The simplified reference tissue model: model assumption violations and their impact on binding potential

Abstract

Reference tissue models have gained significant traction over the last two decades as the methods of choice for the quantification of brain positron emission tomography data because they balance quantitative accuracy with less invasive procedures. The principal advantage is the elimination of the need to perform arterial cannulation of the subject to measure blood and metabolite concentrations for input function generation. In particular, the simplified reference tissue model (SRTM) has been widely adopted as it uses a simplified model configuration with only three parameters that typically produces good fits to the kinetic data and a stable parameter estimation process. However, the model's simplicity and its ability to generate good fits to the data, even when the model assumptions are not met, can lead to misplaced confidence in binding potential (BP_ND) estimates. Computer simulation were used to study the bias introduced in BP_ND estimates as a consequence of violating each of the four core SRTM model assumptions. Violation of each model assumption led to bias in BP_ND (both over and underestimation). Careful assessment of the bias in SRTM BP_ND should be performed for new tracers and applications so that an appropriate decision about its applicability can be made.

Introduction

In quantitative dynamic brain positron emission tomography studies reference tissue models, which avoid the need for arterial blood sampling, have become the methods of choice because they can achieve quantitative accuracy, while maximizing patient comfort. The methods rely on the identification of a brain region devoid of the biologic target of interest, enabling characterization of the behavior of the nondisplaceable signal in this region. These regions may be defined anatomically when a priori information exists, for instance, for G-protein couple receptors this is often the cerebellum, or using cluster analysis based on kinetic information;^{1, 2} for instance, in the case of neuroinflammation studies when anatomic landmarks may not suffice. All the reference tissue methods discussed here are derived from tracer compartmental representations of the target and reference tissues yielding two sets of differential equations involving the plasma concentration. It is the subsequent rearrangement of these equations that allows the elimination of the plasma term to produce an operational equation that describes the target tissue time course as a function of the reference tissue time course and the parameters of interest. Here, it is the binding potential^{3, 4} that is the main parameter of interest as it is proportional to the target availability.

Reference tissue approaches were first developed over 20 years ago and have evolved in the intervening period with a number of compartmental configurations and estimation procedures being introduced. A full list of different reference tissue compartmental (TC) configurations and their mathematical solutions has been given previously.⁵ The early method of choice was the ‘full' reference tissue model,^{6, 7} which estimated four model parameters, including the binding potential of the target region (). Lammertsma and Hume⁸ further refined the technique under the assumption that all compartments in a region could be considered to be in equilibrium leading to the introduction of the simplified reference tissue model (SRTM) that reduced the number of estimated parameters to three and consequently improved the identifiability of the estimated binding potential through a more parsimonious model. Gunn et al⁹ extended its application through the use of basis function techniques that improved the numerical identifiability properties and enabled its used for parametric imaging. More recently, Wu and Carson¹⁰ have developed SRTM2, which uses a two pass approach to the application of the SRTM equations that aims to improve the numerical identifiability of the binding potential further. The method has also been implemented in a multilinear regression framework under the guise of the multilinear reference tissue models MRTM and MRTM2¹¹ and developed to incorporate additional spatial constraints for parametric imaging.¹²

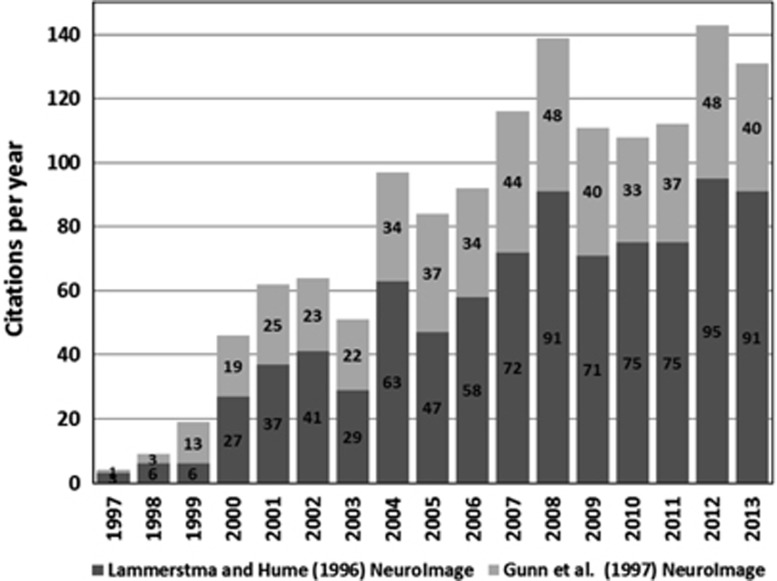
SRTM was initially developed for application to dopamine D2 receptor quantification with [¹¹C]raclopride and since then has become widely used, for a wide variety of brain radiotracers, as can be seen from the growing number of the citations for the two main articles (Lammertsma and Hume⁸ and Gunn et al⁹; Figure 1).

Figure 1.

Summary of simplified reference tissue model (SRTM) citations from the publications of Lammertsma and Hume⁸ and Gunn et al⁹ demonstrating increasing uptake and use of SRTM. Citation source Scopus, Elsevier (www.scopus.com).

However, SRTM's simplicity and its ability to generate good fits to the kinetic data even when the assumption about equilibration of compartments (free, nonspecific and specific) is not met can lead to misplaced confidence in binding potential (BP_ND) estimates. SRTM is based on four key assumptions:

1. The reference region is devoid of specific/displaceable binding.

2. The kinetic behavior of the tracer in both the reference and target tissue can be represented by a one TC model.

3. The blood volume (V_B) contribution to both the reference and target tissues is negligible.

4. Reference and target tissue have the same nondisplaceable volume of distribution (V_ND).

Several publications have considered the consequences of violating some of these assumptions. In the original reference tissue model paper by Cunningham et al,⁷ an extra term was included in the model to simulate the presence of specific binding in the reference region. Later, other groups^{13, 14} showed analytically the bias introduced in BP_ND and target occupancy when this assumption is violated. More recently, Gunn et al¹⁵ have built on this to develop a pseudo reference tissue model (PRTM) that corrects for the bias introduced in BP_ND and occupancy by using an estimate of the specific signal in the reference region. An equivalent approach has also been presented more recently by Turkheimer et al.¹⁶

The model topology has also been studied. Slifstein, Parsey, and colleagues^{17, 18} studied this problem previously after noticing that SRTM estimates of BP_ND for [¹¹C]WAY100635 were significantly different from those derived indirectly using the volumes of distribution (V_T) estimates in the target and reference regions obtained from two tissue compartment (2TC) model analyses with an arterial input function. Computer simulations showed that SRTM underestimated the value of BP_ND when both target and reference tissues were simulated with a 2TC model. In contrast, SRTM overestimated the BP_ND when the target and reference tissue kinetics were represented by a two and one tissue compartment (1TC) model, respectively. The authors also found that the full reference tissue model produced unbiased estimates of binding potential when the target and reference tissues were simulated with a 2TC and 1TC model, respectively, but it failed to converge when both target and reference tissues were simulated with a 2TC model.

There has been little consideration given to the contribution of whole blood activity in the regions of interest. Indeed, as far as blood goes, reference tissue models were by their nature developed to avoid the need for blood measurements.

Similarly, differences in nonspecific binding between the target and reference region, which can arise from different lipophilic properties between regions or as apparent differences because of a lack of tracer selectivity,^{19, 20} are not commonly considered.

The aim of this work was to perform a careful investigation of what happens to SRTM estimates of BP_ND when each of the underlying model assumptions is violated. Further, the article explores how well PRTM performs when the same model assumptions are violated. Investigations are performed on both noiseless and noisy simulated data sets.

Materials and methods

Simulations

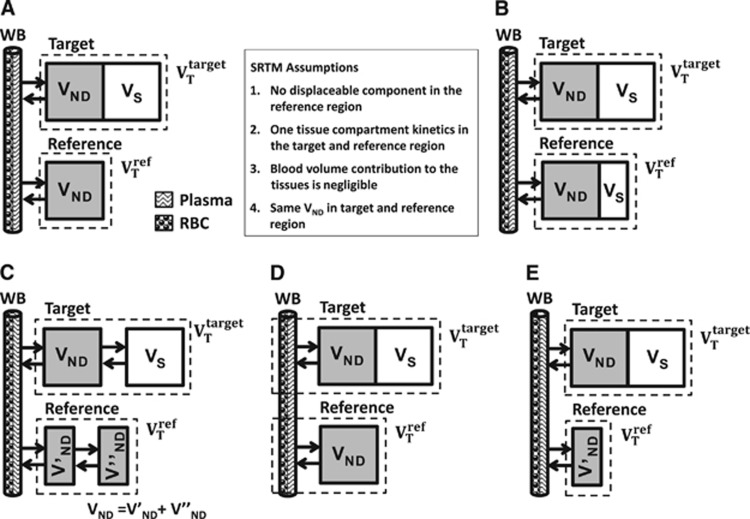
The simplified reference tissue model characterizes the kinetic behavior of a radioligand in both the target and reference region by a 1TC model (Figure 2A). For each tissue, it is possible to derive a differential equation that describes the kinetics of the radioligand as a function of the arterial plasma input function and a set of rate constants. Rearrangement and substitution of the reference tissue equation into the target equation allows elimination of the plasma term and yields the standard operational equation for SRTM,⁸

Figure 2.

Simplified reference tissue model (SRTM) model configuration (A) and violation of model assumptions (B–E): (A) SRTM, (B) displaceable signal in the reference tissue, (C) two tissue compartment model in the target and/or reference tissues, (D) whole blood contribution to target and reference regions, and (E) differences in nonspecific binding between target and reference regions.

where R₁ is the relative target to reference rate of delivery (target to reference K₁ ratio), k₂ is the efflux rate constant, 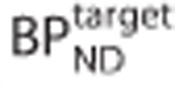is the binding potential in the target region, C_T(t) and C_R(t) are the time activity curves (TACs) in the target and reference regions, respectively.

Computer simulations were used to assess the impact on binding potential estimation when each of the four SRTM model assumptions were violated; specific binding in the reference, incorrect model topology, blood volume contribution, and differences in nonspecific binding (Figure 2). Parameter estimation was performed using nonlinear regression with trust-region-reflective optimization algorithm and residuals weighted by frame duration.

Target and reference TACs were obtained using the exponential convolution forms of the 1TC and/or 2TC model⁵ (Φ_1TC and Φ_2TC, respectively) and a measured arterial input function from a human [¹¹C]PHNO scan. The value of each rate constant was chosen from perturbations around one characteristic parameter set to simulate one or more violations of the SRTM assumptions. Appendix A shows in detail the definition of the rate constants and the generation of the TACs for each case shown in Figure 2.

The V_T associated with each TAC was obtained from the true value of the rate constants used to generate each scenario. For the 1TC, 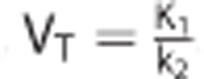. For the 2TC, .

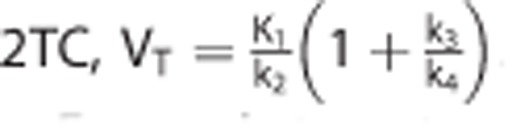For each target-reference pair of simulated TACs, the target BP_ND was defined via what we call the ‘indirect method': .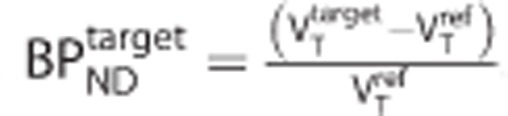

Displaceable Signal in the Reference Region (Assumption 1 Violation)

If the reference tissue is not completely devoid of specific signal, then theory states that the estimated binding potential in the target region will be biased¹⁵ according to,

where 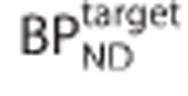is the true binding potential in the target region and is the estimated binding potential and is the binding potential of the pseudo reference region.

Noiseless simulations were performed to assess the effect of a specific signal in the reference region (see Appendix A for details of the implementation). Simulated TACs for the target and reference regions (with no whole blood volume contribution) were generated using a 1TC model. The values of K₁ and V_ND were the same in both regions. A specific binding component in the reference region was simulated for three values of 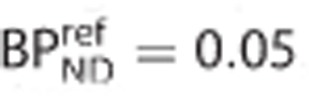. The binding potential in the target region varied from 0.5 to 10. The percentage bias in the estimates of binding potential in the target region were assessed against the true . In addition, the theoretical bias shown in equation 2 was also compared with the simulation data.

Deviation from the Simplified Reference Tissue Model Topology (Assumption 2 Violation)

Noiseless simulations were performed to assess the effect of the model topology on the bias introduced into the SRTM estimates of binding potential (see Appendix A for details of the implementation). Target and reference TACs were generated using a 1TC or 2TC model with no blood volume contribution. All four combinations were explored 1TC-1TC, 1TC-2TC, 2TC-1TC, and 2TC-2TC for target and reference tissues, respectively. The values of K₁ and V_ND were the same for target and reference regions in all simulations. Estimates of binding potential in the target region obtained by solving equation 1 were expressed as a percentage bias in and plotted against the true .

In addition, to enable a more comprehensive evaluation of model topology-induced biases, a large number of simulations (N=30,000) covering the full kinetic space were performed using randomly sampled rate constants for the target and reference regions (constrained to 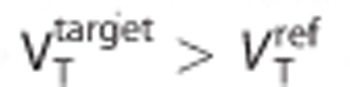and BP_ND<10). After model fitting with SRTM, the absolute binding potential bias (difference between the SRTM estimate and the one derived from the indirect method) was plotted as a function of a model order metric, which measured how close each TAC was to a 1TC model for the target and reference regions.

Model order metric was defined as

where IRF^True2TC is the impulse response of the 2TC model used in the simulation and IRF^Best1TC is the impulse response of the 1TC model fitted to the data simulated by IRF^True2TC. The term 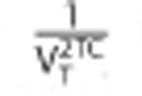is a normalization factor, where 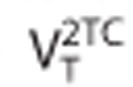is the volume of distribution for the 2TC model. The model order metric provides a measure of how different a TAC is from a 1TC model. A value of zero means the TAC is perfectly described by a 1TC model. Larger values indicate increasing difficulty in representing the TAC by a 1TC model.

Blood Volume-Induced Bias (Assumption 3 Violation)

At equilibrium, the presence of a blood volume component in the target and reference tissues will bias the estimates of V_T by a fraction that will depend on the blood volume fraction V_B and the reciprocal of the plasma-parent to blood ratio P_B. This bias in V_T will be propagated into the estimates of binding potential. By assuming that the fractional blood volume was the same in both the target and reference tissues, Gunn et al⁵ derived an expression to quantify this bias as,

where is the biased estimate of the true binding potential in the target region and V_ND is the nondisplaceable volume of distribution of the radioligand.

Noiseless simulations were performed to assess the bias in binding potential estimates because of a nonnegligible blood volume contribution to both tissues (see Appendix A for simulation details). A whole blood TAC, obtained from the same study as the plasma TAC, was used. TACs in the target and reference regions were simulated with the 1TC model. The value of 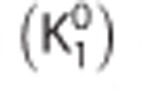and 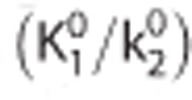were the same in both regions. Estimates of binding potential in the target region obtained by solving equation 1 were expressed as a percentage bias in 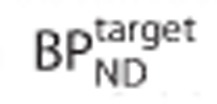and plotted against the true 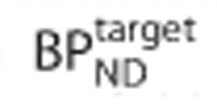for three different values of blood volume contribution in the target and reference regions (V_B=0, 0.1, 0.2). The theoretical bias (equation 4) was calculated using P_B=5 as estimated by the reciprocal of the blood to plasma ratio at 90 minutes (obtained from PHNO data).

Target-Reference Differences in the Nondisplaceable Volume of Distribution (Assumption 4 Violation)

The nondisplaceable volume of distribution V_ND represents the equilibrium partition coefficient between the free plus nondisplaceable bound radiotracer and the plasma concentration and it is assumed to be the same in both target and reference tissues. Theory, derived from equilibrium conditions, states that estimates of BP_ND derived using a reference region that has a different V_ND from that in the target region will be biased according to the following equation,

where 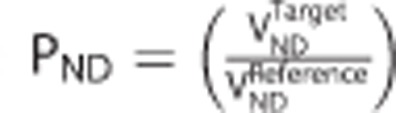is the target to reference V_ND ratio.

Noiseless simulations were performed to assess the bias in binding potential estimates because of differences in nonspecific binding between the target and reference regions (see Appendix A for simulation details). The value of V_ND in the reference region was adjusted to achieve three different values of P_ND (0.8, 1, and 1.2). Estimates of binding potential in the target region obtained by solving equation 1 were expressed as a percentage bias in 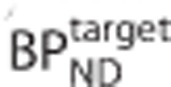and plotted against the true .

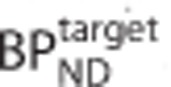Pseudo Reference Tissue Model

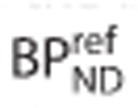The use of a pseudo reference region (assumption 1 violation) introduces a bias in the estimated target binding potential that depends on the binding potential in the reference region . When an estimate of can be obtained, possibly from previous analysis using arterial blood input function and competition data, equation 2 can be rearranged to determine the true binding potential in the target region

This approach is referred to as the PRTM.¹⁵

To explore the validity of this correction when the target and reference tissue uptake is represented by different model topologies, TACs were generated to simulate four different target-reference topology combinations (1TC-1TC, 1TC-2TC, 2TC-1TC, and 2TC-2TC). In all cases, a small specific signal (BP_ND=0.5) was added to the reference region. In all cases, the value of K₁ and V_ND were the same for target and reference regions with no blood volume contribution (V_B=0). PRTM estimates of binding potential were obtained by applying SRTM and then the appropriate correction using equation 6. Both SRTM and PRTM binding potential estimates (expressed as a percentage bias about true binding potential in the target region) were plotted against the true binding potential in the target region .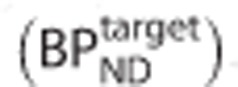

Results

Displaceable Signal in the Reference Region (Assumption 1 Violation)

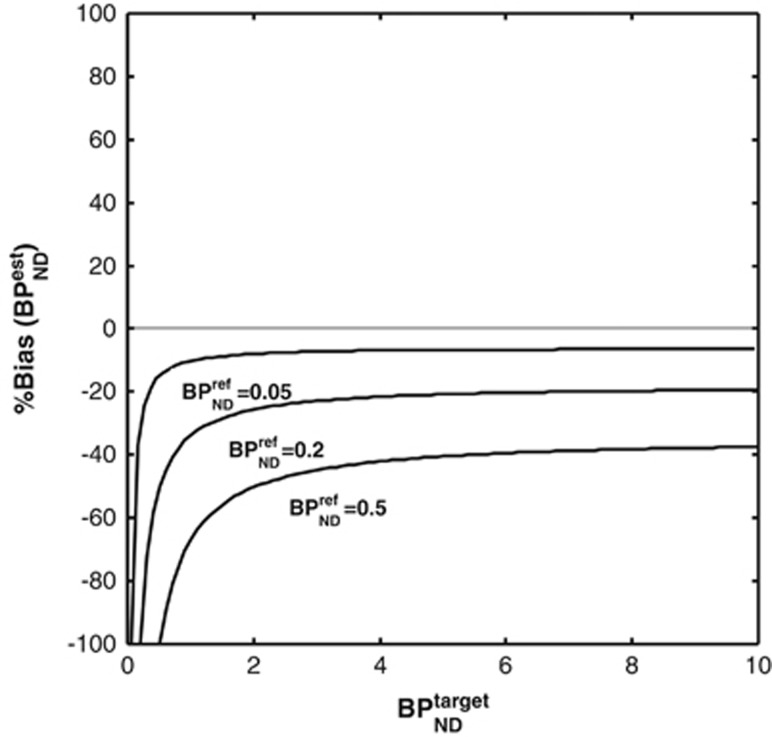
Figure 3 shows the bias in SRTM binding potential estimates (as a percentage of the true value 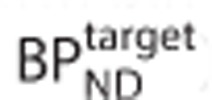) in a noiseless simulation for three different levels of specific binding in the reference region .

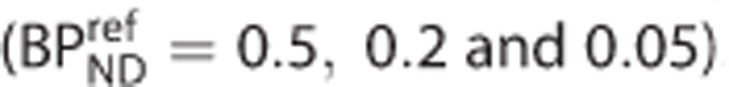Figure 3.

Bias in simplified reference tissue model (SRTM) binding potential estimates when specific binding is present in the reference region. The theoretical bias derived from equation 2 (dashed line) lies exactly underneath the simulation results (solid line).

Deviation from the Simplified Reference Tissue Model Topology (Assumption 2 Violation)

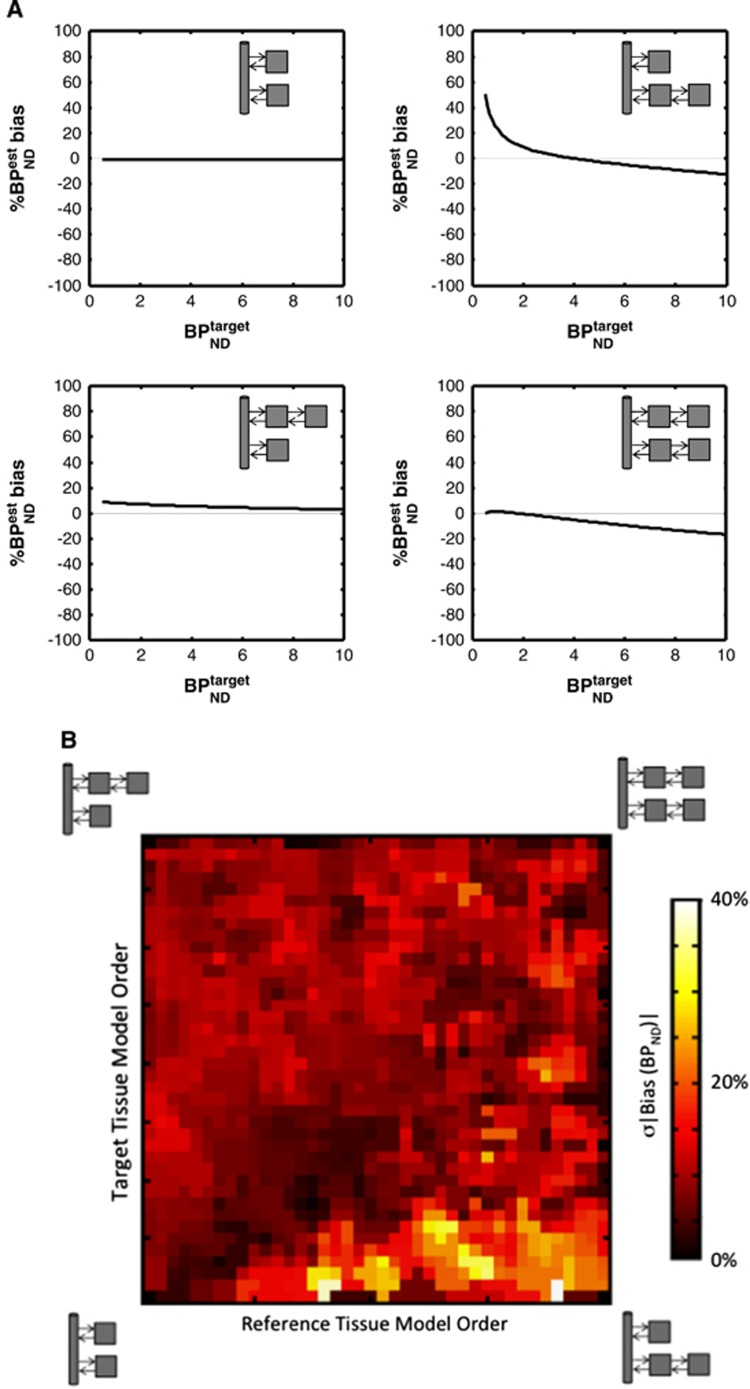
Figure 4A shows the bias in SRTM binding potential estimates in noiseless simulations for different target-reference model topologies. Figure 4B shows a more comprehensive simulation that investigates SRTM binding potential bias in the presence of noise across a wide range of kinetics. When one tissue accurately describes both target and reference regions (bottom left-hand corner), there is no bias as would be expected. When the model order is similar in both regions (the diagonal), the mean bias is generally small. For other topologies, the bias is more evident with the highest values being identified when there is a clear need for 2TCs in the reference tissue and only 1TC in the target region.

Figure 4.

Simplified reference tissue model (SRTM) binding potential bias for different model topologies. (A) Noiseless simulations. The upper left plot represents the nonviolated topology of the SRTM where the true value of binding potential is always correctly estimated (0% bias). In all other cases, the magnitude and direction (overestimation or underestimation) of the biases depends on the value of the true binding potential. (B) Noisy simulations across a wide range of kinetics. The mean absolute SRTM binding potential bias (hot map value) is displayed as a function of the model order metric (MOM) in the target (y-axis) and reference (x-axis) regions. Both x axis and y axis MOM values range from one tissue compartment (1TC) model kinetics up to a clear requirement for a 2TC model representation of the time activity curves.

Blood Volume-Induced Bias (Assumption 3 Violation)

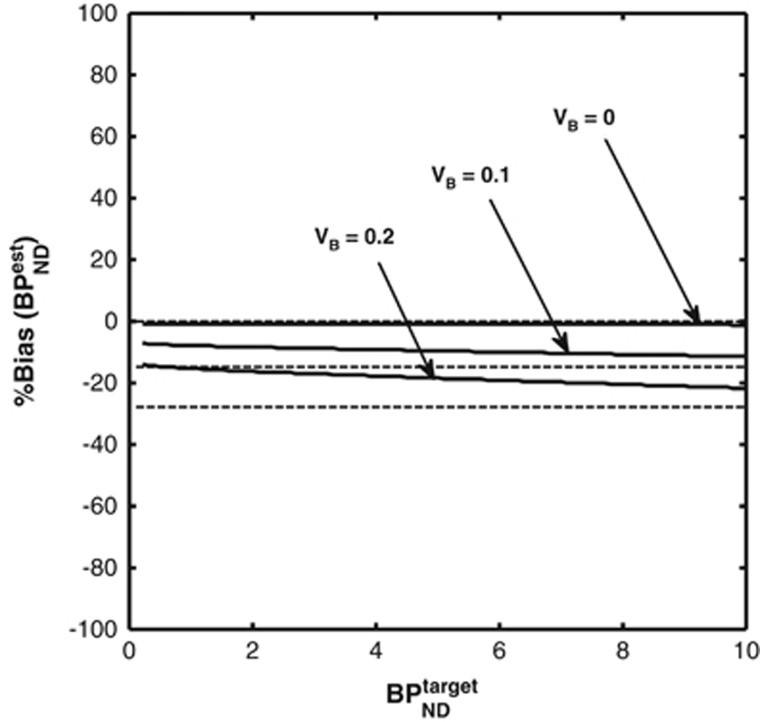
Figure 5 shows the bias in SRTM binding potential estimates in a noiseless simulation for three different blood volume contribution levels (V_B=0, 0.1, 0.2).

Figure 5.

Bias introduced in the simplified reference tissue model (SRTM) estimates of binding potential because of a nonnegligible blood volume contribution. Solid lines represent the simulation results. Dashed lines represent the theoretical bias from equation 4. Only when V_B is zero are non-biased estimates of binding potential obtained.

Target-Reference Differences in the Nondisplaceable Volume of Distribution (Assumption 4 Violation)

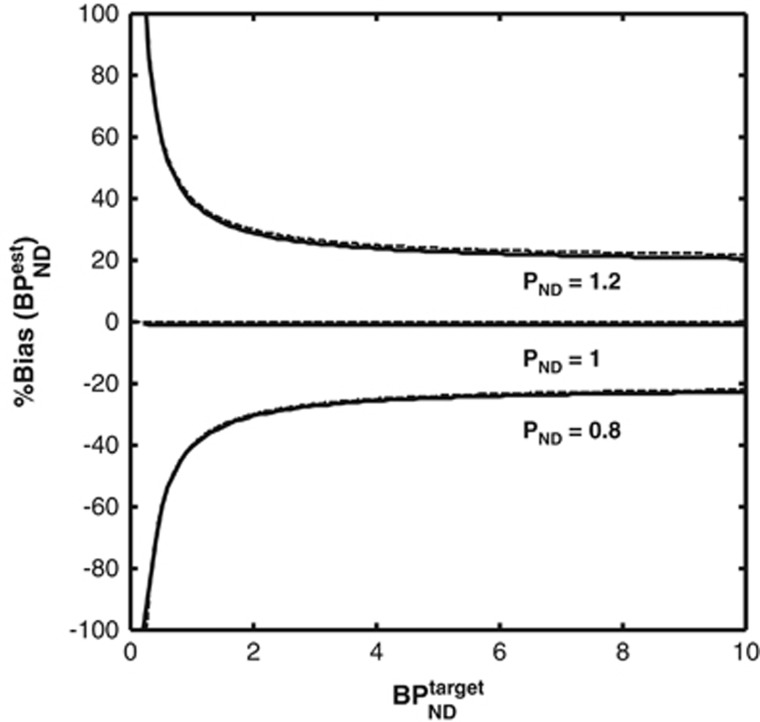
Figure 6 shows the bias in SRTM binding potential estimates from the noiseless simulations considering different target to reference V_ND ratios (P_ND=1.2, 1, 0.8).

Figure 6.

Bias introduced in simplified reference tissue model (SRTM) binding potential estimates because of differences in nondisplaceable binding in the target and references regions. Solid lines represent the simulation results. Dashed lines represent the theoretical bias derived from equation 5. Only when V_ND is the same in the target and reference regions (P_ND=1) are nonbiased estimates of binding potential obtained.

Pseudo Reference Tissue Model

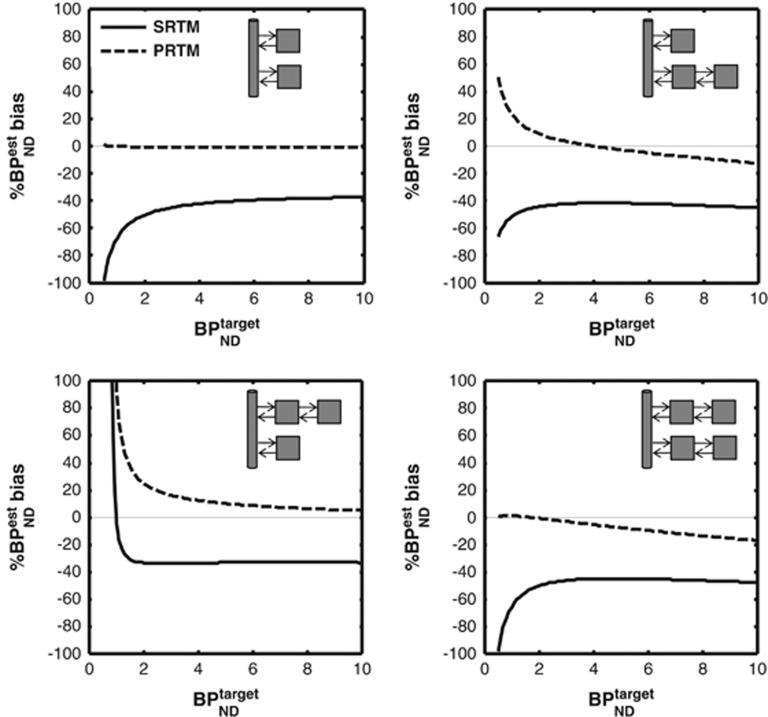
Figure 7 shows the bias in binding potential estimates derived from PRTM in noiseless simulations when the reference tissue has a binding potential of 0.5 for different target-reference topologies. PRTM is able to accurately correct for the presence of specific binding in the reference region when the kinetics are described by 1TC in both target and reference tissue. As the true model topologies increase in model order, PRTM is still able to provide a more accurate estimate of the true .

Figure 7.

Bias in pseudo reference tissue model (PRTM) estimates of binding potential for different model topologies. The solid line in each plots represent the biased simplified reference tissue model (SRTM) estimate of binding potential because of the uncorrected presence of specific binding in the reference region. The dashed line is the bias for PRTM. When one tissue compartment (1TC) is present in both reference and target regions, PRTM is able to provide an unbiased estimate of binding potential, but for more complex model configurations a bias (either positive or negative) is nearly always present.

Discussion

Since its introduction in the late nineties, the SRTM has been rapidly adopted as a parsimonious modeling approach for dynamic brain positron emission tomography imaging that aims to balance quantitative accuracy with patient comfort. By using dynamic data and a tracer compartmental description of the tracer, the approach is able to decouple delivery and binding information and has wide utility for analysis in disease understanding, drug development, and diagnostic settings.

Previous publications along with the work presented in the article have shown that SRTM produces unbiased estimates of binding potential when the model assumptions are met. Herein, we aimed to characterize the bias introduced in binding potential estimates when each of the four key SRTM model assumptions were violated, namely: (1) specific binding in the reference region; (2) more than 1TC required for the tissue kinetics; (3) nonnegligible contribution of whole blood activity to the TACs; and (4) target-reference nonspecific binding differences. We found that violation of each of the four model assumptions led to the introduction of a bias in the SRTM estimates of binding potential.

Violation of assumptions 1 and 4 introduced biases that are mathematically equivalent and can be considered as offsets in the reference tissue partition coefficient that impacts on the binding potential estimates. Nevertheless, in both of these cases the biases were accurately predicted by the mathematical expression given in equations 2 and 5. In fact, these expression could be used in the assessment of individual radiotracers and the potential application of the PRTM where knowledge of is used to enable correct estimation of the binding potential in the target region, for example, see the analysis of [¹¹C]GSK931145 a glycine transporter type 1 radioligand.¹⁵ The mathematics behind these two violations can also be applied to offer insight into what bias would be introduced into BP_ND for tracers that are not selective for a single target.

The bias introduced when the model topology does not conform to 1TC in both the reference and target tissues is more complex and cannot be captured in a simple algebraic expression. Noiseless simulations (Figure 4A) identified the general behavior of these biases as they occur for different model topologies. For the sake of simplicity and because they have been studied elsewhere,^{5, 18} in the noiseless simulations we only studied the bias dependence about the true binding potential in the target region leaving out other factors such as R₁ dependency. However, comprehensive Monte Carlo simulations allowed us to explore the magnitude of the introduced bias across a wide range of tracer kinetics and model configurations (Figure 4B). As the model for both reference and target tissue demands a more obvious need for a second compartment, there is clear evidence of a bias in binding potential. This bias is minimal when the model order of both reference and target tissues are well matched, intermediate when 1TC is required for the reference and 2TCs are required for the target and largest when 2TCs are required for the reference and 1TC is required for the target.

The bias introduced by blood activity contributing to both reference and target tissues can have a significant impact, particularly if the partition coefficient of the tracer is small (cf. the cerebellar region with the 5HT_1A tracer [¹¹C]WAY100635).^{17, 18, 21, 22} Again, it is not possible to come up with an exact algebraic expression for this bias although approximations have been proposed (equation 4), which have been shown here to be a reasonable first-order approximation. Thus, equation 4 allows for an assessment of these biases for individual radiotracers in particular applications.

The impact of SRTM assumption violations in longitudinal or cross-sectional studies will depend primarily on the nature of the assumption(s) being violated. In general, violation of assumption 3 (blood volume) will produce a bias that is more or less constant across a wide range of BP_ND values (Figure 5) and therefore will have little impact unless blood volume constitutes a significant portion of the total tissue signal. For the other cases, if specific binding, model topology or nonspecific binding are altered longitudinally or cross-sectionally then they could introduce confounds into the assessment of differences in BP_ND.

It is important to note that the bias introduced under SRTM model assumption violations is tracer dependent. Therefore, a careful assessment of the bias associated with SRTM for new tracers and applications is critical. To do this properly necessitates the acquisition of dynamic data with associated blood data at baseline conditions and after the administration of a suitable blocking agent (potentially in both a control and disease group). Plasma input function modeling of TACs to identify the most parsimonious compartmental topology will allow for an assessment of assumption 2 (1TC model topology). In addition, these data can be used to assess the impact of blood volume on BP_ND (model assumption 3). Calculation of V_T at baseline and after a blocking dose allows for an assessment of whether there is a displaceable signal in the reference region (assumption 1) and also whether nondisplaceable binding is equal in reference and target tissues (assumption 4).

Although the focus here has been on the core model assumptions specific to SRTM, there are other factors that could lead to the introduction of bias in BP_ND. For example, the presence of brain-penetrant radiolabeled metabolites, partial volume effects affecting primarily small regions of interest surrounded by high uptake regions, inaccurate scatter correction particularly in reference tissues close to the edge of the field of view, and the image reconstruction algorithms themselves (e.g., filtered back projection or iterative methods) can all introduce bias. Although important, these factors have not been considered in this article.

This article has focussed on the bias in BP_ND that may be introduced by SRTM. Other standardized uptake value (SUV)-based reference tissue methods that calculate an SUV ratio (SUVr) between a target and reference region will also be subject to bias. For example, at true equilibrium conditions SUVr can be directly related to the unbiased binding potential estimates obtained via the SRTM 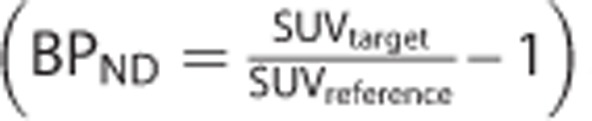. Under these conditions, the SUVr outcome measure will be susceptible to the same bias as SRTM for the model assumption violations 1, 3, and 4 (specific binding in the reference region, blood volume contribution, and unequal V_ND in target and reference tissue) but not 2 (divergence from 1TC behavior). However, measuring these ratios under nonequilibrium conditions will introduce further biases that are dependent on the terminal washout rate of parent plasma and blood flow.²³

where β is the terminal washout rate in plasma. Only at an equilibrium condition (β=0) is the target to reference SUVr equal to 1+BP_ND. Similar biases also apply to the reference graphical method of Logan ²⁴ but in addition there is the factor of noise-induced bias to consider that results from noise on the independent and dependent axes.^{25, 26}

In conclusion, SRTM is a valuable tracer kinetic analysis tool for dynamic positron emission tomography data as it balances quantitative accuracy with patient comfort. However, careful assessment of the level of bias in the binding outcome measure of interest (binding potential) should be performed for new tracers and applications so that an appropriate decision about its applicability can be made.

Appendix A

Details of the model implementation for each of the simulations shown in Figure 2

The authors declare no conflict of interest.