drexplorer: A tool to explore dose–response relationships and drug–drug interactions

Abstract

Motivation: Nonlinear dose–response models are primary tools for estimating the potency [e.g. half-maximum inhibitory concentration (IC) known as IC50] of anti-cancer drugs. We present drexplorer software, which enables biologists to evaluate replicate reproducibility, detect outlier data points, fit different models, select the best model, estimate IC values at different percentiles and assess drug–drug interactions. drexplorer serves as a computation engine within the R environment and a graphical interface for users who do not have programming backgrounds.

Availability and implementation: The drexplorer R package is freely available from GitHub at https://github.com/nickytong/drexplorer. A graphical user interface is shipped with the package.

Contact: jingwang@mdanderson.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Understanding the dose–response relationship of therapeutic compounds is a major focus of clinical oncology. Large-scale drug screening in cancer cell lines has demonstrated that different genomic characteristics (mutations) confer distinct drug sensitivity, supporting patient stratification into treatment regimens on the basis of genomic markers (Barretina et al., 2012; Yang et al., 2013). Cell lines resistant to single-drug treatment may respond to synergistic drug combinations (Lehár, et al., 2009). As cell viability assays become widely used, it is important to provide easily accessible tools to analyze drug profiling data.

We developed drexplorer software in the R environment (R Core Team, 2014) to encompass several aspects of dose–response analysis: assess reproducibility of replicated experiments, detect outlier data points, fit different models, identify the best model, estimate inhibitory concentration (IC) values and evaluate drug–drug interactions.

2 Algorithms

A typical drug screening experiment exposes cells to a range of concentrations (doses) of a drug and quantifies cell viability (response). To account for experimental variations, multiple measurements are obtained for each dose. We denote the jth repeat of the ith dose by $x_{ij}$ and the corresponding response by$y_{ij}$. For anti-cancer drug screening, response $y_{ij}$ is further scaled by the mean response of the controls (i.e. under$x_{ij}=0$) and is called relative viability.

2.1 Outlier detection

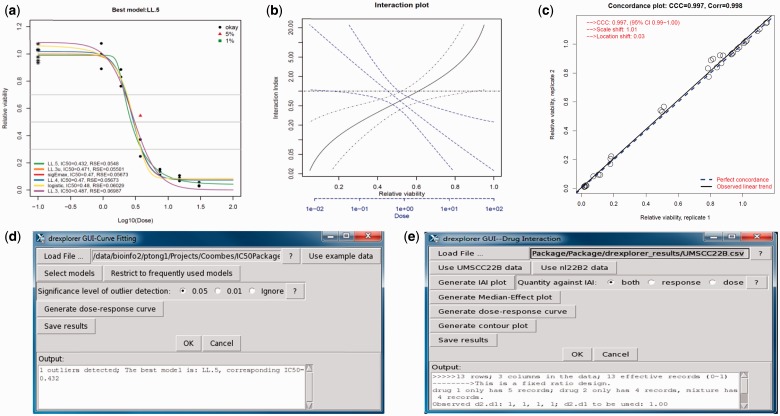
Outlier values in response $y_{ij}$ will affect dose–response curve fitting and IC estimation. We implement the Newman test (Newman, 1939) to detect outliers, defining the test statistic as$q=w/s$, where $w$ is the maximum difference among the response vector $(y_{i1},\dots ,y_{i{m}_i})$ at the ith dose and $s$ is the standard deviation of the response in untreated controls. Once calculated, the test statistic can be compared with the threshold value from the null distribution under the specified type I error ($\alpha =0.01\text{or}0.05$). We apply this test to identify outlier data points at each dose separately. Figure 1a shows outlier detection using the ryegrass data (Ritz and Streibig, 2005).

Fig. 1.

Example of drexplorer output and GUI. (a) Outlier data at type I error = 0.01 and 0.05 are, respectively, indicated by the green square and red triangle. Various dose–response curves are fitted; RSEs are indicated; title indicates model selected by RSE. (b) Interaction index estimated at different doses (blue line) and relative viability (black line); 95% confidence interval also shown. (c) Reproducibility assessment using concordance. Responses from two replicates are highly concordant showing good reproducibility. (d) GUI screenshot for dose–response estimation. (e) GUI screenshot for interaction index estimation.

2.2 Assessing reproducibility

When replicate experiments have been performed, it is necessary to assess the quality of the reproducibility. We use the concordance correlation coefficient (CCC) to capture both the location shift and the scale shift between replicates (Lawrence and Lin, 1989). CCC ranges between −1 and 1, where CCC = 1 means perfect agreement. Figure 1c illustrates the reproducibility assessment for two technical replicates run on different dates.

2.3 The dose–response model

The dose–response model can be expressed as a nonlinear function:

$$y_{ij}=f\left(x_{ij};\text{θ}\right)+{\epsilon }_{ij},i=1,\dots ,n;j=1,\dots ,m_i,$$

where $\text{θ}$ is the vector of unknown parameters, ${\epsilon }_{ij}$ is the measurement error for the response $y_{ij}$, $n$ is the total number of doses administered and $m_i$ is the number of repeats under the ith dose. The error term ${\text{ε}}_{ij}$ is assumed to be identically independently distributed as$N(0,{\text{σ}}^2)$. In the case of the sigmoid Emax model, $f(·)$ has the following form:

$$y_{ij}=E_0+\frac{E_{\text{max}}{x}_{ij}{}^h}{ED{50}^h+x_{ij}{}^h}.$$

Here, $\text{θ}=(E_0,E_{max},ED50,h)$ is the vector of parameters to be estimated.

The dose–response models in drexplorer include all the models in the drc (Ritz and Streibig, 2005) and DoseFinding (Bornkamp, et al., 2010) packages and can be easily used through a uniform interface.

Parameters in the dose–response models can be estimated by minimizing the sum of the squared residuals (SSR):

$$\text{SSR}={\displaystyle \sum }_i{\displaystyle \sum }_j{\{{{\displaystyle y}}_{ij}-f\left(x_{ij};\text{θ}\right)\}}^2.$$

After fitting the model, we estimate the IC at percentile $\tau$ by solving $x$ in equation $\text{τ}=f\left(x;\widehat{\text{θ}}\right),$ where $\widehat{\text{θ}}$ is the vector of the fitted parameters.

Different models can be fit, so we identify the best model as that with minimum residual standard error, calculated as SSR divided by degrees of freedom. Approaches for parametric dose–response models may use the Akaike information criterion or Bayesian information criterion.

2.4 The Interaction Index for Drug Combinations

The interaction index (IAI) is useful to quantify the degree of interaction in drug combinations. For a 2-drug combination, IAI can be defined as

$$\text{IAI}=\frac{d_1}{D_{y,1}}+\frac{d_2}{D_{y,2}}\{\begin{array}{c}<1, \text{synergistic}\\ =1, \text{additive}\\ >1, \text{antagonistic}\end{array}.$$

Here, D_y,1 and D_y,2 and are the doses needed to induce response y for drugs 1 and 2 when administered alone; $d_1$ and $d_2$ are the doses in the mixture that produce the same response y. We adopt the source code used by Lee, et al. (2007) and Lee and Kong (2009) to estimate the IAI and 95% confidence interval (see Fig. 1b using UMSCC22B data; Lee and Kong, 2009). Graphical user interfaces (GUIs) help users without advanced programming skills to analyze dose–response data (Fig. 1d and e).

3 Conclusion

Drexplorer is a versatile R package encompassing several aspects of dose–response and drug–drug interaction analysis. The GUI enables biologists without programming skills to analyze their data.