Evaluating Geographically Weighted Regression Models for Environmental Chemical Risk Analysis

Abstract

In the evaluation of cancer risk related to environmental chemical exposures, the effect of many correlated chemicals on disease is often of interest. The relationship between correlated environmental chemicals and health effects is not always constant across a study area, as exposure levels may change spatially due to various environmental factors. Geographically weighted regression (GWR) has been proposed to model spatially varying effects. However, concerns about collinearity effects, including regression coefficient sign reversal (ie, reversal paradox), may limit the applicability of GWR for environmental chemical risk analysis. A penalized version of GWR, the geographically weighted lasso, has been proposed to remediate the collinearity effects in GWR models. Our focus in this study was on assessing through a simulation study the ability of GWR and GWL to correctly identify spatially varying chemical effects for a mixture of correlated chemicals within a study area. Our results showed that GWR suffered from the reversal paradox, while GWL overpenalized the effects for the chemical most strongly related to the outcome.

Introduction

Humans are exposed to mixtures of chemicals that may be influential for cancer risk. For example, risk of non-Hodgkin lymphoma (NHL) is suspected to be associated with several chemicals through environmental or occupational routes of exposure, and geographic variation in NHL rates suggests the importance of environmental risk factors.¹ Positive associations have been found with persistent organochlorine chemicals, including polychlorinated biphenyls (PCBs),² particularly PCB congener 180,^3–5 and dichlorodiphenyldichloroethylene.^2,3

Environmental exposure patterns are typically complex with inherent correlations among co-occurring chemicals or their metabolites.⁶ For example, many PCB congeners exhibit a high degree of correlation. Important questions in the analysis of mixtures include whether and how the health effect of one chemical should be adjusted for other chemicals present, even when those chemicals are highly correlated. Furthermore, the relationship between environmental chemicals and health effects (eg, cancer risk) is not always constant across a study area.⁶ Exposure levels may be different spatially due to environmental factors. For example, pesticide levels measured in house dust may be higher in agricultural communities (eg, in Iowa) or those in temperate climates where more pesticides are applied throughout the year (eg, Los Angeles) compared to the levels in urban locations (eg, Detroit). Acknowledging the principle that “the dose makes the poison,” the risk of adverse health effects such as NHL is greater in regions where exposure is higher. Thus, environmental health models that account for these spatially changing exposure/risk regions can be informative.

Models with spatially varying coefficients include geographically weighted regression (GWR⁷), which is similar to local linear regression (eg, references 8–10) in that both methods use a kernel function to calculate weights that are applied to observations in a series of local weighted regression models. One issue with GWR is that GWR models have been found to be affected by local collinearity.^11–15 Local collinearity in weighted explanatory variables can lead to GWR coefficient estimates that are correlated locally and across space, have inflated variances, and are at times counterintuitive and contradictory in sign to the global regression estimates, ie, evidence of the reversal paradox.^12,16

To illustrate, Wheeler and Tiefelsdorf¹¹ highlighted the issue of collinearity in GWR in a simple model to explain white male bladder cancer mortality rates (1970–1994) in the 508 State Economic Areas of the US. Their model consisted of two explanatory variables: population density, a proxy for environmental and behavioral differences in urban/rural life, and lung cancer mortality rates, a proxy for the risk factor smoking, a known risk factor for bladder cancer. These two variables had a global correlation estimate of −0.59; however, local correlation estimates were generally more extreme (ie, more strongly negative; median = −0.63; Q3 = −0.71 as approximated from their Fig. 4), with strongest inverse association in parts of Northeastern and Midwestern US (their Fig. 3). The resulting maps of GWR coefficients for population density and the smoking proxy showed a clear inverse map pattern. When the local smoking proxy parameter was high (primarily in the West and Northeast), the local population density parameter was negative. When the local smoking proxy parameter was negligible, the population density parameter was large and positive (primarily in the Midwest and Southeast). As noted by Wheeler and Tiefelsdorf,¹¹ the important question is whether this complementary relationship in the parameters is real, meaningful, and interpretable, or whether it is an artifact of the statistical method. The natural research question is whether such inverse patterning in regression coefficients is an example of the reversal paradox¹⁶ due to strong local correlations between the two variables.

Figure 4.

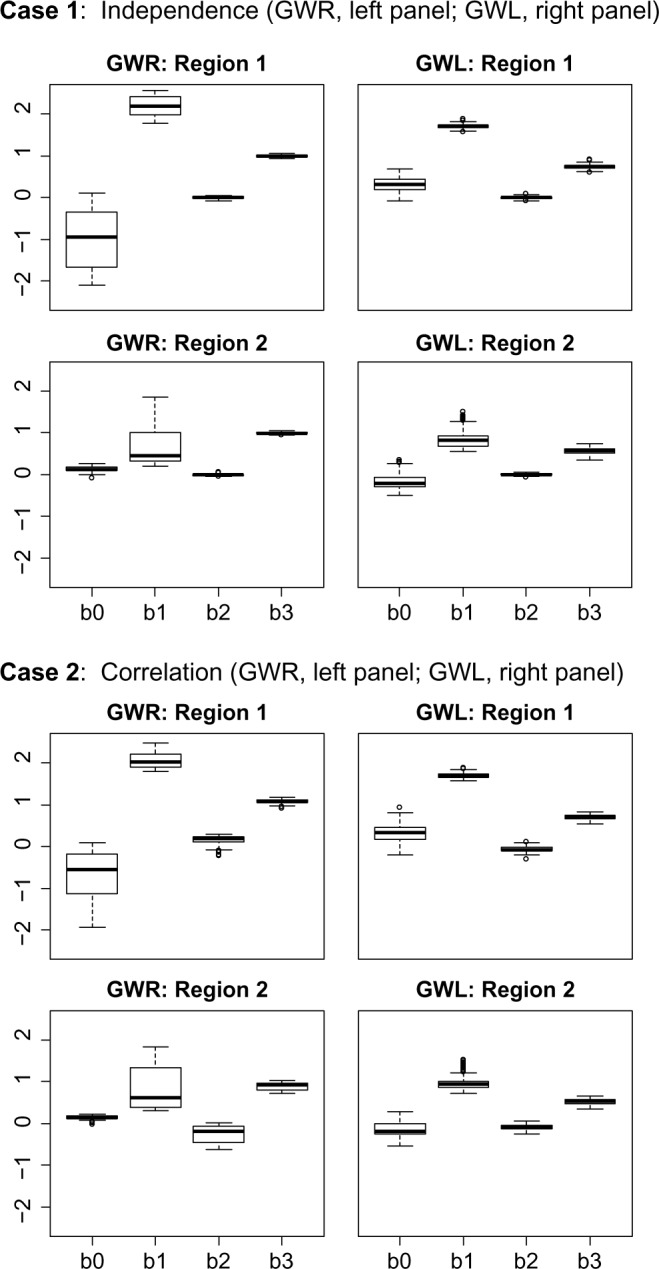
Box plots of average GWR and GWL regression coefficients across 100 simulated data sets for the two study regions for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

Figure 3.

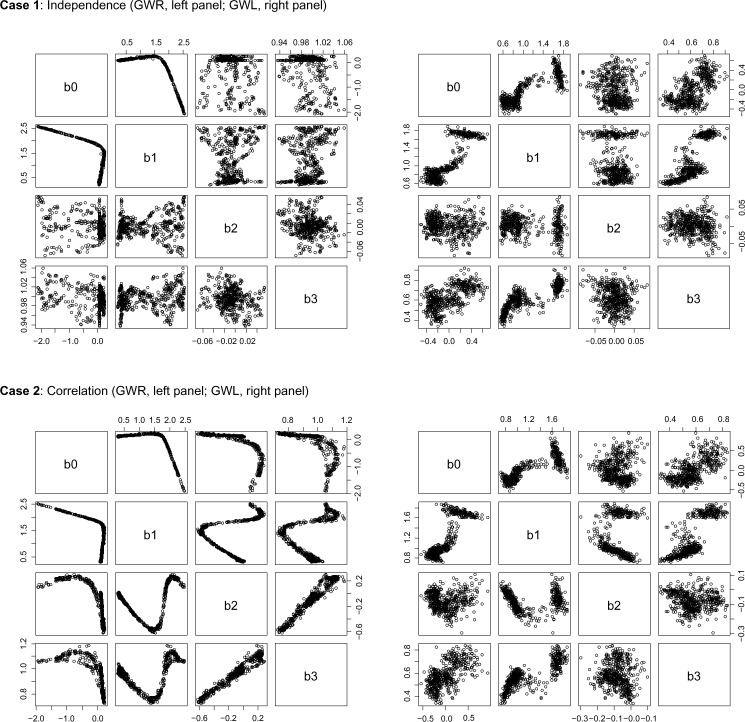
Pairwise plots of average regression coefficients across the 100 simulated data sets for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2) for GWR and GWL.

According to the reversal paradox, the association between two variables can be reversed, diminished, or enhanced when another variable is statistically controlled for.¹⁶ For example, consider two explanatory variables, x₁ and x₂, where the bivariate correlation between x₁ and y is 0.2, and between x₂ and y is 0.1. Figure 1 presents the standardized beta coefficients in the multiple regression model μ = β₀ + β₁x₁ + β₂x₂. As the correlation between the variables increases, the regression coefficient associated with x₁ increases and the coefficient associated with x₂ becomes large and negative – which could lead to a misleading interpretation of the association between x₂ and y. Use of statistical models with correlated data may produce consistent, replicable, yet erroneous results.¹⁶

Figure 1.

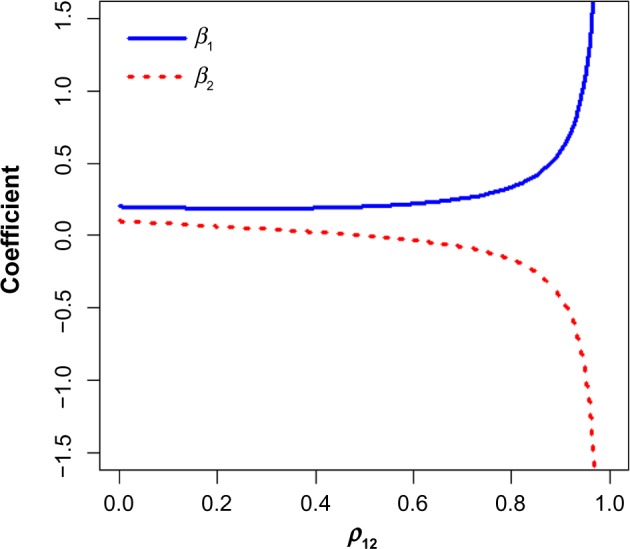
Standardized partial regression coefficients in a multiple regression model with two variables.

Note: ${\beta }_1=\frac{{\rho }_{y1}-{\rho }_{12}{\rho }_{y2}}{1-{\rho }_{12}^2}$ and ${\beta }_2=\frac{{\rho }_{y2}-{\rho }_{12}{\rho }_{y1}}{1-{\rho }_{12}^2}$, where the bivariate correlation between the predictor variables and y are set as ρ_y1 = 0.2 and ρ_y2 = 0.1, respectively.

To address the issue of collinearity with GWR and to limit its effects, the geographically weighted lasso (GWL) adds a constraint on the magnitude of the estimated regression coefficients.¹⁴ The GWL also performs local model selection by potentially shrinking some of the estimated regression coefficients to zero in some locations of the study area, thereby diminishing the adverse effects of the correlation pattern. However, when accurate variable selection is the focus of the analysis, such a strategy makes it difficult to determine whether a variable was excluded from the model due to a lack of association with the outcome or due to its correlation with variables in the model.

Our objective in this study is to evaluate the impact of collinearity of the geographically weighted regression models GWR and GWL in a chemical exposure and risk assessment context. We use a simulated data set for which the truth is known and further assess the ability of GWL to control collinearity effects, such as the reversal paradox, when the effects of correlated environmental chemicals are of interest. We begin by describing the process used to simulate data that we propose are environmentally relevant – ie, regions with low exposure and regions with higher exposures and where different chemicals may have related exposure patterns but not necessarily the same association with a health effect of interest. We conduct GWR and GWL analyses in a scenario with independent chemicals and a scenario with correlated chemicals.

Methods

Simulating spatially varying exposure- and dose- dependent association with an outcome

Consider the scenario in which there are three predictor variables (eg, environmental chemicals) that vary over space in a study area (Fig. 2). We assumed that the first predictor variable, x₁, was present at high enough levels to be associated with an increase in the mean response in the upper region of the study area, while being present only at background levels where there is no increase in mean response in the lower region of the study area. Furthermore, we assumed that both x₂ and x₃ were present at uniform levels across the study area and that x₂ was not related to the response variable, while the relationship between x₃ and the response was moderate. Additionally, we considered two cases for the relationships among the predictor variables: Case 1, where the predictor variables were independent (ie, multivariate normal with zero correlation), and Case 2, where the predictor variables were correlated (ie, ρ₁₂ = 0.7, ρ₁₃ = 0.3, and ρ₂₃ = 0). We used a unit grid as the study area and divided the grid into three equal-sized rows. A total of 500 locations were randomly generated inside the study area, and locations falling in the upper one-third of the study area were defined as belonging to Region 1 (n₁ = 160), while locations falling in the lower two-thirds of the study area were defined as belonging to Region 2 (n₂ = 340)

Figure 2.

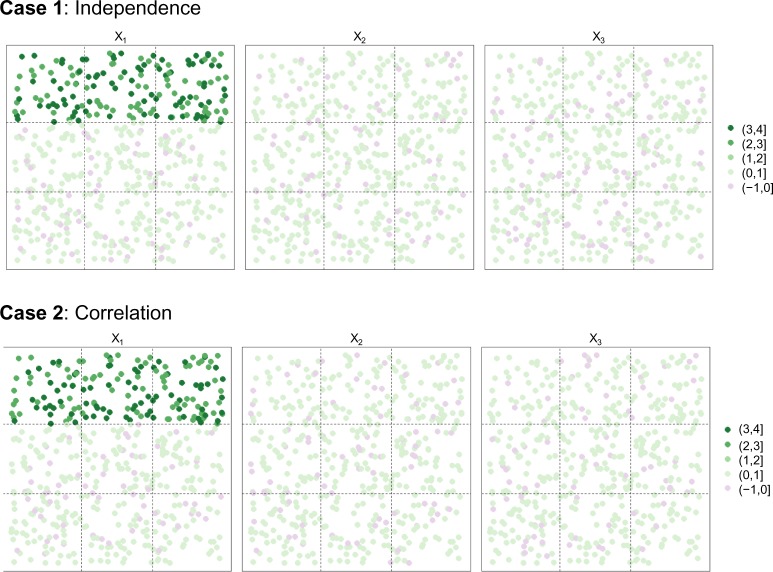
Plots of average simulated concentration values across 100 simulated data sets over a square study area for two scenarios: independent chemicals (Case 1) and correlated chemicals (Case 2).

For each case, multivariate normal data were simulated separately for Region 1 and Region 2. We assumed that the levels of x₁ were the highest in Region 1 (mean of 3.0) and negligible in Region 2 (mean of 0.1). We further assumed that the mean of both x₂ and x₃ was constant (mean of 0.1) across the entire study area. In the case of independence, an identity matrix was used for the covariance, while for the correlated case, the aforementioned correlation pattern was imposed. To simulate the corresponding mean related to the three predictor variables, we used the following nonlinear threshold model:

$$\mu ={\beta }_0+{\beta }_1(x_1>\delta )x_1+{\beta }_2{x}_2+{\beta }_3{x}_3$$ (1)

with parameters defined as β₀ = β₂ = 0, β₁ = 2, β₃ = 1, and δ = 2. The response variable, y, was generated by adding a standard normal error term to the mean. Using this model, we imposed that x₁ was active in Region 1 and inactive in Region 2. More specifically, we allowed x₁ to be present at high enough levels to be associated with an increase in mean response in Region 1, while being present only at background levels (ie, less than the threshold) and not associated with the mean response in Region 2. This specification effectively removed β₁ from the model in Region 2, with β₁ = 0 for almost all of the locations in Region 2 for both the correlated and uncorrelated cases. The parameter β₁ was equal to 2.0 in the majority of locations in Region 1. Hence, there was a simple spatially varying relationship for x₁ and the outcome variable. Finally, we imposed that x₂ was not related to the response variable, while the relationship between x₃ and the response was moderate and uniform across the study area. A total of 100 data sets of size N = 500 were generated for each case, and the results are later presented aggregated over the 100 simulated data sets.

GWR model

In GWR, the spatial coordinates of data are used in the calculation of distances that are input into a kernel function to determine weights for spatial dependence among observations. Local regression models are related through shared data, but the dependence between regression coefficients at different locations is not specified. For example, consider n observations measured at different locations. The GWR model at location i is represented as follows:

$$y_i={\mathbf{X}}_i{\mathbf{\beta }}_i+{\epsilon }_i$$ (2)

where y_i is the dependent variable at location i, X_i is the row vector of explanatory variables at location i, β_i is the column vector of regression coefficients at location i, and ε_i is the random error at location i. The vector of estimated regression coefficients at location i is

$${\widehat{\beta }}_i={\left[{\mathbf{X}}^T{\mathbf{W}}_i\mathbf{X}\right]}^{-1}{\mathbf{X}}^T{\mathbf{W}}_i\mathbf{y}$$ (3)

where X is the design matrix of explanatory variables; W_i is the diagonal weights matrix that is calculated for each location i and applies weights to observations j = 1, …, n; and y is the vector of dependent variable values. Examples of kernel functions for defining the weight matrix include the Gaussian function, the bi-square nearest-neighbor function, and the exponential function, used herein. The weight from the exponential kernel function between any location j and the model location i is calculated as

$$w_j(i)=\exp \left(\frac{-d_{ij}}{\varphi }\right)$$ (4)

where d_ij is the distance between locations i and j, and ϕ is the kernel bandwidth parameter.

GWL model

The lasso is defined¹⁷ as.

$${\widehat{\beta }}^L=\underset{\beta }{\arg \min }{\displaystyle \sum _{i=1}^n{\left(y_i-{\beta }_0-{\displaystyle \sum _{k=1}^p{x}_{ik}}{\beta }_k\right)}^2}+\lambda {\displaystyle {\sum }_k\left|{\beta }_k\right|}$$ (5)

where λ controls the amount of shrinkage of the regression coefficients, the value of which is chosen through algorithms such as least-angle regression (LARS)¹⁸ to find the lowest root-mean-square prediction error (RMSPE). Wheeler¹⁴ extended lasso to a geographically weighted version by defining a weighted X matrix as

$${\mathbf{X}}_W={\mathbf{W}}_i^{1/2}\mathbf{X}$$ (6)

and estimating a lasso model with the LARS algorithm corresponding to each of the ith locations, i = 1, …, n.

Evaluation of models

The focus of the study was to determine whether the methods were able to correctly detect a strong relationship between x₁ and the mean response (β₁ = 2) in the upper third of the study grid and a moderate but uniform relationship between x₃ and the mean response (β₃ = 1) over the entire study area. Additionally, we were also interested in whether or not the methods can correctly discern that there is 1) no relationship between x₁ and the mean response in the lower two-thirds of the study grid and 2) no relationship between x₂ and the mean response over the entire study area. To evaluate the performance of GWR and GWL in identifying the spatially varying patterns in the coefficients, we started by mapping the average of the coefficient estimates at each location over the study area for both methods.

For each model, we calculated the root-mean-square error (RMSE) from estimation, the RMSPE, and the R² value. The RMSE is defined as

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left[y_i-{\widehat{y}}_i\right]}^2}}$$ (7)

while RMSPE is defined as

$$RMSPE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left[y_i-{\widehat{y}}_{(i)}\right]}^2}}$$ (8)

where ${\widehat{y}}_{(i)}$ is the predicted value of observation i with location i left out of the estimation data set. We then described these summary statistics using the median and interquartile range (IQR) over the 100 simulations.

To evaluate the performance of GWL in terms of variable selection, the percentages of coefficient estimates that were positive, negative, or zero were calculated by region for each simulated data set. We summarized the results across the simulated examples using medians and IQRs. Because GWR does not perform variable selection, we calculated the percentage of coefficient estimates that were positive and negative within each region. Additionally, in an effort to further evaluate the performance of GWR, we approximated the variance of the estimated GWR regression coefficients and created confidence intervals for the estimates at each location based on one and two standard errors (SEs) (ie, ${\widehat{\beta }}_{ik}\pm \mathrm{SE}\left({\widehat{\beta }}_{ik}\right)$ and ${\widehat{\beta }}_{ik}+2\mathrm{SE}\left({\widehat{\beta }}_{ik}\right)$, for the i = 1, …, n locations, and k = 0, …, p parameters). The estimates were then classified as positive if the confidence interval was above zero, negative if the confidence interval was below zero, and zero (negligible) if the confidence interval contained zero. The covariance of the estimated regression coefficients was approximated¹⁹ as

$$Var\left[{\widehat{\beta }}_i\right]=\left[{\left({\mathbf{X}}^T{\mathbf{W}}_i\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\mathbf{W}}_i\right]{\left[{\left({\mathbf{X}}^T{\mathbf{W}}_i\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\mathbf{W}}_i\right]}^T{\widehat{\sigma }}^2$$ (9)

where the estimated error variance, ${\widehat{\sigma }}^2$, is given as

$${\widehat{\sigma }}^2={\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2/\left(n-\left(2\mathrm{trace}\left(\mathbf{H}\right)-\mathrm{trace}\left({\mathbf{H}}^T\mathbf{H}\right)\right)\right)}$$ (10)

with the ith row of the hat matrix defined as

$${\mathbf{H}}_i={\mathbf{X}}_i{\left({\mathbf{X}}^T{\mathbf{W}}_i\mathbf{X}\right)}^{-1}{\mathbf{X}}^T{\mathbf{W}}_i$$ (11)

Results

The average observed concentration levels across the 100 simulated examples are plotted over the study area for each case in Figure 2, wherein we see that the average levels of x₂ and x₃ are uniform over the study area, while the mean level for x₁ is higher in Region 1 (the upper one-third of the grid space) as desired. The observed means for both the predictor and response variables are consistent with the study design and are summarized by case and region in Table 1. The observed correlation patterns were also consistent with the study design (results not shown).

Table 1.

Average predictor and response values across the 100 simulated data sets for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

	X1	X2	X3	Y
Case 1
Region 1	3.00	0.11	0.09	5.63
Region 2	0.10	0.11	0.10	0.23
Case 2
Region 1	3.00	0.11	0.11	5.62
Region 2	0.10	0.10	0.11	0.25

The summary statistics across the 100 data sets are listed in Table 2. GWL outperformed GWR in terms of RMSPE in the uncorrelated case, while in the correlated case, GWL outperformed GWR in terms of both RMSPE and RMSE, with a greater improvement for prediction of the outcome (RMSPE) than for estimation of the outcome (RMSE).

Table 2.

Median (interquartile range) of summary statistics for GWR and GWL models across the 100 simulated data sets for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

	RMSE		RMSPE		R2
Case 1
GWR	1.4	(1.4, 1.5)	1.0	(1.0, 1.2)	0.9	(0.9, 0.9)
GWL	1.2	(1.1, 1.2)	1.1	(0.7, 1.2)	0.9	(0.9, 1.0)
Case 2
GWR	1.4	(1.4, 1.5)	1.2	(1.0, 1.2)	0.9	(0.9, 0.9)
GWL	1.2	(1.1, 1.2)	1.1	(0.7, 1.2)	0.9	(0.9, 1.0)

Pairwise plots of the average regression coefficients are shown in Figure 3. Correlation in the parameter estimates is evident for both GWR and GWL in the cases of both independent and correlated chemicals. In the uncorrelated case, the relationship is most pronounced between the intercept and β₁ parameters (denoted by b0 and b1, respectively). In the correlated case, there is a noticeable pattern among all of the parameter estimates, with a strong linear relationship evident between the estimates for β₂ and β₃ (denoted by b2 and b3, respectively). While GWL breaks up some of the strong correlation among the parameter estimates that is evident in GWR, strong relationships are still present between many of the regression coefficients.

As demonstrated in the box plots of the averaged regression coefficients from the models for the 100 simulated data sets (Fig. 4), GWR appears to accurately capture the importance of x₁ in Region 1, with distributions centered around 2.0 for the β₁ estimates in both the independent and the correlated cases. However, we also see that GWR overstates the importance of x₁ in Region 2, with distributions centered above zero for the β₁ estimates regardless of the relationship among the predictor variables. Furthermore, GWL performs shrinkage as expected, demonstrated by the frequent reduction in the magnitude of the parameter estimates when comparing GWR to GWL. However, in both the independent and the correlated cases, GWL often understates the importance of x₁ in Region 1 and overstates its importance Region 2, with distributions for the β₁ estimates centered below 2.0 in Region 1 and around 1.0 in Region 2.

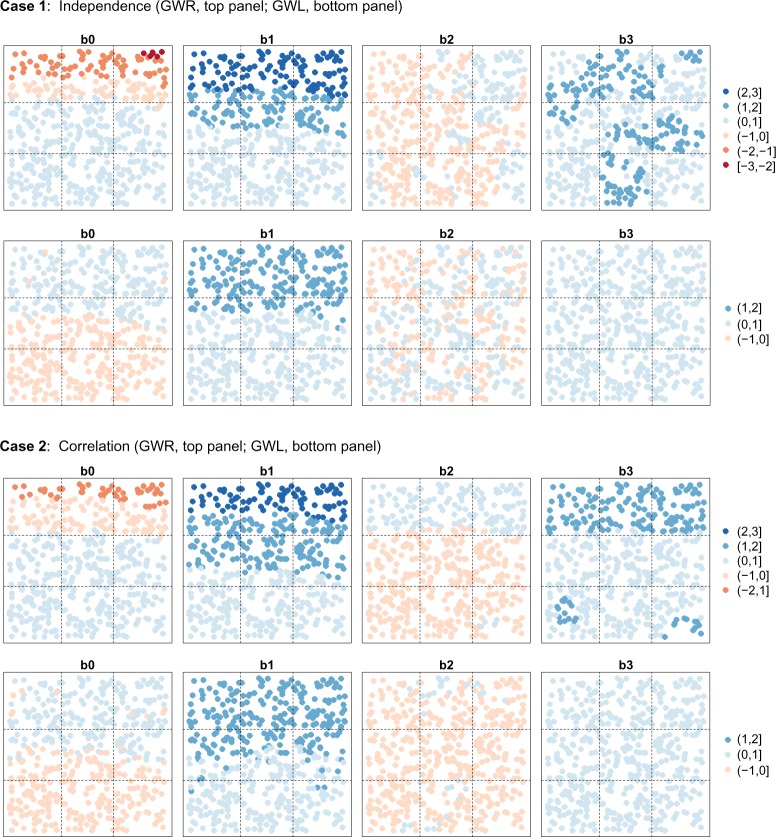
The GWR and GWL regression coefficient estimates from the 100 simulated data sets were averaged at each location and are plotted in Figure 5. The coefficient maps reveal a high degree of correlation between the GWR estimates of β₀ and β₁ in both the independent and the correlated cases. This strong negative relationship is also evident in the pairwise scatter plots of the regression coefficients (Fig. 3). Similarly, correlation in the intercept and β₁ is also apparent in the GWL models, although the correlation between the estimates is not as strong and is largely positive. When examining the coefficient maps for β₁ in both the independent and the correlated cases, GWR and GWL correctly identified Region 1 as the area of highest activity for x₁ but tended to oversmooth the effect into the upper part of Region 2 (ie, the second row of the grid space). GWL also tended to overshrink the parameter estimates for β₁ in Region 1, thereby underestimating the effect of x₁ in the region of activity.

Figure 5.

Average GWR and GWL regression coefficient estimates over 100 simulated data sets for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

When considering the estimated β₂ coefficients, GWR appears to identify several clusters of positive and negative associations in the independent case, while in the case of correlation, it finds a positive association in Region 1 and a negative association in Region 2, probably a reflection of the high degree of correlation between the predictors x₁ and x₂. Although the estimates are small in magnitude, it is clear that GWR is identifying artificial patterns in the β₂ regression coefficients. In contrast, the maps of the GWL estimates for β₂ demonstrate little-to-no systematic patterning in both the correlated and uncorrelated cases, suggesting that GWL is able to break up some of the artificial patterning seen in the GWR estimates of β₂.

Finally, with respect to β₃, GWR appears to incorrectly identify several clusters of a stronger positive relationship between x₃ and the response variable in the uncorrelated case. Furthermore, in the correlated case, GWR incorrectly identifies a strong spatial pattern in the β₃ estimates, with Region 1 appearing to be an area of high activity. The similarity in the GWR coefficient maps of β₂ and β₃ (Fig. 5) reflects the strong linear positive relationship demonstrated in the pairwise plots of the estimated GWR regression coefficients in the correlated case (Fig. 3). The artificial spatial pattern in the GWR estimates of β₃ parallels the true spatial variation in β₁ and is probably induced by the correlation between x₁ and x₃ In contrast, GWL is able to reduce the correlation between the β₂ and β₃ estimates and appears to correctly identify the uniform moderate relationship between x₃ and the response, regardless of the relationship among the predictor variables.

The percentages of positive and negative GWR coefficient estimates are summarized by region for each correlation case in the left side of Table 3. We see that across the simulated data sets, the GWR estimates of β₁ were positive nearly 100% of the time in Regions 1 and 2 for both the independent and the correlated cases. This is further evidence that GWR overstates the importance of β₁ in Region 2. When considering β₂, 53% of the GWR estimates in Regions 1 and 2 were negative in the case of independence for at least half of the simulated data sets, while 28% and 77% of the GWR estimates in Regions 1 and 2, respectively, were negative in the case of correlation. Given that x₂ has no relationship with the outcome in the simulated data, we suspect the presence of the reversal paradox, which could lead to incorrect inference about the impact of this predictor.

Table 3.

Median (interquartile range) percentage of GWR and GWL coefficient estimates that were positive, negative, and zero across the 100 simulated data sets for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

	GWR								GWL
	${\widehat{\beta }}_0$		${\widehat{\beta }}_1$		${\widehat{\beta }}_2$		${\widehat{\beta }}_3$		${\widehat{\beta }}_0$		${\widehat{\beta }}_1$		${\widehat{\beta }}_2$		${\widehat{\beta }}_3$
Case 1
Region 1
Positive	12	(6, 21)	100	(100, 100)	47	(39, 64)	100	(100, 100)	62	(16, 68)	100	(100, 100)	27	(0, 36)	83	(72, 86)
Negative	88	(79, 94)	0	(0, 0)	53	(36, 61)	0	(0, 0)	0	(0, 35)	0	(0, 0)	27	(4, 38)	0	(0, 1)
Zero	–	–	–	–	–	–	–	–	38	(33, 49)	0	(0, 0)	55	(44, 63)	17	(14, 26)
Region 2
Positive	76	(66, 86)	96	(92, 99)	47	(40, 61)	100	(100, 100)	7	(5, 27)	100	(47, 100)	15	(0, 23)	65	(61, 81)
Negative	24	(14, 34)	4	(1, 8)	53	(39, 60)	0	(0, 0)	19	(18, 21)	0	(0, 12)	16	(9, 21)	0	(0, 0)
Zero	–	–	–	–	–	–	–	–	74	(51, 76)	0	(0, 37)	81	(52, 85)	35	(18, 39)
Case 2
Region 1
Positive	15	(8, 25)	100	(100, 100)	73	(64, 83)	100	(100, 100)	57	(17, 66)	100	(100, 100)	0	(0, 36)	85	(75, 88)
Negative	85	(75, 93)	0	(0, 0)	28	(18, 36)	0	(0, 0)	1	(0, 30)	0	(0, 0)	42	(26, 53)	0	(0, 1)
Zero	–	–	–	–	–	–	–	–	42	(34, 51)	0	(0, 0)	44	(37, 55)	15	(13, 23)
Region 2
Positive	78	(69, 89)	97	(92, 100)	23	(13, 31)	100	(100, 100)	8	(5, 26)	100	(46, 100)	0	(0, 20)	65	(63, 82)
Negative	22	(11, 31)	3	(0, 8)	77	(69, 87)	0	(0, 0)	19	(17, 22)	0	(0, 12)	28	(26, 31)	0	(0, 1)
Zero	–	–	–	–	–	–	–	–	74	(50, 76)	0	(0, 40)	68	(54, 72)	35	(16, 37)

Note: On average, the true β₁ parameter was nonzero (ie, β₁ = 2) at 84% of locations in Region 1 and 3% of locations in Region 2 for both Case 1 and Case 2.

Similarly, as shown in the right side of Table 3, the GWL estimates of β₁ were positive nearly 100% of the time in Regions 1 and 2 for both the independent and the correlated cases. This indicates that GWL failed to appropriately perform variable selection for x₁ in Region 2, the region of inactivity. Furthermore, in at least half of the simulated examples, 17% and 35% of the GWL estimates of β₃ in Regions 1 and 2, respectively, were zero in the case of independence, and 15% and 35% of the estimates of β₃ in Regions 1 and 2, respectively, were zero in the case of correlation. Given that x₃ is moderately positively associated with the outcome across the study area, these results could lead to the incorrect conclusion that this predictor is not positively associated with the adverse outcome.

The results of applying one and two SEs to the GWR estimated coefficients to classify them as positive, negative, or zero are listed in Table 4. Using the one-SE criteria, GWR incorrectly classified 83% of β₁ estimates in Region 2 as positive at least half of the time for the independent case and incorrectly classified 84% of β₁ estimates in Region 2 as positive at least half of the time when the predictors were correlated. Similarly, when applying the two-SE criteria, GWR incorrectly classified 64% of β₁ estimates in Region 2 as positive at least half of the time for the independent case and incorrectly classified 66% of β₁ estimates in Region 2 as positive at least half of the time in the correlated case. This implies that GWR frequently yields nonnegligible positive estimates of β₁ in the region of inactivity.

Table 4.

Median (interquartile range) percentage of GWR coefficient estimates that were positive, negative, and zero across the 100 simulated data sets when considering ±1 and ±2 standard errors of regression coefficient estimates for the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

	GWR (1 SE)								GWR (2 SE)
	${\widehat{\beta }}_0$		${\widehat{\beta }}_1$		${\widehat{\beta }}_2$		${\widehat{\beta }}_3$		${\widehat{\beta }}_0$		${\widehat{\beta }}_1$		${\widehat{\beta }}_2$		${\widehat{\beta }}_3$
Case 1
Region 1
Positive	4	(1, 10)	100	(100, 100)	16	(6, 27)	100	(99, 100)	0	(0, 3)	100	(100, 100)	1	(0, 6)	98	(96, 100)
Negative	73	(64, 82)	0	(0, 0)	15	(8, 28)	0	(0, 0)	53	(44, 63)	0	(0, 0)	2	(0, 6)	0	(0, 0)
Zero	21	(16, 28)	0	(0, 0)	64	(54, 73)	0	(0, 1)	45	(36, 54)	0	(0, 0)	94	(88, 98)	2	(0, 4)
Region 2
Positive	35	(22, 44)	83	(73, 92)	12	(7, 18)	100	(100, 100)	8	(4, 14)	64	(54, 78)	1	(0, 3)	99	(98, 100)
Negative	3	(1, 6)	0	(0, 1)	14	(7, 22)	0	(0, 0)	0	(0, 0)	0	(0, 0)	1	(0, 3)	0	(0, 0)
Zero	60	(53, 70)	17	(8, 24)	72	(65, 77)	0	(0, 0)	91	(86, 96)	36	(23, 46)	96	(94, 99)	1	(0, 2)
Case 2
Region 1
Positive	6	(1, 10)	100	(100, 100)	39	(30, 53)	100	(100, 100)	0	(0, 4)	100	(100, 100)	12	(5, 20)	100	(98, 100)
Negative	64	(51, 73)	0	(0, 0)	8	(3, 13)	0	(0, 0)	33	(23, 45)	0	(0, 0)	1	(0, 3)	0	(0, 0)
Zero	28	(21, 38)	0	(0, 0)	51	(42, 59)	0	(0, 0)	64	(53, 72)	0	(0, 0)	86	(79, 93)	0	(0, 3)
Region 2
Positive	39	(27, 50)	84	(69, 92)	3	(0, 9)	100	(100, 100)	8	(3, 16)	66	(49, 76)	0	(0, 0)	99	(97, 100)
Negative	3	(0, 6)	0	(0, 0)	50	(41, 63)	0	(0, 0)	0	(0, 0)	0	(0, 0)	31	(20, 42)	0	(0, 0)
Zero	58	(48, 68)	16	(8, 29)	44	(35, 53)	0	(0, 0)	91	(84, 96)	34	(24, 50)	69	(57, 79)	1	(0, 3)

Notes: On average, the true β₁ parameter was nonzero (ie, β₁ = 2) at 84% of locations in Region 1 and 3% of locations in Region 2 for both Case 1 and Case 2. A parameter estimate was counted as zero if its confidence interval based on one or two standard errors contained zero.

Furthermore, when applying the one-SE rule, we see that in the case of independence, GWR correctly classified 64% and 72% of the β₂ estimates as zero in the upper and lower regions, respectively, at least half of the time. In the case of correlated predictors, only 51% and 44% of the β₂ estimates were correctly classified at least half of the time in the upper and lower regions, respectively. Finally, when using the two-SE criteria, 29% of the β₂ estimates in Region 1 were incorrectly classified as positive at least half of the time when the predictors were correlated. Thus, even when allowing “small” estimates to be considered as negligible, GWR results can still lead to erroneous inferences about the nature of a predictor variable that is not associated with the response.

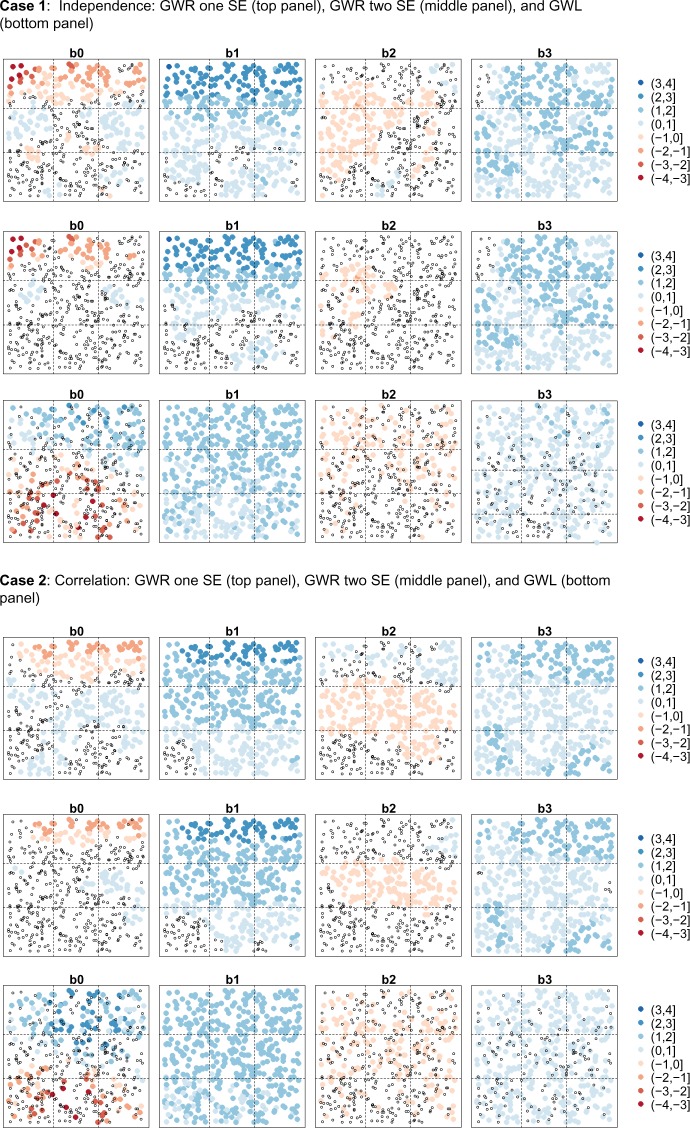
As an illustrative example, we randomly chose one simulated data set for each correlation case and plotted the corresponding estimated regression coefficients from GWR and GWL, using open circles for the negligible estimates (ie, GWR estimates with confidence intervals containing zero or GWL estimates of zero) (Fig. 6). This example visually supports the aggregate results given in Tables 3 and 4. GWR accurately identified Region 1 as the region of high activity for x₁ but overstated the effect of x₁ in Region 2, in which the predictor is inactive. In addition, in the correlated case, GWR produced a cluster of nonnegligible positive estimates for β₂ in Region 1 and nonnegligible negative estimates for β₂ in Region 2. Finally, while GWL was able to correctly perform variable selection for x₂ with some frequency (ie, estimate that β₂ was zero, as shown by the open circles), we see that GWL was again unable to correctly identify the spatially varying pattern of β₁ in the cases of both independence and correlation. More specifically, GWL estimated a nearly uniform effect for β₁ across the study area, understating the effect of x₁ in Region 1 and failing to perform appropriate variable selection for x₁ in Region 2 (implying that x₁ is active in Region 2).

Figure 6.

Estimated regression coefficients from GWR and GWL for one simulation of data under the cases of independent chemicals (Case 1) and correlated chemicals (Case 2).

Discussion and Conclusion

We have evaluated the ability of the geographically weighted regression methods of GWR and GWL to detect signal from noise in the context of modeling the associations of environmental chemicals and an adverse health effect using a simulation study with both independent and correlated chemicals. We found that GWR was able to identify regions of high activity for an important chemical when the predictors were independent and when they were highly correlated, but it demonstrated a tendency to overstate the importance of this chemical in its region of inactivity. Furthermore, GWR suffered from the reversal paradox for less-important chemicals when the chemicals were correlated, as the variable that was not associated with the outcome was largely positive in the upper study region and largely negative in the lower study region. We also found that with GWL, the signal of the most important chemical was diminished, with less distinction between the inactive and active study regions, regardless of the correlation among the chemicals.

Previous work has addressed the issue of collinearity in GWR. Wheeler and Tiefelsdorf¹¹ first demonstrated the link between collinearity in GWR and correlation of estimated regression coefficients using simulation studies. These authors introduced systematic collinearity into the model by adding correlation to a pair of covariates and found consistent evidence of increasing correlation in GWR coefficients with increasing collinearity. Wheeler and Calder¹³ used two simulation studies to evaluate the coverage probability and accuracy of the regression coefficients from GWR. Results of the simulation studies include low coverage probabilities for the GWR coefficients and consistently increasing error in the coefficients when collinearity is increased. Wheeler¹² conducted a simple experiment by systematically increasing collinearity in a data set to demonstrate that a penalized form of GWR, geographically weighted ridge regression, reduces the extreme effects of collinearity that afflict GWR. More recent simulation study work confirms that a nonnegligible amount of spatial variation of and correlation between GWR coefficient surfaces is inherently generated by the method.¹⁵ This work finds that the false-positive rates for GWR coefficients are typically much higher than convention would mandate, from <10% to >50% of the time (depending on the true correlation level between two covariates) when the true underlying process is stationary.

Wheeler¹⁴ expanded the simulation study of Wheeler and Calder¹³ to contain four explanatory variables and 196 observations in a study of the performance of GWR and GWL. This work compared the coefficient accuracy and the predictive performance of the models in the presence of collinearity. In these experiments, 100 realizations of a data-generating process were used with the true local coefficients sampled from a multivariate normal distribution. These simulation studies show that the performance of GWR in terms of both prediction and coefficient accuracy can be improved by constraining the magnitude of its regression coefficients with techniques designed to remediate collinearity. However, the experiments reported in that study show that the correlation between local coefficients is reduced but not eliminated with GWL, and that although GWL can shrink some coefficients to zero to stabilize the model, the estimates still tend to be positively correlated with those from GWR.¹⁵

We have extended these results in the case of three environmental chemicals to identify evidence of the reversal paradox and evaluate the correct identification of local “hot spots” or regions of high activity for one chemical. Our results demonstrate that while GWR can correctly identify a region of high activity for one chemical, it has difficulty in identifying regions of inactivity or low exposure. Additionally, GWR artificially induces spatial patterning and suffers from the reversal paradox in the setting of highly correlated predictor variables. Finally, we have shown that while GWL reduces the correlation among the coefficient estimates and tempers the reversal paradox that is problematic with GWR, it suffers from an inability to adequately distinguish local regions of high activity regardless of the relationship among the predictor variables. The implications of our findings for environmental risk analysis is that GWR may incorrectly identify some chemicals as positively or negatively associated with disease risk, and GWL may not correctly estimate the magnitude of association for an important chemical in some regions of the study area. Given these findings, more methodological development is required to better estimate the effects of correlated environmental chemicals on diseases associated with environmental factors, such as many cancers.