A Respiratory Self-Gating Technique with 3D-Translation Compensation for Free-Breathing Whole-Heart Coronary MRA

Abstract

Respiratory motion remains a major challenge for robust coronary MRA. Diaphragmatic navigator (NAV) suffers from indirect measurement of heart position. Respiratory self-gating (RSG) approaches improve motion detection only in the head-feet direction, leaving motion in the other two dimensions unaccounted for. The purpose of this study was to extend conventional RSG (1D RSG) to RSG capable of 3D motion detection (3D RSG) by acquiring additional RSG projections with transverse-motion-encoding gradients. Simulation and volunteer studies were conducted to validate the effectiveness of this new method. Preliminary comparison was performed between coronary artery images reconstructed from the same data sets using different motion correction methods. Our simulation illustrates that a proper motion-encoding gradient and derivation method enable accurate 3D motion detection. Results from whole-heart coronary MRA show that 3D RSG can further reduce motion artifacts as compared to NAV and 1D RSG and enables usage of larger gating windows for faster coronary imaging.

Introduction

Over the past two decades, tremendous progress has been made for coronary MR angiography (MRA), adding its promise for accurate noninvasive diagnosis of coronary artery diseases (1-5). Conventional coronary MRA performs imaging in a thin volume targeted at a specific coronary artery segment to obtain high resolution three-dimensional (3D) images within a short scan (4,5). Nonetheless, this method necessitates precise determination of an imaging plane for each coronary artery segment and suffers from limited visible vessel length. With the development of fast imaging techniques (e.g. steady state free precession (SSFP) and parallel imaging), whole-heart coronary MRA has emerged as a more reliable approach for coronary imaging with simplified imaging planning and complete visualization of the coronary artery tree (6). However, whole-heart coverage demands free-breathing data acquisition and thereby accurate compensation for respiratory motion during the scan.

Early studies show that respiratory motion of the heart is dominated by one-dimensional (1D) translation along the superior-inferior (SI) direction and is correlated with SI diaphragm displacements (7,8). Based on these properties, diaphragmatic navigator (NAV) monitors diaphragm position in real-time and then estimates SI motion of the heart using an empirical correlation factor (9). This technique is now the most commonly used method for free-breathing coronary MRA. However, as revealed in many studies, the robustness of NAV for coronary MRA is undermined by subject-dependent correlation and hysteresis between heart and diaphragm motion (10-12).

Direct measurement of heart position can potentially address the problem of inter-subject variability. For this purpose, heart navigator was used to monitor the motion of a left ventricular column free of coronary arteries (13). However, this method was found inferior to conventional NAV, due to the reduced SNR of the NAV projection (13) and complicated geometry and motion of the heart (12). Its local motion measurement could be especially problematic for whole-heart coronary MRA, where detection of global heart displacements is desired for correcting the overall motion of the entire coronary artery tree. An alternative approach, respiratory self-gating (RSG) (14-16), is gaining increasing attention in recent years. By repetitively measuring a center k-space RSG line, dominant global translation of the heart could be directly calculated from the shift of the heart profile in the RSG projection (16). A newly proposed dual-projection RSG (DP-RSG) method further improved this projection-based motion detection approach by eliminating chest wall signals (17). Preliminary comparison with NAV has demonstrated its superiority in motion detection and its potential for improving overall delineation of coronary arteries. However, like NAV, RSG methods only compensate for heart translation detected along the SI direction, while breathing-induced heart displacements in the other two dimensions can be sufficiently large to cause considerable motion artifacts (12). Furthermore, transverse heart translation varies largely in extent, direction and its relationship with SI translation among subjects (12,18), indicating that a general linear model would be insufficient to accurately estimate 3D heart displacements based on SI motion only. This restricts conventional RSG to 1D motion detection and its achievable gating window (GW) and acquisition efficiency. Consequently, a long scan time is still needed for high-definition whole-heart coronary MRA, which increases not only patient discomfort but also its susceptibility to changes of the patient's breathing pattern.

Three-dimensional (3D) NAV was proposed to reduce residual respiratory motion artifacts, by acquiring three orthogonal NAV echoes for 3D motion detection (19). Although improvement over conventional NAV was observed in some subjects, the effectiveness of this technique remains limited by its indirect measurement of heart position. Progress was made by Manke, et al, by fitting 3D NAV motion detection into an affine model characterizing more complicated heart motion, consisting of 3D translation and linear transformation (20). This technique has been shown to be able to significantly reduce residual motion and improve coronary artery delineation (20,21). However, this delicate affine motion correction requires additional calibration prescans, manual definition of a heart mask and establishment of an affine model for each subject. Furthermore, variations of the subject's breathing pattern during a study could potentially impair the applicability of the affine model established in a prescan to subsequent coronary imaging. Additionally, these 3D NAV-based techniques require acquisition of 3D NAV echoes crossing the region of interest. Due to the complicated geometry of the coronary artery tree spanning over the myocardial surface, extra caution must be paid for the NAV placement to avoid interfering coronary imaging, especially for whole-heart coronary MRA with full coronary artery coverage.

Based on a previous study comparing different motion models, 3D translation correction could reduce the respiratory motion of coronary arteries into a tolerable scale even with a large GW up to 10mm (22). This implies the potential to significantly reduce respiratory motion artifacts and the scan time and therefore increase the robustness of coronary MRA. Motivated by this promising result, our work was aimed to extend conventional RSG techniques (1D RSG) to 3D RSG, enabling direct measurement of 3D heart translation on the fly, and investigate its feasibility for whole-heart coronary MRA. Preliminary comparison with conventional NAV and 1D RSG was performed to evaluate the effectiveness of this new method for suppressing respiratory motion artifacts.

Theory

It has been demonstrated in (17) that averaging two k-space lines with a properly designed AP dephasing gradient can generate a 1D SI projection containing primarily heart signals. Translation parallel to the projection could be estimated by tracking the shift of the heart profile in this 1D projection. If an additional motion-encoding (ME) gradient perpendicular to the projection is added in acquisition of the 1D projection similar to floating NAV (FNAV) (23), translation along the ME gradient introduces a phase shift in the projection signal proportional to the amount of this translation (Eq. 1).

$$p(x,\omega )=\int f(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z+\mathrm{\Delta }z)·e^{-j\omega ·y}dydz=e^{j\omega ·\mathrm{\Delta }y}\int f(x+\mathrm{\Delta }x,y,z)·e^{-j\omega ·y}dydz=e^{j\omega ·\mathrm{\Delta }y}·p_0(x+\mathrm{\Delta }x)$$ (1)

where x, y and z are three orthogonal axes in image domain; Δx, Δy and Δz are the amount of translation along x, y and z, respectively; ω is the strength of the ME gradient applied along y; f(x,y) represents the magnetization distribution in the image domain; p₀(x,ω) and p(x,ω) are 1D projections at the reference position (Δx, Δy, Δz=0) and a shifted position, respectively. According to Eq. 1, the two translation components, Δx and Δy, can be derived by simply calculating the profile shift and phase shift in this 1D projection, respectively.

It is feasible to integrate DP-RSG and FNAV to detect multiple-dimensional translation of the heart. However, the validity of FNAV relies on an assumption that the object resides in a homogeneous magnetic field such that signal modulation due to background gradients can be ignored. This ideal field cannot be achieved in coronary MRA due to 1. the spatially-varying sensitivity of phase-arrayed coils and 2. the sinusoidal magnitude modulation along AP generated by DP-RSG acquisition (17). Although these two types of background modulation are both relatively smooth and gradual compared to the scale of heart displacements, the additional phase changes in p(x,ω) induced by them can potentially reduce the accuracy of the phase-shift-based motion detection. To alleviate this adverse effect of background modulation, two heart projections were acquired, namely, a non-motion-encoded projection (p(x,0)) and a motion-encoded projection (p(x,ω≠0)). In the non-motion-encoded projection, the profile shift can be used to derive Δx, while the phase shift can be used to estimate the phase change induced by background modulation alone. Accordingly, calculation of Δy is formulated in Eq. 2 taking into account of both Δx and background modulation effects.

$$\mathrm{\Delta }{y}^{\prime }=\frac{arg\left(\underset{R}{\int }\right[p(x-\mathrm{\Delta }{x}^{\prime },\omega )·{p_0}^{\ast }(x,\omega )]·{[p(x-\mathrm{\Delta }{x}^{\prime },0)·p_0^{\ast }(x,0)]}^{\ast }dx)}{\omega }$$ (2)

where Δx′ and Δy′ are the estimated Δx and Δy, respectively; arg and * represent the operators of phase and conjugate calculations, respectively; R indicates a window covering the region of the heart in the 1D projection. Integration of signals over R was performed to calculate the global phase shift of the entire heart.

Based on the preceding steps, separate SI, AP and LR RSG projections can be collected to detect heart displacements in the three dimensions. All the three RSG projections are acquired with x along the SI direction. The SI RSG projection is acquired with ω=0, while a nonzero ME gradient is applied in the AP and LR axes for the AP and LR RSG projections, respectively. SI heart translation is derived from the profile shift in the SI RSG projection. Corrected phase-shift calculation is performed based on Eq. 2 in the AP and LR RSG projections for detection of translations along AP and LR directions, respectively.

Selection of ω is critical for the efficacy of this phase-shift-based approach. Theoretically, increasing ω can increase its sensitivity to AP and LR translation (23). Additionally, using larger ω can reduce the relative contribution of background modulation in the phase shift of p(x, ω) and the resulting errors in motion detection. However, this also reduces the signal-to-noise ratio (SNR) of the AP and LR RSG projections and consequently impairs the accuracy of transverse motion detection (23). The optimal value of ω will be determined using simulation.

Materials and Method

Simulation

Simulation was performed based on a 3D heart model established using real whole-heart images. The whole-heart image set was obtained from a volunteer using the same scanner and receiver coil as will be used for coronary MRA in this study. Sensitivity maps of the receiver coil were estimated from the images reconstructed from individual channels and the square-root-of-sum-of-squares (SOS) images combining data from all channels (24). The estimated coil sensitivity was normalized by SOS combined magnitude. Second-order polynomial surface fitting was performed to reduce noise effects in coil sensitivity estimation (24). 3D magnetization distribution of the heart was extracted by manually selecting the region of the heart in each slice of the whole-heart image set. Heart translation was simulated by shifting this heart model in 3D based on a linear motion model assuming heart translations along AP and LR were 0.25 and -0.25 times of the amount of its SI translation respectively. Background modulation induced by the receiver coil and DP-RSG acquisition was simulated based on the estimated coil sensitivity map and the AP dephasing necessary for chest wall suppression, respectively. The three RSG projections at different heart positions were simulated using Eq. 3.

$$p(x)=\int f(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z+\mathrm{\Delta }z)·s(x,y,z)·cos\left(\frac{\pi ·y}{2·W}\right)·e^{-j({\omega }_{y}y+{\omega }_{z}z)}dydz$$ (3)

where Δx, Δy and Δz are simulated SI, AP and LR translations, respectively; s(x,y,z) represents coil sensitivity distribution; the cosine term represents the magnitude modulation due to DP-RSP acquisition, in which W is the distance between the centers of the heart and chest wall (17); ω_y is the ME gradient applied for the AP RSG projection and is zero for calculating the SI and LR RSG projections; ω_z is the ME gradient for the LR RSG projection and is zero for calculating the SI and AP RSG projections.

3D heart translation was derived from the simulated RSG projections as described in Theory. To evaluate the impact of ω on the accuracy of motion detection, motion derivation was performed using a range of ω values and the mean error with regard to the simulated motion (SOS of the absolute errors in all three dimensions) was calculated for each ω. Considering the concomitant SNR loss in the RSG projections with larger ω, the minimal ω providing a sufficiently small mean error was selected as the optimal ME gradient.

Data Acquisition

The sequence used for this study was modified from a conventional magnetization-prepared (T2 preparation and fat saturation) 3D SSFP sequence with ECG triggering and NAV gating. As illustrated in Fig. 1, 6 additional RSG echoes were acquired immediately following the NAV echo acquisition in each heartbeat. These RSG echoes were comprised of 3 pairs of RSG k-space lines, corresponding to reconstruction of SI, AP and LR RSG projections. Data acquisition for the first pair was similar to that of DP-RSG. Two center k-space lines along the SI direction were collected in two consecutive gradient-echo radiofrequency (RF) cycles. Additional dephasing gradients were applied along AP, generating π/2 and -π/2 dephasing at chest wall for the first and the second RSG echoes, respectively. Acquisition of the second pair was same as the first pair, except that a ME gradient was added in the AP direction before acquisition of each RSG echo. A similar acquisition strategy was used for the third pair with the same ME gradient applied along the LR direction.

Fig. 1.

Upper: the acquisition scheme of the 3D RSG sequence in a heartbeat. Lower: the sequence diagram of RSG data acquisition. G_LR, G_AP and G_SI represent gradients along LR, AP and SI, respectively. Solid, dashed and dotted arrows in the lower figure indicate AP dephasing gradients for DP-RSG and ME gradients along AP and LR, respectively. G_LR and G_AP are scaled up by 20 times to visualize gradients along these two directions.

Coronary MRA was conducted on 9 healthy volunteers (age: 28-58 years) using a 1.5T clinical MRI scanner (MAGNETOM Avanto, Siemens Medical Solutions, Erlangen, Germany) and a 6-pack phased array cardiac coil (2×3 element configuration; 322 mm length; 520 mm width). The experiment protocol was approved by our institutional review board and written informed consent was obtained from each volunteer before a study. In the beginning of each study, a low-resolution localization scan with three standard views was performed to determine the positions of the heart and right hemi-diaphragmatic dome. Next, a 4-chamber view slice was scanned using a cine SSFP sequence. By visually assessing the cardiac motion in the cine image series, the position of the optimal acquisition window in a cardiac cycle with minimal RCA motion was determined. Coronary MRA was then performed in a sagittal slice covering the entire heart using the 3D RSG sequence described above. Free-breathing was allowed during the scan and data acquisition was gated prospectively using NAV. Typical parameters for coronary MRA were used: 320×240 mm² FOV; 120 slices interpolated from 60 slices; 1.0 mm slice thickness after interpolation; 825 Hz/pixel bandwidth; 320×228 matrix; 1.0×1.1 in-plane spatial resolution; 38 lines/segment; 90° flip angle; TE/TR = 1.87/3.74 ms. To reduce eddy-current effects, data were acquired with centric-pair and linear orders along phase- and partition-encoding directions, respectively (17). RSG data were collected from a separate sagittal slice centered at the heart with a thickness of 160 mm. The size of the field-of-view (FOV) of the RSG slice was manually adjusted such that the FOV covers the heart from the apex to the aorta root in the SI direction and its anterior edge was placed at the center of chest wall. The SI range of the FOV was used to define the heart region in RSG projections for motion derivation. The AP width of the FOV was used for automatic calculation of the AP dephasing gradient for chest wall suppression (17). A flip angle of 10° was used for RSG data acquisition. Additionally, to reduce blood-flow-related phase variations, flow compensation was employed in all three gradient axes. The total RSG data acquisition time was 22.5 ms in each heartbeat. For NAV gating, a GW of ±4.5 mm was used. No slice tracking was performed and respiratory motion within the GW was corrected in offline processing.

Motion Derivation

SI, AP and LR RSG projections were reconstructed from the 3 pairs of RSG echoes and used for 3D motion derivation. First, the two RSG k-space lines in each pair were averaged to reconstruct an RSG projection without contamination of chest wall signals (17). To eliminate signals from static tissues on the back, only data received by anterior coils were selected for reconstruction of RSG projections (17). Next, SI and transverse translation components were calculated from the SI RSG projection using a maximum correlation coefficient method (17) and from the AP and LR RSG projections based on phase-shift calculations (Eq. 2), respectively. Both profile matching and phase-shift calculations were confined in R, the manually defined region of the heart.

Respiratory motion signal was also derived from NAV echo. SI displacement of the diaphragm-lung interface in the NAV projection was calculated based on edge detection (2) and was multiplied by 0.6 to estimate SI heart translation during the scan (7,9).

For the above processing, a reference heartbeat was determined by selecting a heartbeat with the highest diaphragm position from the first 10 heartbeats in a scan. The NAV and RSG projections acquired in the reference heartbeat were selected as the reference signals for motion detection.

Image Reconstruction

Image reconstruction was performed using k-space data accepted by NAV gating. For comparison, three image sets were reconstructed on each subject from the same k-space data set based on the following three types of motion compensation.

• NAV: compensating SI heart translation estimated using NAV;

• 1D RSG: compensating SI heart translation using the SI component of the 3D RSG motion signal;

• 3D RSG: compensating 3D heart translation using all components of the 3D RSG motion signal.

Motion compensation was carried out by applying a linear phase modulation along each k-space axis based on the estimated heart translation in the corresponding direction.

Image Analysis

The performance of different motion compensation methods was compared with regard to delineation of coronary arteries. For each subject, NAV, 1D RSG and 3D RSG image sets were reformatted in identical orientations to obtain optimal visualizations of LAD and RCA. The reformatted images for each coronary artery segment from each subject were displayed on the same slide in a random order. The randomized images were graded by two experienced cardiac MR specialists based on depiction of the coronary artery using a 5-scale scoring system (4: excellent; 3: good; 2: fair; 1: poor; 0: undistinguishable).

The image scores of LAD and RCA obtained from each subject were averaged to represent the overall vessel delineation on the subject. These mean scores from all 9 subjects were compared using one-way ANOVA to analyze the difference of the three reconstruction methods. Next, pair-wise comparison was performed using Wilcoxon signed-rank test to compare each pair of the three reconstruction methods. A p-value smaller than 0.05 was considered statistically significant for the above analyses.

Results

Simulation

To be consistent with the 9mm GW used for coronary MRA, the simulated heart translation was confined within a range of –3 ∼ 6 mm in the SI direction. Fig. 2. a∼c plot the detected translation against the simulated translation in all three dimensions using different derivation methods and different ω values. Clearly, the error in motion detection increases as the heart moves farther away from the reference position. Comparing motion curves of the two ω values, ω=5°/mm produces very small errors in all dimensions and is more accurate than ω=2°/mm in both AP and LR directions. Also, without background phase correction, the transverse components of the detected motion deviate from the simulated motion substantially. Fig. 2.d shows the mean errors corresponding to a range of ω values. Generally, larger ω provides higher accuracy. The mean error is reduced to below 0.1 mm with ω=5°/mm, while further increasing producing only minor improvement. Therefore, 5°/mm was selected as the optimal ME gradient and used for all coronary MRA scans in this study.

Fig. 2.

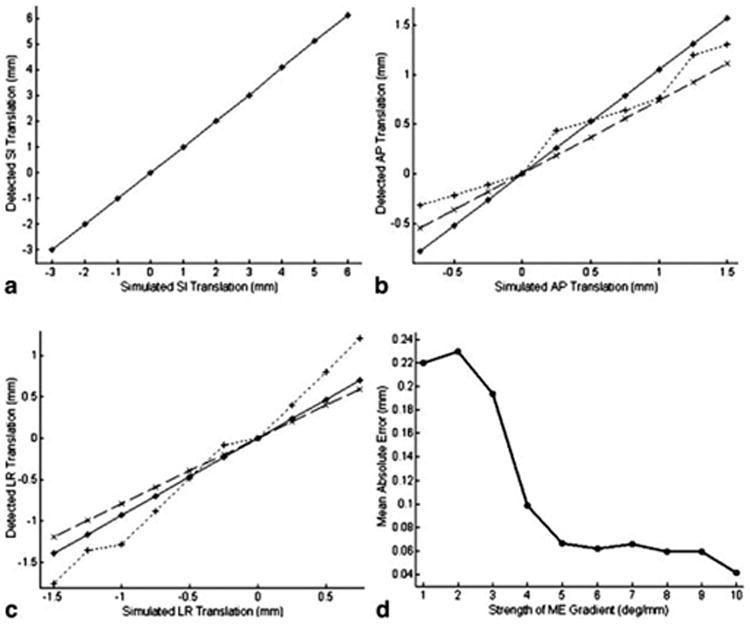
SI (a), AP (b) and LR (c) displacements detected at simulated heart positions with ω=5°/mm (solid *) and 2°/mm (dashed ×) and without background phase correction (ω=5°/mm; dotted +). Note the different scales in y-axes in (a, b, c). The detected motion along SI is the same for different methods and ω values. Only one curve is shown in a) for legibility. d) shows mean absolute errors corresponding to different ω values.

Coronary MRA

Fig. 3 shows motion signals obtained from a subject using NAV and 3D RSG. SI motion detected using NAV and 3D RSG closely follow each other with noticeable difference in magnitude. For 3D RSG, the AP and LR motion components are visually synchronized with the SI component, while the magnitude of the former two components is substantially reduced. On all the 9 volunteers, the means of the corrected motion in image reconstruction are 1.70±0.67 mm, 0.42±0.21 mm and 0.31±0.09 mm in the SI, AP and LR directions, respectively.

Fig. 3.

Motion detection in a temporal segment during a scan. Dark solid curves are heart translation along SI (top), AP (middle) and LR (bottom) detected using 3D RSG. The gray dotted curve is the SI heart translation estimated using NAV.

Reformatted coronary artery images from the same subject are shown in Fig. 4. For both RCA and LAD, 1D RSG better suppresses motion artifacts compared to NAV and 3D RSG further improves vessel delineation. The difference between them can be better appreciated in a sagittal slice across the bifurcation of LAD and left circumflex artery (Fig. 4.c). These two closely located coronary artery branches are completely blurred and merged as a single dot in the NAV image and can hardly be distinguished in the 1D RSG image. In comparison, this bifurcation is clearly depicted in the 3D RSG image.

Fig. 4.

The same RCA slice reconstructed using NAV (left), 1D RSG (middle) and 3D RSG (right). White arrows indicate noticeable image degradation caused by residual motion artifacts using NAV and 1D RSG.

Another example is provided in Fig. 5. On this subject, 3D RSG apparently provides the best delineation of proximal RCA. However, this coronary artery segment is significantly obscured by motion artifacts in the NAV image and also slightly blurred in the 1D RSG image.

Fig. 5.

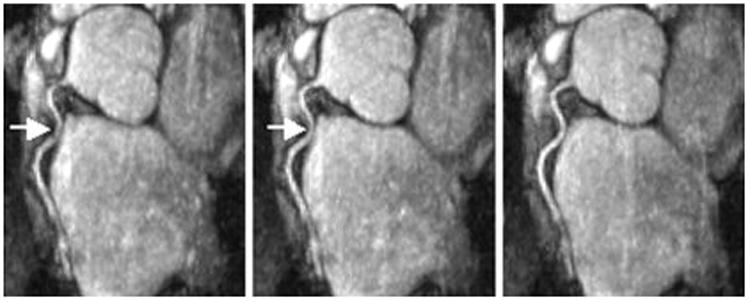
Reformatted RCA images obtained from the same volunteer reconstructed using NAV (left), 1D RSG (middle) and 3D RSG (right). White arrows indicate noticeable image degradation caused by residual motion artifacts.

The mean scores of different reconstruction methods were listed in Table 1. On average, 3D RSG images received the highest scores and 1D RSG images were graded higher than NAV images for both evaluated vessel segments. In the total of 18 coronary artery images, 3D RSG achieved higher scores than 1D RSG in 13 cases and than NAV in 16 cases. Apparent improvement (difference in the score > 0.3) was observed in 7 cases compared to 1D RSG and in 12 cases compared to NAV. Statistically, different motion correction methods introduced significant difference in image scores (p<0.001). Pair-wise comparisons revealed that 1D RSG significantly improved vessel delineation compared to NAV (p=0.013) and 3D RSG achieved significantly higher scores than both 1D RSG (p=0.011) and NAV (p=0.008).

Table 1. Mean scores of LAD and RCA for different motion correction methods.

	NAV	1D RSG	3D RSG
LAD	2.57±0.35	2.89±0.15	2.97±0.20
RCA	2.57±0.41	2.82±0.21	3.19±0.21

Discussion

A new RSG approach with 3D translation detection was presented in this work. Heart displacements along SI and transverse directions could be derived based on profile and phase shifts in additionally collected RSG projections. By visual assessment, transverse translation detected on the 9 volunteers involved in this study is synchronized with SI translation with a pseudo-linear relationship. By performing linear regression, we found the correlation between the two transverse motion components and the SI motion component exhibited large inter-subject variations. The correlation factor between AP and SI translation is 0.14±0.15 ranging in -0.04 ∼ 0.45, while this correlation factor is -0.10±0.13 with a range of -0.28 ∼ 0.09 for the LR direction. Moreover, evident hysteresis exists between different motion components as observed on many subjects in this study. One representative example is shown in Fig. 6. Apparently, in such cases, a linear motion model would introduce substantial errors in motion detection and compensation. These observations indicate that transverse translation, although is of reduced magnitude compared to dominant SI translation, can still result in considerable motion artifacts on a population of subjects, especially with a large GW. Furthermore, transverse motion components must be measured on a subject-by-subject basis and cannot be accurately estimated from SI motion detection using a simple linear model. Although the magnitude and general properties of the heart motion detected in this study are in accordance with results from previous papers (8,12,22), a quantitative evaluation is still needed to fully investigate the accuracy of this new method in measuring 3D heart position.

Fig. 6.

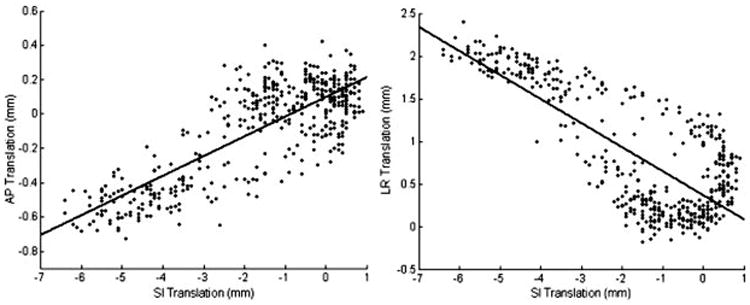
Heart translations along AP (a) and LR (b) v.s SI heart translation detected from the same scan. The black dots indicate heart displacements during a scan detected using 3D RSG. The two bold lines represent the fitted linear models characterizing correlations between transverse and SI translations.

This work compared the effectiveness of three motion correction methods for whole-heart coronary MRA. Consistent with the results in a previous study (17), 1D RSG significantly improved vessel delineation compared to NAV. This improvement is attributed to its direct measurement of heart position, which resolves the major challenge for NAV, namely inconsistency between diaphragm and heart motion. Although 1D RSG can potentially accurately detect and correct dominant heart motion along SI, displacements in the transverse plane remains uncompensated and can generate considerable motion artifacts with a GW larger than 5mm (22). By introducing 3D translation correction, 3D RSG can further reduce residual motion artifacts as demonstrated in our human studies. As expected, this improvement is determined by the scale of transverse motion within the GW and therefore is strongly subject-dependent. In this study, the improvement was apparent in 7 cases and relatively slight in 6 cases, while no improvement was observed in the remaining 5 cases. It must be noted that NAV gating is not necessary for the proposed 3D RSG method. NAV echo was acquired in this work such that different motion correction methods could be compared using the same datasets. In future implementation, respiratory motion signals should be derived from RSG echoes in real-time and used to gate coronary imaging.

For detection of 3D heart translation, additional RSG projections were acquired in each heartbeat during a scan. Compared to FNAV which attempted to encode 2D motion into one NAV echo, this method requires three separate RSG projections for motion detection in three orthogonal directions, among which an SI RSG projection was collected without motion encoding. However, this modification potentially can improve the accuracy of motion detection in all three dimensions. First, a certain nonzero ME gradient is needed for optimal phase-shift-based detection of transverse translation, while a zero ME gradient producing the highest SNR is desirable for profile-shift-based detection of SI translation. This creates a dilemma for FNAV to optimize motion detection in both directions. Contrarily, acquiring separate RSG projections enables usage of the optimal ME gradient for motion detection in each direction. Furthermore, additional phase shift due to background modulation can be estimated from the non-motion-encoded SI RSG projection. As demonstrated in our simulation, the estimated background phase shift can be used for background phase correction and improving the accuracy of transverse motion detection.

The original DP-RSG method acquires RSG echoes between dummy pulses and imaging k-space lines. Therefore, RSG and imaging data must be acquired from the same slice to avoid steady-state artifacts and the optimal orientation is limited to sagittal orientation for motion detection along the SI direction. In this study, RSG echoes were collected in a few gradient-echo RF cycles prior to dummy pulses. Because the magnetization excited for RSG data acquisition is substantially attenuated by the gradient spoiler at the end of each gradient-echo RF cycle and further decays during the dummy pulses, the effect of RSG data acquisition on imaging data acquisition is negligible. Therefore, our new method allows acquisition of RSG and imaging data in two different FOV's. With this flexibility, the optimal orientation and slice coverage for imaging data acquisition can be selected based on the heart geometry of the subject.

Compared to the small GW (usually ±2.5mm) used in conventional free-breathing coronary MRA, this study used a larger GW of ±4.5mm for NAV gating. Although image quality was compromised to some extent in the NAV and 1D RSG images, overall good delineation of coronary arteries (LAD: 2.97±0.20; RCA: 3.19±0.21) was maintained using 3D RSG. On the other hand, substantially higher acquisition efficiency (64.3±8.6%) was achieved with the larger GW than that usually obtained (<40%) with a ±2.5mm GW. This implies that 3D RSG can potentially achieve similar image quality with a reduced scan time. However, it must be noted that the heart does not only translate but also experiences more complicated motion (22), e.g. rotation and deformation, which can not be detected using the present 3D RSG method. The uncompensated motion components can result in additional blurring and ghosting artifacts interfering coronary artery visualization with large GW's. Extending this RSG method to encompass more complete motion detection (e.g. rotation, stretching) could further reduce residual motion artifacts. However, this desirable extension would be not straightforward for this 1D-projection-based motion detection method, because, by collapsing all 2D signals in a transverse plane into a single sample in 1D RSG projections, nontranslational motion of the heart in transverse directions is hidden. Future work should evaluate the effectiveness of 3D RSG with different GW's and determine the optimal GW for coronary MRA.

This work investigated the efficacy of 3D RSG in coronary MRA with an increased GW and a typical ∼2 mm³ spatial resolution. Besides improving acquisition efficiency as demonstrated in this work, this 3D-motion-detection method could potentially be used to achieve higher spatial resolution (e.g sub-millimeter) depiction of coronary arteries as well by reducing residual motion artifacts within a typical GW of 2-5 mm. Future evaluations are necessary to study its performance in such a scenario in comparison with conventional methods. However, it should be pointed out that whole-heart imaging with a small GW and a sub-millimeter spatial resolution requires a long scan time, which can potentially increase the susceptibility to irregular breathing patterns.

In conclusion, this work demonstrated the feasibility of a new RSG technique for whole-heart coronary MRA, capable of detecting and compensating breathing-induced heart translation in all three dimensions. Comparison with NAV and 1D RSG on the same datasets shows that this new method is promising for reducing residual motion artifacts and improving coronary artery delineation. With this capability, larger GW's can be used to accelerate data acquisition. Future work will quantitatively evaluate the accuracy of this new method and implement real-time 3D RSG gating.