Summary
In the U.S., the Centers for Medicare and Medicaid Services uses 30-day readmission, following hospitalization, as a proxy outcome to monitor quality of care. These efforts generally focus on treatable health conditions, such as pneumonia and heart failure. Expanding quality of care systems to monitor conditions for which treatment options are limited or non-existent, such as pancreatic cancer, is challenging because of the non-trivial force of mortality; 30-day mortality for pancreatic cancer is approximately 30%. In the statistical literature, data that arise when the observation of the time to some non-terminal event is subject to some terminal event are referred to as ‘semi-competing risks data’. Given such data, scientific interest may lie in at least one of three areas: (i) estimation/inference for regression parameters, (ii) characterization of dependence between the two events, and (iii) prediction given a covariate profile. Existing statistical methods focus almost exclusively on the first of these; methods are sparse or non-existent, however, when interest lies with understanding dependence and performing prediction. In this paper we propose a Bayesian semi-parametric regression framework for analyzing semi-competing risks data that permits the simultaneous investigation of all three of the aforementioned scientific goals. Characterization of the induced posterior and posterior predictive distributions is achieved via an efficient Metropolis-Hastings-Green algorithm, which has been implemented in an R package. The proposed framework is applied to data on 16,051 individuals diagnosed with pancreatic cancer between 2005-2008, obtained from Medicare Part A. We found that increased risk for readmission is associated with a high comorbidity index, a long hospital stay at initial hospitalization, non-white race, male, and discharge to home care.
Keywords: Bayesian survival analysis, illness-death models, reversible jump Markov chain Monte Carlo, shared frailty, semi-competing risks
1. Introduction
Pancreatic cancer is the fourth leading cause of cancer death in the U.S., with an estimated 37,660 pancreatic cancer-related deaths in 2011 (American Cancer Society, 2011). Since there are no effective screening tools, pancreatic cancer often presents insidiously; the majority of patients are diagnosed with advanced or metastatic disease and only approximately 10% are eligible for curative resection (Lockhart, Rothenberg, and Berlin, 2005). Unfortunately, despite recent advances in treatment, prognosis is extremely poor: 1-year mortality rates are 74% (American Cancer Society, 2011). A consequence of the severity of disease and lack of effective curative treatment is that pancreatic cancer management focuses on palliation of symptoms and the provision of end-of-life care (PLoS Medicine Editors, 2012).
Towards a better understanding of the prognosis of patients with pancreatic cancer, scientific interest often lies with post-diagnosis mortality. For this outcome, a so-called terminal event, standard survival analysis tools for time-to-event data can be used (Cox and Oakes, 1984; Ibrahim et al., 2005). In other settings, scientific interest may focus on a broader range of outcomes, including so-called non-terminal events. Consider, for example, the event of ‘readmission following discharge from the hospitalization at which an initial diagnosis of pancreatic cancer was given’. Readmission is non-terminal in the sense that patients continue to live beyond the experience of an event. Readmission rates are a major target of healthcare policy because readmission is common, costly and potentially avoidable (Joshua et al., 2010; Warren et al., 2011) and hence is seen as an adverse outcome; currently, the Centers of Medicare and Medicaid Services in the U.S. monitors 30-day readmission rates for a number of health conditions (Centers for Medicare and Medicaid Services, 2012). However, in conditions with poor prognosis such as pancreatic cancer, to focus solely on readmission rates is to oversimplify a situation in which patients may die before being readmitted, which clearly is also an adverse outcome. In such situations, healthcare policy should consider both readmission and death rates, which requires the development of models that consider both endpoints simultaneously.
In the statistical literature, data that arise when the observation of the time to some non-terminal event is subject to some terminal event are referred to as ‘semi-competing risks data’ (Fine, Jiang, and Chappell, 2001). Letting T1 and T2 denote the times to the non-terminal and terminal events, respectively, scientific goals in the semi-competing risks setting can broadly be categorized into one (or more) of three types:
Estimation/inference for regression parameters denoting the association between risk factors and T1 and T2 jointly.
Characterization of the within-subject dependence structure between T1 and T2.
Prediction of T1 and T2, given a patient’s covariate profile.
The literature on methods for semi-competing risks data has focused almost exclusively on estimation/inference for regression parameters. While these methods are clearly of use to researchers, when interest lies in characterizing the nature of the within-subject dependence structure between T1 and T2 or in prediction of outcomes (either the non-terminal event or the non-terminal event and the terminal event jointly) the literature is non-existent or sparse at best. Currently, researchers in pancreatic cancer, or any other health condition with a strong force of mortality, do not have a unified semi-competing risks data analysis framework that permits the simultaneous investigation of all three scientific goals.
Towards the analysis of semi-competing risks data, the central statistical challenge is the non-identifiability of the marginal survivor function for T1 (Fine et al., 2001). Let S(t1, t2) = P(T1 > t1, T2 > t2) denote the joint survivor function of the time to the non-terminal and terminal events, and S1(t1) = P(T1 > t1) and S2(t2) = P(T2 > t2) the corresponding marginal survival functions. While S2(t2) is fully identified from semi-competing risks data, S(t1, t2) is solely identified in the upper wedge of the support of (T1,T2), i.e. the region (0 < t1 < t2). Furthermore, S1(t1) is not identified, at least not without addition untestable assumptions and/or models. Methods developed in this context generally fall into one of two groups. The first considers models for the marginal distributions of T1 and T2 and either leaves the dependence between T1 and T2 arbitrary (Cook and Lawless, 1997; Ghosh and Lin, 2000, 2002) or models the dependence via a copula (Fine, Jiang, and Chappell, 2001; Jiang, Fine, and Chappell, 2005; Ghosh, 2006; Peng and Fine, 2007; Lakhal, Rivest, and Abdous, 2008; Hsieh, Wang, and Ding, 2008; Fu, Wang, Liu, Kulkarni, and Melemed, 2012). The second strategy focuses on building conditional models for the hazard functions of the non-terminal and terminal events (Liu et al., 2004; Ye et al., 2007; Zeng and Lin, 2009; Xu et al., 2010; Zeng et al., 2012; Zhang et al., 2013).
To-date, the vast majority of these methods have been developed within the frequentist paradigm, with an emphasis on non-parametric or semi-parametric analysis approaches. While well-suited to the task of estimation and inference for regression parameters, extensions that permit the investigation of dependence structure and the prediction of outcomes are non-trivial. This is especially the case if one is to report estimates of uncertainty. To our knowledge there is only a limited literature on Bayesian methods for semi-competing risks data. Fu et al. (2012), for example, proposed a Bayesian approach using a copula model, although it does not incorporate covariates and also assumes a parametric form for the underlying hazard functions. Bayesian methods have also been developed in the related setting of multi-state models (Sharples, 1993; Pan, Yen, and Chen, 2007; van den Hout and Matthews, 2009; van den Hout, Fox, and Klein Entink, 2011). One particularly relevant paper is that of Kneib and Hennerfeind (2008) who develop a general Bayesian framework for multi-state models. We believe that there are three important distinctions between their paper and ours. First of all, the overarching focus of that paper was on estimation/inference of the global dynamics of a multi-state system, rather than on one specific component; their application considers the transitions across various states during a nights’ sleep. In contrast, the scientific focus here is specifically on the non-terminal event, as well as on understanding within-subject dependence and on providing a framework for prediction of future outcomes. Second, we propose a different framework for modeling the baseline hazard functions; while Kneib and Hennerfeind (2008) use a B-spline with a penalty term on the spline coefficients, we consider a mixture of piecewise constant functions for the log-baseline hazard function to impose smoothness. Lastly, our proposed framework permits researchers to model the ‘from non-terminal event to terminal event’ transition via a model for the sojourn time. Most recently, Zhang et al. (2013) developed a Bayesian framework for semi-competing risks data that arises when patients switch treatments in a randomized trial. Their approach, however, relies on a model for the lifetime risk of the non-terminal event which, given the limited follow-up afforded by most studies, may be difficult to specify and evaluate.
In this paper, we develop a novel Bayesian framework for the analysis of semi-competing risks data. Specifically, the framework uses a shared-frailty illness-death model to characterize an underlying compartment model for the joint distribution of the non-terminal and terminal events (Xu et al., 2010). Two complementary specifications of the illness-death model are considered: a Markov model and a semi-Markov model. In contrast to previous frequentist approaches to estimation/inference for this model, the proposed framework is specifically developed to provide researchers with tools to investigate all three of the aforementioned scientific goals. The remainder of the paper is organized as follows. In Section 2, we describe the proposed Bayesian framework for the analysis of semi-competing risks data. Section 3 provides a detailed application of the methods using Medicare data on patients with pancreatic cancer. Finally, Section 4 concludes with discussion.
2. A Bayesian Framework for Semi-Competing Risks Data
Implementing a shared-frailty illness-death model within the Bayesian paradigm requires overcoming three challenges: (i) specification of three continuous baseline hazard functions; (ii) specification of prior distributions; and, (iii) the development of robust, e cient computational schemes. In this section, following a description of the model, we provide practical solutions to these challenges; the description of our computational scheme and its implementation is brief, with complete details provided in Supplemental material A.
2.1. Illness-Death Models for Semi-Competing Risks Data
In the context of our motivating pancreatic cancer study, an intuitive approach to analyzing semi-competing risks data is to view the data as arising from an underlying illness-death model system in which individuals may undergo one or more of three transitions: (1) discharge to readmission; (2) discharge to death; and (3) readmission to death. Following Xu et al. (2010) we consider modeling this system of transitions via the specification of three hazard functions: a cause-specific hazard for readmission, h1(t1); a cause-specific hazard for death, h2(t2); and a hazard for death conditional to a time for readmission, h3(t2|t1). Specifically, for 0 < t1 < t2, we define:
| (1) |
| (2) |
| (3) |
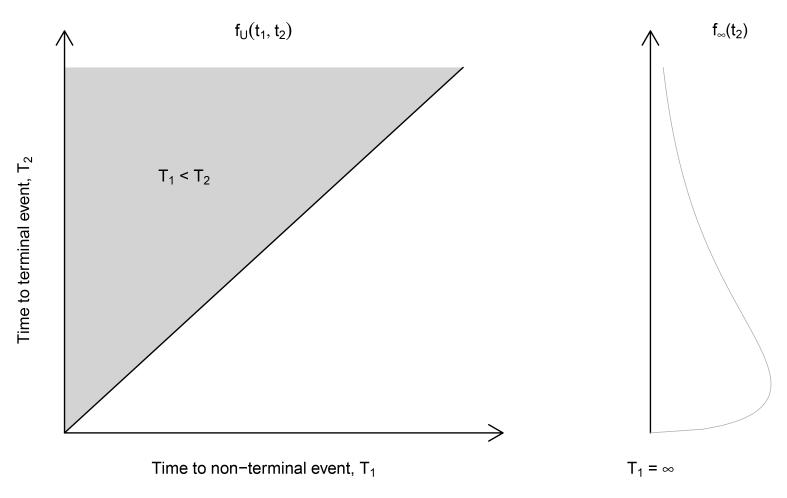
Together, (1)-(3) define the joint distribution on the upper wedge of the support of (T1, T2) that is denoted by fU(t1, t2). However, for any fU(t1, t2) defined solely on the upper wedge,
| (4) |
One strategy for resolving this is to set T1 = ∞ if a subject experiences death prior to readmission (Wang, 2003; Xu et al., 2010); that is, the remaining probability mass in (4) is distributed along the line t1 = ∞, as shown in Figure 1.
Fig. 1.
Specification of joint probability function of (T1, T2)
2.2. Bayesian Estimation/Inference for Semi-parametric Shared Frailty Model
Let T1i be the time to the non-terminal event, T2i the time to the terminal event, Ci a (right) censoring time and xi a p × 1 vector of covariates for the ith subject in an i.i.d sample of size n. Consider the following specification for hazard functions (1)-(3):
| (5) |
| (6) |
| (7) |
where γi is a subject-specific shared frailty, taken to be distributed independently of xi, and for g ∈ {1, 2, 3}, h0g is an unspecified baseline hazard function and βg is a vector of p log-hazard ratio regression parameters.
Two features of models (5)-(7) are worth noting. First, the shared frailty is taken to influence each of the hazards in the same multiplicative way. This is precisely analogous to the use of a subject-specific random intercept in mixed effects models as a mechanism for inducing dependence among longitudinal measures. As such, dependence that is induced between T1 and T2 by the shared frailty is strictly positive. Second, the conditional hazard for death given that a readmission event has occurred is assumed to be Markov with respect to the timing of the readmission event; that is, h3(·) does not depend on t1i. Throughout this paper, therefore, we refer to the model specified by (5), (6) and (7) as the Markov model.
That the risk of death following readmission in the Markov model is taken to be independent of the timing of readmission could be viewed as restrictive. An alternative specification is to model the risk of death following readmission as a function of the sojourn time. Specifically, retaining models (5) and (6), consider modeling h3(·) as follows:
| (8) |
Collectively, we refer to the model specified by (5), (6) and (8) as the semi-Markov model.
Under either the Markov model or the semi-Markov model, estimation and inference could proceed without explicit specification of the three baseline hazard functions, h0g(·) for g ∈ {1, 2, 3}. In the Bayesian paradigm, however, one is required to provide an explicit representation. Our strategy is to parameterize (5)-(8) by taking each of the three log-baseline hazard functions to be a mixture of piecewise constant functions (Haneuse, Rudser, and Gillen, 2008). Towards this, for each transition g ∈ {1, 2, 3}, let sg,max denote the largest observed event time. Then, consider the finite partition of the relevant time axis into Jg + 1 disjoint intervals: 0 < sg,1 < sg,2 < … < sg,Jg+1 = sg,max. For notational convenience, let Ig,j = (sg,j−1, sg,j] denote the jth partition. For given a partition, sg = (sg,1, …, sg,Jg+1), we assume the log-baseline hazard functions is piecewise constant:
| (9) |
where I(·) is the indicator function and sg,0 ≡ 0. Note, this specification is general in that the partitions of the time axes differ across the three hazard functions.
2.3. Observed Likelihood
For the ith individual, the observed data are D = {Y1i, Y2i, δ1i δ2i, xi}, where Y1i = min(T1i, T2i, Ci), δ1i = I(T1i ≤ min(T2i, Ci)), Y2i = min(T2i, Ci), and δ2i = I(T2i ≤ Ci). In the context of the motivating pancreatic cancer application, in which all observations were administratively censored at 90 days (see Section 3.1 below), Table 1 summarizes the four possible scenarios for outcome information.
Table 1.
Observed outcome information in the pancreatic cancer application. Note, administrative censoring was at 90 days post-discharge.
| (Y1i, Y2i) | (δ1i, δ2i) | N | |
|---|---|---|---|
| Readmitted and censored prior to death | (T1i, Ci) | (1, 0) | 2,213 |
| Dead following readmission | (T1i, T2i) | (1, 1) | 2,254 |
| Dead without readmission | (T2i, T2i) | (0, 1) | 7,505 |
| Censored prior to readmission or death | (Ci,Ci) | (0, 0) | 4,079 |
The derivation of the observed data likelihood function follows the formulation of the joint density of (T1, T2) in the context of bivariate survival modeling (Cox and Oakes, 1984, Chapter 10) and the multistate modeling (Putter et al., 2007; Xu et al., 2010; Barrett et al., 2011). The detailed derivation of the observed data likelihood function is provided in Supplemental material B. In this section, we present the grouped data representation of the observed likelihood function. Let and denote the risk sets consisting of individuals who are at risk for both of the readmission and death events at times s1,j−1 and s2,k−1, respectively (i.e. those who have not experienced either event). Also, let denote the risk set of individuals who have experienced the readmission event prior to s3,l−1 and are at risk for the death event at time s3,l−1. Further, let denote the set of indices of individuals who experience the transition g in the interval Ig,j, g ∈ {1, 2, 3}. Finally, let γ = (γ1, …, γn)⊺ and λg = (λg,1, …, λg,Jg+1). In terms of the disjoint intervals, the observed data likelihood, L(β1, β2, β3, λ1, λ2, λ3), has the following computationally convenient form:
| (10) |
where
2.4. Prior Distributions
To complete the Bayesian specification we outline priors for the unknown parameters. For regression parameters βg, we adopt a non-informative flat prior on the real line. For the subject-specific frailties, we adopt the standard convention of assuming the γi arise from some common distribution, specifically a gamma distribution denoted by (parameterized so that E(γi) = 1 and V (γi) = θ). In the absence of direct knowledge on the variation in the subject-specific frailties, we adopt a hyperprior for the precision 1/θ.
For the log-baseline hazard functions, given by (9), given the partition of the time scale sg, one could assign independent priors to each of the Jg + 1 components of λg. However, λ(·) is likely a smooth function over time and, as such, the components of λg are unlikely to be independent of each other a priori. Instead we view specification of a prior for the components of λg as a one-dimensional spatial problem and model dependence via a Gaussian intrinsic conditional autoregression (ICAR) (Besag and Kooperberg, 1995). The ICAR formulation specifies that λg jointly follows a (Jg + 1)-dimensional multivariate normal (MVN) distribution:
| (11) |
where μλg is the overall (marginal) mean, the overall variability in λg,j’s. The details on the ICAR specification including the expression of Σλg are provided in Supplemental material C. In the absence of prior information on the values of μλg and , we introduce hyperpriors on these parameters and update them using Gibbs sampling. Specifically, a flat prior on the real line is adopted for μλg and a conjugate distribution is adopted for the precision .
The MVN-ICAR specification (11) conditions on a fixed number of splits, Jg and partition, sg. In practice, one could perform sensitivity analyses with respect to the partition, to examine its influence on estimation and inference. Rather than doing so, we treat the partition as random, assign a prior and update the ‘unknown’ partition in our computational scheme. Specifically, a priori we take Jg, the number of splits in the partition, to be Poisson distributed with rate parameter, αg. Conditional on the number of splits, we take the split positions sg to be the even-numbered order statistics of 2Jg + 1 points uniformly distributed on [0, sg,max] (Green, 1995). This strategy of using even-numbered order statistics is adopted to prevent the splits from being too close together, which helps avoid having intervals contain only a few or no events. Jointly, the priors for Jg and sg form a time-homogeneous Poisson process prior for the partition (McKeague and Tighiouart, 2000; Haneuse et al., 2008).
To summarize, our prior choices are, for g ∈ {1, 2, 3}:
and
Finally, we note that αg, ag, bg, cλg (see Supplemental material C), ψ, and ω are hyperparameters that require specification. In practice, as with all hyperprior specification, analysts may elicit values from subject-matter experts and/or perform sensitivity analyses to examine the influence of specific choices.
2.5. Computational Scheme
For fixed J1, J2 and J3, the unknown parameters in the likelihood given by (10) together with the MVN-ICAR specifications for the baseline hazard functions are:
To perform posterior estimation and inference, we use a random scan Gibbs sampling algorithm to generate samples from the full posterior distribution. In the resulting MCMC scheme, there are a total of 17 updates/moves. For fixed J1, J2 and J3, the components of φ(J1, J2, J3) are updated by either exploiting conjugacies in the full conditionals or via Metropolis-Hastings steps. Updating J1, J2 and J3 requires a change in the dimension of the parameter space; a reversible jump MCMC Metropolis-Hastings-Green (MHG) algorithm was developed and implemented (Green, 1995). A detailed description of the complete algorithm, together with all necessary full conditional posterior distributions, is provided in Supplemental material A. The algorithm has been implemented in the SemiCompRisks package for R (R Development Core Team, 2012), available from the Comprehensive R Archive Network (CRAN, http://cran.r-project.org).
2.6. Within-Subject Dependence
As outlined in the introduction, the fundamental challenge in the analysis of semi-competing risks data is the non-identifiability of the marginal distribution of the non-terminal event. To overcome this challenge, statistical methods exploit observed information on the within-subject dependence between T1 and T2 by adopting some structure for the dependence. However dependence is structured, it is desirable to have interpretable measures of dependency that can be reported along with results directly from the models. For our proposed model/prior specification, dependence is captured by several components. One component, which can be used as a measure of dependence, is the variance parameter θ in the gamma prior for the subject-specific frailties (see Section 2.4); if θ > 0, then dependence between T1 and T2 is induced marginally, when one integrates over the distribution of the frailties. A second measure, that can be used for the Markov model defined in Section 2.2, is the so-called explanatory hazard ratio (EHR) = h3(t2|t1)/h2(t2) (Clayton, 1978; Xu et al., 2010). Intuitively, the EHR describes how the risk of death changes over time, given that a readmission event occurred at time t1. If the risk of death is not influenced by the risk of readmission (i.e. T1 and T2 are independent), the EHR is equal to 1 for t2 > 0. For the Markov model specified by equations (5)-(7), the EHR is
| (12) |
for t2 > t1. We refer to this expression as the conditional EHR, since the hazards in the numerator and denominator both condition on the individual-specific frailty, γ. We see that, given the Markov structure adopted for h3(t2|t1), the induced conditional EHR does not depend on t1. Nevertheless, the interpretation is conditional on t1 in the sense that expression (12) holds for all t2 > t1 for all fixed t1 > 0. Beyond this, we see that the conditional EHR remains a relatively complex function of t2, the value of x and the interplay between the influence of x on the hazard of death given that a readmission has occurred (i.e. β3) versus when a readmission has not occurred (i.e. β2). Unfortunately however, there is no obvious interpretable analogue of expression (12) for the semi-Markov model defined by (5), (6), and (8), because h2(·) and h3(·) are defined on different time scales for this model.
Within the developed Bayesian computational framework, estimation and the quantification of uncertainty for the conditional EHR follows directly by evaluating their expressions at each scan of the MCMC scheme. In practice, estimates and 95% credible intervals for both measures of dependence would be reported graphically, as a function of time, with several curves representing different covariate combinations of interest.
2.7. Prediction
A key benefit of the proposed Bayesian framework is the ease with which predictions for T1 and T2 can be produced. Specifically, the posterior predictive density for a future observation (, ) is given by:
| (13) |
where θ ∈ Θ denotes a set of all of the unknown model parameters, with the exception of γ, and π(θ|D) and π(γ) are the joint posterior density of θ and the probability density function of γ, respectively. Supplemental material B provides an expression for the full joint probability density function f(t1, t2|θ, γ) based on the model specification in Sections 2.2-2.4. From expression (13), the posterior predictive distribution can be viewed as the posterior expectation of the joint probability function and can, therefore, be directly incorporated into the Gibbs sampling scheme. In particular, given x, we can predict any joint probability involving the two event times such as for and for .
3. Application
As outlined in Section 1, the scientific context that motivated the work is as follows:
the study of hazard models including an investigation of risk factors for hospital readmission among patients diagnosed with pancreatic cancer (specifically, readmission following discharge from the initial hospitalization at which the diagnosis was first given),
the measure of the dependence between the time to readmission and death,
the joint prediction for the risk of readmission and death for a given covariate profile.
Following a description of pancreatic cancer data, we provide results from the semi-competing risks data analysis using our proposed Bayesian framework.
3.1. Pancreatic Cancer Data
The available data consist of information from Medicare Part A on 100% of Medicare enrollees from 01/2005 to 11/2008. During this period a total of 16,051 individuals aged 75 years or older were: (i) hospitalized with a diagnosis of pancreatic cancer, (ii) did not undergo any pancreatic cancer specific procedures (i.e. their disease was sufficiently advanced that curative treatment was not a viable option), and (iii) were subsequently discharged to home, home-care, an intermediate care facility (ICF) or a skilled nursing facility (SNF), or a hospice.
In our analyses, patients were considered at risk for hospital readmission and death from the date of discharge (t=0). Subsequently, as outlined in Table 1, patients were classified into one of four outcome groups, depending on whether or not a readmission and/or death event was observed. For both outcomes, we (administratively) censored observation time at t=90 days since, when taken as a proxy measure for quality of care, scientific interest typically lies in post-discharge readmission within a relatively short time frame (Centers for Medicare and Medicaid Services, 2012).
Towards understanding determinants of risk of readmission, we considered the following covariates: gender (0/1=female/male), age (standardized so that age ‘zero’ corresponds to an actual age of 82 years and so that a one-unit increment corresponds to 5 years), race (0/1=white/non-white), length of initial hospital stay (0/1 = /> 2 weeks), discharge destination (factored, with levels: home (referent), home-care, ICF/SNF, and hospice) and a comorbidity risk score (factored, with levels: 0–1 (referent), 2–3, and 4+). The latter was calculated by counting the number of diagnosis codes given during the initial hospitalization from a list of 27 disease/disorders related to prognosis following hospital discharge.
3.2. Analyses and Specification of Hyperparameters
The main analyses presented here are those that jointly analyze readmission and death, using the proposed Bayesian framework for semi-competing risks data. For illustrative purposes, we also present univariate Bayesian analyses of readmission and death; for readmission we (inappropriately) treat death as an independent censoring mechanism. Hereafter, we call these the univariate data analyses which assume independence between T1 and T2.
As outlined in Section 2.4, the framework requires specification of a number of hyperparameters. For the number of splits, Jg, we consider three values for each Poisson rate parameter: αg=5, 20 and 50, for g ∈ {1, 2, 3}. For the MVN-ICAR specification we set cλg=1, indicating strong a priori spatial dependence between adjacent time intervals. For the precision components and θ−1, we set (ag, bg)=(ψ,ω)=(0.7, 0.7). This choice corresponds to an induced prior distribution for all variance components, and θ, with a median of 1.72 and 95% of central mass between 0.23 and 156. While the results presented below correspond to these specific choices, Supplemental material E provides detailed sensitivity analyses investigating the impact of alternative choices under Markov model. Specifically, we considered the impact of setting cλg=0.5; setting (ag, bg)=(0.2, 0.2) and (0.5, 0.01); and, setting (ψ, ω)=(0.2, 0.2) and (0.5, 0.01).
For both sets of univariate data analyses we considered estimation and inference via a Bayesian analysis of the Cox model that uses the same parameterization of the baseline hazard function as that introduced in Section 2.2, as well as the same values for the hyperparameters specified for the semi-competing risks data analysis (i.e. α = 20, c = 1, and (a, b) = (0.7, 0.7)). We also considered estimation and inference via maximum partial likelihood estimation (MPL) of the Cox model (Cox, 1975).
Results for the Bayesian analyses, both the univariate and joint semi-competing risks data analyses, are based on samples from the joint posterior distribution obtained from three independent reversible jump MCMC chains. Each chain was run for 2 million iterations, with the first half taken as burn-in. Convergence of the Markov chains was assessed via visual inspection of mixing in trace plots as well as through the calculation of the potential scale reduction factor (Gelman et al., 2004). For the latter, a conservative threshold of 1.05 was adopted. For the semi-competing risks data analyses, the overall acceptance rates for the Metropolis-Hastings steps and Metropolis-Hastings-Green steps in the reversible jump MCMC scheme ranged between 40-50%, indicating that the algorithm is relatively efficient.
3.3. Results: Hazard Model - Regression Parameters and Baseline Hazard Functions
Table 2 provides posterior median and 95% credible intervals (CI) for hazard ratio (HR) parameters from the (separate) Bayesian univariate data analyses of readmission and death, and the semi-competing risks data analysis via the proposed Bayesian framework, setting the Poisson rate parameter to α and αg to 20 throughout. While not presented here, results for the regression coefficients were essentially equivalent across different values of αg/α, cλ g, (ag, bg), and (ψ, ω) (see Supplemental material E), or when estimation and inference was based on MPL (see Supplemental material F). For results based on the semi-competing risks data analysis, it is worth emphasizing the conditional interpretation of regression coefficients in the proposed framework. Specifically from models (5)-(8), we see that interpreting βg, or exp(βg), requires conditioning on the subject-specific frailty, γi. This is in contrast to the interpretation of the parameters in our univariate data analyses, in which no such conditioning is performed. We note that this difference is analogous to the differences in interpretations between regression coefficients in generalized linear mixed models for repeated measures data and regression coefficients from marginal models that are estimated via, say, generalized estimating equations.
Table 2.
Posterior medians (PM) and 95% credible intervals (CI) for hazard ratio parameters from (i) univariate Bayesian analyses of readmission and death, separately, and (ii) joint analyses based on the proposed Bayesian framework for semi-competing risks data. Results are based on setting the Poisson rate parameters α and αg, g ∈ {1,2,3}, to 20 for all MVN-ICAR specifications of baseline hazard functions.
| Univariate data analyses | Semi-competing risks data analysis | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Markov model for h3(·) | semi-Markov model for h3(·) | ||||||||
| Readmission | Death | Readmission | Death prior to readmission |
Death after readmission |
Readmission | Death prior to readmission |
Death after readmission |
||
|
|
|||||||||
| PM (95% CI) | PM (95% CI) | PM (95% CI) | PM (95% CI) | PM (95% CI) | PM (95% CI) | PM (95% CI) | PM (95% CI) | ||
| Comorbidity | 0-1 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| indexa | 2-3 | 1.04 (0.97, 1.12) | 1.00 (0.95, 1.05) | 1.03 (0.96, 1.12) | 0.99 (0.93, 1.05) | 0.99 (0.89, 1.10) | 1.03 (0.96, 1.11) | 0.99 (0.92, 1.06) | 0.98 (0.89, 1.11) |
| ≥ 4 | 1.24 (1.15, 1.35) | 1.13 (1.07, 1.19) | 1.26 (1.16, 1.37) | 1.15 (1.07, 1.23) | 1.07 (0.95, 1.21) | 1.26 (1.16, 1.38) | 1.16 (1.08, 1.25) | 1.08 (0.96, 1.23) | |
| Race | White | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Non-white | 1.27 (1.17, 1.37) | 0.94 (0.89, 1.00) | 1.27 (1.17, 1.39) | 0.86 (0.79, 0.93) | 1.13 (1.01, 1.28) | 1.28 (1.17, 1.40) | 0.86 (0.79, 0.93) | 1.15 (1.02, 1.28) | |
| Gender | Female | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Male | 1.06 (1.00, 1.13) | 1.24 (1.19, 1.30) | 1.10 (1.03, 1.18) | 1.30 (1.23, 1.38) | 1.22 (1.12, 1.34) | 1.11 (1.05, 1.19) | 1.32 (1.25, 1.40) | 1.25 (1.14, 1.37) | |
| Ageb | 0.88 (0.86, 0.91) | 1.05 (1.03, 1.07) | 0.87 (0.84, 0.90) | 1.07 (1.04, 1.10) | 1.08 (1.03, 1.13) | 0.87 (0.84, 0.90) | 1.07 (1.04, 1.10) | 1.08 (1.03, 1.13) | |
| Care after | Home | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| discharge | Home care | 1.17 (1.09, 1.26) | 1.38 (1.29, 1.48) | 1.21 (1.12, 1.31) | 1.53 (1.39, 1.69) | 1.23 (1.10, 1.38) | 1.24 (1.14, 1.34) | 1.57 (1.43, 1.74) | 1.28 (1.14, 1.43) |
| ICF/SNF | 0.76 (0.69, 0.83) | 2.39 (2.25, 2.54) | 0.82 (0.75, 0.91) | 3.46 (3.19, 3.79) | 1.76 (1.54, 2.01) | 0.85 (0.77, 0.94) | 3.61 (3.31, 3.97) | 1.84 (1.60, 2.11) | |
| Hospice | 0.15 (0.12, 0.17) | 5.11 (4.85, 5.39) | 0.18 (0.15, 0.21) | 8.96 (8.25, 9.86) | 3.08 (2.38, 3.99) | 0.19 (0.15, 0.22) | 9.69 (8.82, 10.76) | 3.35 (2.59, 4.28) | |
| Hospital stay | ≤ 2 weeks | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| > 2 weeks | 1.21 (1.09, 1.34) | 1.05 (0.98, 1.12) | 1.25 (1.12, 1.39) | 1.09 (1.00, 1.20) | 0.89 (0.76, 1.05) | 1.27 (1.13, 1.42) | 1.11 (1.00, 1.22) | 0.91 (0.78, 1.06) | |
Number of diagnosis codes given during the initial hospitalization from a list of 27 disease/disorders related to prognosis following hospital discharge.
Standardized so that a one-unit contrast corresponds to a difference of 5 years.
Comparing the results from the univariate data analyses for the readmission outcome (first column) to those based on the semi-competing risks data analyses (third and sixth column) we find little difference. Since the results are very similar between Markov and semi-Markov model, hereafter, we refer to the results from Markov model for semi-competing risks data analysis. In both sets of analyses, there is evidence of increased risk for readmission associated with a high comorbidity index, a long (initial) hospital stay, non-white race, male gender, and discharge to home care. However, the semi-competing risks data analysis reveals nuance in how several covariates confer risk for death. For example, while the univariate data analysis indicates decreased risk associated with non-white race for death (HR 0.94; 95% CI 0.89, 1.00) the semi-competing risks data analysis of readmission and death reveals that the association between non-white race and death is in fact stronger among those individuals who have not been readmitted (HR 0.86; 95% CI 0.79, 0.93) and that there is evidence of the increased risk of death for an individual with non-white race after readmission (HR 1.13; 95% CI 1.01, 1.28). In univariate data analyses, being discharged to hospice lowers the risk of being readmitted (HR 0.15; 95% CI 0.12, 0.17) compared to being discharged to home, but increases the risk of death (HR 5.11; 95% CI 4.85, 5.39). In semi-competing risks data analysis, being discharged to hospice compared to home substantially increases the risk of death prior to readmission (HR 8.96; 95% CI 8.25, 9.86) and also increases the risk of death after readmission (HR 3.08; 95% CI 2.38, 3.99).
Figure 2 provides results for the baseline hazard functions, as formulated in Sections 2.2 and 2.4. While not presented here, the uncertainties (posterior standard deviations) associated with Bayesian methods are provided in Supplemental material D and could be used to construct the pointwise 95% credible intervals. From Section 3.1, the baseline hazard functions in all of our models correspond to a population of 82 year old, white females, who had at most one comorbidity (from among the 27 pre-specified conditions), whose hospital stay was less than 2 weeks and were discharged to their own homes. Further, for the semi-competing risks data analysis, the interpretation of the baseline hazard function also conditions on the subject-specific frailty of γ=1.
Fig. 2.
Estimates of the log-baseline hazard functions (baseline covariate profile: 82 years old, white female, at most 1 comorbidity index, less than 2 weeks of hospital stay at initial hospitalization, and discharge to home); estimates from univariate data analyses are provided in panels (a) and (b); results from the proposed Bayesian framework for semi-competing risks data are provided in panels (c), (d), and (e) (Markov), and (f), (g), and (h) (semi-Markov). Three sets of data analyses were performed, with values of α and αg of 5, 20 and 50 adopted for all Poisson rate parameters. Also shown for the univariate data analyses are the smoothed Nelson-Aalen (univariate, frequentist) estimate of the baseline hazard function.
In general, the estimated log-baseline hazard functions are very similar between Markov and semi-Markov model except h03. It is noted that time since readmission is taken as the time scale for h03 under semi-Markov model as seen in Figure 2 (h). We refer to the results from Markov model for semi-competing risks data analysis hereafter. From the top row of Figure 2 we see that, from both the univariate and joint semi-competing risks data analyses, the baseline hazard function for readmission is decreasing over time. However, the baseline estimate from the univariate data analyses indicates lower overall risk for readmission than that based on the semi-competing risks data analysis. This is likely due to the inappropriate treatment of death (i.e. as an independent censoring mechanism) in the univariate data analyses. From the second and the third row, we again find that the semi-competing risks data analysis reveals differences in the risk of death depending on whether or not a readmission event has occurred. Specifically, the log-baseline hazard for death prior to readmission is slowly decreasing around −5.6; however, the log-baseline hazard function for death given that a readmission event has occurred is considerably higher and generally decreases faster over time.
From Figure 2 we also see that, for our pancreatic cancer data, estimation of the log-baseline hazard functions for readmission is relatively robust to the specific choice of the Poisson rate parameter (α for the univariate data analysis and αg, g = 1, 2, 3, for the semi-competing risks data analysis). Similarly, from panels (b), (d) (e), (g), and (h), estimation of the log-baseline hazard function for death is relatively robust to the choice of α or αg. In addition, we consider four different combinations of the covariate vector, x, and the covariate profiles are given in Table 3. In Supplemental material D, we provide estimates of the log-hazard functions using Markov model for the four individuals.
Table 3.
Covariate profiles of the four different individuals considered for the EHR and the posterior predictive probability
| Comorbidity index |
Race | Gender | Age | Care after discharge |
Hospital stay | |
|---|---|---|---|---|---|---|
| Baseline | 0-1 | White | Female | 82 | Home | ≤ 2 weeks |
| Subject 1 | ≥ 4 | Non-white | Male | 92 | Home care | > 2 weeks |
| Subject 2 | 0-1 | Non-white | Female | 92 | Home | ≤ 2 weeks |
| Subject 3 | ≥ 4 | White | Male | 82 | Hospice | > 2 weeks |
3.4. Results: Measure of Within-Subject Dependence
As described in Section 2.6, within-subject dependence between the readmission and death events is captured by several components of the model. The posterior median and 95% CI for the variance component θ are 0.34 and (0.25, 0.44), respectively, indicating relatively low variation in the subject-specific frailties across subjects. Furthermore, we provide posterior medians and 95% credible intervals for the subject-specific frailty, γi, for a random sample of 30 individuals (ordered by posterior median), based on the analysis with αg=20 in Supplemental material D. Across these 30 individuals, there does not appear to be great variation in the posterior medians with the values ranging from 0.32 to 1.35.
Figure 3 presents pointwise posterior median and 95% credible intervals for the conditional EHR from the Markov model, given by expression (12), for the four individuals defined in Table 3. As described in Section 2.6, the EHR describes how the risk of death changes over time given that the readmission event has occurred. For example, in panel (a), a value of conditional EHR for the Baseline subject is around 2.8 at 4 days after discharge, indicating that the occurrence of readmission substantially increases the risk of death (2.8 times) for this subject at day 4 following discharge. For each individual the conditional EHR is generally highest immediately after discharge, decreases over time and significantly increases at 88 day mark, indicating a strong influence of readmission on death soon after discharge. Further, while the pointwise 95% credible intervals do not correspond to a 95% credible band for the entire curve, in panels (a) and (c) they exclude a value of EHR=1.0 through 90 days after discharge, implying the significant dependence between T1 and T2 for a population of corresponding covariate profiles.
Fig. 3.
Pointwise posterior median and 95% credible intervals for the conditional explanatory hazard ratio (EHR) from the Markov model, the ratio of hazards for death after and prior to readmission given by expression (12) in Section 2.6. Shown are results for the four individuals defined in Table 3.
3.5. Results: Posterior Predictive Distribution
In Figure 4, we provide the posterior predictive distribution for the four individuals defined in Table 3. Among the four individuals, the subject 1 in panel (b) has the highest posterior predictive probability of dying following readmission through 90 days after discharge. On the other hand, the subject 3 in panel (h) exhibits the most rapid increase in the posterior predictive probability for death without readmission in first 30 days after discharge. This observation is supported by the results from panel (d) of Figure 3, where the conditional EHR for the subject 3 is generally smaller than 1.0 indicating a higher risk of death without readmission than that following readmission. More specifically, we can see that the subject 3 has posterior predictive probability of 0.02 of dying no later than 50 days and being readmitted within 30 after discharge, while he has the much higher posterior predictive probability (0.83) of dying no later than 50 days without readmission. In contrast, subject 1’s posterior predictive probability of dying within 50 days and being readmitted no later than 30 days after discharge is approximately 0.19 and that without readmission is 0.26.
Fig. 4.
Posterior predictive distribution of (T1, T2) for four individuals defined in Table 3; panels (a)-(d) show the posterior predictive distribution F(t1, t2) for t1 ≤ t2; panels (e)-(h) provide the posterior predictive distribution F∞(t2).
4. Discussion
In this article we have developed a Bayesian framework that permits the researcher to simultaneously address the three important scientific goals in the context of semi-competing risks data: the estimation of regression parameters, the characterization of within-subject dependence between the two event times, and the prediction of outcomes. To our knowledge, this is the first framework that provides the unified solution to the analysis of semi-competing risks data. The proposed framework allows analysts to take advantage of the well-known benefits of the Bayesian paradigm including the ability to incorporate substantive prior information, the automated quantification of uncertainty and prediction, the prescriptive nature of computation for complex problems, the ease with which sensitivity analyses may be structured and the straightforward nature of extending the model to include additional structure/random effects. In particular, as illustrated in Figures 3, one can directly characterize uncertainty in components/features of the model that are specifically pertinent to the semi-competing risks nature of the data. Our proposed Bayesian framework also enables the straightforward prediction through the posterior predictive distribution as shown in Figure 4. Note, while Figures 3 and 4 are relatively easily produced within the proposed framework, they cannot be produced by any current frequentist methods for semi-competing risks data.
In this paper we have presented Bayesian methods for both a Markov and a semi-Markov illness-death model. The fundamental difference between the two models is in the time scales used to index risk of death following readmission. Under the Markov model, expression (7) considers the time-since-discharge; under the semi-Markov model, expression (8) considers the time-since-readmission. In the multi-state modeling literature, use of the time-since-discharge as the time scale is referred to as the ‘clock forward’ approach while use of time-since-readmission is referred to as the ‘clock reset’ approach (Putter et al., 2007). A consequence of having different time scales is that the models differ in the interpretation of how risk of death following readmission is conferred. Furthermore, the interpretation of regression coefficients differ. Under the Markov model, exp{β3} is interpreted as a hazard ratio which holds time-since-discharge fixed, while under the semi-Markov model, the interpretation of exp{β3} holds the time-since-readmission fixed. In practice, if scientific interest lies solely with the non-terminal event, these differences may not be relevant; the model for h1(·) and interpretation of its regression coefficients is the same in the two models. If, however, interest lies in understanding the broader experience of patients post-discharge, these differences may influence the choice that researchers make. For relatively complex models, modeling assumptions need to be well-thought out. For the frailties, we note that their purpose in the adopted model formulation is to induce correlation among the outcomes within a subject. In this sense, they serve the same purpose as random effects in a mixed effects model: there is some latent characteristic that is subject-specific that operates on their outcomes (in our instance through the three hazard functions). We used a gamma distribution in part because it is a relatively common choice in the literature and also because of computational convenience.
With respect to the motivating study of time to hospital readmission among patients with cancer of the pancreas, the proposed Bayesian framework shows evidence of increased risk for readmission associated with a high comorbidity index, a long hospital stay at initial hospitalization, non-white race, male gender, and discharge to home care. While relatively complex, the proposed framework helps avoid the difficult task of fixing the number of the time partitions and their positions by updating them within the MCMC sampling scheme. This results in a notable smoothing effect in the estimation of the baseline hazard functions (see Figure 2). While the global measure of dependence between time to readmission and time to death appears to be quite small (), our proposed Bayesian solution has the ability to provide the within-subject dependence (EHR) over time along with a quantification of uncertainty. The EHR is a measure of dependence between the two event times, one that arises naturally from the specification of the Markov illness-death model. Characterizing and presenting dependence in various ways can help guide discussions among collaborators about how best to model data and about where current models could be improved. The results reveal substantial variation in the dependence structure across differing covariate profiles (see Figure 3). For the subjects we considered, the posterior distribution of the conditional EHR provides strong evidence of dependence between time to readmission and time to death. Using our proposed Bayesian approach, the posterior predictive distribution of time to readmission and time to death is easily obtained via Gibbs sampler (shown in Figure 4) and it can be used to calculate the posterior predictive probability of being readmitted for a future patient.
Finally, although scientific interest at the outset of this work focused on readmission, taking the marginal distribution of T1 to be an inferential target is hugely problematic. First, as pointed out earlier, estimation of the marginal distribution of T1 is solely identified by semi-competing risks data by adopting additional structure/assumptions that cannot be empirically verified. Second, as others have argued (Andersen and Keiding, 2012; Farewell and Tom, 2012), the interpretation of the marginal distribution of T1 requires consideration of a world in which patients do not die. Fortunately, illness-death models provide a framework within which semi-competing risks data can be analyzed with the constituent components being interpretable (i.e. the transition-specific hazards). Within this framework, we adopted the conventional assumption that T1 = ∞ for T1 > T2 and employed a formulation of the observed data likelihood that has been widely accepted for the semi-competing risks data analysis in context of the multi-state models (Wang, 2003; Xu et al., 2010). As mentioned in the Introduction, this is not the only approach that has been considered in the literature. Recently, Zeng et al. (2012) and Zhang et al. (2013) proposed a general framework for the analysis of semi-competing risks data that requires the specification of an additional model; one for the lifetime probability of the non-terminal event. Given the fundamental challenge of never being able to observe a non-terminal event after the terminal event has occurred, the extent to which one approach to handling non-identifiability of S1(t1) is better over another will likely be context specific. Our perspective is that researchers benefit from a broad range of statistical tools, the assumptions of which can be considered and evaluated in the light of the actual data. With this in mind we are currently pursing two related avenues of research. First is a detailed investigation of when results based on a näive model may be expected to exhibit bias. In our application, despite the strong force of mortality, results based on the proposed framework for readmission did not differ substantially from those based on a näive model. Second is a broader evaluation and comparisons of the assumptions used to induce identifiability. When bias is expected in näive analyses, guidance on how to choose between alternative methods will be crucial as researchers conduct analyses of semi-competing risk data.
Supplementary Material
Acknowledgements
We would like to thank Dr. Yun Wang at Harvard School of Public Heath for the assistance and consultation on the Medicare pancreatic cancer data set. We are also grateful for helpful comments from the Dr. R. Chandler (Joint Editor), an Associate Editor and two referees. This work was supported by National Cancer Institute grant (P01 CA134294-02) and National Institutes of Health grants (ES012044, K18 HS021991, R01 CA181360-01).
Contributor Information
Kyu Ha Lee, Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts, USA.
Sebastien Haneuse, Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts, USA.
Deborah Schrag, Dana-Farber Cancer Institute, Boston, Massachusetts, USA.
Francesca Dominici, Department of Biostatistics, Harvard School of Public Health, Boston, Massachusetts, USA.
References
- American Cancer Society . Cancer Facts & Figures 2011. 2011. [Google Scholar]
- Andersen PK, Keiding N. Interpretability and importance of functionals in competing risks and multistate models. Statistics in medicine. 2012;31(11-12):1074–1088. doi: 10.1002/sim.4385. [DOI] [PubMed] [Google Scholar]
- Barrett JK, Siannis F, Farewell VT. A semi-competing risks model for data with interval-censoring and informative observation: An application to the mrc cognitive function and ageing study. Statistics in Medicine. 2011;30(1):1–10. doi: 10.1002/sim.4071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag J, Kooperberg C. On conditional and intrinsic autoregressions. Biometrika. 1995;82(4):733–746. [Google Scholar]
- Centers for Medicare and Medicaid Services [accessed 09/2012];Hospital Inpatient Quality Reporting Program. 2012 http://www.cms.gov.
- Clayton D. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika. 1978;65(1):141–151. [Google Scholar]
- Cook R, Lawless J. Marginal analysis of recurrent and terminal events. Statistics in Medicine. 1997;16:911–924. doi: 10.1002/(sici)1097-0258(19970430)16:8<911::aid-sim544>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Cox D. Partial likelihood. Biometrika. 1975;62(2):269–276. [Google Scholar]
- Cox DR, Oakes D. Analysis of survival data. Vol. 21. Chapman & Hall/CRC; 1984. [Google Scholar]
- Farewell VT, Tom BD. The versatility of multi-state models for the analysis of longitudinal data with unobservable features. Lifetime data analysis. 2012;20:51–75. doi: 10.1007/s10985-012-9236-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine J, Jiang H, Chappell R. On semi-competing risks data. Biometrika. 2001;88:907–919. [Google Scholar]
- Fu H, Wang Y, Liu J, Kulkarni P, Melemed A. Joint modeling of progression-free survival and overall survival by a bayesian normal induced copula estimation model. Statistics in Medicine. 2012;32:240–254. doi: 10.1002/sim.5487. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin J, Stern H, Rubin D. Bayesian data analysis. CRC press; 2004. [Google Scholar]
- Ghosh D. Semiparametric inferences for association with semi-competing risks data. Statistics in Medicine. 2006;25:2059–2070. doi: 10.1002/sim.2327. [DOI] [PubMed] [Google Scholar]
- Ghosh D, Lin D. Nonparametric analysis of recurrent events and death. Biometrics. 2000;56:554–562. doi: 10.1111/j.0006-341x.2000.00554.x. [DOI] [PubMed] [Google Scholar]
- Ghosh D, Lin D. Marginal regression models for recurrent and terminal events. Statistica Sinica. 2002;12:663–688. [Google Scholar]
- Green P. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82(4):711–732. [Google Scholar]
- Haneuse SJ-P, Rudser K, Gillen D. The separation of timescales in Bayesian survival modeling of the time-varying effect of a time-dependent exposure. Biostatistics. 2008;9(3):400–410. doi: 10.1093/biostatistics/kxm038. [DOI] [PubMed] [Google Scholar]
- Hsieh J, Wang W, Ding A. Regression analysis based on semi competing risks data. Journal of the Royal Statistical Society, Series B. 2008;70:3–20. [Google Scholar]
- Ibrahim J, Chen M, Sinha D. Bayesian survival analysis. Wiley Online Library; 2005. [Google Scholar]
- Jiang H, Fine J, Chappell R. Semiparametric analysis of survival data with left truncation and dependent right censoring. Biometrics. 2005;61:567–575. doi: 10.1111/j.1541-0420.2005.00335.x. [DOI] [PubMed] [Google Scholar]
- Joshua V, Larry G, Brock O, Kevin S. Determinants of preventable readmissions in the united states: a systematic review. Implementation Science. 2010;5:88. doi: 10.1186/1748-5908-5-88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kneib T, Hennerfeind A. Bayesian semiparametric multi-state models. Statistical Modeling. 2008;8:169–198. [Google Scholar]
- Lakhal L, Rivest L, Abdous B. Estimating survival and association in semicompeting risks model. Biometrics. 2008;64:180–188. doi: 10.1111/j.1541-0420.2007.00872.x. [DOI] [PubMed] [Google Scholar]
- Liu L, Wolfe R, Huang X. Shared frailty models for recurrent events and terminal events. Biometrics. 2004;60:747–756. doi: 10.1111/j.0006-341X.2004.00225.x. [DOI] [PubMed] [Google Scholar]
- Lockhart A, Rothenberg M, Berlin J. Treatment for pancreatic cancer: Curgent therapy and continued progress. Gastroenterology. 2005;128:1642–1654. doi: 10.1053/j.gastro.2005.03.039. [DOI] [PubMed] [Google Scholar]
- McKeague I, Tighiouart M. Bayesian estimators for conditional hazard functions. Biometrics. 2000;56(4):1007–1015. doi: 10.1111/j.0006-341x.2000.01007.x. [DOI] [PubMed] [Google Scholar]
- Pan S, Yen H, Chen T. A Markov regression random-effects model for remission of functional disability in patients following a first stroke: a Bayesian approach. Statistics in Medicine. 2007;26:5335–5353. doi: 10.1002/sim.2999. [DOI] [PubMed] [Google Scholar]
- Peng L, Fine J. Regression modeling of semi-competing risks data. Biometrics. 2007;63:96–108. doi: 10.1111/j.1541-0420.2006.00621.x. [DOI] [PubMed] [Google Scholar]
- PLoS Medicine Editors Beyond the numbers: Describing care at the end of life. 2012 doi: 10.1371/journal.pmed.1001181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Putter H, Fiocco M, Geskus R. Tutorial in biostatistics: competing risks and multi-state models. Statistics in Medicine. 2007;26(11):2389–2430. doi: 10.1002/sim.2712. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2012. [Google Scholar]
- Sharples L. Use of the Gibbs sampler to estimate transition rates between grades of coronary disease following cardiac transplantation. Statistics in Medicine. 1993;12:1155–1169. doi: 10.1002/sim.4780121205. [DOI] [PubMed] [Google Scholar]
- van den Hout A, Fox J-P, Klein Entinky R. Bayesian inference for an illness-death model for stroke with cognition as a latent time-dependent risk factor. Statistical Methods in Medical Research. 2011;0(0):1–19. doi: 10.1177/0962280211426359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Hout A, Matthews F. Estimating dementia-free life expectancy for parkinson’s patients using bayesian inference and microsimulation. Biostatistics. 2009;10(4):729–743. doi: 10.1093/biostatistics/kxp027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W. Nonparametric estimation of the sojourn time distributions for a multipath model. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2003;65(4):921–935. [Google Scholar]
- Warren J, Barbera L, Bremner K, Yabroff K, Hoch J, Barrett M, Luo J, Krahn M. End-of-life care for lung cancer patients in the united states and ontario. Journal of the National Cancer Institute. 2011;103(11):853–862. doi: 10.1093/jnci/djr145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Kalbfleisch J, Tai B. Statistical analysis of illness-death processes and semi-competing risks data. Biometrics. 2010;66:716–725. doi: 10.1111/j.1541-0420.2009.01340.x. [DOI] [PubMed] [Google Scholar]
- Ye Y, Kalbfleisch J, Schaubel D. Semiparametric analysis of correlated recurrent and terminal events. Biometrics. 2007;63:78–87. doi: 10.1111/j.1541-0420.2006.00677.x. [DOI] [PubMed] [Google Scholar]
- Zeng D, Chen Q, Chen M-H, Ibrahim JG, et al. Estimating treatment effects with treatment switching via semicompeting risks models: an application to a colorectal cancer study. Biometrika. 2012;99(1):167–184. doi: 10.1093/biomet/asr062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng D, Lin D. Semiparametric transformation models with random effects for joint analysis of recurrent and terminal events. Biometrics. 2009;65:746–752. doi: 10.1111/j.1541-0420.2008.01126.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Chen M-H, Ibrahim JG, Zeng D, Chen Q, Pan Z, Xue X. Bayesian gamma frailty models for survival data with semi-competing risks and treatment switching. Lifetime data analysis. 2013;20:76–105. doi: 10.1007/s10985-013-9254-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.