Predictive polymer modeling reveals coupled fluctuations in chromosome conformation and transcription

Summary

A new level of chromosome organization, Topologically Associating Domains (TADs), was recently uncovered by chromosome-confirmation-capture (3C) techniques. To explore TAD structure and function, we developed a polymer model that can extract the full repertoire of chromatin conformations within TADs from population-based 3C data. This model predicts actual physical distances and to what extent chromosomal contacts vary between cells. It also identifies interactions within single TADs that stabilize boundaries between TADs and allows us to identify and genetically validate key structural elements within TADs. Combining the model’s predictions with high-resolution DNA FISH and quantitative RNA FISH for TADs within the X-inactivation center (Xic), we dissect the relationship between transcription and spatial proximity to cis-regulatory elements. We demonstrate that contacts between potential regulatory elements occur in the context of fluctuating structures rather than stable loops and propose that such fluctuations may contribute to asymmetric expression in the Xic during X inactivation.

Introduction

A fundamental question in biology is how genomes are folded in cell nuclei and how their three-dimensional organization influences biological functions, such as transcription. Thanks to the refinement of chromosome conformation capture (3C) techniques (reviewed in de Wit and de Laat, 2012), the fine scale three-dimensional structure of genomes is now starting to emerge. Investigations based on 5C and Hi-C (Dixon et al., 2012; Hou et al., 2012; Nora et al., 2012; Sexton et al., 2012) revealed that the genomes of metazoans are partitioned into topologically associating domains (TADs). These are submegabase-sized regions, within which the chromatin fiber has a particularly high propensity to interact. Remarkably, in mammals TAD positions appear to be conserved (Dixon et al., 2012), implying that they represent some fundamental organizing principle of the mammalian genome.

In addition, TADs may also provide the structural context for transcriptional regulation of genes by long-range elements such as enhancers. Indeed, most identified enhancer/promoter pairs are found to belong to the same TADs (Shen et al., 2012; Smallwood and Ren, 2013). Within single TADs, a fine-scale structural network appears to connect cell-type specific enhancers and CTCF, cohesin and Mediator binding sites (Phillips-Cremins et al., 2013). Disrupting the frontier between two TADs results in transcriptional mis-regulation within them due to the formation of ectopic contacts across the deleted boundary (Nora et al., 2012). This suggests that the three-dimensional clustering of regulatory sequences within TADs may be essential for the appropriate functional interactions between regulatory sequences (Andrey et al., 2013).

Due to the cell population-averaged nature of 5C and Hi-C data, it is unclear what TADs actually represent at the single cell level. Although single cell Hi-C was recently achieved (Nagano et al., 2013), this could not provide sufficient resolution to assess contact frequencies inside single TADs. Super-resolution imaging using fluorescent probes spanning several hundreds of kilobases across TADs revealed that they do differ in size and degree of clustering from one cell to another (Nora et al., 2012). However variation in their internal organization was not evaluated. The question arises at to whether TADs (and their internal structures) represent stable three-dimensional conformations of chromatin present in every cell within a population; or whether they are the result of averaging multiple possible chromatin conformations over millions of cells.

These two alternative scenarios have profoundly different implications for transcriptional regulation. In the first case, which would be compatible with the existence of stable enhancer/promoter chromatin loops between regulatory regions (Tolhuis et al., 2002) a functional enhancer within a TAD would stably engage physical contacts with a promoter in the context of a static chromatin configuration resulting in equivalent regulatory inputs in all cells, transcriptional control being delegated to the action of binding molecules. In the second case, enhancer/promoter contacts would rather emerge as probabilistic events in a fluctuating structural environment (Fudenberg and Mirny, 2012; Nora et al., 2013) and would provide variable regulatory stimulation in the cell population, potentially contributing to cell-to-cell transcriptional variability and control (Amano et al., 2009; Krijger and de Laat, 2013).

To characterize the chromatin structures underlying TAD organization at the single-cell level, we combine physical modeling with high-resolution 3D DNA FISH across the mouse X-inactivation center (Xic) region. We investigate the internal structures of the TADs containing Xist, the master regulator of X chromosome inactivation (XCI), and its antisense transcript, Tsix, which plays a key role in modulating Xist expression during mouse development and is believed to play an important role in the choice of which Xist allele will be expressed during random XCI. To reconstruct the full spectrum of chromatin conformations underlying the observed 5C contacts across this region, we simulate the thermodynamic ensemble of conformations of a physical polymer model with a Monte Carlo method, which reproduces the correct conformational fluctuations of the polymer, and identify the site-specific interactions that are able to recapitulate the experimentally observed contact frequencies. Our physical model predicts the distribution of distances between any two sites across a population of cells. This enables validation of the structural reconstruction of the 5C data, using high-resolution DNA FISH. We demonstrate that chromatin conformation within individual TADs is highly variable, though not random. TADs thus represent an average of multiple diverse conformations across the cell population. We propose that a small number of loci overlapping with cohesin/CTCF binding sites determine specific internal TAD structure and also contribute to shaping a boundary between adjacent TADs. We also test the model’s predictions by inducing a deletion at one such locus and measuring the resulting changes in 3D distances.

The model also predicts that the interactions of Tsix with two putative regulatory elements in its TAD (Linx and Chic1, Nora et al, 2012) only occur in a sub-population of cells at any one time. Using RNA FISH combined with DNA FISH and super-resolution microscopy we find that the transcriptional activity of Tsix is higher in the cell sub-population with the more interactive conformation. Thus, we demonstrate that structural fluctuations of chromatin conformation within TADs can contribute to transcriptional variability by stochastically modulating interactions between regulatory sequences. We propose that such fluctuations might play a role in ensuring asymmetric transcription of Tsix, and therfore of Xist, between the two X chromosomes at the onset of XCI.

Results

Structural modeling of 5C data

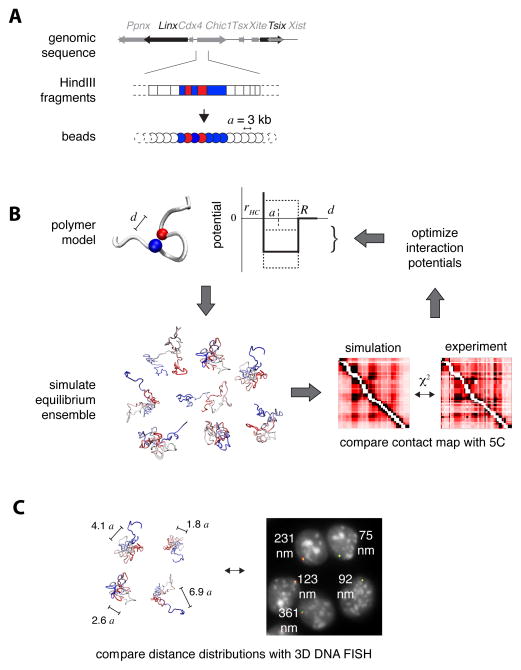
We set out to develop a modeling strategy that would enable us to define realistic thermodynamic ensembles of fiber conformations, which reproduce the contact frequencies experimentally observed in chromosome conformation capture datasets. The same computational scheme can be used to model 3C, 5C or Hi-C data; here we describe its application to 5C. We adopted a statistical interpretation of data, whereby 5C counts are considered to be proportional to the probability of two loci physically contacting each other within a cell population. To simulate the thermodynamics of the chromatin fiber, we represent it as a chain of identical beads separated by distance a (Figure 1A). The only assumption made initially is that a represents 3 kb of genomic sequence, which corresponds to the average size of HindIII restriction fragments in our 5C dataset (Nora et al., 2012) (Figure S1A). Thus, each restriction fragment can be mapped onto a sequence of adjacent beads according to its genomic location and length. The original 5C data, based on pairs of interacting forward/reverse restriction fragments, is thereby converted into a list of interacting pairs of “bead” sequences (Figure 1A, Figure S1B and supplementary model description in Data S1).

Figure 1. Physical modeling of the chromatin fiber.

A. Beads-on-a-string representation of the chromatin fiber. HindIII restriction fragments within the genomic region of interest are mapped onto sequences of adjacent beads in the model. The distance a between adjacent beads represents 3 kb.

B. Structural deconvolution of 5C contact frequencies. Each bead in the model interacts with other beads through a short-range interaction potential (thick line in the scheme), which acts when the three-dimensional distance d between the two beads is smaller than the interaction radius R, and repulses them if their distance is smaller than the hardcore radius r_HC. Given an initial set of interaction potentials, Monte Carlo sampling is performed to simulate the equilibrium ensemble of configurations of the fiber. Contact probabilities of this ensemble are then compared to experimental 5C contact frequencies by measuring their χ² distance, and interaction potentials are optimized (dashed lines in the scheme) to produce a new ensemble with better agreement with 5C. This procedure is iterated until the simulated contacts converge to the experimental 5C map.

C. The optimized ensemble of fiber configurations can be used to predict the physical distances between genomic loci and their distribution in the population of cells. This allows testing the model against single-cell based assays such as 3D DNA FISH.

To mimic interactions that may statistically favor (or disfavor) the colocalization of different parts of the chromatin fiber, each bead was allowed to interact with others via contact interaction potentials (Figure 1B) of range R with a hard-core repulsion at distance r_HC,. As no measurements are available to constrain the values of R and r_HC themselves, we adopted an unbiased approach and tested several values independently for the two parameters. Importantly, although the bead distance a was defined in terms of genomic length (a=3 kb), it was not defined in terms of physical length (i.e. nanometers) as all distances in the model can be expressed as multiples of a when comparing predicted contact frequencies with the 5C data. We thus left this parameter as temporarily undetermined, until further information could be provided by the DNA FISH (see below).

For any given choice of R and r_HC we optimized the strengths of interaction potentials between beads by using an iterative Monte Carlo scheme (Norgaard et al., 2008; see supplementary model description in Data S1) whereby the potentials are successively optimized until the contact probabilities predicted by the model (averaged over 5000 conformations of the fiber) converged to the experimental values, as judged by iterative χ² tests (Figure 1B). This procedure leads to a set of conformations that represent the equilibrium ensemble of the fiber (Metropolis et al., 1953). Our simulation thus enables deconvolution of the average contact frequencies measured by 5C, into the full set of chromatin conformations present within the cell population.

The conformation ensembles that our model produces can be used to predict structural statistical fluctuations in a formally rigorous framework. This has advantages over previous approaches that sought to determine average chromatin structures through mean-field approximations, and assumed that a single predominant structure is present in all cells (Baù and Marti-Renom, 2010; Kalhor et al., 2012; Umbarger et al., 2011). Notably, the fact that our simulation provides a quantitative output for 3D distances between pairs of loci, as well as for their variability across the population, means that an alternative experimental single-cell technique can be used to test it, such as DNA FISH (Figure 1C).

The internal structure of the Tsix TAD is highly variable between cells

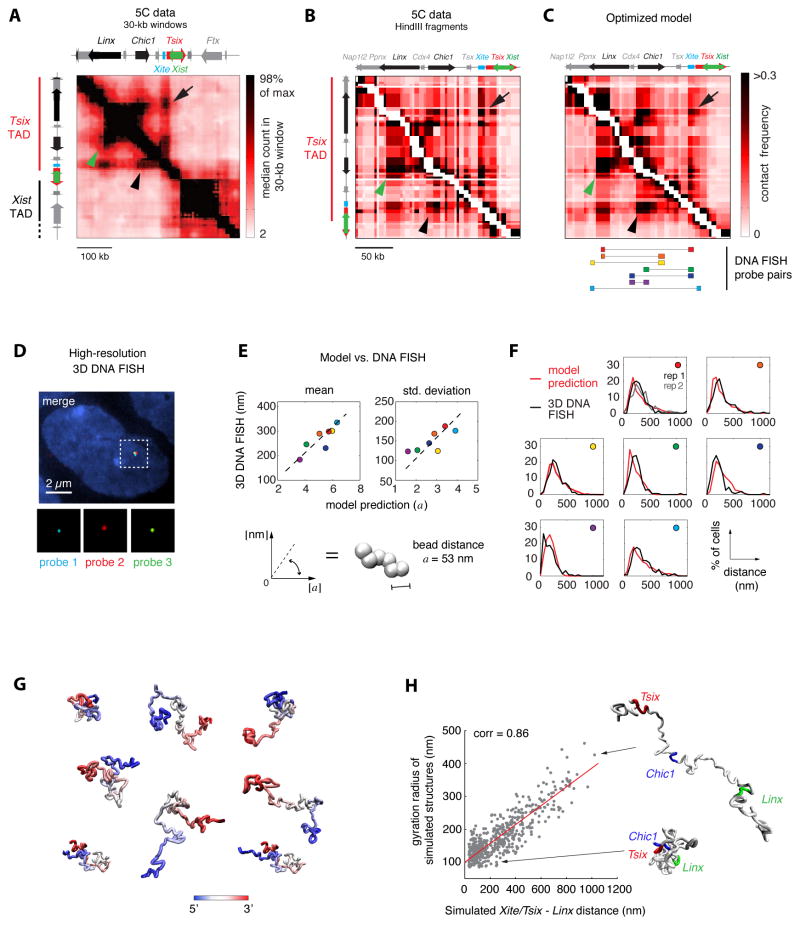
We first applied our method to reconstruct the structure of the 260 kb TAD harboring the Tsix promoter (Figure 2A). This TAD contains the genomic region previously shown to be essential for appropriate Tsix expression by transgenesis and includes a known enhancer of Tsix, Xite (Ogawa and Lee, 2003), as well as a novel non-coding RNA locus, Linx (Nora et al, 2012). Based on the 5C data, this TAD also hosts multiple long-range interactions and putative regulatory elements of Tsix. Indeed, Tsix and Xite interact significantly with Linx, as well as with a region that lies between them, located within the Chic1 gene (Figure 2A). By simply examining the 5C data, it is impossible to deduce whether these three loci interact simultaneously or in a pairwise fashion, and in what proportion of cells. We therefore applied our model to address this.

Figure 2. Physical modeling reveals extensive structural variation at the Tsix TAD.

A. Experimental 5C contact frequencies in the Tsix/Xist region showing the Tsix TAD and part of the Xist TADs. 5C data from (Nora et al., 2012) were smoothed with a 30-kb sliding window filter with 6 kb steps. Long-range interactions between Tsix/Xite and Linx (arrow), Tsix/Xite and Chic1 (arrowhead) and Chic1 and Linx (green arrowhead) are highlighted.

B. 5C data in the Tsix TAD at single HindIII restriction-fragment scale. White pixels along the diagonal indicate adjacent restriction fragments that were not used to constrain the computational model (see supplementary model description in Data S1). Arrows indicate long-range interactions as in panel A.

C. Simulated contact frequencies calculated on the ensemble of fiber configurations obtained by optimizing interaction potentials. The simulation was run with optimal values of parameters R = 1.5 a and r_HC = 0.6 a. Bottom: Positions of high-resolution DNA FISH probes. Arrows as in panels A and B.

D. High-resolution 3D DNA FISH to validate model predictions on three-dimensional distances within the Tsix TAD. Signals from three 9-kb plasmid probes in a male (E14) ES cell are shown after computational correction of chromatic aberrations.

E. Model predictions against experimental measurements for mean 3D distances (left) and standard deviations of 3D distances between seven pairs of loci within the Tsix TAD (colors refer to the probe pairs shown in the bottom part of panel C). Linear fit allows extracting the numerical value of the bead-to-bead distance a as the slope of the best fitting line (a = 53 nm ±2), thus allowing to converting model distances into real physical distances.

F. Comparison of full 3D distance distributions predicted by the optimized model and measured in 3D DNA FISH. n>100 cells were quantified for all distances. Colored circles indicate which probe pair the graph refers to, with reference to panel C.

G. Sample fiber conformations in the optimized ensemble of configurations. Color encodes the position along the model polymer, from 5′ (blue) to 3′ (red).

H. In the optimized ensemble of fiber conformations, Xite/Tsix and Linx tend to be close in space when the entire TAD is in a compact configuration (small gyration radius), and are kept far apart in cells where the TAD is in unfolded configurations.

To model the Tsix TAD, we used 5C data from male ES cells, where the presence of a single X chromosome allows 5C counts to be unambiguously assigned to sequences in cis. For each 5C pair of HindIII restriction fragments in the TAD, we averaged interaction counts from two biological 5C replicates (Figure 2B) and applied the simulation pipeline described above. After optimization of the interaction potentials, we obtained ensembles of fiber conformations the contact frequencies of which closely resembled those observed in 5C, for a wide range of choices of contact and hard-core radii R and r_HC. Optimal agreement was found for R = 1.5a and r_HC = 0.6a (Figure 2C).

To be considered realistic and to make new predictions, a model must be robust with respect to small changes in the parameters that define it. To assess the robustness of the optimized model for any given value of R and r_HC, we ran replicate simulations, starting from different initial sets of non-optimized potentials. Replicate simulations led to optimized potentials that were well correlated (Figure S2A), though not identical. Thus, for any given choice of R and r_HC, multiple sets of interaction potentials exist, that result in similar levels of χ² agreement with the experimental 5C data. However, the corresponding structural ensembles returned equivalent contact frequencies (Figure S2B–C), showing that multiple sets of potentials robustly result in indistinguishable contact probabilities. The model also appeared to be robust with respect to small changes in R and r_HC (Figure S2D), meaning that the precise choice of these parameters is not critical, provided they vary within ~30% of the optimal values R = 1.5a and r_HC = 0.6a.

Although accurately reproducing 5C contact frequencies, the optimized conformation ensemble may not represent a realistic reconstruction of the conformations of chromatin in real cells. To test this, we asked the optimized ensemble to predict pairwise three-dimensional distances between several loci inside the TAD (Figure 2C, bottom) and then compared these distances and their distribution in the population, to actual 3D DNA FISH measurements in ES cells (as illustrated in Figure 1C). Given the small genomic size (260 kb) of the Tsix TAD, the loci tested were separated by only a few tens of kilobases, and could not be resolved by conventional 3D DNA FISH with BAC/fosmid probes. We therefore designed a high-resolution 3D DNA FISH approach using short plasmid- or oligonucleotide-based probes (4–16 kb) to achieve high genomic resolution, together with computational correction of chromatic aberrations to ensure optimal optical resolution in wide-field microscopy (Figure 2D). By applying calibration-bead assisted registration of multi-color images, we could measure distances between sub-diffraction signals in two different colors with an uncertainty of 35 nm (Figure S2E and Extended Experimental Procedures).

For the seven pairs of loci that we tested, the mean distances measured in high-resolution 3D DNA FISH correlated remarkably well with the model’s predictions (Figure 2E, left panel; Spearman correlation 0.89). Notably, the optimized model’s predictions for mean 3D distances were significantly more accurate than those of conformational ensembles obtained from random reshuffling of the optimized interaction potentials (p=0.014), or simpler models in which all beads interact uniformly (Figure S2F).

We also exploited an important attribute of our thermodynamic model, which is to predict statistical fluctuations of 3D distances across the cell population. The model’s predictions were in good agreement with high-resolution DNA FISH for the seven 3D distances measured (Figure 2E right panel; Spearman correlation 0.75) and it correctly predicted the overall shapes of observed distance distributions (Figure 2F). Importantly, the model’s predictions on distance variability were remarkably more precise than the reshuffled models (p<0.002) and uniformly interacting polymers (Figure S2F–G); moreover, these results could be robustly reproduced with conformation ensembles obtained by replicate independent parameter optimizations (Figure S2H).

In conclusion, our optimized model provided a more accurate prediction of the full spectrum of experimental observations (both 5C and DNA FISH mean and variance), than any of the alternative models we tested. These results underline the power of our modeling strategy for deconvolving population-averaged 5C contacts into an ensemble of fiber configurations, capturing the full range of fluctuations in chromatin conformation at this locus.

DNA FISH measurements also allowed us to estimate the numerical value of a, the bead distance in our model. By fitting the correlation between predicted and observed mean distances (Figure 2E, bottom panel; see Extended Experimental Procedures), we obtained a=53±2 nm. Based on this, we conclude that the optimized model represents a fiber of approximately 32 nm in diameter (r_HC=0.6a = 0.6×53 nm), the different parts of which can be crosslinked when closer than approximately 80 nm (R=1.5a). This is compatible with the idea that protein complexes mediate interactions between distal parts of the fiber. Our results therefore support the existence of a 30-nm chromatin fiber in vivo, at least at this locus; however, we cannot exclude that this effective diameter may be due to higher-order folding of a thinner fiber occurring on length scales smaller than our model’s resolution (3 kb) (Fussner et al., 2011).

Both the model-based deconvolution of 5C and the DNA FISH data (Figure 2B–F) suggest that the Tsix TAD chromatin fiber, far from adopting a stable conformation with small fluctuations around an average structure, is highly variable in the cell population. Closer inspection of the model-derived structures revealed that a wide variety of fiber configurations coexist within the population, ranging from tightly folded to very elongated (Figure 2G), with a broad distribution of physical sizes (Figure S2I). Thus, even the most significant long-range interactions, between Tsix/Xite, Chic1 and Linx based on 5C (Nora et al., 2012; see Figure 2A) rather than corresponding to stable loops of intervening DNA, seem to be due to probabilistic events within highly variable distance distributions, occurring in 34% (Tsix/Xite-Linx), 45% (Tsix/Xite-Chic1) and 42% (Chic1-Linx) of cells. Importantly, the model reconstruction predicts that the long-range interactions between Tsix/Xite, Chic1 and Linx are more likely to occur in cells where the whole TAD has a more compact conformation (Figure 2H) than when the fiber adopts elongated configurations. Furthermore, the model predicts that Tsix/Xite, Chic1 and Linx tend to interact as a three-some in compact conformations of the TAD, rather than in a pairwise fashion (24% of model structures have a three-some interaction involving at least one bead in each hotspot locus, while only 1.9–3.1% show any of the possible pairwise interactions excluding the third locus). To confirm this, we performed high-resolution DNA FISH and found that the physical distances between Xite, Chic1 and Linx tend to be reciprocally correlated, in good agreement with the model’s prediction (Figure S2J). Furthermore, when two of these three loci are close in space, the third tends to be close as well, with conformations involving threesomes being more abundant than those with twosomes for a wide range of threshold distances that we used to define colocalization between two FISH signals (Figure S2K). Altogether, these observations argue against stable ‘looped’ configurations of the chromatin fiber within the Tsix TAD, and support the idea that remote chromosomal contacts occur in the context of a compact topology in a subset of cells.

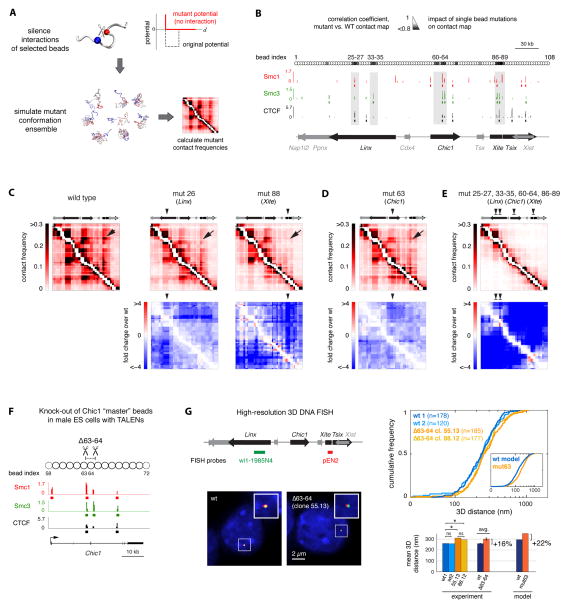
Defining the interactions that determine the internal structure of a TAD

Having found that the results of our model are reliable and robust, we next asked whether it could enable us deduce whether some loci contribute more than others to shaping the overall folding of the fiber and its statistical properties. To address this, we systematically “silenced” the interaction potential of each bead in the chain while leaving the others unchanged (Figure 3A). For each of these virtual “mutations”, we re-simulated the corresponding equilibrium ensemble without further optimizing the interaction potentials of the unaffected beads and calculated the associated contact frequencies (Figure 3A). We found that most simulations of polymers with a silenced bead had very similar contact frequencies when compared to the wild-type model (80% of the silenced beads led to a less than 30% decrease in overall contact frequencies, Figure S3A–B). However, for a few beads, a marked change in contact probabilities was observed when their interactions were silenced. A further indication that these “master” beads are the main determinants of the internal organization of the Tsix TAD came from the fact that the average interaction potentials of these specific beads were the most robust among replicate potential optimizations (Figure S3C). These “master” beads were clustered in four genomic hotspots, which overlap with the highly interacting loci on Xite/Tsix, Chic1 and Linx (Figure 3B). When the sequence/epigenomic features of these hotspots were examined, they were found to significantly colocalise (p<0.005, see Extended Experimental Procedures) with a subset of cohesin/CTCF binding sites in the region (Kagey et al., 2010) (Figure 3B). This is very much in line with the observation that cohesin may play a role in establishing chromosomal interactions (Hadjur et al., 2009; Phillips-Cremins et al., 2013).

Figure 3. Identification of master loci controlling long-range contacts within the Tsix TAD.

A. Virtual “mutations” were generated by silencing the interaction potentials of single beads with all other beads in the model chain. Structural ensembles were re-simulated without further optimizing the potentials of unaffected beads and used to calculate mutant contact frequencies.

B. The similarity between wild-type and “virtual mutant” contact maps was quantified by their Spearman correlation coefficient (small correlation coefficients correspond to big changes in contact frequencies). Hotspots of “master” beads, which strongly affect contact probabilities when mutated, are highlighted in grey. Here, master beads were defined as those corresponding to the lowest 10% quantile of correlation coefficients (see Extended Experimental Procedures). Alignment with ChIP-seq data (Kagey et al., 2010) shows that hotspots overlap with cohesin (Smc1 and Smc3) and CTCF binding sites (p<0.005, see Extended Experimental Procedures).

C. Silencing the interaction potentials of single beads in the Linx and Xite/Tsix hotspots causes the loss of long-range contacts between Linx and Xite/Tsix (indicated by an arrow) as well as a global decrease in contact frequencies throughout the Tsix TAD. Numbers indicate the index of beads that were mutated in the examples shown here.

D. Silencing interaction potentials in the Chic1 hotspot also causes the loss of long-range interaction between Linx and Xite/Tsix (arrow).

E. Simultaneously silencing interaction potentials of all beads in the four hotspots causes the internal organization of long-range contacts within the Tsix TAD to be lost.

F. Generation of mutant male ES cells bearing a 4.4-kb deletion within the Chic1 hotspot (Δ63-64). Two pairs of TALENs were designed to induce double-strand breaks flanking two cohesin/CTCF binding sites that overlap with beads 63 (partly), and 64 (pairs of TALENs are shown here by scissors). Two clones (55.13 and 88.12) bearing a full deletion of the 4.4 kb sequence between the two pairs of TALENs were analyzed.

G. Left panel: High-resolution 3D DNA FISH in mutant vs. wild-type male ES cells with probes against Linx and Xite/Tsix. DNA FISH was performed in in two independent wild-type samples and two Δ63-64 mutant clones. Right panel, top: Comparison of cumulative distributions revealed that 3D distances between Linx and Xite/Tsix are mildly but significantly larger in mutant than in wild-type cells. Model prediction for mutated bead 63 (cf. panel D) is shown in the inset. Bottom: Comparison of mean 3D distances in individual wild-type and mutant samples (* denotes p<0.05 in one-tailed two-sample Kolmogorov-Smirnov tests; ns denotes p>0.85). On average, Linx-Xite/Tsix 3D distances were 16% ± 3% larger in the Δ63-64 mutants than in wild-type cells in agreement with the model prediction (22%).

In order to assess the impact that silencing each of these beads had on the actual contact frequencies between different sequences within the TAD, we quantified the mean 3D distances between all pairs of beads and compared them to the wild-type model. We found that silencing of beads within the four hotspots systematically resulted in decreased contact frequencies throughout the TAD as a consequence of global unfolding of the region (Figure S3D). By silencing single beads within either the Linx or the Xite/Tsix hotspots (beads 25–27, 33–35 and 86–89), we obtained a significant loss of contacts between Linx and Xite/Tsix (Figure 3C) due to an average 50% increase in 3D distances between these two loci and a concomitant loss of contacts of both Linx and Tsix/Xite with Chic1 (Figure S3E). Remarkably, silencing of “master” beads in the Chic1 hotspot (beads 60–64) resulted in decreased contact frequencies, not only between Chic1 and Xite/Tsix or Linx, but also between Xite/Tsix and Linx (Figure 3D and Figure S3F). This suggests that Chic1 may act as a bridging element, helping to bring these two long-range elements into proximity. When all “master” beads were silenced, this resulted in complete loss of structure across the TAD (Figure 3E).

To test the model’s prediction that disrupting master beads in Chic1 would result in increased 3D distances between Linx and Xite/Tsix, we generated mutant male ES cell lines bearing a 4.4-kb deletion within the Chic1 hotspot using transcription activator-like (TAL) effector nucleases (TALENs) (Sanjana et al., 2012) (see Extended experimental procedures). The deletion encompasses two CTCF/cohesin binding sites and overlaps with part of bead 63 and the entire bead 64 in the polymer model (Δ63-64, Figure 3F). To compare distances between Linx and Xite/Tsix in mutant and wild-type cells, we performed high-resolution 3D DNA FISH in two independent wild-type samples and two Δ63-64 mutant clones (Figure 3G). The 3D distances between Linx and Xite/Tsix were consistently found to be significantly larger in the two mutants than in wild-type cells (p<0.05 in one-tailed Kolmogorov-Smirnov tests), whereas they were indistinguishable in the two pairs of wild-type and mutant samples (p>0.85). On average, mean 3D distances were 16% ± 3% larger in Δ63-64 mutants than in wild-type cells (p<0.005 in a one-tailed paired t-test on mean distances). Although moderate, this increase is consistent with the 22% increase predicted by the model for the same pair of probes when either bead 63 (Figure 3D) or 64, or both beads, were silenced; or when beads 63 and 64 were physically deleted from the polymer model alone or in combination (Figure S3G). These in vivo findings, following genetic mutation of master beads identified by our model, demonstrate its predictive power.

Taken together, this analysis suggests that a small number of key loci control the overall conformation of the entire Tsix TAD; and that these master loci thereby supervise the probability that distal sequences such as Tsix/Xite and Linx, physically interact. The importance of these master loci in the overall structure of the TAD could not have been deduced by simple inspection of the 5C data. Our model thus facilitates identification of the key architectural elements within a TAD.

Interactions within TADs contribute to boundary definition between TADs

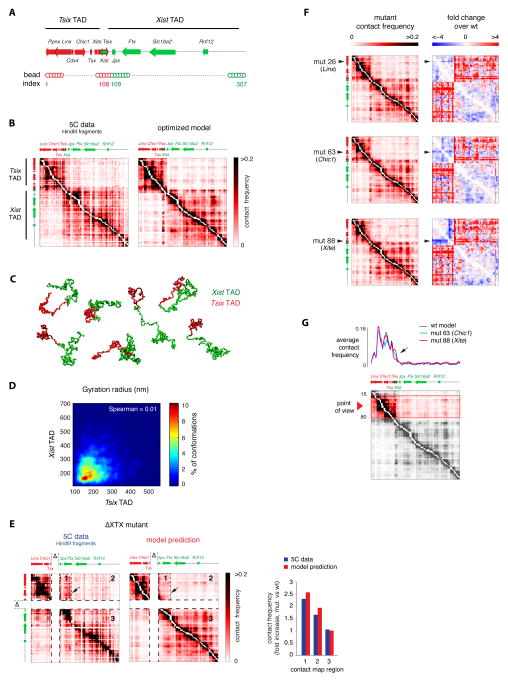
Having used the model to make predictions about the internal organization of a single TAD, we applied it to the reconstruction of the 260-kb Tsix TAD together with the adjacent 520-kb TAD E containing the Xist promoter, and the boundary that separates them. To this end, we added new beads to the existing Tsix TAD D model fiber (Figure 4A) and allowed the simulation pipeline to optimize the interaction potentials in order to reproduce the experimental 5C contacts (Figure 4B, left panel). The model generated an ensemble of fiber conformations that reproduced the existence of the two separate TADs, the contacts within both TADs, and their mutual interactions (Figure 4B, right panel). Similarly to the results for the Tsix TAD, chromatin conformation over both TADs appeared to be highly variable, although in most conformations of the ensemble the Tsix and Xist TADs appeared as two well-separated domains in the chromatin fiber (Figure 4C), with occasional partial overlap giving rise to the weak rather uniform inter-TAD contacts observed in 5C. No correlation between the compaction levels of the two TADs could be found (Figure 4D).

Figure 4. Intra-TAD interactions participate in establishing and maintaining boundaries between adjacent TADs.

A. Extended model fiber for simulating the Tsix and Xist TADs together (represented in red and green, respectively).

B. Experimental and simulated contact frequencies for the Tsix and Xist TADs. The model correctly reproduces the existence of two the TADs and the weak contact frequencies between them. Experimental data from (Nora et al, 2012).

C. Sample conformations from the optimized simulation shown in panel B, highlighting the compartmentalization of the model fiber into two separated domains corresponding to the Tsix and Xist TADs despite extensive structural variability.

D. The gyration radii of the Xist and Tsix TAD were determined for each single fiber conformation in the optimized simulation, showing no mutual correlation. Color scale in the plot corresponds to the percentage of simulated fiber configurations wherein the gyration radius of the Tsix and Xist lie in each corresponding 50 nm × 50 nm bin.

E. Experimental data (from Nora et al., 2012) and model prediction of contact frequencies in the ΔXTX boundary deletion. No further potential optimization with respect to the model shown in panel C was performed. Arrow indicates the position of the ectopic boundary near the Ftx promoter. The model correctly predicts the formation of new boundary between regions 1 and 2 of the contact map, the experimental increase in inter-TAD contact frequencies in regions 1 and 2 and the stability of contacts within the Xist TAD (region 3).

F. Silencing interaction potentials of single beads within hotspots in the Tsix TAD (beads 26, 63 and 88 are shown here as examples) leads to four-fold increased contacts between the Tsix and Xist TADs, as shown by the right-hand side heatmaps.

G. Demarcation of the boundary between TADs is decreased when silencing the interaction potentials of single beads in the Tsix TAD hotspots (beads 63 and 88 shown here as an example). Contact frequencies from multiple viewpoints within the Tsix TAD (red arrowhead, bottom panel) were averaged and plotted against genomic distance to generate the interaction profile in the top panel. Loss of contacts within the Tsix TAD near the boundary (arrow) is at the origin of increased boundary permeability.

To test the predictive power of our two-TAD model, we asked whether it could predict the outcome of a 58 kb deletion (ΔXTX) encompassing the boundary between the TADs (Monkhorst et al., 2008). Deletion of this region had previously been shown to result in ectopic contacts between TAD D and part of TAD E (Nora et al., 2012). Without further optimization of interaction potentials, the model correctly predicted the formation of ectopic contacts in the absence of this region, as well as the appearance of a new boundary near the Ftx transcription start site (Figure 4E). This demonstrates the capacity of our model to make genetically testable predictions. Furthermore, it reveals that the new boundary formed between the two TADs in the presence of the ΔXTX deletion is determined by the fact that in the wild-type, the sub-TAD region extending from Xist to Ftx had significantly higher interactions with the Tsix TAD than the region immediately downstream, which is particularly poorly interactive (Figure S4A). Clearly, these interactions are sufficient, when the ΔXTX boundary is deleted, to favor the spatial proximity of the residual part of this particular sub-TAD with the Tsix TAD.

Our finding that silencing of hotspot loci could lead to global unfolding of chromatin structure within the Tsix TAD (Figure 3C–D) prompted us to investigate the effect of such virtual mutations on the overall structure of the two-TAD fiber and on the presence of a sharp boundary between the two TADs. Silencing master beads within the Linx, Chic1 and Tsix hotspots in Tsix TAD D (beads 25–27, 33–35; 60–64; 86–89 respectively) resulted not only in decreased contact frequencies within this TAD (as before, in Figure 3), but also in increased contacts between the Xist and Tsix TADs and a slight but appreciable loss of contacts within the Xist TAD (Figure 4F). This can be explained by the loosening of the constraints that shape chromatin structure within the Tsix TAD and its partial unfolding, allowing sequences within it to interact more frequently with parts of the neighboring Xist TAD, which in turn adopts a more loosened conformation due to interactions with the other TAD.

These results suggest that interactions within a TAD may not only be necessary to organize the internal structure of the TAD itself, but could also help to prevent interactions with a neighboring TAD, and thus contribute to the presence of a sharp boundary between them. Consistent with this, silencing of master beads within the Tsix TAD also affected the sharpness of the boundary (Figure 4G) by partially unfolding the Tsix TAD. Thus, interactions within TADs participate in the spatial segregation of TADs and can explain, at least partly, boundary stabilization. It should be noted that this may not explain the way in which segregation between TADs is initially established – but rather how this situation is maintained.

Structural variation within the Tsix TAD is related to transcriptional activity

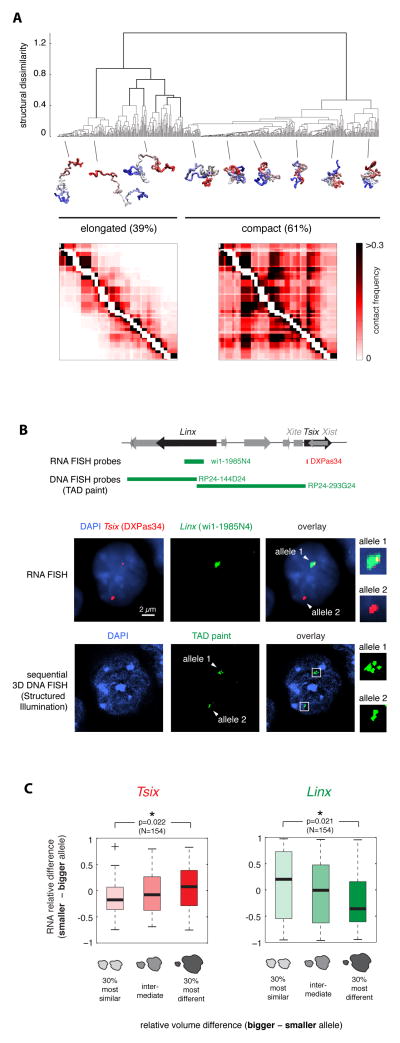
The structural variability that we noted within the Tsix TAD, led us to explore how alternative chromatin configurations might relate to the transcriptional status of Tsix and its putative regulator Linx. Taking the ensemble of chromatin fiber conformations generated by the Tsix TAD model, and hierarchically clustering them according to structural similarity based on root mean square distance (dRMSD) between structures (see Extended Experimental Procedures), we identified two main classes of conformations (Figure 5A). In one cluster (39% of conformations) the chromatin fiber tends to be elongated and almost no long-range contacts take place (Figure S5A); while the other cluster (61% of conformations) is composed of highly folded, compact conformations where multiple long-range contacts frequently occur (Figure S5A), including the high frequency interactions between Xite/Tsix, Chic1 and Linx (each occurring in approximately 55% of these compact conformations). This is consistent with the three loci tending to be closer together when the fiber adopts compact conformations (cf. Figure 2H and Figure S2J). Although each of these structural clusters displays extensive structural variability, they nevertheless have globally distinct volumes (Figure S5B), suggesting that they could be distinguishable by DNA FISH. Indeed, when we performed 3D DNA FISH with tiled probes in different colors spanning the entire Tsix TAD, and acquired the images using structured illumination microscopy, we observed a wide range of different signal geometries ranging from compact to elongated (fiber-like) structures (Figure S5C).

Figure 5. Structural fluctuations at the Tsix TAD are coupled with fluctuations in transcription of Tsix and Linx.

A. Clustering of fiber configurations in the Tsix TAD. Hierarchical clustering of model fiber configurations based on their structural dissimilarity (dRMSD between structures) predicts the coexistence of two conformational classes. Compact conformations are enriched in long-range physical contacts, which are virtually absent in elongated structures.

B. Sequential quantitative RNA/3D DNA FISH allows measuring nascent transcription and TAD compaction in the same cells. Top: Positions of RNA and DNA FISH probes in the Tsix TAD. Middle panel: RNA FISH for Tsix and Linx nascent transcripts in a PGK12.1 female cell showing differential transcription from the two alleles. Bottom panel: sequential 3D DNA FISH in the same cell with the two adjacent BAC probes shown on top; DNA FISH images were acquired by structured illumination microscopy.

C. Single-cell analysis of differential allelic transcription of Tsix and Linx vs. differential allelic TAD volume in female PGK12.1 cells. Tsix (left) tends to be more transcribed from the most compact TAD, whereas Linx (right) shows the inverse trend. Cells were sorted in the G1 phase of the cell cycle, where one copy of the chromatin fiber is present on each allele, to ensure unequivocal quantification of transcription and TAD volume.

We therefore assessed whether these different structural clusters correlated with transcriptional activity within the Tsix TAD. Previous work showed that the genomic region containing Linx and Chic1, both of which interact significantly with Tsix, is required for correct developmental Tsix expression (Nora et al., 2012). According to our model’s predictions, Linx and Chic1 would come into spatial proximity with the Tsix promoter only in the fraction of cells where the TAD is compacted. We hypothesized that in these cells, Tsix might be transcribed more efficiently.

We first characterized the variability of Tsix transcription based on quantitative nascent transcript detection (Figure S5D) in male and female ES cells, by RNA FISH using a probe immediately downstream of the transcription start site (the DXPas34 region, Figure 5B) (Debrand et al., 1999). In undifferentiated female cells, we observed biallelic expression of Tsix in nearly 80% of cells as expected. However, in both male and female cells we detected substantial variations in the actual levels of Tsix transcription between different cells, and verified that this was not due to differences in cell-cycle phase (Figure S5E). Moreover, we noted that in the majority of biallelically expressing female cells, the two Tsix alleles showed different levels of transcription (Figure S5F). We also measured Linx transcription, as this locus has been proposed to be a potential regulator of Tsix (Nora et al., 2012) and it is found to be co-expressed with Tsix in ES cells (Nora et al., 2012), whereas Chic1 and Xite show low correlation with Tsix transcription during differentiation (data not shown). Similarly to Tsix, we found that Linx was biallelically expressed in >80% of cells, but was transcribed at variable levels amongst cells, and between the two alleles in the majority of biallelically expressing cells (Figure S5F). Although cell-to-cell differences in Tsix and Linx transcription could be caused by fluctuations in extrinsic cell-specific conditions (e.g. variable concentrations of trans-acting factors such as pluripotency transcription factors (Graf and Stadtfeld, 2008)), the fact that we detected differential transcription of the two alleles within the same nucleus implies that this could be at least partly due to differential cis-regulation of the two alleles.

To assess whether the above variability in allelic transcription of Tsix and Linx might be associated with TAD structural variability, we correlated allelic differences in transcription for Tsix and Linx with corresponding allelic differences in TAD compaction. Nascent RNA FISH was performed followed by sequential super-resolution 3D DNA FISH in the same cells with tiled probes spanning the entire Tsix TAD (Figure 5B). To rule out possible artifacts in quantification due to the independent folding and transcription from the two sister chromatids on replicated alleles, we analyzed cells in G1 phase of the cell cycle by fluorescence activated cell sorting (FACS) (Figure S5G and Extended Experimental Procedures). To ensure maximum accuracy in our measurements we quantified TAD compaction by measuring the volumes of DNA FISH signals from images acquired using structured illumination microscopy (Figure S5H). We found that in cells where one of the two homologous TADs was significantly smaller than the other, Tsix tends to show higher expression from the smaller TAD (Figure 5C and S5I). Thus we show that even when present in the same nucleus, the two Tsix alleles differ in their transcriptional activity, and that this is related to the conformation of the TAD from which they are expressed. Although a significant correlation between Tsix expression levels and TAD volume could be found in G1 cells, it was less significant in cycling ES cells (data not shown) presumably because > 60% of ES cells are in S or G2/M phase as judged by FACS (Figure S5G), and the presences of two chromatin fibers (after replication) confounds volume and transcript measurements. Measurements in G1 cells are thus essential to ensure that every RNA signal can be compared to the conformation of just a single DNA fiber within the TAD.

We also examined Linx expression in relation to TAD volume. In contrast to Tsix, Linx tended to be more highly transcribed from the TAD with the larger volume (Figure 5C). Consistent with this, we found that although the absolute cellular levels of Tsix and Linx were correlated between different cells (Figure S5J), in fact Linx and Tsix were slightly, but significantly, anti-correlated in their expression levels in cis (Figure S5K), with Tsix being more transcribed on the allele showing lower Linx transcription and vice versa. This unexpected finding, in addition to its implications for Xic regulation, demonstrates that transcription is not a simple correlate of TAD compaction, and that two loci within the same TAD can be oppositely influenced by local compaction.

In conclusion, we show unambiguously that variations in the internal chromatin conformation of a TAD are correlated to differential transcription levels of loci, most likely due to the variability in distances between regulatory sequences.

Discussion

In this paper, we describe a rigorous physical model that can deconvolve sub-TAD contact frequencies measured by 5C into single-cell chromatin configurations. This allows us to make important structural and functional predictions about chromatin folding and its relationship with transcriptional regulation. Unlike previous computational methods (Baù and Marti-Renom, 2010; Kalhor et al., 2012; Umbarger et al., 2011; reviewed in Hu et al., 2013), our model provides thermodynamic sampling of fiber conformations following the associated Boltzmann distribution, which provides precise distance predictions in a formally coherent context. This enables quantitative validation of the model using single-cell assays such as 3D DNA FISH. Combining the model’s predictions with quantitative RNA and DNA FISH revealed a number of important characteristics of chromatin folding inside TADs and their relationship to transcriptional output, which would not have been detected by simple qualitative examination of 5C data, or by performing unsupervised FISH.

Although it was already known that TADs could host interactions between potential regulatory elements, little was known about the conformations that TADs represent in single cells. Here we demonstrate that TADs consist of population-averaged contacts of a multitude of highly diverse configurations of the chromatin fiber. We also show that sub-TAD interactions (including those between potential regulatory elements) emerge as probabilistic events in a subset of cells, thus challenging the more classical view that long-range interactions between regulatory sequences consist of stable DNA loops.

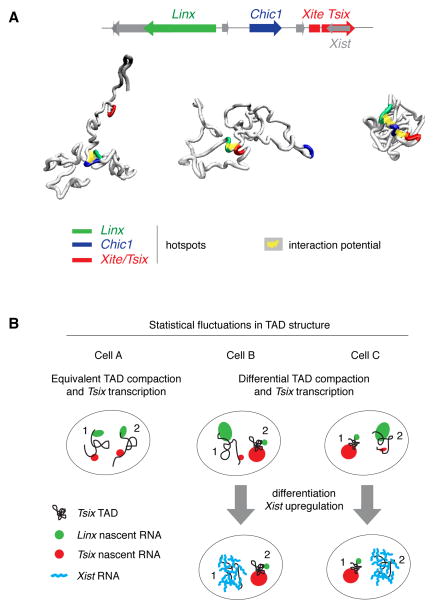
A major advantage of our model is that it makes new predictions, which we exploited here by simulating virtual disruptions and comparing them to experimental data using genetically modified ES cell lines. By simulating the effect of disrupting specific interactions inside the Tsix TAD, a small number of master loci clustered as hotspots within the Linx, Chic1 and Xite/Tsix regions were predicted to organize the internal structure of this TAD, by harboring interactions that favor the conformations whereby the sequences in these hotspots mutually colocalise (Figure 6A). These master loci were found to overlap with cohesin/CTCF binding sites, in agreement with recent findings that cohesin and CTCF mediate long-range functional interactions (Hadjur et al., 2009) and shape sub-TAD structure (Phillips-Cremins et al., 2013). Guided by the model’s predictions, we genetically deleted a small region within the Chic1 hotspot that includes two CTCF/cohesin binding sites (Kagey et al., 2010) and no other specific chromatin features in undifferentiated ESCs. As predicted by the model, the 3D distance between Linx and Tsix increases in ES cells with this region deleted. Although we cannot extrapolate these results to all of the model’s predictions, the above in vivo experiments support the idea that this physical model can be used to make new predictions that can be validated experimentally.

Figure 6. Statistical fluctuations within the Tsix TAD may contribute to the establishment of asymmetric Tsix expression at the onset of XCI.

A. Interactions between the Linx, Chic1 and Xite/Tsix hotspots shape the structure of the Tsix TAD by favoring conformations of the chromatin fiber wherein they mutually colocalise. Three conformations representative of pairwise or three-some interactions between hotspots are shown, taken from the optimized model of the Tsix TAD.

B. Statistical fluctuations in chromatin conformation within the Tsix TAD may contribute to ensuring asymmetric expression from the Xic at the onset of X chromosome inactivation (XCI). In cells where the Tsix TAD is similarly compacted on the two alleles (cell A), Tsix and Linx tend to be similarly transcribed from the two alleles, whereas in cells where the Tsix TADs is significantly more compacted on one allele (as in cells B and C) the two transcripts tend to be differentially expressed. This mechanism may help ensuring that Xist is only transcribed from the allele with lower Tsix transcription at the onset of XCI.

Another remarkable and unexpected prediction is that interfering with the interactions of CTCF/cohesin binding sites within a TAD would result in decreased intra-TAD interactions and increased inter-TAD interactions. Again, this is in line with recent Hi-C results in Rad21 knock-out cells (Sofueva et al., 2013). Our model also correctly predicts that CTCF/cohesin binding sites interact prevalently within one TAD, and to a much lower extent across the boundary with the adjacent TAD, as observed by 4C-seq in the same study (Sofueva et al., 2013). Clearly some mechanism exists to allow asymmetric distribution of interactions across the boundary, such as the presence of an insulator element at the boundary itself (Dixon et al., 2012). Nevertheless, our findings show that maintenance of boundaries may be at least partially accounted for by the propensity of sequences to interact together within TADs.

By extracting the full range of TAD chromatin configurations that exist within a population, our model led us to explore the relationship between chromatin conformation and transcription at a key locus in the Xic, Tsix, and its putative regulator and long-range interacting element, Linx. We demonstrated that, although they show highly correlated expression dynamics during early development, Linx and Tsix in fact display opposing transcriptional states from the same TAD, with the more compact TAD configuration corresponding to higher Tsix transcription levels and lower levels of Linx, while the more elongated conformation appears to favor higher Linx and lower Tsix expression. Thus, the two loci may compete for common regulatory sequences, such that in the clustered configuration Tsix transcription is favored over Linx. The fact that deleting part of the Chic1 intronic interaction hotspot (harboring several CTCF/cohesin binding sites that overlap with essential master beads in our model) led to a measureable change in Linx-Xite/Tsix 3D distances, implies that this Chic1 region may act as a bridging element that enables the more compact chromatin configurations to occur and perhaps, thus, enhances expression of Tsix at the expense of Linx. However this remains to be demonstrated.

In conclusion, our results favor a model whereby both Tsix and Linx are regulated by similar trans-acting factors (e.g. Oct4, Nanog and Sox2) (Navarro et al., 2010), explaining why they tend to be expressed in the same cells, but they could share, or even compete for, one or more common cis-acting regulatory elements.

Although we privilege the hypothesis that fluctuations in chromatin conformation and transcriptional activity occur within timescales that are shorter than a cell cycle, thus giving rise to the observed cell-to-cell variability, we cannot exclude alternative scenarios. For example, chromatin structure and transcription at the Xic may fluctuate slowly over time (> 1 cell cycle) and cell-to-cell differences may be inherited during cell division. We believe that this is unlikely however, as comparable structural and transcriptional variability was found in non-clonal and clonal (early passage) cell populations.

By combining modeling and single-cell analysis we have been able to reveal that intrinsic fluctuations in the conformation of the Tsix TAD are coupled to variation in transcription at the Xic. This may play a role in enabling transcriptional asymmetry between the two Xic alleles (Figure 6B). Such a mechanism could help to ensure that Xist is not activated simultaneously from both alleles during differentiation. Clearly this does not exclude other models for establishing asymmetry, including pairing (Masui et al., 2011; Xu et al., 2007) or feedback loops (Monkhorst et al., 2008). Having defined key sequences that might facilitate chromatin configuration asymmetry, we can now test this model by genetically manipulating them. In conclusion, the modeling approach we describe here provides a powerful means of defining the range of chromosome configurations present in a cell population and exploring their impact on gene regulation.

EXPERIMENTAL PROCEDURES

Simulations

Numerical potential optimization and Monte Carlo sampling of polymer conformations were performed with a custom-made C language-based code and run on a desktop PC. For a detailed description of the physical model and of the simulation algorithm, please refer to the supplementary model description in Data S1.

Cell culture

Feeder-independent mouse ES cells (male: E14; female: PGK12.1) were cultured on gelatin-coated coverslips as previously described (Nora et al., 2012).

Generation of mutant ES cell lines

Customised TALENs were designed and constructed as previously described (Sanjana et al., 2012; see also http://www.epigenesys.eu/en/protocols/genome-engineering), using the TALE Toolbox kit (Addgene). Clone 55.13 harbours a 4380bp deletion (chrX:100566211-100570591, mm9) and clone 88.12 a 4386bp deletion (chrX:100566208-100570594, mm9). Details can be found in the Extended Experimental Procedures.

RNA and DNA FISH

FISH was performed as previously described (Chaumeil et al., 2008). Further details of the procedure, identity of probes, and correction of chromatic aberrations for high-resolution 3D DNA FISH can be found in the Extended Experimental Procedures.

Quantification of DNA and RNA FISH signals

3D image stacks were analyzed analyzed using custom made ImageJ routines. Please refer to Extended Experimental Procedures for a detailed description of the routines; see also Figure S5D for a description of the RNA FISH quantification routine.

Structured illumination microscopy

Structured illumination was carried out using a Delta Vision OMX version 3 system (Applied Precision, Issaquah, WA) coupled to three EMMCD Evolve cameras (Photometrics, Tucson, AZ).