Visual contribution to human standing balance during support surface tilts

Highlights

• •Contributions of visual position and velocity cues to standing balance are analyzed.
• •Both visual cues reduce sway responses to support surface tilt and sway variability.
• •Model simulations are used for data interpretation and data reproduction.
• •Visual cues improve disturbance estimates by reduction of estimation thresholds.
• •Reduction of noise by visual cues appears to be an instrumental factor.

Abstract

Visual position and velocity cues improve human standing balance, reducing sway responses to external disturbances and sway variability. Previous work suggested that human balancing is based on sensory estimates of external disturbances and their compensation using feedback mechanisms (Disturbance Estimation and Compensation, DEC model). This study investigates the visual effects on sway responses to pseudo-random support surface tilts, assuming that improvements result from lowering the velocity threshold in a tilt estimate and the position threshold in an estimate of the gravity disturbance. Center of mass (COM) sway was measured with four different tilt amplitudes, separating the effect of visual cues across the conditions ‘Eyes closed’ (no visual cues), ‘4 Hz stroboscopic illumination’ (visual position cues), and ‘continuous illumination’ (visual position and velocity cues). In a model based approach, parameters of disturbance estimators were identified. The model reproduced experimental results and showed a specific reduction of the position and velocity threshold when adding visual position and velocity cues, respectively. Sway variability was analyzed to explore a hypothesized relation between estimator thresholds and internal noise. Results suggest that adding the visual cues reduces the contribution of vestibular noise, thereby reducing sway variability and allowing for lower thresholds, which improves the disturbance compensation.

1. Introduction

Human balancing during upright stance is more stable with eyes open than with eyes closed (Horak & Macpherson, 1996). Uncertainties remain how the visual cues are integrated in the balance control mechanism and which sensorimotor mechanisms are involved. The current study aims to understand the sensory integration of visual cues in the stabilization of the body center of mass (COM) during support surface tilts and does not consider other aspects, such as a head stabilizing effect in the presence of visual cues (Dietz, Trippel, Ibrahim, & Berger, 1993; De Nunzio, Nardone, & Schieppati, 2005; Mergner, Schweigart, Fennell, & Maurer, 2009). The study investigates the effect of visual cues in a stationary visual scene, as moving visual scenes involve cognitive mechanisms that may mask the stabilizing effect of visual cues (Nashner & Berthoz, 1978; Bronstein, 1986; Guerraz, Thilo, Bronstein, & Gresty, 2001; Blümle, Maurer, Schweigart, & Mergner, 2006). In a stationary visual scene, two visual effects on the COM stabilization stand out. One is the reduction of sway variability in unperturbed stance (spontaneous sway) and the other the reduced sway response amplitudes that are evoked by external disturbances such as support surface tilts. The reduction of sway amplitudes is here considered as an increase in stability, as the body remains closer to the desired upright position, which, however, is not necessarily a valid criterion in other contexts (e.g., pathological conditions).

Spontaneous sway during unperturbed stance is reduced by a factor of about two when viewing a stationary visual scene as compared to conditions without visual space reference (Romberg, 1846; Edwards, 1946; Paulus, Straube, & Brandt, 1984). Model based simulations suggest that spontaneous sway results from internal noise in the balance control mechanism (Peterka, 2000; Maurer & Peterka, 2005), where the resulting sway is determined by the noise source (sensory noise, motor noise, etc.), the neural control mechanism and its dynamics, and the biomechanics of the standing human. The vestibular system appears to be a major noise source (Mergner, 2007; Van der Kooij & Peterka, 2011). In contrast, the visual signals are assumed to contain relatively little noise (Dokka, Kenyon, Keshner, & Kording, 2010; van Beers, Sittig, & Denier van der Gon, 1998).

Although variability in human motor control can be functionally beneficial (Davids, Glazier, Araujo, & Bartlett, 2003; van Emmerik & van Wegen, 2002), internal noise is mostly thought to be disadvantageous for human sensorimotor function (Wolpert & Ghahramani, 2000). Noise has, for example, been discussed to cause an increase in feedback loop gain in the balance control mechanism of Parkinson’s disease patients, evoking a resonant behavior, which largely deteriorates stance stability (Maurer, Mergner, & Peterka, 2004). The general tendency of the sensorimotor system to reduce variability (Dokka et al., 2010; Franklin & Wolpert, 2011) could explain the reduction of spontaneous sway in the presence of a visual space reference. The underlying assumption is that low noise visual cues reduce internal noise by replacement of, or fusion with high noise vestibular cues.

Research using stroboscopic illumination showed that stroboscopic frequencies of about 3 Hz reduce spontaneous sway as compared to eyes closed conditions (Amblard, Crémieux, Marchand, & Carblanc, 1985). Increasing the stroboscopic frequency gradually further reduces spontaneous sway, with sway becoming similar to that during continuous illumination when the stroboscopic frequency reaches 32 Hz (Paulus et al., 1984). During stroboscopic illumination of about 4 Hz strobe frequency and below, the visual system can resolve displacement only as ‘broken motion’ (i.e., a change in position information rather than velocity; Croft, 1971; Wertheimer, 1912), while an increase in stroboscopic frequency leads to a gradual addition of visual velocity cues (Paulus et al., 1984).

The effects of visual position and velocity cues on the closed loop balance control mechanism cannot be identified from spontaneous sway measures. The reason is that the properties of the underlying noise are unknown. This is different when applying known external disturbances, which allow distinguishing between the noise and the response of the balance control mechanism to the stimulus (Van der Kooij, van Asseldonk, & van der Helm, 2005). A previous study from our laboratory investigated combined stroboscopic illumination and support surface tilt to analyze the effect of visual position and velocity cues on the dynamics of the control system (Assländer, Hettich, Gollhofer, & Mergner, 2013). An unpredictable pseudo-random sequence was used as tilt stimulus, where the Low frequency range in the stimulus spectrum had high position and high velocity amplitudes, and the Mid frequency range had high velocity but low position amplitudes. Compared to sway amplitudes observed during eyes closed, 4 Hz stroboscopic illumination reduced the sway responses in the Low-frequency range where tilt position amplitudes were large. In contrast, the 4 Hz stroboscopic illumination did not reduce the sway responses in the Mid-frequency range where tilt position amplitudes were low. Gradually increasing the stroboscopic frequency, thereby adding visual velocity cues, resulted in a gradual decrease of sway in both frequency ranges where tilt velocity amplitudes were high. This result suggests two separate visual contributions in the human balance control mechanism, one based on visual position cues and one based on visual velocity cues.

The separate effects of visual position and velocity cues are in agreement with a model of the balance control mechanism that proposes a separate use of proprioceptive and vestibular position and velocity cues during eyes closed (Maurer, Mergner, & Peterka, 2006; Mergner, Maurer, & Peterka, 2003; Mergner, 2010). The model proposes sensory estimates of external disturbances in the human balance control mechanism for a single inverted pendulum (Disturbance Estimation and Compensation; DEC model), where the disturbance estimator for support surface tilts is based on velocity cues, and the estimator of the gravitational torque in the ankle joints resulting from body lean is based on position cues. The current study investigates whether the effects of the visual position and velocity cues can be explained by parameter changes in the two estimators of the DEC model.

For this purpose, the above described approach using a combination of the pseudo-random tilt stimulus and stroboscopic illumination was extended, applying four different tilt amplitudes, an analysis of sway variability and model simulations. The four tilt amplitudes were applied to identify thresholds that play an important role in the DEC model. The thresholds reproduce the ‘amplitude non-linearity’ observed in human balancing during eyes closed, where large tilt amplitudes are relatively better compensated as compared to small tilt amplitudes (Maurer et al., 2006; Mergner, Maurer, & Peterka, 2003; Peterka, 2002). In the DEC model, two distinct thresholds have been identified to reproduce the amplitude non-linearity, a velocity detection threshold in the support surface Tilt estimator and a position detection threshold in the Gravity estimator (Maurer et al., 2006). These thresholds can be seen in analogy to a central detection threshold in vestibular self-motion perception, which at rest blocks sensory noise from producing illusory perception (Mergner, Siebold, Schweigart, & Becker, 1991). However, the thresholds in the DEC model are clearly lower than the thresholds identified in perceptual studies (see Section 5).

Based on these considerations we hypothesized that the reduction of tilt evoked sway when adding visual velocity and position cues results from an improvement of the support surface tilt and the gravity disturbance estimations. Sway responses and sway variability were measured for four different tilt amplitudes and for the visual conditions ‘eyes closed’, ‘stroboscopic illumination’ (visual position cues), and ‘continuous illumination’ (visual position and velocity cues). The thresholds and other model parameters were identified based on the experimentally measured sway responses using model simulations and optimization techniques. The results showed a specific reduction of the position threshold in the presence of visual position cues and a reduction of the velocity threshold in the presence of visual velocity cues. Sway variability and tilt evoked sway showed similar dependencies on visual conditions and stimulus amplitude. This similarity during support surface tilts is in agreement with the hypothesis that the main effect of visual cues in a stationary visual scene results from a reduction of sensory noise.

2. Model

The current study followed the hypothesis that visual cues reduce subjects’ tilt responses by specifically improving the sensory estimations of the external gravity disturbance and support surface tilt disturbance, which are based on sensory position and velocity cues, respectively. Model simulations were performed to test this hypothesis. Parameters of the model were identified based on the experimentally assessed sway responses using optimization methods (see Section 3.6). In the following, the model and the identified parameters for the three visual conditions are described.

2.1. Model overview

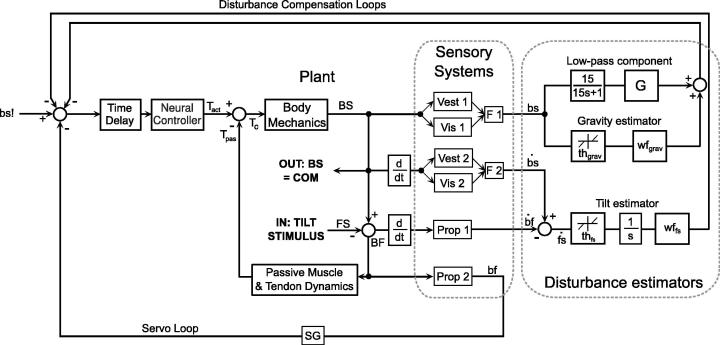
The model is based on a general control concept of human reactive balancing during upright stance (DEC concept; Mergner et al., 2003; Mergner, Schweigart, & Fennell, 2009; Mergner, 2010; Hettich, Assländer, Gollhofer, & Mergner, 2014). The model assumes a sensory estimation and compensation of the four external disturbances that can have impact on body equilibrium during stance: (i) support surface rotation and (ii) translation (iii), field forces such as gravity, and (iv) contact forces such as a push. The model was reduced for the purpose of the current study to the disturbance estimates that mainly contribute during support surface tilt, i.e., i, the Tilt estimator, and iii, the Gravity estimator. The model (Fig. 1) consists of a plant, representing the biomechanics of a standing human, a neural control mechanism commanding the active torque that is driving the plant ($T_{\text{act}}$) and the sensory systems from which the disturbance estimates are derived.

Fig. 1.

DEC posture control model for the simulation of support surface tilt stimuli. Fixed control parameters and parameter values obtained from the optimization procedure are given in Table 1. The model has three neural feedback loops based on sensory signals, which are the reflexive part of the Servo Loop (via box Prop 2) and two Disturbance Compensation Loops. The three loops feed via the summing junction into the neural controller with a time delay. The neural controller and a fourth loop, representing the Passive Muscle and Tendon Dynamics provide the torque that is driving the Body Mechanics, which include the inertia of a single inverted pendulum and gravitational forces. The kinematics of the Body-in-Space angular displacement (BS) are sensed by visual, vestibular and proprioceptive systems, which each provide position and velocity information. BS is also used as the measured output (OUT: BS = COM) for comparison with the human COM sway. The sensory information of visual and vestibular cues is assumed to be fused (boxes F1 and F2) and to provide sensory estimates of BS and its velocity (internal signals, lower case letters). The tilt stimulus represents the input for the support surface tilt sequence that was used in the experiments. Subtracting the tilt signal (which is equal to the Foot-in-Space signal FS) from the BS signal provides the physical variables of body orientation with respect to the foot (BF) and its derivative, both of which are sensed by the proprioceptive system providing the sensory signals bf (box Prop 1) and its derivative (Prop 2). In subsequent processing steps, the sensory information is fused to obtain sensory estimates of the external disturbances acting on the body (disturbance estimators).

2.2. Plant

The biomechanics of the human body swaying in the sagittal plane around the ankle joints is modeled as a single inverted pendulum. The angular position of the body’s COM (excluding the feet) with respect to the space vertical (BS; vertical = 0°) is related to the torque input T_c by

$$BS(s)=1/({\mathit{Js}}^2-\mathit{mgh})\ast T_c(s)\text{,}$$ (1)

where J is the body’s moment of inertia, m the body mass, h the body height, g the gravitational constant, and g the complex argument of the Laplace transform. The torque input T_c is generated in the ankle joints, which reflects the ankle strategy. The contributions of other strategies, such as the hip strategy, are small during the tilt stimuli applied in the experiments and can be neglected (Peterka, 2002). Acceleration of BS through gravitational forces is simplified using the small angle approximation sin(BS) ≈ BS under the assumption that the body remains close to the space vertical. The plant outputs are the physical variables body lean BS and body angular velocity $\dot{\mathit{BS}}$, furthermore the body angular position and velocity with respect to the feet (BF and $\dot{\mathit{BF}}$), which is identical to the orientation to the support surface assuming firm contact of the feet. BF is obtained by subtracting from BS the platform angle in space (FS; horizontal = 0°). By these conventions a body lean of, for example, BS = 5° leads to BF = 5° if the support surface is level (FS = 0°) and to BF = 0° if the support is tilted together with the body in space (BS = FS = 5°).

2.3. Servo loop, passive loop and neural controller

A basic building block of the DEC model is the servo control mechanism. It uses the difference between a desired joint position signal (bs!, transformed through the feedback from the Tilt estimator into a desired body-foot signal) and a sensory derived signal of actual joint position (bf) to calculate a feedback error (Fig. 1). The error and its derivative are amplified in the ‘Neural Controller’ by gain factors (proportional factor Kp and derivative factor Kd, respectively) and are summed to produce the command for the active torque ($T_{\text{act}}$) driving the plant. Such servo mechanisms are often used in engineering and have also been used in motor control physiology (e.g., Merton, 1953; McIntyre & Bizzi, 1993). In addition, a passive torque (passive stiffness and damping; Fig. 1, $T_{\text{pas}}$) is produced by the biomechanical properties of the muscles and tendons (Flash & Hogan, 1985; Hogan, 1984). $T_{\text{pas}}$ is assumed to have zero time delay and to produce 15% of the stiffness and damping of the active loop (Peterka, 2002). Given an appropriate servo gain factor in the active loop (G = 0.85) and an adequate adjustment of the gain factors of the neural controller, the servo generates the dynamics (torques) that are required to produce a desired voluntary movement given by bs!. The gain factors of the neural controller in the servo of the DEC model are set per convention to Kp = mgh and Kd = 0.3 * mgh. The dynamics of voluntary movements that are accurately performed by the servo parameters specified for the given conditions are limited (maximum dominant frequency of signal velocity, <5 Hz). While these servo parameters provide human-like low mechanical impedance, they do not allow the servo to generate sufficient torque to counteract gravity and other external disturbances. Additional context dependent torque is generated in the DEC model through the disturbance estimators (see below).

2.4. Sensory systems

The model assumes that humans use joint proprioception (boxes Prop 1 and Prop 2 in Fig. 1) to sense the physical variables joint angle BF and its derivative $\dot{\mathit{BF}}$ yielding the neural signals bf and $\dot{\mathit{bf}}$, respectively. These signals are derived through fusion of a variety of receptor signals from the muscles, tendons, skin, and structures surrounding the joints (Mergner, 2012). This assumption is intuitive from the human ability to consciously perceive joint angle and angular velocity (see e.g., Mergner et al., 1991). Comparable neural representations of physical variables have been found in single cell recordings in the spinal cord of cats (Bosco & Poppele, 1997; Casabona, Bosco, Perciavalle, & Valle, 2010).

In a stationary visual scene, estimates of BS and $\dot{\mathit{BS}}$ are derived from the head based vestibular system (Vest 1 and Vest 2 in Fig. 1) and the visual system (including the oculomotor system; Vis 1 and Vis 2). The vestibular sensors, centrally fusing canal and otolith transducer signals, provide the neural position signal bs and the rotational velocity signal $\dot{\mathit{bs}}$ (Mergner, Schweigart, & Fennell, 2009). These signals show close to ideal dynamics during rotations in the earth vertical planes, yet contain a high amount of low frequency noise (Mergner, Schweigart, & Fennell, 2009; Van der Kooij & Peterka, 2011). The corresponding signals derived from the visual system involve inputs from several sources, using information on visual landmarks, the ‘subjective visual vertical’, visual motion parallax, optic flow, and more. With the relatively small and slow body-space movements in this study, the visual and vestibular signals are taken to resemble each other in their dynamic characteristics across the Low and Mid frequency ranges (0.0165–0.44 Hz). The sensory cues of the vestibular and the visual systems are assumed to be fused separately for the body-space position cues bs (box F1 in Fig. 1) and the velocity cues $\dot{\mathit{bs}}$ (box F2). The current study aims to characterize the fusion effects in terms of their impacts on the disturbance estimates, without considering details of the visual-vestibular fusion mechanisms.

2.5. Disturbance estimators

During unforeseen external disturbances, the estimators in the model use sensory signals to internally reconstruct the external disturbances and to command the servo to compensate them. Here, the estimations involve the proprioceptive signals bf and $\dot{\mathit{bf}}$ and the visual and vestibular derived signals bs and $\dot{\mathit{bs}}$. Gravity estimator: the estimation of the gravity effect on the ankle torque through body lean uses the neural body-space angle signal bs, as suggested in a previous study (e.g., Maurer et al., 2006). The bs signal contributes in two ways. One is through the Gravity estimator, where the contribution is determined by passing the bs signal through a position detection threshold th_grav and the weighting factor wf_grav. The other contribution consists of a leaky integrator and a gain factor and is referred to as ‘Low-pass component’. This component reduces low frequency sway (Schweigart & Mergner, 2008) and has been realized in functionally similar ways in other models (Peterka, 2002, 2003; Maurer et al., 2006). Tilt estimator: the Tilt estimator is based on an internal reconstruction fs of the tilt stimulus, which is derived from $\dot{\mathit{fs}}=\dot{\mathit{bs}}-\dot{\mathit{bf}}$ using the sensory signals $\dot{\mathit{bs}}$ and $\dot{\mathit{bf}}$. The contribution of the Tilt estimator in the balance control mechanism is derived from the $\dot{\mathit{fs}}$ signal by passing it through a velocity detection threshold th_fs, the weighting factor wf_fs, and a neural integrator.

The estimator signals are fed back to compensate for the gravity and tilt disturbances. The combination of a servo mechanism with low loop gain and the disturbance estimators provides a control structure that tolerates the relatively long time delays found in humans (lumped delay of 180 ms; identified in Peterka, 2002; Maurer et al., 2006). Furthermore, it reproduces human sway responses during eyes closed across a wide range of amplitudes and frequencies, and shows a strong robustness in terms of control stability (Mergner, 2010). The thresholds and the weighting factors are thought to reflect the quality of the estimators, which in turn depend on the quality of the sensory signals. The thresholds (th_fs and th_grav), the weighting factors of the estimators (wf_fs and wf_grav), the gain of the Low-pass component (G) and the lumped time delay (Time Delay) were estimated from the experimental data for the three visual conditions using an optimization procedure (see Section 3.6).

3. Methods

3.1. Subjects

Seven subjects (4 female, 3 male, 27.1 +/− 3.6 years of age) without balance impairments participated in this study after giving their informed consent. Subjects’ mean mass and height were 69.9 +/− 15.0 kg and 1.74 +/− 0.12 m, respectively. As stroboscopic illumination was used in this study, special care was taken that subjects had no history of epilepsy as strobe light may evoke seizures. The study was approved by the Ethics Committee of the Freiburg University Clinics and was in accordance with the 1964 Helsinki Declaration.

3.2. Experimental setup

Subjects stood on a motion platform (Mergner et al., 2003) and held a safety rope in each hand, which was attached to the ceiling and gave hold during outstretched arms, while it gave no orientation cues in the flexed arms position during the experiments. Support surface tilts in anterior-posterior direction with the rotation axis through subjects’ ankle joints were applied. Sway kinematics of the subjects were measured using an optical motion capturing system with active markers, which were attached at hip and shoulder level (Optotrak® 3020; Waterloo, Canada). Stimuli were generated at 100 Hz sampling frequency using a DOS based computer, while stimuli and marker positions were recorded using custom made software written in LabView® (National Instruments; Austin, USA).

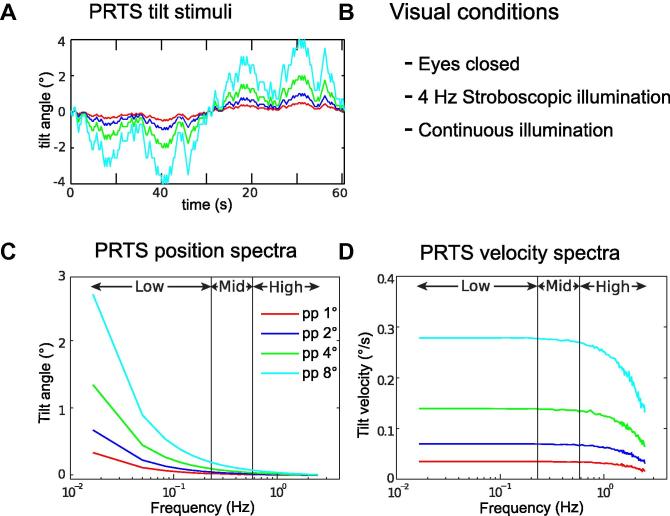
The sequence used as tilt stimulus was based on a 242 state pseudo-random ternary sequence (PRTS; Davies, 1970) with a state duration of 25 ms, giving a cycle length of 60.5 s (Peterka, 2002). The PRTS cycle (shown in Fig. 2A) was repeated six times during each 363 s long experimental trial. The stimulus was applied at four different peak-to-peak tilt amplitudes (pp 1°, pp 2°, pp 4° and pp 8°). The position and velocity amplitude spectra of the four stimuli are shown in Fig. 2C and D, respectively. Note that the PRTS stimulus has the property that only odd frequency points of the discrete spectrum with the fundamental harmonic at 0.0165 Hz have stimulus energy (Davies, 1970) and that even harmonics of the spectrum are not shown in Figs. 2, 3 and 5.

Fig. 2.

Tilt stimulus sequence, its spectral characteristics, and the three visual conditions used in the experiments. Shown are the time courses (A), the visual conditions (B), the position spectra (C) and the velocity spectra (D) for the four peak-to-peak stimulus amplitudes pp 1°, pp 2°, pp 4° and pp 8° (color coding). ‘Low’, ‘Mid’, and ‘High’ indicate the frequency ranges which were used in the analyses.

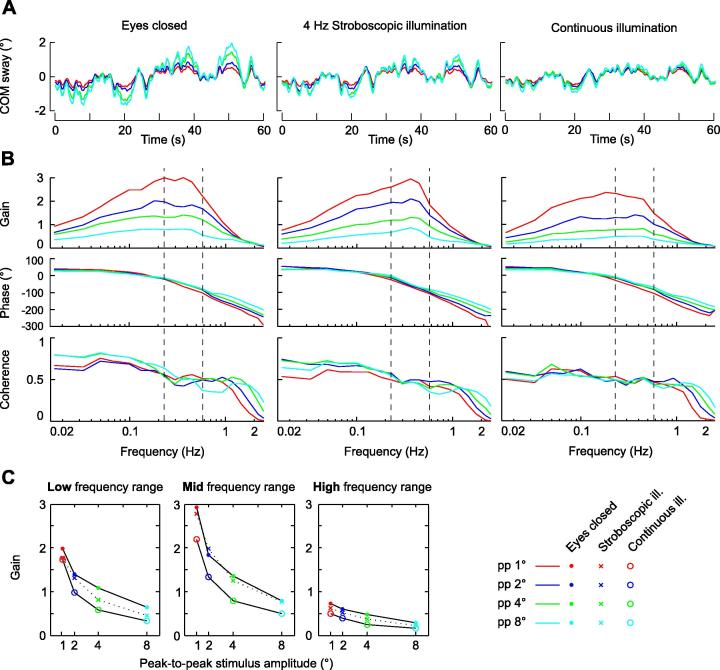
Fig. 3.

Stimulus evoked sway. (A) Stimulus evoked sway in the time domain for the three visual conditions (columns) and the four stimulus amplitudes (color coding); averages across 7 subjects and 10 cycles per subject. (B) Characterization of the stimulus evoked sway in terms of Bode histograms (gain and phase) and coherence functions across frequency. Gain gives the amplitude ratio between sway response amplitudes and tilt stimulus amplitudes. For a gain of one, the sway response amplitude equals the stimulus sway at the given frequency. A gain of zero indicates that the stimulus does not evoke any sway. Phase is a measure of the temporal relation between tilt stimulus and sway response. The body sway is in phase with the platform stimulus at 0° and is in counter phase at +/− 180°. Coherence is a measure of the signal to noise ratio of the stimulus evoked sway. (C) Averages of gain values (shown in B) across the Low, Mid, and High frequency ranges (columns) displayed for the peak-to-peak tilt stimulus amplitudes (abscissa) and for the three visual conditions. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

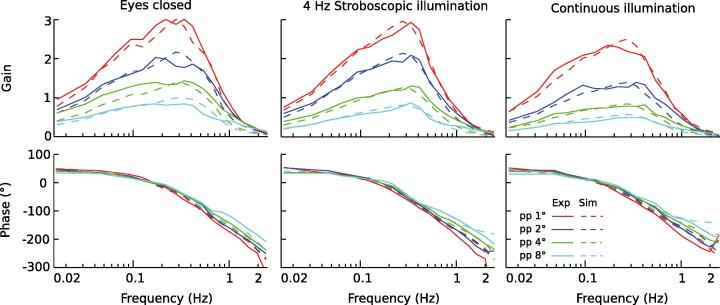
Fig. 5.

Simulation responses (dashed lines) and experimental responses (solid lines; equal to Fig. 3) of the COM to tilt stimulus FRF for the three visual conditions (columns) in terms of gain (top row) and phase (bottom row) over tilt frequency. Each plot gives the stimulus evoked sway results for the four tilt stimulus amplitudes. The simulation results were obtained using the model shown in Fig. 1 and the corresponding set of parameters for each of the three visual conditions (Table 1).

Subjects were tested in three visual conditions, with eyes closed, eyes open with continuous illumination and eyes open with 4 Hz stroboscopic illumination. Illumination during eyes open conditions was provided using a custom made device with 4 super bright LEDs (Neutral White 4000 K; Bridgelux, Livermore, USA). Two LEDs were directed towards the front and one to each side wall from the subjects’ perspective providing an approximately uniform illumination of the visual scene (Assländer et al., 2013). The strobe frequency was set to 4 Hz with a flash duration of 5 ms, where visual velocity cues are minimized (Amblard et al., 1985; Assländer et al., 2013; Paulus et al., 1984). Brightness in the continuous illumination condition was adjusted such that integrated photometric brightness was equal to that in the stroboscopic condition, resulting in approximately constant perceived brightness and constant visual acuity for each subject.

In order to separate visual position and velocity effects, the spectral properties of the PRTS can be exploited in combination with these visual conditions (Assländer et al., 2013). While in the ‘Low frequency range’ (0.0165–0.1818 Hz) position amplitudes of the tilt stimulus are large, they largely diminish in the ‘Mid frequency range’ (0.21–0.45 Hz) and ‘High frequency range’ (0.48–2.46 Hz; Fig. 2C). Therefore, visual position cues and their neural integration show the largest effect in the Low frequency range. Tilt velocity amplitudes are constant throughout Low and Mid, while they decrease in the High frequency range (Fig. 2D). Therefore, visual velocity effects are expected in the Low and Mid frequency ranges.

Four different tilt amplitudes of the PRTS stimulus were applied to assess the characteristics of the amplitude non-linearity, which was used in the model simulations to identify the thresholds. The previous findings on separating visual position and velocity effects (Assländer et al., 2013) are exploited in the setup of the current study to separate the effects of a position threshold, expected mainly in the Low frequency range, and a velocity threshold, expected mainly in the Mid, but also in the Low frequency range.

3.3. Protocol

Each subject performed the experiments twice in up to three different sessions. The first trial of each session was used to familiarize subjects with the experiments and consisted of a pp 4° amplitude stimulus, where subjects had their eyes open during the first 3 cycles and closed during the second 3 cycles. Following, experimental trials for each of the four different amplitudes and three different visual conditions were presented in randomized order. Subjects were instructed to ‘stand upright and comfortable’ and ‘close the eyes’ or ‘look straight ahead’ prior to each trial, defining ‘straight ahead’ as the visual field around eye level without fixating one point. Special care was taken that subjects did not make arm movements or knee movements, to allow the assumption of two rigid body segments in the analysis (see below). During the trials subjects listened to audio books through head phones to distract their attention from the balancing task and to reduce auditory orientation cues. After each eyes open condition, visual acuity was tested using letters of decreasing size in a forced choice procedure (Bach & Kommerell, 1998), where no significant differences were found across visual conditions. In between trials subjects were given breaks of approximately 3 min and a maximum of 8 experimental trials were performed per session.

3.4. Calculation of the center of mass

The recorded data was exported to Matlab (The Mathworks, Natick, USA) for further analysis. Lower and upper body segment angles with respect to the earth vertical were calculated using trigonometric functions, assuming two rigid segments. With the ankle joints fixed in space during the tilt stimuli, the lower body angle was calculated from the horizontal hip displacements and the manually measured height of the opto-electronic hip marker. The upper body angle was calculated from the height difference of the hip and shoulder marker during the upright standing position of a subject and the difference in horizontal displacements of the two markers. Based on anthropometric data of Winter (2009), the center of mass (COM) position was derived from the upper and lower body angles, where the upper body comprises trunk, head and the bent arms, and the lower body the legs without the feet. Body sway, defined as the angle of the COM above the ankle joints with respect to the space vertical was calculated thereof and used as the main output for all further analyses.

3.5. Data analyses

The sway responses to the tilt stimulus were analyzed in terms of frequency response functions (see Peterka, 2002). For each cycle, the discrete Fourier transform of the measured COM sway (output spectrum) and of the tilt stimulus (input spectrum) was calculated using the ‘fft’ function implemented in Matlab. The spectra were averaged across cycles, and frequency response functions were calculated dividing the averaged output spectrum by the averaged input spectrum for each frequency point. Frequency response functions (FRFs) were expressed as gain (absolute value of FRF) and phase (inverse tangent of FRF; Pintelon & Schoukens, 2004). Coherence functions were calculated dividing the squared, absolute value of the averaged cross power spectrum by the product of the averaged input and output power spectra. Gain, phase and coherence curves were smoothed across frequency in Figs. 3 and 5 (compare Peterka, 2002).

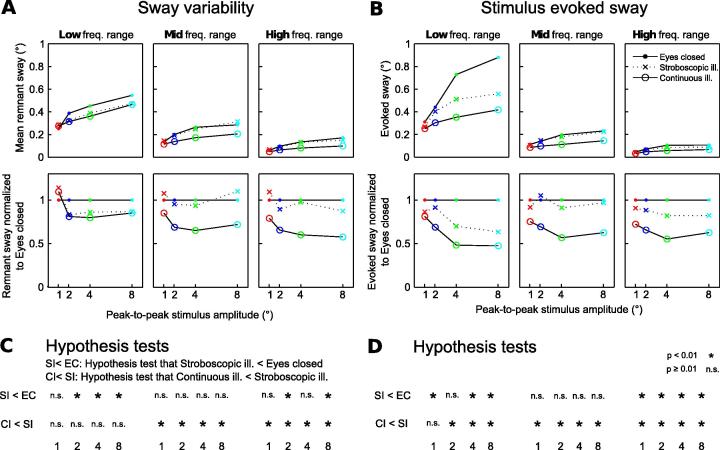
Sway variability was obtained calculating the variance of the amplitude spectra across individual cycles (compare ‘Remnant sway’; Van der Kooij & Peterka, 2011). Sway variability was calculated for the Low, Mid and High frequency ranges and the square root of the variance was displayed across tilt stimulus amplitude conditions for all three visual conditions (Fig. 4A). To compare sway variability with the stimulus evoked sway, power spectra were calculated from the output spectra and averaged across cycles. Sway response power was obtained for Low, Mid and High frequency ranges (see above) by summing across frequencies. Fig. 4B shows the square root of the obtained sway power for each frequency range and each visual condition, plotted across the peak-to-peak tilt stimulus amplitudes (‘Stimulus evoked sway’). Differences of sway response amplitudes and sway variability across visual conditions were statistically compared for each frequency range and stimulus amplitude using a single sided bootstrap hypothesis test (Zoubir & Boashash, 1998), with a significance level of p < .01.

Fig. 4.

COM sway separated into one component that is not correlated to the tilt stimulus (A; sway variability) and one component correlated to the tilt stimulus (B; stimulus evoked sway). COM sway for the three visual conditions is plotted over peak-to-peak tilt stimulus amplitude (abscissa), separately for the Low, Mid, and High frequency ranges. Top rows show the averaged sway, bottom rows the sway normalized to the eyes closed condition to highlight the effect of the visual conditions. (C and D) Results of the bootstrap hypothesis tests comparing sway parameters across visual conditions. SI < EC shows the results of the hypothesis test that sway variability (panel C) or stimulus evoked sway (panel D) is smaller during stroboscopic illumination as compared to Eyes closed. CI < SI show the hypothesis test results that the sway components are smaller in continuous illumination as compared to stroboscopic illumination. The hypothesis tests were performed individually for each stimulus amplitude (abscissa) and for the Low, Mid, and High frequency ranges.

3.6. Simulation methods

Model simulations were performed using Simulink (The Mathworks, Natick, USA). The model used for the simulations is shown in Fig. 1 and is described in Section 2. An optimization procedure was used to find the parameter set that minimized the difference between the experimental data and the simulation results for each of the three visual conditions. Six parameters were varied to reproduce the experimental data (Time delay, G, wf_grav, th_grav, wf_fs, th_fs; see Fig. 1, Section 2. Model, and Section 4.2 Simulation results). Note that, within each visual condition, only one set of parameters was used to fit the responses to all four tilt stimulus amplitudes. For the optimization, a simulation error was calculated using the absolute, squared difference between experimental and simulation data for real and imaginary parts of the frequency response function and summing it across frequency and across all four stimulus amplitudes for a given visual condition. As the main effects of the visual conditions were expected in the Low- and Mid-frequency range, the error was calculated from a smoothed frequency response function, which was averaged across frequency. More frequency points were averaged with increasing frequency such that differences between simulation and experimental results at higher frequencies had less effect on the parameter optimization. The minimized simulation error was also used as a measure for the goodness of the fit. A perfect fit would give a value of zero, while the fit would be worse, the larger the value. The Matlab function ‘fminsearch’ from the ‘Optimization toolbox’ with the ‘Nelder-Mead simplex algorithm’ was used to find the parameter set that minimized the above defined simulation error. Because of the complex interactions between parameters, the algorithm is likely to converge at a local minimum. To find the parameter set which gives the overall smallest simulation error (global minimum), two starting values were chosen for each parameter at approximately 20% and 80% of a range that was considered plausible based on earlier studies and physiological considerations. The algorithm was started from all possible combinations of starting points of the parameters, i.e., the optimization was run with a total of 2⁶ = 64 different combinations of starting points. The parameter set with the smallest simulation error was chosen as the final output. The procedure was repeated for each visual condition, calculating the error function based on the corresponding experimental data.

4. Results

4.1. Experimental results

Fig. 3A shows the COM sway averaged across subjects in the time domain, separately for the three visual conditions and the four stimulus amplitudes. The averaged COM sway represents the sway component that is evoked by the PRTS tilt stimulus. The sway response characteristics resembled those of the stimulus (Fig. 2A) across all three visual conditions. The response amplitude increased with stimulus amplitude within each visual condition. Across visual conditions, adding visual position cues in the stroboscopic condition and furthermore visual velocity cues in the continuous illumination condition reduced sway response amplitudes. The visual cues also reduced the increase in the response amplitudes with increased stimulus amplitude.

Fig. 3B presents the sway response data in the frequency domain in terms of gain, phase and coherence functions. In the eyes closed condition, the characteristics of the gain curves show low gain values (G_{pp 1} = 0.9; G_{pp 8} = 0.4) at the lowest frequency of 0.0165 Hz. The gain increases with frequency reaching a peak between 0.2 Hz and 0.5 Hz (G_{pp 1} = 3; G_{pp 8} = 0.7) and then decreases to G = 0.1 at 2 Hz for all stimulus amplitudes. The amplitude non-linearity, given by the gain differences across stimulus amplitudes, depicts the tendency of humans to compensate larger tilt stimuli relatively better as compared to small tilt stimuli. Fig. 3C summarizes the response gain curves shown in Fig. 3B, presenting across-frequency averages for each stimulus amplitude and each visual condition, separately for the Low, Mid, and High frequency ranges (frequency ranges are indicated by dashed vertical lines in Figs. 3B, 2C and D). These frequency ranges help separating the effect of the visual conditions on the compensation of tilt position amplitudes (large in the Low frequency range) and tilt velocity amplitudes (large in the Low and Mid frequency range; see Fig. 2 and Methods). In the Low frequency range, gain values during 4 Hz stroboscopic illumination show a decrease compared to the Eyes closed condition, and a further decrease during continuous illumination. This effect is similar across all stimulus amplitudes. In the Mid frequency range, in contrast, gain during 4 Hz stroboscopic illumination is similar to Eyes closed across all stimulus amplitudes, while gain clearly decreased during continuous illumination. In the High frequency range, the gain values are reduced during 4 Hz stroboscopic illumination as compared to Eyes closed and show a further small reduction during continuous illumination. These findings show that the illumination dependent gain characteristics across frequency, previously reported for the pp 4° tilt amplitude (Assländer et al., 2013), exist similarly for the pp 1°, pp 2° and pp 8° tilt amplitudes.

Fig. 3B also presents the phase characteristics across frequency. A phase lead was found at the lowest frequencies, which continuously decreases with increasing tilt frequency reaching a phase lag of about −180° at 2 Hz. The phase is similar across tilt amplitudes and visual conditions, apart from small tilt amplitude dependent differences at the highest frequencies, which are present in all three visual conditions. The coherence is similar across the three visual conditions and the four tilt amplitudes, amounting to 0.5 or higher in the Low and Mid frequency ranges. In the High frequency range, coherence decreases, this the more the smaller the tilt amplitude became.

Fig. 4 shows the sway variability, i.e., the sway component that is mathematically not correlated with the stimulus (Fig. 4A), and the stimulus evoked sway (Fig. 4B). Figs. 4B and 3 both show the stimulus evoked sway component. However, while the latter shows the sway amplitude in relation to the stimulus amplitude (gain in Fig. 3B and C), Fig. 4B shows the absolute amplitude of the stimulus evoked sway component. In Fig. 4, both sway components are displayed separately across stimulus amplitudes (abscissas) for the Low, Mid, and High frequency ranges. Note that the exceptionally large stimulus evoked sway observed with Eyes closed in the Low frequency range (Fig. 4B) results from the large position amplitudes in the stimulus spectrum of this range. Sway variability (Fig. 4A) and stimulus evoked sway (Fig. 4B) increased with stimulus amplitude in each of the three frequency ranges and for each of the three visual conditions. Across the three frequency ranges, stimulus evoked sway and sway variability decreased from the Low to the Mid and further to the High frequency range. A similar decrease in sway variability across stimulus frequency has been shown in previous work for the eyes closed condition (Van der Kooij & Peterka, 2011).

To ease comparison across visual conditions, the sway components were normalized to the eyes closed condition (Fig. 4; lower panels). In the Low frequency range adding visual position cues by presenting stroboscopic illumination caused a decrease of sway variability and of the stimulus evoked sway (with the exception of sway variability in pp 1°). In the Mid frequency range, in contrast, visual position cues did not reduce sway. In the High frequency range, visual position cues significantly decreased stimulus evoked sway, while sway variability showed significant reductions only at the stimulus amplitudes pp 2° and pp 8°. Adding visual velocity cues (continuous illumination) further reduced the stimulus evoked sway in all frequency ranges, and sway variability in all but the Low frequency range. Thus, visual velocity cues reduced the two sway components in the Mid frequency range, where the position cues had no sway reducing effect. Statistical comparisons between visual conditions were performed for each stimulus amplitude and frequency range (Fig. 4C and D). Bootstrap methods were used to test the hypotheses that sway in 4 Hz Stroboscopic illumination was smaller as compared to Eyes closed (SI < EC) and that sway in continuous illumination was smaller as compared to 4 Hz stroboscopic illumination (CI < SI; Fig. 4C and D). The statistical comparisons confirmed with few exceptions the above described differences across visual conditions.

4.2. Simulation results

Fig. 5 shows the simulation results (Sim) superimposed on the experimental gain and phase curves (Exp) for the four tilt stimulus amplitudes and the three visual conditions. The simulation results closely resemble the human data in all visual conditions, where one set of parameters (Table 1) reproduced the sway responses of all four stimulus amplitudes within each visual condition. Goodness of fit values were 3.65, 1.92, and 1.74 for eyes closed, stroboscopic, and continuous illumination, respectively. These findings are novel in that they demonstrate that the DEC model is able to describe human sway responses also in the presence of visual cues. A detailed comparison of simulation and experimental data revealed small differences in the gain and phase curves of the frequency response functions above 0.8 Hz, such as slightly lower gain values in the model simulations. In the identified parameters of the optimization procedure (Table 1) the Time Delay converged at about 160 ms in all three visual conditions. The identified gain factor of the low-pass component of the Gravity estimator was also similar across all conditions. The main effects across the three visual conditions on the experimentally observed amplitude non-linearities were reproduced by the model through changes in the thresholds and the weighting factors of the estimators. Specifically, adding visual position cues (4 Hz stroboscopic illumination compared to Eyes closed) did not affect the velocity threshold of the Tilt estimator. However, it reduced the position threshold of the Gravity estimator th_grav from 0.07° to 0.02°. Adding visual velocity cues (continuous compared to 4 Hz stroboscopic illumination) did not affect the position threshold in the Gravity estimator, but reduced the velocity threshold in the Tilt estimator th_fs from 0.33°/s to 0.20°/s.

Table 1.

Fixed model parameters and parameters derived from the optimization procedure.

Fixed model parameters
Body mass kg	CoM height m	Moment of inertia kg m2	Servo gain	Kp Nm/rad	Kd Nm/(rad/s)	Kp passive Nm/rad	Kd passive Nm/(rad/s)
69.0	0.93	72.8	0.85	mgh	0.3 * mgh	0.15 * mgh	0.15 * 0.3 * mgh
Optimization results
Visual condition	Tilt estimate		Gravity estimate		Low pass G	Time delay s	Simulation error
	Threshold°/s	Weight. fact.	Threshold°	Weight. fact.
Eyes closed	0.33	0.75	0.07	0.55	0.13	0.16	3.65
Strobosc. ill.	0.33	0.87	0.02	0.46	0.15	0.16	1.92
Continuous ill.	0.20	0.89	0.03	0.46	0.13	0.15	1.74

The weighting factor of the velocity based Tilt estimator wf_fs increased in the presence of visual position cues (4 Hz stroboscopic illumination compared to Eyes closed) from 0.75 to 0.87 and remained at this increased level (0.89) when adding visual velocity information (continuous compared to 4 Hz stroboscopic illumination). The weighting factor of the position based Gravity estimator wf_grav decreased when adding visual position cues (Eyes closed compared to 4 Hz stroboscopic illumination) from 0.55 to 0.46 and remained at this low value when adding visual velocity cues (continuous compared to 4 Hz stroboscopic illumination).

5. Discussion

The aim of the study was to better understand the neural mechanisms by which visual position and velocity cues help humans to improve their balance during support surface tilts. The study assumed that reduced sway responses result from an improved sensory reconstruction and compensation of the gravity and tilt disturbances. The study proceeded from the hypothesis that it is mainly the reduction of noise in the sensory disturbance estimates, which improves the disturbance compensations. The reduction of noise is thought to result from a fusion of low-noise visual signals with high-noise vestibular signals. Specifically, the study analyzed the effect of visual position and velocity cues on sway responses to support surface tilt stimuli and sway variability. Characteristic reductions of sway were identified when adding visual position cues (4 Hz stroboscopic illumination) and a further characteristic reduction when adding visual velocity cues (continuous illumination). The distinct effects of visual position and velocity cues are in line with previous studies measuring spontaneous sway during stroboscopic illumination (Amblard et al., 1985; Paulus et al., 1984) or sway responses to a pp 4° PRTS tilt stimulus during stroboscopic illumination (Assländer et al., 2013).

The visual effects on sway responses were identified using a tilt stimulus with a broad frequency range and specific characteristics in the velocity and position spectra. The tilt stimulus was applied at four different amplitudes. This experimental setup allowed a model-based interpretation, where the effects of visual position and velocity cues on the sensory disturbance estimations were quantified using parameter identification. The main parameter changes across visual conditions were found in the disturbance estimators, which were sufficient to reproduce the sway response gain and phase curves across the different tilt frequencies and amplitudes (Fig. 5). The changes of the thresholds across the visual conditions allow inferences related to the hypothesized sensory noise effects (addressed in Section 5.1). Identified changes of the weighting factors in the disturbance estimators require additional considerations (addressed in Section 5.2).

5.1. Relations between thresholds and sway variability

The experimental results showed similar changes in sway variability and stimulus evoked sway across the four tilt amplitudes, the three frequency ranges, and the three visual conditions (Fig. 4). The similarity between sway variability and stimulus evoked sway can be interpreted as resulting from signal dependent noise, where the noise amplitude is related to the amplitude of the sway response. One source of signal dependent noise in human sensorimotor control stems from the torque generation process (‘motor noise’), where the variability increases with the exerted force (Harris & Wolpert, 1998; Selen, Franklin, & Wolpert, 2009). However, also noise from sensory systems can be a source for movement variability (Osborne, Lisberger, & Bialek, 2005). For eyes closed human balancing, it has been estimated that motor noise accounts for only about 10% of the overall sway variability and that the vestibular system is the major source of the observed sway variability (Van der Kooij & Peterka, 2011).

The thresholds in the disturbance estimates have been suggested in earlier studies as a central neural mechanism, which can explain sensory reweighting occurring with changes in disturbance magnitude (amplitude non-linearity) and disturbance modality (tilt versus pull stimulus; Maurer et al., 2006). Originally, a noise reducing function of central detection thresholds had been postulated for human self-motion perception of horizontal rotations (Mergner et al., 1991). The authors argued that, in situations where the body is at rest in the dark, the thresholds block vestibular noise to prevent self-motion illusions. Although the thresholds in the balance control mechanism (Maurer et al., 2006) are considerably lower compared to those identified in self-motion perception (Fitzpatrick & McCloskey, 1994; Mergner et al., 1991), these studies suggest that the thresholds do not only affect the stimulus evoked sway (addressed in the model simulations) but also sway variability (Mergner, Schweigart, & Fennell, 2009; Mergner, 2010).

The effect of the thresholds on sway variability is that below threshold, neither the signal, nor the noise of the signal contributes to the torque command of the control mechanism. The larger the signal, the more of the signal and its noise cross the threshold, which in effect results in signal dependent noise. Despite these considerations, the model based interpretation of the observed sway variability across tilt stimulus amplitudes and frequency (Fig. 4A) is not straight forward. While the noise passing the threshold in the Gravity estimator depends on body lean in space, the noise passing the threshold in the Tilt estimator depends on the tilt stimulus. The observed sway variability results from both contributions and from other, supposedly less important, noise sources, such as motor noise.

The above considerations are independent of the effects found across visual conditions, where visual cues affected sway variability and the thresholds that were identified based on the stimulus evoked sway. Adding visual position cues reduced sway variability in the Low frequency range, while adding visual velocity cues reduced sway variability in the Mid and High frequency ranges (Fig. 4A). The identified position threshold in the Gravity estimator was reduced when adding visual position cues and the velocity threshold in the Tilt estimator was reduced when adding visual velocity cues (Table 1). The reductions in sway response amplitudes can be explained by lower thresholds, because lower thresholds allow smaller signals to pass, thereby improving the disturbance compensation. However, the reduction of the thresholds does not explain the reduction in sway variability when adding visual cues, because lowering the thresholds allows more noise to pass the thresholds. The reduction in sway variability therefore likely results from a reduction of noise located upstream at the level of the visual-vestibular fusion mechanisms (F1 and F2 in Fig. 1). Thus, for each visual contribution (position and velocity cues), two improvements can be distinguished: a reduction of sensory noise through visual vestibular fusion and an improvement of disturbance estimates through lowering of the thresholds. It is reasonable to assume that the lowering of the thresholds is related to the lower noise levels.

Variability has been discussed in several studies to be an important factor in motor control. A prominent approach that relates behavior and variability is based on Bayesian statistics. This normative approach has been used, for example, to explain sway responses to visual scene motions (Dokka et al., 2010). Another common approach comes from engineering sciences and uses Kalman filters, where the contribution of individual sensory sources is weighted based on the variability of the sensory signals. Several models based on Kalman filters have been proposed for human balancing (Van der Kooij, Jacobs, Koopman, & van der Helm, 2001; Kuo, 2005; Carver, Kiemel, & Jeka, 2006; Klein, Jeka, Kiemel, & Lewis, 2011). The comparison between these models and the DEC model remains an open issue. However, the explanatory power, reflected in the ability to reproduce human sway responses across a wide range of stimulus amplitudes and frequencies, the simplicity, and the consistency with findings in perception studies provide strong support for the DEC model. Furthermore, the DEC model is the only model that currently provides a consistent interpretation of the sway reduction through visual position and velocity cues.

5.2. Weighting factors of the disturbance estimators

Parameter identification showed changes in the weighting factors of the estimators across visual conditions (Table 1). The weighting factors are necessary to reproduce the experimentally observed sway responses and so far have been found to be below unity, which suggests that humans tend to compensate disturbances only partially (Mergner et al., 2003; Maurer et al., 2006; Mergner, 2010). The weighting factor in a disturbance estimator may be related to two aspects: (i) trust in the quality of a given estimate, and (ii) voluntary control of how strong to use the estimate for disturbance compensation (Mergner, 2010). The results obtained from the parameter identification suggest a qualitatively different cause for the observed changes in the weighting factor of the Tilt estimator as compared to the Gravity estimator.

The weighting factor of the Tilt estimator increased with the change from Eyes closed to 4 Hz stroboscopic illumination, i.e., when adding visual position cues (change: 0.75–0.87; Table 1), whereas further adding visual velocity cues had only a marginal effect (0.87–0.89). The higher weighting factor represents a better compensation of the disturbance. As the sensory input into the Tilt estimator is velocity based, the improvement of its weighting factor when adding visual position cues appears surprising. A possible explanation for the change in the tilt weight could be a higher ‘trust’ in the estimate (see above). Such a change is unlikely to be caused by simple sensory interactions, but rather indicates a higher level, or cognitive mechanism.

The weighting factor of the Gravity estimator decreased from 0.55 to 0.46, when adding visual position cues, while further adding visual velocity cues had again no considerable effect (Table 1). The decrease of this weighting factor was unexpected, as visual cues are thought to improve the estimate, while a reduced weighting factor indicates that the disturbance is less compensated. To resolve this contradictory finding, we included a retrospective report of our subjects into our considerations, indicating that already the addition of the visual position cues, when changing from Eyes closed to 4 Hz stroboscopic illumination, sufficed to allow them a more relaxed standing on the tilting support surface. This led us to consider the possibility that subjects balanced with reduced reflexive and/or passive joint stiffness in the presence of visual cues. The ability in human motor control to modulate joint stiffness is well established (Hogan, 1984; Latash & Zatsiorsky, 1993; van Soest, Haenen, & Rozendaal, 2003). A change in stiffness likely has an effect on the sway response to support surface tilt, as the disturbing effect of tilts results from the passive and reflexive stiffness of the servo mechanism. This stiffness takes the body along with the support surface, while without stiffness inertia would tend to stabilize the body and only gravity would remain as disturbing effect (compare Mergner, 2010). The sway responses to support surface tilts therefore likely modulate with changes of passive and reflexive stiffness, where a reduction of stiffness would help to reduce the disturbing effect. On the other hand, sufficient torque needs to be generated to counteract the gravitational force (Peterka, 2002). In case of reduced stiffness, other components in the balance control mechanism need to increase their contribution. The following section will explore these considerations and explore if a hypothesized change in passive and reflexive stiffness affects the disturbance estimators and can account for the unexpected change in the weighting factor of the Gravity estimator.

5.3. Relation of estimator parameters and joint stiffness

Additional model simulations were performed to test how changes in joint stiffness affect the parameters of the disturbance estimators. To change the stiffness, the passive loop gain (box Passive Muscle & Tendon Dynamics in Fig. 1) and the reflexive servo gain (box SG) were manually changed by increasing or decreasing either the reflexive or the passive loop gain, while leaving the other constant. The above described optimization procedure (see Section 3.6) was repeated to identify the model parameters in dependence on the changes in stiffness. A first finding was that changing either the reflexive loop gain or the passive loop gain by 0.1 * mgh (and damping by 0.03 * mgh) yielded very similar results, allowing to lump the identified control parameter values into corresponding mean values (Table 2). A second finding was that the estimated values for the gain of the low pass component and the time delay showed only minor changes as compared to the results shown in Table 1 and are therefore not included in Table 2, which only presents the identified parameters of the estimators.

Table 2.

Simulation results for the variation of reflexive and passive gain factors.

Visual condition	Change in stiffness	Servo gain factor⁎		Tilt estimate		Gravity estimate
		Reflexive	Passive	Threshold°/s	Weight. fact.	Threshold°	Weight. fact.
Eyes closed	No change	0.85	0.15	0.33	0.75	0.07	0.55
	Reduced	R: ↓0.75 or P: ↓0.05		0.36	0.73	0.07	0.64
	Increased	R: ↑0.95 or P: ↑0.25		0.31	0.77	0.06	0.44
Stroboscopic illumination	No change	0.85	0.15	0.33	0.88	0.02	0.46
	Reduced	R: ↓0.75 or P: ↓0.05		0.35	0.86	0.02	0.55
	Increased	R: ↑0.95 or P: ↑0.25		0.31	0.88	0.00	0.36
Continuous illumination	No change	0.85	0.15	0.20	0.89	0.03	0.46
	Reduced	R: ↓0.75 or P: ↓0.05		0.26	0.91	0.01	0.56
	Increased	R: ↑0.95 or P: ↑0.25		0.18	0.90	0.04	0.37

Bold indicates the main observed parameter changes evoked by the stiffness modification.

^⁎Servo gain factors are units of mgh for the proportional and units of 0.3 * mgh for the derivative component of the controller.

The main effect of the stiffness changes on the estimator parameters was a mutual interrelation between stiffness and the weighting factor of the Gravity estimator, while the other parameters showed only minor changes (Table 2). Increasing stiffness by 0.1 * mgh evokes a decrease in the gravity weight of about 0.1 (amplified by mgh in the neural controller) and vice versa. This relation was consistent across the three visual conditions. In view of these results, the unexpected finding of the reduced gravity weight (Table 1) could alternatively be caused by a change in passive and/or reflexive stiffness. The current simulations are preliminary, as the effects of stiffness and gravity weight cannot be separated in the optimization procedure. In previous studies, the DEC model did not include changes in passive and reflexive stiffness, as the assumption of fixed stiffness parameters was sufficient to explain the experimental data in eyes closed conditions. A decrease in stiffness may be functionally advantageous, as it reflects a shift from the joint stabilization of the Servo Loop to the context dependent Disturbance Compensation Loops (compare Fig. 1).

5.4. Integration of visual cues

The experimental design of the present study proceeded from the assumption that visual and vestibular cues are fused to provide estimates of head and, derived thereof, body orientation and velocity in space (F1 and F2 in Fig. 1). However, the study did not consider details of the fusion mechanisms, but rather the effects of the fused signals on the parameters in the disturbance estimators. Yet, the findings have implications related to the understanding of the visual integration in general. First, the study shows that there are at least two visual-vestibular fusion mechanisms, one for position and one for velocity cues. Second, the study suggests that noise reduction in the input signals of the disturbance estimates leads to, or at least is associated with a lowering of the estimation thresholds. Third, two effects were observed that may relate to changes caused by higher level, or cognitive mechanisms. These two cognitive effects are the increase of the weighting factor of the Tilt estimator and the proposed change in stiffness across visual conditions. Interestingly, these cognitive improvements were already observed when adding visual position cues.

The present study focused on the effects of visual cues on COM sway in a stationary visual scene. One important additional aspect of the visual contribution is the detection of whether, and to what extent the visual scene is stationary or moving and may accordingly be used as a space reference. The visual contribution tends to be suppressed when the visual scene is moving, involving a cognitive mechanism (Bronstein, 1986; Guerraz et al., 2001; Nashner & Berthoz, 1978), where the effect of the cognitive suppression even occurs across stimulus planes (Blümle et al., 2006). A cognitive mechanism has also been identified in visually evoked self-motion perception on a rotation chair in terms of a visual-vestibular conflict mechanism (Mergner, Schweigart, Müller, Hlavacka, & Becker, 2000; Zacharias & Young, 1981). Visual-vestibular conflict was avoided in the present study by always using the interior of the laboratory as stationary visual space reference, such that the integration of the visual cues as a space reference occurred in a conflict free way. The findings in the current study may help in future studies to identify the integration of visual cues into the posture control mechanism in situations where the visual scene is moving.