Abstract
Flagellar assembly in Salmonella is controlled by an intricate genetic and biochemical network. This network comprises of a number of inter-connected feedback loops, which control the assembly process dynamically. Critical among these are the FliA–FlgM feedback, FliZ-mediated positive feedback, and FliT-mediated negative feedback. In this work, we develop a mathematical model to track the dynamics of flagellar gene expression in Salmonella. Analysis of our model demonstrates that the network is wired to not only control the transition of the cell from a non-flagellated to a flagellated state, but to also control dynamics of gene expression during cell division. Further, we predict that FliZ encoded in the flagellar regulon acts as a critical secretion-dependent molecular link between flagella and Salmonella Pathogenicity Island 1 gene expression. Sensitivity analysis of the model demonstrates that the flagellar regulatory network architecture is extremely robust to mutations.
Electronic supplementary material
The online version of this article (doi:10.1007/s11693-015-9160-3) contains supplementary material, which is available to authorized users.
Keywords: Flagella, Salmonella, T3SS, Gene regulation
Introduction
Salmonella enterica serovar typhimurium (S. typhimurium) is a common food-borne pathogen that uses flagella to swim in liquid media and swarm on solid surfaces (Berg 2003). Flagella are located peritrichously on the bacterium’s surface, and number between 6 and 8 per cell (Karlinsey et al. 2000b). Assembly of a functional flagellum involves expression from more than 50 genes located at different regions on the chromosome (Chilcott and Hughes 2000).
Structurally, a flagellum is divided into three parts: basal-body, hook, and the filament (Macnab 1999). The basal body anchors the flagellum to the cell membrane; hook is the flexible joint that links the rigid basal-body with the filament; and the filament, a rigid helical structure which rotates to drive the cell forward (Yonekura et al. 2003). Flagellum synthesis starts from the assembly of basal body first, followed by the hook and the filament. In addition to these parts, the flagellum also needs the chemotaxis and motor proteins to sense gradients and power movement in a particular direction (Mariconda et al. 2006).
The assembly of a flagellum is linked with gene expression. Depending on their timing of activation, the promoters in the flagellar regulon are divided into three classes, namely class 1, 2, and 3 (Fig. 1) (Wada et al. 2011). Environmental and cellular signals are fed into the class 1 promoter which controls expression of two proteins, FlhD and FlhC (Chilcott and Hughes 2000; Kutsukake 1997; Yanagihara et al. 1999). The resulting proteins form a complex FlhD4C2, which activates transcription from class 2 promoters (Ikebe et al. 1999a; Wang et al. 2006). The class 2 promoters control expression of all the proteins required for the assembly of a functional hook-basal body (HBB) structure. Once the HBB assembly is complete and the resulting structure capable of secretion, expression from class 3 promoters takes place resulting in expression and assembly of filament, chemotaxis, and motor proteins. If the HBB structure is not functional, there is no class 3 expression (Hughes et al. 1993).
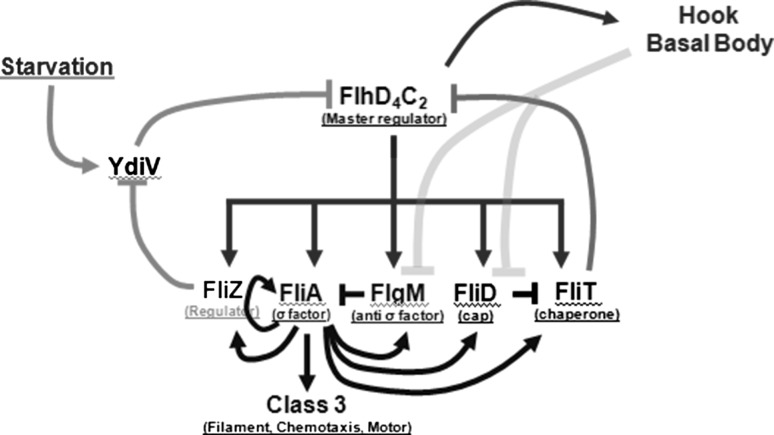
Fig. 1.
Regulatory network controlling flagella gene expression in S. typhimurium. FlhD4C2 (the master regulator) is expressed after combinatorial inputs from a large number of cellular and environmental signals. FlhD4C2 activates genes responsible for HBB, FliA (flagella-specific sigma factor), FlgM (anti-sigma factor), FliZ (regulatory protein), FliD (cap protein), and FliT (cap chaperone, and anti- FlhD4C2 factor). FliZ represses expression of YdiV transcriptionally. YdiV, whose expression is controlled in response to the nutritional status of the cell, controls FlhD4C2 amounts in the cell through control via proteolysis by ClpXP
An important feature of the flagellar biogenesis is that expression of class 3 is contingent on successful assembly of HBB structure. This logic is encoded via the following interactions. In addition to controlling expression of class 2 proteins, which form components of the basal-body structure, the FlhD4C2 complex also activates expression of FlgM and FliA. FliA is the flagella-specific sigma factor (σ28) which is essential for class 3 promoter activation (Ohnishi et al. 1992). FlgM is the anti-sigma factor for FliA. Prior to completion of HBB, FlgM binds FliA and prevents FliA-dependent activation of class 3 promoters (Chadsey and Hughes 2001; Chadsey et al. 1998). On HBB completion, the substrate specificity for export from the HBB structure changes, and FlgM is secreted from the cell (Hughes et al. 1993). The secretion of FlgM frees FliA inside the cell, which leads to activation of class 3 promoters. Interestingly, expression of both, FliA and FlgM, is also controlled by a FliA-dependent class 3 promoter (Ikebe et al. 1999b).
In addition to FliA, FlgM, and the HBB proteins; FlhD4C2 also activates expression of several other regulators. These include FliZ, FliD, and FliT (Karlinsey et al. 2000a; Kutsukake et al. 1999). All three regulators are under the dual control of class 2 (activated by FlhD4C2) and class 3 (activated by FliA) promoters. FliZ is a protein of unknown homology which positively regulates flagella gene expression (Kutsukake et al. 1999; Mytelka and Chamberlin 1996; Saini et al. 2008). FliZ is expressed in the same operon as FliA, and controls class 2 gene expression via a protein YdiV (Wada et al. 2011). YdiV controls the amounts of FlhD4C2 amounts in the cell by controlling its exposure to ClpXP protease (Takaya et al. 2012). In addition, FliZ is also known to activate expression of the genes located on the Salmonella Pathogenicity Island-1 (SPI1) (Chubiz et al. 2010).
FliD is the cap protein of the flagella, and its point of assembly defines the distal end of the flagellum. FliT is the chaperone for FliD and is expressed from the same operon as fliD (Kutsukake et al. 1999; Yamamoto and Kutsukake 2006). Prior to HBB completion, FliT is bound to the intracellular FliD (Aldridge et al. 2010). However, on completion of HBB, FliD is secreted from the flagellum to be assembled at its distal end. This frees the intracellular FliT, which feeds back and interacts with the FlhD4C2 complex, resulting in formation of a FlhD4C2:FliT complex. This FlhD4C2:FliT complex is unable to activate expression from class 2 promoters (Aldridge et al. 2010). Thus, FliT forms a secretion dependent negative feedback loop controlling expression of class 2 genes in the flagella regulon (Fig. 1).
Interestingly, none of FlgM, FliZ, or FliT is essential for assembly of a functional flagellum (or swimming) in Salmonella (Aldridge et al. 2010; Saini et al. 2008, 2011). This leads us to a question that what role do feedback loops encoded by these regulators play in the flagella regulatory network? To answer this question, we developed a mathematical model describing regulation and dynamics of gene expression in the flagellar network. Our model predicts that the feedback loops encoded by FlgM, FliZ, and FliT are essential for correct timing of expression of genes. This is true not only for transition from non-flagellated to a flagellated state, but also when a cell with existing flagella divides. We also show that FliZ likely links flagellar gene expression with SPI1 gene expression in a secretion-dependent manner. SPI1 encodes for a Type 3 Secretion System (T3SS) which is essential for the bacterium gaining entry into the host cell. Collectively, we show that the flagellar regulatory network comprises of many non-trivial interactions, and each is designed for robustness and control over the assembly and function of flagella. Our model also exhibits a role for interlinked feedback loops in regulatory networks, where feedback loops are activated (or deactivated) in response to secretion status of the cell (which corresponds to the flagellar abundance on the cellular surface).
Development of the mathematical model
Mathematical model was developed using a deterministic formulation of flagellar gene regulation. The following species were modeled in our simulations: FlhD4C2 (represented as FlhDC in equations for simplicity), HBB (representing all class 2 proteins), FlgM, FliA, FlgM–FliA complex, FliD, FliT, FliD–FliT complex, FliZ, YdiV, FlhD4C2–FliT complex, and class 3 proteins. All parameter values used in the equations are listed in Table 1. Many of the biochemical interactions in the flagellar network are well established, hence, we have accurate estimates of biochemical parameters. Particularly, the parameters associated with FliA–FlgM interactions are taken from Barembruch and Hengge’s work (2007) the association and disassociation constants from Chadsey et al.’s work (1998) and from a previous mathematical study on flagellar regulation (Saini et al. 2011). For all remaining parameters, there are no quantitative measurements available. However, considerable work on biochemistry of the interactions provides us with inputs regarding the relative magnitudes of parameters. Hence, the remaining parameters are estimated to best fit the data from a number of experimental studies on the flagella system (Aldridge et al. 2003, 2010; Saini et al. 2008, 2011). The model was developed with the following assumptions:
Expression from the class 1 promoter is known to be controlled via a large number of global regulators, via unknown mechanisms (Clarke and Sperandio 2005; Ko and Park 2000; Teplitski et al. 2003; Tomoyasu et al. 2002; Wei et al. 2001). It is also not clear how these inputs are integrated at the class 1 promoter (or post-transcriptionally) leading to the control of FlhD4C2 production. In the absence of these details, these effects have been lumped together as a step function that feeds into the class 1 promoter (Saini et al. 2011). FlhD4C2 autoregulation has been neglected. FlhD4C2 has been observed to auto regulate its expression, (Kutsukake 1997) but this effect has been found to be relatively weak and hence, has been left out from our equations.
FliZ has been assumed to control YdiV expression, which, in turn controls the amounts of FlhD4C2 inside the cell. FliZ has been shown to control protein amounts of FlhD4C2 previously, and we assume in our model, that this happens via YdiV (Wada et al. 2011).
Flagella network has recently been shown to exhibit bistability at class 2 gene expression level (Koirala et al. 2014). This bistability is presumably due to heterogeneity in the induction of the ydiV promoter (as a result of the availability of nutrients in the surrounding environment). However, as there are no details available regarding expression from the ydiV promoter, our model does not capture this bistability, or the cell-to-cell heterogeneity, as observed previously in the flagellar network (Saini et al. 2010a).
FliZ and FliA (and similarly FliD and FliT) are expressed from the same operon (Ikebe et al. 1999b; Kawagishi et al. 1992; Mytelka and Chamberlin 1996; Yokoseki et al. 1995) and the model assumes that their production rates, both from the class 2 and class 3 transcripts, are identical. In addition, we have assumed that the production rates for FliA and FliZ (and similarly, FliD and FliT) are additive with respect to expression from class 2 and class 3 transcripts. This is supported by evidence that the binding sites of FlhDC complex and FliA in both, the fliAZ and fliDST operons do not overlap (Kutsukake and Ide 1995; Tanabe et al. 2011). However, real time data regarding interaction of the two promoters is not available. In addition, there is no known effects of translational coupling on the fliAZ or fliDST operons.
FlgM is assumed to be only exported when bound to FliA. Absence of FliA, reduces secretion of FlgM significantly, and has been ignored in the model (Aldridge et al. 2006). Similarly, it has been assumed in the model that FliD is only secreted from the cell when bound with its chaperone FliT. Free FliD has been assumed to be incapable of secretion (Aldridge et al. 2010).
HBB [which comprises of more than ten proteins (Chilcott and Hughes 2000)] has been assumed as a lumped variable, and its expression has been assumed to be solely dependent on FlhD4C2. Moreover, HBB expression has been assumed to be a continuous variable. In reality, a functional HBB will be a discrete event in the cell, and secretion from completed HBBs will increase in steps. Rather, our model assumes a continuous increase/decrease in HBB amounts, and consequently secretion. While this assumption is clearly an over-simplification of the assembly process, there is little data available on dynamics of HBB assembly inside a cell (Karlinsey et al. 2000b). In the absence of these details, our model proceeds with this over-simplified assumption.
Our model assumes that secretion of regulatory proteins from the HBBs is linear to the amount of HBB produced in the cell (Saini et al. 2011). In reality, the amount of protein secretion would likely reach a saturated state, once the cell has assembled sufficient HBBs. However, there is no experimental data available to provide evidence for this claim. In addition, we also assume that the secretion from a HBB is independent of the developmental stage of an HBB (Rosu and Hughes 2006).
FliS and FlgN, chaperones for filament FliC and hook-associated proteins (HAPs) FlgKL respectively, have also been reported to play a regulatory role in the flagellar cascade (Aldridge et al. 2003; Muskotal et al. 2006). However, these effects are relatively minor and thought to be mechanisms for fine-tuning gene expression. Recently, FliS has also been shown to interact with FlgM, and sequester its binding with FliA (Galeva et al. 2014). Hence, FliS plays a dual role in the cell, where it is interacting with FliC as well as FlgM. In the absence of any data as to how FliS interacts with FlgM in presence of FliC, these effects have not been included in the model.
The FliA. FlgM complex is considered to be stable as compared to FliA and FlgM inside the cell. Hence, in our model, the degradation of FliA. FlgM complex has been ignored (Barembruch and Hengge 2007; Chadsey and Hughes 2001).
Unbound FliA, FlgM, and FliD are unstable, and hence have a fast turnover. This is represented in the model by choosing a high degradation rate constant (same for all three). All other proteins have been assumed to be relatively more stable, and hence a lower degradation rate has been chosen for all other protein species in the system (Table 1). By choosing only two degradation rates in our model, we minimize the number of free parameters used.
We assume that gene expression dynamics is governed by protein numbers per cell rather than protein numbers per volume. Typical size of E. coli is small enough that the time for a protein to diffuse from one to the other is of the order of mseconds (Burton 2000). As a result, time for the proteins to find their targets is small compared to the other processes like transcription, translation (Paulsson 2005). As a result, the effect of dilution in terms of the time required for proteins to find their regulatory targets has been ignored.
With the above listed assumptions, the equations governing the kinetics of expression of flagella genes were developed as follows:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
Table 1.
List of parameters used in the model and their values
| Parameter | Value | Description |
|---|---|---|
| K1 | 3 | Maximal class 1 promoter activity |
| KDCT/KDC.T | 1,000 | Rate constant FlhDC. FliT formation/break |
| Β | 10 | Negative regulation by YdiV |
| K2 | 5 | Activation of HBB expression by FlhDC |
| K2m | 10 | Michaelis constant for HBB activation by FlhDC |
| K3 | 9 | Activation of FlgM by FlhDC |
| K3m | 3 | Michaelis constant for FlgM activation by FlhDC |
| K7 | 5 | Activation of FlgM by FliA |
| K7m | 1 | Michaelis constant for FlgM activation by FliA |
| KA.M/KAM | 333 | Ratio of rate constant of FliA. FlgM complex formation/break |
| K4 | 3 | Activation of FliAZ by FlhDC |
| K4m | 8 | Michaelis constant for FliAZ activation by FlhDC |
| K8 | 10 | Activation of FliAZ by FliA |
| K8m | 6 | Michaelis constant for FliAZ activation by FliA |
| Ksec | 0.1 | Secretion rate constant from HBB |
| K6 | 8 | Activation of class 3 by FliA |
| K6m | 40 | Michaelis constant for class 3 activation by FliA |
| K9 | 1 | Activation of FliDT by FlhDC |
| K9m | 1 | Michaelis constant for FliDT activation by FlhDC |
| K10 | 1 | Activation of FliDT by FliA |
| K10m | 1 | Michaelis constant for FliDT activation by FliA |
| K12 | 0.1 | Activation of FliT by FlhDC |
| K12m | 10 | Michaelis constant for FliT activation by FlhDC |
| K13m | 50 | Michaelis constant for FliT activation by FliA |
| KD.T/KDT | 1,080 | Ratio of rate constant of FliD.FliT complex formation/break |
| K | 0.35 | Maximal rate of expression of YdiV |
| Γ | 30 | Repression coefficient of YdiV by FliZ |
| X | Between 0 and 1 | Starvation status of the cell |
| Kd | 0.1 | Degradation constant |
| Kd2 | 1 | Degradation constant |
Parameters without references in the description column were approximated to best represent the experimental data
The equations were solved in MATLAB 7.10.0. To simulate mutant behavior, we substituted the formation term of the appropriate gene’s equation by a zero. For instance, to capture dynamics in a mutant where FliZ is only produced from the class 2 promoter, we replaced the FliA-dependent formation of FliZ (Eq. 5) by zero. Unless otherwise mentioned, the simulations were performed with initial number of all flagellar proteins equal to zero (Saini et al. 2011).
Cell division, and the consequent gene expression dynamics were modeled in the following manner. Under a given nutritional condition, the equations were simulated to steady state expression levels. At steady state, cell division was assumed to have occurred which would reduce all protein numbers in the cell by a factor of two. This reduced number of protein molecules in the cell was used as the initial condition for simulating dynamics post division. Kinetics of class 2 and class 3 promoters were observed.
Results and discussion
Hierarchical expression of class 2 and class 3 genes in flagellar regulon (WT and mutants)
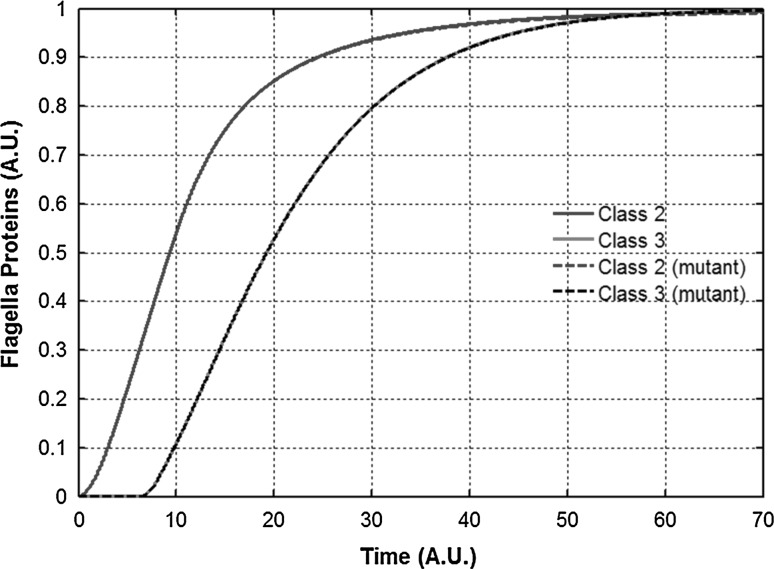
A characteristic feature of flagellar gene expression is hierarchical expression of class 2 and class 3 genes. In wild-type Salmonella, expression of class 3 genes only starts after the HBB assembly has been successfully completed (Saini et al. 2008, 2011). Consistent with these experimental observations, our model captures this qualitative aspect of flagellar regulation (Fig. 2). In addition, simulations of our model in a ΔflgM mutant leads to elimination of the lag in expression of class 3 genes. In a HBB mutant, since no secretion is possible, class 3 expression is eliminated (Kutsukake and Iino 1994). However, there is no significant impact on class 2 gene expression. Similarly, in a ΔfliA mutant, there is no significant effect on class 2 gene expression (either end-point or kinetic) and class 3 expression is eliminated (Kutsukake 1997) (Supplement Fig. 1). Similarly, kinetic experiments from previous reports were used to calibrate and validate our model (Aldridge et al. 2010; Saini et al. 2008, 2011).
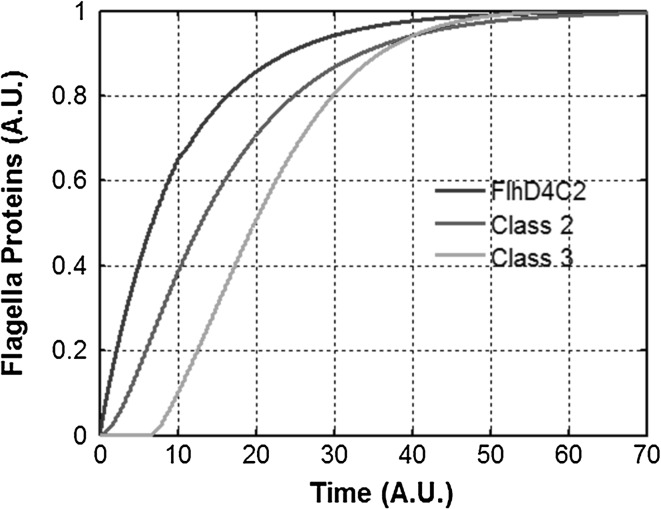
Fig. 2.
Hierarchical expression of flagella genes. Dynamics of expression of class 1, class 2, and class 3 genes in flagella regulatory network in wild-type S. typhimurium. Characteristic of the expression pattern is the delay in induction of class 3. This delay corresponds to the time required by the bacterium to assemble a sufficient number of HBBs to relieve FlgM repression of FliA. The class 1 product in the graph represents the free FlhD4C2 present in the cell, and does not include the FlhD4C2 bound with FliT. Class 2 proteins represent the HBB proteins lumped together. Class 3 proteins represent the filament, chemotaxis, and motor proteins
In addition, our model is able to capture successfully the dynamics of gene expression in fliZ, fliT, and fliD mutants. A ΔfliZ mutant leads to slower and lower expression of class 2 genes, as observed previously (Saini et al. 2008). In addition, impact of FliZ on flagella gene expression was found to be dependent on the nutritional status of the cell, as observed previously (Wada et al. 2011). Specifically, the impact of a fliZ mutation was minimal when the starvation levels are low (i.e., the cells are grown in rich media) but the impact increases as the starvation increases. A ΔfliZ mutation was also found to lead to lower class 3 expression levels, as has been observed previously (Saini et al. 2008). In absence of FliT, our model validates that the expression of both class 2 and class 3 genes is up regulated as compared to wild type, where as in absence of FliD, lower levels of class 2 and class 3 proteins (compared to wild-type) are observed (Aldridge et al. 2010) (Supplement Fig. 1).
We also note that the free-FlhD4C2 (the class 1 product) reaches its maximal value at the time when secretion is just about to begin. Post-secretion, the amount of free class 1 product decreases inside the cell because of sequestration by FliT.
Previous modeling efforts regarding flagella gene regulation have only focused on the FliA–FlgM interaction, or the hook-length control in growing flagella (Barembruch and Hengge 2007; Chadsey and Hughes 2001; Chilcott and Hughes 2000; Saini et al. 2011). There has been no published attempt to capture the dynamics of gene expression with the multiple and coupled feedback loops driving the flagella gene expression. In addition, all earlier gene expression dynamics modeling efforts have focused on studying the transition from a non-flagellated to a flagellated state in Salmonella. However, experimental evidence suggests that the class 1 promoter in Salmonella, unlike in E. coli, is never in the OFF state, (Karlinsey et al. 2000b) and hence, a typical OFF to ON transition does not capture the physiological state of the organism.
Steady state class 2 and class 3 expressions at various nutritional levels
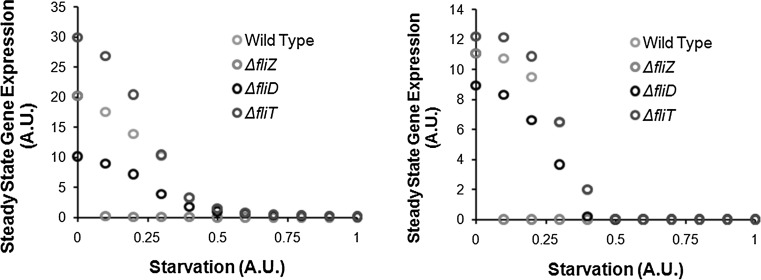
Since flagellar gene expression (via the FliZ-dependent feedback loop) in Salmonella is strongly linked with the nutritional status of the cell, we explored the relationship by studying the steady state class 2 and class 3 gene expression under a variety of nutritional status of the cell. Our model predicts that the flagella assembly is linked with the expression kinetics of the gene ydiV. In our model, we have assumed YdiV expression to be linearly proportional to the nutritional status of the cell. However, in terms of the steady state gene expression of class 2 and class 3 levels, this leads to two distinct regimes. In the first phase (at low starvation levels), the class 2 expression decreases rapidly with increase in starvation (Fig. 3). However, after reaching a certain critical value, the repression from increased starvation shuts down flagella gene expression. This has previously been observed experimentally where in conditions of poor nutrition, a majority of the cells across a population do not have flagella (Aldridge et al. 2010). Thereafter, increasing the starvation levels of the cell do not have any effect on the steady state expression levels of class 2 and class 3 proteins. Interestingly, the mutants exhibit different sensitivities to the nutritional status of the cell. For instance, as compared to the fliD mutant, the fliZ mutant exhibits higher class 2 and class 3 expression levels in conditions of no nutritional stress. However, as stress in introduced in the surroundings, the FliZ-dependent feedback is much more sensitive and as a result, the fliZ mutant exhibits a much steeper decline in class 2 and class 3 expression (Fig. 3a, b). This demonstrates that the relative strength of the various feedback loops in the network is contingent on the precise environmental conditions under which the bacteria are grown. Recently, YdiV has also been shown to be involved in causing bistability in flagellar network in Salmonella (Koirala et al. 2014). However, regulation and kinetics of the ydiV promoter are not yet understood. Hence, the precise cause of this bistability is difficult to comment on.
Fig. 3.
Steady State class 2 (left) and class 3 (right) gene expression in wild type, ΔfliZ, ΔfliD, and ΔfliT mutants. At high starvation levels, flagella gene expression is repressed in Salmonella. Between the two feedback loops, FliZ’s impact on gene expression is the strongest in response to nutritional conditions
From this, we note that the two feedback loops in the network (FliZ- and FliT-dependent) likely serve two distinct purposes. In the absence of FliZ, the rate of decrease in class 2 gene expression (with increasing starvation) is much more rapid as compared to wild type. Thus, the FliZ-phenotype becomes much more significant at low levels of starvation than in poor media. A similar trend is observed for class 3 gene expression. Thus, FliZ helps the cell assemble flagella in rich environmental conditions. On the other hand, FliT and FliD mutants are likely involved in only tuning the gene expression. Our results show that in ΔfliT and ΔfliD mutants, class 2 and class 3 gene expression is up- and down-regulated as compared to the wild type, respectively. This effect is most prominent at low starvation levels. As starvation levels increase, the mutant profile approaches that of the wild-type. This is qualitatively different from the wild type and the ΔfliZ curves, where the difference between the steady state expression curves grows till the curve for the mutant reaches zero expression values.
Response to cell division in WT and mutants
An open question regarding flagellar regulation in Salmonella is how the cell responds to cell division and regulate expression (Aizawa and Kubori 1998). In our model, we have linked gene expression of the flagella genes with protein secretion. On division, the existing flagella are divided among the progenies randomly, which leads to a decrease in the total protein secretion per unit time from a cell. This leads to realignment of the regulatory network in the cell, leading to changes in rate of expression of the different species. Specifically, change in protein secretion rate from the cell changes the amount and ratio of regulators present inside the cell. The changed relative ratios then exert altered control over the network. To check how the cell re-adjusts gene expression after division, we performed simulations where after cell division, the protein amounts present in the cell were halved, and the dynamics of class 2 and class 3 gene expression studied.
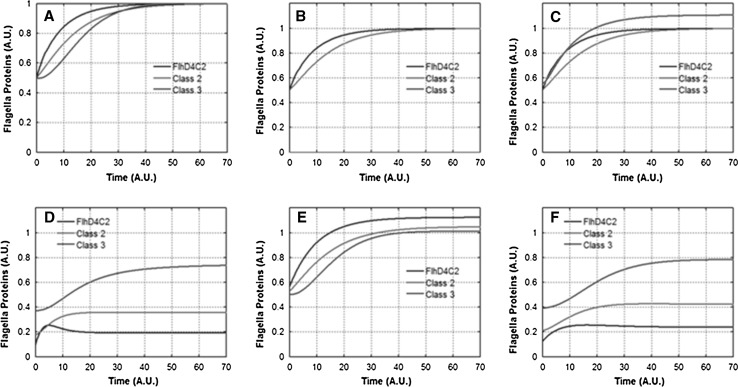
Our simulations show that in wild type, post-division, the cell readjusts its gene expression rates to assemble additional flagella. In this readjustment phase, the hierarchy of gene expression is again maintained (Fig. 4a). This hierarchy is likely important as premature expression of class 3 genes is known to impact the growth of the cell (Chilcott and Hughes 2000). As against this, in ΔflgM, ΔfliZ, and ΔfliD mutants, the hierarchy of gene expression is not maintained post cell-division. In particular, in these mutants, upon division, class 3 gene expression leads class 2 gene expression. Thus, we propose that an additional role of the feedback loops associated with FlgM, FliZ, and FliD is to control the hierarchical expression of genes post cell-division. In ΔfliT mutant, the expression of the three classes of genes is hierarchical, implying that absence of FliT does not directly control hierarchy of expression post division. However, all classes of genes were upregulated as compared to the wild type, suggesting FliT’s role in negatively controlling number of flagella per cell (Fig. 4b–f) (Aldridge et al. 2010).
Fig. 4.
Dynamics of flagella gene expression post cell-division. Class 1, class 2, and class 3 gene expression dynamics after cell division in a Wild Type, b ΔfliA, c ΔflgM, d ΔfliZ, e ΔfliT, and f ΔfliD mutants. Note that in ΔflgM, ΔfliZ, and ΔfliD mutants, class 3 (red) gene expression leads class 2 (green) gene expression. Class 2 proteins represent the HBB proteins lumped together. Class 3 proteins represent the filament, chemotaxis, and motor proteins
We consider this to be a significant input and prediction from our model. Why the flagella gene expression system needs a large number of feedback loops has been an open question, especially because many of these auxiliary regulators are non-essential for motility and only have a limited to no impact on swimming speed. Our model predicts that there is an important physiological role served by these regulators, which is only apparent when studying cell division and the associated regulation of flagella number and assembly.
Secretion dependent FliZ-positive feedback loop is not required for flagellar gene expression regulation
An additional feature of the flagellar gene regulatory network architecture is the presence of different feedback loops at different secretion rates during assembly. At low/no secretion, the FliZ-dependent positive feedback loop is active, whereas at high secretion rates, the FliT-dependent negative feedback loop is active (Aldridge et al. 2010; Saini et al. 2010a). However, at high secretion, another FliZ-dependent positive feedback loop is active. This includes FlhD4C2-dependent activation of FliA. FliA autoregulation and activation of FliZ, and FliZ-dependent positive regulation of FlhD4C2. This implies that at high secretion rates there are two antagonistic feedback loops controlling FlhD4C2 amounts/activity.
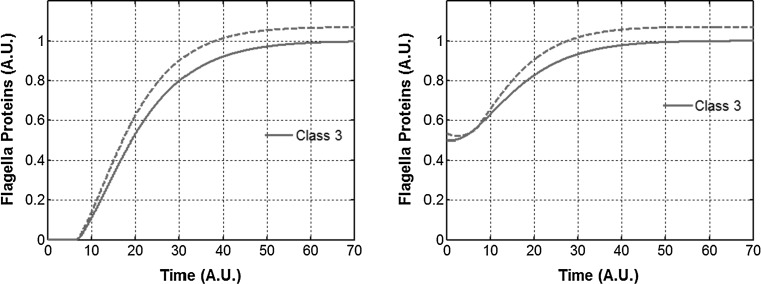
To ascertain the role of these feedback loops we performed a simulation where we set production of FliZ independent of FliA. That is, FliZ expression was solely under the control of the FlhD4C2-dependent promoter. Experimentally, this is equivalent to removing FliZ from its chromosomal locus, and placing it under a class 2 promoter elsewhere on the chromosome. Mathematically, in our model, this is equivalent to replacing the FliA-dependent FliZ production term by zero. Note that in this mutant, FliA is still under both class 2 and class 3 promoters. Class 2 and class 3 dynamics for this mutant show that there is no discernible class 2 or class 3 gene expression difference between the mutant and the wild type (Fig. 5). This suggests that the late FliZ (expressed from class 3) does not have any role in control of flagella gene expression. This likely implies that post-secretion, FliZ made from the class 3 transcript is responsible for activation of SPI1 and SPI4 gene expression. The role of FliZ in activating SPI1 and SPI4 gene expression has been previously reported (Chubiz et al. 2010; Kage et al. 2008; Saini and Rao 2010; Saini et al. 2010b).
Fig. 5.
FliZ from the class 2 transcript controls class 2 gene expression dynamics. Gene expression dynamics in Wild type and a mutant where FliZ production from the class 3 transcript has been set to zero. FliZ is only being produced from the class 2 transcript. Class 2 proteins represent the HBB proteins lumped together. Class 3 proteins represent the filament, chemotaxis, and motor proteins
Hence, our modeling results suggest that late expression of FliZ dictates timely activation of SPI1 and SPI4 in the Salmonella infection cycle, and that FliZ acts as a molecular link between these systems involved in infection. Physiologically, this prediction from our model has important implications for the infection process. Our prediction suggests that the initial role of FliZ in the cell is to aid assembly of sufficient number of HBBs, presumably to help the bacterium locate its preferred site of infection (Iyoda et al. 2001). However, once that is accomplished, late FliZ (from the class 3 promoter) is used by the cell as a signal to prepare for the next phase of infection, i.e. expression of the T3SS encoded on the SPI1 locus (Lostroh and Lee 2001).
FliA-dependent activation of FlgM ensures an effective “off” switch for class 3 gene expression as cells transition from high- to low-secretion regime
Another curious regulatory interaction in the flagella network is activation of FlgM by FliA (post-secretion). Post-secretion, FlgM is constantly secreted from the cell, and hence plays no role in regulation. However, the network not only activates FlgM production via FliA but also stabilizes the class 3 flgM transcript via FlgN (which is the chaperone for the hook-associated proteins, FlgKL) (Karlinsey et al. 2000a). This post-secretion activation of FlgM, intuitively, seems wasteful. To test the possible role for this regulation, we performed simulations in a mutant where post-secretion FlgM production is absent. This is equivalent to making FlgM expression only dependent on FlhD4C2.
In our simulations, we tested the dynamics of class 2 and class 3 gene expression in wild-type and this regulatory mutant (Fig. 6). Our results show that in wild type, FlgM resulting from class 3 transcript is only incremental in halting class 3 expression. In both the wild type and the mutant, post cell-division, class 3 expression is halted for some time, and increases thereafter. The increase in the mutant is however, greater than in the wild type (Fig. 6b). The delay in class 3 expression could be important for the cell. Upon division, the secretion rate from the flagella decreases, and the cell needs to build more HBBs. During this time, when the secretion is low, aggressive expression of class 3 genes could be deleterious to the cell. This is because class 3 products include FliC (flagelllin) and if not secreted effectively, FliC polymerizes inside the cell leading to death (Auvray et al. 2001; Yokoseki et al. 1995). Hence, from a cellular perspective it is very important that class 3 expression is commensurate with the secretion capability of the cell. And our results show that the FlgM activation by FliA is designed to provide a check for this effect.
Fig. 6.
FlgM from the class 3 transcript controls the dynamics of class 3 gene expression. (Left) class 3 gene expression in Wild Type (solid) and a mutant where FliA does not regulate FlgM expression (dash). (Right) class 3 gene expression in WT (solid) and mutant (dash) upon cell division. Class 3 proteins represent the filament, chemotaxis, and motor proteins
Fraction of free-FlhD4C2 complex as a function of class 3 expression (or secretion) in WT, fliZ mutant, fliD mutant, and a fliT mutant
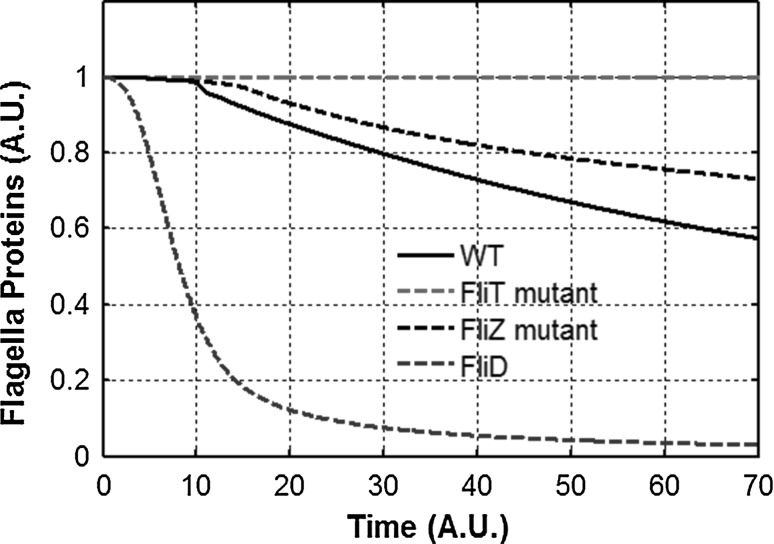
The modes of regulation of FlhD4C2 by FliZ and FliT are different. While FliZ controls FlhD4C2 amounts in the cell, FliT controls the activity of the FlhD4C2 transcription factor complex. However, both control the relative ratio of the FlhD4C2 complex in the active form. By active form, we mean the fraction of FlhD4C2 which is not bound to FliT. Our model demonstrates that there is a significant difference in the fraction of the FlhD4C2 present as free-FlhD4C2 between wild type, ΔfliD, ΔfliT, and a ΔfliZ mutant (Fig. 7).
Fig. 7.
Feedback loops control the amount and fraction of free FlhD4C2 inside the cell. Fraction of free FlhD4C2 complex inside the cell in wild type, ΔfliZ, ΔfliT, and ΔfliD mutant as a fraction of time. FlhD4C2 is assumed to exist either freely or bound with FliT. All values are normalized with respect to the wild type levels of total FlhD4C2 amounts inside the cell
As expected, as compared to the wild type, the fraction of FlhD4C2 which is free is reduced in a ΔfliD and is always equal to one in a ΔfliT mutant. This temporal control of free FlhD4C2 is as shown in Fig. 8. However, contrary to expectation, we also note that the fraction is enhanced in a ΔfliZ mutant (compared to wild type). The absence of FliZ leads to a fall in the intracellular levels of FlhD4C2. As a result, class 2 gene expression (and consequently HBB) is considerably lowered as well. Lower expression of HBB leads to slow secretion, which implies that FliD secretion from the cell is less than as compared to the wild type. This reduced secretion of FliD sequesters the intracellular FliT, and negatively controls the FliT-mediated negative feedback loop in the network. Hence, FliD acts as an anti–anti- FlhD4C2 factor, as proposed before (Aldridge et al. 2010). However, we propose that the strength of the FliT- FlhD4C2 loop is controlled by FliZ present in the cell. The absence of FliZ is “sensed” by the cell in terms of reduced HBB expression, and the cell tried to compensate for this loss of HBB expression by retaining more of FlhD4C2 in the cell in its free form.
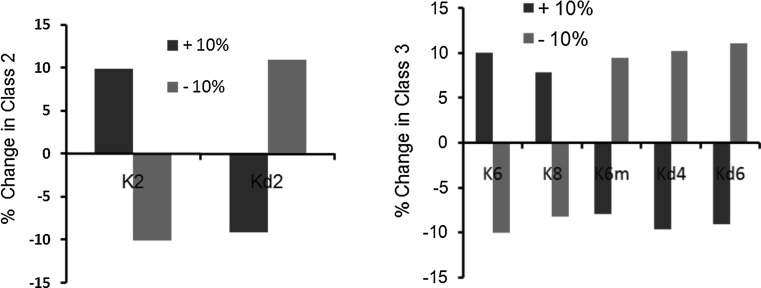
Fig. 8.
Sensitivity analysis. Class 2 (left) and class 3 (right) expression values on making 10 % change in the parameter values. Red bars indicate change in steady state value after increasing the parameter value by 10 %, and green bars indicate the change in steady state value after decreasing the parameter value by 10 %. Changing values of all other model parameters resulted in <10 % change (data not shown). Kd2 is the degradation constant of class 2 genes. Kd4 and Kd6 are the degradation constants of FliA and Class 3 proteins respectively
Sensitivity analysis of model parameters
Salmonella has been a model organism to study regulation and assembly of flagella in a number of studies. This has led to characterization of a number of biochemical and genetic interactions in the system, which has significantly aided in modeling the system. To characterize the relative significance of the various parameters associated with the network, we simulated the network after having changed the value of each parameter (one at a time) by ±10 %, and observed the change in the difference in the steady state values of class 2 and class 3 gene expression levels. Our results identified two sets of eight parameters which were found to be significant in controlling flagella gene expression. The parameters are as presented in (Fig. 8). All other parameters were found to result in a percent change <5 % in our analysis (data not shown).
Our results show that for class 2 gene expression, there are only two model parameters which exhibit a more than 10 % change in steady state values (on changing the parameter value by ±10 %). These two are FlhD4C2-dependent parameter K2, and the degradation rate of class 2 products, Kd2. In the case of class 3 gene products, the expression is sensitive to five parameters, which include: degradation constants of FliA and class 3 products, and constants associated with FliA-dependent activation of Class 3 genes and FliA (Fig. 8). Despite being a complex network, change in value of no other parameter (one at a time) exhibited a significant change in steady state expression of class 2 and class 3 products. From a networks perspective, this indicates that the flagellar regulatory network in Salmonella is extremely robust against mutations.
Conclusions
In this work, we have developed a mathematical model of the flagellar regulatory network in the model organism S. typhimurium. Flagellar gene regulation has been the subject of interest in a large number of experimental studies (Chilcott and Hughes 2000; Jones and Aizawa 1991; Macnab 1977, 1999, 2003; Silverman and Simon 1974). The regulatory network includes a number of coupled feedback loops, which makes it difficult to decouple the role of each interaction experimentally. The modeling efforts in this direction have been limited to only the FliA–FlgM interaction, which has been the most well-understood interaction in the network, and is thought to be the key check-point in the process (Chevance and Hughes 2008; Chilcott and Hughes 2000; Hughes et al. 1993). However, important differences exist between flagellar regulation in E. coli and Salmonella. One, both respond differently to stress. Second, unlike E. coli, in Salmonella, the flagellar regulon is never truly in the OFF state. And last, in Salmonella, motility is a virulence factor, and proteins from the flagellar network have been shown to regulate genes on Pathogenicity Island of the organism (Chubiz et al. 2010; Iyoda et al. 2001; Kage et al. 2008). To study these questions, we develop a model taking into account all major feedback loops in the network, and study the impact of different interactions on the dynamics of gene expression.
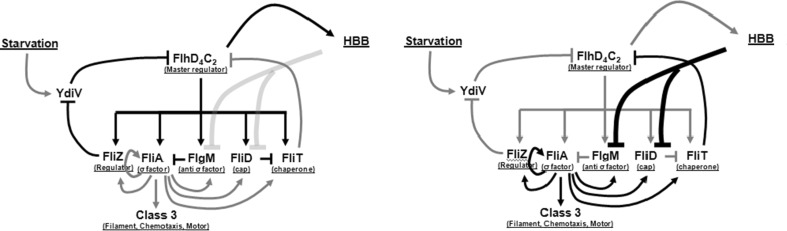
Through the aid of the model, we demonstrate that the number of feedback loops encoded in the network play a role of precisely timing the hierarchical expression of genes in this network. Our model is the first mathematical expression of the flagellar network where we demonstrate that the relative strength of these loops changes with the secretion status of the flagella in a cell. In a non-flagellated state (or in absence of secretion), the regulatory interactions which predominantly drive gene expression are as shown in Fig. 9 (left panel). As the cell assembles more and more number of HBBs capable of secretion, the regulatory network moves towards Fig. 9 (right panel). This transition is continuous as the cell assembles more and more HBBs, but also discrete since completion of a HBB is a discrete event. In addition, we show that one of the major roles of the accessory proteins in the network (FlgM, FliZ, and FliD) could be to ensure hierarchy of expression of class 2 and class 3 genes upon cell division. This is likely important as premature expression of class 3 products is known to be detrimental to cell growth. Another insight from the model is the prediction that FliZ is the secretion-dependent link between flagella and the SPI1 regulatory network. FliZ has been previously shown to be activator of SPI1 gene expression, and our model predicts that this happens post-secretion (Chubiz et al. 2010; Iyoda et al. 2001; Lucas et al. 2000). Previous modeling efforts of the flagellar regulon have been limited to the FliA–FlgM interaction only (Kalir et al. 2005; Saini et al. 2011). As a result, these models have been unable to capture the additional roles of regulators and feedback loops that our model predicts in this study.
Fig. 9.
Flagella regulatory network tunes in response to the secretion from the assembled HBBs. (Left at low secretion rates): FliD sequesters FliT, and FlgM sequesters FliA. As a result, all interactions regulated by free FliA and FliT are inactive (in grey). The active interactions in this regime are highlighted in black. (Right at high secretion rates): FlgM and FliD are actively secreted from the cell. Free FliA activates expression of class fliAZ, fliDST, flgM, and class 3 promoters. FliT interacts with FlhD4C2 to repress FlhD4C2-dependent activation of class 2 promoters. In both figures, black arrows represent active interactions, and grey represent inactive interactions. The transition from black to grey (or vice versa) is gradual
From a networks perspective, more than 50 genes come together leading to a functional flagella (Chilcott and Hughes 2000). In addition to their timely activation and assembly, it is also desirable that the network is immune to mutations and changes in biochemical parameters. We show that the regulatory structure of the flagella network is such that it renders steady state expressions of class 2 and 3 genes dependent on a minimal number of parameters.
From a networks perspective, feedback has been demonstrated to play an important role in control of biological processes, including virulence (Brandman et al. 2005; Freeman 2000; Kim et al. 2007; Mitrophanov and Groisman 2008; Saini and Rao 2010; Shin et al. 2006; Thomas et al. 1995). In this direction, our work adds to the number of behaviors known to be exhibited by living cells using feedback in networks. Among this, the role of secretion to tune the strength of the various feedback loops is a critical and novel one. From the perspective of Salmonella pathogenesis, further work needs to be done to validate and test predictions from our model, and shed more light on the multi-process control of the Salmonella infection cycle (Clegg and Hughes 2002; Ellermeier and Slauch 2003; Iyoda et al. 2001; Saini et al. 2010b; Wu et al. 2012).
Electronic supplementary material
Acknowledgments
This work was funded by the Innovative Young Biotechnologist Award (IYBA) 2010 program of the Department of Biotechnology, Ministry of Science and Technology, Government of India.
Footnotes
Kirti Jain and Amit Pradhan have contributed equally to this study.
References
- Aizawa SI, Kubori T. Bacterial flagellation and cell division. Genes Cells. 1998;3:625–634. doi: 10.1046/j.1365-2443.1998.00219.x. [DOI] [PubMed] [Google Scholar]
- Aldridge P, Karlinsey J, Hughes KT. The type III secretion chaperone FlgN regulates flagellar assembly via a negative feedback loop containing its chaperone substrates FlgK and FlgL. Mol Microbiol. 2003;49:1333–1345. doi: 10.1046/j.1365-2958.2003.03637.x. [DOI] [PubMed] [Google Scholar]
- Aldridge PD, Karlinsey JE, Aldridge C, Birchall C, Thompson D, Yagasaki J, Hughes KT. The flagellar-specific transcription factor, sigma28, is the type III secretion chaperone for the flagellar-specific anti-sigma28 factor FlgM. Genes Dev. 2006;20:2315–2326. doi: 10.1101/gad.380406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldridge C, Poonchareon K, Saini S, Ewen T, Soloyva A, Rao CV, Imada K, Minamino T, Aldridge PD. The interaction dynamics of a negative feedback loop regulates flagellar number in Salmonella enterica serovar typhimurium. Mol Microbiol. 2010;78:1416–1430. doi: 10.1111/j.1365-2958.2010.07415.x. [DOI] [PubMed] [Google Scholar]
- Auvray F, Thomas J, Fraser GM, Hughes C. Flagellin polymerisation control by a cytosolic export chaperone. J Mol Biol. 2001;308:221–229. doi: 10.1006/jmbi.2001.4597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barembruch C, Hengge R. Cellular levels and activity of the flagellar sigma factor FliA of Escherichia coli are controlled by FlgM-modulated proteolysis. Mol Microbiol. 2007;65:76–89. doi: 10.1111/j.1365-2958.2007.05770.x. [DOI] [PubMed] [Google Scholar]
- Berg HC. The rotary motor of bacterial flagella. Annu Rev Biochem. 2003;72:19–54. doi: 10.1146/annurev.biochem.72.121801.161737. [DOI] [PubMed] [Google Scholar]
- Brandman O, Ferrell JE, Jr, Li R, Meyer T. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science. 2005;310:496–498. doi: 10.1126/science.1113834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burton RF. Physiology by numbers: an encouragement to quantitative thinking. 2. Cambridge: Cambridge University Press; 2000. [Google Scholar]
- Chadsey MS, Hughes KT. A multipartite interaction between Salmonella transcription factor sigma28 and its anti-sigma factor FlgM: implications for sigma28 holoenzyme destabilization through stepwise binding. J Mol Biol. 2001;306:915–929. doi: 10.1006/jmbi.2001.4438. [DOI] [PubMed] [Google Scholar]
- Chadsey MS, Karlinsey JE, Hughes KT. The flagellar anti-sigma factor FlgM actively dissociates Salmonella typhimurium sigma28 RNA polymerase holoenzyme. Genes Dev. 1998;12:3123–3136. doi: 10.1101/gad.12.19.3123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevance FF, Hughes KT. Coordinating assembly of a bacterial macromolecular machine. Nat Rev Microbiol. 2008;6:455–465. doi: 10.1038/nrmicro1887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chilcott GS, Hughes KT. Coupling of flagellar gene expression to flagellar assembly in Salmonella enterica serovar typhimurium and Escherichia coli. Microbiol Mol Biol Rev. 2000;64:694–708. doi: 10.1128/MMBR.64.4.694-708.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chubiz JE, Golubeva YA, Lin D, Miller LD, Slauch JM. FliZ regulates expression of the Salmonella pathogenicity island 1 invasion locus by controlling HilD protein activity in Salmonella enterica serovar typhimurium. J Bacteriol. 2010;192:6261–6270. doi: 10.1128/JB.00635-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clarke MB, Sperandio V. Transcriptional regulation of flhDC by QseBC and sigma (FliA) in enterohaemorrhagic Escherichia coli. Mol Microbiol. 2005;57:1734–1749. doi: 10.1111/j.1365-2958.2005.04792.x. [DOI] [PubMed] [Google Scholar]
- Clegg S, Hughes KT. FimZ is a molecular link between sticking and swimming in Salmonella enterica serovar typhimurium. J Bacteriol. 2002;184:1209–1213. doi: 10.1128/jb.184.4.1209-1213.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellermeier CD, Slauch JM. RtsA and RtsB coordinately regulate expression of the invasion and flagellar genes in Salmonella enterica serovar typhimurium. J Bacteriol. 2003;185:5096–5108. doi: 10.1128/JB.185.17.5096-5108.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman M. Feedback control of intercellular signalling in development. Nature. 2000;408:313–319. doi: 10.1038/35042500. [DOI] [PubMed] [Google Scholar]
- Galeva A, Moroz N, Yoon YH, Hughes KT, Samatey FA, Kostyukova AS. Bacterial flagellin-specific chaperone FliS interacts with anti-sigma factor FlgM. J Bacteriol. 2014;196:1215–1221. doi: 10.1128/JB.01278-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes KT, Gillen KL, Semon MJ, Karlinsey JE. Sensing structural intermediates in bacterial flagellar assembly by export of a negative regulator. Science. 1993;262:1277–1280. doi: 10.1126/science.8235660. [DOI] [PubMed] [Google Scholar]
- Ikebe T, Iyoda S, Kutsukake K. Promoter analysis of the class 2 flagellar operons of Salmonella. Genes Genet Syst. 1999;74:179–183. doi: 10.1266/ggs.74.179. [DOI] [PubMed] [Google Scholar]
- Ikebe T, Iyoda S, Kutsukake K. Structure and expression of the fliA operon of Salmonella typhimurium. Microbiology. 1999;145:1389–1396. doi: 10.1099/13500872-145-6-1389. [DOI] [PubMed] [Google Scholar]
- Iyoda S, Kamidoi T, Hirose K, Kutsukake K, Watanabe H. A flagellar gene fliZ regulates the expression of invasion genes and virulence phenotype in Salmonella enterica serovar typhimurium. Microb Pathog. 2001;30:81–90. doi: 10.1006/mpat.2000.0409. [DOI] [PubMed] [Google Scholar]
- Jones CJ, Aizawa S. The bacterial flagellum and flagellar motor: structure, assembly and function. Adv Microb Physiol. 1991;32:109–172. doi: 10.1016/S0065-2911(08)60007-7. [DOI] [PubMed] [Google Scholar]
- Kage H, Takaya A, Ohya M, Yamamoto T. Coordinated regulation of expression of Salmonella pathogenicity island 1 and flagellar type III secretion systems by ATP-dependent ClpXP protease. J Bacteriol. 2008;190:2470–2478. doi: 10.1128/JB.01385-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalir S, Mangan S, Alon U. A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli. Mol Syst Biol. 2005;1(2005):0006. doi: 10.1038/msb4100010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlinsey JE, Lonner J, Brown KL, Hughes KT. Translation/secretion coupling by type III secretion systems. Cell. 2000;102:487–497. doi: 10.1016/S0092-8674(00)00053-2. [DOI] [PubMed] [Google Scholar]
- Karlinsey JE, Tanaka S, Bettenworth V, Yamaguchi S, Boos W, Aizawa SI, Hughes KT. Completion of the hook-basal body complex of the Salmonella typhimurium flagellum is coupled to FlgM secretion and fliC transcription. Mol Microbiol. 2000;37:1220–1231. doi: 10.1046/j.1365-2958.2000.02081.x. [DOI] [PubMed] [Google Scholar]
- Kawagishi I, Muller V, Williams AW, Irikura VM, Macnab RM. Subdivision of flagellar region III of the Escherichia coli and Salmonella typhimurium chromosomes and identification of two additional flagellar genes. J Gen Microbiol. 1992;138:1051–1065. doi: 10.1099/00221287-138-6-1051. [DOI] [PubMed] [Google Scholar]
- Kim D, Kwon YK, Cho KH. Coupled positive and negative feedback circuits form an essential building block of cellular signaling pathways. BioEssays. 2007;29:85–90. doi: 10.1002/bies.20511. [DOI] [PubMed] [Google Scholar]
- Ko M, Park C. Two novel flagellar components and H-NS are involved in the motor function of Escherichia coli. J Mol Biol. 2000;303:371–382. doi: 10.1006/jmbi.2000.4147. [DOI] [PubMed] [Google Scholar]
- Koirala S, Mears P, Sim M, Golding I, Chemla YR, Aldridge PD, Rao CV. A nutrient-tunable bistable switch controls motility in Salmonella enterica serovar typhimurium. mBio. 2014;5:e01611–e01614. doi: 10.1128/mBio.01611-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutsukake K. Autogenous and global control of the flagellar master operon, flhD, in Salmonella typhimurium. Mol Gen Genet. 1997;254:440–448. doi: 10.1007/s004380050437. [DOI] [PubMed] [Google Scholar]
- Kutsukake K, Ide N. Transcriptional analysis of the flgK and fliD operons of Salmonella typhimurium which encode flagellar hook-associated proteins. Mol Gen Genet. 1995;247:275–281. doi: 10.1007/BF00293195. [DOI] [PubMed] [Google Scholar]
- Kutsukake K, Iino T. Role of the FliA-FlgM regulatory system on the transcriptional control of the flagellar regulon and flagellar formation in Salmonella typhimurium. J Bacteriol. 1994;176:3598–3605. doi: 10.1128/jb.176.12.3598-3605.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutsukake K, Ikebe T, Yamamoto S. Two novel regulatory genes, fliT and fliZ, in the flagellar regulon of Salmonella. Genes Genet Syst. 1999;74:287–292. doi: 10.1266/ggs.74.287. [DOI] [PubMed] [Google Scholar]
- Lostroh CP, Lee CA. The Salmonella pathogenicity island-1 type III secretion system. Microbes Infect. 2001;3:1281–1291. doi: 10.1016/S1286-4579(01)01488-5. [DOI] [PubMed] [Google Scholar]
- Lucas RL, Lostroh CP, DiRusso CC, Spector MP, Wanner BL, Lee CA. Multiple factors independently regulate hilA and invasion gene expression in Salmonella enterica serovar typhimurium. J Bacteriol. 2000;182:1872–1882. doi: 10.1128/JB.182.7.1872-1882.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macnab RM. Bacterial flagella rotating in bundles: a study in helical geometry. Proc Natl Acad Sci USA. 1977;74:221–225. doi: 10.1073/pnas.74.1.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macnab RM. The bacterial flagellum: reversible rotary propellor and type III export apparatus. J Bacteriol. 1999;181:7149–7153. doi: 10.1128/jb.181.23.7149-7153.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macnab RM. How bacteria assemble flagella. Annu Rev Microbiol. 2003;57:77–100. doi: 10.1146/annurev.micro.57.030502.090832. [DOI] [PubMed] [Google Scholar]
- Mariconda S, Wang Q, Harshey RM. A mechanical role for the chemotaxis system in swarming motility. Mol Microbiol. 2006;60:1590–1602. doi: 10.1111/j.1365-2958.2006.05208.x. [DOI] [PubMed] [Google Scholar]
- Mitrophanov AY, Groisman EA. Positive feedback in cellular control systems. BioEssays. 2008;30:542–555. doi: 10.1002/bies.20769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muskotal A, Kiraly R, Sebestyen A, Gugolya Z, Vegh BM, Vonderviszt F. Interaction of FliS flagellar chaperone with flagellin. FEBS Lett. 2006;580:3916–3920. doi: 10.1016/j.febslet.2006.06.024. [DOI] [PubMed] [Google Scholar]
- Mytelka DS, Chamberlin MJ. Escherichia coli fliAZY operon. J Bacteriol. 1996;178:24–34. doi: 10.1128/jb.178.1.24-34.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohnishi K, Kutsukake K, Suzuki H, Lino T. A novel transcriptional regulation mechanism in the flagellar regulon of Salmonella typhimurium: an antisigma factor inhibits the activity of the flagellum-specific sigma factor, sigma F. Mol Microbiol. 1992;6:3149–3157. doi: 10.1111/j.1365-2958.1992.tb01771.x. [DOI] [PubMed] [Google Scholar]
- Paulsson J. Models of stochastic gene expression. Physics of Life Reviews. 2005;2:157–175. doi: 10.1016/j.plrev.2005.03.003. [DOI] [Google Scholar]
- Rosu V, Hughes KT. sigma28-dependent transcription in Salmonella enterica is independent of flagellar shearing. J Bacteriol. 2006;188:5196–5203. doi: 10.1128/JB.00299-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini S, Rao CV. SprB is the molecular link between Salmonella pathogenicity island 1 (SPI1) and SPI4. J Bacteriol. 2010;192:2459–2462. doi: 10.1128/JB.00047-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini S, Brown JD, Aldridge PD, Rao CV. FliZ is a posttranslational activator of FlhD4C2-dependent flagellar gene expression. J Bacteriol. 2008;190:4979–4988. doi: 10.1128/JB.01996-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini S, Koirala S, Floess E, Mears PJ, Chemla YR, Golding I, Aldridge C, Aldridge PD, Rao CV. FliZ induces a kinetic switch in flagellar gene expression. J Bacteriol. 2010;192:6477–6481. doi: 10.1128/JB.00751-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini S, Slauch JM, Aldridge PD, Rao CV. Role of cross talk in regulating the dynamic expression of the flagellar Salmonella pathogenicity island 1 and type 1 fimbrial genes. J Bacteriol. 2010;192:5767–5777. doi: 10.1128/JB.00624-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini S, Floess E, Aldridge C, Brown J, Aldridge PD, Rao CV. Continuous control of flagellar gene expression by the sigma28-FlgM regulatory circuit in Salmonella enterica. Mol Microbiol. 2011;79:264–278. doi: 10.1111/j.1365-2958.2010.07444.x. [DOI] [PubMed] [Google Scholar]
- Shin D, Lee EJ, Huang H, Groisman EA. A positive feedback loop promotes transcription surge that jump-starts Salmonella virulence circuit. Science. 2006;314:1607–1609. doi: 10.1126/science.1134930. [DOI] [PubMed] [Google Scholar]
- Silverman M, Simon M. Flagellar rotation and the mechanism of bacterial motility. Nature. 1974;249:73–74. doi: 10.1038/249073a0. [DOI] [PubMed] [Google Scholar]
- Takaya A, Erhardt M, Karata K, Winterberg K, Yamamoto T, Hughes KT. YdiV: a dual function protein that targets FlhDC for ClpXP-dependent degradation by promoting release of DNA-bound FlhDC complex. Mol Microbiol. 2012;83:1268–1284. doi: 10.1111/j.1365-2958.2012.08007.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanabe Y, Wada T, Ono K, Abo T, Kutsukake K. The transcript from the sigma(28)-dependent promoter is translationally inert in the expression of the sigma(28)-encoding gene fliA in the fliAZ operon of Salmonella enterica serovar typhimurium. J Bacteriol. 2011;193:6132–6141. doi: 10.1128/JB.05909-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teplitski M, Goodier RI, Ahmer BM. Pathways leading from BarA/SirA to motility and virulence gene expression in Salmonella. J Bacteriol. 2003;185:7257–7265. doi: 10.1128/JB.185.24.7257-7265.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas R, Thieffry D, Kaufman M. Dynamical behaviour of biological regulatory networks–I. Biological role of feedback loops and practical use of the concept of the loop-characteristic state. Bull Math Biol. 1995;57:247–276. doi: 10.1007/BF02460618. [DOI] [PubMed] [Google Scholar]
- Tomoyasu T, Ohkishi T, Ukyo Y, Tokumitsu A, Takaya A, Suzuki M, Sekiya K, Matsui H, Kutsukake K, Yamamoto T. The ClpXP ATP-dependent protease regulates flagellum synthesis in Salmonella enterica serovar typhimurium. J Bacteriol. 2002;184:645–653. doi: 10.1128/JB.184.3.645-653.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wada T, Tanabe Y, Kutsukake K. FliZ acts as a repressor of the ydiV gene, which encodes an anti-FlhD4C2 factor of the flagellar regulon in Salmonella enterica serovar typhimurium. J Bacteriol. 2011;193:5191–5198. doi: 10.1128/JB.05441-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Fleming RT, Westbrook EM, Matsumura P, McKay DB. Structure of the Escherichia coli FlhDC complex, a prokaryotic heteromeric regulator of transcription. J Mol Biol. 2006;355:798–808. doi: 10.1016/j.jmb.2005.11.020. [DOI] [PubMed] [Google Scholar]
- Wei BL, Brun-Zinkernagel AM, Simecka JW, Pruss BM, Babitzke P, Romeo T. Positive regulation of motility and flhDC expression by the RNA-binding protein CsrA of Escherichia coli. Mol Microbiol. 2001;40:245–256. doi: 10.1046/j.1365-2958.2001.02380.x. [DOI] [PubMed] [Google Scholar]
- Wu KH, Wang KC, Lee LW, Huang YN, Yeh KS. A constitutively mannose-sensitive agglutinating Salmonella enterica subsp enterica serovar typhimurium strain, carrying a transposon in the fimbrial usher gene stbC, exhibits multidrug resistance and flagellated phenotypes. ScientificWorldJournal. 2012;2012:280264. doi: 10.1100/2012/280264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto S, Kutsukake K. FliT acts as an anti-FlhD2C2 factor in the transcriptional control of the flagellar regulon in Salmonella enterica serovar typhimurium. J Bacteriol. 2006;188:6703–6708. doi: 10.1128/JB.00799-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanagihara S, Iyoda S, Ohnishi K, Iino T, Kutsukake K. Structure and transcriptional control of the flagellar master operon of Salmonella typhimurium. Genes Genet Syst. 1999;74:105–111. doi: 10.1266/ggs.74.105. [DOI] [PubMed] [Google Scholar]
- Yokoseki T, Kutsukake K, Ohnishi K, Iino T. Functional analysis of the flagellar genes in the fliD operon of Salmonella typhimurium. Microbiology. 1995;141:1715–1722. doi: 10.1099/13500872-141-7-1715. [DOI] [PubMed] [Google Scholar]
- Yonekura K, Maki-Yonekura S, Namba K. Complete atomic model of the bacterial flagellar filament by electron cryomicroscopy. Nature. 2003;424:643–650. doi: 10.1038/nature01830. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.