Pinning synchronization of coupled inertial delayed neural networks

Abstract

The paper is devoted to the investigation of synchronization for an array of linearly and diffusively coupled inertial delayed neural networks (DNNs). By placing feedback control on a small fraction of network nodes, the entire coupled DNNs can be synchronized to a common objective trajectory asymptotically. Two different analysis methods, including matrix measure strategy and Lyapunov–Krasovskii function approach, are employed to provide sufficient criteria for the synchronization control problem. Comparisons of these two techniques are given at the end of the paper. Finally, an illustrative example is provided to show the effectiveness of the obtained theoretical results.

Introduction

Complex dynamical networks (CDNs), which are coupled by a large collection of dynamic nodes, can emerge some captivating phenomena, such as synchronization, consensus, swarming, flocking and rendezvous. Synchronization of CDNs is always the central topic among these collective behaviors which has received much attention in the past decade (Yu et al. 2013; Jeong et al. 2013; Shen and Cao 2011; Hu et al. 2014). In literature, numerous synchronization patterns have been introduced and studied, such as complete synchronization, local synchronization, generalized synchronization, projective synchronization, partial synchronization, lag synchronization and cluster synchronization. We are interested in the global complete synchronization in this paper. On the other hand, for general CDNs, due to the existence of weak coupling or disconnected communication in the network, synchronization phenomena cannot be achieved autonomously most of the time. And therefore, to reach a global synchronization, some extra controllers need to be designed and imposed on nodes of the network. Recently, pinning control has become a popular choice for synchronization control of CDNs (Wang and Chen 2002; Chen et al. 2007) since such a scheme can greatly reduce the cost of control by controlling only a small fraction of the nodes instead of all the nodes in the network.

As for neural networks, most of the previous publications mainly concentrated on stability analysis and periodic or almost periodic attractors for different kinds of neural networks with or without time delays (Forti and Tesi 1995; Arik 2000; Hu et al. 2013). While authors in Chen et al. (2004) investigated the global synchronization of linearly and diffusively coupled identical delayed neural networks (DNNs) by Lyapunov functional methods and Hermitian matrix theory. Synchronization of coupled neural networks means multiple neural networks can achieve a common trajectory, such as a common equilibrium, limit cycle or chaotic trajectory. Based on Lyapunov functional method and linear matrix inequalities (LMIs), exponential synchronization was studied in Lu and Chen (2004) for coupled connected neural networks with delays. Drive–response synchronization of neural networks with or without time-varying delay was considered in Cao and Lu (2006) based on adaptive feedback control method. By introducing the delayed coupling term, the global exponential synchronization was discussed in Cao et al. (2006) for an array of DNNs with constant and delayed couplings. Furthermore, the hybrid coupling case was considered in Cao et al. (2008), where constant, discrete and distributed-delay couplings coexist. Sufficient conditions were derived for local synchronization of coupled DNNs with discontinuous activation functions (Liu and Cao 2011). Based on sampled-data control, synchronization of neural networks with time-varying delays was investigated in Wu et al. (2012). Drive–response exponential synchronization was formulated in Yang et al. (2014) for a class of neural networks with mixed delays and discontinuous activations. Synchronization for coupled memristive neural networks with time-varying delays was considered recently (Zhang et al. 2013; Wen et al. 2013; Wang et al. 2014). For more studies concerning synchronization of neural networks, see Wu and Park (2013), Yang et al. (2014), Fang and Park (2013) and references cited therein.

In literature, neural network models are always described by first-order differential equations; while inertial electronic neural networks, which are modeled by second-order differential equations, were introduced in Babcock and Westervelt (1987) with small scale number of neurons, such as one-or two-neuron models. It was found that when the neuron coupling was of an inertial nature, the dynamics can be more complex compared with the simpler behavior displayed in standard resistor-capacitor variety. Furthermore, some local stability and Hopf/Bogdanov–Takens bifurcation problems of a single delayed neuron model with inertial terms were investigated in Li et al. (2004), Liu et al. (2009), He et al. (2012). Most of the published investigations concerning the inertial neural networks are always focusing on small-scale neural networks with only one or two neurons with/without time delays, and the general inertial neural network coupled by multiple neurons is rarely seen. Recently, the authors in Ke and Miao (2013) considered the stability and existence of periodic solutions for inertial bidirectional associative memory (BAM) neural networks with time delays. Furthermore, stability analysis was carried out in Ke and Miao (2013) for inertial Cohen–Grossberg-type neural networks with time delays. While in Cao and Wan (2014), the stability of an inertial DNN was investigated by matrix measure strategies and drive–response synchronization was considered as an application at the end of the paper.

Pinning synchronization of coupled neural networks is another interesting research area, which has received much attention. Such as, based on adaptive pinning control, the synchronization problems were investigated in Zhou et al. (2008), Song et al. (2012) for a general weighted neural network with coupling delay. Cluster synchronization problem was studied in Li and Cao (2011) for an array of coupled stochastic delayed neural networks by using pinning control strategy. By pinning impulsive control, exponential synchronization was considered in Yang et al. (2013) for an array of linearly and diffusively coupled reaction-diffusion neural networks with time-varying delays. Robust synchronization problem for the coupled neural networks with mixed delays and uncertain parameters was investigated in Zheng and Cao (2014) by intermittent pinning control. For more studies concerning pinning synchronization of neural networks, we refer to Lu et al. (2009), Wang et al. (2013), Shi et al. (2014) and references cited therein.

Motivated by the above discussions, this paper is intended to investigate the synchronization of coupled inertial delayed neural networks by pinning control. To the best of our knowledge, there are very few studies on the synchronization problem of the coupled inertial DNNs. We shall investigate the pinning synchronization (i.e., leader-following synchronization) for an array of linearly and diffusively coupled inertial delayed neural networks by matrix measure strategy and Lyapunov functional method, respectively. Matrix measure technique has been widely utilized to deal with synchronization problem for complex networks (Sun and Zhang 2004; Chen 2006; Juang and Liang 2009) and neural networks (He and Cao 2009; Cao and Wan 2014). It has been shown that the matrix measure approach has several advantages, such as without needing to construct Lyapunov function or functional, making full use of matrix elements’ information and simple stability criteria (Cao and Wan 2014). We will provide several sufficient synchronization criteria for the coupled inertial DNNs in terms of matrix measure and LMIs. Furthermore, we conclude that the matrix measure may not be appropriate to deal with synchronization of large-scale coupled network with high-dimensional node. The main contributions of this article are listed as follows: (1) leader-following synchronization of inertial neural networks is considered; (2) pinning feedback control is introduced to synchronize the coupled inertial DNNs to the objective trajectory; (3) two different kinds of synchronization criteria are provided by matrix measure and Lyapunov functional methods, respectively.

The rest of this paper is structured as follows. In “Model description and preliminaries” section, model description and some preliminaries are briefly outlined. In “Main results” section, main theorems are given for the synchronization of the coupled inertial DNNs by pinning control. Illustrative example is provided in “Illustrative example” section to demonstrate the utility of the theoretical results. Finally, conclusions are drawn in “Conclusions” section.

Model description and preliminaries

Notation

Throughout this paper, ${\mathbb{R}}^n$ and ${\mathbb{R}}^{n\times m}$ denote the $n$-dimensional Euclidean space and the set of all real $n\times m$ matrices, respectively. $I_n$ denotes the $n\times n$ identity matrix and $\mathrm{diag}\{\mathit{\omega }\}$$(\mathit{\omega }={[{\mathit{\omega }}_1,\dots ,{\mathit{\omega }}_n]}^T\in {\mathbb{R}}^n)$ is the diagonal matrix with diagonal entries ${\mathit{\omega }}_1$–${\mathit{\omega }}_n$. Matrix $A$ is called Hurwitz if all the eigenvalues of $A$ lie in the open left half-plane. The notation $P>Q$, where $P$ and $Q$ are symmetric matrices, means that the matrix $P-Q$ is positive definite, while $P\ge 0$ denotes $P$ is a positive semidefinite matrix. Matrices, if their dimensions are not explicitly stated, are assumed to be compatible for the algebraic operations.

Consider an array of linearly coupled inertial DNNs consisting of $N$ identical nodes with the dynamics of the $i\text{th}$ node described by the following equation:

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}& =-D\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}-C{x}_i(t)+Af(x_i(t))+Bf(x_i(t-\mathit{\tau }(t)))+I(t)\hfill \\ \hfill & +c\sum _{j=1}^N{G}_{ij}\mathit{\Gamma }\left(\frac{\mathrm{d}{x}_j(t)}{\mathrm{d}t}+x_j(t)\right),i=1,\dots ,N,\hfill \end{array}$$ 1

where $x_i(t)={(x_{i1}(t),\dots ,x_{in}(t))}^T\in {\mathbb{R}}^n$ is the state vector of the $i\text{th}$ neural network and $D=\mathrm{diag}\{d_1,\dots ,d_n\},C=\mathrm{diag}\{c_1,\dots ,c_n\}$ are constant positive definite matrices. $A={(a_{ij})}_{n\times n}$ and $B={(b_{ij})}_{n\times n}$ denote the connection weight matrix and the delayed connection weight matrix, respectively. The nonlinear function $f(x_i)={(f_1(x_{i1}),\dots ,f_n(x_{in}))}^T$ is the activation function for the inertial neural network; $I(t)={(I_1(t),\dots ,I_n(t))}^T$ is the external input vector. The second derivative of $x_i(t)$ is called an inertial term of system (1). The positive constant $c$ is the network coupling strength and $\mathit{\Gamma }$ is the inner coupling matrix; $G={(G_{ij})}_{N\times N}$ is the constant coupling configuration matrix defined to be diffusive: $G_{ij}\ge 0(i\ne j)$ and $G_{ii}=-{\sum }_{j=1,j\ne i}^N{G}_{ij}$. The coupling matrix $G$ is not required to be symmetric or irreducible.

The initial conditions associated with system (1) are given as $x_i(\mathit{\omega })={\mathit{\varphi }}_i(\mathit{\omega })\in {\mathcal{C}}^{(1)}([-\mathit{\tau },0],{\mathbb{R}}^n)$, $i=1,\dots ,N$, where ${\mathcal{C}}^{(1)}([-\mathit{\tau },0],{\mathbb{R}}^n)$ denotes the set of all $n$-dimensional continuous differentiable functions defined on the interval $[-\mathit{\tau },0]$ with $\mathit{\tau }={\text{sup}}_{t\ge 0}\{\mathit{\tau }(t)\}$.

To proceed, the following assumptions, definitions and lemmas are given.

Assumption 1

The activation function $f_i(·):\mathbb{R}\to \mathbb{R}(1\le i\le n)$ is bounded and satisfies Lipschitz condition, i.e., there exist constants ${\mathit{\kappa }}_i$ and $M_i$ such that

$$\begin{array}{c}\hfill |f_i(x)-f_i(y)|\le {\mathit{\kappa }}_i|x-y|\mathrm{and}|f_i(x)|\le M_i\end{array}$$

hold for all $x,y\in \mathbb{R}$.

Assumption 2

The time delay $\mathit{\tau }(t)\ge 0$ in (1) is a bounded and differentiable function of time $t$ satisfying $\dot{\mathit{\tau }}(t)\le \mathit{\rho }<1$ for all $t\ge 0$, where $\mathit{\rho }>0$.

Remark 1

The above Assumption 1 is used to ensure the existence and uniqueness of the solution of inertial DNNs (2) with Lipschitzian activation functions without assuming their monotonicity or differentiability (Cao and Wan 2014).

Definition 1

The coupled inertial neural network (1) is said to be globally asymptotically synchronizable to the goal trajectory $s(t)$ if the following discriminant relations

$$\begin{array}{c}\hfill {\text{lim}}_{t\to \infty }\Vert x_i(t)-s(t)\Vert =0,i=1,2\dots ,N,\end{array}$$

hold for all initial functions.

Definition 2

For a matrix $A\in {\mathbb{R}}^{n\times n}$, the matrix measure is defined as follows:

$$\begin{array}{c}\hfill {\mathit{\mu }}_p(A)={\text{lim}}_{\mathit{\epsilon }\to 0^{+}}\frac{\Vert I_n{+\mathit{\epsilon }A\Vert }_p-1}{\mathit{\epsilon }},\end{array}$$

where ${\Vert ·\Vert }_p$ is an induced matrix norm on ${\mathbb{R}}^{n\times n}$ with $p=1,2,\infty ,\mathit{\omega }$. The corresponding matrix norms and measures are given as follows,

Matrix norm	Matrix measure
${\Vert A\Vert }_1={\text{max}}_j{\sum }_{i=1}^n|a_{ij}|$	${\mathit{\mu }}_1(A)={\text{max}}_j\left\{a_{jj}+{\sum }_{i=1,i\ne j}^n|a_{ij}|\right\}$
${\Vert A\Vert }_2=\sqrt{{\mathit{\lambda }}_{\text{max}}(A^{T}A)}$	${\mathit{\mu }}_2(A)=\frac{1}{2}{\mathit{\lambda }}_{\text{max}}(A^T+A)$
${\Vert A\Vert }_{\infty }={\text{max}}_i{\sum }_{j=1}^n|a_{ij}|$	${\mathit{\mu }}_{\infty }(A)={\text{max}}_i\left\{a_{ii}+{\sum }_{j=1,j\ne i}^n|a_{ij}|\right\}$
${\Vert A\Vert }_{\mathit{\omega }}={\text{max}}_j{\sum }_{i=1}^n\frac{{\mathit{\omega }}_i}{{\mathit{\omega }}_j}|a_{ij}|$	${\mathit{\mu }}_{\mathit{\omega }}(A)={\text{max}}_j\left\{a_{jj}+{\sum }_{i=1,i\ne j}^n\frac{{\mathit{\omega }}_i}{{\mathit{\omega }}_j}|a_{ij}|\right\}$

where ${\mathit{\omega }}_i>0,i=1,2,\dots ,n$ are any constant numbers.

Remark 2

Note that the $\mathit{\omega }$-matrix measure was introduced in Cao (2004), which is the generalization of the $1$-matrix measure ${\mathit{\mu }}_1(·)$. On the other hand, a simple interpretation for matrix measure is that the measure ${\mathit{\mu }}_p(A)$ is the derivative of the norm of $exp(At)$ at $t=0$. It is easy to see that if ${\mathit{\mu }}_p(A)<0$, then $A$ is “instantaneously norm-contractive” and, consequently, Hurwitz stable (Bolzern et al. 2006).

Lemma 1

(Halanay 1966) Let$x(·):[t_0-\mathit{\tau },\infty )\to [0,\infty )$be a continuous function such that

$$\begin{array}{c}\hfill D^{+}x(t)\le -ax(t)+b\overline{x}(t)\end{array}$$

is satisfied for$t\ge t_0$. If$a>b>0$, then

$$\begin{array}{c}\hfill x(t)\le \overline{x}(t_0)e^{-\mathit{\lambda }(t-t_0)},t\ge t_0\end{array}$$

where$\overline{x}(t)={\text{sup}}_{t-\mathit{\tau }\le s\le t}x(s)$, and$\mathit{\lambda }>0$is the unique positive real root of the equation$-a+\mathit{\lambda }+b{e}^{\mathit{\lambda }\mathit{\tau }}=0$.

Lemma 2

(Horn and Johnson 2012) For a nonsingular matrix$A\in {\mathbb{R}}^{n\times n}$, the following statements are equivalent:

1. $A$is a nonsingular Minkovski matrix (M-matrix).

2. The off-diagonal elements of matrix$A$satisfy$a_{ij}\le 0$and$A^{-1}$exists with each entry of$A^{-1}$is nonnegative.

3. $A$is a positive stable matrix (all eigenvalues of matrix$A$have positive real parts, i.e.,$\mathcal{R}({\mathit{\lambda }}_i(A))>0$for all$i=1,2,\dots ,n$).

4. There exists a diagonal matrix$\mathit{\Theta }=\mathrm{diag}\{{\mathit{\theta }}_1,\dots ,{\mathit{\theta }}_n\}>0$such that$\mathit{\Theta }A+A^T\mathit{\Theta }>0$.

Main results

In this section, we investigate the global synchronization of the coupled inertial DNNs by pinning control, which means that the feedback injections are only placed on a small fraction of total network nodes and most of network nodes are not directly controlled. The isolated node of network (1) is given by the following inertial delayed DNN:

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^{2}s(t)}{\mathrm{d}{t}^2}=& -D\frac{\mathrm{d}s(t)}{\mathrm{d}t}-Cs(t)+Af(s(t))+Bf(s(t-\mathit{\tau }(t)))+I(t),\hfill \end{array}$$ 2

where $s(t)=(s_1(t),\dots ,s_n(t))\in {\mathbb{R}}^n$. The initial condition for system (2) is given as $s(\mathit{\omega })=\mathit{\phi }(\mathit{\omega })\in {\mathcal{C}}^{(1)}([-\mathit{\tau },0],{\mathbb{R}}^n)$.

The pinning controlled network is given as follows:

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}& =-D\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}-C{x}_i(t)+Af(x_i(t))+Bf(x_i(t-\mathit{\tau }(t)))+I(t)\hfill \\ \hfill & +c\sum _{j=1}^N{G}_{ij}\mathit{\Gamma }\left(\frac{\mathrm{d}{x}_j(t)}{\mathrm{d}t}+x_j(t)\right)-c{\mathit{\sigma }}_i\mathit{\Gamma }\left(\frac{\mathrm{d}(x_i(t)-s(t))}{\mathrm{d}t}+\left(x_i(t)-s(t)\right)\right),\hfill \end{array}$$ 3

where $i=1,\dots ,N$; and ${\mathit{\sigma }}_i=1$ if the node $i$ is pinned, otherwise ${\mathit{\sigma }}_i=0$.

By letting the synchronization error $e_i(t)=x_i(t)-s(t)$, one can derive the following error system:

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2{e}_i(t)}{\mathrm{d}{t}^2}& =-D\frac{\mathrm{d}{e}_i(t)}{\mathrm{d}t}-C{e}_i(t)+Ag(e_i(t))+Bg(e_i(t-\mathit{\tau }(t)))\hfill \\ \hfill & +c\sum _{j=1}^N{G}_{ij}\mathit{\Gamma }\left(\frac{\mathrm{d}{e}_j(t)}{\mathrm{d}t}+e_j(t)\right)-c{\mathit{\sigma }}_i\mathit{\Gamma }\left(\frac{\mathrm{d}{e}_i(t)}{\mathrm{d}t}+e_i(t)\right),i=1,\dots ,N,\hfill \end{array}$$ 4

where $g(e_i)={(f_1(e_{i1}+s_1)-f_1(s_1),\dots ,f_n(e_{in}+s_n)-f_n(s_n))}^T$.

Next, by introducing the following variable transformation:

$$\begin{array}{c}\hfill r_i(t)=\frac{\mathrm{d}{e}_i(t)}{\mathrm{d}t}+e_i(t),i=1,\dots ,n,\end{array}$$

the error system (4) can be written as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\frac{\mathrm{d}{e}_i(t)}{\mathrm{d}t}=-e_i(t)+r_i(t),\hfill \\ \frac{\mathrm{d}{r}_i(t)}{\mathrm{d}t}=-\mathit{C}{e}_i(t)-\mathit{D}{r}_i(t)+Ag(e_i(t))+Bg(e_i(t-\mathit{\tau }(t)))-c{\sum }_{j=1}^N{l}_{ij}\mathit{\Gamma }{r}_j(t)-c{\mathit{\sigma }}_i\mathit{\Gamma }{r}_i(t),\hfill \end{array}\right.\end{array}$$ 5

for $i=1,\dots ,N$, where $\mathit{C}\triangleq C+I_n-D$ and $\mathit{D}\triangleq D-I_n$; $L={(l_{ij})}_{N\times N}=-G$ is the Laplacian matrix of the coupling network.

By letting $e(t)={(e_1^T,\dots ,e_N^T)}^T$ and $r(t)={(r_1^T,\dots ,r_N^T)}^T$, together with the Kronecker product, the error system (5) can be written as the following compact forms:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{e}(t)=-e(t)+r(t),\hfill \\ \dot{r}(t)=-(I_N\otimes \mathit{C})e(t)-(I_N\otimes \mathit{D})r(t)+(I_N\otimes A)g(e(t))\hfill \\ +(I_N\otimes B)g(e(t-\mathit{\tau }(t)))-c((L+\mathit{\Sigma })\otimes \mathit{\Gamma })r(t),\hfill \end{array}\right.\end{array}$$ 6

where $\mathit{\Sigma }=\mathrm{diag}\{{\mathit{\sigma }}_1,\dots ,{\mathit{\sigma }}_N\}$ is the pinning matrix and $g(e)={(g^T(e_1),\dots ,g^T(e_N))}^T$.

The coupled inertial DNNs (3) can be synchronized if the error system (6) is globally asymptotically stable. In the following, two different analysis methods, including matrix measure strategy and Lyapunov–Krasovskii function approach, are employed to provide sufficient criteria for the globally asymptotically stable of the error system (6).

Matrix measure method

In this section, we utilize the matrix measure strategy to derive the stability conditions for the error system. By defining $\mathit{\delta }(t)={(e^T(t),r^T(t))}^T$, the augmented error system can be obtained:

$$\begin{array}{c}\hfill \dot{\mathit{\delta }}(t)=\mathcal{H}\mathit{\delta }(t)+\mathcal{A}\tilde{g}(\mathit{\delta }(t))+\mathcal{B}\tilde{g}(\mathit{\delta }(t-\mathit{\tau }(t))),\end{array}$$ 7

where $\tilde{g}(\mathit{\delta }(t))={(g^T(e_1),\dots ,g^T(e_N),g^T(r_1),\dots ,g^T(r_N))}^T$ and the coefficient matrices are

$$\begin{array}{c}\hfill \mathcal{H}=\left[\begin{array}{cc}-I_{Nn}\hfill & I_{Nn}\hfill \\ -I_N\otimes \mathit{C}\hfill & -I_N\otimes \mathit{D}-c(L+\mathit{\Sigma })\otimes \mathit{\Gamma }\hfill \end{array}\right],\mathcal{A}=\left[\begin{array}{cc}\mathbf{0}\hfill & \mathbf{0}\hfill \\ I_N\otimes A\hfill & \mathbf{0}\hfill \end{array}\right],\mathcal{B}=\left[\begin{array}{cc}\mathbf{0}\hfill & \mathbf{0}\hfill \\ I_N\otimes B\hfill & \mathbf{0}\hfill \end{array}\right].\end{array}$$

Theorem 1

Under Assumptions 1 and 2, if there exists a kind of matrix measure ${\mathit{\mu }}_p(·)(p=1,2,\infty ,\mathit{\omega })$ such that

$$\begin{array}{c}\hfill -{\mathit{\mu }}_p(\mathcal{H})-{\overline{\mathit{\kappa }}\Vert \mathcal{A}\Vert }_p>\overline{\mathit{\kappa }}{\Vert \mathcal{B}\Vert }_p>0,\end{array}$$ 8

where $\overline{\mathit{\kappa }}={\text{max}}_{1\le i\le n}\{{\mathit{\kappa }}_i\}$ is the maximal lipschitz constant, then the pinning controlled coupled inertial DNNs (3) is globally exponentially synchronization.

Proof

According to the error system (7), the upper-right Dini derivative of ${\Vert \mathit{\delta }(t)\Vert }_p$ with respect to $t$ along the solution of (7) is as follows:

$$\begin{array}{cc}\hfill D^{+}{\Vert \mathit{\delta }(t)\Vert }_p& ={\text{lim}}_{h\to 0^{+}}\frac{{\Vert \mathit{\delta }(t+h)\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}={\text{lim}}_{h\to 0^{+}}\frac{\Vert \mathit{\delta }(t)+h\dot{\mathit{\delta }}{(t)+o(h)\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}\hfill \\ \hfill & \le {\text{lim}}_{h\to 0^{+}}\frac{\Vert \mathit{\delta }(t)+h\mathcal{H}\mathit{\delta }(t)+h\mathcal{A}\tilde{g}(\mathit{\delta }(t))+h\mathcal{B}\tilde{g}{(\mathit{\delta }(t-\mathit{\tau }(t)))\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}\hfill \\ \hfill & \le {\text{lim}}_{h\to 0^{+}}\frac{\Vert I_{2Nn}{+h\mathcal{H}\Vert }_p-1}{h}{\Vert \mathit{\delta }(t)\Vert }_p+\Vert \mathcal{A}\tilde{g}{(\mathit{\delta }(t))\Vert }_p+{\Vert \mathcal{B}\tilde{g}(\mathit{\delta }(t-\mathit{\tau }(t)))\Vert }_p\hfill \\ \hfill & \le {\mathit{\mu }}_p{(\mathcal{H})\Vert \mathit{\delta }(t)\Vert }_p+{\overline{\mathit{\kappa }}\Vert \mathcal{A}\Vert }_p·{\Vert \mathit{\delta }(t)\Vert }_p+{\overline{\mathit{\kappa }}\Vert \mathcal{B}\Vert }_p·{\Vert \mathit{\delta }(t-\mathit{\tau }(t))\Vert }_p\hfill \\ \hfill & =\left({\mathit{\mu }}_p(\mathcal{H})+\overline{\mathit{\kappa }}{\Vert \mathcal{A}\Vert }_p\right){\Vert \mathit{\delta }(t)\Vert }_p+\left({\overline{\mathit{\kappa }}\Vert \mathcal{B}\Vert }_p\Vert \right){\text{sup}}_{t-\mathit{\tau }\le s\le t}{\Vert \mathit{\delta }(s)\Vert }_p.\hfill \end{array}$$

By inequality (8) and Lemma 1, one can derive

$$\begin{array}{c}\hfill {\Vert \mathit{\delta }(t)\Vert }_p\le \overline{\mathit{\delta }}(t_0)e^{-\mathit{\lambda }(t-t_0)},t\ge t_0,\end{array}$$

where $\mathit{\lambda }>0$ is the unique positive real root of the equation $-{\mathit{\mu }}_p(\mathcal{H})-{\overline{\mathit{\kappa }}\Vert \mathcal{A}\Vert }_p+\mathit{\lambda }+\overline{\mathit{\kappa }}\Vert \mathcal{B}{e}^{\mathit{\lambda }\mathit{\tau }}=0$.

Therefore, $\mathit{\delta }(t)$ converges exponentially to zero with a convergence rate $\mathit{\lambda }$, that is, the globally synchronization is achieved. This completes the proof. $\square$

Noting that the synchronization condition (8) in Theorem 1 is based on the maximal lipschitz constant $\overline{\mathit{\kappa }}$. The following Theorem 2 gives a more detailed synchronization criterion which utilizes the information of each lipschitz constant ${\mathit{\kappa }}_i$. To derive the main result, the following lemma is needed, stated as follows,

Lemma 3

(He and Cao 2009) Under Assumption 1, let${\mathit{\mu }}_p(·)$ be the corresponding matrix measure associated with the induced matrix norm${\Vert ·\Vert }_p$ on${\mathbb{R}}^{n\times n}$. Then${\mathit{\mu }}_p(AG(e(t)))\le {\mathit{\mu }}_p(AF)$, where$G(e(t))=\mathrm{diag}\left(\frac{g_1(e_1(t))}{e_1(t)},\dots ,\frac{g_n(e_n(t))}{e_n(t)}\right)$,$F=\mathrm{diag}({\mathit{\kappa }}_1,\dots ,{\mathit{\kappa }}_n)$,$p=1,\infty ,\mathit{\omega }$, and

$$\begin{array}{c}\hfill \overline{A}={({\overline{a}}_{ij})}_{n\times n}=\left\{\begin{array}{cc}\text{max}\{0,a_{ii}\},\hfill & i=j,\hfill \\ a_{ij},\hfill & i\ne j.\hfill \end{array}\right.\end{array}$$

Theorem 2

Under Assumptions 1 and 2, if there exists a matrix measure ${\mathit{\mu }}_p(·)(p=1,\infty ,\mathit{\omega })$ such that

$$\begin{array}{c}\hfill -{\mathit{\mu }}_p(\mathcal{H})-{\mathit{\mu }}_p(\overline{\mathcal{A}}\mathcal{F})>\overline{\mathit{\kappa }}{\Vert I_N\otimes B\Vert }_p>0,\end{array}$$ 9

where $\mathcal{F}=\mathrm{diag}({\underbrace{\underline{{\mathit{\kappa }}_1,\dots ,{\mathit{\kappa }}_n},\dots ,\underline{{\mathit{\kappa }}_1,\dots ,{\mathit{\kappa }}_n}}}_N,{\underbrace{1,\dots ,1}}_{N\ast n})$, $\overline{\mathit{\kappa }}={\text{max}}_{1\le i\le n}\{{\mathit{\kappa }}_i\}$, then the pinning controlled coupled inertial DNNs (3) is globally exponentially synchronization.

Proof

Under a simple transformation, the error system (6) is equivalent to the error system (10):

$$\begin{array}{c}\hfill \dot{\mathit{\delta }}(t)=\left(\mathcal{H}+\mathcal{A}\mathbf{G}(e(t))\right)\mathit{\delta }(t)+\mathcal{B}\tilde{g}(\mathit{\delta }(t-\mathit{\tau }(t))),\end{array}$$ 10

where $\mathbf{G}(e(t))=\mathrm{diag}\{\tilde{\mathbf{G}}(e(t)),I_{Nn}\}$ with $\tilde{\mathbf{G}}(e(t))=\mathrm{diag}\{{\tilde{\mathbf{G}}}_1(e_1),{\tilde{\mathbf{G}}}_2(e_2),\dots ,{\tilde{\mathbf{G}}}_N(e_N)\}$, and ${\tilde{\mathbf{G}}}_i(e_i)=\mathrm{diag}\{\frac{g(e_{i1})}{e_{i1}},\frac{g(e_{i2})}{e_{i2}},\dots ,\frac{g(e_{in})}{e_{in}}\}(1\le i\le N)$.

The upper-right Dini derivative of ${\Vert \mathit{\delta }(t)\Vert }_p$ with respect to $t$ along the solution of (10) is as follows:

$$\begin{array}{cc}\hfill D^{+}{\Vert \mathit{\delta }(t)\Vert }_p& ={\text{lim}}_{h\to 0^{+}}\frac{{\Vert \mathit{\delta }(t+h)\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}={\text{lim}}_{h\to 0^{+}}\frac{\Vert \mathit{\delta }(t)+h\dot{\mathit{\delta }}{(t)+o(h)\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}\hfill \\ \hfill & \le {\text{lim}}_{h\to 0^{+}}\frac{\Vert \mathit{\delta }(t)+h\left(\mathcal{H}+\mathcal{A}\mathbf{G}(e(t))\right)\mathit{\delta }(t)+\mathcal{B}\tilde{g}{(\mathit{\delta }(t-\mathit{\tau }(t)))\Vert }_p-{\Vert \mathit{\delta }(t)\Vert }_p}{h}\hfill \\ \hfill & \le {\text{lim}}_{h\to 0^{+}}\frac{\Vert I_n+h\left(\mathcal{H}+\mathcal{A}\mathbf{G}(e(t))\right){\Vert }_p-1}{h}{\Vert \mathit{\delta }(t)\Vert }_p+{\Vert \mathcal{B}\tilde{g}(\mathit{\delta }(t-\mathit{\tau }(t)))\Vert }_p\hfill \\ \hfill & \le {\mathit{\mu }}_p\left(\mathcal{H}+\mathcal{A}\mathbf{G}(e(t))\right){\Vert \mathit{\delta }(t)\Vert }_p+{\overline{\mathit{\kappa }}\Vert \mathcal{B}\Vert }_p·{\Vert \mathit{\delta }(t-\mathit{\tau }(t))\Vert }_p\hfill \\ \hfill & \le \left({\mathit{\mu }}_p(\mathcal{H})+{\mathit{\mu }}_p(\overline{\mathcal{A}}\mathcal{F})\right){\Vert \mathit{\delta }(t)\Vert }_p+\left({\overline{\mathit{\kappa }}\Vert \mathcal{B}\Vert }_p\right){\text{sup}}_{t-\mathit{\tau }\le s\le t}{\Vert \mathit{\delta }(s)\Vert }_p.\hfill \end{array}$$

If the inequality $-{\mathit{\mu }}_p(\mathcal{H})-{\mathit{\mu }}_p(\overline{\mathcal{A}}\mathcal{F})>\overline{\mathit{\kappa }}{\Vert \mathcal{B}\Vert }_p>0$ holds, then by Lemma 1, one can derive

$$\begin{array}{c}\hfill {\Vert \mathit{\delta }(t)\Vert }_p\le \overline{\mathit{\delta }}(t_0)e^{-\mathit{\lambda }(t-t_0)},t\ge t_0,\end{array}$$

where $\mathit{\lambda }>0$ is the unique positive real root of the equation $-{\mathit{\mu }}_p(\mathcal{H})-{\mathit{\mu }}_p(\overline{\mathcal{A}}\mathcal{F})+\mathit{\lambda }+\overline{\mathit{\kappa }}{\Vert \mathcal{B}\Vert }_p{e}^{\mathit{\lambda }\mathit{\tau }}=0$.

Therefore, $\mathit{\delta }(t)$ converges exponentially to zero with a convergence rate $\mathit{\lambda }$, that is, the globally synchronization is achieved. This completes the proof. $\square$

Lyapunov–Krasovskii method

In the pinning controlled coupled network (3), a pinned node can access objective information of the isolated node (2). That is, there is a directed link from the isolated node to the pinned node. If the objective trajectory $s(t)$ is labeled as the dynamic of the node 0, then a new network appears. We use the union of the network $\mathcal{G}$ and the node $\{0\}$ (i.e., $\tilde{\mathcal{G}}\triangleq \mathcal{G}\cup \{0\}$) to denote the pinning joint communication topology (Hu et al. (2014)). The Laplacian matrix of $\tilde{\mathcal{G}}$ is

$$\begin{array}{c}\hfill \tilde{\mathcal{L}}=\left[\begin{array}{cc}0& {\mathbf{0}}_{1\times N}\\ \mathit{\sigma }& L+\mathit{\Sigma }\end{array}\right],\end{array}$$

in which $\mathit{\sigma }={[{\mathit{\sigma }}_1,\dots ,{\mathit{\sigma }}_N]}^T$ and $\mathit{\Sigma }=\mathrm{diag}\{\mathit{\sigma }\}$ is the pinning matrix. Before proposing the main results, we need the following lemma.

Lemma 4

(Song et al. 2012) The matrix$L+\mathit{\Sigma }$ is a nonsingular$M$-matrix if and only if the pinning joint communication topology$\tilde{\mathcal{G}}$ has a directed spanning tree.

Based on the pinning control, if the pinning joint communication topology $\tilde{\mathcal{G}}$ has a directed spanning tree, then matrix $L+\mathit{\Sigma }$ is a nonsingular $M$-matrix. By Lemma 2, there exists a positive diagonal matrix $\mathit{\Theta }=\mathrm{diag}\{{\mathit{\theta }}_1,\dots ,{\mathit{\theta }}_N\}$ such that $\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }>0$.

Theorem 3

Under Assumptions 1 and  2, and the pinning joint communication topology has a directed spanning tree, then the coupled inertial neural network (1) is globally asymptotically synchronization if there exists a positive definite matrix $P$ such that

$$\begin{array}{c}\hfill \mathit{\Phi }=\left[\begin{array}{cc}-I_N\otimes P+\left(\frac{1}{2}+\mathit{\eta }\right)(\mathit{\Theta }\otimes \tilde{F})& I_N\otimes P-\mathit{\Theta }\otimes \mathit{C}\\ \ast & Q\end{array}\right]<0,\end{array}$$ 11

where $\mathit{\eta }>\frac{1}{2(1-\mathit{\rho })}$ is a positive constant and $\tilde{F}=\mathrm{diag}\{{\mathit{\kappa }}_1^2,\dots ,{\mathit{\kappa }}_n^2\}$; and $Q=-\mathit{\Theta }\otimes \mathit{D}+\mathit{\Theta }\otimes \frac{A{A}^T+B{B}^T}{2}-c\left(\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }\right)\otimes \mathit{\Gamma }$.

Proof

To prove the result, one just need to show that the error system (6) is globally asymptotically stable. Consider the following Lyapunov–Krasovskii functional candidate for system (6)

$$\begin{array}{c}\hfill V(t)=\frac{1}{2}{e}^T(t)(I_N\otimes P)e(t)+\mathit{\eta }{\int }_{t-\mathit{\tau }(t)}^t{e}^T(s)(\mathit{\Theta }\otimes \tilde{F})e(s)\mathrm{d}s+\frac{1}{2}{r}^T(t)(\mathit{\Theta }\otimes I_n)r(t).\end{array}$$ 12

Calculating the time derivative of $V(t)$ along the trajectories of system (6), one can obtain

$$\begin{array}{cc}\hfill \dot{V}(t)& =e^T(t)(I_N\otimes P)\left(-e(t)+r(t)\right)+\mathit{\eta }{e}^T(t)(\mathit{\Theta }\otimes \tilde{F})e(t)\hfill \\ \hfill & -\mathit{\eta }(1-\mathit{\rho })e^T(t-\mathit{\tau }(t))(\mathit{\Theta }\otimes \tilde{F})e(t-\mathit{\tau }(t))\hfill \\ \hfill & -r^T(t)(\mathit{\Theta }\otimes \mathit{C})e(t)-r^T(t)(\mathit{\Theta }\otimes \mathit{D})r(t)+r^T(t)(\mathit{\Theta }\otimes A)g(e(t))\hfill \\ \hfill & +r^T(t)(\mathit{\Theta }\otimes B)g(e(t-\mathit{\tau }(t)))-c{r}^T(t)\left(\left(\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }\right)\otimes \mathit{\Gamma }\right)r(t).\hfill \end{array}$$

It follows from Assumption 1 that

$$\begin{array}{cc}\hfill r^T(t)(\mathit{\Theta }\otimes A)g(e(t))& =\sum _{i=1}^N{\mathit{\theta }}_i{r}_i^{T}A{g}_i(e_i)\le \sum _{i=1}^N\left(\frac{{\mathit{\theta }}_i}{2}{r}_i^{T}A{A}^T{r}_i+\frac{{\mathit{\theta }}_i}{2}{g}^T(e_i)g(e_i)\right)\hfill \\ \hfill & \le \sum _{i=1}^N\left(\frac{{\mathit{\theta }}_i}{2}{r}_i^{T}A{A}^T{r}_i+\frac{{\mathit{\theta }}_i}{2}\sum _{j=1}^n{\mathit{\kappa }}_j^2{e}_{ij}^T{e}_{ij}\right)=\sum _{i=1}^N\left(\frac{{\mathit{\theta }}_i}{2}{r}_i^{T}A{A}^T{r}_i+\frac{{\mathit{\theta }}_i}{2}{e}_i^T\tilde{F}{e}_i\right)\hfill \\ \hfill & \le \sum _{i=1}^N\left(\frac{{\mathit{\theta }}_i}{2}{r}_i^{T}A{A}^T{r}_i+\frac{{\mathit{\theta }}_i}{2}{e}_i^T\tilde{F}{e}_i\right)\le \frac{1}{2}{r}^T(\mathit{\Theta }\otimes A{A}^T)r+\frac{1}{2}{e}^T\left(\mathit{\Theta }\otimes \tilde{F}\right)e,\hfill \end{array}$$ 13

and

$$\begin{array}{cc}\hfill r^T(t)(\mathit{\Theta }\otimes B)g(e(t-\mathit{\tau }(t)))& =\sum _{i=1}^N{\mathit{\theta }}_i{r}_i^{T}B{g}_i(e_i(t-\mathit{\tau }(t)))\hfill \\ \hfill & \le \sum _{i=1}^N\left(\frac{{\mathit{\theta }}_i}{2}{r}_i^{T}B{B}^T{r}_i+\frac{{\mathit{\theta }}_i}{2}{e}_i^T(t-\mathit{\tau }(t))\tilde{F}{e}_i(t-\mathit{\tau }(t))\right)\hfill \\ \hfill & \le \frac{1}{2}{r}^T(\mathit{\Theta }\otimes B{B}^T)r+\frac{1}{2}{e}^T(t-\mathit{\tau }(t))(\mathit{\Theta }\otimes \tilde{F})e(t-\mathit{\tau }(t)).\hfill \end{array}$$ 14

Combining inequalities (13) and (14), we have

$$\begin{array}{cc}\hfill \dot{V}(t)& \le -e^T(t)(I_N\otimes P)e(t)+e^T(t)(I_N\otimes P)r(t)+\mathit{\eta }{e}^T(t)(\mathit{\Theta }\otimes \tilde{F})e(t)\hfill \\ \hfill & -\mathit{\eta }(1-\mathit{\rho })e^T(t-\mathit{\tau }(t))(\mathit{\Theta }\otimes \tilde{F})e(t-\mathit{\tau }(t))-r^T(t)(\mathit{\Theta }\otimes \mathit{C})e(t)\hfill \\ \hfill & -r^T(t)(\mathit{\Theta }\otimes \mathit{D})r(t)+\frac{1}{2}{e}^T(t)(\mathit{\Theta }\otimes \tilde{F})e(t)+\frac{1}{2}{r}^T(t)\left(\mathit{\Theta }\otimes (A{A}^T+B{B}^T)\right)r(t)\hfill \\ \hfill & +\frac{1}{2}{e}^T(t-\mathit{\tau }(t))(\mathit{\Theta }\otimes \tilde{F})e(t-\mathit{\tau }(t))-c{r}^T(t)\left(\left(\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }\right)\otimes \mathit{\Gamma }\right)r(t)\hfill \\ \hfill & \le -e^T(t)\left((I_N\otimes P)+(\frac{1}{2}+\mathit{\eta })(\mathit{\Theta }\otimes \tilde{F})\right)e(t)+e^T(t)\left((I_N\otimes P)-(\mathit{\Theta }\otimes \mathit{C})\right)r(t)\hfill \\ \hfill & -r^T(t)\left(\mathit{\Theta }\otimes \mathit{D}+\frac{1}{2}\mathit{\Theta }\otimes (A{A}^T+B{B}^T)-c\left(\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }\right)\otimes \mathit{\Gamma }\right)r(t)\hfill \\ \hfill & \le {\mathit{\psi }}^T(t)\mathit{\Phi }\mathit{\psi }(t),\hfill \end{array}$$

where $\mathit{\psi }(t)={[e^T(t),r^T(t)]}^T$. Thus, by LMI (11), we have $\dot{V}(t)<0$ for $\mathit{\psi }(t)\ne 0$, which indicates that ${\text{lim}}_{t\to \infty }e(t)=\mathbf{0}$ and ${\text{lim}}_{t\to \infty }r(t)=\mathbf{0}$. Therefore, the pinning controlled network (3) can be globally asymptotically synchronized to the objective trajectory. $\square$

Remark 3

In fact, in order to make $\mathit{\Phi }<0$, the matrix $Q$ needs to satisfy $Q<0$. Furthermore, if $\mathit{D}<0$, then $Q<0$ indicates that $\mathit{\Theta }(L+\mathit{\Sigma })+(L^T+\mathit{\Sigma })\mathit{\Theta }>0$ is necessary. On the other hand, by checking the negative definite of $Q$, one can derive the lower bound for the coupling strength $c$.

Illustrative example

In this section, one illustrative example is presented to demonstrate the effectiveness of the obtained theoretical results. Consider the following coupling inertial DNNs with six nodes:

$$\begin{array}{cc}\hfill \frac{{\mathrm{d}}^2{x}_i(t)}{\mathrm{d}{t}^2}& =-D\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}-C{x}_i(t)+Af(x_i(t))+Bf(x_i(t-\mathit{\tau }(t)))+I(t)\hfill \\ \hfill & +c\sum _{j=1}^6{G}_{ij}\mathit{\Gamma }\left(\frac{\mathrm{d}{x}_j(t)}{\mathrm{d}t}+x_j(t)\right),i=1,\dots ,6,\hfill \end{array}$$ 15

where $x_i(t)={(x_{i1}(t),x_{i2}(t))}^T$, $f(x_i(t))={\left(0.5sin(x_{i1}(t)),0.5cos(x_{i2}(t))\right)}^T$, $I(t)={(0.8,0.4)}^T,1\le i\le 6$ and the time delay $\mathit{\tau }(t)=0.15e^t/(1+e^t)$. So it is easy to get ${\mathit{\kappa }}_i=0.5$, $\mathit{\tau }=0.15$ and $\mathit{\rho }=0.0375$. The inner coupling matrix $\mathit{\Gamma }$ in (15) is given with $\mathit{\Gamma }=\mathrm{diag}\{6,4\}$ and the coefficient matrices are given as

$$\begin{array}{c}\hfill D=\left[\begin{array}{cc}0.4& 0\\ 0& 0.3\end{array}\right],C=\left[\begin{array}{cc}1.2& 0\\ 0& 0.4\end{array}\right],A=\left[\begin{array}{cc}0.2& -0.6\\ 0.5& 0.3\end{array}\right],B=\left[\begin{array}{cc}0.3& -0.3\\ -0.2& 0.5\end{array}\right].\end{array}$$

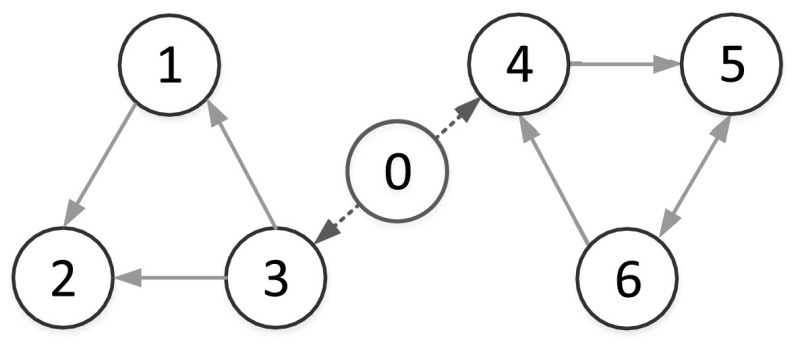
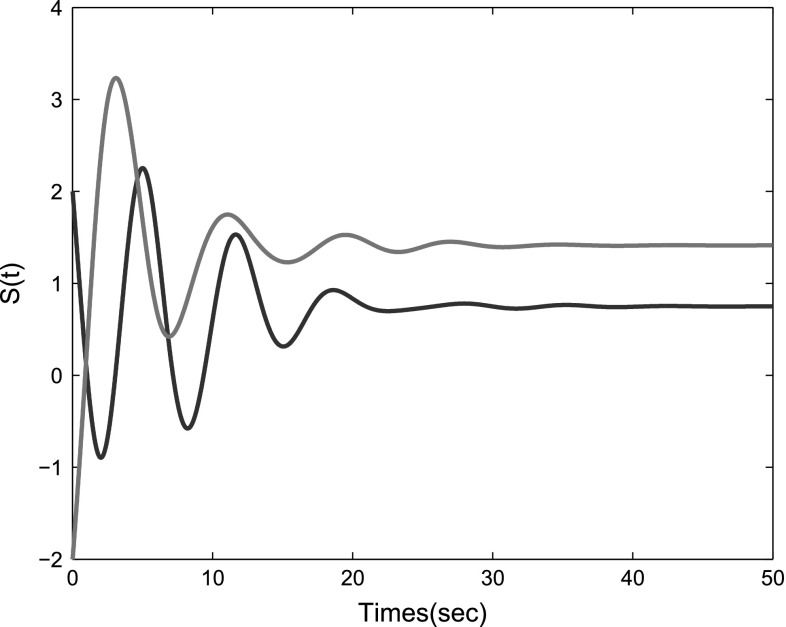
The coupling matrix $G$ is determined by the directed topology given in Fig. 1 with $G_{ij}=0,1(i\ne j)$. Let the initial state of the objective system be $\tilde{\mathit{\varphi }}={[2,-2]}^T$ on the interval $[-0.15,0]$ and initial functions for system (15) are chosen randomly. We use the quantity $E(t)=\sqrt{(1/6){\sum }_{i=1}^6{e}_i^T(t)e_i(t)}$ to measure the quality of the synchronization process. By setting the pinning node set $\mathcal{V}=\{3,4\}$ (see Fig. 1). The objective trajectory of the pinning controlled system (1) is shown in Fig. 2.

Fig. 1.

The coupling communication topology $\mathcal{G}$

Fig. 2.

Objective state trajectory $s(t)$ in system (2)

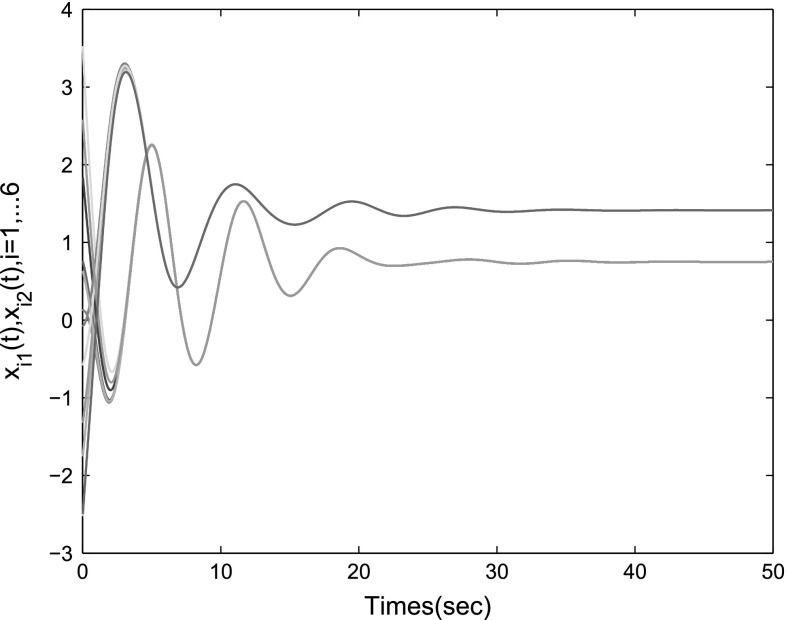
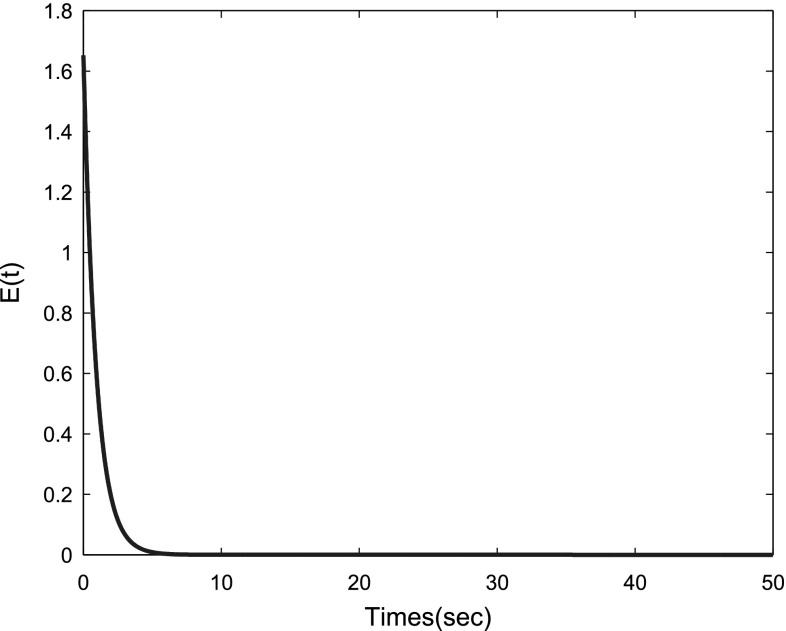
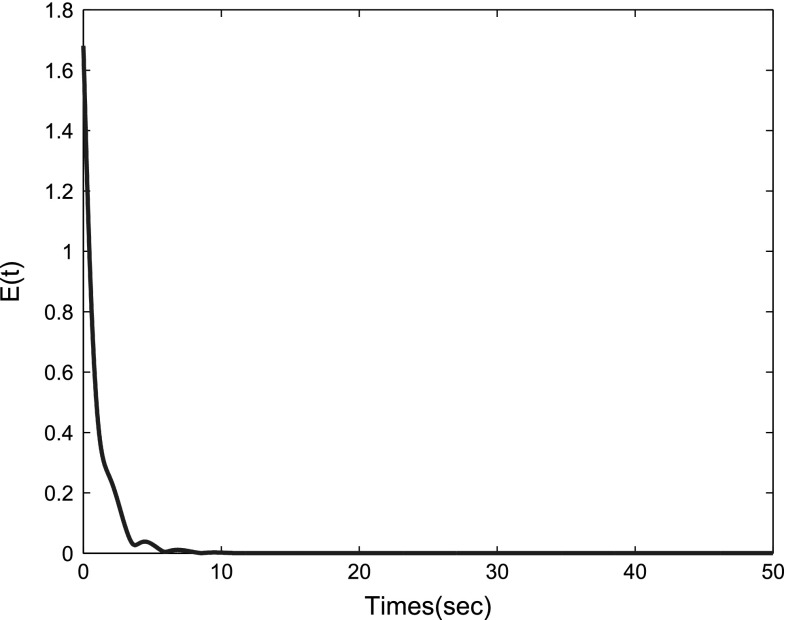
By checking the inequality (8) in Theorem 1, it is easy to compute when $p=2$ and $c=3.5$, ${\mathit{\mu }}_2(\mathcal{H})=-0.6824$, ${\Vert \mathcal{A}\Vert }_2=0.6749$ and ${\Vert \mathcal{B}\Vert }_2=0.6724>0$, which follows that $-{\mathit{\mu }}_2(\mathcal{H})-{\overline{\mathit{\kappa }}\Vert \mathcal{A}\Vert }_2-\overline{\mathit{\kappa }}{\Vert \mathcal{B}\Vert }_2=0.0088>0$. Based on the conclusion in Theorem 1, the coupled inertial DNNs can be exponentially synchronized. The synchronization state trajectories $x_i(t),i=1,2,\dots ,6$ and synchronization error $E(t)$ are given in Figs. 3 and 4.

Fig. 3.

State trajectories $x_i(t)$ in system (15)

Fig. 4.

Synchronization error $E(t)$

Under the pinning node set $\mathcal{V}=\{3,4\}$, one can derive that $\mathit{\theta }=\mathrm{diag}\{0.6935,0.3853,0.9708,0.4258,0.3281,0.5997\}$. By setting $\mathit{\eta }=0.5205$ and the coupling strength $c=1.2$, it is easy to check the LMI (11) in Theorem 3 has a positive definite solution, which ensures that the whole coupled neural network system (15) can be synchronized to the given goal trajectory asymptotically. The state trajectories and the synchronization error of (15) are given in Figs. 5 and 6.

Fig. 5.

State trajectories $x_i(t)$ in system (15)

Fig. 6.

Synchronization error $E(t)$

Remark 4

Matrix measure strategy is an efficient tool to address the stability problem of nonlinear systems. Usually, the established results by using matrix measure are more general than common algebraic criterion due to the fact that matrix measure can be not only taken positive value but also negative value. However, in the synchronization problem for the coupled network, the augmented coefficient matrices of the close-loop controlled system are always high-dimension sparse matrices, which make the verification of the corresponding matrix measure become difficult. On the contrary, the derived condition in the form of LMIs may be more easier to be satisfied with a relatively small coupling strength.

Remark 5

It is difficult to check the inequality (9) in Theorem 2 for $p=1,\infty ,\mathit{\omega }$ under the parameter settings in this example. From the verification conditions in Theorems 1 and 3, one can find that Lyapunov functional method is better than the matrix measure strategy in terms of easy verification for the established criteria when dealing with coupled networks, which suggests that matrix measure strategies are not always better than the classical Lyapunov functional methods.

Conclusions

In this paper, the synchronization control problem has been investigated for coupled inertial DNNs by pinning feedback control. Firstly, matrix measure strategies are utilized to analyze the close-loop error system, under which two sufficient criteria have been established such that the exponential synchronization can be achieved. Furthermore, based on the Lyapunov–Krasovskii method, another sufficient condition has been derived for the asymptotically synchronization for the coupled inertial DNNs. It has been shown that the Lyapunov functional method is more appropriate to deal with the synchronization problem for large-scale coupled CDNs compared with matrix measure strategy.