Deterministic convergence of chaos injection-based gradient method for training feedforward neural networks

Abstract

It has been shown that, by adding a chaotic sequence to the weight update during the training of neural networks, the chaos injection-based gradient method (CIBGM) is superior to the standard backpropagation algorithm. This paper presents the theoretical convergence analysis of CIBGM for training feedforward neural networks. We consider both the case of batch learning as well as the case of online learning. Under mild conditions, we prove the weak convergence, i.e., the training error tends to a constant and the gradient of the error function tends to zero. Moreover, the strong convergence of CIBGM is also obtained with the help of an extra condition. The theoretical results are substantiated by a simulation example.

Introduction

Gradient method (GM) has been widely used as a training algorithm for feedforward neural networks. GM can be implemented in two practical ways: the batch learning and the online learning (Haykin 2008). The batch learning approach accumulates the weight correction over all the training samples before actually performing the update, nevertheless the online learning approach updates the network weights immediately after each training sample is fed. Though GM is widely used in neural network fields, it also has drawbacks of slow learning and getting trapped in local minimum. To overcome those problems, many heuristic improvements have been proposed, such as adding a penalty term to the error function (Karnin 1990), adding a momentum to the weight update (Zhang et al. 2006), injecting noise into the learning procedure (Sum et al. 2012a, b; Ho et al. 2010), etc. Some other nonlinear optimization algorithms such as the Newton method (Osowski et al. 1996), conjugate-gradient method (Charalambous 1992), extended Kalman filtering (Iiguni et al. 1992), and Levenberg–Marquardt method (Hagan and Mehnaj 1994) have also been used for training neural networks. Though these algorithms converge in fewer iterations than GM, they require much more computation per pattern, which makes them not so suitable especially for online learning (Behera et al. 2006). Thus, gradient method remains attractive because of its simplicity and ease of implementation.

As convergence is a precondition for the practical usage of a learning algorithm, the convergence analysis of GM and its various modifications have attracted many researchers in neural network fields (Fine and Mukherjee 1999; Wu et al. 2005, 2011; Wang et al. 2011; Shao and Zheng 2011; Zhang et al. 2007, 2008, 2009, 2012, 2014; Fan et al. 2014; Yu and Chen 2012). Recently, Sum John, Leung Chi-Sing and Ho Kevin theoretically investigated the convergence of noise injection-based online gradient methods (NIBOGM) in Sum et al. (2012a, b) and Ho et al. (2010), where the noises are independent mean zero Gaussian-distributed random variables. For the stability of the noise-induced neural systems and the effects of the noise on neural networks, we refer to Wu et al. (2013), Zheng et al. (2014) and Guo (2011). Besides the independent and identically distributed (i.i.d) noises, chaos noise is also widely used and has been shown to be effective (Ahmed et al. 2011; Uwate et al. 2004) when injected into the gradient training process of feedforward neural networks. Chaos injection enhances the resemblance to biological systems (Li and Nara 2008; Yoshida et al. 2010), and the dynamic variation that it introduces facilitates escaping from local minima and thus improves the convergence (Ahmed et al. 2011). However, as the chaos is not an i.i.d variable, the existing convergence results and the corresponding analysis methods for noise injection-based online gradient methods can not be directly applied to the chaos injection-based gradient methods (CIBGM).

Motivated by the above issues, in this paper we try to theoretically analyze the convergence of CIBGM, covering both the batch learning and the online learning. The weak convergence and strong convergence of the algorithms will be established. The online learning we considered in this paper is the case where the training samples are fed into the network in a fixed sequence, which is also called cyclic learning in literature (Heskes and Wiegerinck 1996). Thus, compared with the convergence results for NIBOGM (Sum et al. 2012a, b; Ho et al. 2010), where the training samples are fed into the network in a totally random sequence, our results will be of deterministic nature.

The remainder of this paper is organized as follows. The network structure and CIBGM are described in “Network structure and chaos injection-based gradient method” section. “Convergence results” section presents some assumptions and our main theorems. The detailed proof of the theorems is given in “Proofs” section. In “Simulation results” section, we use a simulation example to illustrate the theoretical analysis. We conclude the paper in “Conclusion” section.

Network structure and chaos injection-based gradient method

In this section, we first introduce the network structure, which is a typical three-layer neural network. Then we describe the chaos injection-based batch gradient method and the chaos injection-based online gradient method.

Network structure

Consider a three-layer network consisting of p input nodes, q hidden nodes, and 1 output node. Let ${\mathbf{w}}_0={(w_{01},w_{02},\dots ,w_{0q})}^T\in {\mathbb{R}}^q$ be the weight vector between all the hidden units and the output unit, and ${\mathbf{w}}_i={(w_{i1},w_{i2},\dots ,w_{ip})}^T\in {\mathbb{R}}^p$ be the weight vector between all the input units and the hidden unit $i(i=1,2,\dots ,q)$. To simplify the presentation, we write all the weight parameters in a compact form, i.e., $\mathbf{w}={\left({\mathbf{w}}_0^T,{\mathbf{w}}_1^T,\dots ,{\mathbf{w}}_q^T\right)}^T\in {\mathbb{R}}^{q+pq}$ and we define a matrix $\mathbf{V}={({\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_q)}^T\in {\mathbb{R}}^{q\times p}$.

Given activation functions $f,g:\mathbb{R}\to \mathbb{R}$ for the hidden layer and output layer, respectively, we define a vector function $\mathbf{F}(\mathbf{x})={(f(x_1),f(x_2),\dots ,f(x_q))}^T$ for $\mathbf{x}={(x_1,x_2,\dots ,x_q)}^T\in {\mathbb{R}}^q$. For an input $\mathit{\xi }\in {\mathbb{R}}^p$, the output vector of the hidden layer can be written as $\mathbf{F}(\mathbf{V}\mathit{\xi })$ and the final output of the network can be written as

$$\mathit{\zeta }=g({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}\mathit{\xi })),$$ 1

where ${\mathbf{w}}_0·\mathbf{F}(\mathbf{V}\mathit{\xi })$ represents the inner product between the two vectors ${\mathbf{w}}_0$ and $\mathbf{F}(\mathbf{V}\mathit{\xi })$.

Chaos injection-based batch gradient method

Suppose that ${\{{\mathit{\xi }}^j,O^j\}}_{j=1}^J\subset {\mathbb{R}}^p\times \mathbb{R}$ is a given set of training samples. The aim of the network training is to find the appropriate network weights ${\mathbf{w}}^{\ast }$ that can minimize the error function

$$\begin{array}{cc}\hfill E(\mathbf{w})& =\frac{1}{2}\sum _{j=1}^J{\left(O^j-g({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}{\mathit{\xi }}^j))\right)}^2\hfill \\ \hfill & =\sum _{j=1}^J{e}_j\left({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}{\mathit{\xi }}^j)\right),\hfill \end{array}$$ 2

where $e_j(t):=\frac{1}{2}{(O^j-g(t))}^2$.

The gradient of the error function is given by

$$E_{\mathbf{w}}(\mathbf{w})={\left(E_{{\mathbf{w}}_0}^T(\mathbf{w}),E_{{\mathbf{w}}_1}^T(\mathbf{w}),\dots ,E_{{\mathbf{w}}_q}^T(\mathbf{w})\right)}^T$$ 3

with

$$\begin{array}{cc}& E_{{\mathbf{w}}_0}(\mathbf{w})=\sum _{j=1}^J{e}_j^{\prime }\left({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}{\mathit{\xi }}^j)\right)\mathbf{F}(\mathbf{V}{\mathit{\xi }}^j),\hfill \end{array}$$ 4a

$$\begin{array}{cc}\hfill E_{{\mathbf{w}}_i}(\mathbf{w})& =\sum _{j=1}^J{e}_j^{\prime }\left({\mathbf{w}}_0·\mathbf{F}(\mathbf{V}{\mathit{\xi }}^j)\right)w_{0i}{f}^{\prime }({\mathbf{w}}_i·{\mathit{\xi }}^j){\mathit{\xi }}^j,\hfill \\ \hfill & i=1,2,\dots ,q.\hfill \end{array}$$ 4b

Starting from an arbitrary initial value ${\mathbf{w}}^0$, the chaos injection-based batch gradient method updates the weights $\{{\mathbf{w}}^n\}$ iteratively by

$${\mathbf{w}}^{n+1}={\mathbf{w}}^n-{\mathit{\eta }}_n\left(E_{\mathbf{w}}({\mathbf{w}}^n)+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right),n=0,1,2,\dots ,$$ 5

where ${\mathit{\eta }}_n>0$ is the learning rate, A is a positive parameter, $\mathbf{I}={(1,\dots ,1)}^T$, and

$$v(n)=\mathit{\alpha }v(n-1)(1-v(n-1))$$ 6

is the logistic map/Verhust equation which is highly sensitive to the initial value $v(0)$ and the parameter α. For specific values of $v(0)$ (e.g., $0<v(0)<1$) and α (e.g., $3.6<\mathit{\alpha }<4$), the logistic map produces a chaotic time series.

Chaos injection-based online gradient method

The batch gradient method given in (5) updates the weights after all the training samples are fed into the network. This seems not so efficient if the training set is made up of a large number of samples. In this case, the online gradient method is preferred.

We consider the case that the training samples are supplied to the network in a fixed order in the training process. Starting from an arbitrary initial value ${\mathbf{w}}^0$, the chaos injection-based online gradient method updates the weights iteratively by

$${\mathbf{w}}_0^{nJ+j}={\mathbf{w}}_0^{nJ+j-1}+{▵}_j{\mathbf{w}}_0^{nJ+j-1}$$ 7a

$${\mathbf{w}}_i^{nJ+j}={\mathbf{w}}_i^{nJ+j-1}+{▵}_j{\mathbf{w}}_i^{nJ+j-1},i=1,2,\dots ,q$$ 7b

with

$$\begin{array}{cc}\hfill {▵}_k{\mathbf{w}}_0^{nJ+j-1}& =-{\mathit{\eta }}_n\left(e_k^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·\mathbf{F}\left({\mathbf{V}}^{nJ+j-1}{\mathit{\xi }}^k\right)\right)\right.\hfill \\ \hfill & \left.\mathbf{F}({\mathbf{V}}^{nJ+j-1}{\mathit{\xi }}^k)+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right)\hfill \end{array}$$ 8a

$$\begin{array}{cc}\hfill {▵}_k{\mathbf{w}}_i^{nJ+j-1}& =-{\mathit{\eta }}_n\left(e_k^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·\mathbf{F}\left({\mathbf{V}}^{nJ+j-1}{\mathit{\xi }}^k\right)\right)w_{0i}^{nJ+j-1}\right.\hfill \\ \hfill & \left.f^{\prime }\left({\mathbf{w}}_i^{nJ+j-1}·{\mathit{\xi }}^k\right){\mathit{\xi }}^k+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right)\hfill \end{array}$$ 8b

for $j,k=1,2,\dots ,J$, where ${\mathit{\eta }}_n>0$ is the learning rate, whose value may be changed after each cycle of the training procedure, A is a positive parameter, and $v(n)$ is defined by (6).

Remark 1

During the training process, the injected chaos should be large at the beginning in order to help the gradient method avoid trapping into a local minimum, and then be smaller and smaller as the iteration (cycle) proceeds for the sake of ensuring the convergence of the algorithm to a minimum. Thus, in (5) and (8), we use ${\mathit{\eta }}_{n}A$ to control the magnitude of the chaos injected. Here p is used to magnify the effect of the chaos in the early training stage, and ${\mathit{\eta }}_n$ [as suggested by Assumption (A2) in the next section, ${lim}_{n\to \infty }{\mathit{\eta }}_n=0$] is for the purpose of diminishing the effect of the injected chaos on the convergence of the algorithm with the iteration (cycle) increasing.

Convergence results

In this section, we give the convergence results of the CIBGM, covering both the batch learning case (5) and the online learning case (7).

Let $\mathit{\Phi }=\{\mathbf{w}:E_{\mathbf{w}}(\mathbf{w})=0\}$ be the stationary point set of the error function $E(\mathbf{w})$, and ${\mathit{\Phi }}_s=\{w_{ij}:\mathbf{w}=(w_{01},\dots ,w_{ij},\dots ,w_{qp})\in \mathit{\Phi },s=q+(i-1)p+j(\text{if}i>0)\text{or}j(\text{if}i=0)\}$ be the projection of $\mathit{\Phi }$ onto the (s)th coordinate axis, for $s=1,\dots ,pq+q$. The following assumptions are needed for our convergence results.

• (A1) $f^{\prime }(t)$ and $g^{\prime }(t)$ are Lipschitz continuous on any bounded closed interval;

• (A2) ${\mathit{\eta }}_n>0,{\sum }_{n=0}^{\infty }{\mathit{\eta }}_n=\infty ,{\sum }_{n=0}^{\infty }{\mathit{\eta }}_n^2<\infty$;

• (A3) $\{{\mathbf{w}}^n\}$ generated by (5) is bounded over ${\mathbb{R}}^{pq+q}$;

• (A3′) $\{{\mathbf{w}}^{nJ+j}\}$ (or simply denoted by $\{{\mathbf{w}}^m\}$ with $m=nJ+j$) generated by (7) is bounded over ${\mathbb{R}}^{pq+q}$;

• (A4) The set ${\mathit{\Phi }}_s$ does not contain any interior point for every $s=1,\dots ,pq+q$.

Remark 2

Assumption (A1) is satisfied by most of the activation functions, such as sigmoid functions and linear functions. Assumption (A2) is a traditional condition for the convergence analysis of the online gradient method (Sum et al. 2012a, b; Ho et al. 2010). Here we also use this condition in the convergence analysis of the chaos injection-based batch gradient method for the sake of controlling the impact of the chaos on the convergence of the algorithm. Assumption (A3) [or Assumption (A3′)] is a commonly used condition for the convergence analysis of the gradient method in the literature (Wu et al. 2011). In fact, this condition can be easily satisfied by adding a penalty term to the error function (Zhang et al. 2009, 2012). Assumption (A4) is provided to establish the strong convergence.

Now we present our convergence results, where we use “$\Vert ·\Vert$” to denote the Euclidean norm of a vector.

Theorem 1

Suppose that the error function is given by (2) and that the weight sequence $\{{\mathbf{w}}^n\}$is generated by the algorithm (5) for any initial value ${\mathbf{w}}^0$. Assume the conditions (A1)–(A3) are valid. Then there hold the weak convergence results

$$\begin{array}{cc}& (a)Thereis{E}^{\ast }>0suchthat\underset{n\to \infty }{lim}E({\mathbf{w}}^n)=E^{\ast };\hfill \end{array}$$ 9

$$(b)\underset{n\to \infty }{lim}∥E_{\mathbf{w}}({\mathbf{w}}^n)∥=0.$$ 10

Moreover, if Assumption (A4) is valid, then there holds the strong convergence, i.e., there exists a point ${\mathbf{w}}^{\ast }\in \mathit{\Phi }$such that

$$(c)\underset{n\to \infty }{lim}{\mathbf{w}}^n={\mathbf{w}}^{\ast }.$$ 11

Theorem 2

Suppose that the conditions (A1), (A2) and (A3′) are valid. Then, starting from an arbitrary initial value ${\mathbf{w}}^0$, the weight sequence $\{{\mathbf{w}}^m\}$ defined by (7) satisfies the following weak convergence

$$\begin{array}{cc}& (a)Thereis{E}^{\star }>0suchthat\underset{m\to \infty }{lim}E({\mathbf{w}}^m)=E^{\star };\hfill \end{array}$$ 12

$$(b)\underset{m\to \infty }{lim}∥E_{\mathbf{w}}({\mathbf{w}}^m)∥=0.$$ 13

Moreover, if Assumption (A4) is valid, then there holds the strong convergence: there exists${\mathbf{w}}^{\star }\in \mathit{\Phi }$ such that

$$(c)\underset{m\to \infty }{lim}{\mathbf{w}}^m={\mathbf{w}}^{\star }.$$ 14

Proofs

In this section, we first list several lemmas in the literature, then we conduct the proofs of theorems 1 and 2 in “Proof of Theorem 1” and “Proof of Theorem 2” subsections, respectively.

Lemma 1

(See Lemma 1 in Bertsekas and Tsitsiklis 2000) Let$Y_n,W_n$ and$Z_n$ be three sequences such that$W_n$ is nonnegative for all n. Assume that

$$Y_{n+1}\le Y_n-W_n+Z_n,n=0,1\dots$$

and that the series${\sum }_{n=0}^{\infty }{Z}_n$ is convergent. Then either $Y_n\to -\infty$ or else$Y_n$ converges to a finite value and ${\sum }_{n=0}^{\infty }{W}_n<\infty$.

Lemma 2

(See Lemma 4.2 in Wu et al. 2011) Suppose that the learning rate${\mathit{\eta }}_n$satisfies Assumption (A2) and that the sequence $\{a_n\}(n\in \mathbb{N})$ satisfies $a_n\ge 0,{\sum }_{n=0}^{\infty }{\mathit{\eta }}_n{a}_n^{\mathit{\beta }}<\infty$and $|a_{n+1}-a_n|\le \mathit{\mu }{\mathit{\eta }}_n$ for some positive constants βand μ. Then there holds ${lim}_{n\to \infty }{a}_n=0$.

Lemma 3

(See Lemma 5.3 in Wang et al. 2011) Let$F:\mathit{\Omega }\subset {\mathbb{R}}^k\to \mathbb{R},(k\ge 1)$ be continuous for a bounded closed region$\mathit{\Omega }$, and $\mathit{\Phi }=\{\mathbf{z}\in \mathit{\Omega }:F(\mathbf{z})=0\}$. The projection of$\mathit{\Phi }$ on each coordinate axis does not contain any interior point. Let the sequence$\{{\mathbf{z}}^n\}$satisfy:

• (i)${lim}_{n\to \infty }F({\mathbf{z}}^n)=0$;
• (ii)${lim}_{n\to \infty }\Vert {\mathbf{z}}^{n+1}-{\mathbf{z}}^n\Vert =0$.

Then, there exists a unique${\mathbf{z}}^{\ast }\in \mathit{\Phi }$such that${lim}_{n\to \infty }{\mathbf{z}}^n={\mathbf{z}}^{\ast }.$

Proof of Theorem 1

Lemma 4

Suppose the conditions (A1) and (A3) are valid, then $E_{\mathbf{w}}(\mathbf{w})$ satisfies Lipschitz conditon, that is, there exists a positive constant L, such that

$$∥E_{\mathbf{w}}({\mathbf{w}}^{n+1})-E_{\mathbf{w}}({\mathbf{w}}^n)∥\le L∥{\mathbf{w}}^{n+1}-\mathbf{w}{}^n∥.$$ 15

Specially, for $\mathit{\theta }\in [0,1]$, there holds

$$∥E_{\mathbf{w}}({\mathbf{w}}^n+\mathit{\theta }({\mathbf{w}}^{n+1}-{\mathbf{w}}^n))-E_{\mathbf{w}}({\mathbf{w}}^n)∥\le L\mathit{\theta }\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert .$$ 16

Proof

The proof of this lemma is similar to Lemma 2 of Zhang et al. (2012) and thus omitted. $\square$

Proof of (9)

Given that $0<v(0)<1$ and $3.6<\mathit{\alpha }<4$, it is easy to see

$$\begin{array}{cc}\hfill 0<v(n)& =\mathit{\alpha }v(n-1)(1-v(n-1))\hfill \\ \hfill & \le \mathit{\alpha }\frac{{(v(n-1)+1-v(n-1))}^2}{4}=\frac{\mathit{\alpha }}{4}<1.\hfill \end{array}$$ 17

By the differential mean value theorem, there exists a constant $\mathit{\theta }\in [0,1]$, such that

$$\begin{array}{cc}& E({\mathbf{w}}^{n+1})-E({\mathbf{w}}^n)\hfill \\ \hfill & ={\left(E_{\mathbf{w}}({\mathbf{w}}^n+\mathit{\theta }({\mathbf{w}}^{n+1}-{\mathbf{w}}^n))\right)}^T({\mathbf{w}}^{n+1}-{\mathbf{w}}^n)\hfill \\ \hfill & ={\left(E_{\mathbf{w}}({\mathbf{w}}^n)\right)}^T({\mathbf{w}}^{n+1}-{\mathbf{w}}^n)\hfill \\ \hfill & +{\left(E_{\mathbf{w}}({\mathbf{w}}^n+\mathit{\theta }({\mathbf{w}}^{n+1}-{\mathbf{w}}^n))-(E_{\mathbf{w}}({\mathbf{w}}^n))\right)}^T({\mathbf{w}}^{n+1}-{\mathbf{w}}^n)\hfill \\ \hfill & \le {\left(E_{\mathbf{w}}({\mathbf{w}}^n)\right)}^T({\mathbf{w}}^{n+1}-{\mathbf{w}}^n)+L\mathit{\theta }{\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert }^2,\hfill \end{array}$$ 18

where the last inequality is due to (16). Considering (5) and (18), we have

$$\begin{array}{cc}\hfill E({\mathbf{w}}^{n+1})& \le E({\mathbf{w}}^n)+{\mathit{\eta }}_n{\left(E_{\mathbf{w}}({\mathbf{w}}^n)\right)}^T\left(-E_{\mathbf{w}}({\mathbf{w}}^n)-{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right)\hfill \\ \hfill & +L\mathit{\theta }{\mathit{\eta }}_n{∥E_{\mathbf{w}}({\mathbf{w}}^n)+A{\mathit{\eta }}_{n}v(n)\mathbf{I}∥}^2.\hfill \end{array}$$ 19

Using (17) and the inequality $∥E_{\mathbf{w}}({\mathbf{w}}^n)∥\le \frac{\left(1+\Vert E_{\mathbf{w}}({\mathbf{w}}^n){\Vert }^2\right)}{2}$, the second term on the right hand side of (19) can be evaluated

$$\begin{array}{cc}& {\left(E_{\mathbf{w}}({\mathbf{w}}^n)\right)}^T\left[-E_{\mathbf{w}}({\mathbf{w}}^n)-{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right]\hfill \\ \hfill & \le -{∥(E_{\mathbf{w}}({\mathbf{w}}^n))∥}^2+{\mathit{\eta }}_{n}A\sqrt{pq+q}\Vert E_{\mathbf{w}}({\mathbf{w}}^n)\Vert \hfill \\ \hfill & =-{∥(E_{\mathbf{w}}({\mathbf{w}}^n))∥}^2+{\mathit{\eta }}_n\frac{A}{2}\sqrt{pq+q}\left(1+\Vert E_{\mathbf{w}}({\mathbf{w}}^n){\Vert }^2\right).\hfill \end{array}$$ 20

Using inequality ${(a+b)}^2\le 2(a^2+b^2)$, the third term on the right hand side of (19) can be evaluated

$$\begin{array}{cc}& {∥{\mathit{\eta }}_n{E}_{\mathbf{w}}({\mathbf{w}}^n)+A{\mathit{\eta }}_n^{2}v(n)\mathbf{I}∥}^2\hfill \\ \hfill & \le 2{\mathit{\eta }}_n^2{∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2+2{\mathit{\eta }}_n^4{A}^2{\Vert \mathbf{I}\Vert }^2\hfill \\ \hfill & \le 2{\mathit{\eta }}_n^2{∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2+2A^2(pq+q){\mathit{\eta }}_n^4.\hfill \end{array}$$ 21

Combining (19)–(21), we have

$$\begin{array}{cc}\hfill E({\mathbf{w}}^{n+1})& \le E({\mathbf{w}}^n)-{\mathit{\eta }}_n{∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2\hfill \\ \hfill & +{\mathit{\eta }}_n^2\frac{A}{2}\sqrt{pq+q}\left(1+\Vert E_{\mathbf{w}}({\mathbf{w}}^n){\Vert }^2\right)\hfill \\ \hfill & +2L\mathit{\theta }{\mathit{\eta }}_n^2{∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2+2L\mathit{\theta }{A}^2(pq+q){\mathit{\eta }}_n^4\hfill \\ \hfill & =E({\mathbf{w}}^n)-{\mathit{\eta }}_n{\Vert E_{\mathbf{w}}({\mathbf{w}}^n)\Vert }^2\hfill \\ \hfill & +{\mathit{\eta }}_n^2\left(\frac{A}{2}\sqrt{pq+q}+2L\mathit{\theta }{A}^2{\mathit{\eta }}_n^2(pq+q)\right.\hfill \\ \hfill & \left.+\left(2L\mathit{\theta }+\frac{A}{2}\sqrt{pq+q}\right){∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2\right).\hfill \end{array}$$ 22

By Assumptions (A1) and (A3), there is a constant $C_1>0$ such that for all $n=0,1,\dots$

$$∥E_{\mathbf{w}}({\mathbf{w}}^n)∥\le C_1.$$ 23

Thus, there exists a positive constant $C_2$, such that

$$E({\mathbf{w}}^{n+1})\le E({\mathbf{w}}^n)-{\mathit{\eta }}_n{∥E_{\mathbf{w}}({\mathbf{w}}^n))∥}^2+{\mathit{\eta }}_n^2{C}_2.$$ 24

Combining ${\sum }_{n=1}^{\infty }{\mathit{\eta }}_n^2{C}_2<\infty ,E({\mathbf{w}}^n)>0$, and according to Lemma 1, we can conclude that there exists a constant $E^{\ast }$ such that

$$\underset{n\to \infty }{lim}E({\mathbf{w}}^n)=E^{\ast }$$ 25

and

$$\sum _{n=0}^{\infty }{∥E_{\mathbf{w}}({\mathbf{w}}^n)∥}^2{\mathit{\eta }}_n<\infty .$$ 26

This completes the proof of (9).$\square$

Proof of (10)

Using (5), (15) and (23), we have

$$\begin{array}{cc}\hfill \left|∥E_{\mathbf{w}}({\mathbf{w}}^{n+1})∥-∥E_{\mathbf{w}}({\mathbf{w}}^n)∥\right|& \le ∥E_{\mathbf{w}}({\mathbf{w}}^{n+1})-E_{\mathbf{w}}({\mathbf{w}}^n)∥\hfill \\ \hfill & \le L\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert \hfill \\ \hfill & \le {\mathit{\eta }}_{n}L\left(\Vert E_{\mathbf{w}}({\mathbf{w}}^n\right)\Vert +{\mathit{\eta }}_{n}A\Vert \mathbf{I}\Vert )\hfill \\ \hfill & \le C_3{\mathit{\eta }}_n,\hfill \end{array}$$ 27

where $C_3=L(C_1+A\sqrt{pq+q}{sup}_{n\in \mathbb{N}}{\mathit{\eta }}_n)$. Thus, by (26), (27), and Lemma 2, we conclude

$$\underset{n\to \infty }{lim}{E}_{\mathbf{w}}({\mathbf{w}}^n)=0.\square$$

Proof of (11)

Obviously $\Vert E_{\mathbf{w}}(\mathbf{w})\Vert$ is a continuous function under the Assumption (A1). Using (5), (17) and (23), we have

$$\underset{n\to \infty }{lim}\Vert {\mathbf{w}}^{n+1}-{\mathbf{w}}^n\Vert =\underset{n\to \infty }{lim}{\mathit{\eta }}_n∥E_{\mathbf{w}}({\mathbf{w}}^n)+A{\mathit{\eta }}_{n}v(n)\mathbf{I}∥=0.$$ 28

Furthermore, the Assumption (A4) is valid. Thus, applying Lemma 3, there exists a unique ${\mathbf{w}}^{\ast }\in \mathit{\Phi }$ such that ${lim}_{n\to \infty }{\mathbf{w}}^n={\mathbf{w}}^{\ast }$.$\square$

Proof of Theorem 2

Let the sequence $\{{\mathbf{w}}^{nJ+j}\}(n\in \mathbb{N},j=1,2,\dots ,J)$ be generated by (7). For brevity, we introduce the following notations:

$${\mathbf{F}}^{nJ+j,k}=\mathbf{F}({\mathbf{V}}^{nJ+j}{\mathit{\xi }}^k),$$ 29a

$$\begin{array}{cc}& {\mathbf{r}}_i^{n,j}={▵}_j{\mathbf{w}}_i^{nJ+j-1}-{▵}_j{\mathbf{w}}_i^{nJ},\hfill \end{array}$$ 29b

$$\begin{array}{cc}\hfill {\mathbf{h}}_i^{n,l}& ={\mathbf{w}}_i^{nJ+l}-{\mathbf{w}}_i^{nJ}=\sum _{j=1}^l{▵}_j{\mathbf{w}}_i^{nJ+j-1}\hfill \\ \hfill & =\sum _{j=1}^l{▵}_j{\mathbf{w}}_i^{nJ}+\sum _{j=1}^l{\mathbf{r}}_i^{n,j},\hfill \end{array}$$ 29c

$${\mathit{\psi }}^{n,l,j}={\mathbf{F}}^{nJ+l,j}-{\mathbf{F}}^{nJ,j},$$ 29d

for $n\in \mathbb{N};j,k,l=1,2,\dots ,J;i=0,1,2,\dots ,q.$

Lemma 5

(See Lemma 4.1 in Wu et al. 2011) Let $h(x)$ be a function defined on a bounded closed interval $[a,b]$ such that$h^{\prime }(x)$ is Lipschitz continuous with Lipschitz constant$K>0$. Then, $h^{\prime }(x)$ is differentiable almost everywhere in$[a,b]$ and

$$|h^{\prime \prime }(x)|\le K,x\in [a,b].$$ 30

Moreover, there exists a constant$C_4>0$such that

$$\begin{array}{cc}\hfill h(x)& \le h(x_0)+h^{\prime }(x_0)(x-x_0)+C_4{(x-x_0)}^2,\hfill \\ \hfill & \forall x_0,x\in [a,b].\hfill \end{array}$$ 31

Lemma 6

Suppose the conditions (A1) and (A3′) are valid, and the sequence$\{{\mathbf{w}}^{nJ+j}\}$ is generated by (7). Then there are$C_5-C_8$ such that

$$\Vert {\mathbf{F}}^{nJ+j,k}\Vert \le C_5,$$ 32

$$\Vert {\mathbf{h}}_i^{n,l}\Vert \le C_6{\mathit{\eta }}_n,$$ 33

$$\Vert {\mathit{\psi }}^{n,l,j}\Vert \le C_7{\mathit{\eta }}_n,$$ 34

$$\Vert {\mathbf{r}}_i^{n,j}\Vert \le C_8{\mathit{\eta }}_n^2,$$ 35

where$n\in \mathbb{N};j,k,l=1,2,\dots ,J;i=0,1,2,\dots ,q.$

Proof

According to Assumption (A3′), we can define a constant $C_w=sup\Vert {\mathbf{w}}^m\Vert$. Then we have

$$\left|{\mathbf{w}}_i^{nJ+j}·{\mathit{\xi }}^k\right|\le ∥{\mathbf{w}}_i^{nJ+j}∥∥{\mathit{\xi }}^k∥\le C_w\underset{1\le k\le J}{max}\Vert {\mathit{\xi }}^k\Vert =C_9.$$ 36

Accordingly, there exist two positive constants $C_f$ and $C_{f^{\prime }}$ such that

$$\underset{|t|\le C_9}{sup}|f(t)|=C_f,\underset{|t|\le 2C_9}{sup}|f^{\prime }(t)|=C_{f^{\prime }}.$$ 37

Thus we have

$$\Vert {\mathbf{F}}^{nJ+j,k}\Vert =\Vert \mathbf{F}({\mathbf{V}}^{nJ+j}{\mathit{\xi }}^k)\Vert \le \sqrt{q}{C}_f=C_5,$$ 38

and

$$\left|{\mathbf{w}}_0^{nJ+j}·{\mathbf{F}}^{nJ+j,k}\right|\le ∥{\mathbf{w}}_0^{nJ+j}∥∥{\mathbf{F}}^{nJ+j,k}∥\le C_w{C}_5.$$ 39

Then, there is a positive constant $C_{e_j^{\prime }}$ such that

$$\underset{|t|\le C_w{C}_5}{max}\left|e_j^{\prime }(t)\right|\le C_{e_j^{\prime }}.$$ 40

Using (8), (17), (29c), (38) and (40), we have

$$\begin{array}{cc}\hfill ∥{\mathbf{h}}_0^{n,l}∥& =∥\sum _{j=1}^l{▵}_j{\mathbf{w}}_0^{nJ+j-1}∥\hfill \\ \hfill & =∥-{\mathit{\eta }}_n\sum _{j=1}^l\left(e_j^{\prime }({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right){\mathbf{F}}^{nJ+j-1,j}+{\mathit{\eta }}_{n}Av(n)\mathbf{I})∥\hfill \\ \hfill & \le {\mathit{\eta }}_{n}J{C}_{e_j^{\prime }}{C}_5+{\mathit{\eta }}_n^{2}AJ\sqrt{q}\hfill \\ \hfill & \le J\left(C_{e_j^{\prime }}{C}_5+A\sqrt{q}sup{\mathit{\eta }}_n\right){\mathit{\eta }}_n.\hfill \end{array}$$ 41

Similarly, for $i=1,\dots ,q$, we have

$$\begin{array}{cc}\hfill ∥{\mathbf{h}}_i^{n,l}∥& =∥\sum _{j=1}^l{▵}_j{\mathbf{w}}_i^{nJ+j-1}∥\hfill \\ \hfill & =∥-{\mathit{\eta }}_n\sum _{j=1}^l\left(e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right)w_{0i}^{nJ+j-1}\right.\hfill \\ \hfill & \left.f^{\prime }\left({\mathbf{w}}_i^{nJ+j-1}·{\mathit{\xi }}^j\right){\mathit{\xi }}^j+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right)∥\hfill \\ \hfill & \le {\mathit{\eta }}_{n}J{C}_{e_j^{\prime }}{C}_{f^{\prime }}{C}_9+{\mathit{\eta }}_n^{2}AJ\sqrt{p}\hfill \\ \hfill & \le J\left(C_{e_j^{\prime }}{C}_{f^{\prime }}{C}_9+A\sqrt{p}sup{\mathit{\eta }}_n\right){\mathit{\eta }}_n.\hfill \end{array}$$

Let $C_6=Jmax\{C_{e_j^{\prime }}{C}_5+A\sqrt{q}sup{\mathit{\eta }}_n,C_{e_j^{\prime }}{C}_{f^{\prime }}{C}_9+A\sqrt{p}sup{\mathit{\eta }}_n\}$, then we have $\Vert {\mathbf{h}}_i^{n,l}\Vert \le C_6{\mathit{\eta }}_n$ for $i=0,1,\dots ,q$.

Using (29c), (29d), (33) and the mean value theorem, we have

$$\begin{array}{cc}\hfill \Vert {\mathit{\psi }}^{n,l,j}\Vert & =\Vert \mathbf{F}({\mathbf{V}}^{nJ+l}{\mathit{\xi }}^j)-\mathbf{F}({\mathbf{V}}^{nJ}{\mathit{\xi }}^j)\Vert \hfill \\ \hfill & ={\left[\sum _{i=1}^q{\left[f\left({\mathbf{w}}_i^{nJ+l}·{\mathit{\xi }}^j\right)-f\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right)\right]}^2\right]}^{\frac{1}{2}}\hfill \\ \hfill & ={\left[\sum _{i=1}^q{\left[f^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j+{\mathit{\theta }}_i\left({\mathbf{w}}_i^{nJ+l}·{\mathit{\xi }}^j-{\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right)\right){\mathbf{h}}_i^{n,l}·{\mathit{\xi }}^j\right]}^2\right]}^{\frac{1}{2}}\hfill \\ \hfill & \le C_{f^{\prime }}\Vert {\mathit{\xi }}^j\Vert \sum _{i=1}^q\Vert {\mathbf{h}}_i^{n,l}\Vert \le q{C}_{f^{\prime }}\underset{1\le j\le J}{max}\Vert {\mathit{\xi }}^j\Vert C_6{\mathit{\eta }}_n=C_7{\mathit{\eta }}_n,\hfill \end{array}$$ 42

where ${\mathit{\theta }}_i\in (0,1)$ and $C_7=q{C}_{f^{\prime }}{max}_{1\le j\le J}\Vert {\mathit{\xi }}^j\Vert C_6$.

As Assumptions (A1) and (A3′) are valid, it is easy to see that there exists a constant $L^{\prime }$ such that for any $n=0,1,\dots ,$ and $1\le k_1,k_2,j_1,j_2,l_1,l_2\le J$, there holds

$$\begin{array}{cc}& \left|e_j^{\prime }\left({\mathbf{w}}_0^{nJ+k_1}·{\mathbf{F}}^{nJ+j_1,l_1}\right)-e_j^{\prime }\left({\mathbf{w}}_0^{nJ+k_2}·{\mathbf{F}}^{nJ+j_2,l_2}\right)\right|\hfill \\ \hfill & \le L^{\prime }\left|{\mathbf{w}}_0^{nJ+k_1}·{\mathbf{F}}^{nJ+j_1,l_1}-{\mathbf{w}}_0^{nJ+k_2}·{\mathbf{F}}^{nJ+j_2,l_2}\right|.\hfill \end{array}$$ 43

Combining (8), (29), (32)–(34) and (43), we have

$$\begin{array}{cc}\hfill ∥{\mathbf{r}}_0^{n,j}∥& =∥{▵}_j{\mathbf{w}}_0^{nJ+j-1}-{▵}_j{\mathbf{w}}_0^{nJ}∥\hfill \\ \hfill & =∥-{\mathit{\eta }}_n\left(e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right){\mathbf{F}}^{nJ+j-1,j}\right.\hfill \\ \hfill & \left.-e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right){\mathbf{F}}^{nJ,j}\right)∥\hfill \\ \hfill & =∥-{\mathit{\eta }}_n\left[e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right){\mathit{\psi }}^{n,j-1,j}\right.\hfill \\ \hfill & +\left(e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right)-e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}\right)\right){\mathbf{F}}^{nJ,j}\hfill \\ \hfill & \left.+\left(e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}\right)-e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\right){\mathbf{F}}^{nJ,j}\right]∥\hfill \\ \hfill & \le {\mathit{\eta }}_n\left(\left|e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right)\right|\Vert {\mathit{\psi }}^{n,j-1,j}\Vert \right.\hfill \\ \hfill & +\left|e_j^{\prime }\left({\mathbf{w}}_0^{nJ+j-1}·{\mathbf{F}}^{nJ+j-1,j}\right)-e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}\right)\right|\Vert {\mathbf{F}}^{nJ,j}\Vert \hfill \\ \hfill & \left.+\left|e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}\right)-e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\right|\Vert {\mathbf{F}}^{nJ,j}\Vert \right)\hfill \\ \hfill & \le {\mathit{\eta }}_n\left(C_{e_j^{\prime }}\Vert {\mathit{\psi }}^{n,j-1,j}\Vert +L^{\prime }\left|{\mathbf{w}}_0^{nJ+j-1}\right.\right.\hfill \\ \hfill & \left.\times {\mathbf{F}}^{nJ+j-1,j}-{\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}\right|\Vert {\mathbf{F}}^{nJ,j}\Vert \hfill \\ \hfill & \left.+L^{\prime }\left|{\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ+j-1,j}-{\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right|\Vert {\mathbf{F}}^{nJ,j}\Vert \right)\hfill \\ \hfill & \le {\mathit{\eta }}_n\left(C_{e_j^{\prime }}\Vert {\mathit{\psi }}^{n,j-1,j}\Vert +L^{\prime }{C}_5^2∥{\mathbf{h}}_0^{n,j-1}∥+L^{\prime }{C}_w{C}_5\Vert {\mathit{\psi }}^{n,j-1,j}\Vert \right)\hfill \\ \hfill & \le {\mathit{\eta }}_n^2\left(C_{e_j^{\prime }}{C}_7+L^{\prime }{C}_5^2{C}_6+L^{\prime }{C}_w{C}_5{C}_7\right)=C_{10}{\mathit{\eta }}_n^2,\hfill \end{array}$$ 44

where $C_{10}=C_{e_j^{\prime }}{C}_7+L^{\prime }{C}_5^2{C}_6+L^{\prime }{C}_w{C}_5{C}_7$. Similarly, we can show the existence of a constant $C_{11}>0$ such that

$$\Vert {\mathbf{r}}_i^{n,j}\Vert \le C_{11}{\mathit{\eta }}_n^2.$$ 45

Let $C_8=max\{C_{10},C_{11}\}$, then we have $\Vert {\mathbf{r}}_i^{n,j}\Vert \le C_8{\mathit{\eta }}_n^2$ for $i=0,1,2,\dots ,q$.$\square$

Lemma 7

Let the sequence$\{{\mathbf{w}}^{nJ+j}\}$ be generated by (7). Under assumptions (A1) and $(A{3}^{\prime })$, there holds

$$\begin{array}{cc}\hfill E({\mathbf{w}}^{(n+1)J})& \le E({\mathbf{w}}^{nJ})-{\mathit{\eta }}_n{\Vert E_{\mathbf{w}}({\mathbf{w}}^{nJ})\Vert }^2+C_{12}{\mathit{\eta }}_n^2,\hfill \\ \hfill & (n=0,1,\dots )\hfill \end{array}$$ 46

where$C_{12}>0$ is a positive constant.

Proof

By virtue of Assumption (A1) and Lemma 5, we know that $f^{\prime \prime }({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j+t({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j))$ is integrable almost everywhere on $t\in [0,1]$. Then, using Taylor’s mean value theorem we arrive at

$$\begin{array}{cc}\hfill {\mathbf{w}}_0^{nJ}·{\mathit{\psi }}^{n,J,j}& =\sum _{i=1}^q{w}_{0i}^{nJ}\left[f\left({\mathbf{w}}_i^{(n+1)J}·{\mathit{\xi }}^j\right)-f\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right)\right]\hfill \\ \hfill & =\sum _{i=1}^q{w}_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right){\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\hfill \\ \hfill & +\sum _{i=1}^q{w}_{0i}^{nJ}{\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)}^2\hfill \\ \hfill & \times {\int }_0^1(1-t)f^{\prime \prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j+t\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)\right)dt.\hfill \end{array}$$ 47

By virtue of (8), (29), (47) and Lemma 5, there is a constant $C_{13}>0$ such that

$$\begin{array}{cc}& e_j\left({\mathbf{w}}_0^{(n+1)J}·{\mathbf{F}}^{(n+1)J,j}\right)\hfill \\ \hfill & \le e_j\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)+e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\hfill \\ \hfill & \left({\mathbf{w}}_0^{(n+1)J}·{\mathbf{F}}^{(n+1)J,j}-{\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\hfill \\ \hfill & +C_{13}{\left({\mathbf{w}}_0^{(n+1)J}·{\mathbf{F}}^{(n+1)J,j}-{\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)}^2\hfill \\ \hfill & =e_j\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)+e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\hfill \\ \hfill & \left({\mathbf{h}}_0^{n,J}·{\mathbf{F}}^{nJ,j}+{\mathbf{w}}_0^{nJ}·{\mathit{\psi }}^{n,J,j}+{\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\right)\hfill \\ \hfill & +C_{13}{\left({\mathbf{h}}_0^{n,J}·{\mathbf{F}}^{nJ,j}+{\mathbf{w}}_0^{nJ}·{\mathit{\psi }}^{n,J,j}+{\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\right)}^2\hfill \\ \hfill & =e_j\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)+e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right){\mathbf{F}}^{nJ,j}·{\mathbf{h}}_0^{n,J}\hfill \\ \hfill & +e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right){\mathit{\xi }}^j·{\mathbf{h}}_i^{n,J}+{\mathit{\delta }}_1\hfill \\ \hfill & =e_j\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)+e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\hfill \\ \hfill & {\mathbf{F}}^{nJ,j}\times \left(-{\mathit{\eta }}_n\sum _{k=1}^J\left[e_k^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,k}\right){\mathbf{F}}^{nJ,k}+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right]+\sum _{k=1}^J{\mathbf{r}}_0^{n,k}\right)\hfill \\ \hfill & +e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right){\mathit{\xi }}^j·\left(-{\mathit{\eta }}_n\sum _{k=1}^J\left[e_k^{\prime }\right.\right.\hfill \\ \hfill & \left.\left.\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,k}\right)w_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^k\right){\mathit{\xi }}^k+{\mathit{\eta }}_{n}Av(n)\mathbf{I}\right]+\sum _{k=1}^J{\mathbf{r}}_i^{n,k}\right)+{\mathit{\delta }}_1\hfill \\ \hfill & =e_j\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)-{\mathit{\eta }}_n{e}_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\hfill \\ \hfill & {\mathbf{F}}^{nJ,j}·\sum _{k=1}^J{e}_k^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,k}\right){\mathbf{F}}^{nJ,k}\hfill \\ \hfill & -{\mathit{\eta }}_n{e}_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right){\mathit{\xi }}^j\hfill \\ \hfill & \times \sum _{k=1}^J{e}_k^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,k}\right)w_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^k\right){\mathit{\xi }}^k+{\mathit{\delta }}_2,\hfill \end{array}$$ 48

where

$$\begin{array}{cc}\hfill {\mathit{\delta }}_1& =e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)}^2\hfill \\ \hfill & \times {\int }_0^1(1-t)f^{\prime \prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j+t\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)\right)dt\hfill \\ \hfill & +e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right){\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\hfill \\ \hfill & +C_{13}{\left({\mathbf{h}}_0^{n,J}·{\mathbf{F}}^{nJ,j}+{\mathbf{w}}_0^{nJ}·{\mathit{\psi }}^{n,J,j}+{\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\right)}^2\hfill \end{array}$$ 49

and

$$\begin{array}{cc}\hfill {\mathit{\delta }}_2& =e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right){\mathbf{F}}^{nJ,j}·\left(-{\mathit{\eta }}_n^{2}JAv(n)\mathbf{I}+\sum _{k=1}^J{\mathbf{r}}_0^{n,k}\right)\hfill \\ \hfill & +e_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{f}^{\prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j\right){\mathit{\xi }}^j\hfill \\ \hfill & \times \left(-{\mathit{\eta }}_n^{2}JAv(n)\mathbf{I}+\sum _{k=1}^J{\mathbf{r}}_i^{n,k}\right)+{\mathit{\delta }}_1.\hfill \end{array}$$ 50

Summing (48) for $j$ from 1 to J up, and noticing (2), (4a, 4b), (29a), (49) and (50), we have

$$\begin{array}{cc}\hfill E({\mathbf{w}}^{(n+1)J})& \le E({\mathbf{w}}^{nJ})-{\mathit{\eta }}_n\sum _{i=0}^q{∥E_{{\mathbf{w}}_i}({\mathbf{w}}^{nJ})∥}^2+{\mathit{\delta }}_3\hfill \\ \hfill & =E({\mathbf{w}}^{nJ})-{\mathit{\eta }}_n{∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥}^2+{\mathit{\delta }}_3,\hfill \end{array}$$ 51

where

$$\begin{array}{cc}\hfill {\mathit{\delta }}_3& =E_{{\mathbf{w}}_0}({\mathbf{w}}^{nJ})·\left(-{\mathit{\eta }}_n^{2}JAv(n)\mathbf{I}+\sum _{k=1}^J{\mathbf{r}}_0^{n,k}\right)\hfill \\ \hfill & +\sum _{i=1}^q{E}_{{\mathbf{w}}_i}({\mathbf{w}}^{nJ})·\left(-{\mathit{\eta }}_n^{2}JAv(n)\mathbf{I}+\sum _{k=1}^J{\mathbf{r}}_i^{n,k}\right)\hfill \\ \hfill & +\sum _{j=1}^J{e}_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right)\sum _{i=1}^q{w}_{0i}^{nJ}{\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)}^2\hfill \\ \hfill & \times {\int }_0^1(1-t)f^{\prime \prime }\left({\mathbf{w}}_i^{nJ}·{\mathit{\xi }}^j+t\left({\mathbf{h}}_i^{n,J}·{\mathit{\xi }}^j\right)\right)dt\hfill \\ \hfill & +\sum _{j=1}^J{e}_j^{\prime }\left({\mathbf{w}}_0^{nJ}·{\mathbf{F}}^{nJ,j}\right){\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\hfill \\ \hfill & +C_{13}\sum _{j=1}^J{\left({\mathbf{h}}_0^{n,J}·{\mathbf{F}}^{nJ,j}+{\mathbf{w}}_0^{nJ}·{\mathit{\psi }}^{n,J,j}+{\mathbf{h}}_0^{n,J}·{\mathit{\psi }}^{n,J,j}\right)}^2.\hfill \end{array}$$ 52

Considering (17) and (32)–(40), it is easy to see that there exists a constant $C_{12}$ such that

$${\mathit{\delta }}_3<C_{12}{\mathit{\eta }}_n^2.$$ 53

Thus, the desired estimate is deduced by combining (51) and (53). $\square$

Now we are ready to prove the convergence theorem.

Proof of (12)

According to Lemmas 1 and 7, there exists a constant $E^{\star }$ such that ${lim}_{m\to \infty }E({\mathbf{w}}^m)=E^{\star }$ or ${lim}_{m\to \infty }E({\mathbf{w}}^m)=-\infty$. Recall $E({\mathbf{w}}^m)⩾0$, then we have (12). $\square$

Proof of (13)

Using Lemmas 1 and 7, we have that

$$\sum _{n=0}^{\infty }{\mathit{\eta }}_n{∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥}^2<\infty .$$ 54

Similarly to Lemma 4, there exists a Lipschitz constant $L^{″}$ such that

$$∥E_{\mathbf{w}}({\mathbf{w}}^{m+l})-E_{\mathbf{w}}({\mathbf{w}}^m)∥\le L^{″}∥{\mathbf{w}}^{m+l}-\mathbf{w}{}^m∥.$$ 55

where ${\mathbf{w}}^m$ is the weight sequence generated by (7) and $l$ is a positive integer.

Using (55) and (33), for $n=0,1,\dots$, and $j=1,\dots ,J$, we have

$$\begin{array}{cc}& \left|∥E_{\mathbf{w}}({\mathbf{w}}^{(n+1)J})∥-∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥\right|\le ∥E_{\mathbf{w}}({\mathbf{w}}^{(n+1)J})-E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥\hfill \\ \hfill & \le L^{″}\Vert {\mathbf{w}}^{(n+1)J}-{\mathbf{w}}^{nJ}\Vert \hfill \\ \hfill & =L^{″}\sqrt{{\sum }_{i=0}^q{∥{\mathbf{h}}_i^{n,J}∥}^2}\le \sqrt{q+1}{L}^{″}{C}_6{\mathit{\eta }}_n.\hfill \end{array}$$ 56

Combining (54), (56) and Lemma 2, we have

$$\underset{n\to \infty }{lim}∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥=0.$$ 57

Since

$$\begin{array}{cc}\hfill ∥E_{\mathbf{w}}({\mathbf{w}}^{nJ+j})∥& \le ∥E_{\mathbf{w}}({\mathbf{w}}^{nJ+j})-E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥+∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥\hfill \\ \hfill & \le L^{″}{C}_6\sqrt{q+1}{\mathit{\eta }}_n+∥E_{\mathbf{w}}({\mathbf{w}}^{nJ})∥,\hfill \end{array}$$ 58

we have ${lim}_{n\to \infty }∥E_{\mathbf{w}}({\mathbf{w}}^{nJ+j})∥=0$ for $j=1,2,\dots ,J$. $\square$

Proof of (14)

The proof is almost the same as the proof of (11) and thus it is omitted here. $\square$

Simulation results

In this section, we illustrate the convergence behavior of the CIBGM using the sonar signal classification problem.

Sonar signal classification is one of the benchmark problems in neural network field. Our task is to train a network to discriminate between sonar returns bounced off a metal cylinder and those bounced off a roughly cylindrical rock. We obtained the data set from UCI machine learning repository (http://archive.ics.uci.edu/ml/), which comprises 208 samples, each with 60 components. In this simulation, we stochastically choose 164 samples for training and 44 samples for test.

The network for training is with the structure of 60–25–2. The activation functions for both the hidden and output layers are set to be $logsig(·)$ in MATLAB, which is a commonly used sigmoid function. We choose the initial weights to be random numbers in the interval $[-0.5,0.5]$.

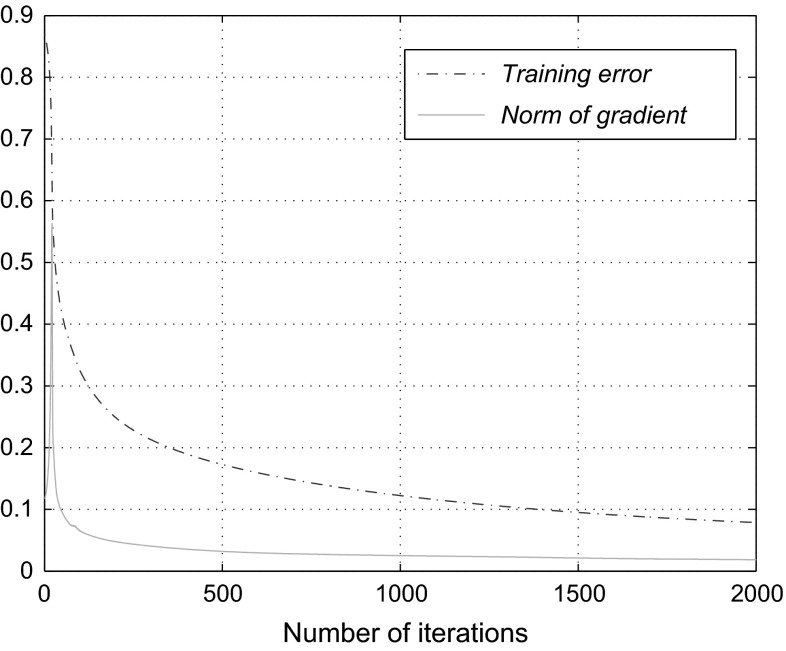
The simulation is carried out by choosing the parameters $A=500,v(0)=0.5$ and $\mathit{\alpha }=3.8$. We set the learning rate ${\mathit{\eta }}_n=\frac{0.08}{164}$ if $n\le 120$ and $\frac{n^{-0.5}}{164}$ if $n>120$, which satisfies Assumption $(A2)$. Here 164 is the number of the training samples. The maximum training iteration (cycle) is 2,000. The learning curves for the chaos injection-based batch gradient method are depicted in Fig. 1, which shows the training error tends to a constant and the gradient of the error function tends to zero. This supports our theoretical analysis. The learning curves for the chaos injection-based online gradient method are almost the same with Fig. 1, with the only change that we should replace the x label “Number of iterations” with “Number of cycles”.

Fig. 1.

Learning curves for chaos injection-based batch gradient method

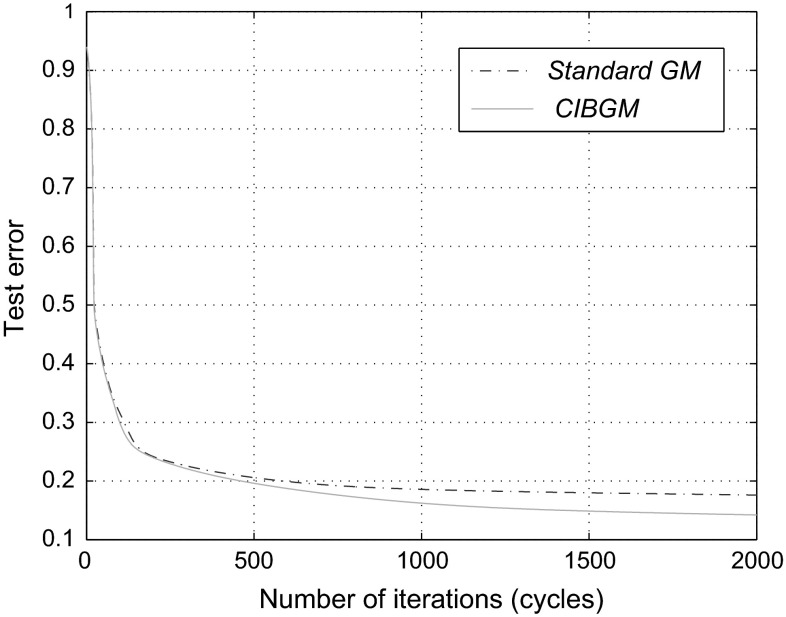
In order to show the effectiveness of the chaos injection method, we compare the test error curves of CIBGM and the standard GM (with no chaos injected) in Fig. 2. We can see that the test error of CIBGM converges faster and tends to a smaller number than that of the standard GM.

Fig. 2.

Test error curves for CIBGM and GM (with no chaos injected)

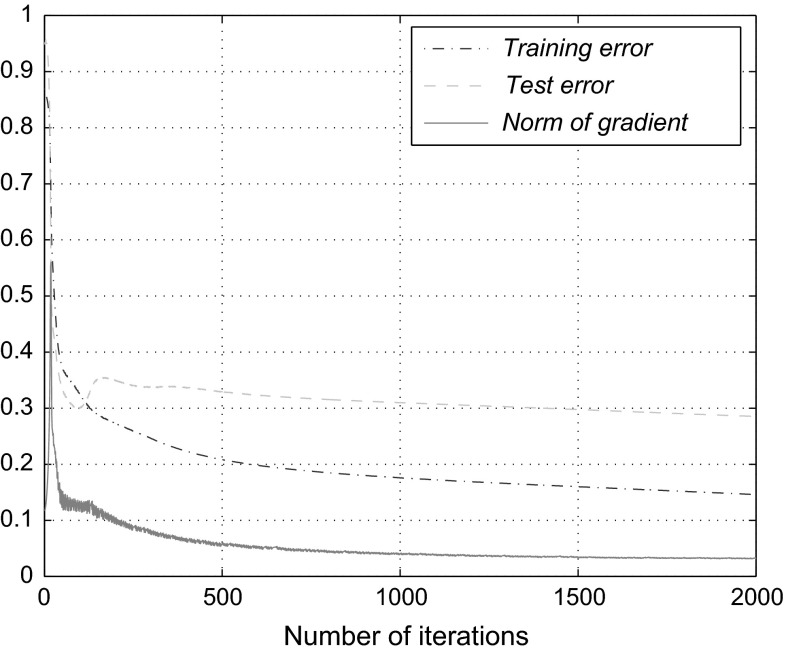
We mention that, though there is no restriction for the parameter A in Theorems 1 and 2, the choice of A is still of great importance. If A is too small, CIBGM will reduce to the standard GM. On the other hand, if A is too large, then the chaos term will dominate the update of the CIBGM especially in the early stage of the training procedure. As a result, the algorithm will converge very slowly and the performance may even be unacceptable. Figure 3 shows the results of the chaos injection-based batch gradient method for $A=5,000$. We can find that the algorithm still converges. However, the performance is much worse than that for $A=500$.

Fig. 3.

Performance for chaos injection-based batch gradient method with $A=5,000$

Conclusion

This paper investigates the chaos injection-based gradient method (CIBGM) for the feedforward neural networks. Two learning mode cases, batch learning and online learning, are considered. Under the conditions that the derivatives of activation functions are Lipschitz continuous on any bounded closed interval and the learning rate ${\mathit{\eta }}_n$ is positive and satisfies ${\sum }_{n=0}^{\infty }{\mathit{\eta }}_n=\infty$ and ${\sum }_{n=0}^{\infty }{\mathit{\eta }}_n^2<\infty$, we derive the weak convergence of the CIBGM, that is the gradient of the error function tends to zero and the error function tends to a constant. The strong convergence is also derived with the assumption that the set ${\mathit{\Phi }}_s$ does not contain any interior point. The theoretical findings and the effectiveness of the CIBGM are illustrated by a simulation example. Future research includes the study on the convergence of the chaos injection-based stochastic gradient method.