Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Apr 10;119(18):5824–5831. doi: 10.1021/acs.jpcb.5b02223

Visualizing KcsA Conformational Changes upon Ion Binding by Infrared Spectroscopy and Atomistic Modeling

Paul Stevenson †,‡, Christoph Götz §,∥,⊥, Carlos R Baiz ‡, Jasper Akerboom ⊥, Andrei Tokmakoff ‡,*, Alipasha Vaziri §,∥,⊥,*
PMCID: PMC4428008  PMID: 25861001

Abstract

graphic file with name jp-2015-02223a_0003.jpg

The effect of ion binding in the selectivity filter of the potassium channel KcsA is investigated by combining amide I Fourier-transform infrared spectroscopy with structure-based spectral modeling. Experimental difference IR spectra between K+-bound KcsA and Na+-bound KcsA are in good qualitative agreement with spectra modeled from structural ensembles generated from molecular dynamics simulations. The molecular origins of the vibrational modes contributing to differences in these spectra are determined not only from structural differences in the selectivity filter but also from the pore helices surrounding this region. Furthermore, the coordination of K+ or Na+ to carbonyls in the selectivity filter effectively decouples the vibrations of those carbonyls from the rest of the protein, creating local probes of the electrostatic environment. The results suggest that it is necessary to include the influence of the surrounding helices in discussing selectivity and transport in KcsA and, on a more general level, that IR spectroscopy offers a nonperturbative route to studying the structure and dynamics of ion channels.

1. Introduction

Over the past decades our atomistic understanding of protein structure and function has been revolutionized by X-ray crystallography and NMR spectroscopy, and magnetic resonance techniques have provided information on the time scales of protein conformational dynamics. However, until recently, no direct experimental techniques existed that could combine atomistic structural information with time resolution sufficient to observe the intrinsic functional time scales of many proteins.1−5

Among the new approaches to studying protein conformational dynamics, infrared (IR) spectroscopy of amide I vibrations (the amide carbonyl stretch between 1600 and 1700 cm–1) has seen a surge of interest as a result of advances in 2D IR spectroscopy and structure-based modeling, which provides an atomistic interpretation of protein IR spectra.6−9 Amide I vibrations are delocalized, involving the concerted vibration of numerous coupled carbonyls of peptide units of the protein backbone. The sensitivity of the coupling between carbonyl groups to their relative position and orientation in space means that the amide I band is influenced by the underlying symmetry, size, and backbone structure of the protein. Though interpretation of protein IR spectra is often complicated by the presence of many broad peaks in a small frequency window, a new generation of atomistic spectral modeling that draws from molecular dynamics (MD) simulations of the protein provides new avenues by which to interpret these experiments.10

In this context, the molecular origin of the observed high ion throughput (>108 ions s–1) and highly selective transport of K+ ions of Na+ (>1000:1)11 in the bacterial potassium channel KcsA is still hotly debated.12,13 Traditional models of the selectivity and transport assume the selectivity filter is inflexible and that differences in the ion binding can be explained by a geometry optimized to bind K+ ions (the “Snug-fit” model).11,14 This is in contrast to other proposed explanations, where significant fluctuations in the selectivity filter are invoked.12,15−17 More recently, simulations have suggested the assumption of alternating K+ ions and water molecules transporting through the selectivity filter may be incorrect, and the K+ ions are more densely packed than previously thought.13 What is clear, however, is that understanding the behavior of the selectivity filter is essential to understanding K+ transport in KcsA, which requires experimental characterization of the dynamical interaction between the ions and the selectivity filter.

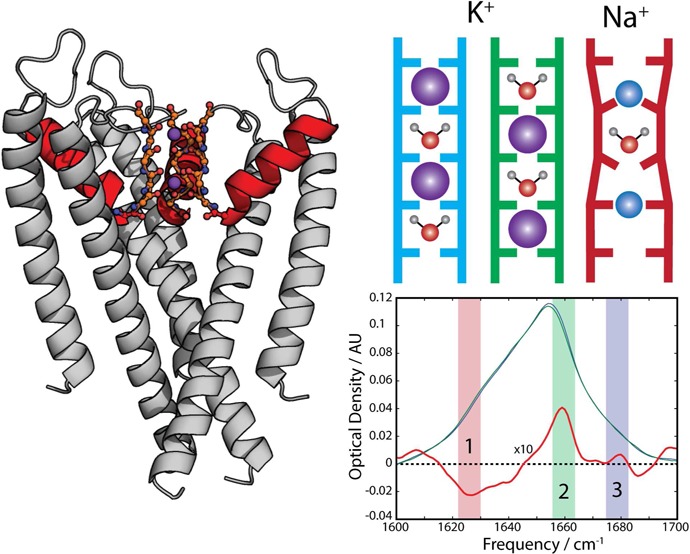
The TVGYG structural motif constituting the selectivity filter is a highly conserved sequence among potassium channels.18 Each subunit of the KcsA tetramer consists of an intracellular gating domain and a ∼15 Å narrow pore domain in which the selectivity filter resides (Figure 1a). The carbonyl groups in this 20-residue filter define a set of binding sites, labeled S1–S4, in which K+ binds in an 8-fold coordinated geometry (Figure 1b). X-ray crystallography indicates that under physiological concentration K+ can bind in one of two configurations, either at sites S1 and S3 or at sites S2 and S4.19 Water is assumed to occupy the respective other binding sites for each configuration, though concerns have been raised over whether this is the case during transport.13 Na+ has been observed to bind primarily in an in-plane position (Figure 1b), though there is still some debate over which residues coordinate Na+.20

Figure 1.

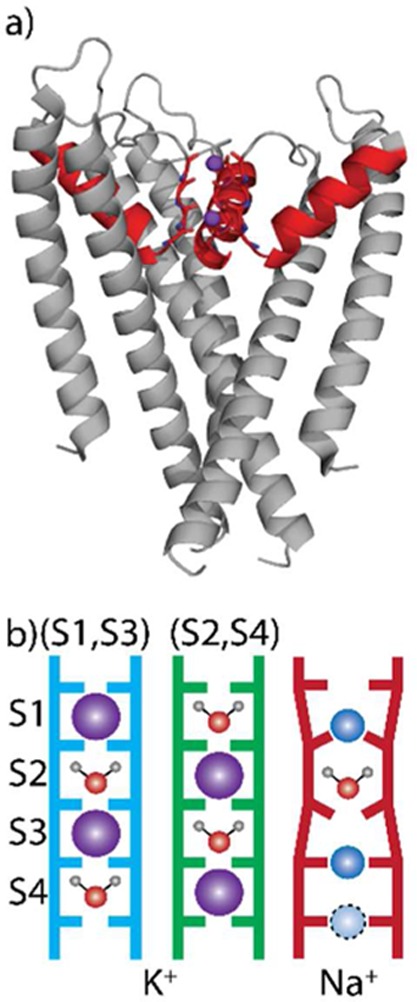
Figure 1

Open in a new tab

(a) Structure of the transmembrane region of KcsA highlighting the extended filter region (red) and K+ ions in the (S1, S3) configuration (purple). (b) Schematic illustration of the ion occupancy within the selectivity filter for the three configurations investigated.

Here we demonstrate on three well-characterized examples of ion-binding in KcsA that the ion-induced conformational changes of KcsA can be characterized using amide I IR spectroscopy in combination with computational modeling. Using attenuated total reflection (ATR) IR spectroscopy, it was recently shown that significant differences in the amide I spectrum can be observed when the buffer cation composition is varied between K+ and Na+, but the origin of these differences remained elusive.21 Here we present new difference IR spectra between K+ and Na+ buffers designed to prepare the binding configurations pictured in Figure 1b and use structure-based spectroscopic modeling that draws on MD simulations to interpret the data. Our analysis reveals the sensitivity of amide I vibrations of the selectivity filter and pore region to the conformational changes which occur on binding K+ or Na+.

2. Methods

a. Sample Preparation

KcsA Expression and Purification

The full-length KcsA channel (167 amino acid length monomer), containing a 6xHis-tag inserted directly after Met1 and cloned into pRSF1 (Merck), was expressed in Escherichia coli BL21 (DE3) cells on induction with 1 mM IPTG (isopropyl-β-d-thiogalactopyranoside). Bacteria were collected and resuspended in buffer A (100 mM NaCl, 50 mM KCl, 50 mM sodium phosphate, pH 8.0) solution and lysed by sonication in the presence of a protease inhibitor cocktail (complete EDTA-free, Roche). The protein was solubilized by 1 h incubation with 20 mM n-dodecyl-β-d-maltopyranoside (DDM, Avanti) which is known to not interfere with the protein’s spectral features in the amide I band, followed by centrifugation at 30000g for 30 min. The supernatant was incubated with Co2+ affinity resin (Thermo) in the presence of 20 mM imidazole for 1 h at 4 °C, loaded onto a column, and washed with 40 mM imidazole and 1 mM DDM in buffer A. The protein was eluted with 400 mM imidazole and 1 mM DDM in buffer A and extensively dialyzed versus NaCl buffer B (150 mM NaCl, 1 mM DDM, 10 mM HEPES, pH 7.5) to remove K+ ions.

To assist with sample transparency in the infrared, all exchangeable protons of KcsA were deuterated by multiple concentration–dilution cycles with D2O-based buffer B in a 10 kDa MWCO spin concentrator (Amicon, Millipore) over the course of several days until the H2O content was below 1% as determined by absorption at 3400 cm–1 on a FTIR spectrometer (Thermo). Temporary heating of the sample to 37 °C and subsequent incubation at 4 °C ensured proper deuteration of the buried parts of the protein. The desalted and deuterated KcsA was concentrated to 7–8 mg/mL, frozen in liquid N2, and stored at −80 °C until further use. Correct secondary structure of KcsA in K+-free buffer B was confirmed via CD spectroscopy. The fraction of correctly folded tetrameric protein was estimated by loading unexchanged samples of KcsA on a normal SDS-gel, and from the densiometry of the monomeric and tetrameric band at approximately 18 and 75 kDa, it was estimated that >95% of the sample was composed of correctly folded tetrameric protein.

Salt Exchange and Sample Preparation

To introduce K+ ions into the sample in a controlled fashion, the KcsA was subjected to further concentration–dilution cycles with a modified buffer B (150 mM KCl, 1 mM DDM, 10 mM HEPES pD 7.9 in D2O).

FTIR Spectroscopy

For the FTIR absorbance spectra, approximately 2.5 μL of KcsA sample in different salt conditions was sandwiched between two 1 mm thick CaF2 windows (CeNing Optics), separated by a 50 μM PTFE spacer. For each sample, 2048 averages were collected on a Nicolet 380 FTIR spectrometer (Thermo Scientific) at 1 cm–1 resolution against a background of dry air at 20 °C. FTIR spectra of each buffer, without protein, were also collected in order to subtract the background D2O absorption from the KcsA spectra. Difference spectra are calculated as FTIR spectra of (KcsA in KCl, buffer subtracted) – (KcsA in NaCl, buffer subtracted).

b. Structure-Based Spectral Modeling

In order to obtain a molecular interpretation of the spectral features above, we used a model of the amide I vibration that maps structure vibrational frequencies and couplings between oscillators.22,23 This procedure draws on MD simulations of KcsA for each ion-binding configuration of interest and uses it to parametrize a quantum-mechanical local mode Hamiltonian for the coupled peptide units of the protein backbone, which govern the vibrational spectroscopy of the amide I band.

Molecular Dynamics Simulations

MD simulations were performed using the GROMACS software package and the CHARMM36 force field. We started with the full-length tetrameric KcsA crystal structure by Uysal et al.24 (PDB accession code 3EFF) and embedded this in a DMPC membrane25,26 using the g_membed function in GROMACS.27 The protein–lipid system was solvated with the TIP3P water model. This system was equilibrated for a total of 2 ns (1 ns NVT equilibration, 1 ns NPT equilibration), before running a further 7 ns trajectory to use as a basis for the spectral calculations. These equilibration and trajectory times are consistent with literature protocols for KcsA simulations.28−30 All stages of the simulation were run with 2 fs time steps, Nosé–Hoover thermostat, semi-isotropic Parrinello–Rahman pressure coupling (where appropriate), and the LINCS constraint algorithm. To compare the effects of different salts on the spectra, we replaced the contents of the selectivity filter prior to equilibration with either 2 K+ ions and 2 water molecules (with K+ in either S1, S3 or S2, S4, water occupying with remaining sites) or 2 Na+ and 2 water molecules (using the positions from Thompson et al.20). During the MD production run, the K+ (Na+) ions were held in place with harmonic position restraints.

Amide I Spectral Modeling

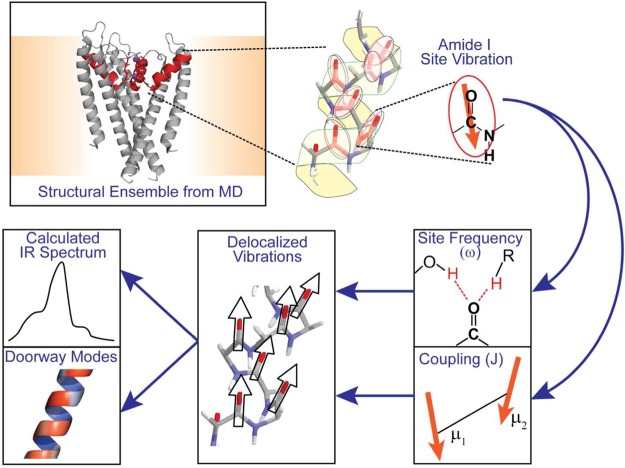
Figure 2 illustrates the simulation protocol used to link the experimentally observed IR spectra with MD simulations, as reviewed in detail in ref (10). The local mode Hamiltonian is constructed in the basis set of the 668 backbone peptide units and was parametrized using frozen configurations of the protein and water. The structure determines the position and orientation of each peptide unit, and the corresponding amide I transition dipole moment for that site is positioned in the plane of the peptide unit between the carbon and oxygen. The diagonal elements of the Hamiltonian are the vibrational transition energies (site frequencies) between the ν = 0 and ν = 1 states of the amide I vibration. Hydrogen-bonding interactions with the carbonyl oxygen downshift these frequencies by an amount that depends on the local electrostatic environment. For this calculation, we used the empirical spectral map in which the frequency of each oscillator is correlated with the electric field acting on the oxygen of the peptide unit along the carbonyl bond developed by Reppert et al.23 The Hamiltonian’s off-diagonal elements, or couplings, are determined by the spatial configuration of the peptide units. In the case of through-space interaction, we used transition dipole coupling, which depends on the distance and angle between the two oscillators.31 For bonded peptide units, the through-bond coupling was obtained from the nearest-neighbor coupling model developed by Jansen et al.,22 which maps the φ and ψ angles of the bonded peptide units onto a coupling. Diagonalizing this Hamiltonian led to eigenstates and eigenvalues which were used to calculate an FTIR spectrum of individual configurations of protein and water. Since parameters used depend intimately on the sub-angstrom configuration of water and protein, we generate Hamiltonians for structural snapshots at 1 ps intervals of the trajectory. In the case of the K+ calculations, an average of the S1, S3 and S2, S4 calculated spectra was used for comparison to experiment.

Figure 2.

Figure 2

Open in a new tab

Simulation strategy for linking MD structures with experimental IR spectra. Individual peptide groups and their associated amide I transition dipoles are identified in structures sampled from MD simulations. A local mode Hamiltonian is parametrized from the structure using the molecular electric field to set the diagonal site frequencies and off-diagonal couplings between sites. The delocalized eigenstates and their corresponding transition dipole moments are used to calculate the IR spectrum and use doorway modes to visualize the vibrations.

This approach is known to qualitatively reproduce spectral features. While it does not quantitatively reproduce exact peak frequencies, line widths, or absolute intensities, the relative frequency shifts and intensities of resonances are reliable metrics for comparison. Our calculations also neglect side chain vibrations that may absorb in the 1600–1700 cm–1 region, such as the amide vibrations from glutamine and asparagine and the CN vibrations of arginine. While side chains certainly contribute, it is at a significantly lower level than amide I, and their frequencies are well-known for the interpretation of experimental spectra. Although the spectral map we use here neglects side chains, it is important to note that other maps have been developed which are developed with the aim of capturing the vibrations of side chain amide groups (Asp, Glu),32 though the application of this maps to side chains in larger proteins has not been characterized.

Doorway Mode Analysis

The diagonalization of the local mode Hamiltonian provides not only the energies of the vibrational modes but also the corresponding eigenstates. Interpretation of these eigenstates, however, is hampered by the sheer number of them (>30 000 in this case), even for a small subset of the protein structure at a reduced sampling rate. Analogously to how principal component analysis can be used to describe which input variables are principally responsible for observed trends, doorway mode analysis shows which amide units contribute most significantly to the IR spectrum in a specific frequency window.33 To obtain a set of representative strongly IR-active states from a subset of eigenvectors, we apply the doorway mode analysis in ref (34), using a ± 3 cm–1 window about the stated center frequency.

Though outlined in detail in ref (34), we briefly review doorway mode analysis. The aim is to find a transformation matrix Φi, which will transform vectors in the site basis to the doorway basis. The doorway mode basis is one where most of the intensity of the transition is contained within the first three modes. First, we define the matrix Ti, a subset of the transformation matrix obtained from the eigenvalue decomposition of the Hamiltonian. The subset is defined to only include eigenstates with eigenvalues within the frequency range Ri. A singular value decomposition (SVD) of the eigenstates of the Hamiltonian transforms them to a basis where each subsequent component contributes less to the transition intensity. Combining the SVD transformation matrix Ui with our eigenstate transformation matrix Ti yields the overall transformation matrix Φi = UiTi. With this matrix, we are able to determine representative modes for each transition.

3. Results and Discussion

a. FTIR Experiments

As shown in Figure 3, the FTIR spectra of KcsA in both KCl and NaCl show a broad peak centered at 1655 cm–1, consistent with the high α-helix content of the protein. The asymmetric line shape features a broad shoulder at lower frequencies, which includes contributions from the side chain absorptions of Asp, Arg, Gln, Tyr, Trp, and Gln residues.35 To specifically capture the spectral changes which arise solely from the binding of ions by the selectivity filter, we focus on the analysis of the difference spectra, i.e., the spectrum of KcsA in KCl buffer minus the spectrum of KcsA in NaCl buffer. The FTIR difference spectrum, in Figure 3, is highly structured, with several distinct features. Of these features, we select three for analysis (labeled 1, 2, and 3) because they are the largest amplitude differences within the amide I window, are not overlapping other features, and are well-reproduced by our calculations. Peak 1 is a strong and broad negative peak at 1625 cm–1, peak 2 is a strong positive band at 1660 cm–1, and peak 3 is a less intense narrow positive band at 1680 cm–1. Given that the amide I vibrations of 668 peptide units contribute to the full FTIR spectra, and that only 16 carbonyls are in direct contact with the bound ions at any one time, it is not surprising that the largest spectral changes between KCl and NaCl buffers are on the order of 4%. Nevertheless, this change is large enough to suggest that a significant number of amide carbonyls are sensitive to the identity of the bound ion.

Figure 3.

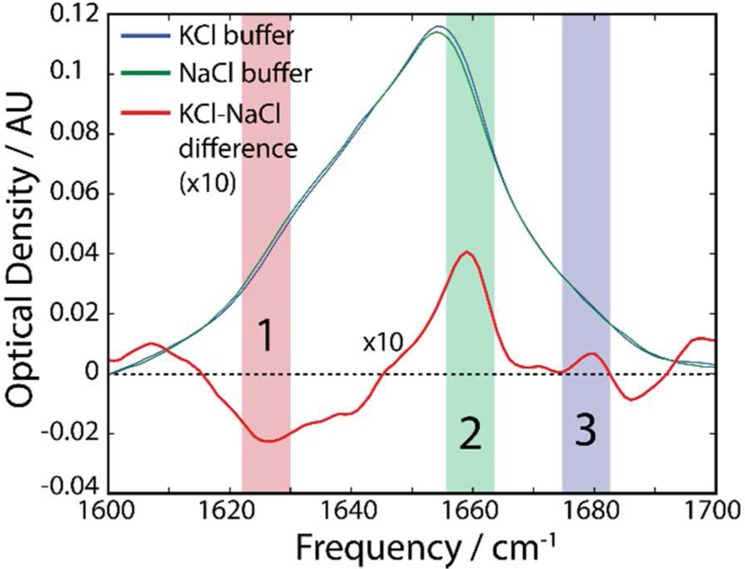
Figure 3

Open in a new tab

Experimental spectra of KcsA with KCl or NaCl buffers and the difference spectrum (KCl – NaCl) illustrating the correspondence of key features.

Our experimental FTIR spectra and difference spectrum are consistent with the difference ATR infrared spectra reported recently by Futurani et al.21 Our peak positions differ by <5 cm–1, but this readily explained by our use of deuterated sample as opposed to experiments in H2O, and the differing chemical environment of the sample (DDM micelles in this work versus Asolectin bilayer).

b. Simulations of FTIR Spectra

Simulated FTIR and FTIR difference spectra, shown in Figures 4a and 4b, respectively, are able to qualitatively reproduce the key experimental features. The full FTIR center frequency and line width are in good qualitative agreement, though as noted earlier, quantitative agreement should not be expected from these calculations. The experimental line shape is not fully reproduced by calculation, notably in the 1620–1650 cm–1 region, in which there is a shoulder in the experimental spectra which is not captured in the calculations. We attribute this primarily to side chain absorptions in this region (namely Arg at 1605 cm–1, Tyr at 1615 cm–1, Trp at 1618 cm–1, and Gln at 1640 cm–1),35 which are not included in our calculation since vibrational frequency and coupling models do not presently exist.

Figure 4.

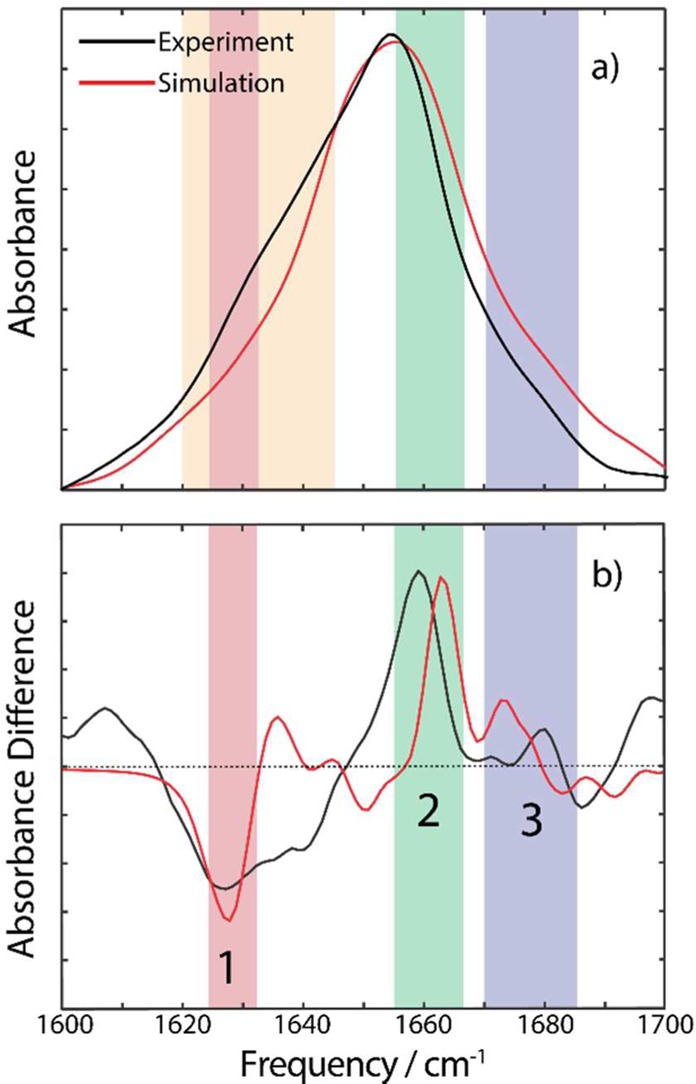
Figure 4

Open in a new tab

Comparison of the experimental and calculated spectra for KcsA in KCl buffer (a) and the difference spectra (b). Peaks 1, 2, and 3 (see main text) are highlighted in red, green, and blue respectively, and the side chain region is highlighted in orange.

In the calculated FTIR difference spectrum, we find the three features highlighted in the experimental data are reproduced well both in peak frequency (differing by only a few wavenumbers) and in relative intensity. The reproduction of both the frequency and intensity in our calculations suggests the nature of the delocalized vibrational modes is well captured.

The most notable region of mismatch between the experimental and calculated difference spectra is again the 1620–1650 cm–1 region. While this could reflect a limitation of the vibrational coupling model, is it more likely to reflect the neglect of side chain vibrations in our calculations. Previous work has shown that the Y78F mutant, which shows similar functional behavior to the WT protein,36 gives rise to a difference spectra distinct from the wild-type, with the most notable differences being in the 1620–1650 cm–1 region.21 However, we note that, while the side chain absorptions may indeed contribute significantly to the experimental difference spectrum, our analysis focuses on peaks which are clearly reproduced by the carbonyl-only modeling, indicating that a discussion of these peaks in terms of delocalized amide I vibrations only is appropriate.

To determine the participation of different regions of the protein to the spectral features observed, we calculated difference FTIR spectra using various subdomains of the full tetrameric protein complex. These sections are (a) the four TVGY chains comprising the selectivity filter, (b) the “extended filter” region comprising the selectivity filter and the four pore helices, and (c) the entire transmembrane region of the protein. Our results are summarized in Figure 5. We found that the calculated FTIR spectra for the transmembrane region and the extended filter differed only in the intensity of some features but were otherwise consistent with each other. The selectivity filter alone could not reproduce the difference spectra, notably the 1660 cm–1 peak, suggesting the larger protein complex and coupling between the monomer units are actively participating in generating the observed experimental spectra.

Figure 5.

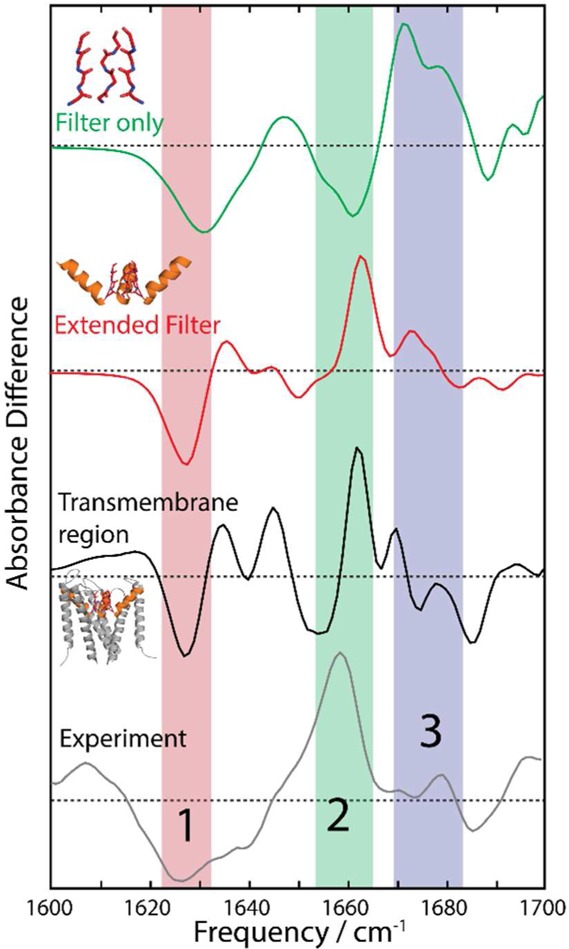
Figure 5

Open in a new tab

Comparison of calculated difference spectra for different subsections of KcsA. The filter-only calculation is unable to reproduce the features observed in the extended filter region, the full transmembrane region, and the experimental spectra.

In order to elucidate the origins of the features in the difference spectra, we show the calculated FTIR spectra for the individual ion-binding configuration of the extended filter region in Figure 6. From this, we see that peaks 1 and 3 come from distinct peaks in the Na+- and K+-bound calculations, respectively, while peak 2 comes from a change in intensity and line shape of a peak present in the K+and Na+ calculations. Taken in conjunction with the calculations on truncated regions of the protein, this suggest the 1660 cm–1 peak in the difference spectra (peak 2) arises from changes in the α-helices surrounding the pores. The nature of these structural changes is discussed below.

Figure 6.

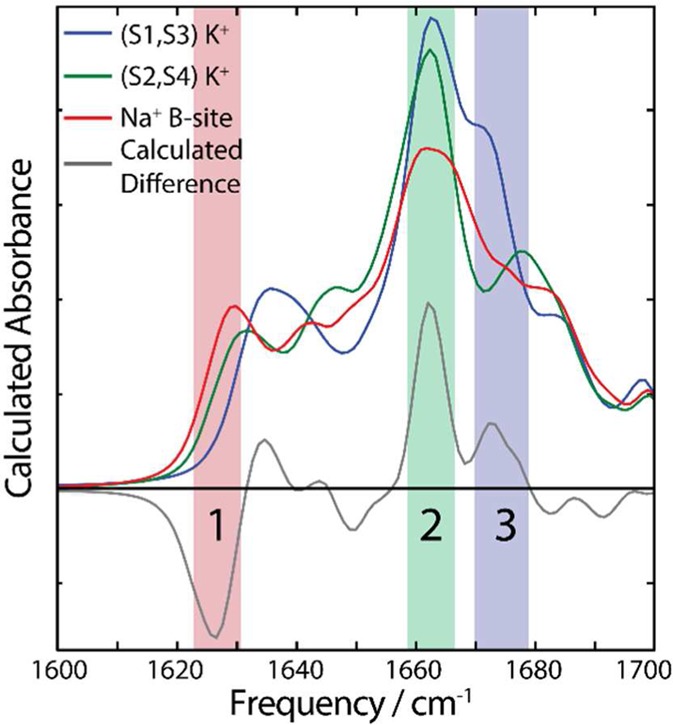
Figure 6

Open in a new tab

Calculated spectra for the extended filter region for the various ion-binding configurations. The calculated difference spectrum is shown in gray.

c. Vibrational Mode Assignment and Visualization

To visualize the molecular origins of the vibrations which contribute to the difference spectrum, we apply a doorway mode analysis to our calculated eigenvectors for the extended filter region. We selected four frequency windows—the first at 1630 cm–1 corresponding to peak 1, 1660 cm–1 (peak 2), 1674 cm–1 (peak 3 for S1, S3 binding), and 1680 cm–1 (peak 3 for S2, S4 binding)—and analyzed eigenstates falling within ±3 cm–1 of the center frequency. On the basis of this calculation, the four frequencies can be assigned to four modes with distinct vibrational motions involving amide units within the extended filter region (see Figure 7). The amide units contributing most significantly to the 1630 cm–1 mode, designated the B-site mode, are T75 carbonyls with some contribution from the carbonyls of the pore α-helices. These carbonyls and the direction of their transition dipoles are identified with outlined arrows in Figure 7a. Carbonyls on opposite monomers of the filter mode vibrate out-of-phase, contracting on one side and extending on the other; however, the net transition dipole moment of all oscillators constructively adds so that the total transition dipole moment (green arrows) is orthogonal to the filters pore. The 1660 cm–1 mode (labeled “Helix”) is present in all cases and is constituted almost exclusively by vibrations from the pore α-helices. Carbonyls in all monomers are in-phase and contribute to an overall dipole moment that is oriented along the pore (Figure 7b). The 1674 cm–1 mode of the (S1, S3) configuration is termed “S3”, due to the strong involvement of the T75 and V76 residues in the filter which define the S3 binding site (Figure 7c). Similarly the 1680 cm–1 mode of the (S2, S4) configuration is termed “S2” due to the large amplitude in the V76 and G77 residues which define the S2 binding site (Figure 7d).

Figure 7.

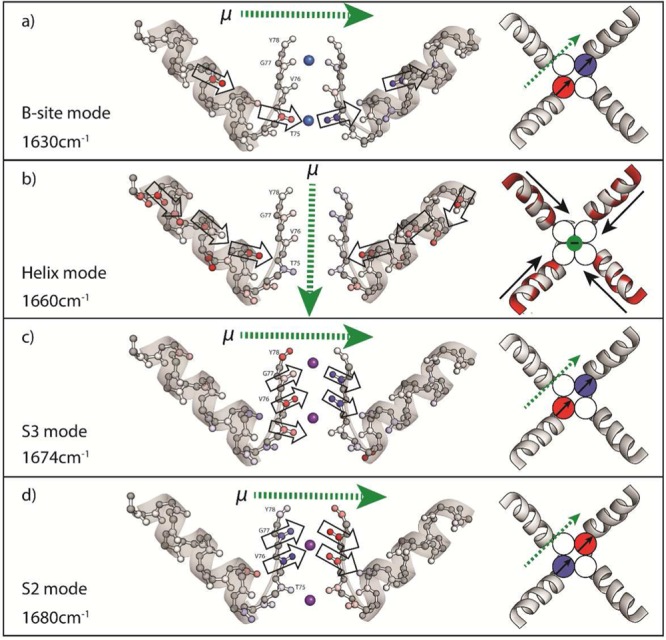
Figure 7

Open in a new tab

Visualizations of calculated doorway modes of the extended filter region presented as side view (left) and top view looking down the pore (right). Color indicates the relative sign of the CO vibrational motion (contraction/extension), while the color intensity indicates its amplitude. Outlined arrows indicate the direction of the transition dipole moment of individual carbonyls contributing most to the mode. The sum of transition dipoles of one monomer is shown as black arrows. The direction of the net transition dipole moment for the whole extended monomer (μ) is shown with dotted green arrows. The colors in circles on the right indicate the overall displacement of the selectivity filter carbonyls in that strand. Na+ and K+ ions are blue and purple, respectively.

Instances of both delocalized and highly localized amide I vibrations are known.37,38 The extent of delocalization determines how specific an IR resonance will be to interactions at a particular site of the protein. The extent of delocalization of vibrations is determined by two competing factors: the strength of couplings between oscillators (J) and the variation in individual site frequencies (Δω). Increasing J and decreasing Δω leads to increasing delocalization. In the case of the “Helix” mode (peak 2); the near-uniform electrostatic environment of the α-helix minimizes Δω while also locking the oscillators into a geometry which gives rise to significant coupling between oscillators, resulting in a vibrational mode which is spread over the length of the pore helix. We believe the delocalized nature of the “Helix” mode is the key to why peak 2 is observed in the difference spectrum. Slight changes in the structure of α-helices, such as a slight bending of the helix from the helical axis, have been predicted to change the intensity and line widths of IR peaks.39,40 The increase in intensity at 1660 cm–1 in the K+ bound data suggests that the α-helices deviate further from an ideal α-helix geometry than the Na+ bound structure.

The remaining three modes we identify, however, are more local in character, because the electrostatic environments that arise from binding K+ and Na+ strongly and selectively influences the frequency of the coordinating carbonyls. These conclusions are borne out in our model. For the B mode, the proximity of Na+ lowers the frequency of the four T75 carbonyls by >25 cm–1 relative to the V76 carbonyls. Considering the weaker coupling between T75 and V76 carbonyls (J < 8 cm–1), binding Na+in plane with the T75 residues largely decouples these vibrations from the rest of the extended filter, creating a site-specific infrared transition. For the S3 mode, the similar frequencies of the K+-binding V76 and G77 carbonyls (Δω ≈ 10 cm–1) and their strong coupling (J > 8 cm–1) lead to a vibrational transition that is largely localized on the eight carbonyls defining the S3 site. Similar factors seem to be responsible for the S2 mode which strongly involves the T75 and V76 residues.

In reality, all of the vibrational motions we observe are neither localized to a single oscillator nor delocalized over the entire protein but have varying degrees of delocalization. Furthermore, the doorway modes do not reflect how these characteristic vibrational motions influence one another or act in concert as would be appropriate for developing a dynamical picture of the protein–ion interaction.

4. Conclusions

Our results show that IR spectroscopy coupled with structure-based spectral modeling can be used as a sensitive tool to investigate functionally relevant conformational changes in large membrane proteins and, furthermore, detect subtle local changes. We have demonstrated this capability in this study by resolving the different environments of the binding sites in the selectivity filter of KcsA and identified unique IR signatures of ion binding states. Structure-based spectroscopic modeling of the extended filter region allowed us to perform the doorway mode analysis which established the link between our experimental data and the ion-induced structural rearrangements in the protein. We found different vibrational couplings for the K+- and Na+-bound states between the TVGY core of the channel and the pore helices, which suggest that the helices are not simply a structural support but may indeed play a central role in determining the different transport properties of KcsA for these ions. It has previously been suggested that the pore helices may act as a mediator between selectivity filter and activation gate, with particular emphasis on the mechanism of C-type inactivation.41,42 Our work suggests the role of the pore helices may extend beyond this and even have a role in determining the energetics and dynamics of ion binding. To what extent these vibrational couplings map onto functionally relevant interactions could be further studied by mutations that alter the interface between the pore helix and selectivity filter.43

Though our work was not designed to directly study KcsA under transport conditions, some of our conclusions have important implications in this area. We find experimental evidence for strong interactions between the T75 carbonyls and Na+. In their recent paper, Köpfer et al.13 emphasize the role of positional fluctuations in the selectivity filter during transport. This suggests perhaps that Na+ ions are not conducted, in part, because of the influence of the Na+ on the coordinating carbonyl dynamics (“rigidifying” them).

On the technical side, one possible extension of our work here is to time-resolved and multidimensional IR spectroscopy. This will capture the dynamics of the protein in real time, shedding light on the underlying molecular mechanisms of the early time events in binding in transport, thus far inaccessible to standard techniques. This provides the tantalizing possibility that mechanisms suggested by MD, such as those for C-type inactivation,44,45 could be directly tested.

Acknowledgments

P.S. thanks Mike Reppert for valuable discussions implementing the spectroscopic modeling. A.V. thanks Joseph Mindell at the early phase of the project for discussion and suggestions for sample preparation and Luke Lavis for the loan of scientific equipment. This project was supported by the Vienna Science and Technology Fund (WWTF) project VRG10-11 and the Research Platform Quantum Phenomena and Nanoscale Biological Systems (QuNaBioS). The Institute of Molecular Pathology is funded by Boehringer Ingelheim. A.T. acknowledges support from the National Science Foundation (CHE-1212557 and CHE-1414486) and the MIT Laser Biomedical Research Center (P41-EB015871). C.B. acknowledges support from the National Institutes of Health in the form of a Ruth L. Kirschstein National Research Service Award (F32GM105104).

Author Present Address

∇ JasperYeast LLC, 818 Cattail Ln, Lessburg, VA 20147.

The authors declare no competing financial interest.

References

  1. Benkovic S. J.; Hammes-Schiffer S. A Perspective on Enzyme Catalysis. Science 2003, 301, 1196–1202. [DOI] [PubMed] [Google Scholar]
  2. Kern D.; Zuiderweg E. R. The Role of Dynamics in Allosteric Regulation. Curr. Opin. Struct. Biol. 2003, 13, 748–757. [DOI] [PubMed] [Google Scholar]
  3. Henzler-Wildman K.; Kern D. Dynamic Personalities of Proteins. Nature 2007, 450, 964–972. [DOI] [PubMed] [Google Scholar]
  4. Ihee H.; Rajagopal S.; Srajer V.; Pahl R.; Anderson S.; Schmidt M.; Schotte F.; Anfinrud P. A.; Wulff M.; Moffat K. Visualizing Reaction Pathways in Photoactive Yellow Protein from Nanoseconds to Seconds. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 7145–7150. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Schotte F.; Lim M.; Jackson T. A.; Smirnov A. V.; Soman J.; Olson J. S.; Phillips G. N.; Wulff M.; Anfinrud P. A. Watching a Protein as It Functions with 150-ps Time-Resolved X-Ray Crystallography. Science 2003, 300, 1944–1947. [DOI] [PubMed] [Google Scholar]
  6. Zanni M.; Hochstrasser R. Two-Dimensional Infrared Spectroscopy: A Promising New Method for the Time Resolution of Structures. Curr. Opin. Struct. Biol. 2001, 516–522. [DOI] [PubMed] [Google Scholar]
  7. Ganim Z.; Chung H. S.; Smith A. W.; Deflores L. P.; Jones K. C.; Tokmakoff A.; Amide I. Two-Dimensional Infrared Spectroscopy of Proteins. Acc. Chem. Res. 2008, 41, 432–441. [DOI] [PubMed] [Google Scholar]
  8. Hayashi T.; Mukamel S. Vibrational-Exciton Couplings for the Amide I, II, III, and A Modes of Peptides. J. Phys. Chem. B 2007, 111, 11032–11046. [DOI] [PubMed] [Google Scholar]
  9. Bloem R.; Dijkstra A. G.; Jansen T. L. C.; Knoester J. Simulation of Vibrational Energy Transfer in Two-Dimensional Infrared Spectroscopy of Amide I and Amide II Modes in Solution. J. Chem. Phys. 2008, 129, 055101. [DOI] [PubMed] [Google Scholar]
  10. Baiz C. R.; Reppert M. E.; Tokmakoff A.. An Introduction of Protein 2D IR Spectroscopy. In Ultrafast Infrared Vibrational Spectroscopy; Fayer M. D., Ed.; CRC Press: Boca Raton, FL, 2013; pp 361–405. [Google Scholar]
  11. Doyle D. A.; Morais-Cabral J. H.; Pfuetzner R. A.; Kuo A.; Gulbis J. M.; Cohen S. L.; Chait B. T.; MacKinnon R. The Structure of the Potassium Channel: Molecular Basis of K+ Conduction and Selectivity. Science 1998, 280, 69–77. [DOI] [PubMed] [Google Scholar]
  12. Andersen O. S. Perspectives on: Ion Selectivity. J. Gen. Physiol. 2011, 137, 393–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kopfer D. A.; Song C.; Gruene T.; Sheldrick G. M.; Zachariae U.; de Groot B. L. Ion Permeation in K+ Channels Occurs by Direct Coulomb Knock-On. Science 2014, 346, 352–355. [DOI] [PubMed] [Google Scholar]
  14. Lockless S. W.; Zhou M.; MacKinnon R. Structural and Thermodynamic Properties of Selective Ion Binding in a K+ Channel. PLoS Biol. 2007, 5, e121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Noskov S.; Bernèche S.; Roux B. Control of Ion Selectivity in Potassium Channels by Electrostatic and Dynamic Properties of Carbonyl Ligands. Nature 2004, 431, 2–6. [DOI] [PubMed] [Google Scholar]
  16. Bernèche S.; Roux B.. Energetics of Ion Conduction through the K+ Channel. Nature 2001, 414. [DOI] [PubMed] [Google Scholar]
  17. Roux B.; Bernèche S.; Egwolf B.; Lev B.; Noskov S. Y.; Rowley C. N.; Yu H. Ion Selectivity in Channels and Transporters. J. Gen. Physiol. 2011, 137, 415–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Heginbotham L.; Lu Z.; Abramson T.; MacKinnon R. Mutations in the K+ Channel Signature Sequence. Biophys. J. 1994, 66, 1061–1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zhou Y.; MacKinnon R. The Occupancy of Ions in the K+ Selectivity Filter: Charge Balance and Coupling of Ion Binding to a Protein Conformational Change Underlie High Conduction Rates. J. Mol. Biol. 2003, 333, 965–975. [DOI] [PubMed] [Google Scholar]
  20. Thompson A. N.; Kim I.; Panosian T. D.; Iverson T. M.; Allen T. W.; Nimigean C. M. Mechanism of Potassium-Channel Selectivity Revealed by Na(+) and Li(+) Binding Sites within the KcsA Pore. Nat. Struct. Mol. Biol. 2009, 16, 1317–1324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Furutani Y.; Shimizu H.; Asai Y.; Fukuda T.; Oiki S.; Kandori H. ATR-FTIR Spectroscopy Revealing the Different Vibrational Modes of the Selectivity Filter Interacting with K+ and Na+ in the Open and Collapsed Conformations of the KcsA Potassium Channel. J. Phys. Chem. Lett. 2012, 3, 3806–3810. [DOI] [PubMed] [Google Scholar]
  22. La Cour Jansen T.; Dijkstra A. G.; Watson T. M.; Hirst J. D.; Knoester J. Modeling the Amide I Bands of Small Peptides. J. Chem. Phys. 2006, 125, 44312. [DOI] [PubMed] [Google Scholar]
  23. Reppert M.; Tokmakoff A. Electrostatic Frequency Shifts in Amide I Vibrational Spectra: Direct Parameterization against Experiment. J. Chem. Phys. 2013, 138, 134116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Uysal S.; Vásquez V.; Tereshko V.; Esaki K.; Fellouse F. A.; Sidhu S. S.; Koide S.; Perozo E.; Kossiakoff A. Crystal Structure of Full-Length KcsA in Its Closed Conformation. Proc. Natl. Acad. Sci. U. S. A. 2009, 106, 6644–6649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jämbeck J. P. M.; Lyubartsev A. P. Derivation and Systematic Validation of a Refined All-Atom Force Field for Phosphatidylcholine Lipids. J. Phys. Chem. B 2012, 116, 3164–3179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jämbeck J. P. M.; Lyubartsev A. P. An Extension and Further Validation of an All-Atomistic Force Field for Biological Membranes. J. Chem. Theory Comput. 2012, 8, 2938–2948. [DOI] [PubMed] [Google Scholar]
  27. Wolf M. G.; Hoefling M.; Aponte-Santamaría C.; Grubmüller H.; Groenhof G. G_membed: Efficient Insertion of a Membrane Protein into an Equilibrated Lipid Bilayer with Minimal Perturbation. J. Comput. Chem. 2010, 31, 2169–2174. [DOI] [PubMed] [Google Scholar]
  28. Allen T. W.; Kuyucak S.; Chung S.-H. Molecular Dynamics Study of the KcsA Potassium Channel. Biophys. J. 1999, 77, 2502–2516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Bernèche S.; Roux B. Molecular Dynamics of the KcsA K(+) Channel in a Bilayer Membrane. Biophys. J. 2000, 78, 2900–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Compoint M.; Carloni P.; Ramseyer C.; Girardet C. Molecular Dynamics Study of the KcsA Channel at 2.0-A Resolution: Stability and Concerted Motions within the Pore. Biochim. Biophys. Acta 2004, 1661, 26–39. [DOI] [PubMed] [Google Scholar]
  31. Torii H.; Tasumi M. Model Calculations on the Amide-I Infrared Bands of Globular Proteins. J. Chem. Phys. 1992, 96, 3379. [Google Scholar]
  32. Wang L.; Middleton C. T.; Zanni M. T.; Skinner J. L. Development and Validation of Transferable Amide I Vibrational Frequency Maps for Peptides. J. Phys. Chem. B 2011, 115, 3713–3724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Torii H.; Tasumi M. Application of the Three-Dimensional Doorway-State Theory to Analyses of the Amide-I Infrared Bands of Globular Proteins. J. Chem. Phys. 1992, 97, 92. [Google Scholar]
  34. Chung H. S.; Tokmakoff A. Visualization and Characterization of the Infrared Active Amide I Vibrations of Proteins. J. Phys. Chem. B 2006, 110, 2888–2898. [DOI] [PubMed] [Google Scholar]
  35. Barth A. The Infrared Absorption of Amino Acid Side Chains. Prog. Biophys. Mol. Biol. 2000, 74, 141–173. [DOI] [PubMed] [Google Scholar]
  36. Splitt H.; Meuser D.; Borovok I.; Betzler M.; Schrempf H. Pore Mutations Affecting Tetrameric Assembly and Functioning of the Potassium Channel KcsA from Streptomyces Lividans. FEBS Lett. 2000, 472, 83–87. [DOI] [PubMed] [Google Scholar]
  37. Cheatum C. M.; Tokmakoff A.; Knoester J. Signatures of Beta-Sheet Secondary Structures in Linear and Two-Dimensional Infrared Spectroscopy. J. Chem. Phys. 2004, 120, 8201–8215. [DOI] [PubMed] [Google Scholar]
  38. Mukherjee P.; Krummel A. T.; Fulmer E. C.; Kass I.; Arkin I. T.; Zanni M. T. Site-Specific Vibrational Dynamics of the CD3zeta Membrane Peptide Using Heterodyned Two-Dimensional Infrared Photon Echo Spectroscopy. J. Chem. Phys. 2004, 120, 10215–10224. [DOI] [PubMed] [Google Scholar]
  39. Higgs P. W. The Vibration Spectra of Helical Molecules: Infra-Red and Raman Selection Rules, Intensities and Approximate Frequencies. Proc. R. Soc. A: Math. Phys. Eng. Sci. 1953, 220, 472–485. [Google Scholar]
  40. Wang J.; Hochstrasser R. M. Characteristics of the Two-Dimensional Infrared Spectroscopy of Helices from Approximate Simulations and Analytic Models. Chem. Phys. 2004, 297, 195–219. [Google Scholar]
  41. Perozo E. Structural Rearrangements Underlying K+-Channel Activation Gating. Science 1999, 285, 73–78. [DOI] [PubMed] [Google Scholar]
  42. Cuello L. G.; Jogini V.; Cortes D. M.; Pan A. C.; Gagnon D. G.; Dalmas O.; Cordero-Morales J. F.; Chakrapani S.; Roux B.; Perozo E. Structural Basis for the Coupling between Activation and Inactivation Gates in K(+) Channels. Nature 2010, 466, 272–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Cordero-Morales J. F.; Jogini V.; Chakrapani S.; Perozo E. A Multipoint Hydrogen-Bond Network Underlying KcsA C-Type Inactivation. Biophys. J. 2011, 100, 2387–2393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ostmeyer J.; Chakrapani S.; Pan A. C.; Perozo E.; Roux B. Recovery from Slow Inactivation in K+ Channels Is Controlled by Water Molecules. Nature 2013, 501, 121–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Chakrapani S.; Cordero-Morales J. F.; Jogini V.; Pan A. C.; Cortes D. M.; Roux B.; Perozo E. On the Structural Basis of Modal Gating Behavior in K(+) Channels. Nat. Struct. Mol. Biol. 2011, 18, 67–74. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES