AN AGE-PERIOD-COHORT ANALYSIS OF CANCER INCIDENCE AMONG THE OLDEST OLD

Abstract

Separating and understanding the effects of age, period, and cohort on major health conditions in the population over eighty-five, the oldest-old, will lead to better population projections of morbidity and mortality. We used age-period-cohort (APC) analyses to describe the simultaneous effects of age, period and cohort on cancer incidence rates in an attempt to understand the population dynamics underlying their patterns. Data from the Utah Cancer Registry (UCR), the US Census, the National Center for Health Statistics (NCHS) and the National Cancer Institute’s Surveillence Epidemiology and End Results (SEER) program were used to generate age-specific estimates of cancer incidence for ages 65–99 from 1973–2002 for Utah. Our results showed increasing cancer incidence rates up to the 85–89 age group followed by declines for ages 90–99 when not confounded by the distinct influence of period and cohort effects. We found significant period and cohort effects, suggesting the role of environmental mechanisms in cancer incidence trends between the ages of 85 and 100.

Introduction

The demographic profile of the United States is changing, with proportionately more individuals surviving to very old ages. The oldest-old population (ages 85+) is projected to more than triple from its current estimate of 5.7 million to 24 million by 2050 (Vincent et al. 2010), making it the fastest growing segment of the population. This substantial growth makes the study of morbidity and mortality for this age group increasingly important. The study we report contributes to the understanding of morbidity trends in the oldest-old population by examining age, period, and cohort trends of cancer incidence from 1973 to 2002 for ages 65 to 99.

While the association between morbidity and mortality is complex (Siegel 2011), studying patterns of human morbidity gives insight into the age-related changes in morbidity and mortality (Ukraintseva and Yashin 2001), particularly for prevalent diseases such as cancer. The deceleration of mortality at advanced ages is a commonly observed phenomenon in both humans and animal species (Horiuchi and Wilmoth 1998; Vaupel et al. 1998). Mortality deceleration can be explained at the macro level due to changes in population composition (i.e. heterogeneity hypothesis) or at the micro level attributable to physiological changes related to aging, (i.e. individual risk hypothesis) (Horiuchi and Wilmoth 1998). Alternatively, this observed trend may be the result of age misreporting in the oldest age categories, heterogeneous birth cohorts, and inaccurate measures of mortality in the oldest age categories (Gavrilov and Gavrilova 2011). A more complete understanding of the determinates of cancer and how these factors change over time can yield better predictions of morbidity and mortality trends at advanced ages. The study reported here disentangles age, period, and cohort effects for a major health condition in the oldest-old categories, allowing for more definitive assertions about the possible causes of mortality deceleration and increased accuracy in forecasting of future trends used to predict the fiscal burdens of an aging population.

Little is known about age-specific disease incidence and prevalence among the oldest-old, including cancer (Boscoe 2008). Unfortunately, traditional surveillance methods limit our ability to examine age-specific cancer incidence in this subpopulation. The National Cancer Institute’s Surveillance Epidemiology and End Results (SEER) program aggregates cancer incidence information for the 85+ age group, making it difficult to study cancer trends in the oldest-old. In 2000, the oldest-old age group accounted for 8 per cent of all incident cancer cases, and this number is projected to rise to 17 per cent by 2050 assuming current incidence rates continue (Hayat et al. 2007). Expanding our knowledge of cancer incidence trends in this subpopulation is crucial.

The few studies that examine cancer incidence trends after age 85 present evidence of a deceleration in cancer incidence, prevalence, and mortality at the oldest ages. (Saltzstein et al. 1998; Kaplan and Saltzstein 2005; Harding et al. 2012). While patterns for different time periods are presented for the oldest-old population, the literature is limited with regard to analyzing change in the trends over time. Recent studies have shown the importance of considering not only the effect of age, but also the role of period and cohort experiences when studying health outcomes (Yang 2008; Reither et al. 2009). Sex-specific trends in both all-site and site-specific cancer should also be considered because there may be different biological and social determinants of cancer for men and women that vary by site (Yancik 2005). The aim of the study presented here was to contribute to the current literature by examining age, period, and cohort trends in cancer incidence from 1973 to 2002 for ages 65 to 99 using data from the Utah Cancer Registry (UCR), the National Cancer Institute’s Surveillance, Epidemiology and End-Results Program (SEER), the decennial Census, and the National Center for Health Statistics (NCHS).

Background

Disentangling Age, Period, and Cohort Effects

Age effects are generally understood to represent the biological characteristics of an individual. Cross-sectional studies of all-site cancer incidence and death rates show that rates generally increase with age, peaking between ages 75 and 85, and then plateauing before declining in advanced ages (Stanta et al. 1997; Saltzstein et al. 1998; Andersen et al. 2005; Arbeev et al. 2005a; Harding et al. 2008). However, many of these studies can only offer limited conclusions about cancer trends in the oldest-old because they aggregated ages 85+, examined a single period, or failed to consider period and cohort influences.

Period effects can be described as the social and environmental context that modifies risk for all individuals in a population at a specific point in time. Changes in cancer screening technology may affect cancer incidence rates at all ages. Changes in health care policy may also create period effects in cancer incidence. For example, Medicare began covering mammograms in 1991(Kelaher and Stellman 2000) and colon cancer screening in 2001 (Berkowitz et al. 2008). Thus, the introduction of new diagnostic tools into the health care market, and changes in screening policies and medical practices have an impact on cancer incidence rates over time.

Cohort effects describe the social or ecological environment unique to individuals born in the same group of years. Epidemiologists often describe cohort effects as the interaction between age and period, while sociologists conceptualize them as a measure of social forces that shape health throughout the life course (Keyes et al. 2010). For example, changes in smoking patterns or other environmental exposures over time may lead to cohort specific trends in cancer incidence. A more comprehensive understanding of the age, period, and cohort (APC) factors contributing to cancer incidence rates in the oldest-old is essential for developing effective screening and treatment recommendations for this population.

Cross-sectional analyses show a decline in cancer incidence for the oldest-old that is similar for men and women. However, results from previous studies indicate that the shape, height, and peak of age-specific incidence curves are sensitive to historical period, cancer site, and study (Saltzstein et al. 1998; Kaplan and Saltzstein 2005; Harding et al. 2008). If cancer incidence rates in this age group were based strictly on the biological factors contributing to aging, one would expect to see consistency in age-specific rates over multiple periods of study. However, the fluctuation in rates is evidence of the influence of external factors, related to period and birth cohort, contributing to cancer incidence. Treating the pattern of decline as an effect of aging neglects evidence of a social and ecological context that may alter age-specific trends and ignores the multifaceted determinates of cancer risk (Stanta et al. 1997; Kaplan and Saltzstein 2005). In this study, we used a comprehensive approach to study cancer trends over time and accounted for period and cohort effects. This approach provides a more accurate depiction of the age-specific trends in cancer incidence.

Aging and Cancer

Disagreement exists among theories explaining the relationship between cancer and aging and the observed decline in cancer incidence in the oldest-old (Anisimov 2003; Ukraintseva and Yashin 2003). The prevailing hypothesis can be grouped into three broad categories that have previously been used to explain mortality deceleration (Horiuchi and Wilmoth 1998; Gavrilov and Gavrilova 2011); hypotheses that suggest deceleration is an artifact, heterogeneity hypotheses, and individual risk hypotheses.

Deceleration is an Artifact

Several theories of cancer causation predict increases of cancer incidence with age. If these theories are true, then deceleration in incidence may be an artifact of cohort differences. The multistage theory predicts that cancer incidence rates should increase with age because the neoplastic transformation of cells occurs through several successive steps (Armitage and Doll 1954; Anisimov 2003). Under this scheme, the path to cancer is step-wise and irreversible, with each step leading to an increased probability of malignant transformation with exposure time and therefore age. However, exposure risks between cohorts may vary, giving rise to different patterns of age-related incidence between birth cohorts and an illusory deceleration in incidence when using cross-sectional data.

Physiological mechanisms may also explain increases in cancer incidence with age. The cancer-longevity tradeoff hypothesis suggests that the cost of living a long life is cancer. Physiological changes in the tissue microenvironment, telomere dysfunction, a decline in immune surveillance, loss in tumour suppressor function, and mutation accumulation are additional factors that have been cited as possible mechanisms leading to the increasing rates of cancer incidence with age (Anisimov 2003; Campisi 2003; Ukraintseva and Yashin 2003). Many of these factors may be modified by environmental exposures and therefore the context of time. Cohort differences in factors such as diet, smoking, exposure to infectious disease (Ukraintseva and Yashin 2003); and environmental interventions such as exercise, social support, and screening practices, may create misleading declines in cancer incidence when using cross-sectional data.

Heterogeneity Hypotheses

Population heterogeneity, differential risk patterns within a population, can be the result of both within and between cohort differences, making the context of cohort an important consideration. Within a single cohort there is differential selection in a heterogeneous population with the frail being selected out of the population at earlier ages (Horiuchi and Wilmoth 1998; Hawkes et al. 2012). Individuals selected out of the population may have a genetic or environmental predisposition to cancer, leaving their robust counterparts to survive to the oldest ages with a survival advantage that protects them from cancer (Morgenthaler et al. 2004). For example, individuals with deleterious mutations, such as the BRCA1 mutation, have elevated post-reproductive mortality rates as compared to the general population, making them less likely to survive to advanced ages (Smith et al. 2011).

Population heterogeneity can also arise because different cohorts have experienced different mortality schedules, environmental exposures, public health initiatives (such as anti-smoking campaigns), and cancer screening recommendations. It has been suggested that the multi-stage theory is correct, and a plateau or decline in cancer incidence rates at old ages may reflect period and cohort trends (Yang 2008). If exposure to different carcinogens such as tobacco smoke, changes in diet, or other environmental carcinogens, fluctuates over time the deceleration in incidence rates at the oldest ages may reflect these changes rather than somatic aging per se. A decline or deceleration in cancer trends in old ages may be a function of cohort experiences such as screening practices or health behaviors for this age group.

Individual Risk Hypotheses

The individual risk hypothesis argues that the deceleration in morbidity and mortality rates at older ages can be explained in terms of physiology, evolution, and health behaviors (Horiuchi and Wilmoth 1998; Vaupel et al. 1998). Although physiological mechanisms have been used to explain increasing cancer incidence with age, they may also predict the opposite - that cancer incidence in the oldest-old age categories decelerate and decline. Physiological changes can contribute to the decline in cancer incidence in the oldest-old through age-related declines in rates of cellular metabolism, suppression of tumour generation, and increased cellular doubling time (Ukraintseva and Yashin 2003).

Natural selection may also affect age-related declines in cancer incidence. Mutation accumulation theory argues that age-related declines in the force of natural selection may result in an accumulation of mutations that result in an increase in mortality beginning near the end of reproductive ages followed by mortality deceleration in the oldest age categories (Horiuchi and Wilmoth 1998). In addition, mechanisms which may protect against cancer may increase longevity, suggesting that individuals in the oldest-old age groups may be less susceptible to cancer (Campisi 2003).

Variation in age-related health behaviors could also explain a decrease in cancer incidence in the oldest-old age groups. Cancer trends periodically shift due to changes in screening procedures and recommendations, but these period effects may not be equal across all ages. Routine cancer screening has increased in the general population (Edwards et al. 2002); however, studies have suggested that there is a decrease in surveillance for the oldest-old and an increase in misdiagnosed or unreported tumours (Stanta et al. 1997; Kaplan and Saltzstein 2005). These factors may lead to cohort specific trends in cancer incidence.

Understanding the relationship between cancer incidence and age will not only improve future predictions of cancer incidence, it will help us understand the mechanisms leading to mortality deceleration in the oldest-old population. The aim of the study presented here was to improve upon current literature by examining temporal trends of cancer incidence from 1973 to 2002 for ages 65 to 99.

Methods

Data

This study used data for the state of Utah from 1973 to 2002 collected from the Utah Cancer Registry (UCR), the National Cancer Institute’s Surveillance, Epidemiology and End-Results Program (SEER), the decennial Census, and the National Center for Health Statistics (NCHS). This study considered using data from 2003 to 2008 but because we did not have access to the counts of the population exposed for this period at the time when the denominators were being constructed this interval was excluded. As will be discussed in more detail in the discussion, we do not believe that the additional period of data will substantially change the results presented in this paper. Cancer incidence cases and the US Census Bureau’s Population Estimates for the state of Utah for ages 65 to 84 were obtained from SEER*Stat software (2010, 2012). Statewide cancer data are collected by the UCR as part of routine cancer surveillance for the Utah Department of Health and the National Cancer Institute’s SEER Program. Cancer cases are reported to the UCR through health service providers and death certificates on which cancer is listed as a cause of death. Site and histology have been coded according to the International Classification of Diseases for Oncology (ICD-O) at the time of diagnosis (Stroup et al. 2008).

Age-specific incidence rates for ages 85 to 99 are not reported by the SEER program. At these ages, age misstatement is a widely recognized problem, making population estimates less reliable (Boscoe 2008). Tabulated incidence data by year and age were provided by the UCR. Intercensal population estimates were calculated via the cohort-component and extinct-cohort methods using decennial data from the US Census Bureau and mortality data from the National Center for Health Statistics (Shryock et al. 1980). The cohort-component method starts with the cohort populations reported in the decennial census and then subtracts deaths to estimate population sizes. The use of census and death certificate data has been criticized because upward age-misstatement can lead to a downward bias of incidence rates for this population. However, age misstatement has been shown to be a relatively rare occurrence with error rates improving over time (Preston et al. 1999; Hill et al. 2000; Boscoe 2008). Data collection issues have also caused errors in population estimates for the oldest-old (Siegel and Passel 1976). The extinct-cohort method is an alternative method of calculating population counts. It relies on death certificate data and is thought to be more reliable when cohorts are close to extinction because it is less subject to bias caused by age misreporting. Rates from both methods were compared and we found that when cohorts are farther from extinction estimates using the extinct-cohort method become less reliable. The cohort component method was selected as the basis for the final models.. The final data set consisted of population level cancer incidence counts (numerators) and cohort-component population estimates (denominators) for the 65 to 99 year old Utah population from 1973 to 2002 by sex.

Statistical Methods

Sex- and site-specific cancer incidence trends from 1973–2002 for ages 65 to 99 for the state of Utah were selected for analysis. There were no incidence cases above age 100 from 1973–82 and 1988–97 for males and 1973–77 for females; therefore we did not include this age category in the analysis. Cancer incidence rates were calculated as the ratio of incident cases to person years of exposure. Age-specific incidence rates were tabulated in age a by calendar year period p arrays with diagonal elements of the matrix corresponding to the birth cohorts c, where the oldest cohort is observed for the oldest age interval during the earliest calendar period and the youngest cohort is observed for the youngest age interval during the latest calendar period. Seven five-year age groups, ranging from 65–69 to 95–99, and six five-year time periods, from 1973–77 to 1998–2002 were used in the analysis. There is some ambiguity in the measurement of cohorts because data are tabulated into five year age and period groupings. For example, an individual age 69 in 1973 would have a birth year of 1904 while an individual age 65 in 1978 would have a birth year of 1913. This yielded 12 successive ten year birth cohorts with midpoints ranging from 1878–1933, which were used for the age, period, and cohort (APC) analyses.

Traditional APC analyses suffer from an “identification problem” resulting from the linear dependency between age, period and cohort (c=a +p), precluding a unique solution. This problem can be remedied by imposing constraints to the model to allow for an identifiable solution (Arbeev et al., 2005a; Arbeev et al., 2005b; Carstensen, 2007; Yang et al., 2004). However, selection of the constraint requires some a priori knowledge of the disease under investigation and models are sensitive to the constraint selected. Other authors have suggested using a proxy characteristic for cohort (O’Brien 1989, 2000; O’Brien et al. 1999). Although, cohort characteristics may not entirely explain cohort effects and the residuals may still be confounded in the model estimates with age and period effects.

The Intrinsic Estimator (IE) proposed by Yang and colleagues (Yang et al. 2004; Yang et al. 2008) can also be viewed as a constrained approach; however, it does not require a priori assumptions about the constraints. Other studies have shown that the IE produces substantively meaningful and empirically valid results (Yang et al. 2008), and the effects can be interpreted like conventional regression coefficients (Harding 2009). The limitations to this approach include the lack of a simple explanation of its assumptions and the lack of a full investigation of its properties (Smith 2004; Harding 2009). The validity of this approach has been recently challenged (Luo 2013). The IE, however, is an appropriate approach when applied correctly (Yang and Land 2013). While the results from this method are the first of its kind for cancer incidence among the oldest-old (Yang et al. 2008; Yang and Land 2013), they provide an important basis for extending our knowledge of temporal trends in cancer incidence from ages 66–99. After initial estimations of a series of Poisson log-linear models, we selected the IE to estimate the APC effects of cancer incidence based on evidence of distinct age, period, and cohort effects and model fit.

Descriptive plots were produced by age group and sex for all-site, breast, colon, and prostate cancers to assess the APC cancer incidence trends. Trends in lung cancer incidence rates were not assessed as part of this analysis because the incidence rates in Utah are very low (Jemal et al. 2008) and the case counts above age 85 were sparse. A similar approach to that used by Yang et al. (2004, 2008) was used to identify an appropriate model to analyse the temporal trends in all-site and site-specific cancer incidence rates. A series of Poisson log-linear models were estimated for each site and sex:

$$ln({\mathrm{m}}_{\mathit{ijk}})=ln({\mathrm{c}}_{\mathit{ijk}}/n_{\mathit{ijk}})=\mu +{\alpha }_i+{\beta }_j+{\gamma }_k$$ (eq. 2.1)

where rate_ijk indexes the expected cancer incidence rate in cell (i, j, k); c_ijk indexes the observed number of cancer incidence cases; n_ijk indexes the number of person years; μ indexes the intercept of age adjusted mean rate; α_i indexes the ith row age effect for i = 1, …, a age groups; β_j represents the jth column period effect for j =1, …, p periods; and γ_k represents the kth diagonal cohort effect for k =1, …, (a + p −1) cohorts.

One-way models (a, p, or c), two factor models (ap, pc, ca) and IE models were compared. Both descriptive analyses and model fit, based on the Akaike Information Criterion (AIC), were used to select the final models. Full analyses are available upon request. The log-linear regression coefficients, standard errors, and model fit were computed using Stata 11. 2. Estimates of the full APC models using the IE approach and the apc_ie.ado downloaded from the Stata command line. To test whether our findings were sensitive to method of denominator construction, the final models were replicated using denominators constructed using the extinct cohort method.

Results

Table 1 shows the total number of cancer cases and person years from 1973–2002 by five-year age group. To assess the variation in age-specific incidence by period a series of age-period plots were created. Figure 1 shows the sex-specific age and period all-site cancer incidence rate plots (plots with 95 per cent CI are available upon request). Each panel displays the age-specific incidence trends by calendar period, ranging from 1973–78 to 1998–2002. The solid lines present the full 85+ age-specific rates and the dashed lines display the trend when cancer rates are top-coded at age 85. These plots also show that the trends are not stable over time. If the only factor influencing cancer incidence trends were age, one would expect the age-specific curves for all periods to follow similar trajectories. However, the plots show variation in the intercept (depicted for age 65– 69), slope, and shape of the curve. There has been a steady increase in the level of cancer incidence over time, with the most recent periods having the highest rates for a majority of the age groups.

Table 1.

Total Number of Cancer Cases and Person Years: 1973 – 2002

Age	Cancer Cases		Person Years
	Female	Male	Female	Male
65 – 69	7,585	11,344	719,026	633,882
70 – 74	7,363	11,934	612,236	501,670
75 – 79	6,765	10,084	484,294	353,977
80 – 84	5,020	6,240	331,194	209,935
85 – 89	3,013	3,147	181,326	95,156
90 – 94	1,067	886	70,155	30,693
95 – 99	249	172	16,201	6,005

Figure 1.

Age-specific incidence of all-site cancer incidence by Period, female and male, Utah 1973 – 2002. Panel A: Female. Panel B: Male.

Note: The scale of the y-axis is smaller than the graphs for the male graphs to allow for the visibility of the variation.

Source: Utah Cancer Registry, US Census Bureau, and National Center for Health Statistics

Age-cohort plots were created to assess the variation in the age trends by birth cohort and sex. Figure 2 displays the variation in shape, slope, and peak in all-site cancer incidence age trends by cohort for both males and females. We were unable to observe a single cohort for the entire age range because we have data for a 30 year window only, from 1973–2002. Age trends for the 1903 and 1908 cohorts had the longest follow-up, with incidence calculated for ages 70 to 99 and 65 to 94 respectively. There is less variation in the trend in age specific incidence rates between cohorts for females as compared to males. The plots suggest that for men the peak in incidence is moving to younger ages for more recent birth cohorts; however, these peaks coincide with the expected rise in incidence that resulted from the PSA testing for prostate cancer. There is a general increase in cancer incidence rates at younger ages for more recent cohorts for both males and females. For both sexes, the largest differences in cancer incidence occurred at ages 90–99. The imprecision at advanced ages was partially a function of decreased sample sizes. The age-period and age-cohort plots indicate period and cohort factors may confound observed trends in age specific cancer incidence.

Figure 2.

Age-specific incidence of all-site cancer incidence by birth cohort, female and male, Utah 1888 – 1923. Panel A: Female. Panel B: Male.

Note: The scale of the y-axis is smaller than the scale for the male graphs to allow for the visibility of the variation. Female incidence rates are lower than male incidence rates and increase with age at a slower rate.

Source: Utah Cancer Registry, US Census Bureau, and National Center for Health Statistics

A series of Poisson log-linear and IE models were used to further investigate APC effects. The goodness-of-fit statistics for the log linear models are displayed in table S1 in the online supplement. The IE model provided the best fit for both male and female all-site cancer, female breast cancer, and prostate cancer incidence. The fit statistics suggest weak cohort effects for women, with the IE model only providing a slightly better fit than the age-period models for both all-site and breast cancer incidence. The age-period model provided the best fit for both male and female colon cancer incidence models.

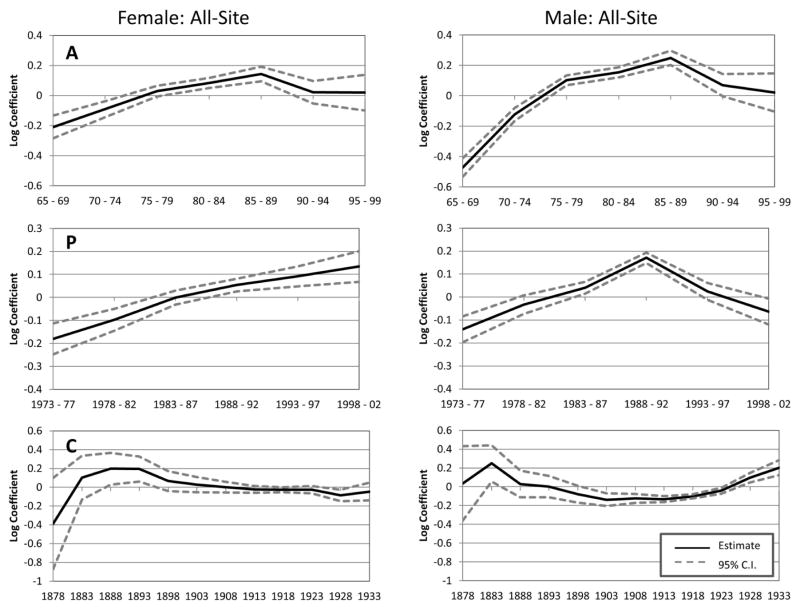
Figure 3 shows the IE results for all-site cancer incidence by sex. The estimated coefficients represent the temporal trends of cancer incidence along each of the APC dimensions. The figure shows an increase across ages in cancer incidence up to age 85. All-site cancer incidence rates are the highest for the 85 to 89 age group when not confounded by the distinct influence of period and cohort effects for both males and females. Female all-site incidence rates for ages 90 and above level off and the estimated coefficients are not statistically significant. There is a steeper decline in the all-site incidence rate for males after age 85; however, it is noteworthy that the estimated coefficient for rates at age 90 (p=0.06) is still higher than the estimated rates for both the 60–64 and 65–69 age groups.

Figure 3.

APC IE estimated trends of all-site cancer incidence rates for ages 65 to 99 in the state of Utah. Panel A: Age effects that are not confounded by the distinct influence of period and cohort. Panel P: Period effects that are not confounded by the distinct influence of age and cohort. Panel C: Cohort effects that are not confounded by the distinct influence of age and period.

Source: Utah Cancer Registry, US Census Bureau, and National Center for Health Statistics

The period specific trends show that there has been a gradual increase in cancer incidence over time. While this gradual increase in cancer incidence with time may be indicative of changes in screening behaviors or environmental exposures, it may also be an artifact of changes in cancer surveillance methods, with more complete identification of cases recorded over time. The period effects for males are as expected based on the descriptive analyses and the known increase in cancer incidence between 1988 and 1992 attributable to shifts in prostate screening practices. The rates drop to pre-1988 levels in the next period and continue their decline into the 1998–2002 periods.

Figure 3 also shows that there are moderate cohort effects for females. All-site cancer incidence was significantly higher for the 1888 and 1893 birth cohorts and lower for the 1928 birth cohort. The cohort effects for males resemble a trough, with slightly elevated risk (albeit insignificant) for early cohorts, followed by a decline and leveling off for the 1903 to 1917 birth cohorts, and ending with an increase that almost reaches the height of the 1883 birth cohort.

Figure 4 displays the IE estimates for breast and prostate cancer. The age effects for the site specific cancers are somewhat different than the all-sites trends. For females, the highest level of breast cancer incidence and the only estimate significantly different from zero, is found between the ages of 75 to 79 (p=0.03). This is a somewhat surprising finding; however this finding is not an artifact of the IE method. The CGLIM estimates show that in a model using only age, breast cancer incidence is higher at ages 75–79, 80–84, and 85–89 compared to ages 65–69 and when controlling for period the size of this effect is attenuated and loses significance for the 80–84 age group. The examination of the age-period plots also supports this finding. The period effects are similar to those observed in the all-site rates as there is a gradual increase in female breast cancer incidence over time. Cohort effects play a small role in determining female breast cancer incidence over age 65. The decline in breast cancer incidence for the 1928 birth cohort is somewhat consistent with previous studies that show a decline in breast cancer incidence for the 1924–38 birth cohorts (Lacey et al. 2002). For prostate cancer, the age effect steadily increases up to age 75 where it reaches a plateau followed by a decline at age 90. Male prostate cancer incidence steadily increases up to 1988 and then sharply declines over time, again for reasons of PSA testing. Male cohorts between 1898 and 1918 have slightly lower rates of prostate cancer incidence. A steady rise in prostate cancer rates is seen in subsequent cohorts.

Figure 4.

APC IE estimates of female breast and male prostate cancer incidence rates for ages 65 to 99 in the state of Utah. Panel A: Age effects that are not confounded by the distinct influence of period and cohort. Panel P: Period effects that are not confounded by the distinct influence of age and cohort. Panel C: Cohort effects that are not confounded by the distinct influence of age and period.

Source: Utah Cancer Registry, US Census Bureau, and National Center for Health Statistics

Figure 5 shows the estimated coefficients for the log-linear AP models of colon cancer incidence. Fit statistics showed that the two-factor model provided the best fit for colon cancer incidence, meaning that cohort effects can be constrained to zero. Fig. 5 indicates that there is a steady increase in colon cancer incidence with age up to age 85, followed by a slight decline (albeit still significantly higher than the referent category of 65 – 69) at the advanced ages. The period trends show a slight elevation in colon cancer incidence between 1983 and 1987 for females and between 1983 and 1992 for males as compared to the sex specific incidence rates in 1973–77.

Figure 5.

To test the sensitivity of our findings, the final models were estimated using denominators created using the extinct cohort method. The results did not substantively change the findings presented and are not shown here.

Discussion

In the study reported in this paper, we found evidence supporting hypotheses of an increase in all-site cancer incidence up to ages 85–89 when not confounded by the distinct influence of period and cohort effects, followed by a modest decline up to age 99. Although incidence appears to drop after age 90, the rates up to age 99 are still higher than rates for individuals aged 65–74. Our findings are supported by other studies and highlight the importance of disaggregating cancer incidence rates for the oldest-old (Smith 1996; Harding et al. 2008). We found evidence of period and cohort effects influencing cancer trends, suggesting the need to consider the social factors that influence biology when studying cancer trends in this population. The benefits of disaggregated estimates for the oldest-old far outweigh the potential challenges related to age misreporting. As more people reach these advance ages, it will become increasingly important to understand the biological and social mechanisms affecting cancer trends in the oldest-old. These results answer Boscoe’s call for greater specificity in age-specific data for the oldest-old (Boscoe 2008).

We conclude that the age, period, and cohort effects of site-specific cancer incidence vary by site and sex. Physiological mechanisms have been the primary mechanisms used to explain the decline in incidence by other authors. Harding and colleagues propose a simple senescence theory, claiming that increasing senescence reduces the ability of cells to divide and limits cancer incidence in the oldest-old population (Harding et al. 2008; Harding et al. 2012). Our results suggest that age is not the only factor contributing to the decline in cancer incidence in the oldest-old age group. We are not arguing against a biological model of cancer decline, but we do advocate a more inclusive theory that considers socio-environmental factors and mortality selection, which may influence the age-specific trends.

The period trends in breast cancer incidence reported here are consistent with previously reported trends in breast cancer (Saltzstein et al. 1998; Kaplan & Saltzstein 2005; Harding et al. 2008). For women, the gradual increase in all-site and breast cancer incidence over time may be partially due to increased detection by mammographic screening (Edwards et al. 2002), improvements in data collection and classification, and elevated risk of new primary malignancies in cancer survivors. A study by Curtis and colleagues (2006) showed that women surviving 2 months or more after an invasive breast cancer diagnosed from 1973–2000, had an 18 per cent elevated risk of new primary malignancies. It is possible that some increased survival rates and elevated risk of new primaries in cancer survivors has contributed to the increase in cancer incidence over time. This pattern of risk also appears to vary by age; Curtis and colleagues (2006) found that those having their first primary diagnosed over the age of 70 did not have an excess risk of subsequent cancer diagnosis, an age group that is largely the focus of this investigation. Future research should examine the APC effects of the risk of subsequent primaries in cancer survivors.

For men the dramatic increase in cancer incidence up to the 1988–92 periods is consistent with other studies of period trends in prostate cancer incidence (Edwards et al. 2002) and the introduction of the PSA screening test. This peak may be due to the early detection of prostate cancer after the introduction of PSA and the decline attributable to the identification of preexisting cancers at an earlier stage (Edwards et al. 2002). The period trends in colon cancer incidence are also consistent with other studies showing an increase during the 1990s as a result of changes in colorectal screening (Edwards et al. 2002). The decline in colon cancer incidence in the late 1990s may be the result of early detection of cancer and the removal of precancerous polyps. The clear period trends observed for both men and women bring attention to the importance of understanding how period factors, and notably changes in cancer screening technologies and recommendations, influence cancer incidence. Our primary focus on cancer for those over age 65 necessarily condition our analysis and conclusions on period and cohort effects.

In our study, cohort effects played a larger role for males than females and did not affect colon cancer incidence rates. Birth cohort did not explain variation in incidence trends for all sites in this study. The absence of a cohort trend in colon cancer incidence is inconsistent with other studies of colon cancer trends (Chu et al. 1994); however, cancer mortality trends may reflect improvements in detection and treatment that prevent colon cancer mortality but do not necessarily modify the risk of colon cancer incidence (which was not reported in this study). Failing to account for heterogeneity between cohorts may lead to erroneous conclusions about deceleration in trends where none exists (Gavrilov & Gavrilova 2011). We have shown that there is a difference in cancer susceptibility between cohorts, but controlling for these differences does not alter the conclusion that cancer incidence rates do not exponentially increase with age.

Heterogeneity within a birth cohort may be an important mechanism driving the deceleration and decline in cancer incidence in the oldest-old. Exceptionally long lived populations may be more homogeneously robust because those with a predisposition to cancer are selected out at early ages. The gradual increase in cancer incidence for males in more recent birth cohorts reported here suggests changing cohort susceptibility to cancer, a position inconsistent with the argument that there is less within-cohort heterogeneity in more recent birth cohorts (Lynch and Brown 2001). While it is difficult to separate the environmental factors from the changes in population heterogeneity, this finding emphasizes the importance of both improved surveillance in cancer trends for the oldest-old and consideration of cohort effects when studying oldest-old cancer trends.

Variation in health and cancer screening behaviors with age is another common argument used to explain the decline in incidence with age and sex differences in period and cohort effects. It is unlikely that between-cohort variability or period specific shifts in health behaviors are strong determinants of the age-specific trend in cancer incidence because incidence rates decline above age 90 when controlling for cohort and period trends. Sex differences in cohort experiences may reflect sex differences in the timing, prevalence, and frequency of smoking; sex differences in environmental exposures to carcinogens in the work place; or sex differences in other risky behaviors that are patterned by generational experiences. For example, Preston and Wang (2006) have demonstrated the close relationship between a cohort’s mortality trajectory and its history of cigarette smoking as well as sex differences in smoking prevalence within the cohort.

Screening bias is another individual level component that may reduce cancer incidence for the oldest-old. The Agency for Healthcare Research and Quality does not recommend routine colonoscopies after the age of 75 (National Guideline), and questions about the efficacy of cancer screening for the oldest-old have also been raised (Østbye et al. 2003). The American Cancer Society recommends PSA screening for males over the age of 50 who have a life expectancy of at least 10 years (Wolf et al. 2010). This study suggests that screening bias may not be the reason for decreases in cancer incidence with age. SEER data collection processes include checking death certificate information. Any cancer occurrence contributing to the cause of death of an individual is reported to the SEER registries. Only cancers that are not an underlying factor in the death would be missed by the system, suggesting that detection bias is not a likely cause in the observed decrease in cancer at advanced ages.

Our results differ slightly from previously reported trends in cancer incidence. The estimated peak in incidence in the 85–89 age category for males and females is higher than Harding et al.’s estimates of 80 (Harding et al. 2008). However, our results are consistent with Saltzstein et al.’s observed peak in age-specific incidence rates for males (Saltzstein et al. 1998). There are three possible explanations for the variation in the estimated peaks in age-specific incidence rates. First, previous studies of age-specific cancer incidence in the oldest-old age group have not considered the role of period and cohort effects. Ignoring exogenous factors that may contribute to cancer incidence oversimplifies the problem and leads to the age-specific incidence rates that are confounded by period and cohort differences in cancer incidence. APC analyses of cancer incidence may provide less biased estimates of the true relationship between cancer and aging.

Second, the differences may be caused by error in the estimated denominators. Preston et al. (1999) found that the difference between the correct population distribution and one estimated with age overstatement increased with time (Preston et al. 1999). Any difference between the estimated peak cancer incidence and the true peak cancer incidence should be negative. If age-misstatement led us to overestimate the size of the oldest-old population, then our estimate of a peak in incidence between the ages of 85 and 89 is conservative. Furthermore, because other studies have also used decennial census data to construct their denominators (Harding et al. 2008; Harding et al. 2012), we argue that this is not the reason for the observed differences in peak age-specific incidence rates.

Third, while not directly assessed, our findings are suggestive of geographic variation in cancer incidence trends given the difference in the estimated peak of cancer incidence between our study and other U.S. studies of overlapping time periods (Saltzstein et al. 1998; Harding et al. 2008; Harding et al. 2012). Regional differences in cancer incidence trends may be attributable to differences in sociodemographic characteristics, health beliefs, access to resources, reproductive characteristics, and exposure to environmental carcinogens. Utah consistently has one of the lowest cancer incidence and mortality rates in the U.S. for both males and females and the lowest rates of lung cancer incidence and mortality (Jemal et al. 2008). However, Utah does not have low incidence rates for all cancer sites. Age-adjusted prostate cancer incidence rates are higher in Utah than the national averages (Stroup et al. 2008). More research should be done to quantify geographic differences as it will provide valuable information about the social forces shaping cancer incidence rates in these age groups.

The IE approach to estimating APC effects of cancer incidence in the oldest-old improved upon previous reports of cancer incidence in this age group in several ways. In addition to estimating the separate effects of age, period, and cohort, the APC approach incorporates cases from 1973–2002, greatly increasing the sample size that we use to estimate the effects. This is an advantage because there is a fair amount of variability in incidence cases above the age of 85, making estimates drawn from a single period of data less reliable. As with all observational data from entire populations, the data for this study consists of a finite number of time periods and it may be argued that we would get different results if we had additional years of cancer incidence data. Yang et al. (2004) show that the IE converges asymptotically to the “true” parameters and is relatively efficient, the variance is smaller for data with a fixed number of time periods, when compared to CGLIM estimates. Essentially, this means that it is unlikely that our conclusions that cancer incidence peaks between ages 85 and 89 would change if we had additional years of Utah data, though this will need to be subjected to testing as more data become available.

As with all APC estimates, the results presented in this paper should be treated with caution (Yang et al. 2008) and more work should be done to replicate the APC trends in cancer incidence in the oldest-old reported here. There are also several structural limitations to studying cancer trends in the oldest-old age groups. Use of clinical and death certificate diagnoses may lead to an underreporting of trends in the oldest-old (Kaplan and Saltzstein 2005; Stanta et al. 1997). Trends calculated using cancer registry and census data are subject to error because the reliability of age estimates for individuals over the age of 85 may be questionable (Edwards et al. 2002; Vincent et al. 2010). However, we used several different methods to create measures of population size and found no substantive differences in the APC trends in all-site cancer incidence.

There is not widespread consensus in the cause of the decline in cancer rates at advanced ages because it has been largely understudied. This study contributes to the current literature by providing estimates of cancer incidence for the 85+ population within the broader context of period and cohort effects. This study supports the individual risk hypothesis and mortality selection arguments that predict a deceleration in incidence at advanced ages. Our findings do not support the position that deceleration is an artifact of variability in morbidity profiles between cohorts, nor do they support arguments that cancer incidence trends are strictly a function of biological mechanisms. Studies utilizing an APC approach to the analysis of cancer trends may provide less biased estimates of the relationship between cancer and aging and improve knowledge about the role of biological and social influences that modify trends. Repeating this analysis using all SEER sites would be a natural extension to this research. This would allow for the study of geographic differences in APC trends and other allow for analyses of other cancer sites. The existence of cohort and period effects also justifies the use of direct measures of the exogenous factors contributing to cancer incidence. Future studies should evaluate the proportion of variation in cancer incidence explained by direct measures of period influences and cohort characteristics. Future studies should also investigate morbidity trends in other major causes of death and explore the relationship between these trends and mortality deceleration. We also show that there is variation in cancer incidence trends in the oldest-old population and reiterate the importance of treating this population as heterogeneous. In order to gain a more comprehensive understanding of morbidity and mortality patterns for this rapidly growing segment of the population, cancer incidence and US Census population estimates need to be disaggregated for the oldest-old population.