Differential Adaptation of Descending Motor Tracts in Musicians

Abstract

Between-group comparisons of musicians and nonmusicians have revealed structural brain differences and also functional differences in motor performance. In this study, we aimed to examine the relation between white matter microstructure and high-level motor skills by contrasting 2 groups of musicians with different instrument-specific motor requirements. We used diffusion tensor imaging to compare diffusivity measures of different corticospinal motor tracts of 10 keyboard players, 10 string players, and 10 nonmusicians. Additionally, the maximal tapping rates of their left and right index fingers were determined. When compared with nonmusicians, fractional anisotropy (FA) values of right-hemispheric motor tracts were significantly higher in both musician groups, whereas left-hemispheric motor tracts showed significantly higher FA values only in the keyboard players. Voxel-wise FA analysis found a group effect in white matter underlying the right motor cortex. Diffusivity measures of fibers originating in the primary motor cortex correlated with the maximal tapping rate of the contralateral index finger across all groups. The observed between-group diffusivity differences might represent an adaptation to the specific motor demands of the respective musical instrument. This is supported further by finding correlations between diffusivity measures and maximal tapping rates.

Introduction

Research has demonstrated associations between variations in neuroanatomical features and motor skills using various imaging techniques (Dayan and Cohen 2011). Musicians are an ideal population to investigate the neuroanatomical underpinnings of exceptional sensorimotor skills (Schlaug 2001; Munte et al. 2002; Hyde et al. 2009; Herholz and Zatorre 2012; Luo et al. 2012). Some researchers have shown specialized anatomical and functional features within musician groups (Elbert et al. 1995; Bangert and Schlaug 2006), which have been used to support the interpretation that specialized long-term skill training of particular instruments can lead to instrument-specific adaptations (Stewart 2008). However, the relation between white matter architecture and sensorimotor skills is not well examined (Jancke 2009; Zatorre et al. 2012).

Diffusion tensor imaging (DTI) allows for the reconstruction of white matter tracts and the characterization of their microstructural status using diffusivity measures, such as fractional anisotropy (FA; Basser et al. 1994). Previous studies comparing musicians with nonmusicians yielded contradictory results with regard to FA values in corticospinal motor tracts, and none of the studies related diffusivity measures to motor performance measures (Schmithorst and Wilke 2002; Bengtsson et al. 2005; Han et al. 2009; Imfeld et al. 2009). Studies examining neural effects of long-term instrumental music practice have been complemented by studies showing white matter plasticity in response to the acquisition of other nonmusical sensorimotor skills (Scholz et al. 2009; Hanggi et al. 2010; Landi et al. 2011) as well as in response to recovery from neurological disorders (Schlaug et al. 2009; Wrigley et al. 2009; Lindenberg et al. 2010; Granziera et al. 2012; Keil et al. 2012; Zipse et al. 2012) or neural effects of immobilization (Langer et al. 2012).

In the current study, we compared diffusivity measures of descending motor tracts between musicians and nonmusicians and within the musician group between keyboard players and string players, and correlated these measures with subjects' maximal finger tapping rates. We not only examined the pyramidal tract (PT), but also so-called alternate motor fibers (aMF). These aMF might comprise the cortico-rubro-spinal and the cortico-reticulo-spinal tracts (Canedo 1997). They have been found to play an important role and show adaptations in motor recovery after lesions to the PT (Lindenberg et al. 2010; Rüber et al. 2012). The aims of our study were to test the hypotheses that (1) diffusivity measures of PT and aMF would show characteristic differences between keyboard players, string players, and nonmusicians and that (2) diffusivity measures of PT and aMF would be related to functional motor performance.

Materials and Methods

Subjects

Our cohort consisted of 30 healthy subjects divided into 3 groups of 10 subjects each: Keyboard players (4 women; mean age ± SD, 24.6 ± 4.0 years), string players (violinists and cellists, 5 women; mean age, 24.9 ± 6.1 years), and a control group of nonmusicians (5 women; mean age, 26.5 ± 4.2 years). All musicians were active at the time of inclusion in the study. The mean age of commencement of musical training was 6.0 ± 2.5 years for the string players and 7.0 ± 2.1 years for the keyboard players; there was no significant between-group difference (P = 0.34). All musicians were asked to report daily hours of practice of their primary instrument during different educational stages: Under the age of 10 years, between 10 and 15 years, between 16 and 18 years, between 19 and 22 years, and at the time of inclusion in the study. There were no significant between-group differences in the hours practiced for the respective time brackets (see above) between the 2 musician groups (all P > 0.34). Eight of the 10 subjects in the nonmusician group had never played any instrument. Two subjects in this group had 1 year of instrumental music training at the age of 10 (see Table 1 for details). Subjects were recruited through posting ads on Craigslist and bulletins at music conservatories in the greater Boston area.

Table 1.

Demographical and retrospective data

	Keyboard playersa	String playersa,b	2-sample, 2-tailed t-test between musician groups		Nonmusicians
Female	4	5			5
Age at scan	24.6 ± 4.0	24.9 ± 6.1	t(18) = −0.13	P = 0.90	26.5 ± 4.2
Age of commencement	7.0 ± 2.1	6.0 ± 2.5	t(18) = 0.99	P = 0.34	10.0 ± 0.0c
dph, <10	1.0 ± 1.0	1.0 ± 1.5	t(16) = 0.08	P = 0.94
dph, 10–15	2.0 ± 1.7	2.1 ± 1.9	t(16) = −0.09	P = 0.93
dph, 16–18	2.6 ± 2.3	1.6 ± 1.5	t(16) = 0.98	P = 0.34
dph, 19–22	3.3 ± 2.5	2.5 ± 3.1	t(16) = 0.67	P = 0.51
dph, currently	2.8 ± 2.3	2.0 ± 2.5	t(17) = 0.78	P = 0.44

Note: Mean values ± standard deviations are reported.

dph: daily practice hours; <10: under the age of 10; 10–15: between the age of 10 and 15; 16–18: between the age of 16 and 18; 19–22: between the age of 19 and 22.

^aFive musicians were nonprofessional (3 string players and 2 keyboard players); however, they had been interested in a professional career at some point in their lives and resembled the other 15 professional musicians with regard to commencement of musical training and amount of practice hours.

^bTwo string players did not report daily practice hours.

^cOnly 2 subjects in the nonmusician group have ever played an instrument: The first subject had 1 year of piano lessons at the age of 10. The second subject was instructed in playing trombone also for 1 year at the age of 10. Whereas the subject playing piano could not remember daily practice hours at that time (but told us that he did not practice much), the subject playing trombone reported having practiced for a maximum of 1h a day.

All subjects were tested for their handedness using the Edinburgh Handedness Inventory (Oldfield 1971) and were verified as consistent right-handers. The study was approved by the local Institutional Review Board. Written informed consent was obtained from all subjects.

Finger Tapping Test

Twenty-eight of the 30 subjects (10 keyboard players, 10 string players, and 8 nonmusicians) performed an index finger tapping test (Jancke et al. 1997). Here, subjects were instructed to tap with their index finger as fast as possible onto the space bar of a computer keyboard for 20 s with the palm of the hand resting on the table in order to determine the maximal tapping rate. Participants underwent the test twice with each index finger, and the trial in which they performed faster was taken for further analysis.

Image Acquisition

Using a 3-T GE scanner, a T₁-weighted anatomical sequence (voxel size: 0.93 × 0.93 × 1.5 mm³) and a DTI sequence (2.5 × 2.5 × 2.5 mm³; 50 contiguous axial slices covering the entire brain including the brainstem) with 30 noncollinear diffusion directions with a b-value of 1000 s/mm², and 6 with a b-value of 0 s/mm², were acquired for all subjects.

Preprocessing of Diffusion Tensor Imaging Data

Preprocessing and fiber tracking were performed with FSL (http://www.fmrib.ox.ac.uk/fsl). A 3-dimensional affine registration was applied to correct for eddy currents and head motion (Jenkinson and Smith 2001) and followed by brain extraction (Smith 2002). Probability distributions of fiber directions were then calculated, allowing estimates of 2 directions per voxel (Behrens et al. 2007). Directional diffusivities were determined as λ₁ > λ₂ > λ₃, and FA was calculated from these eigenvalues. Axial diffusivity (AD) (λ_‖) corresponds to λ₁ and radial diffusivity (RD) (λ_┴) to (λ₂ + λ₃)/2 (Basser 1995; Beaulieu 2002). We normalized individual FA images to the FSL template (1 × 1 × 1 mm³) using linear and nonlinear algorithms. The resulting transformation matrices were also used to normalize λ maps and also individual tracts.

Probabilistic Tractography

To reconstruct different portions of PT and aMF according to their origins in primary and nonprimary motor cortices, 3 different regions of interest (ROIs) were drawn on the same axial slice in the subcortical white matter (Lindenberg et al. 2012; Rüber et al. 2012). The border between primary (M1) and dorsal premotor cortices (PMd) cannot be easily determined since their cytoarchitectonic boundaries do not correspond to gross-anatomic landmarks (Geyer et al. 2000). The M1 ROI was therefore defined at the posterior bank of the precentral gyrus from the deepest point of the central sulcus to the lateral crest of the precentral gyrus. The anterior bank of the precentral gyrus and the lateral aspect of the adjacent superior frontal gyrus comprised the PMd ROI. The anterior border of the PMd ROI coincided with the rostral end of the supplementary motor cortex (SMA) ROI. The SMA ROI was drawn on the medial aspect of the superior frontal gyrus; the anterior border was determined by a vertical line through the anterior commissure perpendicular to a line connecting the anterior and posterior commissures (Lehericy et al. 2004), and the posterior border was marked by a vertical line through the posterior commissure (Schlaug et al. 1996). Further ROIs were drawn in the posterior limb of the internal capsule and the pons. According to the previous work, 2 different pontine ROIs were used in order to differentiate PT (basis pontis) and aMF (tegmentum pontis) (Lindenberg et al. 2010). All ROIs were manually defined on the individual FA maps in native space.

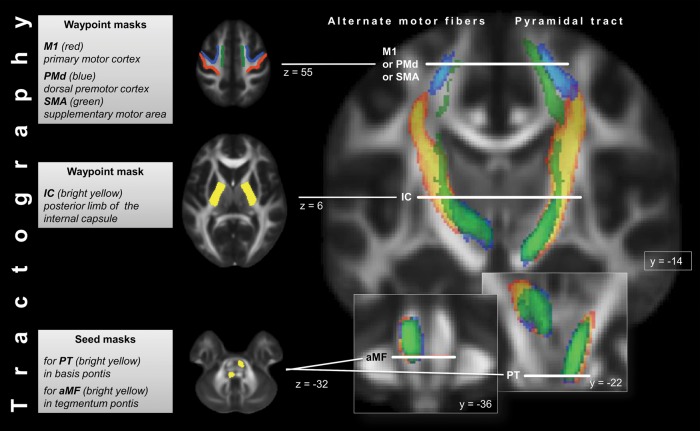
Using the brainstem ROIs as seed regions and the ROI in the ipsilateral internal capsule and the subcortical ROIs as waypoint masks, we reconstructed 6 different tracts in both hemispheres: Fibers originating from each of the motor regions, passing through the internal capsule and descending to either the anterior (^M1PT, ^PMdPT, and ^SMAPT) or posterior pons (^M1aMF, ^PMdaMF, and ^SMAaMF). Sagittal exclusion masks were applied in the corpus callosum and along the midline in the brainstem to include only unilateral fibers. A coronal exclusion mask was added at the posterior bank of the central sulcus on the same axial slice as the subcortical ROIs to restrict tractography to fibers originating in motor cortices. See Figure 1 for a schematic overview of masks used for tractography and of the reconstructed tracts.

Figure 1.

Schematic overview of masks used for tractography as well as of course of reconstructed canonical PT (right side) and aMF (left side) as they descend from the motor cortex to the pons. To generate the canonical images, individual tracts from all subjects were normalized, converted to binary images, and then summed. Cortical contributions from the 3 following cortical areas to PT and aMF are displayed in different colors: red-yellow = contribution from M1 to PT/aMF; blue = contribution from PMd to PT/aMF; green = contribution from SMA to PT/aMF. Color brightness indicates the degree of voxel-by-voxel overlap of the individual normalized tracts. Tractography masks are described in charts on the left side of the figure. “y” and “z” indicate slice position along y- and z-axis in MNI space.

Probabilistic maps were generated by iterations of the streamline process (Behrens et al. 2003). For every seed voxel in the brainstem ROIs, 5000 “particles” were propagated through the multitensor field. Probabilistic streamlines were restricted to white matter by using binarized individual gray matter masks as termination masks. These masks were derived from the T₁-weighted image with FreeSurfer's automated tools for segmentation (Dale et al. 1999; Fischl et al. 1999). We binarized the resulting masks and registered them to the b0 image applying a within-subject, cross-modal approach using a boundary-based cost function to gain gray matter masks, which aligned well with the FA maps in native space. The resulting maps of streamline intensities were finally constrained (Heiervang et al. 2006) to voxels with >1% of the individual robust range. After their reconstruction, all tracts were overlaid onto the individual FA maps in order to visually inspect their course. See Supplementary Table 1 for mean ± SD of individual tract volume in the 3 groups.

Tractography-Based Analysis of Diffusivity Parameters

We performed (1) an analysis of tract-specific diffusivity parameters and (2) a voxel-wise analysis of diffusivity parameters within delineated tracts.

For tract-specific analysis, individual tracts were binarized and used to extract averaged FA and λ values across all voxels of the respective tract in native space. Tract-specific diffusivity parameters were subjected to a 3-way analysis of variance (ANOVA) [group (keyboard players/string players/nonmusicians) × hemisphere (left/right) × tract (^M1PT, ^PMdPT, ^SMAPT, ^M1aMF, ^PMdaMF, and ^SMAaMF)] with hemisphere and tract as repeated measures. This ANOVA and post hoc t-tests allowed us to differentially evaluate absolute differences in diffusivity parameters. For analysis of potentially group-dependent hemispheric asymmetries in diffusivity parameters, which may reflect instrument-specific motor demands, a widely used asymmetry score [(left − right)/(left + right)] was calculated for FA/λ_‖/λ_┴ and subjected to a 2-way ANOVA [group (keyboard players/string players/nonmusicians) × tract (^M1PT, ^PMdPT, ^SMAPT, ^M1aMF, ^PMdaMF, and ^SMAaMF)] with tract as repeated measure. In addition, post hoc t-tests were performed. All post hoc t-tests were protected by Fisher's least significant difference (Milliken and Johnson 2009). Greenhouse-Geiser correction was used in both ANOVAs when Mauchly's sphericity test indicated nonsphericity.

For voxel-wise analyses of diffusivity parameters, we normalized the subjects' individual tracts in order to build canonical tracts. These canonical tracts were thresholded so that only voxels which were common to at least 50% of all subjects (i.e., n = 15/30) were included. FA, λ_‖, and λ_┴ of voxels within ^M1PT were subjected to a 1-way voxel-wise ANOVA with post hoc t-tests in order to evaluate voxel-wise group differences between keyboard players, string players, and nonmusicians. The analysis was restricted to ^M1PT after this tract was found to be most relevant in the tract-specific analysis. We applied nonparametric permutation methods (Nichols and Holmes 2002) performing 5000 permutations for every voxel within this tract. To avoid an arbitrary initial cluster-forming threshold, we used threshold-free cluster enhancement (Smith and Nichols 2009) for final voxel-wise inference.

Results

Diffusivity Measures

Tract-Specific FA Analysis—Absolute Values

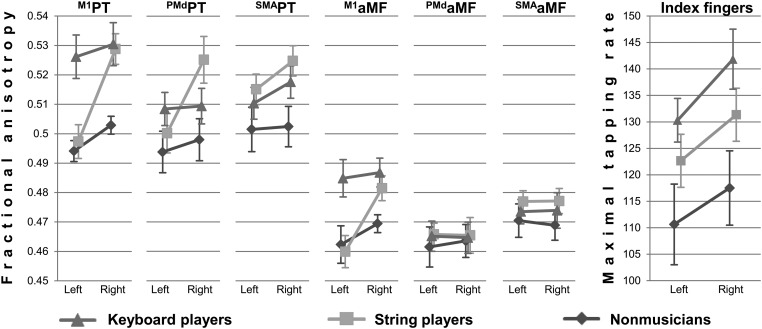
Tract-specific FA values were subjected to a 3-way ANOVA [group (keyboard players/string players/nonmusicians) × hemisphere (left/right) × tract (^M1PT, ^PMdPT, ^SMAPT, ^M1aMF, ^PMdaMF, and ^SMAaMF)]. The main effects of hemisphere and tract were significant (F_1,27 = 27.346, P < 0.001, ${\eta }_{\mathrm{p}}^2=0.\text{5}0\text{3;}$ F_3,80 = 115.146, P < 0.001, ${\eta }_{\mathrm{p}}^2=0.810$). The main effect of group was borderline significant (F_2,27 = 3.303, P = 0.052, ${\eta }_{\mathrm{p}}^2=0.\text{197}$). Post hoc t-tests indicated that string players and keyboard players have higher FA values than nonmusicians (P = 0.063 and 0.022) with no significant difference between string players and keyboard players (P = 0.624) (see Figure 2 and Table 2 for details).

Figure 2.

Tract-specific FA as a function of group × hemisphere × tract. Maximal tapping rate as a function of hand × group. Error bars denote standard error of the mean. Please note: left and right may refer to the hemisphere as well as to the index finger in this figure.

Table 2.

Results of a 3-way ANOVA [hemisphere (2) × tract (6) × group (3)] of tract-specific absolute FA/AD/RD values of corticospinal tracts

Effect	Df	F	P	${\eta }_{\mathrm{p}}^2$
Fractional anisotropy
Group	2	3.303	0.052	0.197
Hemisphere	1	27.346	<0.001	0.503
Tract	2.968	115.146	<0.001	0.810
Hemisphere × group	2	8.775	0.001	0.394
Hemisphere × tract	3.053	4.370	0.006	0.139
Tract × group	5.936	3.152	0.008	0.189
Hemisphere × tract × group	6.106	1.928	0.085	0.125
Axial diffusivity
Group	2	0.329	0.722	0.024
Hemisphere	1	19.204	<0.001	0.416
Tract	3.360	99.589	<0.001	0.787
Hemisphere × group	2	2.226	0.127	0.142
Hemisphere × tract	2.839	4.590	0.006	0.145
Tract × group	6.719	2.955	0.009	0.180
Hemisphere × tract × group	5.677	2.009	0.078	0.130
Radial diffusivity
Group	2	3.235	0.055	0.193
Hemisphere	1	13.788	0.001	0.338
Tract	3.498	70.397	<0.001	0.723
Hemisphere × group	2	6.419	0.005	0.322
Hemisphere × tract	3.431	2.806	0.037	0.094
Tract × group	6.995	1.749	0.107	0.115
Hemisphere × tract × group	6.862	1.128	0.353	0.077

Note: Hemisphere and tract were repeated measures.

Tract-Specific FA Analysis—Asymmetry Score

The computed FA asymmetry score was subjected to a 2-way ANOVA [group (keyboard players/string players/nonmusicians) × tract (^M1PT, ^PMdPT, ^SMAPT, ^M1aMF, ^PMdaMF, and ^SMAaMF)]. There were significant main effects of group and tract (F_2,27 = 8.434, P = 0.001, ${\eta }_{\mathrm{p}}^2=0.\text{385};$ F_3,83 = 4.330, P = 0.007, ${\eta }_{\mathrm{p}}^2=0.\text{138}$). Post hoc t-tests indicated that string players' hemispheric asymmetry score differed from keyboard players' and nonmusicians' asymmetry score (P < 0.001; P = 0.003), whereas the difference between keyboard players' and nonmusicians' asymmetry score was not significant (P = 0.647) (see Figure 2 and Table 3 for details).

Table 3.

Results of a 2-way ANOVA [tract (6) × group (3)] of hemispheric asymmetry score of tract-specific FA/AD/RD values (see Materials and Methods) of corticospinal tracts

Effect	Df	F	P	${\eta }_{\mathrm{p}}^2$
Fractional anisotropy
Group	2	8.434	0.001	0.385
Tract	3.073	4.330	0.007	0.138
Tract × group	6.146	1.877	0.093	0.122
Axial diffusivity
Group	2	2.159	0.135	0.138
Tract	2.832	4.577	0.006	0.145
Tract × group	5.663	2.007	0.079	0.129
Radial diffusivity
Group	2	6.821	0.004	0.336
Tract	3.428	2.937	0.031	0.098
Tract × group	6.855	1.110	0.363	0.076

Note: Tract was a repeated measure.

Tract-Specific Analyses of Directional Diffusivities—Absolute Values and Asymmetry Scores

Tract-specific λ_‖ and λ_┴ values were analyzed the same way as tract-specific FA values (i.e., the absolute diffusivity values of λ_‖/λ_┴ and the hemispheric asymmetry score of both parameters were subjected to a 3-way/2-way ANOVA; see Tables 2 and 3).

No group effect was found in the analysis of absolute λ_‖ values (P = 0.722); however, absolute λ_┴ values showed between-group differences (F_2,27 = 3.235, P = 0.055, ${\eta }_{\mathrm{p}}^2=0.\text{193}$): compared with nonmusicians, keyboard players and string players both had significantly lower absolute λ_┴ values (P = 0.031 and 0.043) as revealed by post hoc t-tests, whereas there was no significant difference between keyboard players and string players (P = 0.888).

The analysis of the λ_‖ asymmetry score did not yield a significant group effect (P = 0.135), but a significant group effect was found in the analysis of the λ_┴ asymmetry score (F_2,27 = 6.821, P = 0.004, ${\eta }_{\mathrm{p}}^2=0.\text{336}$): Post hoc t-tests showed that string players' λ_┴ asymmetry score differed from keyboard players' and nonmusicians' λ_┴ asymmetry score (P = 0.001 and 0.03), with no difference between keyboard players' and nonmusicians' asymmetry score (P = 0.185). Left and right group averages of tract-specific λ_‖ and λ_┴ values for all tracts are presented in Supplementary Figure 1.

Voxel-Wise FA Analysis

The analysis of tract-specific diffusivity measures was complemented by a voxel-wise ANOVA (see Materials and Method section). The F-test showed a significant group effect for one cluster in the juxtacortical white matter underlying right M1 (P < 0.05, FWE-corrected; size: 6 voxels, p-max in Montreal Neurological Institute (MNI) space: x = 13, y = −31, z = 55; Fig. 3).

Figure 3.

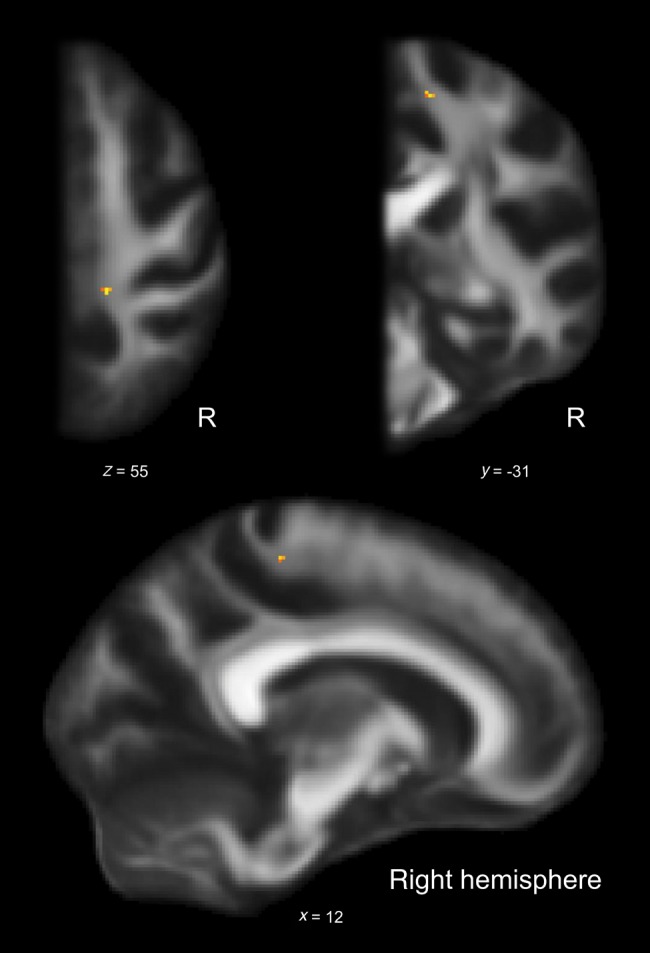
A voxel-wise 1-way ANOVA of FA. Cluster shows group effect within right ^M1PT as indicated by F-test (P ≤ 0.05, FWE-corrected; size: 6 voxels, p-max in MNI space: x = 13, y = −31, z = 55). R: right hemisphere; x, y, z: coordinates in MNI space.

Voxel-wise post hoc t-tests indicated that keyboard players have higher FA values than string players (P < 0.05, FWE-corrected; size: 7 voxels, p-max in MNI space: x = 12, y = −31, z = 56) and nonmusicians (P < 0.05, FWE-corrected; size: 4 voxels, p-max in MNI space: x = 13, y = −31, z = 55) in the juxtacortical white matter underlying right M1.

Voxel-wise analysis of other diffusivity parameters and tests of the opposite contrasts did not yield significant results.

Maximal Finger Tapping Rate

The maximal finger tapping rate was subjected to a 2-way ANOVA [group (keyboard players/string players/nonmusicians) × hand (right hand/left hand)] with repeated measurements of one factor (hand). There were significant main effects of group (F_2,25 = 3.471, P = 0.047, ${\eta }_{\mathrm{p}}^2=0.\text{217}$) and hand (F_1,25 = 15.981, P < 0.001, ${\eta }_{\mathrm{p}}^2=0.\text{39}0$), but the interaction between group and hand was not significant (F_2,25 = 0.328, P = 0.723, ${\eta }_{\mathrm{p}}^2=0.0\text{26}$). Subjects were faster when tapping with the right hand (mean: 134.6 taps/20 s) compared with the left (mean: 124.9 taps/20 s). Keyboard players achieved the highest maximal tapping rate (mean, left-right average: 138.8 taps/20 s), followed by string players (mean, left-right average: 130.3 taps/20 s) and nonmusicians (mean, left-right average: 117.9 taps/20 s). Post hoc t-tests, which were protected by Fisher's least significant difference (Milliken and Johnson 2009), revealed that only the difference between the keyboard players and the nonmusicians reached significance (P = 0.014; string players − nonmusicians: P = 0.132; keyboard players − nonmusicians: P = 0.265; (see Fig. 2).

Correlations Between Diffusivity Measures and Maximal Finger Tapping Rate

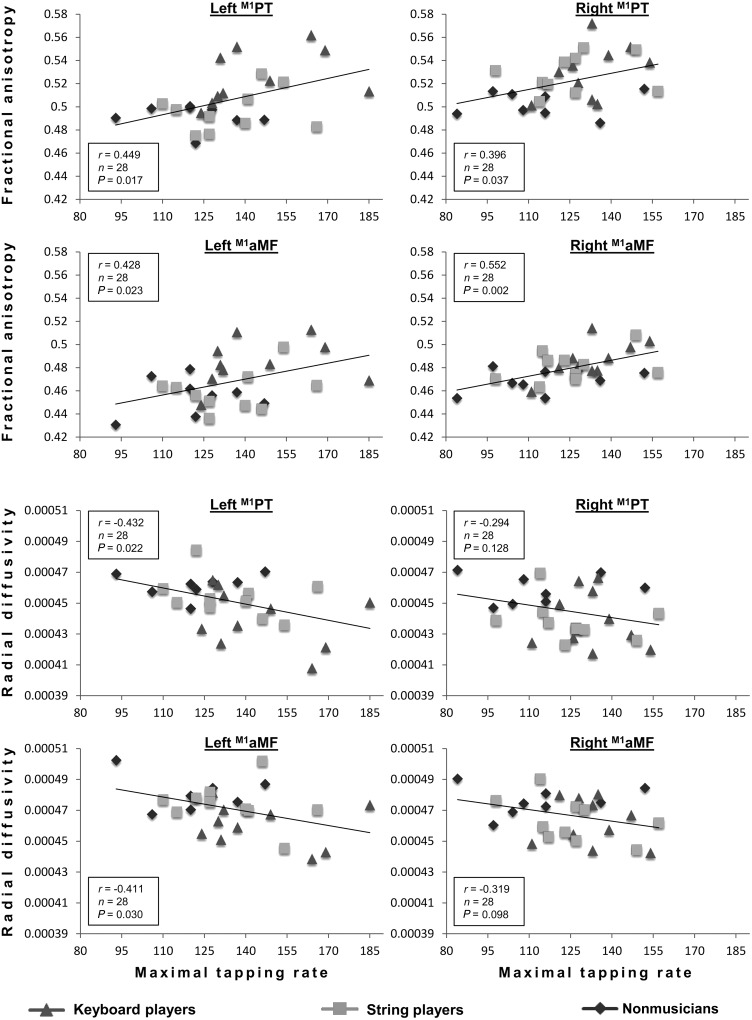
Tract-specific FA values of right and left ^M1PT and ^M1aMF showed significant correlations with the maximal finger tapping rate of the contralateral index fingers (please see Figure 4 for details). Among the contributions to the PT, the correlations were highly specific to fibers originating in M1 (for ^PMdPT and ^SMAPT: all P > 0.34). With regard to aMF, the distinction between ^M1aMF and ^PMdaMF/^SMAaMF was not as clear cut, although correlations between ^M1aMF and tapping speed were always characterized by the highest r-values when compared with ^PMdaMF/^SMAaMF. Repeating this analysis for other diffusivity measures (λ_‖ and λ_┴) of tracts originating in M1, inverse correlations were revealed for tract-specific λ_┴ (see Fig. 4; for λ_‖: all P > 0.15). No correlations were found between diffusivity measures or maximal finger tapping rate and biographical data on musical training (i.e., age of commencement, total hours of practice, or years practiced). To test whether the relation between diffusivity parameters and maximal finger tapping was moderated by musical expertise, a regression analysis (tract-specific FA of the left and right ^M1PT and ^M1aMF predicting the maximal finger tapping rate) with musical expertise as a second independent variable was run. It did not yield significant results (all P > 0.197).

Figure 4.

Correlations between tract-specific FA/RD of left/right ^M1PT/^M1aMF and maximal tapping rate of contralateral index finger. Pearson's coefficient (r), sample size (n), and level of significance (P) are provided.

Discussion

Several studies have revealed differences in white matter composition when comparing individuals trained in sensorimotor skills with novices (Johansen-Berg et al. 2010): for example, a recent study from our group showed that singers exhibited lower FA values than instrumental musicians in the arcuate fasciculus (Halwani et al. 2011). Stronger evidence for the effects of training on white matter is available from 2 longitudinal studies reporting FA increases after individuals learned to juggle (Scholz et al. 2009) or underwent memory training (Engvig et al. 2012). In the current cross-sectional study, we also found higher FA values in experts in fine motor tasks (comparing musicians with nonmusicians) in descending motor tracts with characteristic differences between instrumental musician groups. This favors our interpretation that white matter tracts can be modified to reflect specific motor demands of the respective musical instrument: String players have to acquire fine finger motor skills particularly in their left hands that may lead to structural remodeling of right- more than left-hemispheric tracts, whereas keyboard players have to develop fine finger motor skills in both hands that may lead to structural remodeling of tracts in both hemispheres. The alternative view, that certain pre-existing anatomical features favor the study of instruments with specific motor requirements, appears to be unlikely but cannot be ruled out completely. Functional specializations and differences in gross-anatomical markers have been demonstrated comparing different instrumental musician groups with each other (Pantev et al. 2001; Bangert and Schlaug 2006); however, to the best of our knowledge, they have not been reported for white matter so far. Previous studies have focused on musicians versus nonmusicians white matter differences, but these studies differed in finding either higher or lower FA values within descending motor tracts (Schmithorst and Wilke 2002; Bengtsson et al. 2005; Han et al. 2009; Imfeld et al. 2009). Whereas our study complements the work of Bengtsson et al. (2005) as well as that of Han et al. (2009), differences have emerged between our results and those of Imfeld et al. (2009) as well as those of Schmithorst and Wilke (2002), who found lower FA values in musicians relative to nonmusicians. Methodological issues might account for these differences such as the use of a subcortical ROI that included Brodmann Areas 1–4 (Imfeld et al. 2009) leading to the inclusion of ascending sensory tracts, whereas our ROIs were defined to only include fiber tracts from distinct primary and nonprimary motor areas; and differences in scanning parameters may have to be considered as well. It is still unclear how diffusivity properties can be interpreted in terms of their underlying white matter structure (Beaulieu 2002; Wheeler-Kingshott and Cercignani 2009). Several studies have demonstrated a correspondence between λ_┴ values and myelin integrity (Song et al. 2002; Budde et al. 2007; Klawiter et al. 2011). In the current study, musicians exhibited lower λ_┴ values. Comparably lower λ_┴ values and the observed FA difference could be interpreted as a difference in myelination between musicians and nonmusicians. It is important to note, in this context, that results of the 3 ANOVAs of FA, λ_‖, and λ_┴ have not been corrected for multiple comparisons (k = 3), since the ANOVAs of AD and RD were performed under the presumption that differences in FA exist. Nevertheless, we are aware of the risk of false positives in the 2 ANOVAs of AD and RD, which were only conducted to further explain the observed FA differences, and the results of these ANOVAs should be interpreted with caution.

Diffusivity differences were mainly observed in the PT, suggesting that aMF might not show as much adaptation in response to the predominantly fine-skilled motor demands required by the 2 instruments studied here. In previous studies, aMF showed adaptations in cases of severe lesions to the PT (Belhaj-Saif and Cheney 2000; Lindenberg et al. 2010; Rüber et al. 2012). Overall, this would support the notion that the PT might be more involved in the execution and control of fine-grained distal finger movements, while aMF might be more involved in proximal motor control and that aMF only show adaptations in response to distal motor requirements when the PT system is damaged (Canedo 1997; Lemon 2008).

In agreement with previous studies (Toosy et al. 2003; Kraus et al. 2007; Imfeld et al. 2009), we found a right-greater-than-left asymmetry of FA values in corticospinal motor tracts across all subgroups (see Fig. 2 and Tables 2 and 3). On a first glance, it seems puzzling that left-hemispheric tracts, which control the dominant (right) hand, show comparably lower FA values, but that intensive motor training is accompanied by higher FA values. However, it has been questioned whether structural asymmetries in corticospinal tracts are actually related to handedness (Westerhausen et al. 2007) and even in case they are, differences might not be caused by more extensive use of the dominant right hand which is why our results do not have to be deemed intrinsically inconsistent. Indeed, the notion that interhemispheric differences across groups and between-group differences in FA describe unequal features of the underlying anatomy is emphasized by the observation that they are driven by diverse contributions of λ_‖ and λ_┴: Interhemispheric FA differences across groups are driven by both (higher) λ_‖ and (lower) λ_┴ values, whereas group differences in FA are mainly driven by (lower) λ_┴ values (Table 2; supplementary figure 1).

Consistent with previous studies (Jancke et al. 1997; Kopiez et al. 2010), we found significant between-group differences in maximal tapping rates of keyboard players, string players, and nonmusicians. However, as indicated by the nonsignificant group × hemisphere interaction, the asymmetry gradient of the maximal finger tapping rates of left and right index fingers was not different between groups. Previous studies (Jancke et al. 1997; Kopiez et al. 2010) have reported lower asymmetry gradients in musicians. Jancke et al. (1997) additionally found that a diminished asymmetry of the tapping rate in musicians was related to early commencement of musical training. Possible explanations might be the larger sample size of these previous studies and our selection of strongly right-handed participants.

The observed correlation between diffusivity properties of corticospinal motor tracts and the maximal finger tapping rate in our study is a novel finding. There was no evidence in our data, suggesting that this relation was moderated by age of commencement or intensity of musical training. A possible explanation might be the inclusion of highly trained musicians without large variance in their age of commencement or intensity of musical training. Interestingly, positive correlations between tapping speed and tract-specific FA values of the PT appeared to be specific to contributions from the ROI representing the primary motor cortex in our current study; this is a remarkable finding considering the substantial overlap of the contributions from M1, PMd, and SMA. However, it is in agreement with several other studies concluding that fast finger tapping is mainly controlled by M1 motorneurons (Humphrey 1972; Ashe and Georgopoulos 1994; Lutz et al. 2005). Furthermore, the RD measure (λ_┴) of tracts originating in M1 showed significant negative correlations with the maximal tapping rate, suggesting a higher degree of myelination of the PT in those with faster tapping rates (Song et al. 2002; Budde et al. 2007). Overall, our finding of a correlation between FA/λ_┴ values and maximal finger tapping rates supports the notion that between-group white matter differences are the results of practice-induced myelination changes.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/.

Funding

This work was supported by the National Institutes of Health (DC008796 and DC009823), the Mary Crown and William Ellis Foundation, the Rosalyn and Richard Slifka Family Foundation, and the Suzanne and Tom McManmon Family Foundation.