Abstract
Attachment of dissimilar materials is prone to failure due to stress concentrations that can arise at interfaces. A compositionally or structurally graded transition can dissipate these stress concentrations and thereby toughen an attachment. The interface between compliant tendon and stiff bone utilizes a monotonic change in hydroxylapatite mineral (“mineral”) content to produce a gradient in mechanical properties and mitigate stress concentrations. Previous efforts to mimic the natural tendon-to-bone attachment have included electrospun nanofibrous polymer scaffolds with gradients in mineral. Mineralization of the nanofiber scaffolds has typically been achieved using simulated body fluid (SBF). Depending on the specific formulation of SBF, mineral morphologies ranged from densely packed small crystals to platelike crystal florets. Although this mineralization of scaffolds produced increases in modulus, the peak modulus achieved remained significantly below that of bone. Missing from these prior empirical approaches was insight into the effect of mineral morphology on scaffold mechanics and on the potential for the approach to ultimately achieve moduli approaching that of bone. Here, we applied two mineralization methods to generate scaffolds with spatial gradations in mineral content, and developed methods to quantify the stiffening effects and evaluate them in the context of theoretical bounds. We asked whether either of the mineralization methods we developed holds potential to achieve adequate stiffening of the scaffold, and tested the hypothesis that the smoother, denser mineral coating could attain more potent stiffening effects. Testing this hypothesis required development of and comparison to homogenization bounds, and development of techniques to estimate mineral volume fractions and spatial gradations in modulus. For both mineralization strategies, energy dispersive x-ray analysis demonstrated the formation of linear gradients in mineral concentration along the length of the scaffolds, and Raman spectroscopic analysis revealed that the mineral produced was hydroxylapatite. Mechanical testing showed that the stiffness gradient using the new method was significantly steeper. By analyzing the scaffolds using micromechanical modeling techniques and extrapolating from our experimental results, we present evidence that the new mineralization protocol has the potential to achieve levels of stiffness adequate to contribute to enhanced repair of tendon-to-bone attachments.
1. INTRODUCTION
Connections between dissimilar materials can lead to high stresses and interfacial failure. One approach to minimizing these destructive forces involves incorporation of a functional gradient between the materials, as is done in nature and by materials engineers (Birman and Byrd, 2007; Miserez et al., 2008). At the interface between compliant tendon and stiff bone, a gradient in mechanical properties serves to mitigate stress concentrations (Liu et al., 2011b; Liu et al., 2012b). The two main components of this transitional tissue are nanofibers of collagen and nanometer-scale plates of a stiff, carbonated, hydroxylapatite (“mineral”) Stiffening of the collagen occurs via a monotonic rise in mineral content (Genin et al., 2009; Schwartz et al., 2012). The increasing mineral content results in a stiffness increase from ~400 MPa to ~20 GPa, a difference of almost two orders of magnitude (Currey, 2001; Maganaris and Paul, 1999). Unfortunately, this graded transitional tissue is not regenerated during tendon-to-bone healing or repair of the rotator cuff (Thomopoulos et al., 2003b), leading to high failure rates in surgical repairs of rotator cuffs (Galatz et al., 2004; Harryman et al., 1991). Using the healthy tendon-tobone attachment system as a guide, we created a polymer-hydroxylapatite nanofiber-based material with gradients in mineral content, and investigated the mechanical effects of these gradients.
The stiffness of a composite material depends upon several factors, including the mechanical properties and morphologies of the constituent phases, and the nature of their interactions (Torquato, 2001). By tailoring these factors, materials can be combined to produce a composite material that is mechanically superior to its individual constituents. These same factors also control the mechanics of composite materials whose composition exhibits a spatial gradation (Genin and Birman, 2009). For the graded fibrous scaffolds of interest here, the mechanics, distributions, morphology, and interactions of nanofibers and mineral control the mechanical properties of the resulting composite material.
In this study, we used electrospinning to create scaffolds of aligned nanofibers, and deposited mineral in a graded fashion on the fibers using modifications of a biomimetic ion solution known as “simulated body fluid” (SBF). We synthesized mineral gradients over the fibers by submerging the scaffolds into SBF. Two different mineralization formulations were used to create mineral coats that were compositionally similar but morphologically different (Liu et al., 2011a; Tas and Bhaduri, 2004). The first formulation resulted in plate-like mineral morphology and has been used previously to generate nanofiber scaffolds with gradients in mineral (Li et al., 2009). The second formulation resulted in a dense mineral morphology and was described in a study investigating the effects of homogeneous (i.e., non-graded) mineralization of nanofiber scaffolds (Liu et al., 2011a). We asked whether either of the mineralization methods we developed holds potential to achieve adequate stiffening of the scaffold. We hypothesized that mineral of both types would stiffen the polymer networks, manifesting itself as lower strains in the mineralized regions and larger calculated moduli. Furthermore, we hypothesized that the stiffening effect would depend on the morphology of the mineral, with denser coatings leading to a more potent stiffening effect. Testing of this hypothesis required development of the homogenization bounds and of a technique for estimating spatial gradations in elastic modulus in a graded scaffold. Understanding the stiffening mechanisms of mineral on nanofiber polymer scaffolds is critical for the development of mechanically competent scaffolds for tendon-to-bone tissue engineering. We adapted a newly developed digital image correlation algorithm to measure local strain patterns and analyzed these strain fields to estimate the relationship between mineral volume fraction and mechanical properties.
2. MATERIALS AND METHODS
2.1. Scaffold synthesis
Fibrous scaffolds with gradients in mineral content were generated using electrospinning and two different simulated body fluid (SBF) solutions (10 times SBF (10SBF) and modified 10SBF (m10SBF)) (Liu et al., 2011a; Tas and Bhaduri, 2004) (Table 1). Scaffolds of nanofibers were generated by electrospinning poly lactic co-glycolic acid (PLGA, 85:15 lactic:glycolic ratio, Sigma, St. Louis, MO) onto conducting collectors, as described previously (Liu et al., 2011a). The fiber diameters were 400 - 900nm (as measured using scanning electron microscopy images) and the fiber mats were ~60 microns thick (as measured by a laser micrometer; Keyence LK-081). After electrospinning, the samples were cut into pieces and mounted onto carbon tape-covered wire frames. The mounted samples were then plasma treated for eight minutes to increase surface energy and hydrophillicity (Harrick Plasma PDC-001) (Qu et al., 2007). m10SBF samples were incubated for four hours with heparin and then four hours with chitosan along with cross-linking agent N-(3-Dimethylaminopropyl)-N’-ethylcarbodiimide hydrochloride (EDC) (Sigma, St. Louis, MO). This combination of surface modifications generated negatively charged ions on the surface, allowing for attachment of calcium ions that are thought to encourage mineral nucleation (Cui et al., 2010; Kim et al.; Liu et al., 2011a; Wang et al., 2003; Zhu et al., 2002). 10SBF samples did not receive this surface treatment. Both groups were then soaked in 10SBF without sodium bicarbonate for 30 minutes to bind calcium to the surface. The mineralization solutions 10SBF or m10SBF were then applied (Table 1) (Liu et al., 2011a; Tas and Bhaduri, 2004): a syringe pump was used to fill vials containing the samples with mineralization solution at a constant rate to create linear gradients in mineral content, as described previously (Li et al., 2009). Due to the high porosity of the scaffolds (~13 vol% polymer) no diffusion limitations were expected for mineralization through the thickness of the samples.
Table 1.
Concentrations of ion constituents in simulated body fluid solutions (mM).
| Mg2+ | K+ | Ca2+ | (PO4)3− | Na+ | H+ | Cl− | |
|---|---|---|---|---|---|---|---|
| 10SBF | 5 | 5 | 25 | 10 | 1,010 | 20 | 1,065 |
| m10SBF | 0 | 0 | 25 | 10 | 1,010 | 20 | 1,065 |
2.2. Scaffold Characterization
Scanning Electron Microscopy (SEM) was used to visualize the fibers and mineral morphologies. Samples were mounted on carbon tape-coated aluminum SEM posts and sputter coated with Au-Pd for ~45 s to allow a charge path for the primary electrons. Posts were then imaged under high vacuum using an FEI Nova NanoSEM 2300 and accelerating voltages of between 5 and 10kV.
Energy dispersive X-ray (EDX) was performed using the FEI Nova NanoSEM 2300 during SEM imaging to determine the spatial variation of mineral content along the length of the scaffold. Moving in 1–3 mm increments, regions were assessed for their atomic content. Three regions were analyzed for each measurement along the mineral gradient and averaged for atomic content. Calcium and carbon signals were calculated from the resulting EDX spectra using EDAX Genesis software (EDAX, Mahwah, NJ). Mineral content was measured as an atomic percent of Ca/(Ca+C), which was subsequently converted to volume fractions (see Supplemental Materials).
Raman spectroscopy analysis was performed with a fiber-optically coupled Raman microprobe (HoloLab Series 5000 Raman Microprobe, Kaiser Optical System, Inc., Ann Arbor, MI). The 532 nm excitation was delivered by a Nd:YAG laser (Coherent), which was coupled to a Leica microscope (Germany) with an ultra-long-working-distance MSPlan 80× objective (Olympus, Japan). The spectral region of 400–4000 cm−1 was recorded with a spectral resolution of 2.5 Δcm−1. The power of the incident laser was 10 milliwatts, as measured at the surface of the sample. Intensity, wavelength, and Raman shift position were calibrated based on a NIST secondary standard, gas emission lines, and a laboratory standard. Reproducibility of the Raman shift position for a silicon wafer was 520.5±0.1cm−1. The acquisition time per analysis spot (~1 µm diameter) was 32×4 seconds.
2.3. Scaffold mechanical testing and analysis
Uniaxial tensile tests were performed using an Instron Electropuls E1000 (Norwood, MA) with custom grips, and analyzed using custom code written in Matlab (Mathworks, Natick, MA). To prepare the test strips, the samples were cut out of wire frames with a no. 15 scalpel blade. Using the EDX trace for each sample, the location of the gradient was marked with 5 mg/ml alizarin-red S stain solution (Sigma, St. Louis, MO) and test strips were cut out using a machined 3 mm wide stainless steel template along the direction of fiber orientation. The thickness of each strip was then measured in several places using a Keyence LK-081 laser micrometer (Elmwood Park, NJ), and the average value was taken as the thickness of the sample. The test strips had their ends placed between small pieces of sandpaper, with the grit sides facing the grip. Samples were tested under uniaxial tension at quasi-static conditions, with a constant strain rate of ~0.4 % per second. Video was captured concurrently at 3 frames per second with a resolution of 1360 × 1024 pixels (Olympus DP70). Images from the video were analyzed for their gage length and width. Cross-sectional area was then calculated as width multiplied by thickness. Engineering stress was calculated by dividing force by initial cross-sectional area. The raw data were analyzed to find the stiffness (slope of the linear region of the force-displacement curve), maximum force, maximum stress, ductility, and toughness.
Video was analyzed to identify local strains using digital image warping and the Lucas-Kanade algorithm (Baker and Matthews, 2004; Boyle et al., 2014). This technique provides accurate calculation of regional strains in two dimensions throughout the mechanical tests. The local moduli were determined from linear regressions of the engineering stress and regional strain (Figure 1). EDX data of Calcium (Ca) and Carbon (C) were used to calculate Ca/(Ca+C) as a proxy for relative mineral content. Using the known molecular formulas for 85:15 PLGA and carbonated hydroxylapatite, we were able to estimate mass fractions for both polymer and mineral (see Supplemental Materials). Using the published densities of these materials, the mass fractions could be converted into volume fractions (Leung et al., 2008; Roberts et al., 1974). A small number of samples had local defects due to fabrication issues or mishandling. These defects were readily apparent during testing through the appearance of local strain concentrations. Any samples that displayed this behavior were excluded. The mineral volume was then plotted against the average modulus for each transverse slice, and if the modulus measurements did not indicate zones of failure (negative moduli) the data were included in a larger dataset for each mineralization method (m10SBF 4/5 included, 10SBF 7/7). This larger dataset was analyzed for the overall trends, and a linear fit was found to estimate the relationship between modulus and mineral.
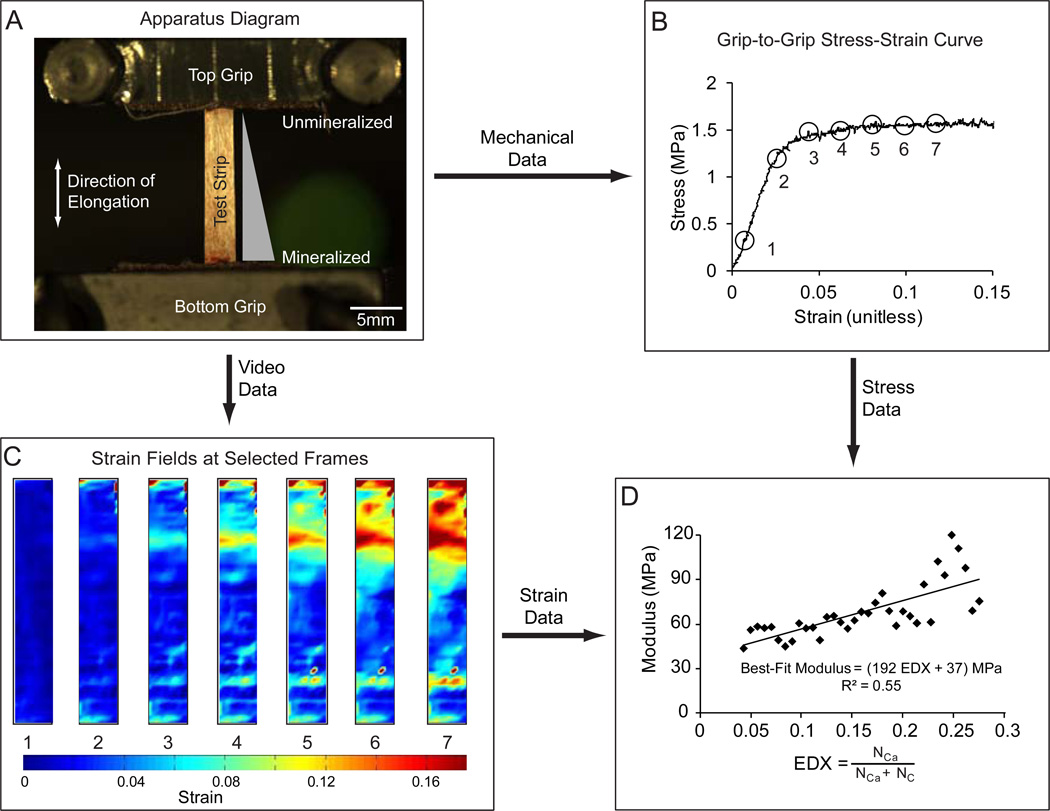
Figure 1.
(A) Testing was performed from slack conditions, and conducted with a strain rate of 0.4 %/sec to achieve quasi-static loading conditions. (B) Locations were selected from the grip-to-grip stress-strain curve. The images were then analyzed to demonstrate the effect of mineral content on the strain fields and mechanical properties. (C) Local strain fields were calculated directly. The first principal strain is shown using a heat map. (D) The relationship between modulus and mineral content was approximately linear, with the slope representing the stiffening effect of the mineral (R: Pearson’s correlation coefficient).
2.4. Mechanical Modeling
Homogenization bounds and estimates were studied to estimate the maximum and minimum stiffening possible by combining PLGA fibers, mineral, and a third phase (air) that had no mechanical resistance. Four bounds were studied: a parallel estimate, a series estimate, and Hashin-Shtrikman-type upper and lower bounds (see Supplemental Document). The parallel estimate was the stiffest guideline considered for a mineralized scaffold, and provided an estimate of stiffening for the case in which mineral accrues in sheaths on the fibers. The series estimate was the most compliant guideline considered, and provided an estimate for the stiffening that would occur in a composite with mineral added in series with the fibers. The Hashin-Shtrikman bounds represent maximum and minimum elastic moduli for a composite of two isotropic phases that are homogeneously mixed (Hashin and Shtrikman, 1963). These were adapted to account for the fibrous nature of the scaffolds. The added mineral was assumed to replace air in the composite, and the polymer volume fraction was assumed to remain constant with the addition of mineral (based on measures of constant scaffold thickness with increasing mineral content, we concluded that the polymer volume fraction did not change during mineralization [data not shown]). The following properties were used: polymer volume fraction of 0.13 (based on measurements of apparent density and published densities), polymer modulus of 700 MPa (from 4-pt bending tests of solid beams), and mineral modulus of 114 GPa (Gilmore and Katz, 1982; Leung et al., 2008). Although there are likely small differences in the mechanical properties of bulk PLGA compared to electrospun nanofiber PLGA, 700 MPa is on the order of recent results for single PLGA fiber mechanical tests (Kolluru et al., 2013). We also note that, while 114 GPa is a reliable estimate for geologic hydroxylapatite, much debate persists on the mechanical properties of biological hydroxylapatite, with recent estimates as low as 55–65 GPa (Deymier-Black et al., 2012; Deymier-Black et al., 2010).
2.5. Statistical Methods
We tested two questions statistically: (1) was there a significant stiffening effect of the mineral and (2) did the stiffening effect differ for m10SBF compared to 10SBF? Standard algorithms native to MATLAB (The Mathworks, Natick, MA) environment were employed. To test the first question, a comparison was made between the measured slope (determined by a linear regression to the data for each group) and a slope of zero (i.e., no stiffening effect). To test the second question, an analysis of covariance was performed for the two datasets to compare the regression line coefficients. The analysis of covariance interactively allows for the comparison of both the intercepts and slopes of regression lines. Confidence ellipses representing the observed statistical spread of modulus and volume fraction data were drawn based upon the eigenvectors and eigenvalues of the two datasets estimated using principal component analysis. After scaling to represent a 95% confidence interval, these and the mean values of modulus and volume fraction defined the major axes and center, respectively, of an ellipse representing a 95% confidence region for the data. The confidence ellipses were drawn using the using a custom MATLAB script (“confellipse2”) (Schwarz, 1998).
3. RESULTS
3.1. Scaffold Characterization
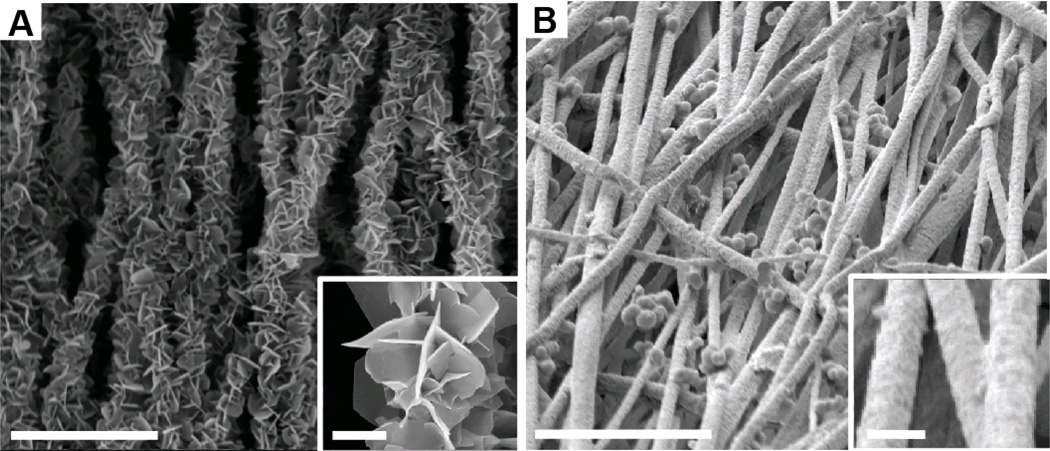
Based on EDX analysis, a linear gradient in mineral content was achieved with both mineralizing solutions (Figure 2). The mineral morphology, as observed using SEM, was dramatically different when comparing the two mineralizing solutions. Mineral deposited using 10SBF was distinctly plate-like and diffuse, arranged in florets over fibers. In contrast, mineral deposited using m10SBF was dense and largely conformal to the fibers, except for some bunched, bead-like accumulations similar to those seen on fracture surfaces in natural bone (Thurner et al., 2007) (Figure 3).
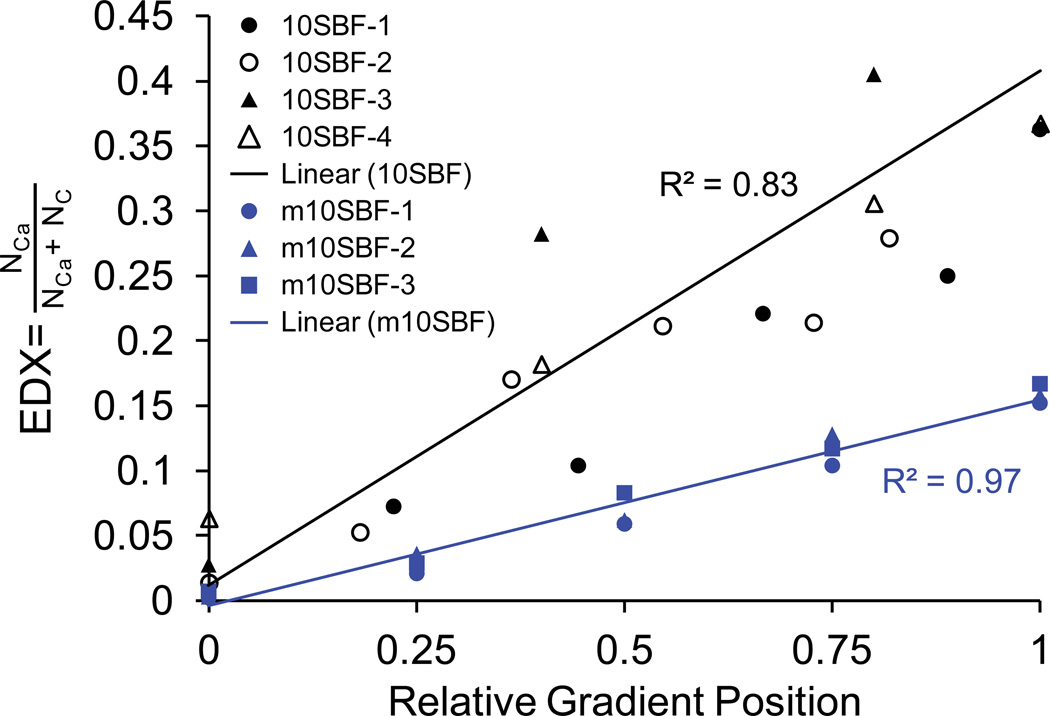
Figure 2.
A linear gradient in hydroxylapatite mineral content was achieved with both 10SBF and m10SBF. The ratio of the number of Ca atoms per unit volume to the combined numbers of Ca and C atoms, as measured with EDX, increased linearly along the length of the scaffold’s mineral gradient (measurements are shown for 4 10SBF samples and 3 m10SBF samples).
Figure 3.
(A) Plate-like mineral morphology was observed in the 10SBF group. (B) A dense coat of small mineral crystals was observed in the m10SBF group. (Outer scale bar = 10 µm, inset scale bar = 1 µm).
Using Raman spectroscopy, we characterized the scaffolds to confirm that the mineral was in fact hydroxylapatite. A suite of peaks from samples with both coatings, and were attributed to hydroxylapatite, confirming its identification: 433, 583, 959, and 1045 cm−1. Small amounts of calcite were found in the 10SBF sample, but previous XRD results suggest that the calcite is likely confined to crystals at the surface (Wopenka and Pasteris, 2005). These results confirm that the two mineral coatings produced bone-like mineral that was identical in chemical composition but different in morphology.
3.2. Mechanical Properties
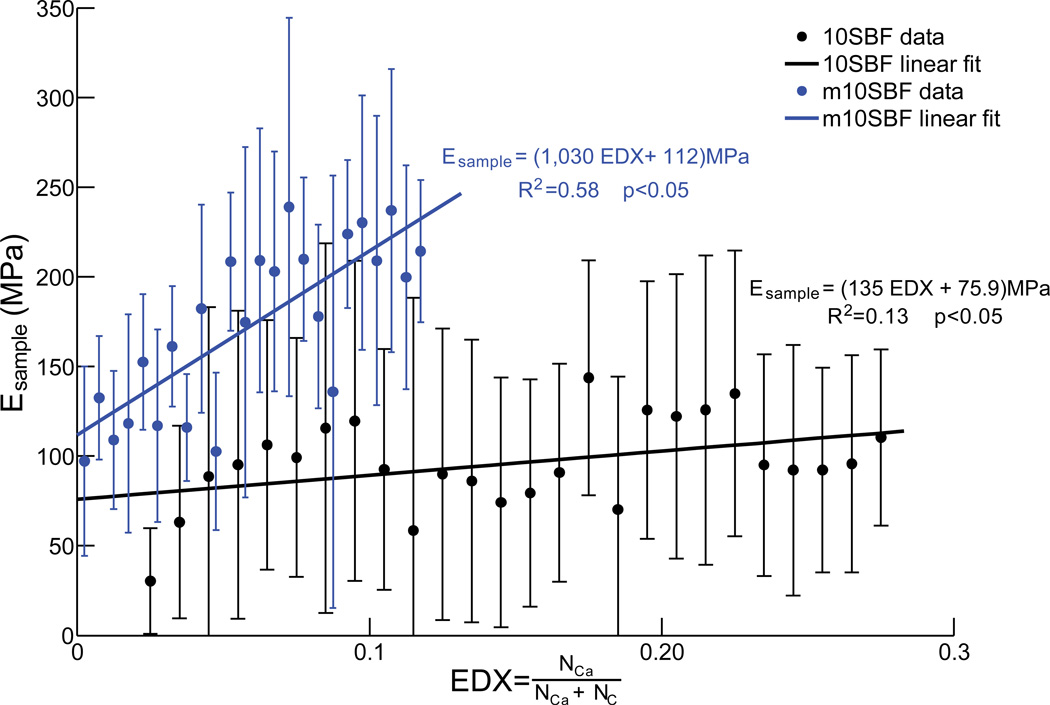
Both mineral volume fraction and mineral morphology strongly affected the mechanical properties of the scaffolds. When the graded scaffolds were loaded mechanically, strain was higher on the low mineral content ends than the high mineral content ends (Figure 1). The elastic modulus of scaffolds generated using both coating methods increased with increasing mineral content. This relationship was statistically significant based on linear regression analysis (Figure 4). A high correlation coefficient was found for the m10SBF group, indicating that the variation in modulus can largely be explained by changes in mineral content for this group. In contrast, a relatively low correlation coefficient was found for the 10SBF group, indicating that the variation in modulus can only partially be explained by changes in mineral content for that group. In other words, the denser mineral coat produced by m10SBF led to more rapid stiffening compared to the plate-like 10SBF coat (Figure 4).
Figure 4.
Plots of modulus relative to mineral content demonstrate the stiffening effects of 10SBF and m10SBF (error bars represent standard deviation). The stiffening effect of m10SBF was significantly greater than 10SBF, as evidenced by a higher slope (analysis of covariance; p<0.05).
3.3. Modeling
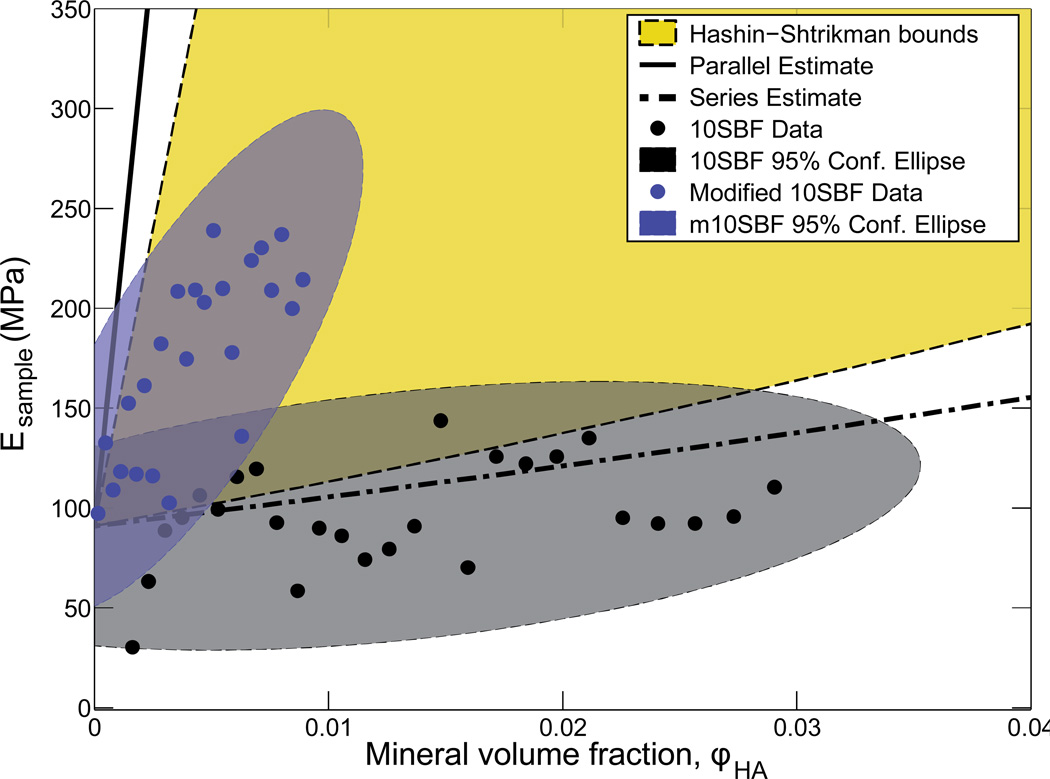
We derived parallel and series estimates to study these data in the context of the weakest and strongest stiffening effects possible for a continuous fibrous material comprised of PLGA and hydroxylapatite mineral. For the scaffolds mineralized using 10SBF, the data were generally coincident with or below the series estimate, indicating stiffening effect as weak as or weaker than the lowest possible for a mechanically continuous material (Figure 5). Note that the volume fraction of mineral in Figure 5 is the scaffold-level volume fraction. The equivalent fiber-level volume fractions can be found by dividing these by the scaffold-level volume fraction of fibers, ~0.13. The Hashin-Shtrikman-type upper and lower bounds were used to describe the minimum and maximum stiffening of fibers consisting of mineral and PLGA mixed homogeneously. When compared to all of these bounds and estimates, the stiffening exhibited by the 10SBF mineralized scaffolds was revealed to be extremely weak. However, the m10SBF data lay well within the bounds and estimates, indicating far superior stiffening.
Figure 5.
Modeling results demonstrated that 10SBF had a small stiffening effect on the scaffold, following the lower series bound, whereas m10SBF had a large stiffening effect, closer to the upper Hashin-Shtrikman bound. This suggests that differences in mineral morphology can affect stiffening effects of the coating.
4. DISCUSSION
This work presented a framework for measuring and assessing the stiffening of nanofibrous scaffolds by a gradient of mineral. Although the levels of mineralization studied are far below those of bone, we see promise in the approach. The stiffening effect of m10SBF on PLGA nanofibers reached levels that are appropriate for tendon-to-bone tissue engineering. The PLGA scaffolds produced have fibers with moduli similar to that of collagen within tendon (1.4–2.3 GPa for PLGA fibers vs. 1.2 GPa for collagen fibers) (Kolluru et al., 2013; Pollock and Shadwick, 1994). To extrapolate the data for mineralized scaffolds to volume fractions of PLGA and mineral of 50%, representative of the mineral volume fraction in bone (e.g. (Alexander et al., 2012; Glimcher, 2006; Liu et al., 2014)), two steps must be undertaken. First, the modulus for a scaffold with a PLGA volume fraction of φPLGA=0.13 and hydroxylapatite volume fraction of φHA=0.13 can be estimated from the fits in Figure 4 and the relationship between EDX and hydroxylapatite volume fraction, (Equation 8 in the Supplemental Document), as:
| (1) |
where α=2.7 is a fitting factor (Supplemental Document). Then, this estimate can be scaled up to a fibril that is 50% PLGA and 50% hydroxylapatite as Emax = 807 MPa (0.5 / 0.13) = 3.1 GPa. This is still a factor of 5 lower than bone (Currey, 2001), due in part to the fact that mineral cannot penetrate the PLGA fibers studied. Further modification of the mineralizing solution or pre-mineralization functionalization may produce even more effective stiffening effects on graded scaffolds. Stronger interfacial bonding between the polymer and the mineral could lead to a more potent stiffening effect, although the effect of this on the remarkable strain tolerance of polymer fibers would have to be tested.
Composites bounds provided a context for the stiffening effects of the mineralization methods. The bounds represent the stiffening that arises from idealized physical arrangements of the polymer and mineral in the scaffolds, enabling investigation of how the mineralized scaffolds performed relative to the best and worst stiffening that could be expected (Milton, 2002). The series estimate described the stiffness of polymer and mineral combined in series. In this scenario, the stiffness of the composite at low mineral volume fraction was driven primarily by the more compliant of two materials, and therefore represents the lowest possible stiffening. In contrast, the parallel estimate describes the stiffness of the polymer and mineral combined in parallel. In this scenario, mineral contributes in proportion to its volume fraction even at very low volume fraction. With the stiffness of the scaffolds driven primarily by the contribution of mineral, this estimate represents the highest possible stiffening; note that this is not a theoretical bound due to Poisson mismatch between the materials. The Hashin-Shtrikman bounds are the tightest bounds for the stiffening when two isotropic phases are mixed homogeneously. A broad range of particulate-reinforced composite materials follow the Hashin-Shtrikman lower bound for volume fractions, with relatively small contributions the composite stiffness below a percolation threshold (Genin and Birman, 2009; Milton, 2002); the idea here is that the stiffer phase does not stretch significantly compared to the compliant phase until it forms a contiguous mechanical network (Marquez et al., 2010; Milton, 2002). Comparing the experimental results with the various bounds, the 10SBF mineralization stiffened the scaffolds roughly along the series lower bound, while the m10SBF mineralization stiffened the scaffolds closer to the Hashin-Shtrikman upper bound. These patterns of stiffening imply that the m10SBF methods were more effective in combining a stiff phase (mineral) with a compliant phase (polymer) whereas 10SBF methods were relatively ineffective.
Gradients like those achieved in the present work are used to achieve a number of mechanical and biologic functions, including compositional and structural gradients for attachment of stiff and compliant tissues (Schwartz et al., 2012; Thomopoulos et al., 2003a). Tissue engineers have therefore attempted to reproduce gradients in the laboratory using collagen density, mineral content, retrovirus immobilization, and microsphere delivery systems (Hadjipanayi et al., 2009; Li et al., 2009; Phillips et al., 2008; Wang et al., 2009). In vitro experiments have demonstrated that gradients can guide cell migration, attachment, morphology, fate, and gene expression (DeLong et al., 2005; Li et al., 2005; Wang et al., 2009). In the current work, simple fabrication techniques consisting of electrospinning and simulated body fluids were used to generate a functionally graded scaffold for potential use in soft-tissue-to-bone repair.
This work adds to the body of literature on electrospinning as a technique for creating fibrous scaffolds that mimic the structure and organization of fibrous tissues (Liu et al., 2012a), and to mineralize these scaffolds (Li et al., 2009; Liu et al., 2011a). Simulated body fluid solutions have been used to deposit bone-like mineral on a wide variety of materials (Chen et al., 2006a; Takeuchi et al., 2003; Tas and Bhaduri, 2004). Previous work has demonstrated that mineral precipitated on both gelatin-coated polymer fibers and titanium alloy is similar to bone hydroxylapatite (Li et al., 2008; Tas and Bhaduri, 2004) and that these solutions can be used to produce linear gradients in mineralization (Li et al., 2009). Mineral deposited by simulated body fluids has been shown to increase pre-osteoblast alkaline phosphatase activity and osteocalcin expression, as well as adhesion and proliferation of stem cells (Chen et al., 2007a; Chen et al., 2006b; Chen et al., 2007b; Li et al., 2009; Murphy et al., 2005). The engineered scaffolds presented in the current paper used a nanofibrous matrix with a gradient of mineral to mimic the mineral compositional gradient found at the tendon-to-bone attachment. The two mineral coatings examined mimicked many aspects of the apatite structure of mineral found in natural bone.
The moduli of both PLGA nanofibers and biological hydroxylapatite are uncertain, but we believe the moduli used in our models to be reasonable estimates. The intercepts of the linear fits of both 10SBF and m10SBF scaffold moduli data are an indication of the modulus of the unmineralized scaffolds. These intercepts, combined with an estimated 13% scaffold-level volume fraction of PLGA, yielded a modulus of PLGA ranging between 580 and 890 MPa. Although the modulus of biological hydroxylapatite is not known to within a factor of 2, hydroxylapatite is at least a factor of 100 stiffer than the PLGA, and this uncertainty is therefore less important at the volume fractions considered.
The mechanical properties of the scaffold are dictated by effects at multiple hierarchical levels. At the fiber level, if the coating is dense and well-bonded to the fiber, load will be transferred via shear stress to the coating, stiffening the fiber. If the coating is poorly bonded to the fiber, little stress can be transferred, and the fiber will remain compliant. If the coating is well-bonded but not mechanically continuous, it will not be able to carry load, and the stiffness will remain the same. Therefore, both the morphology of the coating and its bonding strength to the underlying material are important determinants of the overall mechanics. Furthermore, scaffold mechanics are also dependent on the interactions between fibers. If the fibers become stiffer, then the scaffold becomes stiffer to the extent that the fibers lengthen with the scaffold. If the main deformation mechanism of the scaffold is fiber realignment, then friction between the fibers will increase the apparent stiffness, regardless of fiber stiffness. If the coating bonds adjacent fibers together, then those fibers will have the break those bonds before they can rearrange, leading to increased stiffness.
At the single fiber level, recent work using a microelectromechanical testing frame examined the effect of mineral coatings on single PLGA nanofibers. Results indicated that 10SBF-based mineral coatings do not substantially change the modulus of the individual fibers (Kolluru et al., 2013). This surprising result implies that the stiffening effect of the mineral in the current study occurred at the hierarchical level of the fiber network, not at the level of individual fibers. Stiffening therefore likely resulted from increased fiber-fiber interactions, e.g., mineral bridges connecting adjacent fibers. Indeed, at higher levels of mineral, continuous mineral layers between multiple fibers were apparent on SEM images (Figure 6). Future experiments will directly test whether scaffold-level mechanics can be improved with increased fiber-fiber bonding.
Figure 6.
SEM analysis demonstrated mineral bonding between fibers. (white arrows: mineral bridges; arrowheads: mineral bridge fractures, black arrows: polymer fibers with little to no mineral. Scale bars = 5 µm, inset scale bar = 1 µm) (A) An image from a 10SBF scaffold shows a fractured mineral bridge with crystalline morphology. (B) An image from the m10SBF group shows a more conformal layer of mineral that bonds adjacent fibers. Inset is magnified image of a mineral bridge fracture.
Several features of the native tendon-to-bone attachment remain to be implemented in the nanofiber scaffolds presented in the current study. The scale of the mineral gradient at the natural attachment of tendon to bone is on the order of tens of micrometers (Genin et al., 2009; Schwartz et al., 2012), whereas the mineral gradient in the scaffolds was on the order of millimeters. Implementation of a smaller gradient is possible with the fabrication techniques used, but mechanical characterization of such a gradient would be technically challenging. The natural tendon-to-bone attachment contains a fibrocartilaginous transition between tendon and bone, with a corresponding mechanically compliant region (Liu et al., 2012b; Thomopoulos et al., 2003a). This complexity has yet to be implemented using the current scaffold fabrication approach. Finally, the scaffolds presented in the current study are thin relative to the natural tissue at the attachment of tendon to bone. However, these scaffolds can form the basis of larger scaffolds, e.g., using a layering approach (Manning et al., 2013). Furthermore, thin scaffolds may improve outcomes by guiding the healing process rather than fully replacing the injured tissue.
Previous work has shown that the mineral generated by 10SBF has a different morphology, but similar composition, to the mineral generated by modified 10SBF (Li et al., 2008; Liu et al., 2011a). The different surface treatments used for these coatings could also affect the bonding strength of the coating to the underlying fiber. Changes in bonding strength could have dramatic effects on the interaction between mineral and polymer, and bonding strength between the different phases presents challenges for the mechanics of the fibers. Rogel et al. indicated that most composites that include a ceramic such as hydroxylapatite suffer from weak interfacial adhesive interactions between the phases (Rogel et al., 2008). The covalently bonded heparin and chitosan surface on the PLGA fibers in the m10SBF group may have improved the bonding between the mineral and polymer. It is likely that the strong bonding between the chitosanheparin- mineral complex is responsible for these effects. Previous work with chitosan-calcium phosphate materials has shown that chitosan can enhance bonding of the ceramic phase, maintenance of osteoblast phenotype, in vivo osteogenesis, osteoblast attachment and osteoblast proliferation (Kawakami et al., 1992; Zhu et al., 2002). Further research into the effect of these coatings on electrospun scaffolds with m10SBF could elucidate how much this surface treatment contributes to the mechanical effects of mineralization. The methods presented here for quantifying and assessing these effects comprise an important tool for these efforts.
5. CONCLUSION
In this work, we estimated the stiffening effects of two different mineralization methods on nanofiber polymer scaffolds and compared these to mechanical models to measure how efficient the stiffening was. This is the first study to rigorously examine the mechanics of nanofiber PLGA scaffolds with gradients in mineral. New methods were developed to determine the local mechanical properties and the mineral volume fractions, and a mathematical model was developed to compare the experimental results to theoretical bounds. We found that both mineralization methods stiffened the scaffolds, but that their magnitudes varied substantially, with modified simulated body fluid (m10SBF) giving a more potent effect than simulated body fluid (10SBF). When compared to the composite bounds we developed, the stiffening by mineralization achieved using 10SBF proved to be weaker than the lowest possible stiffening predicted by homogenization theory, indicating that mineral was not well connected to the scaffold. In contrast, mineralization using m10SBF achieved stiffening that was nearly an order of magnitude greater than 10SBF, supporting our initial hypotheses. This stiffening was close to that predicted by the Hashin-Shtrikman upper homogenization bound, suggesting that the new method might be suitable for tendon-to-bone tissue engineering.
Supplementary Material
HIGHLIGHTS.
Functionally graded transitions can dissipate stress concentrations and toughen attachments
Two mineralization methods were used to generate nanofiber scaffolds with gradients in mineral
Scaffold stiffening depended on mineral content and morphology
Micromechanical modeling showed that stiffening may be adequate for enhanced tendon repair
ACKNOWLEDGMENTS
This work was supported in part by the National Science Foundation (NSF) (CAREER 844607 to S.T.), the National Institutes of Health (NIH) (DP1OD000798 to Y.X. and AR060820 to Y.X. and S.T.), NIH/NSF (U01 AR063632 to S.T. and G.G.), and the Center for Materials Innovation at Washington University. Single fiber testing of unmineralized fibers that helped our interpretation of our results was performed in the Chasiotis lab at University of Illinois at Urbana-Champaign. SEM was performed at the Nano Research Facility at Washington University. Raman spectroscopy was performed with assistance from Dr. Jill Pasteris and Zhen Li.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Alexander B, Daulton TL, Genin GM, Lipner J, Pasteris JD, Wopenka B, Thomopoulos S. The nanometre-scale physiology of bone: steric modelling and scanning transmission electron microscopy of collagen–mineral structure. J. R. Soc. Interface. 2012;9:1774–1786. doi: 10.1098/rsif.2011.0880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker S, Matthews I. Lucas-Kanade 20 Years On: A Unifying Framework. Int. J. Comput. Vision. 2004;56:221–255. [Google Scholar]
- Birman V, Byrd LW. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007;60:195–216. [Google Scholar]
- Boyle J, Kume M, Wyczalkowski M, Taber L, Pless R, Xia Y, Genin G, Thomopoulos S. Simple and accurate methods for quantifying deformation, disruption, and development in biological tissues. J. R. Soc. Interface. 2014 doi: 10.1098/rsif.2014.0685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Cho MR, Mak AFT, Li JS, Wang M, Sun S. Morphology and adhesion of mesenchymal stem cells on PLLA, apatite and apatite/collagen surfaces. J. Mater. Sci.-Mater. M. 2007a;19:2563–2567. doi: 10.1007/s10856-007-3195-2. [DOI] [PubMed] [Google Scholar]
- Chen Y, Mak AFT, Wang M, Li J. Composite coating of bonelike apatite particles and collagen fibers on poly L-lactic acid formed through an accelerated biomimetic coprecipitation process. J. Biomed. Mater. Res. B. 2006a;77B:315–322. doi: 10.1002/jbm.b.30356. [DOI] [PubMed] [Google Scholar]
- Chen Y, Mak AFT, Wang M, Li J, Wong MS. PLLA scaffolds with biomimetic apatite coating and biomimetic apatite/collagen composite coating to enhance osteoblast-like cells attachment and activity. Surf. Coat. Tech. 2006b;201:575–580. [Google Scholar]
- Chen Y, Mak AFT, Wang M, Li JS, Wong MS. In vitro behavior of osteoblast-like cells on PLLA films with a biomimetic apatite or apatite/collagen composite coating. J. Mater. Sci.-Mater. M. 2007b;19:2261–2268. doi: 10.1007/s10856-007-3335-8. [DOI] [PubMed] [Google Scholar]
- Cui W, Li X, Xie C, Chen J, Zou J, Zhou S, Weng J. Controllable growth of hydroxyapatite on electrospun poly(dl-lactide) fibers grafted with chitosan as potential tissue engineering scaffolds. Polymer. 2010;51:2320–2328. [Google Scholar]
- Currey JD. Bone and Natural Composites: Properties. In: Buschow KHJ, Cahn RW, Flemings MC, Ilschner B, Kramer EJ, Mahajan S, Veyssière P, editors. Encyclopedia of Materials: Science and Technology. Second Edition. Oxford: Elsevier; 2001. pp. 776–781. [Google Scholar]
- DeLong SA, Moon JJ, West JL. Covalently immobilized gradients of bFGF on hydrogel scaffolds for directed cell migration. Biomaterials. 2005;26:3227–3234. doi: 10.1016/j.biomaterials.2004.09.021. [DOI] [PubMed] [Google Scholar]
- Deymier-Black AC, Almer JD, Stock SR, Dunand DC. Variability in the elastic properties of bovine dentin at multiple length scales. J. Mech. Behav. Biomed. Mater. 2012;5:71–81. doi: 10.1016/j.jmbbm.2011.08.005. [DOI] [PubMed] [Google Scholar]
- Deymier-Black AC, Almer JD, Stock SR, Haeffner DR, Dunand DC. Synchrotron X-ray diffraction study of load partitioning during elastic deformation of bovine dentin. Acta Biomater. 2010;6:2172–2180. doi: 10.1016/j.actbio.2009.11.017. [DOI] [PubMed] [Google Scholar]
- Galatz LM, Ball CM, Teefey SA, Middleton WD, Yamaguchi K. The outcome and repair integrity of completely arthroscopically repaired large and massive rotator cuff tears. J. Bone Joint Surg. Am. 2004;86-A:219–224. doi: 10.2106/00004623-200402000-00002. [DOI] [PubMed] [Google Scholar]
- Genin GM, Birman V. Micromechanics and Structural Response of Functionally Graded, Particulate-Matrix, Fiber-Reinforced Composites. Int. J. Solids Struct. 2009;46:2136–2150. doi: 10.1016/j.ijsolstr.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genin GM, Kent A, Birman V, Wopenka B, Pasteris JD, Marquez PJ, Thomopoulos S. Functional Grading of Mineral and Collagen in the Attachment of Tendon to Bone. Biophys. J. 2009;97:976–985. doi: 10.1016/j.bpj.2009.05.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore RS, Katz JL. Elastic properties of apatites. J. Mater. Sci. 1982;17:1131–1141. [Google Scholar]
- Glimcher MJ. Bone: Nature of the Calcium Phosphate Crystals and Cellular, Structural, and Physical Chemical Mechanisms in Their Formation. Rev. Mineral Geochem. 2006;64:223–282. [Google Scholar]
- Hadjipanayi E, Mudera V, Brown RA. Guiding cell migration in 3D: A collagen matrix with graded directional stiffness. Cell Motil. Cytoskel. 2009;66:121–128. doi: 10.1002/cm.20331. [DOI] [PubMed] [Google Scholar]
- Harryman DT, Mack LA, Wang KY, Jackins SE, Richardson ML, Matsen FA. Repairs of the rotator cuff. Correlation of functional results with integrity of the cuff. J. Bone Joint Surg. Am. 1991;73:982–989. [PubMed] [Google Scholar]
- Hashin Z, Shtrikman S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids. 1963;11:127–140. [Google Scholar]
- Kawakami T, Antoh M, Hasegawa H, Yamagishi T, Ito M, Eda S. Experimental study on osteoconductive properties of a chitosan-bonded hydroxyapatite self-hardening paste. Biomaterials. 1992;13:759–763. doi: 10.1016/0142-9612(92)90014-f. [DOI] [PubMed] [Google Scholar]
- Kim I-Y, Seo S-J, Moon H-S, Yoo M-K, Park I-Y, Kim B-C, Cho C-S. Chitosan and its derivatives for tissue engineering applications. Biotechnol. Adv. 26:1–21. doi: 10.1016/j.biotechadv.2007.07.009. [DOI] [PubMed] [Google Scholar]
- Kolluru PV, Lipner J, Liu W, Xia Y, Thomopoulos S, Genin GM, Chasiotis I. Strong and tough mineralized PLGA nanofibers for tendon-to-bone scaffolds. Acta Biomater. 2013;9:9442–9450. doi: 10.1016/j.actbio.2013.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leung L, Chan C, Baek S, Naguib H. Comparison of morphology and mechanical properties of PLGA bioscaffolds. Biomed. Mater. 2008;3:025006–025014. doi: 10.1088/1748-6041/3/2/025006. [DOI] [PubMed] [Google Scholar]
- Li B, Ma Y, Wang S, Moran PM. Influence of carboxyl group density on neuron cell attachment and differentiation behavior: Gradient-guided neurite outgrowth. Biomaterials. 2005;26:4956–4963. doi: 10.1016/j.biomaterials.2005.01.018. [DOI] [PubMed] [Google Scholar]
- Li X, Xie J, Lipner J, Yuan X, Thomopoulos S, Xia Y. Nanofiber scaffolds with gradations in mineral content for mimicking the tendon-to-bone insertion site. Nano Lett. 2009;9:2763–2768. doi: 10.1021/nl901582f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Xie J, Yuan X, Xia Y. Coating Electrospun Poly(ε-caprolactone) Fibers with Gelatin and Calcium Phosphate and Their Use as Biomimetic Scaffolds for Bone Tissue Engineering. Langmuir. 2008;24:14145–14150. doi: 10.1021/la802984a. [DOI] [PubMed] [Google Scholar]
- Liu W, Thomopoulos S, Xia Y. Electrospun Nanofibers for Regenerative Medicine. Adv. Healthcare Mater. 2012a;1:10–25. doi: 10.1002/adhm.201100021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Yeh YC, Lipner J, Xie J, Sung HW, Thomopoulos S, Xia Y. Enhancing the Stiffness of Electrospun Nanofiber Scaffolds with a Controlled Surface Coating and Mineralization. Langmuir. 2011a:9088–9093. doi: 10.1021/la2018105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Birman V, Chen C, Thomopoulos S, Genin GM. Mechanisms of Bimaterial Attachment at the Interface of Tendon to Bone. J. Eng. Mater-T ASME. 2011b;133:011006–011008. doi: 10.1115/1.4002641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Thomopoulos S, Birman V, Li JS, Genin GM. Bi-material attachment through a compliant interfacial system at the tendon-to-bone insertion site. Mech. Mater. 2012b;44:83–92. doi: 10.1016/j.mechmat.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Thomopoulos S, Chen C, Birman V, Buehler MJ, Genin GM. Modelling the mechanics of partially mineralized collagen fibrils, fibres and tissue. J. R. Soc. Interface. 2014;11:20130835. doi: 10.1098/rsif.2013.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maganaris CN, Paul JP. In vivo human tendon mechanical properties. J. Physiol. 1999;521:307–313. doi: 10.1111/j.1469-7793.1999.00307.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquez JP, Elson EL, Genin GM. Whole cell mechanics of contractile fibroblasts: relations between effective cellular and extracellular matrix moduli. Philos. Transact. A Math. Phys. Eng. Sci. 2010;368:635–654. doi: 10.1098/rsta.2009.0240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milton GW. The Theory of Composites. Cambridge: Cambridge University Press; 2002. [Google Scholar]
- Miserez A, Schneberk T, Sun C, Zok FW, Waite JH. The Transition from Stiff to Compliant Materials in Squid Beaks. Science. 2008;319:1816–1819. doi: 10.1126/science.1154117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy WL, Hsiong S, Richardson TP, Simmons CA, Mooney DJ. Effects of a bone-like mineral film on phenotype of adult human mesenchymal stem cells in vitro. Biomaterials. 2005;26:303–310. doi: 10.1016/j.biomaterials.2004.02.034. [DOI] [PubMed] [Google Scholar]
- Phillips JE, Burns KL, Le Doux JM, Guldberg RE, García AJ. Engineering graded tissue interfaces. P. Natl. Acad. Sci. USA. 2008;105:12170–12175. doi: 10.1073/pnas.0801988105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollock CM, Shadwick RE. Relationship between body mass and biomechanical properties of limb tendons in adult mammals. Am. J. Physiol. 1994;266:R1016–R1021. doi: 10.1152/ajpregu.1994.266.3.R1016. [DOI] [PubMed] [Google Scholar]
- Qu X, Cui W, Yang F, Min C, Shen H, Bei J, Wang S. The effect of oxygen plasma pretreatment and incubation in modified simulated body fluids on the formation of bonelike apatite on poly(lactide-co-glycolide) (70/30) Biomaterials. 2007;28:9–18. doi: 10.1016/j.biomaterials.2006.08.024. [DOI] [PubMed] [Google Scholar]
- Roberts WL, Rapp GRJ, Weber J. Encyclopedia of minerals. 1974 [Google Scholar]
- Rogel MR, Qiu H, Ameer GA. The role of nanocomposites in bone regeneration. J. Mater. Chem. 2008;18:4233–4241. [Google Scholar]
- Schwartz AG, Pasteris JD, Genin GM, Daulton TL, Thomopoulos S. Mineral Distributions at the Developing Tendon Enthesis. PLoS ONE. 2012;7:e48630. doi: 10.1371/journal.pone.0048630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz D. Bootstrapped 95% Confidence Ellipse. Math Forums. 1998 [Google Scholar]
- Takeuchi A, Ohtsuki C, Miyazaki T, Tanaka H, Yamazaki M, Tanihara M. Deposition of bone-like apatite on silk fiber in a solution that mimics extracellular fluid. J. Biomed. Mater. Res. A. 2003;65A:283–289. doi: 10.1002/jbm.a.10456. [DOI] [PubMed] [Google Scholar]
- Tas AC, Bhaduri SB. Rapid coating of Ti6Al4V at room temperature with a calcium phosphate solution similar to 10× simulated body fluid. J. Mater. Res. 2004;19:2742–2749. [Google Scholar]
- Thomopoulos S, Williams GR, Gimbel JA, Favata M, Soslowsky LJ. Variation of biomechanical, structural, and compositional properties along the tendon to bone insertion site. J. Orthop. Res. 2003a;21:413–419. doi: 10.1016/S0736-0266(03)00057-3. [DOI] [PubMed] [Google Scholar]
- Thomopoulos S, Williams GR, Soslowsky LJ. Tendon to Bone Healing: Differences in Biomechanical, Structural, and Compositional Properties Due to a Range of Activity Levels. J. Biomech. Eng. 2003b;125:106–113. doi: 10.1115/1.1536660. [DOI] [PubMed] [Google Scholar]
- Thurner PJ, Erickson B, Jungmann R, Schriock Z, Weaver JC, Fantner GE, Schitter G, Morse DE, Hansma PK. High-speed photography of compressed human trabecular bone correlates whitening to microscopic damage. Eng. Fract. Mech. 2007;74:1928–1941. [Google Scholar]
- Torquato S. Random Heterogeneous Materials. Springer; 2001. [Google Scholar]
- Wang X, Wenk E, Zhang X, Meinel L, Vunjak-Novakovic G, Kaplan DL. Growth factor gradients via microsphere delivery in biopolymer scaffolds for osteochondral tissue engineering. J. Control. Release. 2009;134:81–90. doi: 10.1016/j.jconrel.2008.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XH, Li DP, Wang WJ, Feng QL, Cui FZ, Xu YX, Song XH. Covalent immobilization of chitosan and heparin on PLGA surface. Int. J. Biol. Macromol. 2003;33:95–100. doi: 10.1016/s0141-8130(03)00072-2. [DOI] [PubMed] [Google Scholar]
- Wopenka B, Pasteris JD. A mineralogical perspective on the apatite in bone. Mater. Sci. Eng. C. 2005;25:131–143. [Google Scholar]
- Zhu A, Zhang M, Wu J, Shen J. Covalent immobilization of chitosan/heparin complex with a photosensitive hetero-bifunctional crosslinking reagent on PLA surface. Biomaterials. 2002;23:4657–4665. doi: 10.1016/s0142-9612(02)00215-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.