Estimation of GFR in South Asians: A Study From the General Population in Pakistan

Abstract

Background

South Asians are at high risk for chronic kidney disease. However, unlike those in the United States and United Kingdom, laboratories in South Asian countries do not routinely report estimated glomerular filtration rate (eGFR) when serum creatinine is measured. The objectives of the study were to: (1) evaluate the performance of existing GFR estimating equations in South Asians, and (2) modify the existing equations or develop a new equation for use in this population.

Study Design

Cross-sectional population-based study.

Setting & Participants

581 participants 40 years or older were enrolled from 10 randomly selected communities and renal clinics in Karachi.

Predictors

eGFR, age, sex, serum creatinine level.

Outcomes

Bias (the median difference between measured GFR [mGFR] and eGFR), precision (the IQR of the difference), accuracy (P₃₀; percentage of participants with eGFR within 30% of mGFR), and the root mean squared error reported as cross-validated estimates along with bootstrapped 95% CIs based on 1,000 replications.

Results

The CKD-EPI (Chronic Kidney Disease Epidemiology Collaboration) creatinine equation performed better than the MDRD (Modification of Diet in Renal Disease) Study equation in terms of greater accuracy at P₃₀ (76.1% [95% CI, 72.7%–79.5%] vs 68.0% [95% CI, 64.3%–71.7%]; P <0.001) and improved precision (IQR, 22.6 [95% CI, 19.9–25.3] vs 28.6 [95% CI, 25.8–31.5] mL/min/1.73 m²; P < 0.001). However, both equations overestimated mGFR. Applying modification factors for slope and intercept to the CKD-EPI equation to create a CKD-EPI Pakistan equation (such that eGFR_CKD-EPI(PK) = 0.686 × eGFR_CKD-EPI^1.059) in order to eliminate bias improved accuracy (P₃₀, 81.6% [95% CI, 78.4%–84.8%]; P < 0.001) comparably to new estimating equations developed using creatinine level and additional variables.

Limitations

Lack of external validation data set and few participants with low GFR.

Conclusions

The CKD-EPI creatinine equation is more accurate and precise than the MDRD Study equation in estimating GFR in a South Asian population in Karachi. The CKD-EPI Pakistan equation further improves the performance of the CKD-EPI equation in South Asians and could be used for eGFR reporting.

Chronic kidney disease (CKD) is now recognized as a global public health challenge.¹ The adverse outcomes of CKD, including kidney failure, accelerated cardiovascular disease, and premature mortality, have a profound impact on the national economies of low- and middle-income countries.² The problem is magnified further in the South Asian populations of India, Pakistan, Bangladesh, and Sri Lanka, where risk factors for CKD, including hypertension and diabetes, are widely prevalent and increasing.^3–5

Clinical assessment of kidney function is a routine part of medical practice for overall health evaluation, drug dosing, and administration of intravenous contrast for diagnostic testing and therapeutic procedures.⁶ Glomerular filtration rate (GFR) is widely regarded as the best indicator of kidney function in both health and disease. GFR can be assessed best by measuring urinary clearance of an ideal exogenous marker like inulin. However, measuring GFR is costly, time consuming, and difficult to do. Thus, GFR estimating equations based on serum creatinine level, age, sex, and body size have been developed and are recommended for routine use in clinical practice.

In the United States and United Kingdom, estimated GFR (eGFR) is reported by >75% of clinical laboratories when serum creatinine is measured, using either the isotope-dilution mass spectrometry (IDMS)-traceable 4-variable MDRD (Modification of Diet in Renal Disease) Study equation or the more recently developed CKD-EPI (CKD Epidemiology Collaboration) creatinine equation.^7–12 A recent systematic review showed that this CKD-EPI equation was more accurate in estimating measured GFR (mGFR) than the MDRD Study equation, and a recent meta-analysis showed that GFR estimates based on the CKD-EPI equation more accurately predict the risk of progression to kidney failure and mortality than those based on the MDRD Study equation.^13,14 Clinical laboratories in South Asian countries do not routinely report eGFR, in part because both muscle mass and meat intake are lower in South Asian populations compared with North American and European populations, which might lead to inaccuracy of eGFR, and neither of these equations has been validated in South Asian general populations.¹⁵ Therefore, we performed a cross-sectional population-based study of adults 40 years and older in Karachi, Pakistan, to: (1) evaluate the accuracy of existing creatinine-based GFR estimating equations in this South Asian population, and (2) improve the accuracy of GFR estimation by modifying existing GFR estimating equations or developing a new equation for use in the South Asian population.

METHODS

Study Design and Participants

Participants were drawn from 2 sources. The first was a population-based sample from 10 randomly selected low- to middle-income communities in Karachi. Because the general population was expected to have few people with decreased kidney function, we enriched our sample with 40 patients with a serum creatinine level ≥2.0 mg/dL from the renal clinic (Fig S1, available as online supplementary material), so that 20% of our study sample would have a GFR <60 mL/min/1.73 m² (ie, CKD stage 3 or worse). The details regarding recruitment and stratification have been published previously.¹⁶ The Aga Khan University Ethics Review Committee approved the study.

Screening Visit and Visit to Research Laboratory

All participants attended the research clinic in the morning after an overnight fast with a single 24-hour urine collection. Details of assessment have been published.¹⁶

Laboratory Measurements

As previously described, blood samples were collected for measurement of serum creatinine (Jaffé kinetic rate reaction method with alkaline picrate solution with SynchronCX7 Delta analyzer [Beckman Coulter Inc]), hemoglobin, fasting blood glucose, serum albumin, and serum urea nitrogen. Urine was collected for 24 hours for measurement of urine creatinine, albumin, and urea nitrogen.¹⁶ All assessments were performed to a standard protocol that conformed to international standards for definitions, and measurements and external quality control were performed by the Bio-Rad Laboratories Inc, Irvine, CA.

Calibration of Serum Creatinine Assays

Serum creatinine assays were calibrated to the Roche enzymatic method (Roche-Hitachi P-Module instrument with Roche Creatininase Plus assay; Hoffman-La Roche Ltd), traceable to National Institute of Standards and Technology (NIST) creatinine standard reference material 967 at the Cleveland Clinic.¹⁷ The values from Pakistan were higher than the Roche enzymatic method at the Cleveland Clinic by a mean of 0.21 (standard error, 0.01) mg/dL and hence a calibration factor [(−0.1256) + 0.9557×] based on a significant intercept and slope was derived (Fig S2).

GFR Measurement

GFR was measured (mGFR) using urinary clearance of inulin as the reference standard.¹⁶ A loading dose of 30 mg/kg of Inutest 25% (Fresenius Kabi, Austria) was given, followed by a continuous infusion of 40 mg/kg of inulin diluted in a 10% mannitol solution. Two clearance periods of 30 minutes each were analyzed after an equilibration period of 45 minutes. If urine flow rate differed by 30 mL between the 2 periods, a third 30-minute clearance was performed. Inulin in plasma and urine samples was assayed using an enzymatic method at the Renal Laboratories, Saint-Etienne Hospital, University of Jean Monnet, Saint-Etienne, France. GFR was measured as the mean of at least 2 urinary clearance periods of inulin and expressed per 1.73 m² of body surface area (BSA) by multiplying measured values by 1.73/BSA (BSA =height^0.725[cm] × body weight^0.425[kg] × 0.007184). mGFR adjusted for BSA served as the gold standard for comparison.

Statistical Analysis

Analyses were performed using Stata Statistical Software, release 12.1 (StataCorp LP). Baseline characteristics of the study population were presented as overall and compared across the 3 categories of mGFR (ie, ≥90, 60–89, and <60 mL/min/1.73 m²). Mean values and proportions were compared using one-way analysis of variance and χ² tests, respectively, whereas the median eGFRs for the MDRD Study and CKD-EPI equations were compared using the Kruskal-Wallis test. Performance of the MDRD Study and CKD-EPI equations was assessed for the entire data set of 581 participants. Using the performance metrics, the correction factors for modification of the CKD-EPI equation were derived, new estimating equations were developed, and their performance was assessed.

Modification of the CKD-EPI Equation

Correction factors for the CKD-EPI equation were derived from the linear regression models of ln(mGFR) versus ln(eGFR) calculated by the CKD-EPI equation. The statistically significant (P <0.05) intercept and slopes were back transformed to exponential form and used as correction factors to modify the equation to the CKD-EPI Pakistan equation, referred to here as CKD-EPI_PK (eGFRs calculated with this equation denoted as eGFR_CKD-EPI(PK)).

Development of New Estimating Equations

We developed new GFR estimating equations based on this Pakistani population to assess whether their performance was substantially better than the existing or modified equations. Because a 2-slope spline for serum creatinine cannot be assessed in the same model as linear or other functions of linear terms of the same variable, 2 regression models were built. Each equation was developed using stepwise linear regression to relate mGFR to serum creatinine level and clinical characteristics available in the data set with forward selection using an entry and removal criteria of P = 0.05 and P = 0.20, respectively. We transformed mGFR and serum creatinine level to the natural logarithmic scale to reflect their multiplicative (inverse) relationship and stabilize variance across the range of GFRs. For the first model, spline terms of the natural logarithm of serum creatinine were used. For the second model, we used a linear term for the natural logarithm of serum creatinine along with quadratic and cubic terms as the main predictors. Details of these models are presented in Item S1. Other covariates for both models were age, sex, body mass index (BMI), waist circumference, total body fat, hemoglobin level, serum albumin level, serum urea nitrogen level, fasting blood glucose level, blood pressure, hypertension, and diabetes status. All continuous variables were used in their natural (untransformed) form.

Metrics for Equation Performance

The metrics for comparison of estimation equations with mGFR were bias, precision, root mean squared error (RMSE), and accuracy with 95% confidence intervals (CIs). Bias was expressed as the median of the differences between mGFR and eGFR (ie, mGFR − eGFR), with negative values indicating overestimation of GFR. Precision was expressed as the inter-quartile range (IQR) of the differences of mGFR and eGFR. RMSE was defined as the square root of the average squared difference of mGFR and eGFR. Accuracy (P₂₀ and P₃₀) was defined as the percentage of individuals with eGFRs within 20% and 30% of mGFR, respectively. The CIs for all these estimates were computed with normal approximation by the bootstrap method based on 1,000 replications with predefined seed. P values for assessing differences in RMSE, and IQR, of various GFR estimating equations were computed by paired t test on 1,000 bootstrapped estimates, whereas P values for P₂₀ and P₃₀ were computed by McNemar test on the observed data. The differences between estimates of various estimating equations were considered statistically significant when 95% CIs were nonoverlapping or P values were <0.05, and substantially different when both criteria were met.

We also compared eGFR and mGFR for each participant graphically by plotting the bias (mGFR − eGFR) against eGFR to assess the performance of each equation. The smoothed regression lines were plotted using 95% of the data and the 95% CIs were based on the quantile regressions of the 10th and 90th percentiles of the bias.

Cross-validation of Modified and New Equations

We bootstrapped 500 samples with replacement from the original data (N = 581) to internally validate the modified CKD-EPI equation and new estimating equations developed in this data set.^18,19 Based on the method described by Harrell et al,²⁰ estimates and 95% CIs were validated by adding or subtracting the optimism indexes calculated as the differences of estimates drawn from the equations developed on bootstrapped samples and after applying those on the original data set. Details of cross-validation are given in Item S1 and tables a-d of Item S2. The comparison of performance was done in the overall study population, as well as in participants with eGFR_CKD-EPI(PK) ≥90 and <90 mL/min/1.73 m².

Comparison of Modified and Newly Developed Estimating Equations by Subgroups

In order to assess generalizability among various subgroups, we evaluated the modified CKD-EPI (CKD-EPI_PK) and the new estimating equations in subgroups defined by clinical characteristics, including the presence or absence of hypertension or/ and diabetes, as well as factors related to muscle mass and diet, including BMI (<18.5, 18.5–24.9, 25.0–29.9, and ≥30.0 kg/m²) and tertiles of urine creatinine and urine urea nitrogen excretion.^14,15

RESULTS

Participant Characteristics

Characteristics of the study population are described in Table 1. Of 581 enrolled participants, 50% were men. Median mGFR, eGFR_MDRD, and creatinine-based eGFR_CKD-EPI values were 91.0 (IQR, 36.7), 100.5 (IQR, 40.4), and 104.4 (IQR, 25.4) mL/min/1.73 m², respectively. Participants with mGFR <60 mL/min/ 1.73 m² were older than those with higher mGFRs (P <0.001) and had greater waist circumference (P = 0.02), lower lean body mass (P = 0.007), lower hemoglobin level (P <0.001), and higher systolic blood pressure (P = 0.001) compared with those with higher mGFRs.

Table 1.

Characteristics of Study Participants

Characteristics	Overall (N = 581)	mGFR (mL/min/1.73 m2)			Pa
		≥90 (n = 300)	60–89 (n = 188)	<60 (n = 93)
Age (y)	50.6 ± 10.0	47.2 ± 7.2	51.8 ± 10.3	59.0 ± 11.7	<0.001
Male sex	292 (50.3)	144 (48.0)	100 (53.2)	48 (51.6)	0.5
Clinical status					<0.001
Hypertension onlyb	197 (33.9)	99 (33.0)	69 (36.7)	29 (31.2)
Diabetes onlyc	163 (28.1)	99 (33.0)	42 (22.3)	22 (23.7)
Both	33 (5.7)	9 (3.0)	3 (1.6)	21 (22.6)
Neither	188 (32.4)	93 (31.0)	74 (39.4)	21 (22.6)
Weight (kg)	66.1 ± 13.2	66.9 ± 12.4	65.0 ± 13.6	66.0 ± 14.9	0.3
Height (cm)	159.7 ± 9.1	159.8 ± 8.7	159.9 ± 9.8	158.7 ± 8.8	0.6
Body surface area (m2)	1.7 ± 0.2	1.7 ± 0.2	1.7 ± 0.2	1.7 ± 0.2	0.4
Body mass index (kg/m2)	26.0 ± 5.1	26.2 ± 4.9	25.4 ± 4.8	26.2 ± 6.0	0.2
Waist circumference (cm)	93.3 ± 11.7	93.0 ± 10.7	92.4 ± 11.8	96.3 ± 14.1	0.02
Total body fat (%)	34.8 ± 9.1	34.2 ± 8.9	34.8 ± 9.0	36.6 ± 10.2	0.08
Lean body mass (%)	65.0 ± 9.4	65.8 ± 8.9	65.2 ± 9.0	62.3 ± 11.5	0.007
Systolic BP (mm Hg)	130 ± 21	127 ± 19	131 ± 23	136 ± 22	0.001
Diastolic BP (mm Hg)	81 ± 12	81 ± 11	80 ± 12	79 ± 13	0.3
Hemoglobin (g/dL)	12.5 ± 1.8	12.7 ± 1.8	12.6 ± 1.8	11.6 ± 1.8	<0.001
Serum albumin (g/dL)	3.7 ± 0.3	3.7 ± 0.3	3.7 ± 0.3	3.5 ± 0.4	<0.001
Fasting plasma glucose (mg/dL)	127 ± 65.2	136.8 ± 71.8	115.2 ± 50.1	119.1 ± 65.6	0.001
Urine creatinine (g/d)	1.0 ± 2.8	1.2 ± 3.9	0.9 ± 0.4	0.8 ± 0.3	0.4
Urine creatinine (mg/kg/d)d	13.9 ± 5.0	14.4 ± 5.1	14.1 ± 5	11.9 ± 4.1	<0.001
Urine urea nitrogen (g/d)d	5.1 ± 3.1	5.3 ± 2.5	4.8 ± 2.3	4.9 ± 5.6	0.3
24-h urine volume (L/d)	1.4 ± 0.6	1.5 ± 0.6	1.3 ± 0.5	1.5 ± 0.6	0.01
Serum creatinine (mg/dL)e	0.9 ± 0.7	0.7 ± 0.2	0.8 ± 0.2	2.0 ± 1.4	<0.001
Serum urea nitrogen (mg/dL)	13.3 ± 10.1	10.3 ± 3.7	11.5 ± 3.9	26.6 ± 18.6	<0.001
mGFR (mL/min/1.73 m2)	91.0 [36.7]	109.5 [24.5]	80.8 [12.5]	34.6 [32.0]	—
eGFRMDRD (mL/min/1.73 m2)	100.5 [40.4]	114.3 [25.3]	93.4 [31.7]	43.8 [47.5]	<0.001
eGFRCKD-EPI (mL/min/1.73 m2)	104.4 [25.4]	110.2 [14.8]	97.9 [23.8]	45.0 [54.0]	<0.001

Note: Values for categorical variables are given as number (percentage); values for continuous variables are given as mean ± standard deviation or median [interquartile range]. Conversion factors for units: serum creatinine in mg/dL to μmol/L, ×88.4; serum urea nitrogen in mg/dL to mmol/L, ×0.357; fasting plasma glucose in mg/dL to mmol/L, ×0.05551; urine creatinine in g/d to mmol/d, ×8.84; urine urea nitrogen in g/d to mmol/d, ×35.7.

Abbreviations: BP, blood pressure; eGFR, glomerular filtration rate; eGFR_CKD-EPI, eGFR calculated by Chronic Kidney Disease Epidemiology Collaboration creatinine equation; eGFR_MDRD, eGFR calculated by Modification of Diet in Renal Disease Study equation; mGFR, measured glomerular filtration rate.

^aP for differences across mGFR categories.

^bHypertension defined as systolic BP ≥ 140 or diastolic BP ≥ 90 mm Hg or receiving antihypertensive medications.

^cDiabetes defined as fasting blood glucose ≥126 mg/dL or receiving antidiabetic medications.

^dThree missing values (n = 578).

^eLocal serum creatinine assays were calibrated to isotope-dilution mass spectrometry at the Cleveland Clinic Research Laboratory for using Roche enzymatic method: y = [−0.1256 + (0.9557×)]; where y = standardized serum creatinine and x = local serum creatinine.

CKD-EPI_PK and New Estimating Equations

Table 2 lists coefficients for the modified and newly developed equations. The regression of ln(mGFR) on ln(eGFR) computed using the CKD-EPI equation had intercept of −0.376 and slope of 1.059, both significantly different from 0 and 1, respectively (P <0.001). Therefore, the “Pakistani correction factor” for the CKD-EPI equation can be rendered as eGFR_CKD-EPI(PK) = 0.686 × eGFR_CKD-EPI^1.059.

Table 2.

Regression Coefficients for CKD-EPI_PK and New GFR Estimating Equations Developed in a Pakistani Population

Variables	CKD-EPIPK	New Estimating Equation 1	New Estimating Equation 2
Constant	0.686 (0.560 to 0.841)	114.6 (87.0 to 150.9)	97.0 (73.0 to 128.8)
CKD-EPI equation	1.059 (1.014 to 1.104)	—	—
Age (y)	—	0.992 (0.990 to 0.994)	0.992 (0.99 to 0.994)
Sex	—	0.902 (0.852 to 0.955)	0.741 (0.694 to 0.791)
Body mass index (kg/m2)	—	1.015 (1.007 to 1.022)	1.015 (1.007 to 1.023)
Waist circumference (cm)	—	0.996 (0.993 to 1.000)	0.996 (0.993 to 1.000)
Hemoglobin (g/dL)	—	1.016 (1.002 to 1.031)	1.016 (1.001 to 1.031)
Fasting blood glucose (mg/dL)	—	1.001 (1.000 to 1.001)	1.001 (1.000 to 1.001)
Serum urea nitrogen (mg/dL)	—	0.994 (0.990 to 0.998)	0.993 (0.988 to 0.997)
Serum creatinine (mg/dL)a	—		−0.947 (−1.063 to −0.831)
If ≤0.83 (for male)a	—	−0.286 (−0.442 to −0.130)	—
If >0.83 (for male)a	—	−1.064 (−1.174 to −0.953)	—
If ≤0.64 (for female)a	—	−0.286 (−0.442 to −0.130)	—
If >0.64 (for female)a	—	−1.064 (−1.174 to −0.953)	—
(ln[SCr])2,b	—	—	0.762 (0.701 to 0.827)
(ln[SCr])3,c	—	—	1.154 (1.068 to 1.246)

Note: Values in parentheses are 95% confidence intervals.

Abbreviations: CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; CKD-EPI_PK, CKD-EPI equation with Pakistani correction factors; eGFR, estimated glomerular filtration rate; SCr, serum creatinine.

^aRegression coefficients in natural logarithm form whereas for all other variables, coefficients are transformed to exponential form.

^bSquare of ln(SCr).

^cCube of ln(SCr).

In addition, 2 new GFR estimating equations were developed based on this Pakistani population: equation 1 with a single sex-specific knot for serum creatinine level (for men, 0.83 mg/dL; and for women, 0.64 mg/dL), and equation 2 with the linear term of the natural logarithm of serum creatinine along with quadratic and cubic terms. Other statistically significant (P < 0.05) variables in both models were age, sex, BMI, waist circumference, hemoglobin level, fasting blood glucose level, and serum urea nitrogen level (Table 2).

Formulas for the existing MDRD Study and CKD-EPI equations, CKD-EPI_PK, and new estimating equations are reported in Box 1.

Box 1. Existing, Modified, and New GFR Estimating Equations.

Existing Equations

MDRD Study equation:

$$175\times {\mathit{SCr}}^{-1.154}\times {\mathit{Age}}^{-0.203}\times 0.742(\text{if}\text{female})$$

CKD-EPI equation:

$$\begin{array}{l}\text{If}\text{SCr}\le 0.9(\text{for}\text{male}):141\times {(\mathit{SCr}/0.9)}^{-0.411}\times {0.993}^{\mathit{Age}}\\ \text{If}\text{SCr}>0.9(\text{for}\text{male}):141\times {(\mathit{SCr}/0.9)}^{-1.209}\times {0.993}^{\mathit{Age}}\\ \text{If}\text{SCr}\le 0.7(\text{for}\text{female}):144\times {(\mathit{SCr}/0.7)}^{-0.329}\times {0.993}^{\mathit{Age}}\\ \text{If}\text{SCr}>0.7(\text{for}\text{female}):144\times {(\mathit{SCr}/0.7)}^{-1.209}\times {0.993}^{\mathit{Age}}\end{array}$$

Modified Equation

CKD-EPIPK equation:

$$0.686\times \text{CKD-}{\text{EPI}}^{1.059}$$

New Equations

Equation 1:

$$\begin{array}{l}\text{If}\text{SCr}\le 0.83(\text{for male}):114.6\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.994}^{\mathit{SUN}}\times {(\mathit{SCr}/0.83)}^{-0.286}\\ \text{If}\text{SCr}>0.83(\text{for male}):114.6\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.994}^{\mathit{SUN}}\times {(\mathit{SCr}/0.83)}^{-1.064}\\ \text{If}\text{SCr}\le 0.64(\text{for}\text{female}):114.6\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.994}^{\mathit{SUN}}\times {(\mathit{SCr}/0.64)}^{-0.286}\times 0.902\\ \text{If}\text{SCr}>0.64(\text{for female}):114.6\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.994}^{\mathit{SUN}}\times {(\mathit{SCr}/0.64)}^{-1.064}\times 0.902\end{array}$$

Equation 2:

$$\begin{array}{l}97.0\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.993}^{\mathit{SUN}}\times {\text{SCr}}^{-0.947}\times {0.762}^{{[ln\text{(SCr)}]}^2}\times {1.154}^{{[ln(\text{SCr})]}^3}\\ 97.0\times {0.992}^{\mathit{Age}}\times {1.015}^{\mathit{BMI}}\times {0.996}^{WC}\times {1.016}^{Hb}\times {1.001}^{\mathit{FBG}}\times {0.993}^{\mathit{SUN}}\times {\text{SCr}}^{-0.947}\times {0.762}^{{[ln(\text{SCr})]}^2}\times {1.154}^{{[ln(\text{SCr})]}^3}\times 0.741(\text{if}\text{female})\end{array}$$

Note: Modified and new estimating equations developed in a Pakistani population; see Methods.

Abbreviations: BMI, body mass index; CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration CKD-EPI_PK, CKD-EPI equation with Pakistani correction factors; FBG, fasting blood glucose; Hb, hemoglobin; MDRD, Modification of Diet in Renal Disease; SCr, serum creatinine; SUN, serum urea nitrogen; WC, waist circumference.

Comparison of Performance

Table 3 and Figs 1 and 2 compare the performance among equations.

Table 3.

Performance of GFR Estimating Equations

GFR Estimating Equation	RMSEa	Biasb	Precisionc	Accuracyd
				P20	P30
Overall Study Population (N = 581)
MDRD Study equation	0.295 (0.269 to 0.321)	−8.5 (−10.1 to −6.8)	28.6 (25.8 to 31.5)	54.7 (50.9 to 58.6)	68.0 (64.3 to 71.7)
CKD-EPI equation	0.265 (0.240 to 0.290)	−6.8 (−8.2 to −5.4)	22.6 (19.9 to 25.3)	57.8 (53.8 to 61.8)	76.1 (72.7 to 79.5)
CKD-EPIPK equation	0.265 (0.240 to 0.290)	NA	22.8 (20.3 to 25.2)	65.9 (62.1 to 69.7)	81.6 (78.4 to 84.8)
New estimating equation 1	0.259 (0.234 to 0.284)	NA	22.8 (20.6 to 25.0)	66.8 (62.9 to 70.7)	82.7 (79.8 to 85.7)
New estimating equation 2	0.263 (0.238 to 0.288)	NA	23.1 (20.4 to 25.7)	68.7 (65.0 to 72.4)	82.5 (79.4 to 85.5)
Participants With eGFRCKD-EPI(PK) ≥ 90 mL/min/1.73 m2(n= 300)
MDRD Study equation	0.247 (0.215 to 0.280)	−14.6 (−17.9 to −11.3)	35.2 (30.6 to 39.8)	51.0 (45.8 to 56.2)	64.8 (59.9 to 69.6)
CKD-EPI equation	0.246 (0.215 to 0.278)	−9.9 (−12.9 to −7.0)	26.6 (22.4 to 30.9)	59.0 (53.8 to 64.2)	77.9 (73.7 to 82.2)
CKD-EPIPK equation	0.226 (0.194 to 0.258)	NA	32.6 (28.7 to 36.5)	68.1 (63.0 to 73.2)	86.6 (82.5 to 90.6)
New estimating equation 1	0.218 (0.187 to 0.250)	NA	29.3 (25.6 to 33.0)	71.9 (66.9 to 76.9)	90.3 (86.8 to 93.9)
New estimating equation 2	0.221 (0.189 to 0.253)	NA	30.5 (26.5 to 34.5)	71.4 (66.5 to 76.3)	89.7 (86.1 to 93.4)
Participants With eGFRCKD-EPI(PK) < 90 mL/min/1.73 m2 (n = 281)
MDRD Study equation	0.304 (0.264 to 0.344)	−1.1 (−4.0 to 1.8)	18.4 (15.3 to 21.5)	60.3 (54.0 to 66.7)	72.8 (67.2 to 78.4)
CKD-EPI equation	0.291 (0.251 to 0.331)	−4.8 (−6.9 to −2.8)	16.8 (13.9 to 19.8)	56.0 (49.7 to 62.4)	73.3 (67.8 to 78.8)
CKD-EPIPK equation	0.316 (0.275 to 0.358)	NA	11.8 (9.1 to 14.5)	63.3 (57.2 to 69.3)	74.2 (69.1 to 79.4)
New estimating equation 1	0.307 (0.267 to 0.346)	NA	12.5 (9.5 to 15.6)	57.7 (51.7 to 63.6)	72.7 (67.6 to 77.8)
New estimating equation 2	0.302 (0.262 to 0.343)	NA	10.9 (7.8 to 14.1)	58.3 (52.2 to 64.4)	73.8 (68.7 to 79.0)

Note: Values in parentheses are 95% confidence intervals.

Abbreviations and definitions: CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; CKD-EPI_PK, CKD-EPI equation with Pakistani correction factors; GFR, glomerular filtration rate; MDRD, Modification of Diet in Renal Disease; mGFR, measured GFR; NA, not applicable, bias is expected to be zero; RMSE, root mean squared error.

^aSquare root of the average squared difference of mGFR and eGFR.

^bMedian of mGFR − eGFR, expressed in mL/min/1.73 m².

^cIQR of difference of mGFR and eGFR, expressed in mL/min/1.73 m².

^dAccuracy (P₂₀ and P₃₀) refers to percentages of participants with eGFRs within 20% and 30% of mGFR, respectively; the 95% CIs are based on bootstrapping by 1,000 replications.

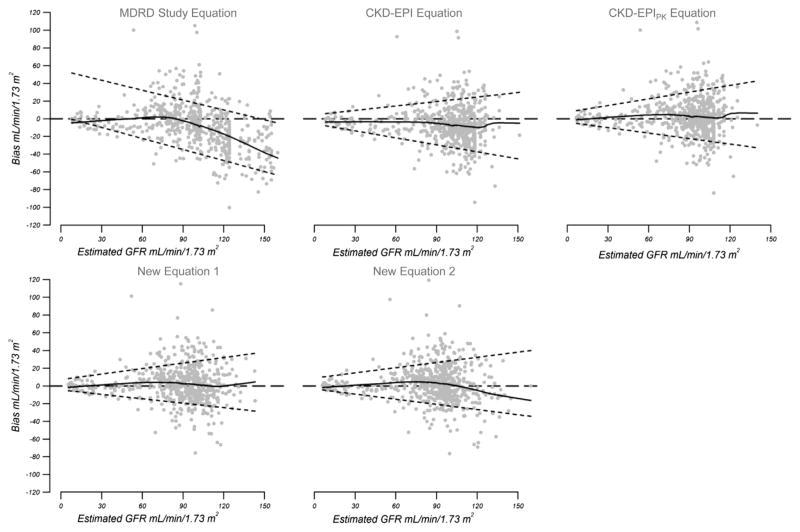
Figure 1.

Bias (measured glomerular filtration rate [GFR] − estimated GFR) by levels of estimated GFR. Solid curved lines indicate smoothed regression lines created using 95% of the data by smoothing function (LOWESS), short dashed lines are the quantile regressions of 10th and 90th percentiles of bias; and dashed horizontal lines represent a reference. Abbreviations: CKD-EPI, Chronic Kidney Disease Epidemiology Collaboration; CKD-EPI_PK, CKD-EPI equation with Pakistani correction factors; MDRD, Modification of Diet in Renal Disease.

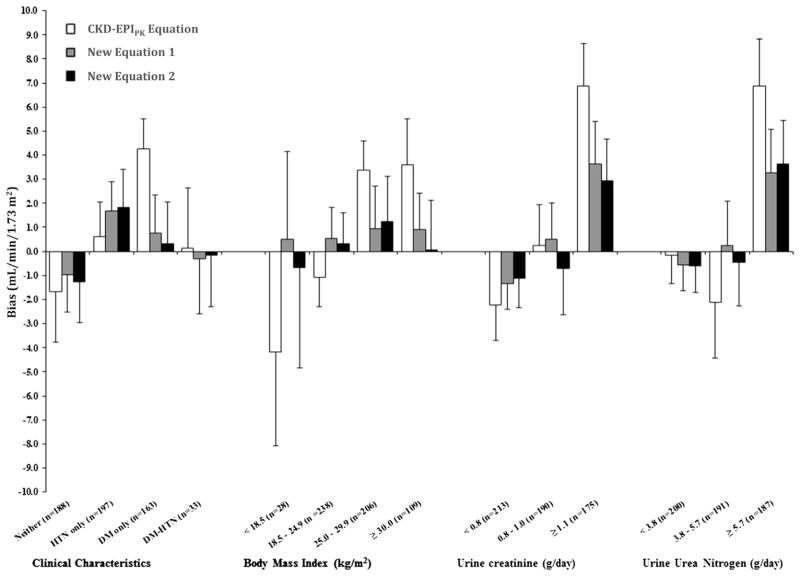
Figure 2.

Comparison of bias (measured glomerular filtration rate [GFR] − estimated GFR) for CKD-EPI_PK (CKD-EPI [Chronic Kidney Disease Epidemiology Collaboration] equation with Pakistani correction factors) equation and new estimating equations 1 and 2 among subgroups. Bars denote median bias, error bars represent standard error of median bias based on 1,000 bootstrapped samples. Bias values that are negative represent overestimation. Conversion factors for units: urine creatinine in g/d to mmol/d, ×8.84; urine urea nitrogen in g/d to mmol/d, ×35.7. Abbreviations and definitions: Neither, nonhypertensive nondiabetic; HTN only, hypertensive; DM only, diabetic; DM-HTN, diabetic and hypertensive.

CKD-EPI and MDRD Study Equations

The CKD-EPI creatinine equation had significantly greater accuracy (P_30, 76.1% [95% CI, 72.7%–79.5%]) and better precision (IQR, 22.6 [95% CI, 19.9–25.3] mL/min/1.73 m²; P < 0.001) compared to the MDRD Study equation (P_30, 68.0% [95% CI, 64.3%–71.7%; IQR, 28.6 [95% CI, 25.8–31.5] mL/ min/1.73 m²; Table 3). However, both equations overestimated mGFR; bias (ie, median mGFR− eGFR values) for the CKD-EPI and MDRD Study equations were −6.8 (95% CI, −8.2 to −5.4) and −8.5 (95% CI, −10.1 to −6.8) mL/min/1.73 m², respectively. Figure 1 shows less variation in bias across the range of eGFRs with the CKD-EPI equation versus MDRD Study equation.

Among participants with eGFR_CKD-EPI(PK) ≥ 90 mL/min/1.73 m², the performance of CKD-EPI was better than that of the MDRD Study equation, whereas in participants with eGFR_CKD-EPI(PK) <90 mL/min/ 1.73 m², there was no difference between them.

CKD-EPI_PK Equation

As expected, modification of the CKD-EPI equation with the Pakistan correction factor eliminated bias and there was no apparent variation across the range of eGFRs (Fig 1). Furthermore, accuracy improved; P₂₀ was 65.9% (95% CI, 62.1%–69.7%) versus 57.8% (95% CI, 53.8%–61.8%; P <0.001), and P₃₀ was 81.6% (95% CI, 78.4%–84.8%) versus 76.1% (95% CI, 72.7%–79.5%; P < 0.001), respectively, for the CKD-EPI_PK and CKD-EPI equations, respectively. Although the 95% CIs of P₃₀ were overlapping, the difference was statistically significant on the basis of P value (see Table 3 and Table S1 for P values).

Among participants with eGFR_CKD-EPI(PK) ≥ 90 mL/min/1.73 m², performance of the CKD-EPI_PK equation was better than the CKD-EPI equation itself (P₃₀, 86.6% [95% CI, 82.5%–90.6%] vs 77.9% [95% CI, 73.7%–82.2%], respectively), whereas in participants with eGFR_CKD-EPI(PK) <90 mL/min/1.73 m², there was no difference between them.

New Estimating Equations

Although both new estimating equations developed in this Pakistani population (equations 1 and 2) had significantly better P₂₀ and P₃₀ accuracy compared to the original CKD-EPI equation (P < 0.001 for each estimate), their performance was comparable to that of the CKD-EPI_PK equation in terms of all parameters with overlapping 95% CIs (RMSE, precision [IQR], and accuracy [P₂₀ and P₃₀]) across the range of eGFRs (ie, overall, as well as eGFR_CKD-EPI(PK) ≥ 90 and <90 mL/min/1.73 m²; see Table 3 and Table S1 for P values). The new estimating equation 2 appeared to overestimate at higher GFRs compared to equation 1 (Fig 1).

Figure 2 compares bias among the CKD-EPI_PK equation and the new estimating equations in subgroups by hypertension and diabetes status and for different ranges of BMI, urine creatinine excretion, and urea nitrogen excretion. Although the new estimating equations appeared to have slightly lower bias compared to the CKD-EPI_PK equation, all 3 equations over- or underestimated GFR to some extent according to participant characteristics, and this was more pronounced in individuals with low BMI and obesity, diabetes, high urine creatinine excretion, and high urine urea nitrogen excretion.

DISCUSSION

The new KDIGO CKD guideline recommends using the CKD-EPI creatinine equation to report eGFR unless an alternative equation has been shown to be more accurate in the local population.²¹ This is the first report of the performance of existing GFR estimating equations in the general population from a South Asian country using a directly measured GFR method as a reference. Using urinary inulin clearance as the gold standard, we found that the CKD-EPI creatinine equation is significantly more accurate and more precise compared to the MDRD Study equation in this largely unselected South Asian population in Karachi, Pakistan. However, both equations overestimated mGFR at the high levels observed in this population. The Pakistan correction factors in the CKD-EPI_PK equation reduced bias and improved accuracy in estimating GFR compared to the original equation in the overall population, mainly due to improvement in individuals with eGFR_CKD-EPI(PK) ≥90 mL/min/ 1.73 m². Performance of the CKD-EPI_PK equation was comparable to that of the new estimating equations developed in this Pakistani population, which did not offer substantial advantage and required using additional variables that are not routinely collected by clinical laboratories. Our findings have potentially significant implications for clinical practice and public health policy in South Asians.

The better performance of the CKD-EPI equation versus the MDRD Study equation in South Asians in Pakistan is consistent with observations in whites²² and Southeast Asian populations.^14,23–25 However, the correction factor in our study accounted for both the slope and the intercept in the regression analysis and therefore had 2 terms (0.686 × eGFR_CKD-EPI^1.059) instead of the single terms proposed for correcting the MDRD Study or CKD-EPI equations in Japanese and Chinese individuals.^23,26,27 Nevertheless, the terms potentially are readily programmable in the equations for automated reporting of eGFR. The new estimating equations described here include terms for individual characteristics (eg, BMI and waist circumference) not included in the CKD-EPI or MDRD Study equations, which would be more difficult for clinical laboratories implementing automatic eGFR reporting.

Compared to the original CKD-EPI creatinine equation, the improvements in accuracy for the CKD-EPI_PK equation and the new estimating equations were significant; however, some variations in their performance remained across categories of BMI, urine excretion of creatinine, and urea nitrogen, and the variations were more apparent at the extremes (Fig 2). This is consistent with the expectation that difference in muscle mass and diet affect serum creatinine concentration independently of GFR. These findings support the contention that no creatinine-based equation will perform equally well across the full spectrum of clinical characteristics observed in any clinical population.¹⁴

The main strength of this study was its community-based (door-to-door) sampling frame, which is representative of the general population. These equations previously have been evaluated predominantly in patients with CKD or kidney donors. Thus, our findings would be generalizable to the general population. Moreover, we recruited additional participants from the clinic so our results also apply to South Asian patients with advanced CKD. Second, this is the first evaluation of estimation equations from a South Asian country. Furthermore, we used optimal approaches to measure GFR (inulin clearance), urinary inulin clearance as the gold-standard GFR reference method, standardized serum creatinine assays (traceable to the IDMS procedure), and the unbiased cross-validated estimates based on 500 bootstrapped samples. Furthermore, the significance of comparison metrics relied on 1,000 bootstrapped replications for 95% CIs and parametric tests for pairwise comparisons. Finally, the performance of the CKD-EPI creatinine equation in our study generally is consistent with the observations in other populations^24,25,28,29 (Table S2). Thus, we have confidence in the accuracy of our GFR estimating equation and believe it can be generalized to the general population for estimating GFR in health screening programs and epidemiologic studies in Pakistan and possibly other South Asian countries.

Our study has limitations. The MDRD Study and CKD-EPI equations were developed using iothalamate clearance to measure GFR, whereas we used urinary clearance of inulin in our study; thus, some of the differences in bias may be due to GFR measurement method.^30,31 Second, there was no external validation data set. However, cross-validation using bootstrapping is recommended as a method for obtaining unbiased results.^18–20 Moreover, this limitation would not apply to our finding that the original CKD-EPI equation outperformed the original MDRD Study equation. Third, the few participants with low GFR limited evaluation of performance in participants with various stages of advanced CKD. However, the main objective of the study was to test the application of the GFR estimating equations in the general population from Karachi, Pakistan, which we were able to achieve. Last, urine samples for inulin clearance were collected by spontaneous voiding and not by catheterization. Thus, incomplete bladder emptying is a potential source of measurement bias. However, use of a mean of 2 inulin clearance periods and a mean of 3 periods in case the difference in volume was > 30 mL would minimize this limitation.

The Pakistan coefficient will need to be tested in other South Asian populations to assess whether this equation can serve as a common correction factor for wider application of the CKD-EPI creatinine equation across South Asia and whether it also enhances prediction of risk of progression to kidney failure, onset of cardiovascular disease, and mortality better than the original CKD-EPI equation in this population.¹³ Such information relating estimates closer to mGFR with outcomes will enable evaluation of the clinical utility and efficiency of the CKD-EPI_PK equation in Pakistan. At the same time, it is also important to emphasize that with overall accuracy of 82%, this CKD-EPI_PK equation has substantial room for further improvement in GFR estimation, especially in those with low GFRs. One possibility involves the addition to the equation of other filtration markers, including the combination of creatinine and cystatin C, which has been shown to perform better and is recommended as a confirmatory test in the subgroup of patients of European origin with low GFRs.³²

In conclusion, our findings suggest that modification of the CKD-EPI equation with a Pakistan correction factor is the most accurate and practicable creatinine-based GFR estimating equation for the South Asian population, at least in Pakistan. The performance of new estimating equations that were developed in this Pakistani population and that incorporate creatinine and additional variables was comparable to that of the CKD-EPI_PK equation. The need for efficient decision making in clinical practice and public health policy requires implementation of eGFR reporting with a single equation across a wide region. Our results suggest that CKD-EPI_PK, the CKD-EPI equation modified for Pakistan, would be the most valid and easy to implement in South Asia. We suggest that these findings be shared with clinical laboratories in Pakistan and neighboring countries to facilitate reporting of eGFR when serum creatinine is measured. These efforts ultimately may translate into better management and improved patient outcomes.