Finite Element Analysis of Patient-Specific Condyle Fracture Plates: A Preliminary Study

Abstract

Various patterns of internal fixation of mandibular condyle fractures have been proposed in the literature. This study investigates the stability of two patient-specific implants (PSIs) for the open reduction and internal fixation of a subcondylar fracture of the mandible. A subcondylar fracture of a mandible was simulated by a series of finite element models. These models contained approximately 1.2 million elements, were heterogeneous in bone material properties, and also modeled the muscles of mastication. Models were run assuming linear elasticity and isotropic material properties for bone. The stability and von Mises stresses of the simulated condylar fracture reduced with each of the PSIs were compared. The most stable of the plate configurations examined was PSI 1, which had comparable mechanical performance to a single 2.0 mm straight four-hole plate.

Fractures of the mandibular subcondylar area are common.^{1 2} Although the techniques of open reduction and internal fixation (ORIF) for most fractures of the facial skeleton are widely accepted as best practice, the discussion over the optimal management of mandibular subcondylar fractures persists.^{3 4 5 6} Upon electing to treat mandibular subcondylar fractures by ORIF, the surgeon must then make a reasoned decision on the type of implant to be used to reduce the fracture.^{1 3 7 8 9 10 11 12} The most stable fracture reduction is achieved by using the largest plate possible; however, due to anatomical and clinical restraints, it is desirable to minimize the size of any implant placed. Thus, there are two opposing influences in the design of bone plates with the optimal design balancing the need to minimize the degree of surgical insult by using small plates, with the requirement to bestow sufficient stability to permit fracture healing to occur. Patient-specific implants (PSIs) have theoretical and practical advantages including a superior fit compared with generic implants, reduced operating time due to decreased need to manually manipulate plates to fit the reduced fracture, and the ability to more readily achieve precise anatomical bone alignment.^{13 14} The addition of finite element analysis (FEA) to existing techniques of computer-aided surgery confers the ability to manipulate and compare several possible designs to determine which one yields the most stable reduction before implant manufacture and placement. With advances in computer-aided design and printing technologies allowing the rapid three-dimensional (3D) printing of titanium objects, it may be feasible in the near future to routinely design and manufacture PSI in a cost and time effective manner.

Engineers routinely use the computational technique of FEA to simulate the mechanical performance of structures including engine parts, buildings, and aircraft, and the application of FEA to research questions in medicine and biology is escalating.^{1 15 16 17} The use of FEA is particularly apt when objects have complicated geometries, intricate loading patterns, and multiple material properties. The technique of FEA has been summarized previously¹; however, in brief, it simplifies a complex continuous structure by treating it as a finite number of elements in which each element is described by an algebraic equation that describes each elements behavior. Factors influencing the accuracy of a finite element method (FEM) prediction include the complexity and number of elements used, how exactly the geometry is replicated in the model, the accuracy of the figures for the material properties incorporated into the model, and how realistically the loading of the model reflects the in vivo situation being modeled.¹ The analysis of facial fractures utilizing this numerical technique is well established^{1 18 19 20 21 22 23 24 25} and its utility for this purpose is accepted.^{21 26}

Materials and Methods

Using techniques described previously by the authors, a FEM of a dry cadaveric human mandible was constructed.¹ The computer program Mimics (v.13.02, Materialise, Belgium) was used to generate “masks” for the cranium and mandible from DICOM (Digital Imaging and Communications in Medicine) data from a computerized tomographic scan of the cranium and mandible. Further manipulation of the mandibular mask created a simulated typical subcondylar fracture with separated proximal and distal parts (Fig. 1). 3D surface meshes were exported into Strand7 FEA software (version 2.4, Strand7 Pty Ltd, Sydney, Australia) and tet4 “bricks” (low order tetrahedral elements with four nodes) elements were used to create a volumetric mesh. Truss elements (beams that can only transmit axial loads) attached to the anatomical origin and insertion sites of the associated musculature were used to model the muscles.²⁷ The medial pterygoid, lateral pterygoid, masseter, and temporalis muscles were modeled bilaterally with 50 muscle trusses on each side of the skull. Trusses were distributed among different muscle groups on the basis of their origin and insertion areas.¹ Associated muscle forces were estimated using the “dry-skull” method.^{27 28} The number and properties of trusses assigned to each muscle are shown in Table 1.

Fig. 1.

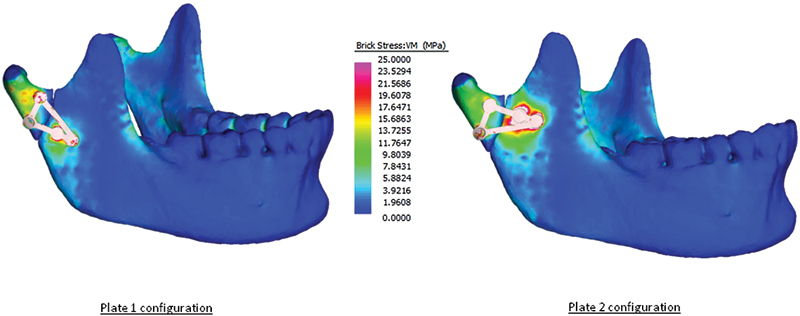
Solved finite element models for configurations 1 and 2 showing the placement of the fracture line and the shape and orientation of each patient-specific implant.

Table 1. The allocation and properties of muscle trusses within the finite element model.

	Number of truss elements on one side	Force/truss (N)	Truss diameter (mm)	Young modulus (MPa)	Density (T/mm3)
Medial pterygoid	6	3	5	0.1	1 × 10−09
Lateral pterygoid	2	3	5	0.1	1 × 10−09
Temporalis	31	3.58	3.90	0.1	1 × 10−09
Masseter	11	17.91	8.72	0.1	1 × 10−09

Two unique triangular-shaped plates were designed using Rhino (version 4.0) and STL files of these designs were made. The triangular plates were designed to have the same width, thickness, screw hole size, and edge curvature and edge beveling of the bar regions as the other straight plates included in the study. This was done to limit potentially confounding effects of subtle differences, or nuances, in plate geometries, as opposed to the effects of the overall (triangular) geometry of the plates, on the results. The plates were 1.5 mm thick and when used in the FEM, they were assigned the material properties of titanium. The STL files were then digitally manipulated (“warped”) to conform passively to the surface of the mandible once the fracture had been anatomically reduced^{1 29} (see Fig. 1). This process results in the formation of a PSI. The two designs were designated as PSI 1 and PSI 2 (see Fig. 2). The two unique designs were based on the expected stress distributions of the mandibular condyle area bearing in mind the AO principle of utilizing the location of bone strains in the placement and selection of implants. It is acknowledged that the online AO reference manual³⁰ suggests that if two plates are used to reduce a subcondylar fracture, the “two miniplates plates should be applied in a triangular fashion with one plate below the sigmoid notch and one plate along the posterior border,” and this principle informed the design and evaluation of the two plate configurations.

Fig. 2.

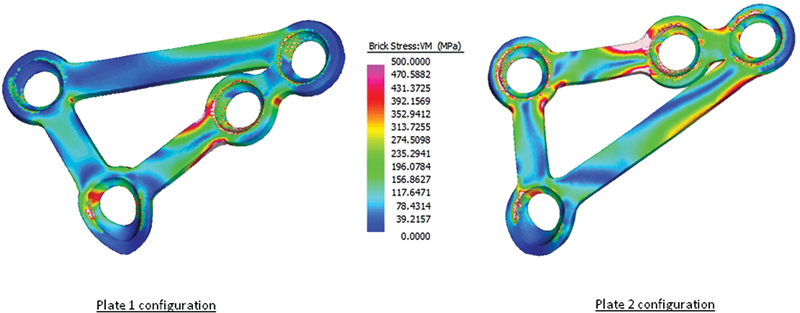
Solved finite element models for each patient-specific implant examined.

The FEM had eight material properties assigned on the basis of bone density as determined by Hounsfield units from the computed tomographic scan (Table 2)³¹ and it was assumed that linear elastic material behavior applied. Each completed model contained approximately 1.2 million elements.

Table 2. The allocation of material properties to brick elements in the finite element model as determined by the distribution of Hounsfield units (HU) in the computed tomography scan.

Brick material properties	Density (T/mm3)	Young modulus (MPa)
MAT1	2.508 × 10−10	1,527
MAT2	2.916 × 10−10	1,868.6
MAT3	3.325 × 10−10	2,223.4
MAT4	1.094 × 10−09	10,786.8
MAT5	1.855 × 10−09	21,734.2
MAT6	2.190 × 10−09	27,082.2
MAT7	2.525 × 10−09	32,704.3
MAT8	2.860 × 10−09	38,575.4

Each model had a linear static solve performed in Strand7. These calculations yielded the relative movement between the fracture fragments and the distribution of von Mises (VM) stress of the relevant plate and screw configuration.¹ The relative movement of 10 points along the fracture line was also determined to identify areas of greater displacement. The points were numbered starting at the coronoid notch end of the fracture and ending at the posterior condylar neck section. Comparison of the relative displacement and the VM stress distribution of different implant configurations facilitate prediction of the most stable implant type. In particular, a smaller relative interfragmentary movement and lower volume-weighted VM stress is associated with more stable fixation.^{23 24 25 32}

Results

The relative displacements of the proximal and distal fragments compared with the volume-weighted mean VM stress of each plate configuration are given in Table 3. Fig. 3 shows graphically the displacement of individual points along the fracture line. The VM stress distributions predicted in the mandible and the plates are graphically displayed in Figs. 1 and 2.

Table 3. Relative interfragmentary movement and volume-weighted mean VM stress of each plate configuration.

	Relative movement, µm (SD)	Volume-weighted mean VM stress	Plate volume (mm3)
PSI 1	179.0 (29.6)	91.3	68.4
PSI 2	267.3 (65.8)	145.3	67.1

Abbreviations: PSI, patient-specific implant; SD, standard deviation; VM, von Mises.

Fig. 3.

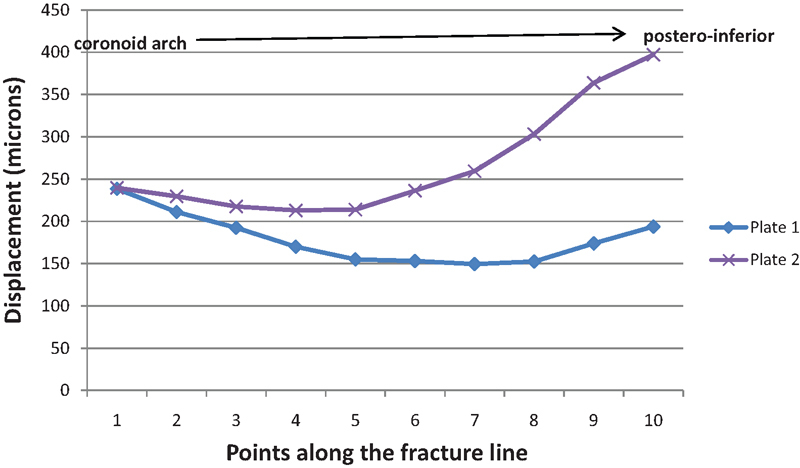
Graphical representation of the degree of displacement across the fracture line for each patient-specific implant.

PSI 1 showed superior biomechanical behavior compared with PSI 2 both in terms of relative movement and volume-weighted mean stress. PSI 1 also showed better overall of restriction in interfragmentary movement with a smaller range of movement. The pattern and location of movement along the fracture line (Fig. 3) also indicated that PSI 1 was likely to be better than PSI 2 in this particular fracture. In particular, PSI 2 displayed a marked increase in interfragmentary movement toward the posteroinferior border of the fracture (points 5–10), whereas in contrast, PSI 1 showed a decrease in movement from points 5 to 8 and a slight increase between point 8 and 10; however, points 8 to 10 were still lower than points 1 to 5. PSI 1 showed mechanical performance which was comparable to a thicker 2.0 mm straight plate.¹

Discussion

The clinical management of fractures of the mandibular condyle region has changed from being predominantly treated by closed reduction in the recent past to the present time in which many surgeons would advocate ORIF for selected mandibular subcondylar fractures. Once the decision to treat a fracture by ORIF has been made, the surgeon must then decide on the configuration and type of implant(s) to be used.^{1 7 8 9 11 33 34 35 36 37} Advances in computing and manufacturing processes open up the possibility of surgeons designing a PSI to fit a particular fracture and to then virtually analyze its performance before implanting it in the patient. Thus several designs can be quickly evaluated and the implant with the optimal mechanically performance selected.

In this preliminary study, we designed two novel implants for the reduction of a subcondylar fracture. The implant design was influenced by the anatomical constraints of the fracture and by analyzing the various vectors of muscle action on the condylar region. The triangular shape and orientation of the plates was intended to counteract areas of strain causing separation of the fracture. Theoretically, as both plates were designed to accommodate the expected forces applied during function to the fracture, both plates were expected to perform adequately. The strength of applying FEA to this process is that it gives the surgeon further information about a particular designs likely in vivo performance before manufacture and implantation. In this study, PSI 1 was clearly better from a biomechanical viewpoint than PSI 2.

Presently, the cost and time of production for PSI mitigate against their use in routine fractures of the facial skeleton. However, in keeping with most technological advances, it is expected that in the near future, the cost, ease, and speed of computer-aided design and 3D printing technologies will rapidly move to make it viable to regularly design PSI for the management of condylar and other facial fractures.

Although there is some literature arguing that there is no benefit in treating mandibular condyle fractures with ORIF compared with closed reduction, the tendency of recent research is to support the use of ORIF in these fractures.^{3 6 11 38}

There is still considerable discussion as to what the best form of internal fixation for mandibular condyle fractures is, but in summary, the literature suggests that two plates are more stable than a single plate,^{1 10 11 19 34 37 39} that bicortical screws are more stable than monocortical screws,¹⁰ and that thicker plates are more stable than thinner plates.^{10 12}

The senior author's (P.A.) clinical experience has been that the placement of two straight plates onto a mandibular condylar neck fracture is often problematic secondary to the often small area available for plate placement. This is especially so if an endoscopic technique is used. Another practical consideration is that often the straight plates used are the plates designed for use in mandibular body, angle, or parasymphyseal fractures and they are relatively thick which compounds the difficulty in accurately bending the plate to passively sit onto the complex 3D surface of the condylar neck. It is envisaged that the use of a PSI that accurately fits the reduced fracture will facilitate treatment of these fractures, especially if an endoscopic approach is used.

Compared with previous FEM of mandibular condyle fractures, our model has the advantages of analyzing the cranium and mandible as an articulated entity, differentiates between cortical and cancellous, and more accurately models the architectures of the jaw musculature.³⁷ The clinical situation is more realistically modeled by this FEM for several reasons; the muscle attachments are included to more closely mimic the anatomical loading of the model, each screw models the mechanical interface between bone and implant, and the virtual plates are “bent” to sit passively on the reduced fracture fragments and with the exception of the author's previous models,¹ this has not been done with other published models.

The FEM used in the present study each comprised around 1.2 million elements and is heterogeneous, considerably larger than other comparable models of the human mandible. Previous reported models have 47,525 elements and 72,899 nodes and homogeneous properties,²² 59,000 elements and 14,000 node and homogeneous properties,²³ 130,259 elements and homogeneous,⁴⁰ and 7,700 elements with 11,500 nodes and homogeneous properties.⁴¹ For geometrically complex structures that have significant heterogeneous properties, the predictive accuracy of a FEM tends to increase with increasing number of brick elements.¹⁶ Another advantage of this FEM is that the force vectors applied to the model have been designed to simulate the forces applied by the musculature attached to the mandible. When compared with testing plate configurations in a conventional mechanical testing system, this FEM results in a more realistic pattern of physiological loading.