Abstract
Rationale and Objectives
Accuracy and speed are essential for the intraprocedural nonrigid MR-to-CT image registration in the assessment of tumor margins during CT-guided liver tumor ablations. While both accuracy and speed can be improved by limiting the registration to a region of interest (ROI), manual contouring of the ROI prolongs the registration process substantially. To achieve accurate and fast registration without the use of an ROI, we combined a nonrigid registration technique based on volume subdivision with hardware acceleration using a graphical processing unit (GPU). We compared the registration accuracy and processing time of GPU-accelerated volume subdivision-based nonrigid registration technique to the conventional nonrigid B-spline registration technique.
Materials and Methods
Fourteen image data sets of preprocedural MR and intraprocedural CT images for percutaneous CT-guided liver tumor ablations were obtained. Each set of images was registered using the GPU-accelerated volume subdivision technique and the B-spline technique. Manual contouring of ROI was used only for the B-spline technique. Registration accuracies (Dice Similarity Coefficient (DSC) and 95% Hausdorff Distance (HD)), and total processing time including contouring of ROIs and computation were compared using a paired Student’s t-test.
Results
Accuracy of the GPU-accelerated registrations and B-spline registrations, respectively were 88.3 ± 3.7% vs 89.3 ± 4.9% (p = 0.41) for DSC and 13.1 ± 5.2 mm vs 11.4 ± 6.3 mm (p = 0.15) for HD. Total processing time of the GPU-accelerated registration and B-spline registration techniques was 88 ± 14 s vs 557 ± 116 s (p < 0.000000002), respectively; there was no significant difference in computation time despite the difference in the complexity of the algorithms (p = 0.71).
Conclusion
The GPU-accelerated volume subdivision technique was as accurate as the B-spline technique and required significantly less processing time. The GPU-accelerated volume subdivision technique may enable the implementation of nonrigid registration into routine clinical practice.
Keywords: Nonrigid image registration, GPU-accelerated image processing, B-spline, mutual information
Introduction
Computed tomography (CT) is used commonly to guide percutaneous tumor ablations of liver tumors (1–3). CT can provide high-quality three-dimensional (3D) images of the liver intraprocedurally, which help radiologists understand spatial relationship of the tumor with respect to the surrounding structures (4). However, typically only sectional unenhanced CT images are used and hence tumor margins may not be delineated well (5); this limitation may contribute to inadequate ablation (6–10). A recent study showed that the rate of local recurrence following percutaneous radiofrequency ablation of hepatocellular carcinoma decreased significantly from 23% to 0% when the ablation margin, the shortest distance between the outer margin of the tumor and the outer margin of the ablation, was increased from less than 1 mm to larger than 3 mm (11). Therefore, visualizing tumor margins intraprocedurally is important. One way to delineate tumor margins intraprocedurally is to register preprocedural MR images to the intraprocedural CT images; tumor margins depicted by MRI can be directly compared to ablation effects depicted with intraprocedural CT (12). In addition, the same data can be used to depict tumor and ablation volumes (12).
Nonrigid image registration techniques can be used to correct accurately the misalignment between structures in two images caused by physiologic variations (13). For example, the liver may be misaligned due to diaphragmatic motion. B-spline registration (14,15) is a commonly used nonrigid registration technique that parameterizes a deformation of an image as displacements of control points on a regular grid, and calculates the displacements of the voxels between the control points using basis spline (B-spline) interpolation (16). However, nonrigid registration techniques are not widely used clinically for intraprocedural registration, because the registration takes too long to perform and often needs a dedicated software operator. While computation time for B-spline registration can be shortened by reducing the control points, fewer control points may impact the registration accuracy negatively. In particular, the B-spline cannot model local deformations well with limited control points. A previous analysis of 4D CT by Schreibmann et al used 15 control points per direction to model the deformations of liver images accurately (17). This number of control points is much larger than those used in previous studies on intraoperative registration, typically 3–5 control points per direction, which still takes up to 2 minutes (12,16). To attain sufficient registration accuracy, a region of interest (ROI) is often employed (12,16,18,19). A ROI can restrict the region to be registered on the liver only, and can reduce the effect of local displacement in the surrounding structures. A ROI also helps reduce computation time by reducing the number of voxels to be processed. However, a ROI must be defined by contouring the target organ. Robust automatic contouring of the target organ is a challenging problem and would invariably introduce additional computation time. Manual contouring has been used in past studies (12,16), but would require an additional human resource for routine clinical use. The long computation time and the need for manual contouring hinder widespread use of nonrigid image registration.
The volume subdivision approach (20) could avoid having to conduct a time-consuming manual contouring, while achieving acceptable registration accuracy. The volume subdivision approach models a deformation by multiple local 6 degrees-of-freedom (DOF) full rigid-body transformations (21). Because the volume subdivision approach corrects for misalignment of individual subvolumes independently, it can often model local displacements better than the B-spline technique, particularly when the number of control points for the B-spline technique is limited. Although the computation time for the volume subdivision approach is also long due to its hierarchical process of refining local matching between two images, and the lack of a ROI that limits the number of processed voxels, it can be significantly reduced by accelerating the algorithm using the stream processing capability of general-purpose graphic processing units (GPGPUs). GPGPUs, which are now widely available in consumer-grade graphics processing unit (GPU) products, are specifically designed for stream processing. The stream processing is a computing model, where a series of arithmetic operations (kernels) are applied to streams of data; because the data streams can be loaded and supplied to the kernels sequentially without waiting for the result of operations, the operations are not constrained by the latency of the memory access unlike the conventional computing model. In addition, if the operations are independent from each other, which is the case in many graphics processing operations, multiple streams can be processed simultaneously. This stream processing model allows the GPUs to use their processing units effectively and to achieve higher computational throughput than conventional CPUs for preprocessing (21), resampling (22), and similarity metrics (23) on personal computers. The use of the volume subdivision approach combined with GPU acceleration might eliminate the need for time-consuming manual contouring without increasing the computation time or a loss of registration accuracy, and thus render nonrigid registration feasible for clinical use. We tested the clinical feasibility of the GPU-accelerated volume subdivision technique by comparing the registration accuracy and processing time to those of the conventional nonrigid B-spline registration technique, which has been validated in the previous clinical studies (12, 16,19).
Materials and Methods
Subjects
Following IRB approval, a HIPAA-compliant, retrospective study was carried out. The inclusion criteria were subjects 1) who underwent CT-guided liver ablations performed by one radiologist (S.T.) between January 2013 and October 2013, and 2) had preprocedural MRI studies. Using these criteria, 14 subjects (ages 45–84 years; 6 males and 7 females; one male underwent two ablations during two separate procedures) were included in the study. Tumor ablations were conducted using microwave ablation (n=8) (AMICA, HS Medical Inc. Boca Raton, FL), cryoablation (n=6) (Galil Medical Ltd., Yokneam, Israel), or radiofrequency (RF) ablation (n= 1) (Covidien, Mansfield, MA). In one patient, both cryoablation and microwave ablation were used to treat separate tumors in a single session.
Imaging Protocol
MR images were acquired within 30 days prior to the procedure using a 1.5 Tesla MRI scanner (MAGNETOM Espree or Aera, Siemens AG, Erlangen, Germany, or Signa EXCITE or HDxt 1.5T, GE Healthcare, Waukesha, WI, USA,) or 3 Tesla MRI scanner (MAGNETOM Trio, Verio, or Skyra, Siemens AG, Erlangen, Germany). We obtained contrast-enhanced MRI (CE MRI) during this preprocedural imaging session using T1-weighted 3D fat-suppressed volume interpolated spoiled gradient echo sequence (TR/TE: 3.3–5.5/1.2–2.7 ms; flip angle: 9–12°; matrix size: 220×320–512×512; pixel spacing: 0.7031–1.7185 mm; slice thickness: 3–5 mm; slice gap: 0 mm) acquired before and 30, 60, and 90 seconds after intravenous administration of 0.1 mmol/kg of gadolinium-based contrast material (Magnevist, Berlex Laboratories, Wayne, NJ, USA). Only the contrast-enhanced images were used as preprocedural MR images in this study for the consistency. Contrast-enhanced MRI (CE-MRI) is widely accepted as an imaging modality for the detection of tumors (24–27), and therefore, it fits our goal of delineating the ablation margin on the intraprocedural CT by fusing them. A board-certified radiologist (S.T.) reviewed the MR images for each case and selected the phase that delineated the tumor best for the following evaluation. Intraprocedural CT scans were obtained with a 40-channel multi-detector row CT scanner (Sensation Open, Siemens Medical Solutions, Forchheim, Germany), with a matrix size of 512 × 512, 0.6 mm collimation, 0.5 sec/rotation, 120kV and 168 to 398 mA, and reconstructed as 3-mm axial sections.
Image Registration Algorithms
GPU-accelerated Nonrigid Registration using Volume Subdivision Approach
All MR and CT images were loaded onto open-source image-processing and visualization software, 3D Slicer (28,29) running on a computer workstation (processor: Intel Core i7 quad-core 4.1GHz; random access memory: 8 GB; Ubuntu 12.04 operating system). For each procedure, we registered the preoperative MR image to the intraoperative CT image using the GPU-accelerated volume subdivision technique implemented as in-house software. The software was integrated into 3D Slicer as a plug-in module for comparison with the B-spline registration available in 3D Slicer using the same data and workflow.
The GPU-accelerated volume subdivision technique was based on a volume subdivision algorithm (23). The multilevel algorithm begins by performing a rigid registration between the two volumes (i.e., volumetric images). In every subsequent level, every volume is divided into eight smaller volumes by dividing along each of the axes and an independent rigid registration takes places between the corresponding subvolumes. By repeating the division and registration process, local displacements due to deformations are determined and nonrigid registration is achieved (Figure 1). A normalized mutual information (NMI) (30) is used to calculate the similarity between the corresponding subvolumes, where the solutions from previous levels contribute to NMI at local volumes to improve local stability while retaining speed. NMI was selected as it has been shown to be a robust metric of MR and CT images including when fields of view between the two images are disparate (30). We implemented the registration algorithm to utilize GPU’s parallel computing capability. In particular, the calculation of NMI between the original fixed image and the transformed floating image, which was the most computationally intensive step in the algorithm, was accelerated in a GPU kernel. We applied two levels of parallelism in the kernel to take advantage of the GPU’s multi-core, multi-processor architecture. At the first level, the image is divided into subvolumes, which are assigned to individual processors and processed in parallel. At the second level, each subvolume is further divided into voxels, which are assigned to individual cores in each processor and processed in parallel. As a result, the calculation of NMI is parallelized at both subvolume and voxel levels (Figure 2). Each subvolume is optimized independently of the others. While voxels within a subvolume share memory resources within a multiprocessor to optimize the computing resources for the algorithm, voxels in different subvolumes do not, enabling subvolumes to be mapped to different multiprocessors. Once an optimized set of 6-degrees-of-freedom (6-DOF) rigid transformations for all the subvolumes are found, a resampling GPU kernel takes these final transforms, interpolates them to derive a smooth transformation field, and applies it to the floating image to produce a final registered image. The 6-DOF rigid transformation of each voxel is estimated by interpolating the transformations of the subvolume centers surrounding the voxel (21). In our implementation, the independent components of the transformation are interpolated separately; three translations along the coordinate axes are determined by tricubic interpolation, whereas the 3D rotational pose is determined by spherical cubic quaternion interpolation (31). The application of the transform, interpolation, and final resampling are independent at the voxel level, permitting the mapping of each voxel to a single thread. In both of these kernels, the use of thread groups and threads for the implemented algorithm ensures high utilization of the GPU for these time-consuming kernels.
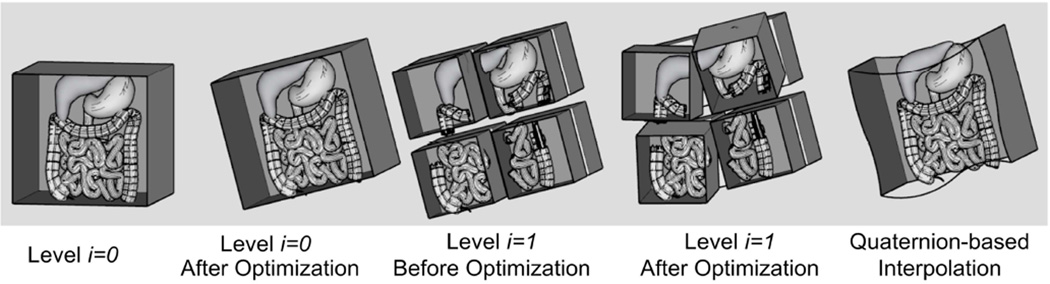
Figure 1.
Pictorial representation of volume subdivision registration algorithm used with GPU acceleration. The algorithm begins with a rigid registration between the two volumes. In every subsequent level, every volume is divided into eight subvolumes and an independent rigid registration takes places between corresponding subvolumes. By repeating the division and registration process, local displacements due to deformations can be determined.
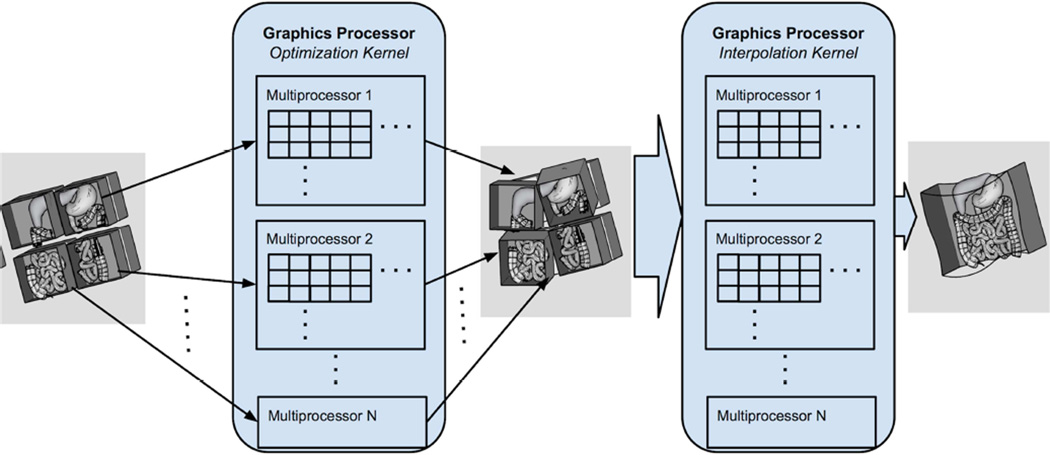
Figure 2.
The nonrigid image registration with image subdivision approach was accelerated in a GPU kernel at both voxel and subvolume levels. A subvolume is assigned to one group of threads, which is executed by a GPU multiprocessor, and a voxel within a subvolume is assigned to a thread, which executes on a single core in a multiprocessor. Once an optimized set of subvolume transformations is found, a resampling GPU kernel takes the transforms of the subvolumes, derives a smooth transformation field, and applies it to the floating image to produce a final registered image. The computation for each pixel is independent, permitting the mapping of each voxel to a single thread.
To optimize registration accuracy, we tuned the following parameters of the registration algorithm using four data sets as training data: window level, flexibility, and subdivision rate. This was intended to be done once per registration scenario; once trained, the same parameters are used throughout the study. For window leveling, a preprocessing step is applied to rescale the 16-bit intensity values of the MR and CT images to 8-bit intensity values. Based on the number of bits allocated to the input image voxel intensities, the dynamic range is high, but voxel intensity histograms often have long tails. For visualization and analysis, image contrast is derived from window level that highlights structures of interest. To focus the registration algorithm we searched the space of possible window levels by tracking a registration quality metric DSC. We evaluated candidates for window level in the design space defined by a high and a low voxel intensity threshold. This was a semi-automated training process, where a set of window levels were manually chosen from previously used window levels for other image data sets, and a program ran all of them over the training data set and summarized the result. Images were rescaled according to these intensity thresholds for each input image. We recorded the candidate by an iterative search through the training data thereby focusing the similarity metric on a meaningful dynamic range of intensity values.
The second parameter we tuned was the default subdivision rate in the superior-inferior (SI) axis relative to the right-left (RL) and anterior-posterior (AP) axes. Image dimensions along the SI axis are often smaller than the dimensions along the RL and API axes. By changing when SI divides relative to RL and AP, the subdivision technique can achieve more cube-like volumes as it proceeds through the registration.
The third parameter we tuned was flexibility, which defines the amount of flexibility given to every subvolume to move from its current position as it begins a new level. While the algorithm always enforces some level of restriction on movement to ensure physically possible deformations, additional flexibility restrictions can help better guide the optimization engine by capturing how large the space is for candidate transformations. While these three parameters (window level, flexibility and subdivision rate) may influence one another, we have found independent evaluation of each on pilot cases being often sufficient. Once determined, the tuned parameters were kept fixed for the rest of the study.
After the nonrigid transformation that registered preprocedural MR image and intraprocedural CT image was determined, the preprocedural MR image was resampled using the determined transformation. The resampled (or registered) preprocedural MR image was saved as an electronic file for further analysis described in the following section. The computation times for the rigid registration, nonrigid registration, and resampling were measured using the internal clock of the computer. The total processing time for the registration was calculated by summing those computation times.
Nonrigid B-Spline Registration
All MR images were loaded into the open-source image-processing and visualization software, 3D Slicer (28,29) running on a computer workstation (Processor: Intel Dual Hexa-Core Xeon 3.06GHz; random access memory: 6 GB; Fedora 14 operation system). For each set of preoperative MR image and intraoperative CT image, first, a region of interest (ROI) including only the liver was defined manually on both MRI and CT by contouring the liver using 3D Slicer’s drawing function and was saved as a ROI image. The livers were contoured initially by a research scientist (J.T.) and then visually confirmed and corrected by a board-certified radiologist (S.T.). This manual contouring minimized registration error due to motion of the anatomy outside the liver and corrected the bias of the pixel intensities within the ROI on the MR image due to the inhomogeneities in the B0 and B1 fields. For the correction of intensity bias, the improved nonparametric non-uniform intensity normalization approach (32) available as the N4ITK Bias Correction Module in 3D Slicer was used. The N4ITK is a variant of N3 bias correction, which is a de facto standard method for the bias correction of intensity inhomogeneity on various images (32–35), but incorporates more robust bias approximation algorithm. It has been used in other studies using the same B-spline registration methods (12,16). We set the grid resolution for the N4ITK Bias Correction at 4×4×4.
Image registration was performed using the BRAINSFit module in 3D Slicer (36). Four steps of registrations were sequentially applied to the image set: alignment of the centers of ROIs; a rigid registration to correct for global misalignment of the liver, an affine registration to correct for global deformation, and a nonrigid B-spline registration to correct for local deformation of the liver. In the step of aligning the centers of ROIs, the center of mass of the ROIs on the MR and CT images were aligned in order to correct for the offset of the coordinate systems. In the following three steps, the preoperative MR image was transformed so that Mattes’ mutual information (MMI) (37) of the two images as a similarity measure was maximized using Limited memory Broyden Fletcher Goldfarb Shannon optimization with simple bounds (L-BFGS-B) (38). Mutual information has been shown to be the most effective currently available metric for multimodality image registration (12,16,37). Specifically, Mattes’ implementation of mutual information (37) is used in BRAINSFit module in 3D Slicer (16,36). The L-BFGS-B, a limited-memory, quasi-Newton minimization method, is used for the optimization of registration parameters. The limited-memory method is useful because it is suitable for optimization with a large number of variables and allows bound constraints on the independent variables (37). We used the ROI to limit the area to be registered. In the final stage of the nonrigid B-spline registration step, deformation of the preoperative MR image was regulated by a uniform B-spline grid. The number of control points of the B-spline grid was 5 per direction (5×5×5) as in our previous study (12).
Once the nonrigid transformation that registered preprocedural MR image and intraprocedural CT image was determined, the preprocedural MR image was resampled using the determined transformation. The resampled (or registered) preprocedural MR image was saved as an electronic file. Time required for manual contouring of the liver on both the preprocedural MR image and intraprocedural CT image, and computation times for the rigid registration, nonrigid registration, and resampling were measured using the internal clock of the computer. The total processing time for the registration was calculated by summing the time needed for contouring and the computation times of the rigid and nonrigid registrations.
Comparison of Registration Accuracy and Processing Time
For each image registration technique, registration accuracy or the degree of volumetric misalignment of the liver between the intraprocedural CT image and the registered preprocedural MR image was evaluated using two metrics: 95% Hausdorff Distance (HD) and the Dice Similarity Coefficient (DSC) (39,40). The 95% HD provides the mismatch distance between two contours from the registered livers. Perfect alignment would yield a 95% HD equal to 0 mm. The DSC is defined as DSC = (2 ×|A∩B|)/(A|+|B|), where |A|, |B| and |A ∩ B| are the volumes of the liver in the two images and the overall between them, respectively. Perfect alignment of the two data sets would provide a DSC value of 1. The HD and DSC are both derived from the same contours, but have distinctive interpretations; the DSC can be translated as what percent of the area in the registered image represents the true area, while the HD can be translated as a misalignment of the region between the two images.
The processing times including the times required for computation (both the GPU-accelerated volume subdivision technique and the B-spline technique) and manual ROI contouring (the B-spline technique only) were measured as described in the previous section. In addition to the processing times, the voxel throughputs for the two registration techniques were calculated. The voxel throughput was defined as the number of processed voxels divided by the total computation time. Because the B-spline registration technique registered only the voxels within the ROI while the GPU-accelerated registration registered the entire image, the numbers of processed voxels for the two techniques were different. Therefore, voxel throughput was considered an appropriate performance measure because it compensated for the different quantity of data processed during the registration.
The mean values of DSC, 95% HD, computation times, total processing times, and voxel throughput were compared between B-spline and GPU-accelerated volume subdivision technique by a paired Student’s t-test. Type 1 error (α) was pre-set at 0.05 and only 2-sided p-values were reported. All analysis was done in Stata version 11 (StataCorp LP, TX, USA).
Results
Table 1 shows the summary of the comparison of registration accuracy and processing time. There was no significant difference in registration accuracy (p = 0.41 for DSC and p = 0.15 for 95% HD) between the two techniques (Table 1 and Figure 3, 4). The total processing time including manual ROI contouring (B-spline technique only) for registration using the GPU-accelerated volume subdivision technique was significantly shorter than the B-spline technique (p = 0. 000000002). However, there was no significant difference in computation time between the two methods (p = 0.71). When the computation times were divided into the 3 computational steps, the GPU-accelerated registration took significantly less time than the B-spline registration to perform the rigid registration (p < 0.002) and the resampling steps (p < 0. 0000000001), while the GPU-accelerated volume subdivision technique took significantly longer than the B-spline technique to perform the nonrigid registration step (p < 0. 00002). The voxel throughput for the GPU-accelerated volume subdivision technique was significantly higher than that of the B-spline technique (p < 0.0004). Table 2 shows the field strengths of the MR scanners (i.e. 1.5 T or 3.0T), phases of CE MRI, and registration performances for individual procedures. There was no significant difference in DSC and 95% HD between the groups with 1.5 T and 3.0 T scanners for both GPU-accelerated volume subdivision technique and B-spline technique (GPU-accelerated volume subdivision: p=0.56 (DSC) and p=0.36 (95% HD); B-spline: p=0.57 (DSC) and p=0.50 (95% HD) using an unpaired two-sided Student’s t-test). We could not compare the processing times between the two groups, because the volumes of the livers were significantly different (p<0.05).
Table 1.
Summary of Results of Nonrigid Registration between Preprocedural MRI and Intraprocedural CT Images using B-Spline and GPU-accelerated Registration Techniques
| Mean ± SD | Range | p-value | ||
|---|---|---|---|---|
| DSC (%) | GPU | 88.30 ± 3.74 | 80.49 – 93.11 | 0.41 |
| B-Spline | 89.32 ± 4.90 | 79.70 – 94.46 | ||
| 95% HD (mm) | GPU | 13.14 ± 5.19 | 6.43 – 24.54 | 0.15 |
| B-Spline | 11.44 ± 6.32 | 5.43 – 23.04 | ||
| Time - Rigid Reg. (s) | GPU | 8.58 ± 6.31 | 4.36 – 29.28 | < 0.002 |
| B-Spline | 20.53 ± 7.01 | 14.56 – 40.08 | ||
| Time - Nonrigid Reg. (s) | GPU | 76.90 ± 10.75 | 61.5 – 91.43 | < 0.00002 |
| B-Spline | 42.48 ± 11.39 | 19.38 – 68.57 | ||
| Time - Resampling (s) | GPU | 2.07 ± 0.47 | 1 – 3 | < 0.0000000001 |
| B-Spline | 27.72 ± 5.02 | 19.87 – 40.71 | ||
| Time – Total Computation (s) |
GPU | 87.55 ± 14.26 | 69.10 – 118.25 | 0.71 |
| B-Spline | 90.72 ± 21.81 | 58.42 – 149.36 | ||
| Voxel Throughput (voxels/s) |
GPU | 195024.67 ± 141785.32 | 104192.50 – 614978.60 | < 0.0004 |
| B-Spline | 18050.36 ± 6324.58 | 12001.98 – 32628.07 | ||
| Time – Manual ROI Contouring |
GPU | N/A | N/A | N/A |
| B-spline | 466 ± 104 | 300–701 | ||
| Time –Total Processing | GPU | 87. 55 ± 14.26 | 69.10 – 118.25 | <0.000000002 |
| B-spline | 557.08 ± 116.47 | 375.83 – 850.36 | ||
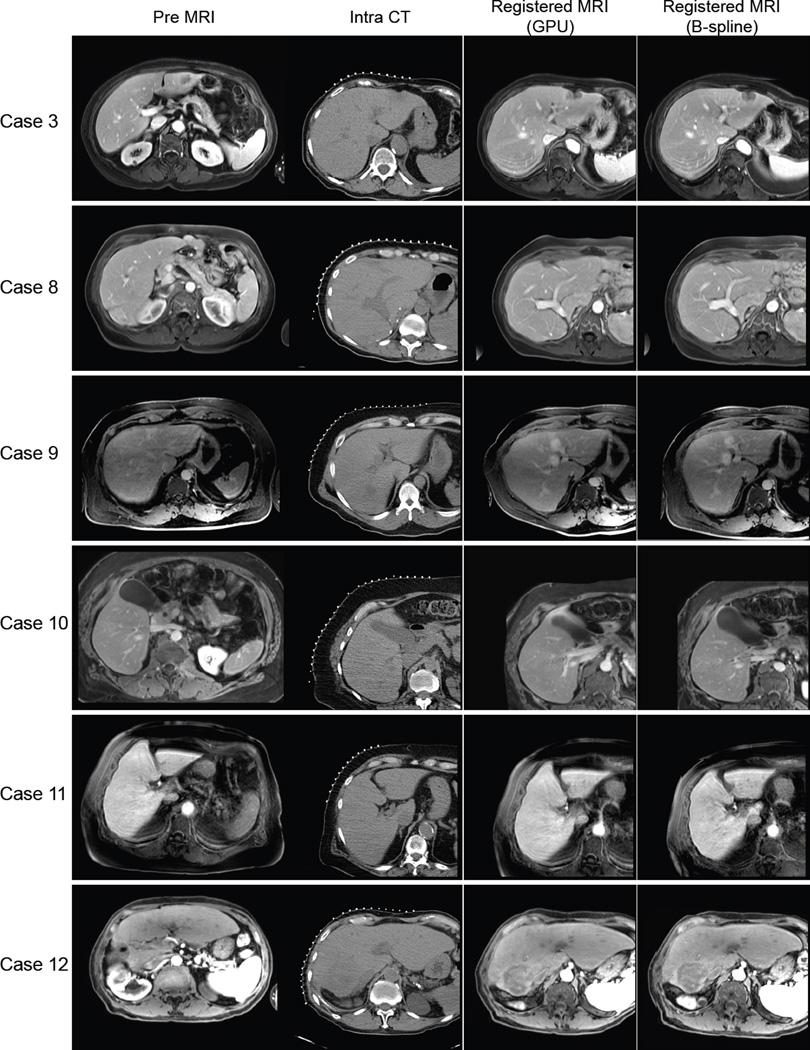
Figure 3.
The original preprocedural MRI, intraprocedural CT, and resampled MR images registered using the B-spline registration technique and the GPU-accelerated registration technique for representative cases are shown. Each row shows different procedures. The case numbers correspond to Table 2.
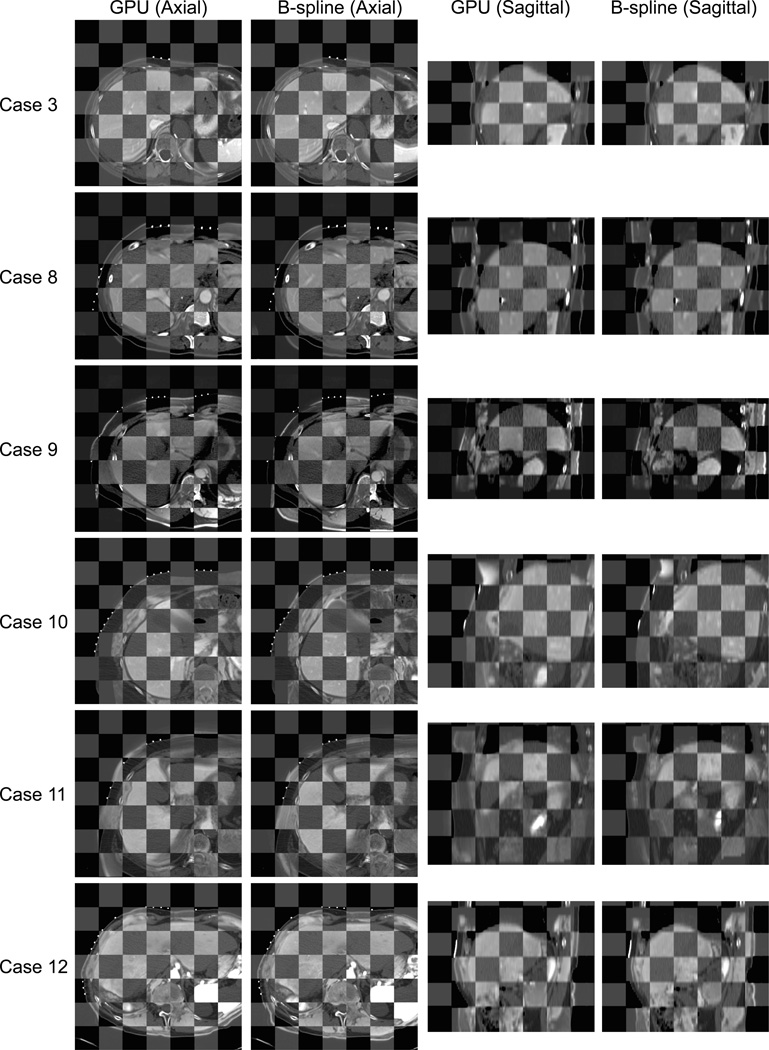
Figure 4.
Registered preprocedural MRI and intraprocedural CT are compared using a checkerboard for each case. While both the B-spline registration technique and the GPU-accelerated registration provide accurate alignment in the liver area, the checkerboards demonstrate that the GPU-accelerated registration often aligned the surrounding structures more accurately.
Table 2.
Type of MRI scanner, phase of CE MRI used for registration, and registration performances including DSC, 95% HD, processing time, and voxel throughput for each subject.
| Case | MRI Scanner |
CE MRI Phase |
DSC (%) | HD (mm) | Process time: rigid reg. (s) |
Process time: nonrigid reg. (s) |
Process time: resampling (s) |
Total process Time (Sec) |
Time: manual contouring (s) |
Total workflow time (s) |
Voxel throughput (voxels/s) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GPU | BS | GPU | BS | GPU | BS | GPU | BS | GPU | BS | GPU | BS | GPU | BS | GPU | BS | GPU | BS | |||
| 1 | 1.5T | 2 | 87.9 | 87.7 | 13.1 | 18.1 | 7.0 | 40.1 | 65.3 | 68.8 | 2.0 | 40.7 | 74.3 | 149.4 | - | 701.0 | 74.3 | 850.4 | 614978.6 | 29900.7 |
| 2 | 3.0T | 2 | 83.0 | 79.7 | 24.5 | 23.0 | 9.7 | 16.0 | 90.6 | 36.6 | 2.0 | 29.4 | 102.4 | 82.1 | - | 499.0 | 102.4 | 581.1 | 107551.5 | 22465.2 |
| 3 | 3.0T | 3 | 91.7 | 92.4 | 10.0 | 10.2 | 5.2 | 23.7 | 62.9 | 51.9 | 1.0 | 28.9 | 69.1 | 104.6 | - | 419.0 | 69.1 | 523.6 | 288972.5 | 18045.4 |
| 4 | 1.5T | 1 | 88.5 | 93.4 | 10.2 | 5.6 | 4.9 | 26.5 | 81.5 | 51.4 | 2.0 | 33.7 | 88.4 | 111.6 | - | 512.0 | 88.4 | 623.6 | 237207.6 | 12002.0 |
| 5 | 3.0T | 1 | 80.5 | 88.7 | 20.9 | 9.0 | 7.3 | 16.0 | 83.8 | 38.9 | 2.0 | 24.1 | 93.1 | 79.0 | - | 550.0 | 93.1 | 629.0 | 109813.3 | 14060.3 |
| 6 | 3.0T | 2 | 90.3 | 80.5 | 12.0 | 19.7 | 12.0 | 14.6 | 72.1 | 34.4 | 2.0 | 24.7 | 86.1 | 73.7 | - | 484.0 | 86.1 | 557.7 | 106612.1 | 17557.9 |
| 7 | 1.5T | 3 | 84.2 | 83.1 | 18.7 | 13.5 | 4.4 | 26.9 | 65.5 | 42.4 | 2.0 | 19.9 | 71.9 | 89.2 | - | 571.0 | 71.9 | 660.2 | 335427.6 | 17322.2 |
| 8 | 1.5T | 2 | 93.1 | 93.2 | 6.4 | 6.6 | 9.0 | 21.2 | 61.5 | 46.5 | 2.0 | 27.8 | 72.5 | 95.5 | - | 417.0 | 72.5 | 512.5 | 190781.1 | 14972.4 |
| 9 | 3.0T | 3 | 89.2 | 91.0 | 10.0 | 6.4 | 5.2 | 19.3 | 74.4 | 43.0 | 2.0 | 26.1 | 81.6 | 88.4 | - | 420.0 | 81.6 | 508.4 | 135680.3 | 13036.0 |
| 10 | 3.0T | 3 | 89.1 | 89.6 | 13.2 | 20.4 | 29.3 | 15.1 | 87.0 | 19.4 | 2.0 | 23.9 | 118.3 | 58.4 | - | 518.0 | 118.3 | 576.4 | 104192.5 | 32628.1 |
| 11 | 3.0T | 3 | 85.1 | 92.8 | 16.4 | 6.1 | 7.0 | 19.6 | 91.4 | 51.1 | 3.0 | 30.5 | 101.4 | 101.2 | - | 429.0 | 101.4 | 530.2 | 131795.6 | 12035.0 |
| 12 | 3.0T | 1 | 91.1 | 90.6 | 10.8 | 10.2 | 7.3 | 15.7 | 90.1 | 36.0 | 3.0 | 26.7 | 100.3 | 78.4 | - | 371.0 | 100.3 | 449.4 | 122826.9 | 18354.8 |
| 13 | 3.0T | 2 | 90.5 | 93.3 | 9.3 | 6.0 | 5.8 | 14.8 | 71.4 | 36.1 | 2.0 | 25.0 | 79.2 | 75.8 | - | 300.0 | 79.2 | 375.8 | 109240.5 | 13329.1 |
| 14 | 1.5T | 2 | 91.9 | 94.5 | 8.4 | 5.4 | 6.2 | 18.1 | 79.0 | 38.2 | 2.0 | 26.7 | 87.2 | 83.0 | - | 338.0 | 87.2 | 421.0 | 135265.2 | 16996.0 |
CE MRI phase: 1=30 s; 2=60 s; 3=90s
Discussion
We evaluated the performance of the GPU-accelerated nonrigid registration in the context of intraprocedural assessment of ablation margins based on preprocedural MR during CT-guided percutaneous ablations. Alternatively, intraprocedural MRI can be used to guide percutaneous ablations (41–43). Intraprocedural MRI has several advantages over intraprocedural CT; it provides better delineation of the tumor and better monitoring of the thermal effect (41); it does not expose the patient and clinical staff to ionizing radiation. The intraprocedural use of MRI is, however, somewhat cumbersome due to a limited access to the patient in a gantry and imaging time longer than that of CT. Furthermore, facilities that can perform intraprocedural MRI are not commonly available. Registration of preprocedural MRI can potentially provide the same or equivalent information to intraprocedural MRI even in conventional CT-guided procedures in many cases.
The B-spline technique for performing nonrigid registrations has been validated clinically (12,13,44), but is not used widely because the time needed to perform the registrations, including the time for manual contouring of an ROI, is too long. Our study showed that the novel, GPU-accelerated volume subdivision technique can be used to perform nonrigid registrations that are just as accurate as the B-spline technique and in less time. The GPU-accelerated volume subdivision approach significantly shortened the total processing time and improved the feasibility of nonrigid image registration in the intraoperative use by removing the manual segmentation step. With this new approach, nonrigid image registration can be deployed in routine clinical practice without having a skilled software operator on site. However, the total processing time of 88 s may slow the procedure in some cases, especially when nonrigid registration is used to quickly confirm the needle placement with respect to the target. In such instances, the speed could be improved by combining rigid registration technique; once preprocedural MR image is registered to an intraprocedural CT image using the nonrigid registration, the registered MR image could be registered to subsequent CT images by rigid image registration unless there is significant deformation. One could also shorten the processing time further by optimizing the software for GPU architecture. Since mutual information is a memory intensive, scatter-gather type algorithm, the bottleneck is data transfer through the bus that connects the main memory and the cores in the GPU. Our current utilization of the bandwidth on the bus is about 10% indicating that there is room for further optimization. The challenge is to organize the memory operations in the calculation of mutual information so that data can be accessed contiguously to achieve high memory bandwidth.
When the three steps of the computation (rigid registration, nonrigid image registration, and resampling) were timed individually, the rigid registration and resampling steps using the GPU-accelerated technique were significantly faster than the B-spline technique. The speed advantage of the resampling step is particularly helpful when the same transform is applied to multiple images. For example, when multiple MR images from the same examination (e.g. T1-, T2-, and diffusion-weighted) are registered to an intraprocedural CT image, image registration is needed only once; the rest of the images can be just resampled using the same transformation, as long as there is no misalignment among the MR images. Even if there is misalignment due to patient motion during the preprocedural study, it could be corrected beforehand by using rigid or nonrigid registration depending on the degree and nature of misalignment. The GPU-accelerated volume subdivision technique took longer to perform the nonrigid registration step because of the complexity of the algorithm and the higher number of voxels processed, but the overall time was still less.
The comparison of the voxel throughputs showed that the GPU-accelerated technique could process significantly more voxels per unit time than the B-spline technique. GPUs provide acceleration through many light-weight cores. While single-threaded execution is typically slower on a GPU than a CPU, an application with many light-weight threads is often faster on a GPU than a CPU, even if the CPU has multiple cores. The key to the GPU’s ability to accelerate the application is by having hundreds to thousands of cores simultaneously running these threads. A CPU will be able to run threads simultaneously also, but there are dozens of cores available at most. This order-of-magnitude difference between the number of cores more than makes up for the single-threaded performance gap between a GPU core and a CPU core (45). The GPU’s organization of cores, memory, and interconnection between them are designed to keep program data streaming efficiently to the cores. Cores are grouped together into a multiprocessor, sharing local memory and interconnection resources and multiprocessors are replicated across the GPU, sharing only global memory.
Our qualitative assessment did reveal some differences between the two registration techniques (Figure 3). First, the B-spline technique was affected less by the discontinuous displacement (or sliding) (46) at the boundaries between the liver and the surrounding structures, likely because the use of an ROI masked the region outside it; the GPU-accelerated volume subdivision technique did not take account of the discontinuity and tended to be affected by the displacement of the surrounding structures. Second, the GPU-accelerated volume subdivision technique, on the other hand, performed better in regions of the liver where there was a relatively large local deformation such as segments 2 and 6. The B-spline technique could have corrected the local deformation better if the number of control points was increased. However, a large number of grids would have increased the computation time, and introduced unrealistic deformation to the image registration. Third, the GPU-accelerated volume subdivision technique’s ability to correct global motion had a positive impact on the registration accuracy when the patient’s position during the preprocedural MRI was significantly different from the position during the procedure. Fourth, a limited field-of-view, commonly used during CT-guided interventions to focus the interventionist on the relevant anatomy, reduced registration accuracy for the B-spline technique. If the field of view of the intraprocedural CT image does not include the whole liver when the preprocedural MRI does, the centers of the ROIs on the two images will not dictate the same anatomical point. Therefore, a significant misalignment of the liver can remain even after aligning the centers of the ROIs as the first step of the registration. In fact, a limited field of view affected the accuracy of B-spline technique more than the GPU-accelerated volume subdivision technique in two cases.
There are several limitations in this study. First, the comparison of two algorithms (volume subdivision vs B-spline) optimized for different types of hardware (GPU vs CPU) may not tease apart the different contributions to speed gains. However, intermediary comparison with either GPU-accelerated B-spline registration or CPU-based volume subdivision-based registration were not straightforward, because of the number of combinations of factors that impact the registration performance (23). Those factors include: types of transforms (e.g. B-spline or volume subdivision), similarity measures (e.g. normalized cross correlation, gradient correlation, MMI, NMI, sum of squared differences, sum of absolute differences), optimizers (e.g. Powell, Simplex, gradient descent, Quasi-Newton, etc), preprocessing (e.g. filtering, rectification, bias correction, gradient computation, pyramid construction, feature detection, etc.), features of computing hardware (e.g. masking, clock speed, number of cores, size and bandwidth of on-board random access memory for GPU). Since the two registration programs used in this study were developed independently in the prior studies, those factors were not necessarily the same between them. Therefore, we only focused on the clinical feasibility of the new GPU-accelerated registration by comparing with the well-validated B-spline registration software as a baseline rather than detailed assessment of the speed gains by the use of different algorithms and hardware. To reveal the performance gain by the GPU acceleration, we calculated the voxel throughput. Second, the types of metrics used to evaluate registration accuracy are limited to DSC and HD. The Target Registration Error (TRE) is also used to evaluate registration accuracy. The TRE provides direct interpretation of how accurate the targeting would be if the needle were guided by the registered image. However, we did not evaluate the TRE in this study to avoid any bias originating from landmark selection, because our goal was to compare the two registration approaches.
A specific challenge in image registration of the liver is the modeling of its deformation and discontinuous displacement at the boundaries between the liver and the surrounding structures. Like any transformation model that parameterizes a smooth, continuously differentiable deformation field (e.g. B-splines, thin plate splines), the volume subdivision algorithm cannot exactly model shearing (e.g., the liver sliding across the rib cage) or tearing (e.g., resection). Fortunately for percutaneous liver ablation, the misalignment in the internal organs tends to be well handled by our registration, because the tearing or shearing effects are minimal. In our experimental setup, the volume subdivision approach handled such types of registration problem better than the B-spline approach. By virtue of being based on mutual information and having no segmentation nor landmark identification steps, the registration engine for the GPU-accelerated volume subdivision approach can be applied to other imaging modalities, and other abdominal organs. There are parameters to tune to improve the engine’s robustness and accuracy: window levels, flexibility, and levels of refinement. But beyond these explicitly stated parameters nothing else was done to tune the engine to liver ablations.
In this study, four images were used for the parameter tuning in the GPU-accelerated volume subdivision approach. While more training data might improve the robustness of the system for widespread deployment, our results have shown that the parameters optimized for the training data sets worked well throughout the study, hence the registration approach is feasible as a fully automated solution to map preprocedural MR onto intraprocedural CT for guiding percutaneous liver ablations.
In conclusion, the GPU-accelerated volume subdivision technique is just as accurate as the B-spline technique for performing nonrigid registrations but faster. These results are particularly relevant to performing registrations intraprocedurally when it is important to view images as quickly as possible. The GPU-accelerated volume subdivision technique may enable routine use of nonrigid registration in the clinical practice.
Acknowledgements
This study is supported by The National Institutes of Health (5R42CA137886, 5R01CA138586, and 5P41EB015898). The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. Nobuhiko Hata is a member of the Board of Directors of AZE Technology, Cambridge, MA and has an equity interest in the company. AZE Technology develops and sells imaging technology and software. NH’s interests were reviewed and are managed by the Brigham and Women’s Hospital and Partners HealthCare in accordance with their conflict of interest policies.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Orlacchio A, Bazzocchi G, Pastorelli D, Bolacchi F, Angelico M, Almerighi C, et al. Percutaneous cryoablation of small hepatocellular carcinoma with US guidance and CT monitoring: initial experience. Cardiovasc. Intervent. Radiol. 2008;31(3):587–594. doi: 10.1007/s00270-008-9293-9. [DOI] [PubMed] [Google Scholar]
- 2.Antoch G, Kuehl H, Vogt FM, Debatin JF, Stattaus J. Value of CT volume imaging for optimal placement of radiofrequency ablation probes in liver lesions. J. Vasc. Interv. Radiol. 2002 Nov;13(11):1155–1161. doi: 10.1016/s1051-0443(07)61958-7. [DOI] [PubMed] [Google Scholar]
- 3.Sato M, Watanabe Y, Tokui K, Kawachi K, Sugata S, Ikezoe J. CT-guided treatment of ultrasonically invisible hepatocellular carcinoma. Am. J. Gastroenterol. 2000 Aug;95(8):2102–2106. doi: 10.1111/j.1572-0241.2000.02275.x. [DOI] [PubMed] [Google Scholar]
- 4.Goshima S, Kanematsu M, Kondo H, Yokoyama R, Miyoshi T, Nishibori H, et al. MDCT of the liver and hypervascular hepatocellular carcinomas: optimizing scan delays for bolus-tracking techniques of hepatic arterial and portal venous phases. AJR. Am. J. Roentgenol. 2006 Jul;187(1):W25–W32. doi: 10.2214/AJR.04.1878. [DOI] [PubMed] [Google Scholar]
- 5.Paushter DM, Zeman RK, Scheibler ML, Choyke PL, Jaffe MH, Clark LR. CT evaluation of suspected hepatic metastases: comparison of techniques for i.v. contrast enhancement. AJR. Am. J. Roentgenol. 1989 Feb;152(2):267–271. doi: 10.2214/ajr.152.2.267. [DOI] [PubMed] [Google Scholar]
- 6.Montorsi M, Santambrogio R, Bianchi P, Donadon M, Moroni E, Spinelli A, et al. Survival and recurrences after hepatic resection or radiofrequency for hepatocellular carcinoma in cirrhotic patients: a multivariate analysis. J Gastrointest Surg. 2005;9(1):62–68. doi: 10.1016/j.gassur.2004.10.003. [DOI] [PubMed] [Google Scholar]
- 7.Chen MS, Li JQ, Zheng Y, Guo RP, Liang HH, Zhang YQ, et al. A prospective randomized trial comparing percutaneous local ablative therapy and partial hepatectomy for small hepatocellular carcinoma. Ann Surg. 2006;243(3):321–328. doi: 10.1097/01.sla.0000201480.65519.b8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Abu-Hilal M, Primrose JN, Casaril A, McPhail MJ, Pearce NW, Nicoli N. Surgical resection versus radiofrequency ablation in the treatment of small unifocal hepatocellular carcinoma. J Gastrointest Surg. 2008;12(9):1521–1526. doi: 10.1007/s11605-008-0553-4. [DOI] [PubMed] [Google Scholar]
- 9.Liang HH, Chen MS, Peng ZW, Zhang YQJ, Li JQ, Lau WY. Percutaneous radiofrequency ablation versus repeat hepatectomy for recurrent hepatocellular carcinoma: a retrospective study. Ann Surg Oncol. 2008;15(12):3484–3493. doi: 10.1245/s10434-008-0076-y. [DOI] [PubMed] [Google Scholar]
- 10.Peng ZW, Zhang YJ, Chen MS, Lin XJ, Liang HH, Shi M. Radiofrequency ablation as first-line treatment for small solitary hepatocellular carcinoma: long-term results. Eur J Surg Oncol. 2010;36(11):1054–1060. doi: 10.1016/j.ejso.2010.08.133. [DOI] [PubMed] [Google Scholar]
- 11.Kim YS, Lee WJ, Rhim H, Lim HK, Choi D, Lee JY. The minimal ablative margin of radiofrequency ablation of hepatocellular carcinoma (>2 and < 5 cm) needed to prevent local tumor progression: 3D quantitative assessment using CT image fusion. AJR Am J Roentgenol. 2010;195(3):758–765. doi: 10.2214/AJR.09.2954. [DOI] [PubMed] [Google Scholar]
- 12.Elhawary H, Oguro S, Tuncali K, Morrison PR, Tatli S, Shyn PB, et al. Multimodality non-rigid image registration for planning, targeting and monitoring during CT-guided percutaneous liver tumor cryoablation. Acad Radiol. Elsevier Ltd. 2010 Nov;17(11):1334–1344. doi: 10.1016/j.acra.2010.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Rohlfing T, Maurer CR, Jr, O’Dell WG, Zhong J, Maurer CR, Dell WGO. Modeling liver motion and deformation during the respiratory cycle using intensity-based nonrigid registration of gated MR images. Med Phys. 2004;31(3):427–432. doi: 10.1118/1.1644513. [DOI] [PubMed] [Google Scholar]
- 14.Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. Med. Imaging, IEEE Trans. 1999;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- 15.Wells WM, 3rd, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Med Image Anal. 1996;1(1):35–51. doi: 10.1016/s1361-8415(01)80004-9. [DOI] [PubMed] [Google Scholar]
- 16.Fedorov A, Tuncali K, Fennessy FM, Tokuda J, Hata N, Wells WM, et al. Image registration for targeted MRIguided transperineal prostate biopsy. J Magn Reson Imaging. 2012;36(4):987–992. doi: 10.1002/jmri.23688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schreibmann E, Chen GTY, Xing L. Image interpolation in 4D CT using a BSpline deformable registration model. Int. J. Radiat. Oncol. Biol. Phys. 2006 Apr 1;64(5):1537–1550. doi: 10.1016/j.ijrobp.2005.11.018. [DOI] [PubMed] [Google Scholar]
- 18.Rietzel E, Chen GTY. Deformable registration of 4D computed tomography data. Med. Phys. American Association of Physicists in Medicine. 2006 Oct 31;33(11):4423. doi: 10.1118/1.2361077. [DOI] [PubMed] [Google Scholar]
- 19.Oguro S, Tokuda J, Elhawary H, Haker S, Kikinis R, Tempany CMC, et al. MRI signal intensity based B-spline nonrigid registration for pre- and intraoperative imaging during prostate brachytherapy. J. Magn. Reson. Imaging. 2009 Nov;30(5):1052–1058. doi: 10.1002/jmri.21955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hellier P, Barillot C, Mémin E, Pérez P. Hierarchical estimation of a dense deformation field for 3-D robust registration. IEEE Trans Med Imaging. 2001 May;20(5):388–402. doi: 10.1109/42.925292. [DOI] [PubMed] [Google Scholar]
- 21.Walimbe V, Shekhar R. Automatic elastic image registration by interpolation of 3D rotations and translations from discrete rigid-body transformations. Med. Image Anal. 2006 Dec;10(6):899–914. doi: 10.1016/j.media.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 22.Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. elastix: a toolbox for intensity-based medical image registration. IEEE Trans Med Imaging. 2010;29(1):196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
- 23.Shams R, Sadeghi P, Kennedy R, Hartley R. A survey of medical image registration on multicore and the GPU. IEEE Signal Process. Mag. IEEE. 2010 Mar 1;27:50–60. (March) [Google Scholar]
- 24.Ito K, Choji T, Nakada T, Nakanishi T, Kurokawa F, Okita K. Multislice dynamic MRI of hepatic tumors. J Comput Assist Tomogr. 1993;17(3):390–396. doi: 10.1097/00004728-199305000-00010. [DOI] [PubMed] [Google Scholar]
- 25.Yamashita Y, Mitsuzaki K, Yi T, Ogata I, Nishiharu T, Urata J, et al. Small hepatocellular carcinoma in patients with chronic liver damage: prospective comparison of detection with dynamic MR imaging and helical CT of the whole liver. Radiology. 1996;200(1):79–84. doi: 10.1148/radiology.200.1.8657948. [DOI] [PubMed] [Google Scholar]
- 26.Peterson MS, Baron RL, Murakami T. Hepatic malignancies: usefulness of acquisition of multiple arterial and portal venous phase images at dynamic gadolinium-enhanced MR imaging. Radiology. 1996;201(2):337–345. doi: 10.1148/radiology.201.2.8888220. [DOI] [PubMed] [Google Scholar]
- 27.Semelka RC, Martin DR, Balci C, Lance T. Focal liver lesions: comparison of dual-phase CT and multisequence multiplanar MR imaging including dynamic gadolinium enhancement. J Magn Reson Imaging. 2001;13(3):397–401. doi: 10.1002/jmri.1057. [DOI] [PubMed] [Google Scholar]
- 28.Gering DT, Nabavi A, Kikinis R, Hata N, O’Donnell LJ, Grimson WE, et al. An integrated visualization system for surgical planning and guidance using image fusion and an open MR. J Magn Reson Imaging. 2001;13(6):967–975. doi: 10.1002/jmri.1139. [DOI] [PubMed] [Google Scholar]
- 29.Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin J-CC, Pujol S, et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging. 2012 Nov;30(9):1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 1999 Jan;32(1):71–86. [Google Scholar]
- 31.Shoemake K. Quaternion calculus and fast animation, computer animation: 3-D motion specification and control. SIGGRAPH’87. 1987 [Google Scholar]
- 32.Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, et al. N4ITK: improved N3 bias correction. IEEE Trans. Med. Imaging. 2010 Jun;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Arnold JB, Liow JS, Schaper KA, Stern JJ, Sled JG, Shattuck DW, et al. Qualitative and quantitative evaluation of six algorithms for correcting intensity nonuniformity effects. Neuroimage. 2001 May;13(5):931–943. doi: 10.1006/nimg.2001.0756. [DOI] [PubMed] [Google Scholar]
- 34.Boyes RG, Gunter JL, Frost C, Janke AL, Yeatman T, Hill DLG, et al. Intensity non-uniformity correction using N3 on 3-T scanners with multichannel phased array coils. Neuroimage. 2008 Feb 15;39(4):1752–1762. doi: 10.1016/j.neuroimage.2007.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zheng W, Chee MWL, Zagorodnov V. Improvement of brain segmentation accuracy by optimizing non-uniformity correction using N3. Neuroimage. 2009 Oct 15;48(1):73–83. doi: 10.1016/j.neuroimage.2009.06.039. [DOI] [PubMed] [Google Scholar]
- 36.Johnson HJ, Harris G, Williams K. BRAINSFit: Mutual Information Registrations of Whole-Brain 3D Images, Using the Insight Toolkit. Insight J. 2007 [Google Scholar]
- 37.Mattes D, Haynor DR, Vesselle H, Lewellen TK, Eubank W. PET-CT image registration in the chest using free-form deformations. Med. Imaging, IEEE Trans. 2003;22(1):120–128. doi: 10.1109/TMI.2003.809072. [DOI] [PubMed] [Google Scholar]
- 38.Byrd RH, Lu P, Nocedal J, Zhu C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. SIAM PUBLICATIONS, 3600 UNIV CITY SCIENCE CENTER PH#382-9800, PHILADELPHIA, PA 19104-2688. 1995 Sep;16(5):1190–1208. [Google Scholar]
- 39.Bharatha A, Hirose M, Hata N, Warfield SK, Ferrant M, Zou KH, et al. Evaluation of three-dimensional finite element-based deformable registration of pre- and intraoperative prostate imaging. Med Phys. 2001 Dec;28(12):2551–2560. doi: 10.1118/1.1414009. [DOI] [PubMed] [Google Scholar]
- 40.Zou KH, Warfield SK, Bharatha A, Tempany CM, Kaus MR, Haker SJ, et al. Statistical validation of image segmentation quality based on a spatial overlap index. Acad Radiol. 2004;11(2):178–189. doi: 10.1016/S1076-6332(03)00671-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Morikawa S, Inubushi T, Kurumi Y, Naka S, Sato K, Tani T, et al. MR-guided microwave thermocoagulation therapy of liver tumors: initial clinical experiences using a 0.5 T open MR system. J. Magn. Reson. Imaging. 2002 Nov;16(5):576–583. doi: 10.1002/jmri.10198. [DOI] [PubMed] [Google Scholar]
- 42.Morrison PR, Silverman SG, Tuncali K, Tatli S. MRI-guided cryotherapy. J. Magn. Reson. Imaging. 2008 Feb;27(2):410–420. doi: 10.1002/jmri.21260. [DOI] [PubMed] [Google Scholar]
- 43.Rempp H, Waibel L, Hoffmann R, Claussen CD, Pereira PL, Clasen S. MR-guided radiofrequency ablation using a wide-bore 1.5-T MR system: clinical results of 213 treated liver lesions. Eur. Radiol. 2012 Sep;22(9):1972–1982. doi: 10.1007/s00330-012-2438-x. [DOI] [PubMed] [Google Scholar]
- 44.Passera K, Selvaggi S, Scaramuzza D, Garbagnati F, Vergnaghi D, Mainardi L. Radiofrequency ablation of liver tumors: quantitative assessment of tumor coverage through CT image processing. BMC Med. Imaging. 2013 Jan;13:3. doi: 10.1186/1471-2342-13-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Asanovic K, Bodik R, Demmel J, Keaveny T, Keutzer K, Kubiatowicz J, et al. A View of the Parallel Computing Landscape. Commun. ACM. 2009;52(10):56–67. [Google Scholar]
- 46.Xie Y, Chao M, Xiong G. Deformable image registration of liver with consideration of lung sliding motion. Med. Phys. 2011 Oct;38(10):5351–5361. doi: 10.1118/1.3633902. [DOI] [PubMed] [Google Scholar]