Graph theoretic analysis of structural connectivity across the spectrum of Alzheimer's disease: The importance of graph creation methods

Abstract

Graph theory is increasingly being used to study brain connectivity across the spectrum of Alzheimer's disease (AD), but prior findings have been inconsistent, likely reflecting methodological differences. We systematically investigated how methods of graph creation (i.e., type of correlation matrix and edge weighting) affect structural network properties and group differences. We estimated the structural connectivity of brain networks based on correlation maps of cortical thickness obtained from MRI. Four groups were compared: 126 cognitively normal older adults, 103 individuals with Mild Cognitive Impairment (MCI) who retained MCI status for at least 3 years (stable MCI), 108 individuals with MCI who progressed to AD-dementia within 3 years (progressive MCI), and 105 individuals with AD-dementia. Small-world measures of connectivity (characteristic path length and clustering coefficient) differed across groups, consistent with prior studies. Groups were best discriminated by the Randić index, which measures the degree to which highly connected nodes connect to other highly connected nodes. The Randić index differentiated the stable and progressive MCI groups, suggesting that it might be useful for tracking and predicting the progression of AD. Notably, however, the magnitude and direction of group differences in all three measures were dependent on the method of graph creation, indicating that it is crucial to take into account how graphs are constructed when interpreting differences across diagnostic groups and studies. The algebraic connectivity measures showed few group differences, independent of the method of graph construction, suggesting that global connectivity as it relates to node degree is not altered in early AD.

Highlights

• •Cortical thickness networks were compared across the spectrum of AD.
• •The impact of graph creation methods on diagnostic group differences was examined.
• •Path length, clustering coefficient, and Randić index differed across groups.
• •Graph measures may be useful for tracking and predicting AD progression.
• •Group differences (size and direction) were dependent on the graph creation method.
• •Awareness of how graphs are created is crucial for interpreting AD-related changes.

1. Introduction

Graph theory, a branch of mathematics, is increasingly being used to study the connectivity properties of structural and functional brain networks in individuals across the spectrum of Alzheimer's disease (AD) (for reviews, see Griffa et al., 2013; Tijms et al., 2013b). These investigations have been partially motivated by the finding that AD is characterized by changes in brain connectivity resulting from synaptic dysfunction and loss (Brickman et al., 2009; D'Amelio and Rossini, 2012; Scheff et al., 2011; Scheff and Price, 2006; Selkoe, 2002), as well as neuronal loss and global atrophy (Braak and Braak, 1991; Gomez-Isla et al., 1996; Kordower et al., 2001; Whitwell et al., 2012). In fact, the progressive synaptic and neural degeneration across the continuum of AD has led to the proposal that AD may be considered a ‘disconnection syndrome’ (for a review, see Delbeuck et al., 2003), whereby the normal functional and structural connectivity of the brain becomes increasingly disturbed. Although the precise mechanisms underlying neuronal injury in AD are unclear, it is hypothesized to result from the aggregation of β-amyloid and tau (Fein et al., 2008; Henkins et al., 2012; Takahashi et al., 2010), the two neuropathological hallmarks of AD.

Graph theory provides a set of tools that can be used to quantify the connectivity patterns of complex networks. In this framework, ‘nodes’ represent brain regions and ‘edges’ the network connections between them. Based on the number and distribution of the edges, a variety of measures can be computed to describe global and local connectivity properties (for an overview, see Rubinov and Sporns, 2010). The application of graph theory to the study of AD is appealing because AD pathology progresses throughout the brain in an orderly fashion (Braak and Braak, 1991), suggesting that connectivity properties may also change in an ordered manner over the course of the disease and may have diagnostic and prognostic utility.

Prior graph theoretic studies of AD dementia and Mild Cognitive Impairment (MCI) have used a variety of methods, including structural MRI (He et al., 2008; Li et al., 2012; Tijms et al., 2013a, 2014; Yao et al., 2010) and diffusion tensor imaging (DTI) (Bai et al., 2012; Lo et al., 2010; Shu et al., 2012; Sun et al., 2014) to study anatomic connectivity, as well as resting state functional MRI (rsfMRI) (Sanz-Arigita et al., 2010; Sun et al., 2014; Supekar et al., 2008; Zhao et al., 2012), electroencephalography (EEG) (de Haan et al., 2009; Stam et al., 2007), and magneto-encephalography (MEG) (de Haan et al., 2012a; Stam et al., 2009) to study functional connectivity. Although there is agreement among these studies that AD dementia and Mild Cognitive Impairment are associated with changes in network properties, there is surprisingly little agreement about the nature of these changes. For example, inconsistent results have been reported for the two metrics that have been most frequently examined: characteristic path length, a measure of the average network distance between regions, and the clustering coefficient, a measure of local interconnectivity. Some studies have reported increases in the clustering coefficient as a function of disease severity (He et al., 2008; Yao et al., 2010; Zhao et al., 2012), others have reported a decrease (Li et al., 2012; Stam et al., 2009; Sun et al., 2014; Tijms et al., 2013a) and still others found no difference (Bai et al., 2012; Lo et al., 2010; Sanz-Arigita et al., 2010; Stam et al., 2007). Likewise, for the characteristic path length, AD-related increases (Bai et al., 2012; He et al., 2008; Lo et al., 2010; Shu et al., 2012; Yao et al., 2010; Zhao et al., 2012) and decreases have been reported (Sanz-Arigita et al., 2010; Tijms et al., 2013a, 2014).

While some of the variability in prior findings likely reflects differences in the underlying biological substrates of the networks (e.g., white matter fiber track networks, cortical thickness networks, or resting state functional networks), part of the inconsistency may also reflect methodological differences in network creation. For example, some studies used binary edges, whereby the strength of all connections is weighted equally (He et al., 2008; Li et al., 2012; Shu et al., 2012; Stam et al., 2007; Supekar et al., 2008; Tijms et al., 2013a; Yao et al., 2010), while others have used weighted edges, meaning that connections can differ in strength (Bai et al., 2012; Lo et al., 2010; Stam et al., 2009; Sun et al., 2014). Additionally, different methods have been used to construct the correlation matrix (or adjacency matrix) that is used to determine the presence of an edge, such as ordinary Pearson correlations (e.g., Li et al., 2012; Sun et al., 2014; Tijms et al., 2013a, 2014; Yao et al., 2010), partial correlations (e.g., He et al., 2008; Zhao et al., 2012), or synchronization likelihood for functional connectivity data (e.g., de Haan et al., 2012a; Sanz-Arigita et al., 2010; Stam et al., 2007). Although it has been documented that different methods of edge creation can alter the topological properties of brain graphs (e.g., Liang et al., 2012; Van Schependom et al., 2014), prior studies of AD have each used only one method of network creation and it remains unclear how different methods influence the magnitude and direction of topological differences between cognitively normal individuals, individuals with MCI, and patients with AD-dementia.

The first aim of the current study is to address this issue for one imaging modality, structural MRI, by investigating how cortical thickness (CT) networks differ across the spectrum of AD as a function of the type of correlation matrix and method of edge weighting. Positive, negative, and absolute correlations were examined separately (see Gong et al., 2012), resulting in 24 different graphs that were compared. Consistent with prior studies, characteristic path length and the clustering coefficient were examined. The second aim is to investigate three graph measures that have received little or no attention in the study of AD: (1) the Randić index, a measure of assortativity, or the tendency of similar nodes to connect to one another (Randić, 1975), (2) the Fiedler value, also known as algebraic connectivity, a graph spectral measure that contains information about the global connectivity of a network (de Haan et al., 2012b; Fiedler, 1973), and (3) the normalized Fiedler value, which is similar to the Fiedler value, but normalized for the number of edges in a graph (Chung, 1997). These measures are all indices of global connectivity (for a review, see Kincaid and Phillips, 2011), which we hypothesized would be affected in AD. Lastly, to our knowledge, prior studies have not examined the utility of graph theoretic measures to predict the progression of AD. Therefore, the third aim of this study is to examine the predictive utility graph measures for differentiating patients with stable and progressive MCI, based on their CT networks obtained at baseline.

2. Methods

2.1. Subjects

All subjects in this study were selected from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database (http://adni.loni.usc.edu/). We analyzed data available as of May 2013. ADNI is a comprehensive, multisite longitudinal study designed to identify biomarkers to predict the progression of MCI and AD. It was launched in 2003 as a public–private partnership. The MRI data used in this study was obtained at baseline from subjects enrolled in the initial phase (ADNI-1). Study subjects gave written informed consent at enrollment for data collection, storage and use for research. Each participating institution's Institutional Review Board approved the study. The data were anonymized before being made publicly available. At baseline, subjects were medically stable, free from significant neurological and psychiatric conditions, and did not have significant cerebrovascular risk factors. For additional information about ADNI, including data collection and full inclusion and exclusion criteria, see http://www.adni-info.org.

Data from four groups of subjects were included in the current study: 127 individuals who were cognitively normal at baseline and remained cognitively normal for at least 3 years (stable normal group); 104 individuals diagnosed with MCI at baseline who retained a diagnosis of MCI for at least 3 years (stable MCI group); 106 individuals who were diagnosed with MCI at baseline and progressed to AD-dementia within 3 years; and 108 participants with a baseline diagnosis of AD-dementia. All participants had an MRI scan at their baseline visit and were administered the Clinical Dementia Rating (CDR) scale (Morris, 1993). The baseline CDR score was 0 for the cognitively normal group, 0.5 for the stable and progressive MCI groups and 0.5–1 for AD-dementia group. See Table 1 for participant characteristics at baseline. One-way analyses of variance (ANOVAs) indicated that there was no age difference across diagnostic groups (p > 0.6), but that education differed between groups (F = 7.45, p < 0.0001), such that patients with AD-dementia had fewer years of education than the other three groups (all p < 0.003). A chi-square test indicated that the distribution of males and females also differed across diagnostic groups, with significantly fewer females in the Stable MCI group than in the normal and AD-dementia groups (both p < 0.05). To remove any effects of age, gender, and education on the resulting CT graphs, we controlled for these variables as described below.

Table 1.

Participant characteristics at baseline.

Variable	Cognitively normal (N = 127)	Stable MCI (N = 104)	Progressive MCI (N = 108)	AD-dementia (N = 106)
Age, mean number of years (SD)	80.8 (4.8)	79.7 (7.9)	79.5 (6.9)	80.0 (7.7)
Age range (years)	65–96	61–94	61–94	63–97
Gender, females (%)*	49.6	35.6	43.5	53.8
Education, mean number of years (SD)**	16.1 (2.6)	15.7 (2.9)	15.6 (3.0)	14.4 (3.0)
MMSE, mean score (SD)**	29.1 (1.0)	27.5 (1.7)	26.7 (1.7)	23.4 (1.9)

Abbreviations: MMSE = Mini Mental Status examination.

^*Indicates significant difference across groups (p < 0.05), as assessed by a chi-square test.

^**Indicates significant difference across groups (p < 0.0001), as assessed by one-way ANOVA.

2.2. MRI data acquisition and cortical thickness reconstructions

Standard T1-weighted MR images were acquired sagittally with different 1.5 T scanners using a three-dimensional magnetization prepared rapid gradient-echo (MPRAGE) sequence varying in repetition time and echo time with an in-plane resolution of 1.25 × 1.25 mm and 1.2 mm slice thickness. Additional details about the MRI acquisition procedures are available at the ADNI website (http://www.adni-info.org).

Cortical reconstruction and automated thickness measures were performed using the Freesurfer software, version 5.1 (Fischl and Dale, 2000), which is documented and freely available for download online (http://surfer.nmr.mgh.harvard.edu). Only images that passed a quality review were included in the present analyses. Cortical thickness was measured in subjects' native space. The average CT for each of the 68 cortical regions of interest (ROIs) as provided by Freesurfer (34 regions per hemisphere, Desikan et al., 2006) was used to construct the brain graphs.

2.3. Construction of cortical networks

First, for each cortical region, a linear regression was performed to remove the effects of age, gender, and education. The resulting residuals were then used instead of the raw CT values to construct the graphs. Note that past studies generally controlled for age and gender in the same manner, but did not usually control for education. However, we felt that it was important to do so because years of education were inversely associated with cortical thickness of many regions in all diagnostic groups, in line with prior findings (e.g., Querbes et al., 2009).

Consistent with previous studies, each ROI represented a node in a graph and a connection (or edge) was defined as a statistical association in cortical thickness between brain regions (e.g., He et al., 2008). For each diagnostic group, a set of 8 inter-regional correlation matrices (68 × 68 ROIs) were then computed by calculating correlation coefficients across individuals between every pair of regions: (1) absolute Pearson correlation, (2) positive Pearson correlation values only, (3) absolute Pearson correlation, controlling for mean CT, (4) positive Pearson correlation values only, controlling for mean CT, (5) negative Pearson correlation values only, controlling for mean CT, (6) absolute partial correlation, (7) positive partial correlation values only, and (8) negative partial correlation values only. Negative Pearson correlation matrices were not computed because the majority of the Pearson correlations were positive. The absolute Pearson correlation matrix, controlled for mean CT, was computed by including each individual's mean CT value (across all regions) as an additional variable in the linear regressions, along with age, gender, and education, prior to construction of the correlation matrix. The partial correlation between two regions represents their conditional dependencies after partialling out the effects of all of the other regions (e.g., He et al., 2008). This approach allowed us to examine different methods for accounting for overall CT: at the level of the linear regressions, by partialling out the effect of all other regions, and by using CT weighting (see below). Positive, negative, and absolute CT correlations were examined separately because prior work suggests that they show a differential relationship to white matter diffusion connectivity and may measure different aspects of connectivity (Gong et al., 2012).

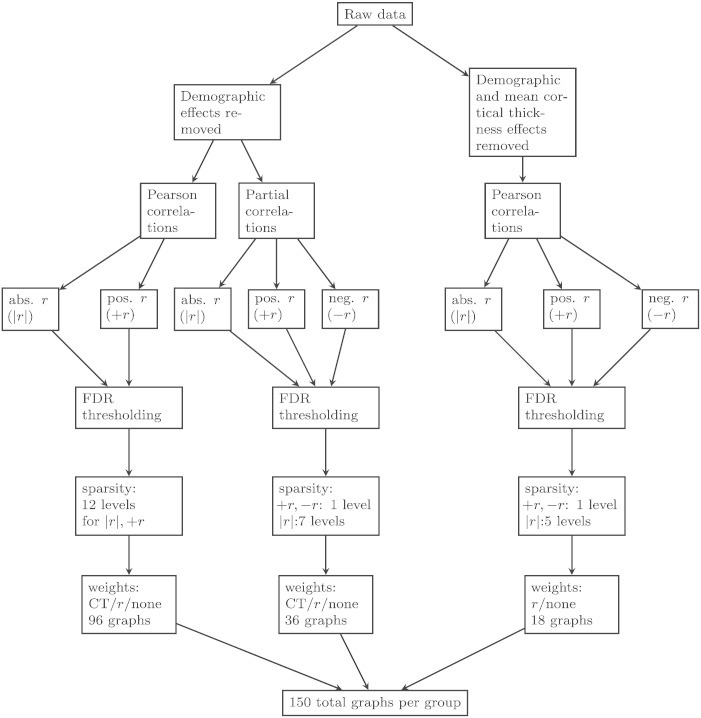
Two brain regions were defined as being connected in a graph when there was a significant correlation between them, corrected for multiple comparisons using the false discovery rate (FDR) at a q value of 0.05 (Genovese et al., 2002). For connected brain regions (i.e., those whose correlation meets the FDR threshold), three different types of edge weights were applied to investigate how different methods of edge weighting affect graph measures: uniform weights (i.e., unweighted graphs), correlation-coefficient weights, and cortical-thickness weights. For unweighted graphs, all significant edges received a weight of 1; all other edges were set to 0. For correlation-weighted graphs, significant edges received a weight corresponding to the actual correlation coefficient between two regions and non-significant edges were set to 0. For cortical-thickness weighted graphs, significant edges received a weight corresponding to the normalized product of the actual thicknesses of the two regions. This latter weighting method has not been used previously, to our knowledge. We reasoned that if two regions are connected (as indicated by a significant correlation between them), but both regions are very thin (due to AD-related atrophy) then the actual amount of information that can be transferred between regions would be low. Likewise, when two regions are thick, they would be expected to communicate more efficiently because they have more neurons and/or synapses. When one region is thin and one region is thick, the thin region may impose an upper bound on the amount of information transfer between the two regions, which we modeled by using the product of the thickness of the two regions (rather than the average thickness). There are other potential methods of edge weighting one could use to model different underlying biological properties (such as amount of amyloid or tau burden in a given ROI), but we restricted ourselves to these as a starting point. Note that the CT weights could not be applied to graphs where mean CT was controlled at the level of the linear regressions because the resulting thickness values were both positive and negative (centered around 0) and negative weights cannot applied. Thus, in total we constructed 24 types of graphs for each diagnostic group (see Fig. 1 for a summary of how the graphs were constructed). All graphs were undirected.

Fig. 1.

This figure depicts the different graph creation methods. Starting from the raw data, there were two possible linear regressions used, one of which controlled for mean cortical thickness and both controlled for the demographic effects of age, gender, and education. For the latter regression, either Pearson or partial correlations were calculated whereas only Pearson correlations were used when the effect of mean cortical thickness was removed. Then, an FDR thresholding was applied to determine significant edges on (1) absolute r-values, (2) positive r-values only, or (3) negative r-values. Then sparsity thresholding was applied at various levels. Finally, edge weights were applied (uniform, r-values, or cortical thickness).

2.3.1. Graph theoretic analysis

The graph measures were computed using in-house software written in R (version 3.0.2) and C. For each graph and diagnostic group, five graph measures were calculated: the mean network characteristic path length, the mean clustering coefficient, the Randić index, the Fiedler value, and the normalized Fiedler value. Briefly, the characteristic path length, CPL, is the average of the shortest path lengths over all pairs of nodes in a graph (Watts and Strogatz, 1998). CPL represents a measure of graph efficiency, in the sense that it represents the average arc distance between any pair of nodes.

The mean clustering coefficient, CC, is the average of the clustering coefficients over all nodes in a network. For unweighted graphs, the clustering coefficient, C_i, of node i is defined as the number of connections among the immediately connected neighbors of the node divided by all their possible connections (Watts and Strogatz, 1998). For weighted graphs, the clustering coefficient represents the sum of weights from node i to adjacent nodes neighboring i divided by the potential sum of weights. More precisely, let w_jk denote the weight between nodes j and k and let $w_i={\sum }_j{w}_{ij.}$ Note that we define w_jk to be zero if there is no edge between nodes j and k. Define A_ij to be 1 if there is an edge between nodes i and j and let d_i denote the number of edges touching node i. Then, for weighted graphs, the clustering coefficient of node i when d_i > 1 is $C_i=\frac{2}{(d_i-1)w_i}{\sum }_{j,k}\frac{w_{ij}+w_{ik}}{2}\left(A_{ij}{A}_{ik}{A}_{jk}\right)$, where j and k range over the neighbors of i. If d_i is equal to 1, then node i has only one neighbor, so we set C_i to zero. We assume that all nodes have at least one neighbor. For both weighted and unweighted graphs, CC = $\frac{1}{n}\sum _{i=1}^n{C}_i$ where n denotes the number of nodes in the graph. The clustering coefficient for a network reflects, on average, the prevalence of clustered connectivity around individual nodes.

The Randić index can be considered a measure of assortativity, or similarity between connected nodes (Randić, 1975). It measures the degree to which nodes with a similar number of edges are connected to one another. A high Randić index indicates that nodes with high “degree” (i.e., many edges) tend to be connected to other high-degree nodes, similar to the “rich club phenomenon”. For a graph G, the general Randić index R_α(G) is defined as the sum of (w_iw_j)^α over all edges ij of G, where w_i denotes the weighted degree of a node i of G and α is an arbitrary real number. Thus, in the case where we have a binary graph, the weight of every edge is one, and w_i is the number of adjacent edges, i.e., the degree, and when the graph is weighted, w_i is the sum of the weights of the adjacent edges. The Randić index is a generalization of the assortativity coefficient (Bollobás and Erdős, 1998). Whereas Randić initially proposed using a = −1/2, we are using a = 1, in which case the Randić index is the same as the assortativity coefficient. For further details about measures of assortativity see (Estrada, 2011).

The Fiedler value, or algebraic connectivity, was introduced by Fiedler in 1973 and can be thought of as a measure of network robustness (Fiedler, 1973). The Fiedler value is equal to the second-smallest eigenvalue of the Laplacian matrix. The second smallest eigenvalue is used as it can be proven that the smallest eigenvalue of the Laplacian is always zero (Fiedler, 1973). The Laplacian matrix combines both degree information and connectivity information in the same matrix. Specifically, the Laplacian matrix is derived by subtracting the adjacency matrix from the degree matrix. We denote the number of nodes by n. The degree of a node is equal to the number of edges adjacent to the node. The degree matrix is an n by n diagonal matrix where the main diagonal consists of the degrees of each node in the graph. The adjacency matrix of a graph is an n by n matrix where the ijth entry is equal to one if there is an edge between nodes i and j, for all i,j = 1,…, n. The study of the eigenvalues of the Laplacian and adjacency matrix is a part of algebraic graph theory known as spectral graph theory (see, Chung, 1997; Spielman, 2007).

Because the Fiedler value is weakly increasing in the number of edges in a graph, we are also interested in the normalized Fiedler value (Chung, 1997). Let s_i denote the square root of the degree of node i, and L_ij denote the ijth entry of the Laplacian. The normalized Laplacian is defined as the matrix where the ijth entry is L_ij / (s_is_j). The normalized Fiedler value is the second smallest eigenvalue of the normalized Laplacian. Intuitively, the relationship between the Laplacian and the normalized Laplacian is analogous to the relationship between the covariance and correlation matrices, respectively.

Consistent with prior studies, we employed a sparsity thresholding approach to control for the number of edges in a graph across diagnostic groups (He et al., 2008). This was done because the network topology measures used are sensitive to the number of edges in a graph and our diagnostic groups had different numbers of edges for a given type of graph. Thus, without this (or some other correction), group differences in network measures would not only reflect differences in the topology of a graph, but also differences in the number of edges. Sparsity (S) is defined as the total number of edges in a graph divided by the maximum number of possible edges. In general, for a graph with n nodes, there are n choose 2 = n(n − 1) / 2 possible edges assuming all edges are between distinct nodes and only one edge is allowed between nodes. Graph measures were examined over a range of sparsity values, 4% ≤ S ≤ 17%, except for graphs based on Pearson correlations, where the maximum connectivity density examined was 47% (see Results). This range was chosen because it is comparable to what has been used in prior studies (e.g., Gong et al., 2012; He et al., 2008; Yao et al., 2010) and because at the lower connectivity density ranges (S < 10%), there seems to be a better correspondence between CT correlations and actual fiber connections as determined with DTI (Gong et al., 2012). The sparsity correction was implemented by removing edges sequentially in order of least significance. Once all edges had been removed, the largest subgraph was selected and graph topology measures were always calculated on the largest component (i.e., disconnected nodes were not included in the calculation of any graph measure). Sparsity for all graphs, including subgraphs with fewer than 68 nodes, was always calculated as the percentage of edges out of the total number of possible edges in a fully connected graph with 68 nodes (i.e., out of 2278 edges). This way, the absolute number of edges in each graph and the correlation threshold for selecting significant edges was the same across diagnostic groups after sparsity thresholding.

2.3.2. Statistical analysis

To determine if the network topology measures were statistically different across diagnostic groups, nonparametric permutation testing was used (He et al., 2008). For each type of graph, the five graph measures were computed at each level of sparsity, separately for each diagnostic group. Then, we randomly assigned each subject to one of the four possible diagnostic groups, recomputed the correlation matrix for each randomized group, applied the FDR correction, and then recomputed the five network measures for each randomized group. This procedure was repeated 10,000 times and the 95th percentile of each distribution was used as the critical value for a two-tailed test of the null hypothesis with a probability of type I error of 0.05. The procedure was repeated for each sparsity threshold. For each level of sparsity and type of graph, initially only the normal and AD-dementia groups were compared. If this comparison was not significant, no further group comparisons were performed. If the normal and AD-dementia groups differed significantly, the remaining 5 group comparisons were performed, correcting for multiple hypothesis testing at the group level (i.e., 6 comparisons) at FDR < 0.05.

3. Results

Table 2 shows the sparsity of each of the 24 graphs after the FDR correction. For all types of graphs, the connectivity density increased with disease severity, such that cognitively normal participants and individuals with stable MCI had the fewest edges and patients with progressive MCI and AD-dementia had the most edges. Similar findings have been reported for gray matter networks (Tijms et al., 2013b). This ordering likely reflects the fact that there is greater variability in the CT values among the cognitively impaired individuals due to a greater range of atrophy among these individuals compared to cognitively normal participants. Thus, individuals with high levels of atrophy in one region likely also had high levels of atrophy in other regions, leading to more significant correlations (and more edges) for the AD-dementia and progressive MCI groups relative to the other two groups. Consistent with this interpretation, the mean variance of CT values (computed as the standard deviation of mean CT for each ROI across subjects) was significantly lower for the cognitively normal participants and stable-MCI groups relative to the other two groups (both p < 0.01, as assessed by t-tests). Additionally, those ROIs showing greater increases in variability between the normal and AD-dementia groups also showed greater increases in their average correlations with other regions (r(66) = 0.40, p = 0.0008, see Supplementary Figures 1 and 2).

Table 2.

Sparsity of graphs as a function of the type of correlation matrix.

Diagnostic group	Pearson correlation		Pearson correlation (controlling for mean cortical thickness)			Partial correlation
Absolute values	Pos. values	Absolute values	Pos. values	Neg. values	Absolute values	Pos. values	Neg. values
Normal	80.3%	80.3%	12.7%	7.9%	4.6%	8.5%	5.0%	3.3%
MCI-stable	78.0%	77.9%	10.5%	6.5%	3.7%	14.9%	8.9%	6.0%
MCI-progressive	87.4%	87.4%	20.1%	12.0%	8.2%	15.8%	9.1%	6.8%
AD-Dementia	89.5%	89.5%	20.3%	11.7%	8.6%	22.6%	12.9%	9.7%

Abbreviations: Pos. = positive; Neg. = negative.

Note: In each graph, all edges are significant using FDR correction of q < 0.05.

For graphs based on absolute partial Pearson correlations, the connectivity density (after FDR correction) ranged from 8.5% (normal group) to 22.6% (AD-dementia group), see Table 2. Therefore, graph measures were examined for sparsities ranging from 4 to 9%, in 1% increments. For graphs based on only positive or negative partial correlations, the sparsities ranged from 5.0% (normal group) to 12.9% (AD-dementia group) and 3.3% (normal group) to 9.7 % (AD dementia group), respectively. Because these graphs were very sparse, the corresponding graph measures were only evaluated at these sparsities (i.e., 5% for positive partial correlations and 3.3% for negative partial correlations). For graphs based on Pearson correlations that controlled for mean CT, the lowest connectivity density across groups was 10.5% for absolute values, 6.5% for positive values, and 3.7% for negative values. The graph measures were therefore evaluated at sparsities ranging from 4% to 10% for absolute values, 5% for positive values, and 3.7% for negative values. Lastly, for graphs based on absolute and positive Pearson correlations (not controlling for mean CT), sparsity values were S > 75% for all groups. We therefore examined the graph measures at the same sparsities values as for the other graphs to be able to compare them directly to one another (i.e., 4% for 10%), as well as at 17%, 33%, 40%, 47%. Given that most of the Pearson correlations (not controlling for mean CT) were positive, the results for graphs based on absolute and positive correlation values were the same and we only present the results for the absolute values.

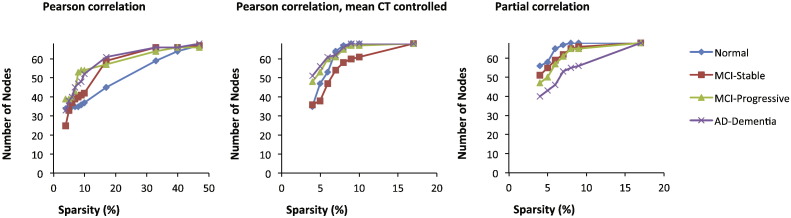
Because the graphs based on partial correlations and those based on Pearson correlations controlling for mean CT were not fully connected at their maximum connectivity density values (and thus had different numbers of nodes across groups, see Fig. 2), we also examined the graph metrics at a sparsity threshold, 17%, at which all of these graphs were fully connected. For these analyses, an FDR threshold of q < 0.1 was used. Although this likely introduces more spurious connections, this analysis allowed us to determine whether the pattern of results observed at lower connectivity densities (based on the largest sub-graphs) was the same as for the fully connected graphs. This analysis was important because a difference in the number of nodes across graphs with fixed sparsities can affect graph measures.

Fig. 2.

Number of nodes in each graph as a function of graph sparsity for three types of correlation matrixes: absolute Pearson correlations (left), absolute Pearson correlations, controlling for mean cortical thickness (center), and absolute partial correlations (right).

3.1. Characteristic path length

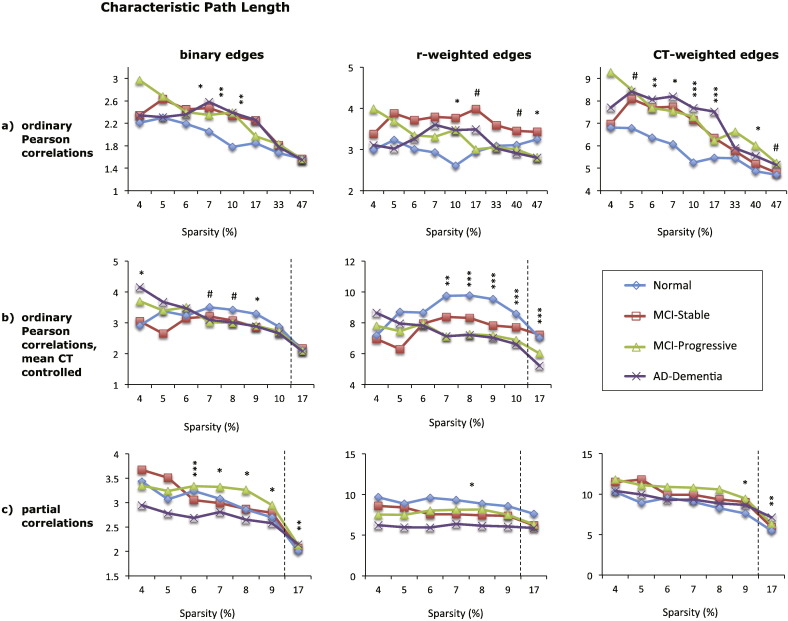
The results for characteristic path length for the 9 graphs based on absolute correlation values are shown in Fig. 3. Overall, the type of edge weights affected the magnitude of group differences, whereas the type of correlation matrix also affected the direction of those differences.

Fig. 3.

Mean characteristic path length (CPL) of eight different cortical networks for the four diagnostic groups (see legend). The top row (a) shows CPL values for graphs based on absolute Pearson correlations, the middle row (b) shows CPL values for graphs based absolute Pearson correlations with mean cortical thickness controlled, and the bottom row (c) shows CPL values for graphs based on absolute partial correlations. Each column shows the results for graphs with different edge weights: binary edges (left column), correlation-weighted edges (middle column), and cortical thickness weighted edges (right column). The x-axis shows the sparsity level (S) at which the CPL values were compared across diagnostic groups. For each level of S shown, only edges that met the FDR correction of q < 0.05 were included, except where S = 17% for graphs shown in (b) and (c), where q < 0.1. Significant differences between the normal and AD-dementia groups are indicated as follows: ^#p < 0.1, * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.005 (all p-values two-tailed).

For graphs based on Pearson correlations (not controlling for mean CT), CPL was shortest for the cognitively normal group relative to the other three groups, particularly over sparsity values ranging from 7 to 17%. The best discrimination between groups was obtained with the thickness-weighted graph, which demonstrated significantly lower CPL values for the cognitively normal group compared AD-dementia group over a wide range of sparsity values (see Fig. 3a, right column), and the MCI groups showed intermediate values.

For graphs based on Pearson correlations that control for mean CT, the pattern of results tended to be in the opposite direction, with cognitively normal individuals showing a longer path length relative to the AD-dementia patients. The best group discrimination was evident for the correlation-weighted graph (Fig. 3b, middle panel), where CPL was greater for the cognitively normal individuals relative to the progressive MCI and AD-dementia groups (all p < 0.007 over a sparsity range of 7–17%), with the stable MCI group showing intermediate values. For graphs based on partial correlations, CPL also tended to decrease with disease severity, although there was not a clear ordering of CPL values across the four diagnostic groups (see Fig. 3c). Additionally, the direction of group differences reversed for the binary partial-correlation graphs at the uncorrected sparsity threshold of 17%, such that CPL increased with disease severity. This reversal may reflect the fact at the lower connection densities, the graphs for the AD dementia group had fewer nodes (and hence higher relative connection density) than the graphs for the cognitively normal group (see Fig. 2) and CPL values tend to be shorter in denser graphs. By comparison, at 17% sparsity the graphs for all groups were the same size, so group differences in CPL values only reflect topological differences.

The results for graphs based on only positive or negative correlations (using FDR-corrected edges) revealed no differences in CPL across groups, except for the graph based on positive partial correlations with binary edges, where individuals with AD-dementia demonstrated a shorter path length than the other three groups (p < 0.05, data not shown).

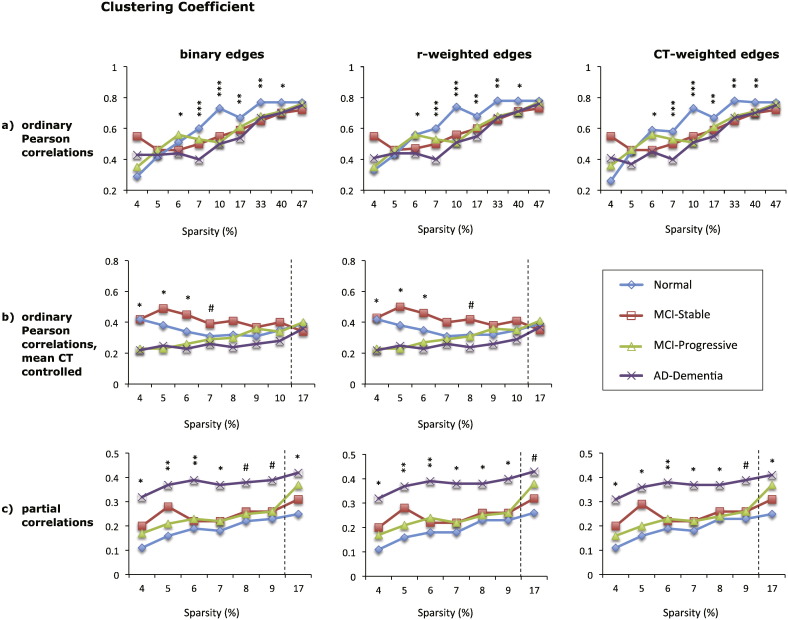
3.2. Clustering coefficient

The mean clustering coefficient for each diagnostic group for the 9 graphs based on absolute correlation values is shown in Fig. 4. While the type of edge weights had little impact on the results, the magnitude and direction of group differences in CC was dependent on the type of correlation matrix.

Fig. 4.

Mean clustering coefficient (CC) of eight different cortical networks for the four diagnostic groups (see legend). The top row (a) shows CC values for graphs based on absolute Pearson correlations, the middle row (b) shows CC values for graphs based absolute Pearson correlations with mean cortical thickness controlled, and the bottom row (c) shows CC values for graphs based on absolute partial correlations. Each column shows the results for graphs with different edge weights: binary edges (left column), correlation-weighted edges (middle column), and cortical thickness weighted edges (right column). The x-axis shows the sparsity level (S) at which the CC values were compared across diagnostic groups. For each level of S shown, only edges that met the FDR correction of q < 0.05 were included, except where S = 17% for graphs shown in (b) and (c), where q < 0.1. Significant differences between the normal and AD-dementia groups are indicated as follows: ^#p < 0.1, * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.005 (all p-values two-tailed).

For graphs based on absolute Pearson correlations, CC tended to decrease for individuals with AD-dementia relative to the cognitively normal group. Specifically, when mean CT was not controlled, CC was significantly lower for the AD-dementia group than for the cognitively normal group over sparsity values of 6–40% (all p < 0.05, see Fig. 4a). Individuals with MCI had intermediate values, but did not differ significantly from the AD-dementia or from the cognitively normal group. While these group differences may partially reflect difference in network size across groups, the same pattern of results was obtained for sparsities of 62% and 70% (data not shown), where all graphs where fully connected. When mean CT was controlled, the magnitude of differences was smaller and less consistent, though in the same direction (see Fig. 4b). When positive and negative correlations were considered separately, there was no difference across groups for graphs using the FDR-corrected sparsity threshold. At 17% connection density, the AD-dementia group had higher CC values than the cognitively normal individuals when positive correlations were considered and mean CT was controlled, and lower CC values when negative correlations were considered (see Supplementary Fig. 3).

Graphs based on absolute partial correlations produced consistent group differences, although the direction of differences was reversed compared to the graphs based on Pearson correlations, with AD-dementia patients showing significantly higher CC values compared to cognitively normal participants over sparsity values of 4–17% (all p  ≤ 0.07). The two MCI groups had intermediate CC values that were significantly lower than the AD-dementia group in some cases, see Fig. 4c. Graphs based on negative partial correlations demonstrated the same pattern of results as those based on absolute correlations, with the AD group having higher CC values than the normal group (p  ≤ 0.06 for graphs at S = 3.3% and S = 17%). However, graphs based on positive partial correlations had clustering values of zero for all groups at S = 5% and significantly lower CC values for the AD-dementia group than the stable MCI and normal groups at S = 17% (all p ≤ 0.05).

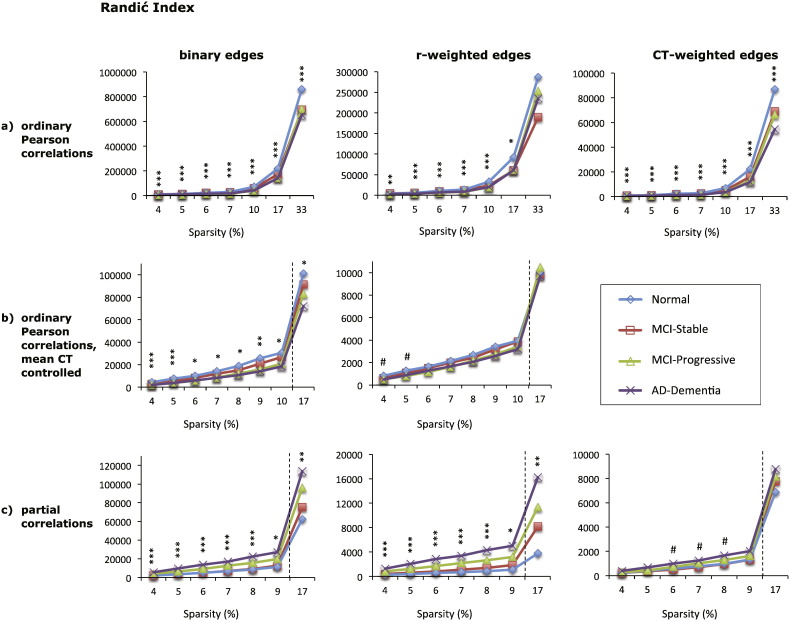
3.3. Randić index

Similar to the clustering coefficient, the type of edge weighting did not affect the direction of group differences in the Randić index, but had some impact on the magnitude of those differences. By comparison, the type of correlation matrix altered the direction of group differences, with graphs based on Pearson correlations demonstrating a decrease in the Randić index with increasing disease severity and graphs based on partial correlations exhibiting the reverse pattern.

In particular, for graphs based on Pearson correlations that did not control for mean CT, the Randić index was lower for individuals with AD-dementia compared to individuals with normal cognition over all sparsity levels examined for binary and CT-weighted graphs (all p < 0.005) and at sparsities of 4–17% for r-weighted graphs (all p < 0.05), see Fig. 5a. The two MCI groups had intermediate values that were lower relative to the cognitively normal group at sparsities of 7–33% for CT-weighted graphs and 10–47% for binary graphs (all p < 0.05). The stable-MCI group had higher Randić index values than the progressive MCI and the AD-dementia groups at sparsity values of 4–10% for binary and CT-weighted graphs (all p < 0.05). When mean CT was controlled, the Randić index was also lower for the AD-dementia group relative to the cognitively normal group for binary graphs (all p < 0.05 at S = 4–17%), while for r-weighted graphs, this difference did not reach significance, see Fig. 5b.

Fig. 5.

Mean Randić index of eight types of cortical networks for the four diagnostic groups. The Randić index of graphs based on absolute Pearson correlations is shown in (a), top row, for graphs based absolute Pearson correlations with mean cortical thickness controlled in (b), middle row, and for graphs based on absolute partial correlations in (c), bottom row. Each column shows the results for graphs with different edge weights: binary edges (left column), correlation-weighted edges (middle column), and cortical thickness weighted edges (right column). The x-axis shows the sparsity level (S) at which the Randić index was compared across diagnostic groups. For each level of S shown, only edges that met the FDR correction of q < 0.05 were included, except where S = 17% for graphs shown in (b) and (c), where q < 0.1. Significant differences between the normal and AD-dementia groups are indicated as follows: ^#p < 0.1, * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.005 (all p-values two-tailed).

For graphs based on partial correlations, the cognitively normal and stable MCI groups had lower Randić index values than the progressive MCI and AD-dementia groups over sparsity levels of 4–17% (all p ≤ 0.05 for binary and r-weighted graphs, see Fig. 5c). Thus, individuals who progressed from MCI to AD within 3 years had higher Randić index values at baseline than those who did not progress over the same time period (see Supplementary Fig. 4). Graphs based on positive and negative partial correlations showed similar patterns as the corresponding graphs based on absolute partial correlations at both the FDR-corrected sparsity threshold and at S = 17% (data not shown), although the difference between the two MCI groups did not reach significance.

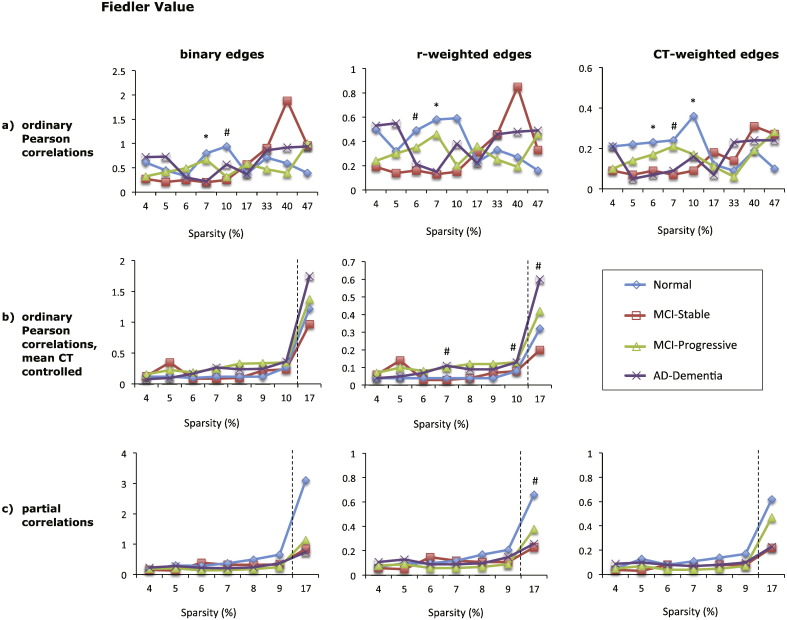
3.4. Fiedler value

There were few differences across diagnostic groups in the Fiedler value for any of the graphs and for many graphs there was no clear ordering in the magnitude of the Fiedler value as a function of disease severity (see Fig. 6). The type of edge weighting had little impact on the result. Graphs based on positive and negative correlations also showed no reliable group differences, suggesting that the Fiedler value does not change significantly with AD.

Fig. 6.

Mean Fiedler value of eight types of cortical networks for the four diagnostic groups. The Fiedler value of graphs based on absolute Pearson correlations is shown in (a), top row, for graphs based absolute Pearson correlations with mean cortical thickness controlled in (b), middle row, and for graphs based on absolute partial correlations in (c), bottom row. Each column shows the results for graphs with different edge weights: binary edges (left column), correlation-weighted edges (middle column), and cortical thickness weighted edges (right column). The x-axis shows the sparsity level (S) at which the Fiedler value was compared across diagnostic groups. For each level of S shown, only edges that met the FDR correction of q < 0.05 were included, except where S = 17% for graphs shown in (b) and (c), where q < 0.1. Significant differences between the normal and AD-dementia groups are indicated as follows: ^#p < 0.1, * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.005 (all p-values two-tailed).

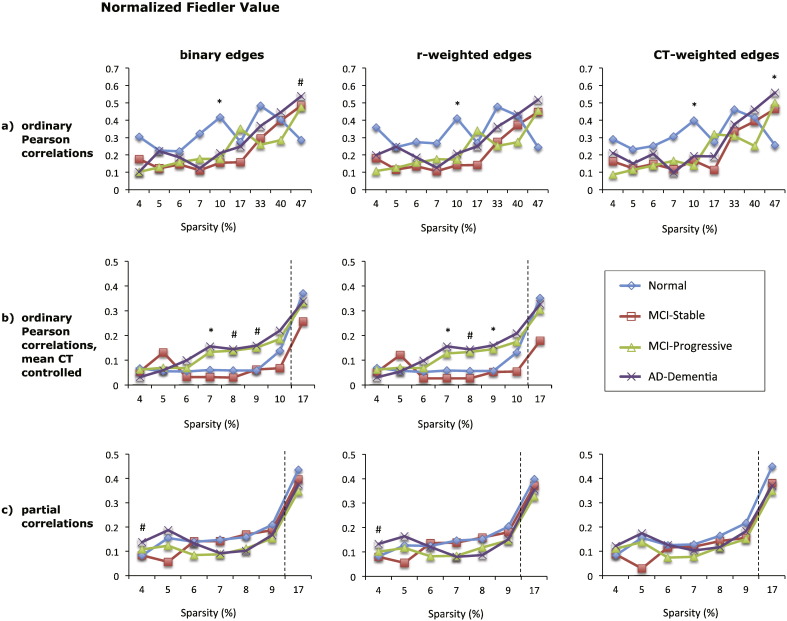
3.5. Normalized Fiedler value

Similar to the Fiedler value, the normalized Fiedler value also showed little difference across diagnostic groups for graphs based on absolute correlations. The type of edge weighting had little effect on the results (see Fig. 7). There were also no significant group differences for graphs based on positive partial correlations, while for graphs based on negative partial correlations there was a decrease in the normalized Fiedler value with increasing AD severity at the 17% sparsity threshold (see Supplementary Fig. 5). At the 17% sparsity threshold, graphs based on positive Pearson correlations with mean CT controlled also demonstrated a decrease of the normalized Fiedler value with AD severity.

Fig. 7.

Mean normalized Fiedler value of eight types of cortical networks for the four diagnostic groups. The normalized Fiedler value of graphs based on absolute Pearson correlations is shown in (a), top row, for graphs based absolute Pearson correlations with mean cortical thickness controlled in (b), middle row, and for graphs based on absolute partial correlations in (c), bottom row. Each column shows the results for graphs with different edge weights: binary edges (left column), correlation-weighted edges (middle column), and cortical thickness weighted edges (right column). The x-axis shows the sparsity level (S) at which the normalized Fiedler value was compared across diagnostic groups. For each level of S shown, only edges that met the FDR correction of q < 0.05 were included, except where S = 17% for graphs shown in (b) and (c), where q < 0.1. Significant differences between the normal and AD-dementia groups are indicated as follows: ^#p < 0.1, * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.005 (all p-values two-tailed).

3.6. Descriptive comparison of graphs based on different correlation matrices

The type of correlation matrix used to construct each graph in some instances changed the direction of significant group differences. While this may be partially attributable to the fact that the number of nodes in each graph differed across diagnostic groups at the low connection densities, the pattern of results was the same for the complete networks in many instances. This indicates that the topology of networks based on different correlation matrices is qualitatively different. To further explore these differences, we compared a subset of the graphs based on three types of correlation matrices in greater detail. Specifically, we compared the hubs (10 nodes with greatest number of edges, summing across hemispheres) and types of connections formed by edges (i.e., ipsilateral vs. contralateral, within-lobe vs. across lobes) in three types of graphs (absolute Pearson correlations, absolute Pearson correlations with mean CT controlled, and absolute partial correlations) for cognitively normal individuals and those with AD-dementia at a fixed sparsity level of S = 9%. This threshold was chosen because all edges included in each of the three types of graphs were significant at the FDR threshold of q < 0.05, thus minimizing the presence of false positive edges.

As shown in Table 3, one of the greatest differences across the three types of graphs is the number of common edges shared by the cognitively normal individuals and those with AD-dementia. Whereas in graphs based on Pearson correlations (with or without mean CT controlled) roughly half of the edges were the same for the two groups of individuals, in graphs based on partial correlations, only 19% of the edges were the same for the two groups of individuals. Likewise, many of the hub regions were the same in the graphs based on Pearson correlations with and without mean CT controlled, whereas graphs based on partial correlations not only had fewer hubs, but also many different hubs (see Supplementary Table 1). Other differences include the relative number of contralateral edges for the two groups of individuals, the number of local edges (i.e., within the same hemisphere and lobe), and the percentage of edges involving temporal and occipital lobe regions (see Table 3). For example, in graphs based on Pearson correlations (with and without mean CT controlled), close to 50% of the edges for the cognitively normal group were contralateral edges, whereas only 20–30% of the edges for the AD-dementia group represented contralateral connections. By comparison, in graphs based on partial correlations, both groups of subjects had close to 50% of contralateral edges. In summary, these and other differences indicate that graphs based on partial correlations and those based on Pearson correlations can be qualitatively different on a number of levels, which may explain why differences in graph measures between diagnostic groups were in opposite directions.

Table 3.

Comparison of edges between cognitively normal individuals and AD-dementia patients for three types of graphs at 9% sparsity.

Type of edge	Pearson correlation		Pearson correlation (controlling for mean cortical thickness)		Partial correlation
Normal	AD	Normal	AD	Normal	AD
Common edges	58%		43%		19%
Contralateral edges	47%	23%	49%	33%	45%	47%
Within lobe & hemisphere	29%	35%	24%	38%	19%	17%
Frontal	58%	49%	56%	54%	51%	59%
Parietal	66%	52%	58%	46%	40%	39%
Temporal	21%	35%	22%	29%	45%	39%
Occipital	5%	6%	10%	12%	20%	24%
Frontal–parietal	29%	17%	23%	19%	10%	12%
Frontal–temporal	4%	6%	7%	7%	14%	17%
Frontal–occipital	0%	0%	0%	1%	8%	11%
Parietal–temporal	10%	12%	8%	9%	15%	10%
Parietal–occipital	4%	3%	6%	2%	4%	7%
Temporal–parietal	0%	3%	0%	3%	4%	4%

Note: Common edges refers to edges that are present in the graphs of both the normal and the AD group; within lobe and hemisphere refers to edges that connect nodes representing brain regions within the same lobe and hemisphere (i.e., local connections); frontal refers to edges that connect a node representing frontal lobe cortex to a node in the same lobe or in another lobe; parietal, temporal, and occipital are defined similarly as frontal; frontal–parietal represent edges that connect a node representing frontal lobe tissue to a node representing parietal lobe tissue.

4. Discussion

This study examined how cortical thickness networks differ across the spectrum of AD as a function of the type of correlation matrix and method of edge weighting. Five different graph measures were compared across 24 different graphs for four diagnostic groups. There are several notable findings. First, different types of correlation matrices gave rise to graphs with different topological properties. Not only the magnitude, but also the direction of group differences in graph measures was dependent on the type of correlation matrix used to construct the graphs. Second, while three of the graph measures showed little sensitivity to the type of edge weighting (i.e., clustering coefficient, Fiedler value, and normalized Fiedler value), the characteristic path length and the Randić index showed significant variability depending on the type of edge weights used. These two findings are of significance because they indicate that it is of critical importance to take into account how graphs are constructed when interpreting differences in graph measures across groups or individuals and when comparing findings across different studies.

Third, contrary to our predictions, we found that the Fiedler value and the normalized Fiedler value do not change reliably with increasing AD severity, independent of how graphs were constructed. The Fiedler value is bounded above by the minimum degree in the graph (weighted degree if the graph has edge weights), and as such, it can be considered a measure of global connectivity as it relates to node degree. Our results suggest that the global connectivity of cortical thickness networks as it relates to node degree is not significantly altered in mild to moderate AD. Interestingly, the characteristic path length, which is also considered a measure of global connectivity, demonstrated some significant group differences. Taken together, these findings indicate that while AD pathology does not significantly affect the node degree of cortical thickness networks, it may alter the routing between brain regions in the generated networks. Consistent with the interpretation that the routing between regions is altered in AD, we found that only 19%–58% of the edges were identical for the cognitively normal and AD-dementia groups at 9% sparsity, see Table 3. At the same time, many of the most highly connected regions were the same for the two groups of subjects (Supplementary Table 1), which may help explain why the path length, but not the Fiedler and normalized Fiedler were altered in AD. That is, while the regions with the most connections (i.e., highest degree nodes) were largely the same for the normal and AD-dementia groups, the connections between them were very different. Additionally, the proportion of edges connecting specific lobes were also comparable for the cognitively normal and AD-dementia groups (see Table 3), suggesting that aspects of global connectivity were not changed in AD.

Fourth, the Randić index, which has not previously been examined with respect to AD, appeared to be the most sensitive of the five graph measures in terms of differentiating between diagnostic groups. This suggests that AD disrupts the degree to which highly connected brain regions are connected to other highly connected brain regions. We also found that the Randić index of brain graphs obtained at baseline was the only graph measure to differentiate between MCI subjects who remained stable over 3 years and MCI subjects who progressed to AD over the same time period. As such, the Randić index may be a useful measure for predicting the progression of AD when applied to individual subject brain networks. Overall, our results provide evidence for the utility of graph theoretic measures for tracking and predicting the progression of AD, but they also highlight the need for methodological consistency across studies, especially if the goal is to understand the neurobiological significance of AD-related connectivity changes.

As outlined in the introduction, there has been little consistency in the literature examining AD-related changes in graph theoretic measures, even when considering studies using the same imaging modality. For example, prior studies using structural MRI have reported both increases in the clustering coefficient and characteristic path length with AD (He et al., 2008; Yao et al., 2010), as well as decreases in both measures (Li et al., 2012; Tijms et al., 2013a, 2014). Likewise, resting state fMRI studies of functional connectivity have found increases in the clustering coefficient and path length (Zhao et al., 2012), as well as decreases or null results for the same measures (Sanz-Arigita et al., 2010; Sun et al., 2014). Our results indicate that at least some of the discrepancy in prior findings may be attributable to differences in graph creation, which has varied across studies (see Tijms et al., 2013b, supplementary material, for preliminary evidence supporting this view). Furthermore, our results suggest that comparing results across studies may only be feasible for graphs constructed using the same type of correlation matrix and edge weights. Future studies should therefore consider reporting graph measures for more than a single type of graph.

There are multiple methodological reasons for why the magnitude and direction of group differences was altered for the different ways of constructing graphs. First, when the same sparsity threshold is used for each diagnostic group to determine which edges to include in a graph, the resulting graphs may differ in the number of nodes across groups, which, in turn alters the relative connectivity density of each group's graph. Both network size and connectivity density are known to affect the graph measures examined in this study, except for the normalized Fiedler value. Second, the average connection weight across all possible edges increased with AD symptom severity in this study, which may have led to the inclusion of more spurious edges for the cognitively normal participants than the AD-dementia group, particularly when connection density was higher (i.e., 17%). Third, our results suggest that the type of correlation matrix used to construct each graph can alter network properties. As shown in Table 1, controlling for mean CT reduces the number of edges in the normal group by a factor of 6.3 (80.3%–12.7%) whereas it reduces the number of edges in the AD-dementia group by a factor of 4.4 (89.5%–20.3%). The difference is more extreme when using partial correlations, which reduces the number of edges in the normal group by a factor of 9.4 (80.3%–8.5%) versus a factor of 4.0 (89.5%–22.6%) in the AD-dementia group. Controlling for mean CT or using partial correlations removes the effect of regional interdependencies on given pairs of nodes. Thus, our findings indicate a higher amount of regional interdependency among the CT values for the normal group than among the AD-dementia group. We further conjecture that this pattern of regional interdependency reduction (due to partialling or controlling for mean CT) may have the effect of reversing the order of group differences.

The only prior study comparing group-level cortical thickness networks between cognitively normal individuals and individuals with AD-dementia (i.e., He et al., 2008) created graphs based on absolute partial correlation matrices and used unweighted edges. Consistent with the results of this study, we found an increase in the clustering coefficient among AD-dementia patients for similarly constructed graphs (Fig. 4c), as well as a higher characteristic path length in the fully connected network (i.e., 17% sparsity). At the lower connectivity density ranges (6–9%), our results showed the reverse trend and the ordering across groups was not consistent. Additionally, some of the hub regions identified by He et al. (2008) are the same as the ones identified in the current study, including the lateral orbital frontal gyrus, superior temporal gyrus, and middle frontal gyrus (see Supplementary Table 1). Overall, this may indicate that when graphs are constructed in the same manner, consistent results can emerge across studies with different imaging parameters, network sizes, and subject populations. However, whereas He et al. (2008) interpreted the increased clustering coefficient and path length among AD patients as reflecting an increase in local specialization and an AD-related shift toward a more regular network, our results suggest that this interpretation does not generalize across graphs, as other types of graphs produced different results.

Unfortunately, too little is currently known about the biological underpinnings of cortical thickness or gray matter volume correlations across subjects or within subjects. It is therefore, unclear how different methods of graph construction map onto different biological processes that influence anatomical correlations, such as the presence of white matter tracts, direct and indirect functional coupling, neurotrophic influences between regions, experience-dependent plasticity, developmental effects, and genetic influences. In fact, it is unlikely that a single type of structural connectivity graph can be identified that best captures the connectivity between two brain regions. Rather, different kinds of graphs are likely useful for describing different kinds of underlying neurobiological processes.

One of the few studies that has examined this issue (Gong et al., 2012) showed that when cortical thickness graphs are constructed based on Pearson correlations, controlling for mean CT, about 40% of the positive correlations but only 10% of the negative correlations map onto fiber connections as determined by diffusion tensor imaging. Gong et al. (2012) suggested that the negative correlations and some positive correlations might instead correspond to direct and indirect functional connections. Providing some support for this view, a recent study found relatively high similarity (~60%) between gray matter volume networks and resting state fMRI networks based on positive correlations, as well as low to moderate similarity (10–40%) for negative correlations (Hosseini and Kesler, 2013). It is also possible, however, that some correlations are artificially induced by data processing, such as controlling for mean signal strength, thickness, or volume. For example, negative correlations only emerge when controlling for mean CT, or when using partial correlations. While these approaches may reduce spurious correlations and noise, they may also introduce artificial correlations (Van Dijk et al., 2010). In the current study, three of the graph measures (characteristic path length, Randic index, and Fiedler value) showed the same general pattern of results for positive, negative, and absolute correlations, though significance values were often reduced for positive and negative correlations. By comparison, the clustering coefficient and normalized Fiedler showed some dependence on the sign of correlations, such that some group differences were evident only for positive or negative correlations, or group differences were reversed for positive and negative correlations. Future studies using multiple imaging modalities will be needed to sort out how different types of correlations map onto different neurobiological mechanisms underlying structural and functional connectivity.

5. Conclusion

In sum, our findings suggest that the magnitude and direction of AD-related differences in some graph measures, including the small-world measures of clustering and characteristic path length, is strongly dependent on the choice of correlation matrix and edge weights used to construct the graphs. These findings likely apply to group-level structural gray matter networks more generally. Consequently, extreme caution is needed when interpreting the presence or absence of group differences in these measures within the context of underlying biological processes. However, even in the absence of an understanding of the nature of different types of gray matter correlations, our findings provide evidence for the clinical utility of some graph measures. The Randić index in particular may be useful for tracking and predicting the progression of AD, especially when used in combination with traditional AD biomarkers.

Appendix A. Supplementary data

Supplementary material.