Thoracic Cavity Definition for 3D PET/CT Analysis and Visualization

Abstract

X-ray computed tomography (CT) and positron emission tomography (PET) serve as the standard imaging modalities for lung-cancer management. CT gives anatomical detail on diagnostic regions of interest (ROIs), while PET gives highly specific functional information. During the lung-cancer management process, a patient receives a co-registered whole-body PET/CT scan pair and a dedicated high-resolution chest CT scan. With these data, multimodal PET/CT ROI information can be gleaned to facilitate disease management. Effective image segmentation of the thoracic cavity, however, is needed to focus attention on the central chest. We present an automatic method for thoracic cavity segmentation from 3D CT scans. We then demonstrate how the method facilitates 3D ROI localization and visualization in patient multimodal imaging studies. Our segmentation method draws upon digital topological and morphological operations, active-contour analysis, and key organ landmarks. Using a large patient database, the method showed high agreement to ground-truth regions, with a mean coverage = 99.2% and leakage = 0.52%. Furthermore, it enabled extremely fast computation. For PET/CT lesion analysis, the segmentation method reduced ROI search space by 97.7% for a whole-body scan, or nearly 3 times greater than that achieved by a lung mask. Despite this reduction, we achieved 100% true-positive ROI detection, while also reducing the false-positive (FP) detection rate by >5 times over that achieved with a lung mask. Finally, the method greatly improved PET/CT visualization by eliminating false PET-avid obscurations arising from the heart, bones, and liver. In particular, PET MIP views and fused PET/CT renderings depicted unprecedented clarity of the lesions and neighboring anatomical structures truly relevant to lung-cancer assessment.

I. Introduction

X-ray computed tomography (CT) and positron emission tomography (PET) serve as the de facto standard imaging modalities for lung-cancer management [1]–[3]. CT gives anatomical detail on diagnostic regions of interest (ROIs), while PET gives highly specific functional information. During the lung-cancer detection and staging process, a patient generally receives a co-registered whole-body PET/CT scan pair, collected as the patient breathes freely, and a dedicated high-resolution chest CT scan, collected during a breath hold. With this scan combination, multimodal PET/CT ROI information can be gleaned from the co-registered PET/CT scan pair, while the dedicated chest CT scan enables precise planning of follow-on chest procedures such as bronchoscopy and radiation therapy [3]–[5].

For all of these tasks, effective image segmentation of the thoracic cavity is important to help focus attention on the central-chest region. The thoracic cavity, also referred to as the innerthoracic region or thorax, encompasses the lungs and mediastinum, where the mediastinum contains the heart, major vessels, central-chest lymph nodes, and esophagus, among other structures [6]. We present an automatic method for thoracic cavity extraction from 3D CT scans. We then demonstrate how the method facilitates 3D ROI localization and visualization in the PET/CT studies of lung-cancer patients.

In current clinical practice, the physician employs 2D section scrolling to interactively search for suspect cancer ROIs, be they lymph nodes or nodules. Unfortunately, a typical 3D PET or CT scan contains hundreds of scan sections, many of which do not pertain to the thoracic cavity. Because of this “data explosion,” interactive search proves to be highly tedious [7].

While segmentation of the lungs and other organs in CT has received much attention [8]–[13], extraction of the mediastinum and complete thoracic cavity have proved to be more difficult [14]–[18]. Zhang et al. proposed a method for mediastinal segmentation, considered for the analysis of pulmonary emboli [14]. They pointed out, however, that the mediastinum has no obvious boundary. In addition, their method did not consider the lower diaphragmatic surface or the complete thoracic cavity. Chittajallu et al. were the first to propose a specific method for segmenting the thoracic cavity [15], [16]. Their method, nominally directed toward the diagnosis of cardiovascular disease, proposed a graph-based global energy-minimization method for defining the thoracic cavity. Unfortunately, the method only extracts the chest wall and does not consider the actual top and bottom of the cavity. In addition, the method is computationally intensive, not suitable for high-resolution 3D image data, and only tested with non-contrast CT scans. Finally, Cheirsilp et al. proposed a preliminary thoracic-cavity definition method that did not satisfactorily define the diaphragmatic interface, upper mediastinum, or heart [18].

Bae et al. presented the most complete effort to date for segmenting the thoracic cavity [17]. They proposed a semi-automatic method, whereby the airways, lungs, and ribs are first segmented. In the second step, the segmented organs contribute toward defining five surfaces delimiting the thoracic cavity. Next, heart segmentation, assisted by two manually selected seed points, is performed, and the previous results are then combined to yield the final segmented region. The method was successfully tested on a series of CT scans from patients suffering from chronic obstructive pulmonary disorder (COPD). Limits of their method include the need for manual interaction, the imprecise interpolated definition of the superior mediastinal surface, and the use of subsampled data during surface definition. In addition, their tests only considered non-contrast CT scans, all reconstructed with the same parameters.

Depending upon the clinical application, it is clear from the discussion above that significant latitude exists in the definition of the thoracic cavity. We consider the thoracic cavity from the standpoint of facilitating lung-cancer detection and staging. In particular, our interest lies in limiting the search space for detecting central-chest lymph nodes and nodules. To this end, physicians now universally draw upon the Mountain-Dressler TNM (tumor-node-metastasis) system guidelines to help localize relevant ROIs during interactive search [1], [19], [20]. In particular, to localize the central-chest lymph nodes, physicians use the TNM system’s International Association for the Study of Lung Cancer (IASLC) lymph-node map. The IASLC lymph-node map gives anatomical criteria specifying 14 distinct thoracic nodal stations. Unfortunately, these stations involve complex, overlapping, loosely-defined 3D zones. Regarding thoracic nodule localization, the TNM system’s guidelines entail elaborate 3D juxtapositions of various organs and airways. Thus, the TNM system is difficult to translate when analyzing a 3D scan consisting of a stack of 2D sections.

Our proposed method for segmenting the thoracic cavity from a 3D CT scan involves three major steps: organ segmentation, contour approximation, and volume refinement. Following established anatomical criteria and TNM-system specifications, the method assumes that the thoracic cavity is delineated by the rib cage and spine, bounded below by the diaphragm/liver interface, and approximately bounded above by the top of the sternum [6], [14]–[17], [19], [20]. The various method steps draw upon 3D digital topological and morphological operations, active-contour analysis, and key anatomical landmarks derived from the segmented organs [21]–[25]. The result is a fully-automatic computationally-efficient method for 3D thoracic-cavity segmentation.

We next show how the segmentation greatly facilitates ROI localization in patient PET/CT imaging studies by effectively focusing the search space on all 2D scan sections. The segmented thoracic cavity produces an especially large data reduction for ROI localization in co-registered PET/CT scan pairs, which span the whole body. Finally, we demonstrate how thoracic cavity segmentation greatly improves the multimodal visualization of 3D PET/CT data sets by removing considerable obscuring scan data.

Section II describes the thoracic-cavity segmentation method. Drawing upon a 3D PET/CT scan database derived from a series of lung-cancer patients and spanning a wide range of scan protocols, Section III then presents results demonstrating the segmentation method’s accuracy and computational efficiency. Section III also illustrates how the segmented thoracic cavity effectively focuses PET/CT ROI search and enables improved fused PET/CT visualization in a multimodal image-analysis system. Finally, Section IV offers concluding comments.

II. METHODS

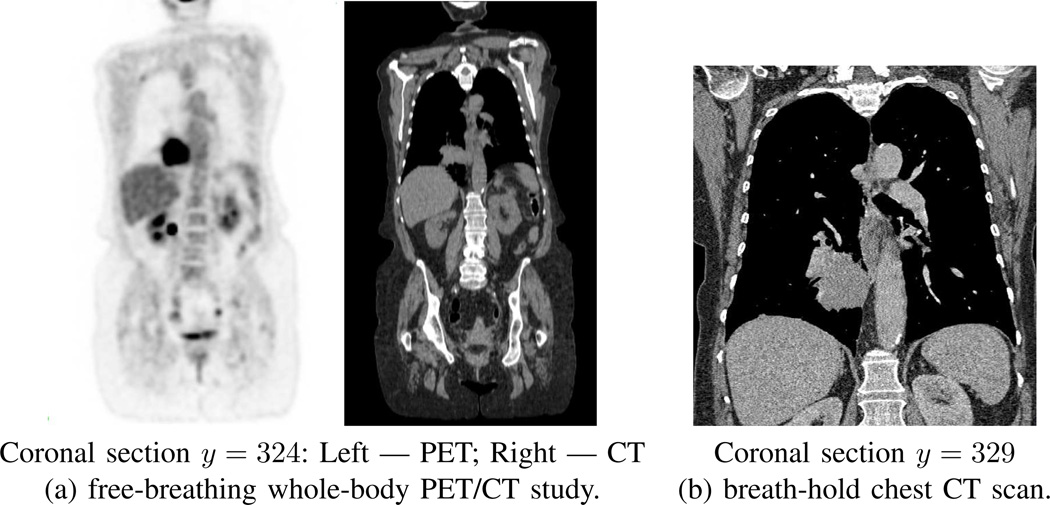
A patient’s CT scan I serves as the input for our method, where I is a 3D digital image consisting of N_z 2D transverse-plane sections. Quantity I(x, y, z) denotes the intensity value in Houndsfield units (HU) for voxel (x, y, z). Equivalently, I_z(x, y) will denote the HU value of voxel (x, y) on section I_z. For the CT scans arising in our work, we draw upon either whole-body co-registered PET/CT studies, acquired while the patient freely breathes, or on focused chest CT scans, acquired while the patient maintains a breath hold (Fig. 1). For these situations, the spacing Δz between sections equals either 3.0 mm (free-breathing scans) or 0.5 mm (breath-hold scans). For both scan types, the number of sections per scan varies, depending on the patient’s size. All scans have transverse-plane resolutions Δx, Δy < 1.2 mm, per Table I in Section III.

Fig. 1.

Examples of two types of scans involved for a typical human study. Data from case 21405.106. (a) whole-body free-breathing co-registered PET/CT study; Philips Gemini True Flight PET/CT scanner used; PET scan details: N_z = 271 sections, section dimensions = 144 × 144, scan resolution (Δx, Δy, Δz) = (4.0 mm, 4.0 mm, 3.0 mm); CT scan details: N_z = 271 sections, section dimensions = 512 × 512, scan resolution (Δx, Δy, Δz) = (1.0 mm, 1.0 mm, 3.0 mm). (b) breath-hold chest CT scan; Siemens Sensation 40 scanner used; scan details: N_z = 658 sections, section dimensions = 512 × 512, scan resolution (Δx, Δy, Δz) = (0.6 mm, 0.6 mm, 0.5 mm).

TABLE I.

Patient scan database. “Scan Type” indicates the type of CT scan, “No.” indicates the number of scans used for an indicated group, “N_z Range” denotes the [min, max] range for the number sections constituting a scan in a given group, “Contrast” indicates the number of scans of a given scan type involving a contrast-agent injection, and “Resolution” specifies the [min, max] range of the axial-plane resolution (Δx, Δy) in mm for a scan in a given group.

Scan Type	No.	Nz Range	Contrast	Resolution
whole body*	17	[251, 312]	1	[0.9, 1.2]
LR chest	6	[93, 373]	0	[0.3, 0.7]
HR chest*	14	[372, 752]	7	[0.5, 0.8]
entire database	37	[93, 752]	8	[0.3, 1.2]

The scanners we employ abide by standard chest-CT HU-calibration conventions [26]. In particular, pure air and water correspond to the calibrated values of −1000 HU and 0 HU, respectively. Image data constituting the lung parenchyma generally appears with values near −1000 HU. Soft-tissue structures, such as fat, muscle, vessels, blood, and lymph nodes exhibit HU values in the range [−200 HU, 200 HU], while blood in contrast-enhanced scans can exhibit values in the range [200 HU, 400 HU]. Solid (pure) bone exhibits values near 1000 HU, while metallic structures, such as pacemakers and certain stents, exhibit high HU values > 1000 HU. Note that partial volume effects, arising from the limitations of having sampled data, adversely influence the HU values of voxels interfacing multiple regions [8], [27]. For example, thin bony structures, such as the ribs, typically exhibit values > 300 HU, but substantially < 1000 HU. In addition, voxels bordering the lung parenchyma and diaphragm/chest-wall muscles often give values in the range [−400 HU, 0 HU].

Given CT scan I, our goal is to define a solid 3D region delineating the thoracic cavity ℛ^thorax. Our method involves three major steps (Fig. 2). First, Organ Segmentation extracts several organs and related anatomical structures pertinent to localizing ℛ^thorax. Next, Contour Approximation defines a set of 2D contours giving an initial approximation to ℛ^thorax. Finally, Volume Refinement performs additional operations to arrive at the final ℛ^thorax. Sections II-A through II-C give a complete description of these steps. Finally, Section II-D discusses implementation details.

Fig. 2.

Block diagram of proposed 3D thoracic-cavity definition method.

A. Organ Segmentation

Because ℛ^thorax occurs inside the body, the first operation in Organ Segmentation defines the body region. Subsequent operations then segment the airway tree, aorta, lungs, and bones. These structures either constitute or partially delimit ℛ^thorax and prove useful in later analysis steps. Details on these operations appear below.

As a convention, all 3D (2D) digital topology operations we use, such as connected-components analysis and cavity filling, assume 26-connectivity (8-connectivity) [21], [22]. In addition, many anatomical landmarks contribute toward defining the thoracic cavity. A number of these arise from a segmented regions’s 3D minimum bounding cuboid (MBC), or bounding box. We use the notation Ω(ℛ) to signify the 3D MBC of region ℛ, where Ω(ℛ) is represented by the following set of six limits in 3D digital image I’s x-y-z coordinate space [28]:

$$\text{right to left}:x_{\text{min}}\le x\le x_{\text{max}}$$ (1)

$$\text{anterior to posterior}:y_{\text{min}}\le y\le y_{\text{max}}$$

$$\text{top to bottom}:z_{\text{min}}\le z\le z_{\text{max}}$$

MBC limits of the form (1) will be used freely in the discussion to follow. Since each anatomical region has its own MBC limits, we will use superscripts to refer to region-specific limits. For example, quantity $z_{\text{min}}^{\text{tree}}$ refers to the top 2D CT section containing the segmented airway tree. Because the lungs correspond to the dominant structure constituting ℛ^thorax, we will use the unsubscripted MBC limits (1) to refer to quantities defining Ω(ℛ^lungs).

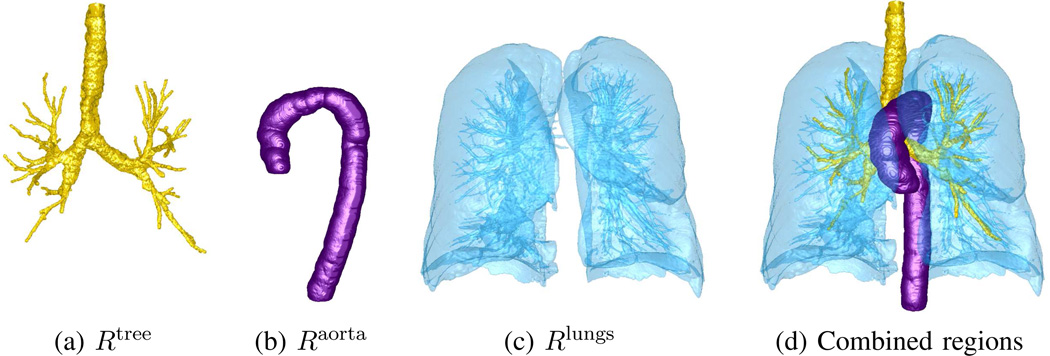
Body segmentation masks out the body, while deleting the external air, scanner bed, and any blanket that may cover the patient during scanning. A series of morphological and 3D topological operations applied to input scan I easily produce the result I^body, a body-masked version of the original CT scan. Given the simplicity of this task, we omit the details and refer the reader to reference [29]. In parallel with body segmentation, the airway tree ℛ^tree and aorta ℛ^aorta are also segmented in scan I, using the methods of Graham and Taeprasartsit, respectively [13], [30]. We have successfully applied both methods to many real pulmonary CT applications [28], [31], [32].

Continuing, lung segmentation in a chest CT scan is straightforward, as demonstrated by many previous methods. Our method draws upon digital topology operations, similar to [10], [13], [14], [17], [28]. It begins by extracting likely air voxels:

$${ℛ}^{\text{lungs}}(x,y,z)=\{\begin{array}{cc}1,\hfill & I^{\text{body}}(x,y,z)\le -400\mathrm{H}\mathrm{U}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

Next, operation

$${ℛ}^{\text{lungs}}={ℛ}^{\text{lungs}}-{ℛ}^{\text{tree}},$$

removes the airway tree, while

$${ℛ}^{\text{lungs}}=\text{conn}\_{\text{comp}}_{26}({ℛ}^{\text{lungs}},\mathrm{\Omega }({ℛ}^{\text{tree}}))$$ (2)

gives the final lung fields. Operation (2) denotes a 3D connected-component operation that keeps all connected components in ℛ^lungs that: (i) intersect the airway tree’s MBC; and (ii) have a volume ≥ 30% of the largest component’s volume. Operation (2) effectively handles situations where a given lung appears disconnected into two parts because of phenomena such as lung scarring. It also rejects the pulmonary vasculature and other small air-filled regions, such as any remnants of the esophagus, stomach, or visible intestine. An important consequence of lung segmentation is that it sets both the top-to-bottom section limits [z_min, z_max] and the right-to-left horizontal limits [x_min, x_max] we use throughout to delimit I_body and, as suggested by Zhang et al., ℛ^thorax [14]. Fig. 3 gives examples of airway tree, aorta, and lung segmentation.

Fig. 3.

Example organ segmentations: (a) airway tree; (b) aorta (rotated 90° about z-axis for clarity); (c) lungs; (d) rendering combining all segmented regions. CT scan of Fig. 1b used.

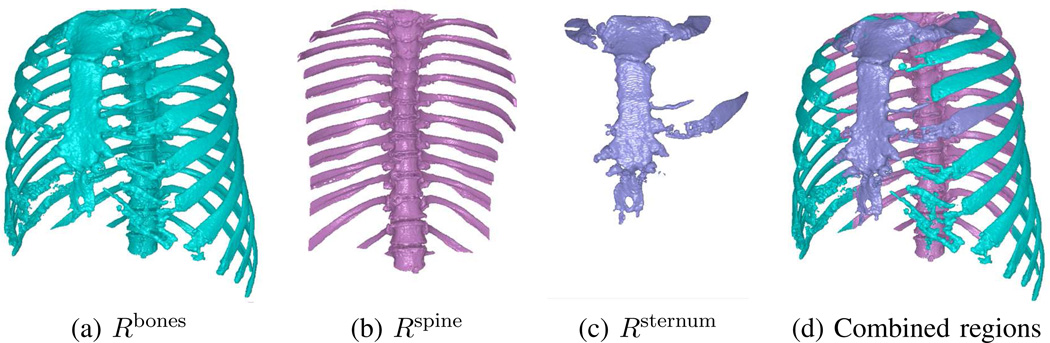
The final segmentation operation extracts bony structures situated within the thoracic cavity’s scope; namely, the ribs, spine, and sternum. They are readily segmented using topological operations and landmarks from previously segmented regions [17], [28], [33]. To begin,

$${ℛ}^{\text{bones}}(x,y,z)=\{\begin{array}{cc}1,\hfill & 160\le I_{\text{body}}(x,y,z)\le 1000\mathrm{H}\mathrm{U}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (3)

extracts likely bone voxels while rejecting suspect metal regions. Next, all cavities are filled in each 2D section of ℛ^bones.

As noted in the Introduction, the IASLC lymph-node map specifies criteria for localizing the central-chest lymph-node stations [19]. As several stations — and, hence, our desired ℛ^thorax — depend on specific landmarks delimiting the spine and sternum, the next several operations derive approximations to the spine and sternum from ℛ^bones.

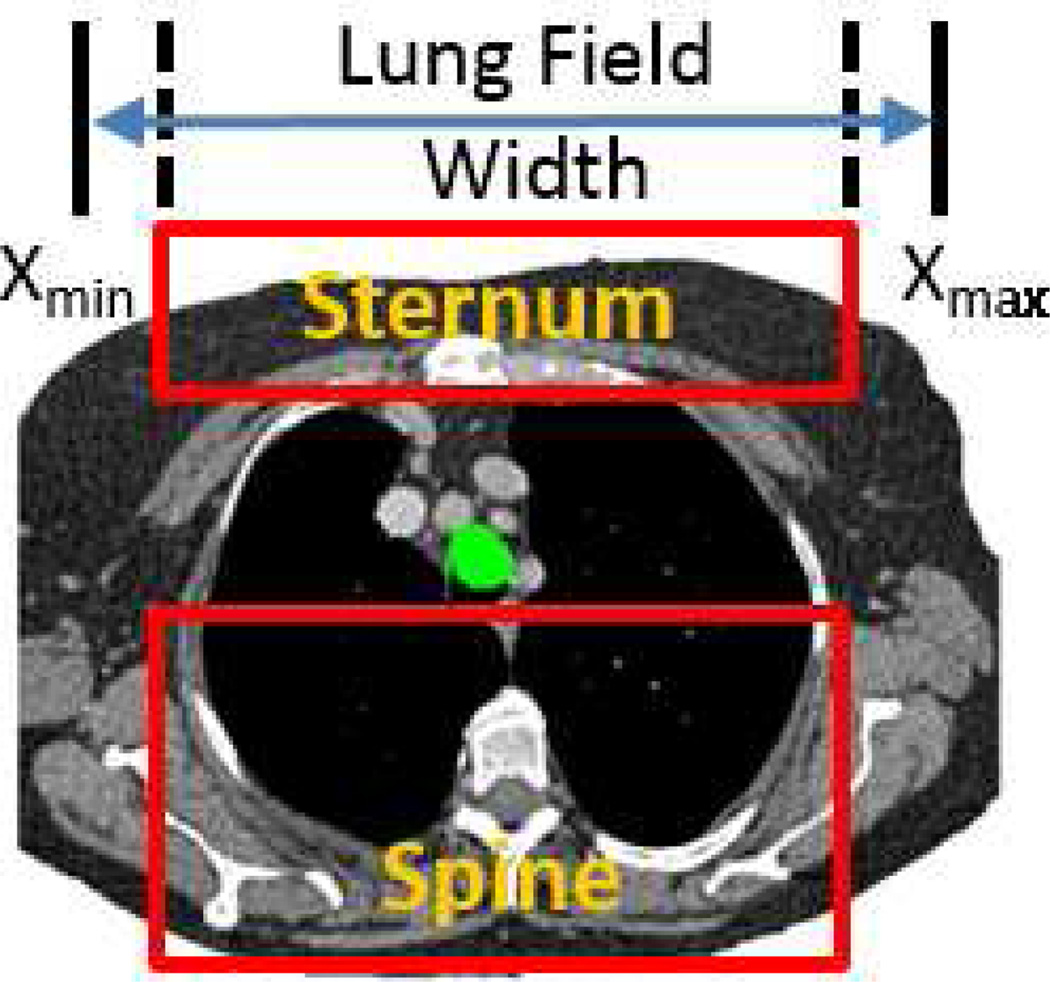
The spine and sternum are long, vertical, centrally-situated structures that are approximately parallel to each other. The spinal and sternal MBCs, Ω(ℛ^spine) and Ω(ℛ^sternum), thus share the right-to-left limits

$$[x_{\text{min}}^{\text{spine}},x_{\text{max}}^{\text{spine}}]=80\%\text{of the range}[x_{\text{min}},x_{\text{max}}],$$ (4)

while their top-to-bottom limits are given by [z_min, z_max]. The liberal right-to-left limits of (4) help focus analysis on centrally-situated bony structures (Fig. 4), while the top-to-bottom limits restrict attention to the lung-field range. Anterior-to-posterior (y) limits, of course, differ for the spine and sternum because the spine must be posterior to the trachea. For the spine, we identify a reference 2D tracheal cross-section situated a short distance below the lung-field apex. This cross-section is found via

$${ℛ}^{\text{trachea}}=\text{conn}\_{\text{comp}}_8({ℛ}_{z_{\text{trachea}}}^{\text{tree}}),$$ (5)

where z_trachea = z_min + 2 cm and conn_comp₈(·) finds the largest 2D connected-component of its argument. Next,

$${ℛ}^{\text{spine}}(x,y,z)=\{\begin{array}{cc}1,\hfill & {ℛ}^{\text{bones}}(x,y,z)\in \mathrm{\Omega }({ℛ}^{\text{spine}})\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

isolates bony components posterior to the trachea and within the lungs, where the anterior-to-posterior limits of Ω(ℛ^spine) are given by

$$[y_{\text{min}}^{\text{spine}},y_{\text{max}}^{\text{spine}}]=[y_{\text{max}}^{\text{trachea}},y_{\text{max}}^{\text{body}}].$$ (6)

The final estimated spinal region is then given by the longest 3D connected component in the z direction in ℛ^spine.

Fig. 4.

Left-to-right and anterior-to-posterior limits for spine and sternum definition. CT scan of Fig. 3 considered. Axial-plane spine and sternum MBC rectangles depicted for 2D section I₁₁₃; x limits set per (4), while the spine’s y limits are given by (6); green structure = projected tracheal cross-section per (5).

Sternum definition begins by finding bony components anterior to the lungs. This is done via

$${ℛ}_z^{\text{sternum}}(x,y)=\{\begin{array}{cc}1,\hfill & {ℛ}_z^{\text{bones}}(x,y)=1,y<y_{z,\text{min}},x_{\text{min}}^{\text{spine}}\le x\le x_{\text{max}}^{\text{spine}}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (7)

for all sections ${ℛ}_z^{\text{bones}}$, z_min ≤ z ≤ z_max. In (7), the quantity y_{z, min} refers to the specific minimum (frontal) location of the lung field located on section ${ℛ}_z^{\text{lungs}}$. This restriction takes into account how the lung field’s shape — and corresponding neighboring sternal location — changes from top to bottom. Next, we project the reference 2D tracheal cross-section ℛ^trachea onto each 2D section of the initial sternal mask ℛ^sternum and locate the topmost section that contains a bony component anterior to the tracheal section — this section index $z=z_{\text{min}}^{\text{sternum}}$ denotes the top of the sternum (Fig. 4c). Finally, we apply

$${ℛ}_z^{\text{sternum}}(x,y)=\{\begin{array}{cc}1,\hfill & {ℛ}_z^{\text{sternum}}(x,y)=1,\text{and}z\ge z_{\text{min}}^{\text{sternum}}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$

and identify the longest 3D connected component in ℛ^sternum in the z direction. Fig. 5 gives examples of segmented bony structures. Notice that the segmented spine and sternum also contain portions of the ribs. This is of no consequence, as all of these bony structures will be removed from ℛ^thorax during Volume Refinement.

Fig. 5.

Examples of segmented bony structures for CT scan of Fig. 4. Renderings for R^bones and combined regions rotated 30° about z-axis for clarity.

B. Contour Approximation

Contour Approximation defines a set of 2D closed contours within I^body that approximately circumscribe the desired thoracic cavity ℛ^thorax (Fig. 2). Denote this set of contours as

$$\mathbf{C}=\{{𝒞}_{z_{\text{min}}},{𝒞}_{z_{\text{min}}+1},\dots ,{𝒞}_z,\dots ,{𝒞}_{z_{\text{max}}-1},{𝒞}_{z_{\text{max}}}\},$$ (8)

where one contour 𝒞_z ≡ 𝒞(x, y, z) is derived for each transverse-plane section $I_z^{\text{body}}$, z = z_min,…, z_max.

For this purpose, we employ active-contour analysis. In its general form, active-contour analysis employs an iterative procedure driven by a cost function to derive an optimal contour circumscribing a desired region [23], [24]. The cost function combines contour shape constraints and gray-scale-based region-edge characteristics to drive the optimization. The method has been applied successfully in many chest CT applications [25], [34], [35]. We incorporate active-contour analysis to define C as follows:

1. Reference Contour Definition: Compute reference contour 𝒞_zref on section $I_{z_{\text{ref}}}^{\text{body}}$.

2. Sequential Section Analysis: For the remaining subvolume sections in I^body, use 𝒞_zref to sequentially derive the remaining contours.

This process assumes that the desired region consists of one cavity-free component per section, has a slowly changing shape from one section to the next, and has automatically identifiable seed boundary points on every section. The discussion below gives complete detail on this two-step process.

1) Reference Contour Definition

To begin, we identify reference section $I_{z_{\text{ref}}}^{\text{body}}$ that contains the largest 2D lung cross-section. Next, a three-stage procedure derives reference contour 𝒞_zref. First, we transform $I_{z_{\text{ref}}}^{\text{body}}$ into a 2D cylindrical-coordinate space:

$$I_{z_{\text{ref}}}^{\mathrm{c}}(r,\theta )=I_{z_{\text{ref}}}^{\text{body}}(r\text{cos}\theta +c_x,r\text{sin}\theta +c_y),$$ (9)

where (c_x, c_y) is the centroid of ${ℛ}_{z_{\text{ref}}}^{\text{lungs}}$, r is the distance from (c_x, c_y), and θ is an angle in the range [0°, 360°]. Transformation (9), suggested by Chittajallu et al., exploits the observation that the thoracic cavity has approximately a cylindrical shape with its central axis roughly parallel to the spinal column [15]. In addition, (9) facilitates seed-point detection and ordering for our method as discussed below. For each (r, θ) in (9), $I_{z_{\text{ref}}}^{\mathrm{c}}(r,\theta )$ is found using nearest-neighbor interpolation on $I_{z_{\text{ref}}}^{\text{body}}$. Radial coordinate r is sampled such that Δr = Δx(= Δy), while θ takes on integer values between [0°, 360°]. See Fig. 6a for an example transformed section $I_z^{\mathrm{c}}$.

Fig. 6.

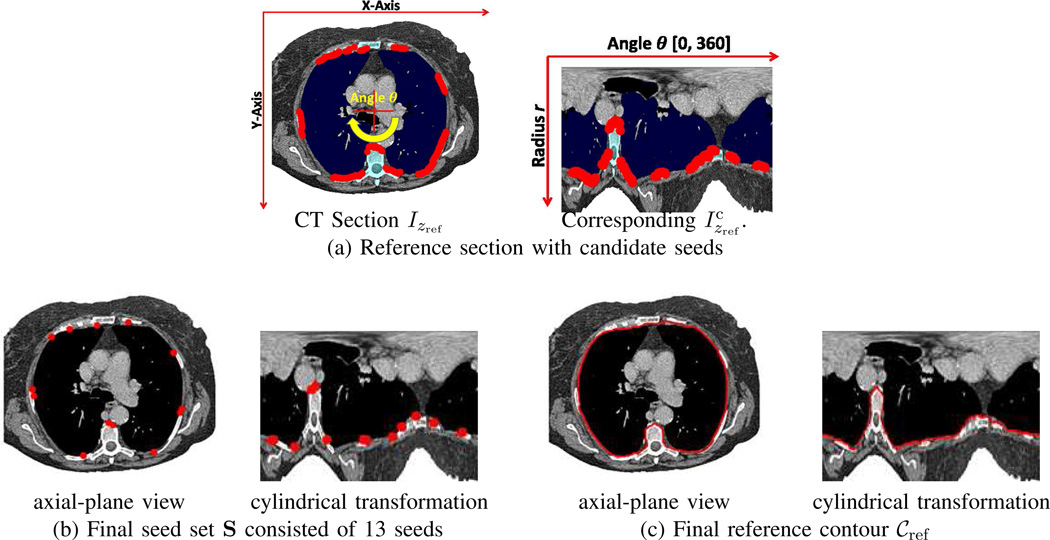
Example of reference contour definition for CT scan of Figs. 3–5. (a) Reference section: [left] Original CT section I_zref for z_ref = 226, plus 236 detected candidate seeds — intersection of the red axes denotes the transformation center (c_x, c_y); [right] Transformed version $I_{z_{\text{ref}}}^{\mathrm{c}}$ (dimensions, 360×248) — the segmented lung and bone regions are in navy blue and cyan, respectively, while the red dots represent detected candidate seeds. (b) Final seed set S consisted of 13 seeds. (c) Final reference contour 𝒞_ref.

We next detect a set of pixels $\mathbf{S}\in I_{z_{\text{ref}}}^{\mathrm{c}}$ that will serve as boundary seeds for active-contour analysis. To find candidate seeds, we search each column of $I_{z_{\text{ref}}}^{\mathrm{c}}$ to find the first pixel, if any, bordering the lungs and before any bony structures. Specifically, for each column, $I_{z_{\text{ref}}}^{\mathrm{c}}(·,{\theta }_j)$, θ_j = 0°, 1°, …, 360°, we find the maximum radius r_lungs such that (r_lungs, θ_j) = last location in ℛ^lungs and the minimum radius r_bones such that (r_bones, θ_j) = first location in ℛ^bones, ℛ^spine, or ℛ^sternum, where ℛ^bones is given by the largest 3D connected component contained in the likely bone mask of (3). We then select the largest r_i in the half-closed interval [r_lungs, r_bones), if any exists, such that $I_{z_{\text{ref}}}^{\mathrm{c}}(r_i,{\theta }_j)>-300\mathrm{H}\mathrm{U}$. (Radius r_i increases from the body center outward.)

At most one potential seed s = (r_i, θ_j) is found per column. As shown in Fig. 6, a typical section may yield 50–250 seeds and clusters of connected seeds often occur between bone/lung interfaces. Therefore, to reduce the computation of the next step, we reduce this set to n = 16 seeds that are approximately evenly spaced across the 360° range of θ. The final set

$$\mathbf{S}=\{{\mathbf{s}}_1,{\mathbf{s}}_2,\dots ,{\mathbf{s}}_j,\dots ,{\mathbf{s}}_n\}$$ (10)

specifies a set of confirmed boundary seeds in $I_{z_{\text{ref}}}^{\mathrm{c}}$ ordered by increasing θ_j.

We now apply active-contour analysis to produce the desired 𝒞_zref. Our method, given by Algorithm 1, derives a closed contour by finding the optimal segment connecting each consecutive pair of seeds in S on section I_zref. It builds upon a method for connecting two pixels first suggested by Mortensen and Barrett and later modified by Lu and Higgins [34], [35]. In Algorithm 1, a search process finds the optimal segment linking each pair of ordered seeds (s_i, s_i+1). For each seed pair, an active pixel list L is first reset, and the cost of L’s initial member b is initialized to 0 (lines 9–10 of Algorithm 1).

Next, the main optimization search occurs between lines 11 and 23. To obtain an optimal segment, the method draws on Dijkstra’s algorithm to build a weighted graph [36]. Each graph node represents a pixel p in image I_zref, while each edge designates the local cost of moving from pixel p to one of its neighbors q ∈ N(p), where N(p) denotes the 8-neighborhood of p. Before the search begins, no pixel p has yet been expanded in the search; this condition is designated by the default pixel setting e(p) = FALSE. At line 12, function min-cost(L) identifies the next pixel p ∈ L having the lowest-cost path tracing back to beginning seed b — p is the next pixel to expand in the search. During this expansion (lines 15 through 21), each suitable neighbor q gets assigned (i) a path tracing back to b via the pointer function ptr(q) and (ii) a path cost g(q). To compute path cost g(q), we add the local cost between pixels p and q, as computed by function local-cost(p, q), to p′s path cost g(p) (line 16).

Eventually, the termination pixel t is identified as the next pixel to expand — this implies that the optimal segment from b to t has been found and the algorithm moves on to the next segment. Function path(b, t) then computes the complete segment of pixels from b to t by tracing back through the pointers. This segment is retained in data structure 𝒞, and the previous end seed t now begins the next segment. After the optimization completes, 𝒞 traces out a complete sequence of pixels defining the optimal closed contour 𝒞_zref passing through seed set S.

Algorithm 1.

— 2D Contour Definition.

1:	Input: ordered seed set S = {s1, s2, …, sn}
2:	𝒞 = ∅ // Initialize contour
3:	i = 1
4:	while i ≤ n do
5:		if i ≠ n then
6:			b = si, t = si+1 // Set beginning/end seeds for ith segment
7:		else
8:			b = sn, t = s1 // Get segment connecting last and first seeds
9:		L = ∅ // Reset active pixel list for ith segment
10:		b → L, g(b) = 0 // Start active list and initialize segment cost
11:		while L ≠ ∅ do // Main search for ith segment
12:			min-cost(L) → p
13:			e(p) = TRUE // p is the active list’s next pixel to expand
14:			if p ≠ t then
15:				for each q ∈ N(p) such that e(q) == FALSE do
16:				gtmp = g(p) + local-cost(p, q)
17:				if q ∈ L and gtmp < g(p) then
18:				g(q) = gtmp, p → ptr(q)
19:				else if q ∈ L then
20:				q → L // Place q onto active list
21:				g(q) = gtmp, p → ptr(q)
22:			else // Optimal path found for ith segment
23:				go to 24 // Terminate search
24:		path(b, t) → 𝒞 // Append segment to contour
25:		i = i + 1
26:	return 𝒞

Function local-cost(p, q) computes the quantity

$$l(\mathbf{p},\mathbf{q})=w_G{f}_G(\mathbf{q})+w_Z{f}_Z(\mathbf{q})+w_{D_1}{f}_{D_1}(\mathbf{p},\mathbf{q})+w_{D_2}{f}_{D_2}(\mathbf{p},\mathbf{q})+f_M(\mathbf{q})$$ (11)

as the local cost to travel from p to q. The quantity l(p, q) in (11) represents a modified form of the function l(p, q) first suggested by Mortensen and Barrett [34]. In (11),

$$f_G(\mathbf{q})=1-\frac{G(\mathbf{q})}{\text{max}G(\mathbf{q})}$$

is a normalized gradient-magnitude cost at q, where

$$G(\mathbf{q})=\sqrt{{(\frac{\partial }{\partial x}{I}_{z_{\text{ref}}}(\mathbf{q}))}^2+{(\frac{\partial }{\partial y}{I}_{z_{\text{ref}}}(\mathbf{q}))}^2},$$

is the gradient magnitude of image I_zref at pixel q. Also, as defined in [35], f_Z (q) is a Laplacian zero-crossing cost, and f_D1(p, q) and f_D2(p, q) are gradient-direction costs between p and q, with I_zref serving as the input image. Quantity f_M is a new term, defined as

$$f_M(\mathbf{q})=\{\begin{array}{cc}\hfill 0,& \text{if}\mathbf{q}\in ℳ\hfill \\ \hfill \infty ,& \text{otherwise}\hfill \end{array},$$ (12)

effectively forces a possible contour pixel q to be a member of control region ℳ by assigning an infinite cost to non-member pixels; i.e., pixels q ∉ ℳ are skipped during the search. For the reference section, ℳ = ℛ^body. Finally, we employ the weights w_G = 0.4, w_Z = 0.17, ,w_D1 = 0.33, and w_D1 = 0.1 as done previously in a general chest CT segmentation application and used successfully for segmenting lymph nodes, nodules, and other structures in chest CT scans [28], [31], [32], [35]. Fig. 6 gives a complete example of Reference Contour Definition.

2) Sequential Section Analysis

The reference contour 𝒞_zref now drives the computation of the remaining contours of C per (8); i.e., contours 𝒞_z, z_min ≤ z ≤ z_max, such that z ≠ z_ref. This involves a sequential process for each series of sections in I^body above and below z = z_ref. This process, which adapts a general 3D segmentation method of Lu and Higgins to thoracic-cavity definition, entails three basic operations for each involved section [28]: 1) defining a working area, 2) detecting a set of seeds, and 3) applying active contour analysis to derive the desired contour. Details appear below.

The process for the bottom series of sections in I^body with indices z = z_ref + 1, …, z_max, begins with the assignment

$${𝒞}_{\text{ref}}={𝒞}_{z-1},$$

where 𝒞_ref represents the optimal contour derived from the previous adjacent section $I_{z-1}^{\text{body}}$. To continue, we next project 𝒞_ref onto $I_z^{\text{body}}$ and perform the 2D dilation

$$ℳ={𝒞}_{\text{ref}}\oplus B_4,$$ (13)

where ℛ⊕B₄ denotes the binary dilation of region ℛ by structuring element B₄ and B₄ is a disk-shaped structuring element of radius 7.5 mm [22]. Fig. 7b illustrates how ℳ appears as a thickened ring-like version of the projected contour 𝒞_ref. As such, it restricts the scope of 𝒞_z’s allowed deviation from reference contour 𝒞_ref. ℳ also serves as the working area for subsequent seed selection. B₄’s radius in (13) conservatively defines an expected lung/bone interface zone for locating seeds and accounts for the Δz = 3 mm section spacing encountered in our PET/CT studies.

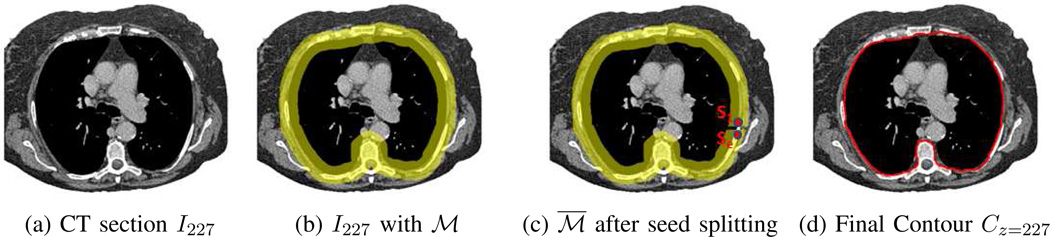
Fig. 7.

2D section result for Sequential Section Analysis. Same CT scan as Fig. 6 used. (a) Beginning bottom-series CT section I₂₂₇. (b) Section with working area ℳ per (13) in yellow (thickness slightly exaggerated for clarity). (c) Results after seed splitting at seed s₁, with split working area ℳ̅ shown. (d) Final contour C_z=227 in green.

A transformation as in (9) now converts $I_z^{\text{body}}$ and ℳ into cylindrical-coordinate analogs, $I_z^{\mathrm{c}}$ and ℳ^c, with (c_x, c_y) equal to the centroid of 𝒞_z−1. Next, a set of seed pixels S as in (10) is detected, using the process of Section II-B1 with two enhancements. First, candidate seeds must lie within the working area ℳ^c, which again in general can result in a candidate seed set S having many seeds.

As before, S is reduced to a set of ≤16 seed pixels. Note that if reduced set S only contains two seeds, s₁ and s₂, then subsequent active contour analysis is guaranteed to trace a segment from s₁ to s₂ and back again on the same segment from s₂ to s₁, resulting in a degenerate “contour.” As another case, if S only contains one seed s₁, then no valid contour can be defined using Algorithm 1. Managing these cases necessitates the second enhancement to the Section II-B1 process.

To begin, we cut ℳ^c into an open ring $\overline{{ℳ}^{\mathrm{c}}}$ at the column (·, θ_j) containing seed s₁ — note that the open region $\overline{{ℳ}^{\mathrm{c}}}$ is only “open” in the sense that column (·, θ_j+1) is no longer considered to be connected to column (·, θ_j). We then “split” seed s₁ into two seeds situated on opposite sides of the cut: the original seed s₁ at its original location (r_i, θ_j) and a new seed s_e = (r_i, θ_j−1) located on the opposite side of the cut. Thus, each seed lies on opposing ends of $\overline{{ℳ}^{\mathrm{c}}}$. This process of cutting ℳ^c and splitting seed s₁ gives the final seed set S and ensures that a proper closed contour 𝒞_z can now be computed for the degenerate cases highlighted above. Fig. 7c illustrates an example ℳ̅ in Cartesian coordinates after seed splitting.

We now apply Algorithm 1 to define 𝒞_z. The algorithm uses S as the seed set and ℳ̅ as the control region for cost f_M in (12). Fig. 7d gives example of a final contour. The process above then repeats for section z = z + 1 until all bottom-series sections have been processed. Two situations cause the sequential process to terminate. First, if the seed set contains no seeds (S = ∅) for section $I_z^{\mathrm{c}}$, then the process stops and no further action occurs for the remaining sections $I_{\overline{z}}^{\text{body}}$, z < z̄ ≤ z_max. As a second situation, if S contains one seed but the dilation (13) produces a filled region ℳ having no cavities, then this seed cannot be split and the process again must terminate. These situations occur for more peripheral sections where weak lung and muscle/tissue interfaces exist and where ℛ^thorax has a small cross-sectional area.

The upper series of sections (z_min ≤ z < z_ref) are then processed in a similar manner. Completion of this step results in a preliminary estimate of ℛ^thorax as delineated by contour set C.

C. Volume Refinement

Many sections near the top and bottom of the preliminary ℛ^thorax as defined by 2D contour set C in (8) tend to consist of disconnected components and have a small cross-sectional area. Hence, these sections are likely to be ill-defined. Furthermore, contour set C in general also encompasses extraneous regions corresponding to the heart and portions of the bones, liver, and diaphragm. Volume Refinement removes these regions in two stages, as discussed below.

1) Heart Definition

The heart is a region that definitely must be avoided during a cancer-staging procedure. It also, of course, contains no lymph nodes or suspect cancer nodules. Furthermore, the heart often exhibits “false alarm” regions of high PET avidity [1]. For these reasons, we delete the heart from ℛ^thorax. Unfortunately, the heart’s considerable motion as manifested in a typical chest CT scan I makes precise heart definition problematic. Also, Bae et al. noted the inherent challenges in defining the heart accurately in a CT scan [17]. Our goal, therefore, is to derive a suitable approximation.

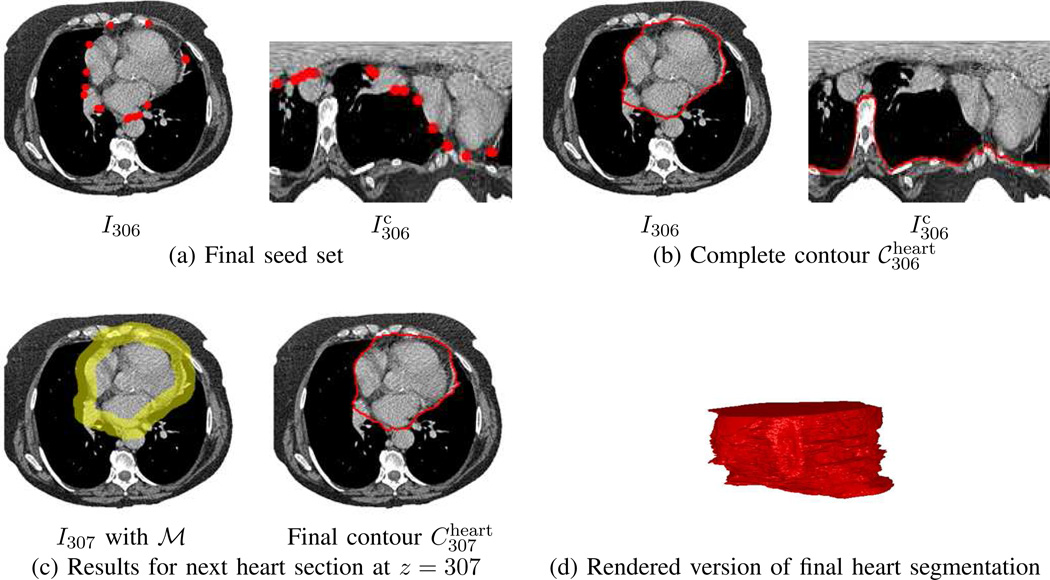
Since the ascending aorta emanates from the heart, heart definition starts by designating the ascending aorta’s bottom-most 2D section as the heart’s top-most section. We denote this 2D section as ${ℛ}_{z_{\text{min}}^{\text{ascend}}}^{\text{aorta}}$. The next operation involves applying active contour analysis, similar to the approach of Section II-B. In particular, for $z=z_{\text{min}}^{\text{ascend}},\dots ,z_{\text{max}}$, the following operations occur:

1. Convert 2D section $I_z^{\text{body}}$ into a cylindrical-coordinate form $I_z^{\mathrm{c}}$ as in (9). For the first section, (c_x, c_y) equals the centroid of the ascending aorta as it appears in 2D section ${ℛ}_{z_{\text{min}}^{\text{ascend}}}^{\text{aorta}}$, while for subsequent sections (c_x, c_y) equals the centroid of the previously computed contour.

2. Identify a preliminary set of candidate seeds (r, θ). Candidate seeds must be a member of one of three previously segmented structures that bound the heart’s exterior boundary; these structures in order of precedence are the descending aorta, lungs, and contour set C. Thus, candidate seeds (r, θ) are found as follows. For each θ ∈ [0°, 360°], we find the minimum r > 0, if any, where either ${ℛ}_z^{\text{descend}}(r,\theta ),{ℛ}_z^{\text{lungs}}(r,\theta )$, or 𝒞_z(r, θ) is non-zero, where ${ℛ}_z^{\text{descend}}$ represents the 2D descending aorta cross-section in ${ℛ}_z^{\text{aorta}}$. The candidate seed set is then reduced to a set of at most 16 seeds approximately evenly sampling the [0°, 360°] range for θ.

3. Apply Algorithm 1 to compute the desired 2D contour ${𝒞}_z^{\text{heart}}$.

This gives a set of contours ${𝒞}_z^{\text{heart}},z=z_{\text{min}}^{\text{ascend}},\dots ,z_{\text{max}}$, approximating ℛ^heart. Fig. 8 gives an example of heart definition.

Fig. 8.

Example of heart definition for CT scan of Fig. 7. Seeds and computed contours are depicted in red, while the working area ℳ appears in yellow. For this example, the top-most section of the heart occurs at $z=z_{\text{min}}^{\text{ascend}}=306$.

2) Extraneous Region Removal

Final refinement entails removing the aforementioned extraneous regions. To begin, few, if any, clinically relevant ROIs occur in the mediastinal region situated between the lungs and above the aorta and sternum; i.e, image sections I_z, z < z_med, where

$$z_{\text{med}}=\text{min}\{z_{\text{min}}^{\text{aorta}},z_{\text{min}}^{\text{sternum}}\}$$ (14)

Constraint (14) effectively defines the superior border of the mediastinum and is easily incorporated into a modified version of ℛ^thorax via:

$${ℛ}_z^{\text{thorax}}=\{\begin{array}{cc}{ℛ}_z^{\text{lungs}}\cup {ℛ}_z^{\text{tree}},\hfill & \text{if}{z}_{\text{min}}\le z<z_{\text{med}}\hfill \\ {ℛ}_z^{\text{thorax}}-{ℛ}_z^{\text{heart}}-{ℛ}^{\text{spine}}-{ℛ}^{\text{sternum}},\hfill & \text{if}{z}_{\text{med}}\le z\le z_{\text{max}}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array},$$ (15)

where (15) also removes the heart and bony structures. In addition, because the trachea contains no relevant ROIs, (15) uses a version of ℛ^tree that has the trachea deleted above z = z_med. (This portion of the trachea is easily found by identifying the largest 2D component in ${ℛ}_z^{\text{tree}}$ for each section z in the affected range.) Note that (14) accommodates the requirements of station-1 superior mediastinal nodes of the IASLC lymph-node map. Related to this point, over the 37 CT scans considered in Section III (Table I), we found that on average the distance from the top of the aortic arch $z_{\text{min}}^{\text{aorta}}$ to the top of the sternum $z_{\text{min}}^{\text{sternum}}$ was 1.57 cm ± 1.58 cm (range: [−2.1 cm, 4.7 cm]) [29].

The next operation refines the bottom surface of the thoracic cavity. The lungs and heart largely determine the vast bulk of this surface, while the remaining residual, if any, is determined by the liver/diaphragm combination. While CT-based diaphragmatic surface definition has been considered [12], [16], given the heterogeneous nature of the types of CT scans we consider (Fig. 1), liver/diaphragm definition can be problematic and is, in fact, unnecessary [17]. Instead, we define the bottom-surface function

$$S_{\mathrm{B}}^{\text{thorax}}(x,y)=\{\begin{array}{c}\text{maximum}z\text{over}z\in [z_{\text{min}}^{\text{ascend}},z_{\text{max}}]\text{such that}{ℛ}_z^{\text{lungs}}(x,y)\ne 0\hfill \\ z_{\text{min}}^{\text{ascend}}\text{otherwise}\hfill \end{array}$$

Finally, we use the bottom-surface function to modify each 2D section of ℛ^thorax via

$${ℛ}_z^{\text{thorax}}(x,y)=\{\begin{array}{cc}0,\hfill & \text{if}z>S_{\mathrm{B}}^{\text{thorax}}(x,y)\hfill \\ {ℛ}_z^{\text{thorax}}(x,y),\hfill & \text{otherwise}\hfill \end{array}$$ (16)

over the range z = z_min, …, z_max, to give the final definition of the thoracic cavity. Fig. 9 illustrates the final output after Volume Refinement.

Fig. 9.

Final thoracic-cavity segmentation for CT scan of Fig. 8.

D. Implementation Comments

All software was coded in C++ and developed using Visual Studio 2012. Tests were run on a Dell Precision T5500 64-bit workstation, running Windows 7, equipped with 24 GB of RAM, dual Intel Xeon six-core 2.79 GHz processors, and an nVidia Quadro 4000 video card (2 GB video memory). Since each core can run two threads in parallel, the workstation can run up to 24 threads in parallel. To exploit this capability, we used OpenMP, a multiprocessing application program interface for cross-platform scalable parallel processing, to parallelize many of the operations employed by our method [37].

In Organ Segmentation, all 2D transverse-plane computations such as thresholding, 2D morphological operations, and 2D connected-components analysis, were performed in parallel; this includes all operations except those employing 3D connected-components analysis (e.g., (2)). During Sequential Section Analysis, both series of 2D sections above and below reference section $I_{z_{\text{ref}}}^{\text{body}}$ were processed in parallel.

The greatest benefit gained from parallel processing occurred through our implementation of Algorithm 1. Separate threads running Algorithm 1 were invoked for every seed in S, with one thread deriving a segment connecting (s₁, s₂), another for a segment connecting (s₂, s₃), and so forth, with the final thread deriving a segment connecting (s_n, s₁).

III. Results

The tests presented herein draw upon a database of 37 CT scans derived from 20 lung-cancer patients, as summarized in Table I. All studies were collected under IRB approval and informed consent. Each patient went through a standard imaging protocol involving two studies:

1. A PET/CT study consisting of:

   1. Whole-body co-registered PET and CT scans, collected as the patient breathed freely (Fig. 1a). The CT scan, which consisted of 512×512 sections spaced Δz = 3.0 mm apart, provides anatomical information. The PET scan, consisting of 144×144 sections also spaced 3.0 mm apart and axial-plane resolution Δx = Δy = 4.0, gives diagnostic cancer biomarker data in the form of standard uptake values (SUVs) [38].
   2. A breath-hold chest CT scan, consisting of 1024×1024 sections spaced Δz = 3.0 mm apart. Because it consists of thick sections, we will refer to this scan as a low-resolution (LR) chest CT scan.

2. A dedicated chest CT study consisting of a breath-hold chest CT scan made up of 512×512 sections spaced Δz = 0.5 mm apart (Fig. 1b). We will refer to this scan as a high-resolution (HR) chest CT scan.

We employed a Philip Gemini TrueFlight integrated PET/CT scanner for all PET/CT studies and either a Siemens Sensation-40 or Siemens SOMATOM Definition scanner for dedicated chest CT studies. Both the LR and HR chest CT scans give information essentially free of breathing-motion artifact. The HR chest CT, however, by virtue of its thin sections, provides far better airway trees — essential for follow-on procedure planning — than the PET/CT study’s LR chest CT [13]. Our selection of scans was random, but we did strive to cover the variety of situations arising in the clinical protocols. Regarding the distribution of the 37 scans over 20 patients, 12 patient studies contributed a whole-body CT (1 contrast) and an HR chest CT (5 contrast), 5 patient studies contributed a whole-body CT and an LR chest CT, and 3 patient studies provided a single CT scan (2 contrast), where the contrast agent helped better distinguish vascular structures from surrounding soft tissues.

The performance results presented in Section III-A employ the following standard metrics [39], [40]:

$$\text{Dice}(G,S)=\frac{2|G\cap S|}{|G|+|S|},\text{Jaccard}(G,S)=\frac{|G\cap S|}{|G\cup S|},\text{coverage}(G,S)=\frac{|G\cap S|}{|G|},\text{leakage}(G,S)=\frac{|S-G|}{|G|},$$ (17)

where |·| signifies the volume of its argument and G and S represent the volumes of a ground-truth region and corresponding segmented region, respectively. The Dice and more stringent Jaccard metrics measure similarity between the ground-truth and segmented regions, coverage measures the amount of the ground-truth region covered by a segmented region, and leakage denotes the erroneous portion of the segmented region situated outside the ground truth. The Dice, Jaccard, and coverage metrics are bounded to the range [0, 1], with 1 signifying a perfect correspondence. The ground-truth regions were defined by two imaging experts and a pulmonary physician in two passes. First, a combination of the general semi-automatic live-wire method of Lu [35] and an early variant of automatic 2D contour-definition method of Algorithm 1 were applied to generate an initial ground-truth segmentation on each 2D scan section. Next, region defects were corrected section by section using either interactive region filling, region erasing, or section tracing.

Section III-A presents tests measuring the performance of the proposed thoracic-cavity definition method. Section III-B then considers application to 3D thoracic PET/CT image analysis and visualization.

A. Segmentation Performance

The first series of tests benchmark parameter sensitivity and computation time for the proposed method. Three CT scans, one of each type, were used in these tests, as summarized in Table II.

TABLE II.

CT scans used in benchmark tests. “Resolution” signifies the axial-plane resolution in mm.

CT Scan	Nz	Resolution
whole-body (case 21405.111)	293	0.9
LR chest (case 21405.98)	100	0.3
HR chest (case 21405.111)	664	0.6

By and large, the method parameters specifying structuring element dimensions or air/bone HU thresholds in Organ Segmentation either have minimal consequence or are well accepted from extensive chest CT imaging experience, while Volume Refinement has no variable parameters. Two parameters used in Contour Approximation, however, warrant careful consideration: 1) the number of seeds n contained in seed set S per (10) during 2D contour definition; and 2) the thickness of the search region ℳ in (13) as determined by structuring element B₄ during sequential section analysis. Tables III–IV detail sensitivity tests for these two parameters. Performance metrics are presented as mean±SD in percentage (%) averaged over the three test scans. For both parameters, the best segmentation results were achieved with the Section II default values of n = 16 and radius = 7.5 mm. Increasing or decreasing their values beyond the defaults did decrease method performance, but these decreases were modest.

TABLE III.

Sensitivity of thoracic-cavity segmentation as function of the number of seeds n in seed set S per (10).

n	Performance Metric (mean ± SD in %)
	Dice	Jaccard	Coverage
8	99.85 ± 0.07	99.71 ± 0.14	99.95 ± 0.01
12	99.84 ± 0.07	99.68 ± 0.14	99.95 ± 0.01
16	99.86 ± 0.07	99.72 ± 0.14	99.98 ± 0.01
24	99.79 ± 0.08	99.58 ± 0.15	99.96 ± 0.01
32	99.78 ± 0.07	99.57 ± 0.13	99.97 ± 0.01

TABLE IV.

Sensitivity of thoracic-cavity segmentation to the radius of B₄ defining working area ℳ in (13).

Radius	Performance Metric (mean ± SD in %)
	Dice	Jaccard	Coverage
2.5	99.35 ± 0.33	98.71 ± 0.66	99.91 ± 0.04
5.0	99.79 ± 0.09	99.58 ± 0.18	99.96 ± 0.02
7.5	99.86 ± 0.07	99.72 ± 0.14	99.98 ± 0.01
10.0	99.86 ± 0.06	99.72 ± 0.13	99.95 ± 0.02

Table V benchmarks the method’s computation time for the three test CT scans, using the Dell Precision T5500 workstation mentioned previously. Contour Approximation required the majority of computation, ranging from 52% to 73%. Notably, despite the many separate operations performed during Organ Segmentation, this step required only between 11% and 34% of the total computation time. Note that while the LR chest CT contains roughly the same number of sections as the whole-body CT, the computation time for this scan was much greater. This is expected, however, as the 2D sections contain 4 times the number of pixels as the other scans. Overall, the method produces complete segmentations of ℛ^thorax in < 20 sec for a typical whole-body CT scan and < 3 min for a large HR chest CT scan.

TABLE V.

Computation time of thoracic-cavity segmentation for three test scans. “Time” equals the total time in sec. for the complete 3-step method. For each method step, the table lists the computation time (sec) and percentage (%) of the total time taken.

Scan Type	Nz	Time	Organ Segmentation	Contour Approximation	Volume Refinement
whole body	83	17.6	6.0, 34.1	9.2, 52.1	2.4, 13.8
LR chest	88	101.0	15.7, 15.6	65.4, 64.7	19.9, 19.7
HR chest	487	151.4	16.5, 10.9	110.5, 73.0	24.4, 16.1

Tables VI–VII next present segmentation performance results for the complete CT-scan database using the default parameter values of Section II, while Figs. 9 and 10 present sample segmentations for three cases. Performance metrics are presented as mean±SD in % over scans of a specified type.

TABLE VI.

Segmentation performance — Complete thoracic cavity considered.

Scan Type	Scans	Performance Metric (mean ± SD in %)
		Dice	Jaccard	coverage	leakage
entire database	37	99.32 ± 1.28	98.68 ± 2.43	99.19 ± 2.28	0.52 ± 0.52
whole body	17	99.30 ± 1.26	98.65 ± 2.41	99.17 ± 2.19	0.53 ± 0.50
LR chest	6	98.61 ± 2.07	97.34 ± 3.89	98.10 ± 3.94	0.78 ± 0.75
HR chest	14	99.64 ± 0.49	99.30 ± 0.96	99.69 ± 0.70	0.39 ± 0.34
contrast	8	99.58 ± 0.63	99.17 ± 1.24	99.53 ± 0.89	0.36 ± 0.39

TABLE VII.

Segmentation performance — Lungs removed from ℛ^thorax.

Scan Type	Scans	Performance Metric (mean ± SD in %)
		Dice	Jaccard	coverage	leakage
entire database	37	97.30 ± 4.34	95.05 ± 7.24	97.29 ± 7.03	2.41 ± 2.16
whole body	17	97.63 ± 3.32	95.56 ± 5.88	97.66 ± 5.55	2.23 ± 1.70
LR chest	6	94.12 ± 8.11	89.90 ± 13.03	93.27 ± 13.49	3.79 ± 3.93
HR chest	14	98.26 ± 1.66	96.63 ± 3.06	98.56 ± 2.53	2.02 ± 1.12
contrast	8	98.14 ± 2.16	96.42 ± 3.98	98.05 ± 3.10	1.73 ± 1.28

Fig. 10.

Example segmentations of ℛ^thorax for two CT scans.

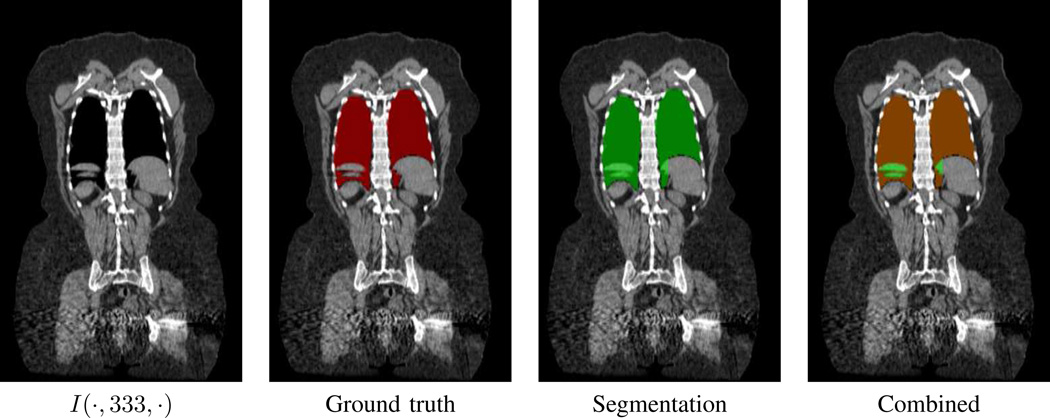
Note that the lungs constitute a high percentage of ℛ^thorax. For our database, ℛ^lungs occupied on average 80.4%±6.8% of ℛ^thorax (min, 60.8%; max, 91.1%) [29]. Therefore, because the lungs are relatively easy to segment, removing the lung field from consideration provides a more telling test of method performance that focuses on the mediastinum. Table VII gives results for this more stringent test. As the tables make evident, segmentation performance was very high, with the performance metrics for the complete ℛ^thorax averaging near 99% for the entire thoracic cavity and 97% with the lungs removed. Leakage errors over all cases ranged between 0.1% and 2.2% (entire thoracic cavity) and 0.4% and 11.2% (no lungs).

B. PET/CT Image Analysis and Visualization

We now consider how thoracic cavity segmentation facilitates PET/CT image analysis and visualization. Results are presented for two tasks arising during the assessment of a lung-cancer patient’s imaging studies: 1) ROI localization and detection; and 2) multimodal image visualization.

1) ROI Localization and Detection

A chest radiologist, pulmonary physician, and two imaging scientists identified and defined all thoracic PET-avid ROIs in the PET scans of 10 patients who had whole-body co-registered PET/CT scan pairs {I_PET, I_CT}. These studies correspond to 10 consecutive patients considered in Table I who presented ROIs satisfying the criteria given below. Only ROIs deemed significant to lung-cancer assessment were identified. Thus, PET-avid regions situated in the heart/vasculature or arising from false indications such as lung scarring were disregarded.

For a given ROI voxel (x, y, z), I_PET(x, y, z) > 0.0 denotes the voxel’s SUV value. A significant suspicious ROI satisfied two criteria [38]: (1) SUV_mean > 2.0 or SUV_max > 3.0; (2) short-axis length > 1 cm on at least one 2D section. 3D regions were defined using a combination of semi-automatic region growing, live-wire contour definition, and region filling/erasing [29], [41]. This resulted in 44 identified ground-truth ROIs for the 10 scans, with PET avidity ranging from mild to intense as judged by the physicians (Table VIII).

TABLE VIII.

Ground-truth ROI characteristics. “Mean” and “Range” denote the mean value and range for a given characteristic over the set of 44 ground-truth ROIs.

Characteristic	Mean	Range
volume	5.9 cm3	[0.6 cm3, 90.3 cm3]
short-axis length	1.7 cm	[1.0 cm, 6.4 cm]
SUVmean	3.62	[2.16, 6.76]
SUVmax	5.83	[2.29, 16.21]

Using this database, we illustrate how CT-based thoracic-cavity segmentation improves PET ROI search and detection performance for a previously developed semi-automatic central-chest lesion-detection method [41]. The method is summarized below, where co-registered PET/CT scan pair {I_PET, I_CT} serves as the input:

1. Mask out voxels in I_PET not contained in a mask derived from I_CT. This gives a masked image $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{\text{mask}}$ with a reduced ROI search space.

2. Histogram the SUV values of voxels constituting $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{\text{mask}}$. Based on the histogram, identify threshold T₁ that maximizes the inter-class variance between the foreground (PET-avid) and background voxels.

3. Threshold $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{\text{mask}}$ using T₁ to give image $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{T_1}$.

4. Delete 3D connected components in $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{T_1}$ having volume < 100 mm³. All remaining 3D connected components correspond to ROI detections.

5. Iterate steps 2)–4) on $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{T_1}$ to produce successively more stringent thresholds T_i > T_i−1 and associated thresholded images $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{T_i}$, i = 2, 3, …, until achieving the desired result.

The method, a 3D multimodal variant of Otsu’s thresholding technique [22], is discussed in full detail in [29], [41]. In past research, we had iterated this process until we observed a satisfactory result as gleaned by interactive visualization [41]. For our current study, we iterated the process until a threshold T_i caused the true-positive (TP) detection rate of I_PET’s ground-truth ROIs to drop below 100%; i.e., T_i−1 was the highest threshold giving a 100% TP rate. We then retained $I_{\mathrm{P}\mathrm{E}\mathrm{T}}^{T_{i-1}}$ as the final result.

Table IX gives study results for three CT-based masks applied in step 1:

1. No mask — Corresponds to a purely PET-based ROI detection.

2. Lung mask — Corresponds to the MBC of the CT-based segmented lungs ℛ^lungs.

3. Thoracic cavity — ℛ^thorax is used as the mask.

In Table IX, “ROI Search Space” signifies mean ROI search volume, presented as mean±SD cm³ over all PET scans, “SUV Threshold” specifies the mean final SUV threshold found by the semi-automatic method giving a 100% TP rate for the ground-truth lesions, “Detected Regions” denotes the total number of isolated regions, “True Positives” gives the total number of detected regions containing a ground-truth ROI (over 44 total ground-truth ROIs), “False Positives” (FPs) indicates the total number of detected regions not containing a ground-truth ROI, and “FP/case” gives the mean number of FPs per case.

TABLE IX.

Overall PET ROI search-space and detection results for 10-scan database.

Mask Type	ROI Search Space	SUV Threshold	Detected Regions	True Positives	False Positives	FP/case
none	196, 088 ± 31, 786	3.15 ± 1.29	506	32	474	47.4
Lung	12, 338 ± 1, 579	3.24 ± 1.19	247	37	210	21.0
Thorax	4, 584 ± 620	3.39 ± 1.04	80	41	39	3.9

First note the size reduction of the ROI search space afforded by each CT-based mask relative to the complete scan. The lung mask reduced the search space by 93.7% over the whole volume, while the thoracic cavity reduced the search space by 97.7%, or an additional 63.5% more than the lung mask. State differently, the thoracic cavity reduced the PET-only search space by a factor of 43 and the lung-mask’s search space by nearly a factor of 3. Nevertheless, 100% ROI detection was still feasible with this greatly reduced PET sub-volume. Furthermore, ℛ^thorax gave a 100% coverage metric for 38/44 ground-truth ROIs, with > 82% coverage for 4 other ROIs. Overall, these observations imply that ℛ^thorax reliably encompasses the necessary data for comprehensive lung-cancer-based lesion detection. As a related observation, Table X shows that ℛ^thorax also greatly reduced the CT-based ROI search space for all CT scan types, with nearly a factor of 3 reduction over the lung mask’s search space.

TABLE X.

CT-based ROI search-space reduction for the 37-scan database of Table I. “Raw Volume” gives the volume of a raw unmasked CT scan as mean±SD cm³ over all scans of a given type. “Lung Mask” and “ℛ^thorax” columns list the search-space reduction in terms volume (cm³) and percentage (%) of the raw scan volume for the specified mask.

Scan Type	Raw Volume	Lung Mask		ℛthorax
		Volume	Percentage	Volume	Percentage
whole-body	209, 783 ± 44, 219	12, 442 ± 2, 458	94.1	4, 677 ± 1, 060	97.8
LR chest	34, 301 ± 10, 202	14, 481 ± 2, 436	57.8	5, 120 ± 691	85.1
HR chest	34, 081 ± 9, 836	14, 254 ± 3, 436	58.2	5, 336 ± 1, 005	84.3

The mask type also had a major effect in reducing false positives. Without a CT-based mask (i.e., PET-only ROI detection), the lesion-detection method essentially fails, as 93.7% of detected ROIs were FPs with a mean 47.4 FP/case. While the lung mask reduced the number of FPs by 55.7%, this still yielded 21 FP/case. Notably, the thoracic cavity reduced the FP rate by an impressive 91.8%, resulting in only 3.9 FP/case. Thus, ℛ^thorax helped reduce the number of FPs by a factor of 12 when compared to a raw scan and 5 when compared to the lung mask. Finally, the refined search space afforded by ℛ^thorax enabled more more stringent SUV thresholds, and, hence, produced more detected regions containing only one ground-truth ROI. In particular, 38/41 (93%) TP regions encompassed only one ground-truth ROI, with 8/10 cases exhibiting no detections that merged ground-truth ROIs. The other masks, on the other hand, merged many more ground-truth ROIs into the same detected regions, reflecting how the poor search-space reduction of these masks adversely affected the lesion detection method.

2) Multimodal Visualization

In this section, we demonstrate how visualization of PET/CT study data is greatly enhanced by use of the CT-based thoracic cavity.

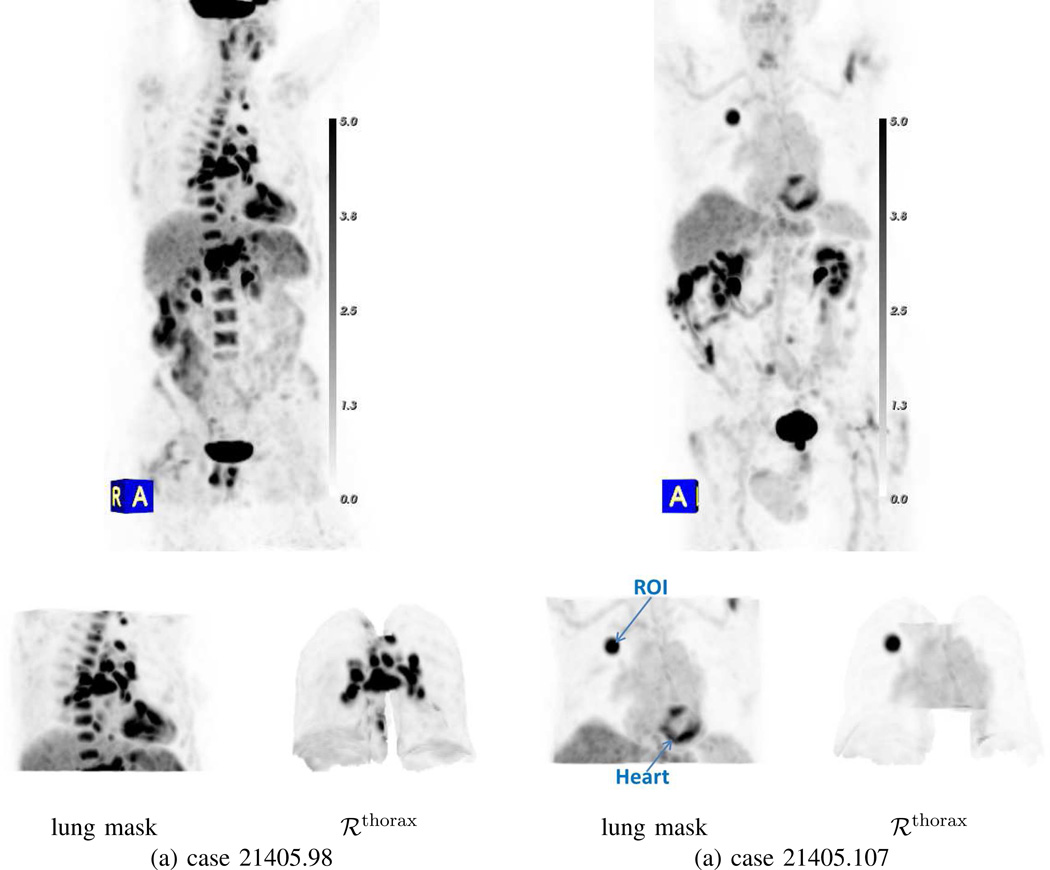
A standard means for viewing whole-body 3D PET data is through interactive maximum-intensity projection (MIP) [2], [42]. Such a view, which integrate all available 3D PET scan data into a single rendering, is useful, because it gives the physician a global picture of potential PET-avid “hot spots.” Unfortunately, the large data volume constituting a typical PET scan often obscures mild-to-moderate PET-avid ROIs. Fig. 11 illustrates how CT-based data masking greatly improves 3D PET MIP visualization. While the lung mask does remove considerable data from consideration in the MIP view, the spine, heart, and remaining parts of the diaphragm/liver still obscure clear viewing of the thorax, especially in the inferior region. These obscurations are especially confounding for case 21405.98, while for case 21405.107 the presence of the heart and its propensity for exhibiting FDG activity confuses the distinction of the true PET-avid lesion. Use of the thoracic mask, on the other hand, gives a much clearer and less ambiguous view of the desired PET-avid ROIs.

Fig. 11.

Improvement in 3D whole-body PET/CT MIP visualization through multimodal data masking. Column (a): case 21405.98; column (b): case 21405.107. Top row shows raw whole-body PET MIP view for each case with [0.0, 5.0] SUV gray-scale; PET-avid regions have high (dark) SUV values. Bottom row shows the indicated PET MIP view produced after applying a specific CT-based mask.

Multimodal volume rendering of a fused whole-body 3D PET/CT volume also greatly improves through data masking. Fig. 12 dramatically demonstrates the superiority of thoracic-cavity masking for unobscured visualization of relevant PET-avid regions — notice how the distracting PET-avid liver region in the lung-masked rendering greatly deteriorates the clarity of the rendering versus the result achieved using the thoracic cavity. As another example, Fig. 13a clearly shows how the location of a PET-avid chest lesion relates to nearby anatomical structures. By using the mask, major obscurations from the rib cage, sternum, heart, and superfluous soft tissue are deleted. In addition, the distracting bladder, which typically appears PET-avid because of the intravenous administration of a F-18 FDG tracer prior PET scanning, is deleted. Given this improved rendering capability, the simultaneous visualization of various multiplanar reformatted 2D sections — both unimodal and fused PET/CT — synchronized to a 3D ROI location selected in the multimodal volume rendering becomes easily achieved and feasible, as shown in Fig. 13 [2].

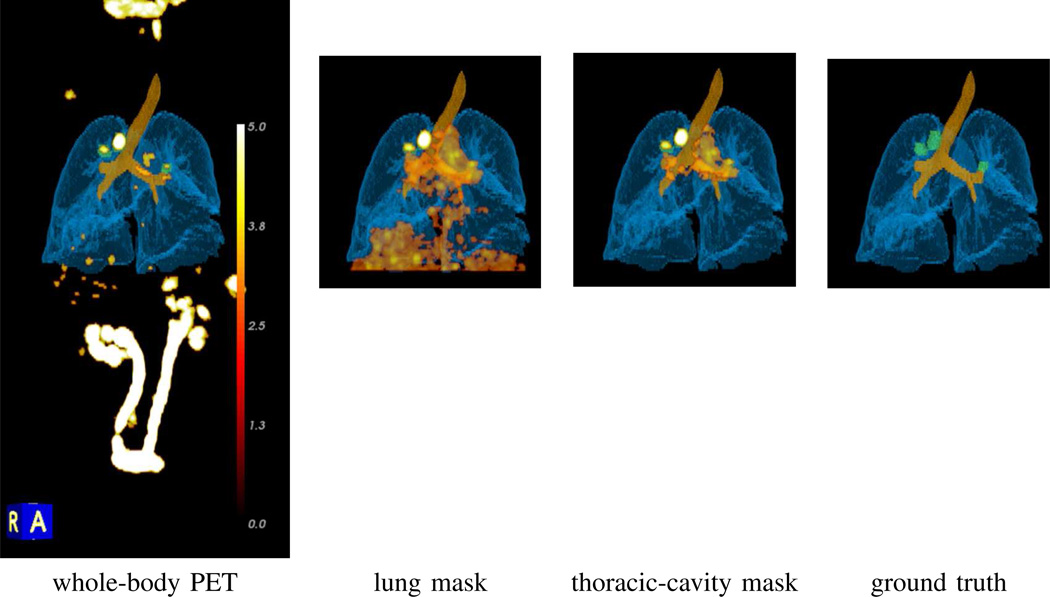
Fig. 12.

Impact of data masking on the visualization of PET-avid ROIs in 3D multimodal volume renderings for case 21405.116. All renderings combine the masked whole-body PET scan, along with the segmented airway tree (brown) and lungs (light blue) derived from the corresponding whole-body CT scan. The PET data is rendered using a [0.0, 5.0] SUV scale mapped to the standard 8-bit “heat” color scale (see Fig. 14). Actual whole-body PET view truncated for brevity; actual view extends from the knees to the neck. Rendering in the Ground Truth column depict the ground-truth ROIs (green).

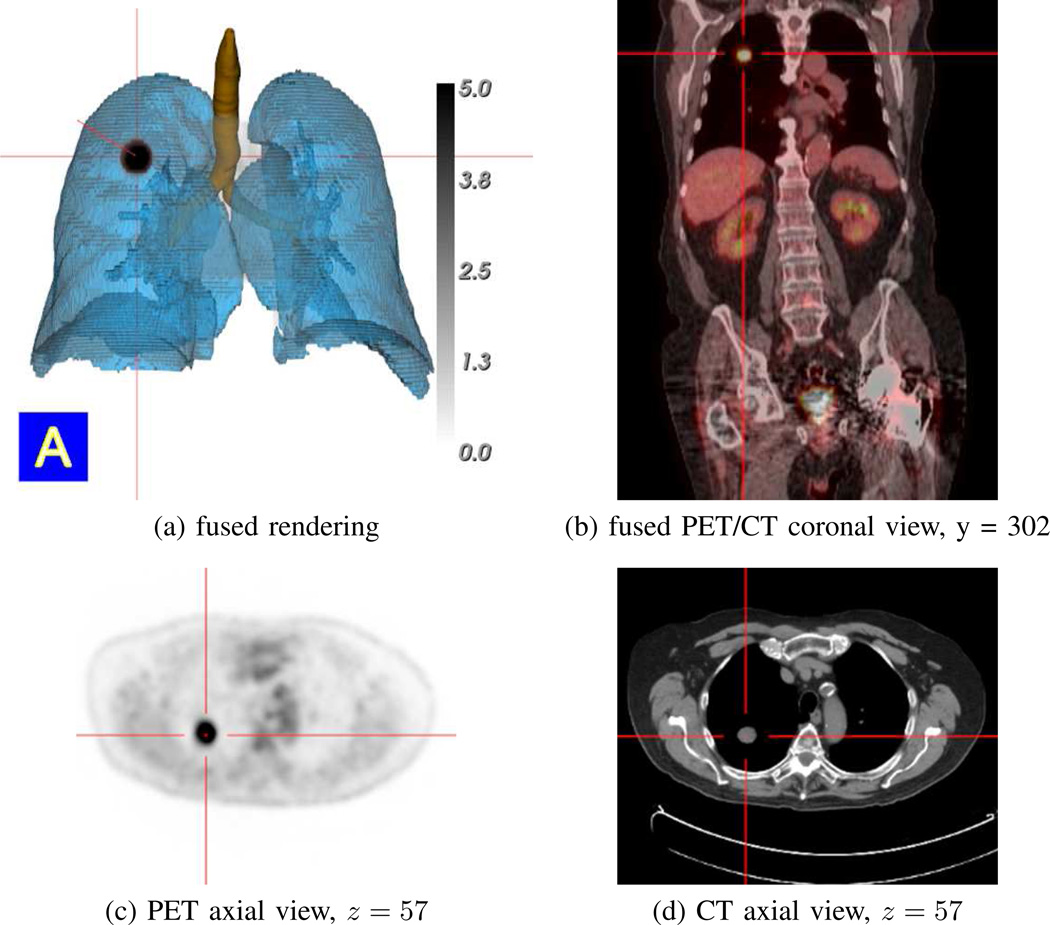
Fig. 13.

Synchronized multimodal visualization of a PET-avid RUL nodule for case 21405.107. All views derived from the whole-body PET/CT study pair {I_PET, I_CT}. (a) ℛ^thorax-masked PET volume fused with surface renderings of the segmented CT-based airway-tree (brown), lungs (light blue), and RUL nodule (black, indicating an intense PET-avid location); PET data rendered using indicated [0.0, 5.0] SUV scale. (b–d) present sample MPR views synchronized to the selected nodule location, as indicated by the red cross-hairs in all views. Fused PET/CT view truncated slightly for brevity, as in Fig. 12.

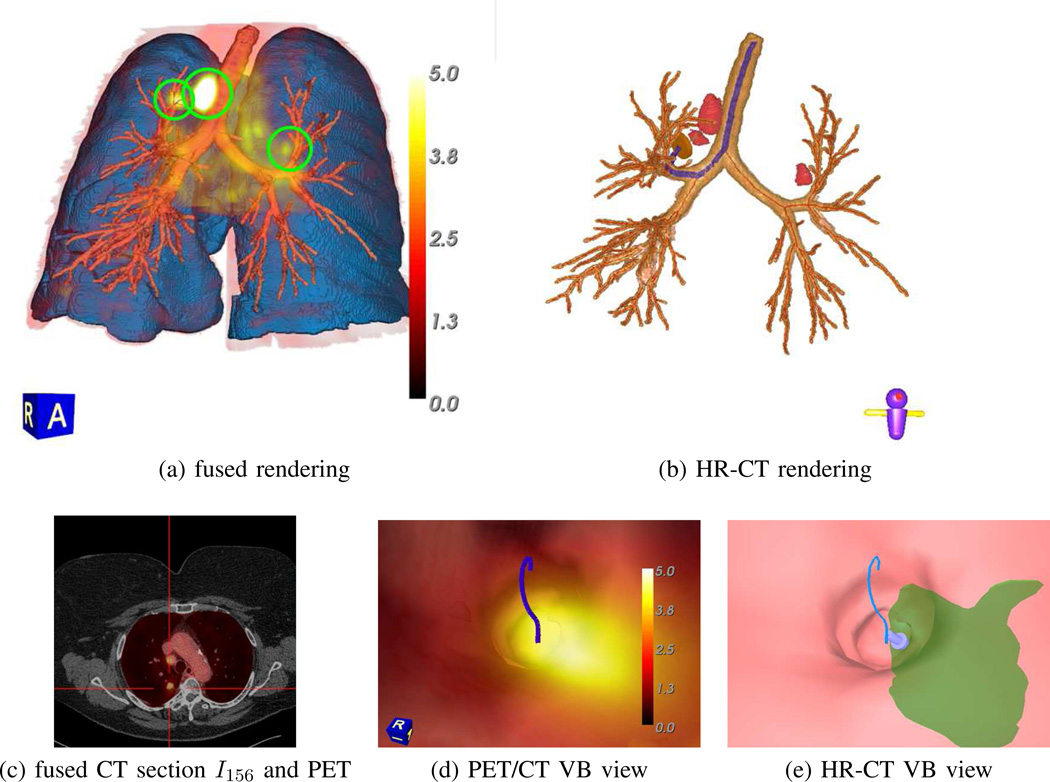
As a final example, Fig. 14 illustrates how detailed synergistic multimodal lung-cancer image assessment and procedure planning become feasible. In particular, the figure illustrates the fusion of a whole-body free-breathing PET/CT study with the corresponding breath-hold HR chest CT scan. As described more fully in the references, to produce these results, we first performed a deformable registration between the PET/CT scans and the HR chest CT scan [29], [43], [44]. We then mapped the masked PET data into the 3D space of the HR chest scan and generated the displayed views. The fused renderings offers a multimodal view of fused 3D functional-imaging data, only available from the PET scan, and the detailed high-resolution airway-tree structure captured only by the HR chest CT scan (Fig. 14a–c). In addition, associated virtual bronchoscopy (VB) views enable virtual navigation through the airway tree and depict an optimal navigation route terminating near a RUL nodule (Fig. 14de) [45]. Note that the navigation route, which is invaluable for follow-on guidance of bronchoscopic lung-cancer staging biopsy, could only be produced with the HR chest CT scan [32].

Fig. 14.

Composite multimodal visualization of three PET-avid ROIs for case 21405.116. (a) ℛ^thorax-masked PET volume fused with CT-based surface rendering of the segmented airway-tree (brown), airway centerlines (red), and lungs (light blue). The whole-body PET/CT scans were registered and deformed to the space of the patient’s HR chest CT scan, while the segmented structures were derived from the HR chest CT scan. The PET-avid ground-truth ROIs are highlighted by green circles. (b) Surface rendering of airway tree, centerlines (red), and ground-truth ROIs (red) derived from the HR chest CT scan. The highlighted blue path represents the optimal navigation route leading to the ground-truth RUL nodule, while station 4R and 3P lymph nodes also appear. (c) Axial section of HR chest CT scan fused with ℛ^thorax-masked version of corresponding registered/deformed whole-body PET section (red); red cross-hairs highlight the RUL nodule. (d) fused whole-body PET/CT VB rendering near site of the PET-avid RUL nodule (bright yellow), along with blue navigation route. (e) HR-CT-based VB rendering of same location as (d), with the HR-CT version of the RUL nodule (green) also appearing. In (a) and (d), PET data is rendered using the indicated [0.0, 5.0] SUV scale. Compare to related visualizations for this case in Fig. 11, third row, and Fig. 12, second row.

IV. Discussion

We proposed a method for segmenting the thoracic cavity in 3D CT scans of lung-cancer patients. We also showed how the method greatly helps analyze and visualize pertinent diagnostic structures in multimodal PET/CT imaging studies. The method is fully automatic and proved to be robust to parameter variations and differences in patient-scanning protocol.

Using a large database, the segmentation method showed very high agreement to ground-truth regions, with a mean coverage = 99.2% and leakage = 0.52%. This compares favorably to other methods: one method, which considered COPD analysis, reported a mean coverage = 98.2% and leakage = 0.49% [17], while a second method, directed toward cardiovascular disease, reported a mean coverage = 99.1% (leakage performance not reported) [15]. Notably, each of these studies only considered scans using one fixed scanning protocol on one scanner. Our results, on the other hand, considered both whole-body and chest-focused scans, a variety of scanning protocols (free-breathing and breath-hold; contrast and no-contrast), and scanners from multiple vendors. In addition, our method’s inherent parallelization enabled extremely fast computation: 20 sec for a typical whole-body scan and 3 min for a typical high-resolution chest scan. While other methods did not report computation time, the approach of Bae et al. sub-sampled the data to facilitate faster computation, while Chittajalu et al.’s 3D directed-graph formulation appears to be intense computationally [15], [17].

We point out that leakage errors near the ribs sometimes existed, as seen in Fig. 15 and as also noted by Bae et al. [17]. We further observed that the enhanced vessels in a contrast-enhanced CT scan occasionally contributed fragments to adjacent bones. Yet, both of these sources tended to be small modest and located around ℛ^thorax’s periphery, a location of little consequence for ROI selection. Another potential error source arose in defining the mediastinum’s superior boundary, even though our method employs well-known landmarks to delimit the region. Both Zhang et al. and Bae et al. acknowledged the inherent vagueness in determining “where to draw the line” for this region [14], [17]. In addition, El-Sherief et al. further noted ambiguity in this region with respect to the IASLC lymph-node map [46]. This ambiguity particularly manifests itself for station 1 (supraclavicular zone), a station that arguably is shortchanged by our definition of the superior mediastinal boundary.

Fig. 15.

Segmentation of ℛ^thorax with extra leakage for case 21405.126 (coverage = 99.94%, leakage = 0.98%, 5.00% (no lungs)). Respiratory motion caused incorrect “intermixing” of the thoracic and diaphragm regions. Ground truth = red regions, Segmentation = green regions, overlap between ground truth and segmentation = brown regions.

The largest observed errors occurred in the inferior portion of the thoracic cavity. Breathing motion and the accompanying reconstruction/blurring artifacts gives rise to some undersegmentation of ℛ^thorax’s inferior surface, while heart motion makes accurate heart definition difficult. Fig. 15 depicts motion errors in the inferior portion of ℛ^thorax. Such errors could cause ℛ^thorax to shortchange IASLC station 9 near the pulmonary ligament. Note, however, that such lymph nodes are not accessible via bronchoscopy. In addition, Bae et al. acknowledged the difficulty of heart and diaphragm segmentation, despite resorting to manual landmark selection to help delineate the heart [17]. While clinically treatable ROIs — i.e., ROIs that can be safely biopsied or surgically removed without compromising patient safety — are not adjacent to the heart, more accurate heart definition would be useful. One promising idea is the define an oblique plane constraining the heart’s superior surface.

The segmentation method proved especially useful for reducing the ROI search space for PET/CT lesion analysis. For a whole-body scan, the average search-space reduction was 97.7%, which was nearly 3 times greater than that achieved by a simple lung mask. Despite this reduction, we achieved 100% true-positive detection, while also reducing the false-positive detection rate 91.8% over using the whole scan volume. Stated differently, this implied a 3.9 FP/scan rate, or >5 times fewer FPs than that achieved with a lung mask.

In addition, the method greatly improved PET/CT visualization by eliminating false PET-avid obscurations arising from the heart, bones, and liver. The resulting PET MIP views and fused PET/CT renderings enabled unprecedented clarity of the central-chest lesions and neighboring anatomical structures truly relevant to lung-cancer assessment and follow-on procedure planning. On a related front, we also demonstrated how whole-body free-breathing PET/CT data could be registered, deformed, and fused with high-resolution chest CT to enable detailed procedure planning; this effort in turn facilitates ongoing research focused on devising a computer-based system for multimodal imaging-based lung-cancer planning and guidance [29], [43], [44].

SUMMARY.

X-ray computed tomography (CT) and positron emission tomography (PET) serve as the standard imaging modalities for lung-cancer management. CT gives anatomical detail on diagnostic regions of interest (ROIs), while PET gives highly specific functional information. During the lung-cancer management process, a patient receives a co-registered whole-body PET/CT scan pair, collected as the patient breathes freely, and a dedicated high-resolution chest CT scan, collected during a breath hold. With this scan combination, multimodal PET/CT ROI information can be gleaned from the co-registered PET/CT scan pair, while the dedicated chest CT scan enables precise planning of follow-on chest procedures such as bronchoscopy and radiation therapy. For all of these tasks, effective image segmentation of the thoracic cavity is important to help focus attention on the central-chest region. We present an automatic method for thoracic cavity extraction from 3D CT scans. We then demonstrate how the method facilitates 3D ROI localization and visualization in the PET/CT studies of lung-cancer patients.

Our method for segmenting the thoracic cavity involves three major steps: organ segmentation, contour approximation, and volume refinement. The various method steps draw upon 3D digital topological and morphological operations, active-contour analysis, and key anatomical landmarks derived from the segmented organs. Using a large patient database, the segmentation method showed very high agreement to ground-truth regions, with a mean coverage = 99.2% and leakage = 0.52%. Also, unlike previously proposed methods, our method was shown to be effective for a wide range of patient-scanning protocols and image resolutions. In addition, our method enabled extremely fast computation: 20 sec for a typical whole-body scan and 3 min for a typical high-resolution chest scan.

The segmentation method proved especially useful for reducing the ROI search space for PET/CT lesion analysis. For a whole-body scan, the average search-space reduction was 97.7%, which was nearly 3 times greater than that achieved by a simple lung mask. Despite this reduction, we achieved 100% true-positive ROI detection, while also reducing the false-positive (FP) detection rate 91.8% over considering the whole scan volume. Stated differently, this implied a 3.9 FP/scan rate, or >5 times fewer FPs than that achieved with a lung mask.

Finally, the method greatly improved PET/CT visualization by eliminating false PET-avid obscurations arising from the heart, bones, and liver. The resulting PET MIP views and fused PET/CT renderings enabled unprecedented clarity of the central-chest lesions and neighboring anatomical structures truly relevant to lung-cancer assessment. Overall, we believe these efforts will facilitate further development of computer-based systems for multimodal lung-cancer procedure planning, guidance, and treatment delivery.