Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2015 May 13;5:10026. doi: 10.1038/srep10026

Local electrical control of magnetic order and orientation by ferroelastic domain arrangements just above room temperature

L C Phillips 1,a,*, R O Cherifi 1,*, V Ivanovskaya 1,b,*, A Zobelli 2, I C Infante 3, E Jacquet 1, N Guiblin 3, A A Ünal 4, F Kronast 4, B Dkhil 3, A Barthélémy 1, M Bibes 1, S Valencia 4,c
PMCID: PMC4429553  PMID: 25969926

Abstract

Ferroic materials (ferromagnetic, ferroelectric, ferroelastic) usually divide into domains with different orientations of their order parameter. Coupling between different ferroic systems creates new functionalities, for instance the electrical control of macroscopic magnetic properties including magnetization and coercive field. Here we show that ferroelastic domains can be used to control both magnetic order and magnetization direction at the nanoscale with a voltage. We use element-specific X-ray imaging to map the magnetic domains as a function of temperature and voltage in epitaxial FeRh on ferroelastic BaTiO3. Exploiting the nanoscale phase-separation of FeRh, we locally interconvert between ferromagnetic and antiferromagnetic states with a small electric field just above room temperature. Imaging and ab initio calculations show the antiferromagnetic phase of FeRh is favoured by compressive strain on c-oriented BaTiO3 domains, and the resultant magnetoelectric coupling is larger and more reversible than previously reported from macroscopic measurements. Our results emphasize the importance of nanoscale ferroic domain structure and the promise of first-order transition materials to achieve enhanced coupling in artificial multiferroics.

Electrical control of magnetic properties1,2 is an important research goal for low-power write operations in spintronic data storage and logic3. Previously, interfacial strain/charge effects have been used to effect electrical control of magnetic anisotropy4,5, domain structure6,7, spin polarization8,9 and exchange bias10. Magnetic order has also been electrically controlled11, but demonstrations have been restricted to interchanging ferromagnetism and paramagnetism via small changes in the Curie temperature TC. Such changes only work in a small temperature range near TC.

We recently controlled magnetic order between antiferromagnetism and ferromagnetism above room temperature, by driving the first-order magneto-structural transition of a Fe50Rh50 (FeRh) thin film grown on ferroelectric/ferroelastic BaTiO3 (BTO), creating a very large magnetoelectric (ME) effect12. The FeRh transition is interesting because first-order transitions are rare in metals, because one can drive the transition by temperature13, pressure14 or magnetic field15, and because it exhibits magnetic phase separation, i.e. coexistence of the ferromagnetic and antiferromagnetic phases in small spatial regions over a range of experimental conditions. Recent imaging studies16,17,18 showed that the FeRh transition proceeds by the formation of robustly ferromagnetic sub-micron-sized regions that subsequently grow and coalesce.

Here we use magnetic imaging by photoelectron emission microscopy with X-ray excitation (XPEEM) and X-ray magnetic circular dichroism (XMCD) contrast to reveal that the ME effect in FeRh on BTO is driven by the creation and annihilation of the same ferromagnetic regions, due to coupling to ~10 μm-wide BTO ferroelastic domains. The two domain structures are easily distinguished due to their different length scales. Ab initio calculations confirm the enhanced relative stability of antiferromagnetic FeRh on BTO c-domains compared to a-domains, suggesting that local ME effects are driven by strain. The local ME effects are greater than our previously observed macroscopic ME effects, and amount to complete local interconversion between antiferromagnetism and ferromagnetism.

Experiment concept

We deposit and anneal our FeRh film at high temperature (see Methods), where BTO is in the non-ferroelectric cubic (C) phase with lattice constant aC. FeRh grows with the ordered body-centred cubic (bcc) CsCl-type structure, and is unstrained but highly aligned, with [100]FeRh || [110]BTO and [001]FeRh || [001]BTO. On cooling, both components undergo non-diffusive first-order phase transitions. BTO transforms sharply at the ferroelectric Curie temperature TC ~ 400 K to the ferroelectric tetragonal (T) phase with parameters aT < cT and ferroelectric polarization P || [001]T [Fig. 1(a)]. If no external electric field is applied, the T-BTO divides into ferroelastic domains separated by 90° walls, each subdivided into non-ferroelastic ferroelectric domains separated by 180° walls19. On the (001)C-oriented top surface of BTO, one sees ferroelastic c-domains (a-domains) with polarization perpendicular (parallel) to the surface and a square (rectangular) unit cell projection with surface area aT2 (aTcT) per unit cell. The balance of a-domains and c-domains can be altered by applying a voltage V across the thickness of BTO. Several domain arrangements are observed experimentally5,6 depending on the thermal and electrical history of the BTO [Fig. 1(b)]. For example, cooling through TC with no applied voltage across BTO yields a T-BTO texture with mostly a-domains separated by 90° domain walls. On the other hand, cooling through TC in the presence of a voltage, or applying voltage isothermally below TC, yields an almost fully c-domain state. Removing an applied voltage isothermally below TC creates small a-domains separated from c-domains by buried 90° domain walls. The creation of a-domains may be driven by the elastic energy of in-plane-aligned defect dipoles20.

Figure 1. Experiment concept sketches.

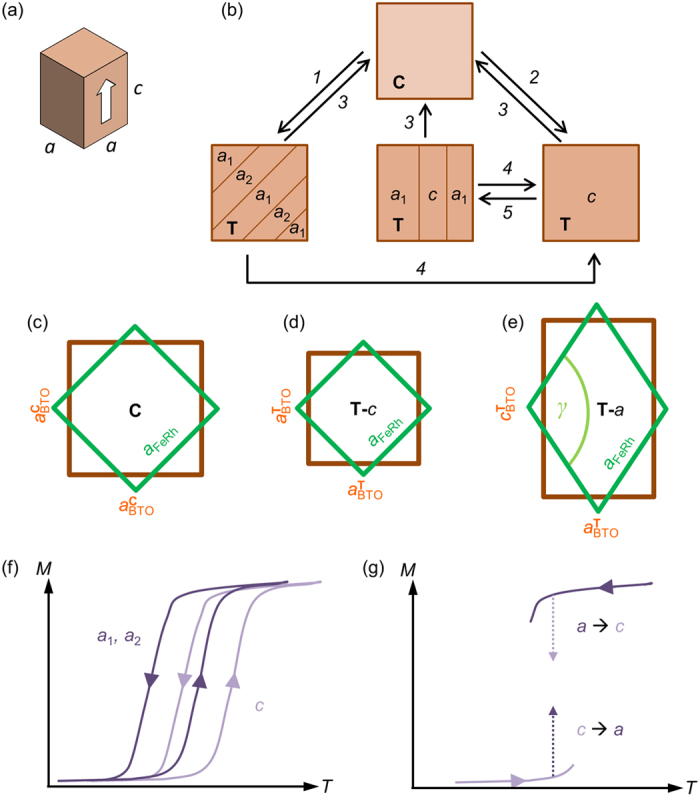
Figure 1

Open in a new tab

(a) 3D sketch of the unit cell shape of tetragonal BTO. A white arrow indicates the polarization direction. (b) 2D projection of ferroelastic domains on the BTO (001)C surface: crystal phase [C = cubic; T = tetragonal] and tetragonal ferroelastic domain orientations [(a1, a2) = a-domains; c = c-domains]. Arrows indicate operations that convert between the observed domain states: 1-cool through TC without voltage V; 2-cool through TC in applied V; 3-heat through TC; 4-apply V; 5-remove applied V. (c-e) Overlaid unit cell shapes of FeRh (green) and BTO (brown) for (c) cubic BTO, and (d) c-domains and (e) a-domains of tetragonal BTO. (f) Sketch of the expected magnetization (M) versus temperature (T) for a strained FeRh film on c-domains and a-domains of tetragonal BTO. (g) Proposed experiments for large magnetoelectric effects: heat (cool) FeRh from low (high) temperature on BTO c-domains (a-domains), then transform BTO to a-domains (c-domains) to obtain a large increase (decrease) of magnetization.

FeRh becomes ferromagnetic (FM) below its Curie temperature TC ~ 700 K, then transforms gradually between ~420 K and ~360 K via a wide range of phase separation, to a phase with antiferromagnetic (AF) order and the same cubic lattice, albeit with a ~0.3% smaller lattice constant14. The mechanical coupling of FeRh and BTO creates interplay between the two transitions. On C-BTO [Fig. 1(c)], FM-FeRh experiences only a small biaxial strain from thermal expansion mismatch [−0.2% on cooling from the deposition temperature of 903 K to the BTO TC of 400 K]21,22. On T-BTO, FM-FeRh experiences either a further biaxial compression on c-domains [Fig. 1(d)] or a monoclinic distortion on a-domains [Fig. 1(e)]. As the greater compressive strain of c-domains shifts the AF-FM transition to higher temperatures [Fig. 1(f)], large ME effects [Fig. 1(g)] are expected if we first heat (cool) from low (high) temperature on BTO consisting of c-domains (a-domains), and transform isothermally towards a-domains (c-domains) by changing the voltage across BTO.

Results

We studied FeRh on BTO in XPEEM (see Methods), controlling the sample temperature T and the voltage V across BTO. Tuning the incident X-ray energy, we find the expected absorption peaks for Fe and Rh [Fig. 2(a)]. The peak position and shape imply that both are in the metallic state. A small FeOx shoulder at 710 eV develops only after irradiation for several days, so our film is essentially stable in our measurement conditions. XMCD images at Fe and Rh edges [Fig. 2(b)] reveal identical magnetic maps over a 20-μm field of view, confirming the presence of the FM phase with the Fe & Rh moments being parallel. Hereafter we will show images at the Fe L3 edge (706.8 eV) whose dichroism is larger23. Blue (red) regions with positive (negative) XMCD are unequivocally identified as FM phase regions whose in-plane magnetization component lies parallel (antiparallel) to the incoming X-rays. White regions with zero XMCD may be either AF phase regions, or FM phase region whose magnetization lies perpendicular to the incoming X-rays. We see phase separation on a ~1 μm length scale, which is longer than previous reports16, probably due to different thickness and strain in our sample. The third phase at FM-AF interfaces18, in which Rh magnetism is supposed to exceed Fe magnetism, is not observed. The relatively large phase separation scale implies a small interfacial phase volume fraction.

Figure 2. X-ray absorption and XMCD in XPEEM.

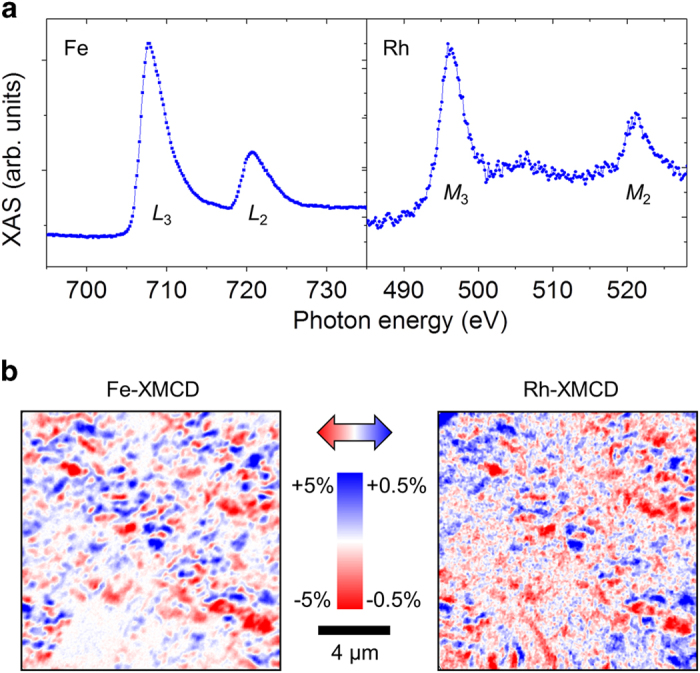
Figure 2

Open in a new tab

(a) X-ray absorption spectra of FeRh with horizontal linear polarization averaged over a 20-μm field of view, showing Fe L3,2 and Rh M3,2 peaks. (b) XMCD images of the same area at Fe L3 and Rh M3 edges. Blue (red) areas have a magnetization component parallel (antiparallel) to the incoming X-rays.

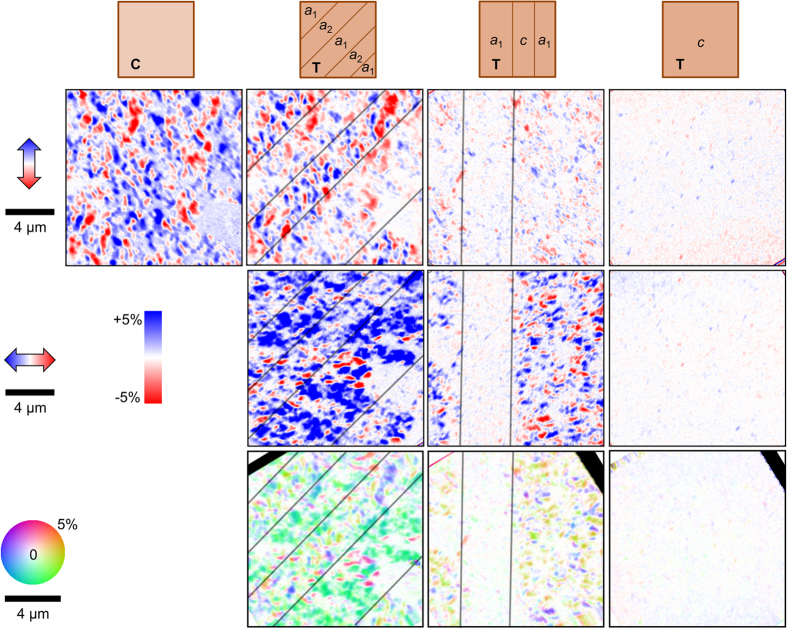
We access the four BTO domain arrangements of Fig. 1(b) by appropriately changing T and V. XMCD images at azimuthal angles of 0° and 90° reveal how FeRh responds to changes in the substrate [Fig. 3]. Single XMCD images do not uniquely identify AF and FM regions, so we combine pairs of XMCD images with perpendicular incoming X-ray directions into vector maps (Fig. 3 and Methods) to directly image the phase-separated texture. White areas in vector maps have no magnetization component in any in-plane direction, and are therefore identified as AF phase regions. On spatially homogeneous BTO states i.e. C-BTO or a single large c-domain of T-BTO, we see a FeRh microstructure consisting of 1 μm-wide equiaxed FM & AF regions. On inhomogeneous BTO states e.g. mixed a1-a2 or a-c domains, we also observe a superstructure of 5–10 μm-wide lamellar regions separated by parallel straight lines. Given that these lamellar structures are very similar to ferroelastic 90° domain walls of BTO (001) crystals6,21 both in size and in angle with respect to the crystal axes, we identify them as regions of FeRh above different BTO ferroelastic domains. XMCD vector maps [Fig. 3, bottom] reveal that FeRh acts as an indicator film to reveal the underlying BTO domains in two ways: either by alternating magnetization orientation on a1-a2 domain patterns, or of ferromagnetic phase fraction on a-c domain patterns. The changes in FeRh are due either to ferroelastic strain or ferroelectric charge. We exclude charge effects that are permitted within one exchange length24 of the FeRh/BTO interface, because XPEEM probes the top ~5 nm of our 22-nm film, and therefore cannot probe the charge-affected region. We conclude that FeRh is affected by dynamic strain from ferroelastic BTO domains which extends through the sample thickness.

Figure 3. XMCD on various BTO domain arrangements.

Figure 3

Open in a new tab

From top to bottom: sketches of expected BTO domains with reference to Fig. 1(b); corresponding Fe-XMCD images at azimuthal angle 0° with incident X-rays along page vertical; Fe-XMCD images at azimuthal angle 90° with incident x-rays along page horizontal; in-plane XMCD vector maps. Black lines mark inferred ferroelastic domain wall locations. Double-headed red-white-blue arrows indicate the component of magnetization that is measured in each row.

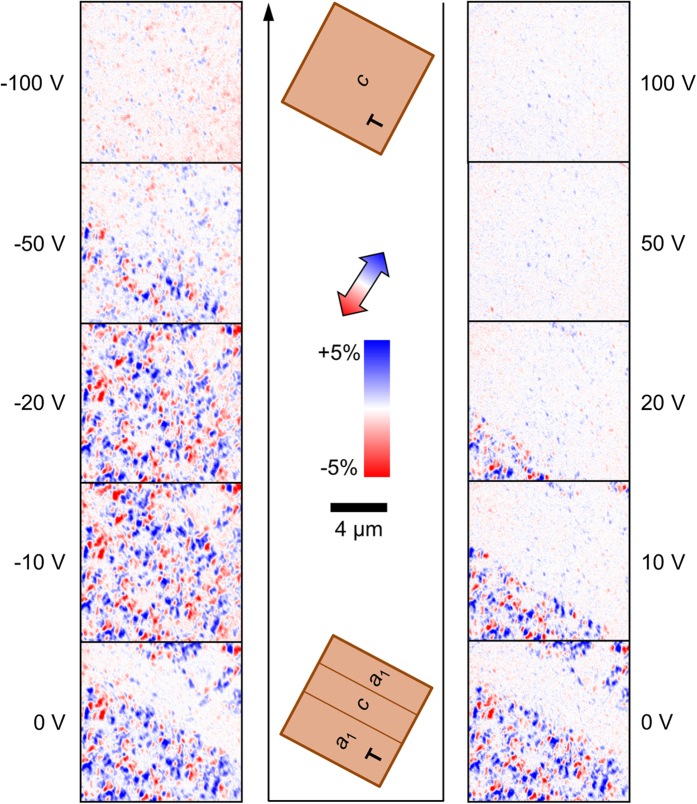
In order to observe local dynamic electric-field-induced changes in FeRh, we performed an isothermal voltage study as sketched in Fig. 1(g), similar to our previous macroscopic measurement12. We heat from ~300 K to the measurement T of 385 K with a large applied voltage V = +150 V, preserving a c-domain BTO state [Fig. 1(b)] and a mostly AF FeRh state [Fig. 1(g)] with negligible XMCD. Reducing the voltage to zero, we create BTO a-domains which propagate slowly across the field of view, transforming FeRh to a mixed state with ~40–60% FM phase [Fig. 4]. Applying a large voltage in the opposite direction, we reconvert the a-domains to c-domains and partly reverse the FeRh transformation. Some FM-FeRh remains, just as for our macroscopic measurement12. The average XMCD over the images for red and blue domains [Fig. 5(a)] shows a peak at a small negative voltage Vpk ≈ −15 V. Vpk also corresponds to a maximum(minimum) in a-(c-)domain population [Fig. 5(b)] and a minimum in the FeRh out-of-plane lattice constant [Fig. 5(c)] that were measured simultaneously in high-T X-ray diffraction during a similar voltage study of a nominally identical sample at 385 K. These measurements provide further proof that the magnetic changes in FeRh are driven by strain arising from interconversion of BTO a- and c-domains.

Figure 4. Magnetoelectric effect by XMCD.

Figure 4

Open in a new tab

XMCD images at 385 K at several voltages V during a stepwise sweep from +100 V to −100 V. The black arrow indicates the order of images in time. Sketches show the expected BTO domains for large and small |V|.

Figure 5. Voltage dependence of XMCD and structural parameters.

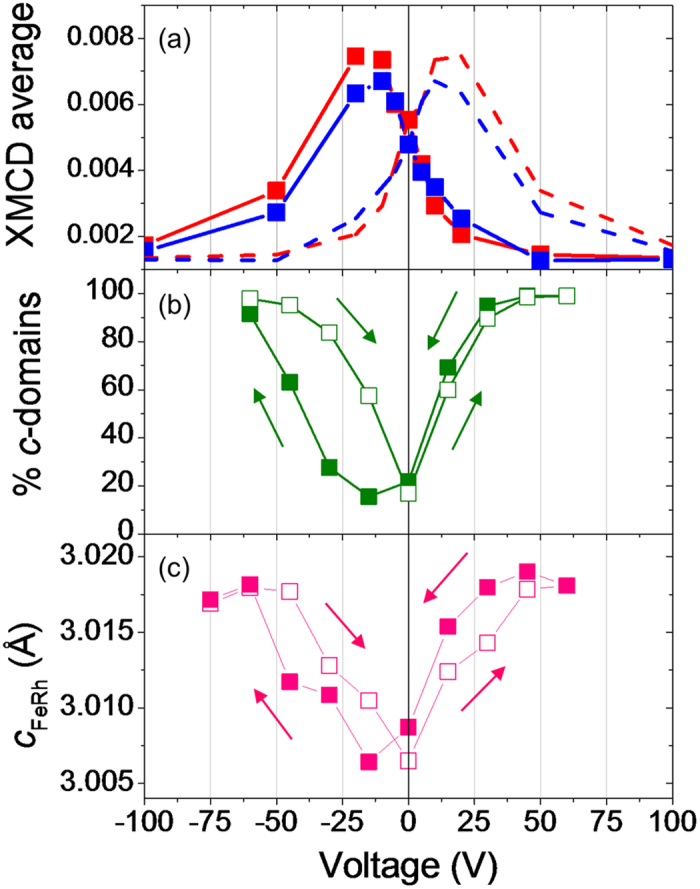
Figure 5

Open in a new tab

(a) Points connected by solid lines represent average XMCD asymmetry vs. voltage for red (XMCD < 0) and blue (XMCD > 0) domains in XPEEM images at 385 K. Dashed lines show the same data mirrored about the voltage axis. Some of the source images are also shown in Fig. 4. (b,c) HTXRD data at 385 K in a nominally identical sample, taken during stepwise negative (closed symbols) and positive (open symbols) sweeps of the voltage across BTO: (b) fraction of BTO c-domains, from the relative areas of BTO 002 and 200 + 020 peaks; (c) FeRh out-of-plane lattice parameter. Data were deduced by fitting pseudo-Voigt functions to observed peaks in θ/2θ scans.

Discussion

We have observed and dynamically altered two properties of FeRh at a local scale: the magnetization orientation in the FM phase, and the AF/FM phase balance. We have thus demonstrated simultaneous electrical control of magnetic order and magnetic anisotropy at the micron and sub-micron length scales. The changes of magnetization orientation arise from ME coupling, specifically the anisotropic part of magnetostriction λt, which was previously discounted as negligible24,25. Our XPEEM images on a1-a2 BTO domains show that λt is non-zero and positive. The changes of phase fraction arise from relative changes in the free energies of AF and FM phases. The phase fraction changes we have seen in XPEEM appear to be larger and more reversible than in our previous macroscopic measurements12, where we achieved an isothermal magnetization change ΔM = 280 e.m.u. cm−3 equal to ~25% of the saturation magnetization of FM-FeRh. This may be because: local changes in our XPEEM field of view can exceed global changes over the whole film; we use a larger voltage to bring BTO to electrical saturation; the out-of-plane FM component is hardly detected in XPEEM; and because our macroscopic measurements were performed in a large saturating magnetic field H = 2 T, which can in principle change the dynamics of the transition.

To understand the link between imposed strain and the relative stability of AF and FM phases, we perform first-principles calculations in the framework of density-functional theory (see Methods). In a previous work, we compared the effect of hydrostatic “isotropic” and biaxial tetragonal “anisotropic” strain in FeRh12, and showed that the AF phase is favoured by compressive distortions of both types. Here we consider the additional effect of transforming FeRh from tetragonal to monoclinic via in-plane shear. We impose values of the in-plane parameter aFeRh and monoclinic angle γ [Fig. 1(e)] and allow the out-of-plane parameter to relax. In this way, we explore possible strain states of FeRh on a- and c-domains of T-BTO.

Calculations of the strain- and γ-dependence of internal energy for AF-FeRh [Fig. 6(a)] and FM-FeRh [Fig. 6(b)] reveal that for all angles γ, compressive strain causes a steep rise in energy in FM-FeRh, and a weaker rise in energy in AF-FeRh, as we saw previously12 for γ = 90 °. In contrast, the two phases respond similarly to changes in γ. The zero-T internal energy difference ΔE between FM and AF phases for the same strain and γ [Fig. 6(c)] is correlated with the AF-FM transition temperature, with a larger ΔE implying a higher transition temperature12. We find that ΔE is sensitive to the strain via the imposed aFeRh, but is almost independent of γ. For the estimated strain states of FeRh on BTO in our XPEEM study [markers, Fig. 6(c)], ΔE is larger on BTO c-domains than on a-domains at the same T. As the AF phase is favoured on BTO c-domains, we anticipate higher (lower) transition temperatures on BTO c-domains (a-domains), in agreement with our experiments.

Figure 6. First-principles energies of FeRh under strain.

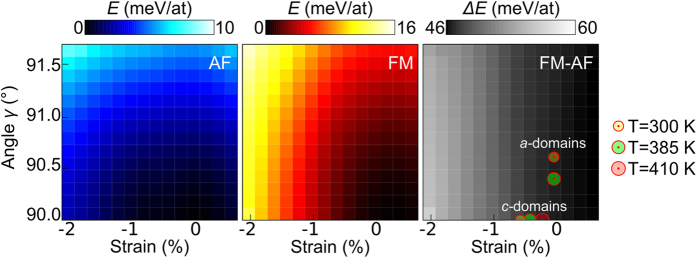
Figure 6

Open in a new tab

(a,b) Internal energy variations with strain and γ for (a) AF-FeRh and (b) FM-FeRh. In each of (a) and (b), energy is given relative to the unstrained ground state energy of the magnetic phase under consideration. In both (a) and (b), strain is given relative to the unstrained equilibrium FM-FeRh cell parameter a0,FeRhFM, i.e. strain = (aFeRh – a0,FeRhFM)/a0,FeRhFM. (c) Internal energy differences ΔE between FM-FeRh and AF-FeRh for the same strain and γ. Red dots represent the estimated experimental percentagewise strain states of FeRh on BTO c-domains and a-domains at the three temperatures indicated on the right.

Conclusions

In summary, we have directly imaged complete local interconversion between antiferromagnetic and ferromagnetic phases of FeRh just above room temperature in response to voltage across the BTO substrate. The effects persist through the thickness of the film. Ab initio calculations confirm that the ME effects are driven by local strain due to the enhanced AF-FeRh stability on ferroelastic BTO c-domains.

Our large local ME coupling could be further increased in thicker FeRh films where the metamagnetic transition can be sharper26, or by working with Pd-doped FeRh27 close to room temperature where the BTO tetragonality c/a and associated strains are larger. More broadly, our work shows that giant changes in functional properties can be achieved with moderate stimuli by combining ferroic domain structures with phase-separated materials with first-order transitions.

Methods

Sample preparation

22-nm-thick FeRh thin films were deposited on a 5 × 5 × 0.5-mm3 BTO (001) crystal (SurfaceNet GmbH) by radiofrequency sputtering at 903 K with a power of 45 W and in argon pressure of 0.860 Pa. The films were then annealed in situ at 1003 K for 90 min. To apply voltage across BTO we use FeRh for the top electrode, and a layer of conducting silver paste or sputtered Pd for the back electrode.

XPEEM and XMCD measurements

High-resolution magnetic images were taken at the spin-resolved photo-emission electron microscope at the synchrotron radiation source BESSY II operated by the Helmholtz-Zentrum-Berlin. This set-up is based on an Elmitec III instrument with an energy filter, permanently attached to an undulator beamline with full polarization control, in an energy range from 80 to 2,000 eV. The lateral resolution of the spin-resolved photo-emission electron microscope is about 25 nm for X-ray excitation. For magnetic imaging the photon energy was tuned to the L3 resonance of iron (706.8 eV), exploiting the element-specific XMCD. Each of the XMCD images shown was calculated from a sequence of images taken with circular polarization (90% of circular photon polarization) and alternating helicity. After normalization to a bright-field image, the sequence was drift-corrected, and frames recorded at the same photon energy and polarization have been averaged. The Fe magnetic contrast is shown as the difference of the two average images with opposite helicity, divided by their sum. The magnetic contrast represents the magnetization component pointing along the incidence direction of the X-ray beam, and we study different in-plane components by rotating the sample azimuth in the beam. Vector maps were created by combining two XMCD images with the incident beam along two perpendicular in-plane directions, after correction for drift and distortion.

High-temperature X-ray diffraction

We used a home-made two axis X-ray diffractometer in the Bragg-Brentano geometry with Cu-Kα1 radiation emitted by a 18 kW rotating anode (Rigaku). A designed sample holder allows in-situ X-ray measurements by varying simultaneously the temperature and the applied voltage.

First-principles calculations

We use a plane-wave pseudopotential approach as implemented in the Quantum ESPRESSO package28. The exchange-correlation functional is treated in the Perdew-Burke- Ernzerhof revised for solids (PBEsol) generalized gradient approximation. Atomic relaxation calculations were performed using a shifted 8 × 8 × 8 Monkhorst-Pack grid for k-point sampling and an energy cutoff of 80 Ry for the plane-wave basis. Atomic positions were converged until the Hellmann-Feynman forces on each atom became less than 20 meV/Å. Simulated AF and FM phases of bcc FeRh have equilibrium cell parameters of 2.95 Å and 2.97 Å in a good agreement with experiments14. Similarly to previous ab initio studies12,29, the AF phase is more stable by 45 meV/atom. The estimated bulk moduli for AF and FM phases are 227 and 222 GPa, respectively, agreeing well with previous theoretical calculations (Ref. 29 and references therein) and consistent with experimental estimates30.

Author Contributions

M.B. and A.B. initiated the study. A.B., R.O.C. and S.V. conceived the experiments. R.O.C. prepared the samples with the assistance of E.J., L.C.P., A.A.Ü., S.V. and F.K. characterized the sample by XPEEM. L.C.P., S.V. and F.K. analyzed the XPEEM data. L.C.P., I.C.I., B.D., N.G. and R.O.C. carried out the X-ray diffraction experiments. V.I. and A.Z. performed the first-principles calculations. L.C.P. and V.I. wrote the manuscript with input from M.B. and A.B. All authors contributed to the manuscript and the interpretation of the data.

Additional Information

How to cite this article: Phillips, L. C. et al. Local electrical control of magnetic order and orientation by ferroelastic domain arrangements just above room temperature. Sci. Rep. 5, 10026; doi: 10.1038/srep10026 (2015).

Acknowledgments

We are very grateful to S. Hämäläinen, S. van Dijken and A. Mougin for magneto-optical characterization. This work received financial support from the French Agence Nationale de la Recherche through project NOMILOPS (ANR-11-BS10-0016) and the European Research Council Advanced Grant FEMMES (contract no. 267579). R.O.C. acknowledges financial support by Thales through a CIFRE PhD grant.

References

  1. Fusil S., Garcia V., Barthélémy A. & Bibes M. Magnetoelectric Devices for Spintronics. Annu. Rev. Mater. Res. 44, 91–116 (2014). [Google Scholar]
  2. Vaz C. A. F. Electric field control of magnetism in multiferroic heterostructures. J. Phys.: Condens. Matter 24, 333201 (2012). [DOI] [PubMed] [Google Scholar]
  3. Chappert C., Fert A. & Nguyen Van Dau F. The emergence of spin electronics in data storage. Nature Mater. 6, 813–823 (2007). [DOI] [PubMed] [Google Scholar]
  4. Weiler M. et al. Voltage controlled inversion of magnetic anisotropy in a ferromagnetic thin film at room temperature. New J. Phys. 11, 013021 (2009). [Google Scholar]
  5. Chopdekar R. et al. Spatially resolved strain-imprinted magnetic states in an artificial multiferroic. Phys. Rev. B 86, 014408 (2012). [Google Scholar]
  6. Lahtinen T. H. E., Franke K. J. A. & van Dijken S. Electric-field control of magnetic domain wall motion and local magnetization reversal. Sci. Rep. 2, 258 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ghidini M. et al. Non-volatile electrically-driven repeatable magnetization reversal with no applied magnetic field. Nature Commun. 4, 1421–1427 (2013). [DOI] [PubMed] [Google Scholar]
  8. Garcia V. et al. Ferroelectric control of spin polarization. Science 327, 1106–1110 (2010). [DOI] [PubMed] [Google Scholar]
  9. Pantel D., Goetze S., Hesse D. & Alexe M. Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nature Mater. 11, 289–93 (2012). [DOI] [PubMed] [Google Scholar]
  10. Allibe J. et al. Room temperature electrical manipulation of giant magnetoresistance in spin valves exchange-biased with BiFeO3. Nano Lett. 12, 1141–1145 (2012). [DOI] [PubMed] [Google Scholar]
  11. Ohno H. et al. Electric-field control of ferromagnetism. Nature 408, 944–6 (2000). [DOI] [PubMed] [Google Scholar]
  12. Cherifi R. O. et al. Electric-field control of magnetic order above room temperature. Nature Mater. 13, 345–51 (2014). [DOI] [PubMed] [Google Scholar]
  13. Kouvel J. S. & Hartelius C. C. Anomalous Magnetic Moments and Transformations in the Ordered Alloy FeRh. J. Appl. Phys. 33, 1343 (1962). [Google Scholar]
  14. Zakharov A. I., Kadomtseva A. M., Levitin R. Z. & Ponyatovskii E. G. Magnetic and magnetoelastic properties of a metamagnetic Iron-Rhodium alloy. Sov. Phys. JETP 19, 1348–1353 (1964). [Google Scholar]
  15. Ponomarev B. K. Investigation of the antiferro-ferromagnetism transition in an FeRh alloy in a pulsed magnetic field up to 300 kOe. Sov. Phys. JETP 36, 105–107 (1973). [Google Scholar]
  16. Baldasseroni C. et al. Temperature-driven nucleation of ferromagnetic domains in FeRh thin films. Appl. Phys. Lett. 100, 262401 (2012). [Google Scholar]
  17. Mariager S. O., Guyader L. Le, Buzzi M., Ingold G. & Quitmann C. Imaging the antiferromagnetic to ferromagnetic first order phase transition of FeRh. ArXiv 1301.4164 (2013). at < http://arxiv.org/abs/1301.4164>(date of access: 09/02/2015)
  18. Choi Y. et al. Critical phenomena of nano phase evolution in a first order transition. ArXiv 1405.4319 (2014). at < http://arxiv.org/abs/1405.4319>(date of access: 09/02/2015)
  19. Lagos L, P. et al. Identification of ferroelectric domain structures in BaTiO3 for Raman spectroscopy. Surf. Sci. 532-535, 493–500 (2003). [Google Scholar]
  20. Ren X. Large electric-field-induced strain in ferroelectric crystals by point-defect-mediated reversible domain switching. Nature Mater. 3, 91–4 (2004). [DOI] [PubMed] [Google Scholar]
  21. Von Hippel A. Ferroelectricity, Domain Structure, and Phase Transitions of Barium Titanate. Rev. Mod. Phys. 22, 221–237 (1950). [Google Scholar]
  22. Ibarra M. & Algarabel P. Giant volume magnetostriction in the FeRh alloy. Phys. Rev. B 50, 4196–4199 (1994). [DOI] [PubMed] [Google Scholar]
  23. Stamm C. et al. Antiferromagnetic-ferromagnetic phase transition in FeRh probed by x-ray magnetic circular dichroism. Phys. Rev. B 77, 184401 (2008). [Google Scholar]
  24. Abo G. S. et al. Definition of Magnetic Exchange Length. IEEE T. Magn. 49, 4937–4939 (2013). [Google Scholar]
  25. Marquina C. et al. Magnetic and magnetoelastic behavior of mechanically alloyed FeRh compound. J. Appl. Phys. 81, 2315 (1997). [Google Scholar]
  26. Suzuki I., Koike T., Itoh M., Taniyama T. & Sato T. Stability of ferromagnetic state of epitaxially grown ordered FeRh thin films. J. Appl. Phys. 105, 07E501 (2009). [Google Scholar]
  27. Wayne R. Pressure Dependence of the Magnetic Transitions in Fe-Rh Alloys. Phys. Rev. 170, 523–527 (1968). [Google Scholar]
  28. Giannozzi P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009). [DOI] [PubMed] [Google Scholar]
  29. Gruner M., Hoffmann E. & Entel P. Instability of the rhodium magnetic moment as the origin of the metamagnetic phase transition in α-FeRh. Phys. Rev. B 67, 064415 (2003). [Google Scholar]
  30. Cooke D. W. et al. Thermodynamic Measurements of Fe-Rh Alloys. Phys. Rev. Lett. 109, 255901 (2012). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES