HCV Kinetic Models and Their Implications in Drug Development

Abstract

Chronic infection with hepatitis C virus (HCV) affects about 170 million people worldwide and is a major cause of liver complications. Mathematical modeling of viral kinetics under treatment has provided insight into the viral life cycle, treatment effectiveness, and drugs' mechanisms of action. Here we review the implications of viral kinetic models at the different stages of development of anti-HCV agents.

Chronic infection with hepatitis C virus (HCV) affects about 170 million people worldwide and is a major cause of liver complications such as cirrhosis, liver cancer, and transplantation.1 The goal of anti-HCV therapy is to achieve a sustained virologic response (SVR), defined as undetectable viral load (viral load) 12–24 weeks after treatment cessation.2,3 The chance of SVR depends on many host and viral factors, such as the presence of cirrhosis or HCV genotype (GT).4 Until 2011, the standard treatment was based on a combination of weekly injections of pegylated interferon (peg-IFN) and daily oral ribavirin (RBV), but this treatment only yielded an SVR rate of about 30–50% in patients infected with HCV GT-1 after a 48-week treatment and of 75–85% in GT-2/3 patients after a 24-week treatment.5,6

In 2011, two direct antiviral agents (DAAs), the protease inhibitors telaprevir and boceprevir, were approved to be used in combination with peg-IFN/RBV for GT-1 infected patients, allowing the SVR rate to rise to about 70% in treatment naïve noncirrhotic patients.7,8 In recent clinical trials, combinations of two or more DAAs (e.g., polymerase inhibitor, protease inhibitor, or NS5A inhibitor) targeting different viral proteins yielded SVR rates of more than 90% after 8–12-week treatments.9–13 Currently, dozens of DAA combinations are being tested, holding the promise that universal IFN-free treatments will be available in the coming years.14

Viral kinetic modeling aims to characterize the mechanisms governing the virologic response during treatment. Initiated in the mid-1990s to understand the effects of HIV protease inhibitors initiation on the HIV RNA, it has rapidly been applied to other viruses. In 1998, a seminal paper that characterized the so-called “biphasic” virologic response during IFN-based treatment was published.15 With the burst of DAA, viral kinetic modeling has expanded in the last decade to embrace a large number of objectives, such as elucidating drugs' mechanisms of action, characterizing the dose/response effect, and optimizing treatment duration. Here we review the role of modeling in the revolution of HCV treatment and how it has contributed at various stages of drug development.

BASIS OF VIRAL KINETIC MODELING

Standard viral kinetic model

Neumann et al., inspired from previous models for viral infection in HIV, proposed the following mathematical model to describe the viral kinetics in HCV patients during IFN-α treatment 1, 15

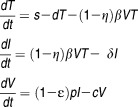Eq 1

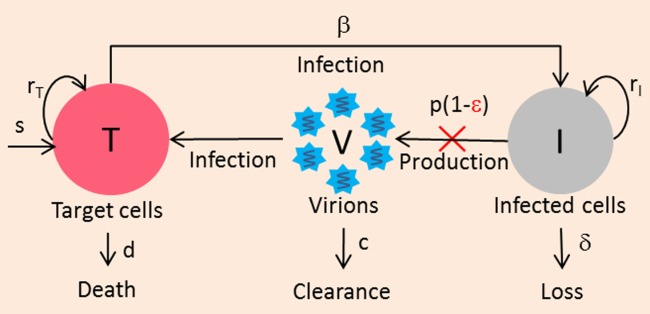
The model considers two populations of hepatocytes, the target cells, T, and the infected cells, I (Figure 1). The target cells are produced at a rate s, are eliminated with a rate d, and become de novo infected by circulating virions, V, with a rate β. Once infected, the hepatocytes are cleared with a rate δ. The free virions are released from the infected cells at a rate p per cell per day and are cleared from the circulation with a rate c. In this model IFN is assumed to act by blocking new infection with an effectiveness η, or by blocking viral production with an effectiveness ɛ. These treatment effect parameters are comprised between 0, meaning no drug effect, and 1, meaning total suppression.

Figure 1.

Standard viral kinetic model. Target cells (T) are produced at rate s, die with death rate d, and become infected cells (I) with infection rate β by free virus (V). Infected hepatocytes die with rate constant δ. V are released from infected cells at a rate of p and are cleared with a rate c. Treatment is assumed to act by blocking new infection with an effectiveness η, or by blocking virion production with an effectiveness ε.

Biphasic model

If one assumes that all parameters (including those related to treatment effect) are constant and that the number of target cells after treatment initiation is equal to their pretreatment value, the model has an explicit solution given by the following biexponential function15:

Eq 2

where

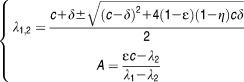Eq 3

In this model, HCV RNA initially declines with rate λ₁ ≈ ɛc, and if the treatment is potent (ɛ ≈ 1), viral load declines with a rate equal to c. This declining phase continues until the viral load reaches a value V₁ that reflects the new equilibrium between the viral production and clearance under treatment given by V₁ = (1-ɛ)V₀. Thus, for instance, if ɛ = 0.99, there will be a rapid decline of 2 log₁₀ of viral load in the first 2 days.

The pretreatment steady-state implies that not only the virus but also the infected cells are in equilibrium, i.e., the infected cells that are naturally eliminated with rate δ are compensated by the newly infected cells. With a lower level of viral production, there are fewer viruses in serum and hence, less de novo infection. As the number of newly infected cells declines, viral production is further reduced. Therefore, the treatment effect, even if modest, triggers a fatal circle of events for the infection that will lead to a continuous decline of virus as long as treatment is maintained. The rate of this second phase decline, noted λ₂, is approximately equal to δ[ɛ+ η(1-ɛ)]. Thus, if ɛ∼1 and δ>0, the second phase is approximately given by ɛδ≈δ. Of note, an additional treatment effect in blocking cell infection will result in only a minor enhancement of viral decline as long as ɛ is high. For instance, if ɛ = 0.99, an additional effect of η = 0.99, will enhance the second phase by only 1%.

If the treatment reduces only cell infection (η>0, ɛ = 0), either directly by blocking the new infection or indirectly by rendering the virus noninfectious, only the second phase will be observed and the viral load will decline linearly with a rate λ₂ approximately equal to ηδ. Thus, for an entry inhibitor or a drug that yields noninfectious virus, modeling predicts that no rapid first phase decline due to blocking of viral production would be observed.

Extended viral kinetic model

The standard viral kinetic model assumes that new hepatocytes are due to migration or differentiation of hepatocyte precursors with a rate s, but ignores the fact that the liver is an organ capable of natural regeneration controlled by homeostatic mechanisms. This feature can be captured in an extended model which considers the proliferation of both uninfected and infected hepatocytes (Figure 2).16

Figure 2.

Extended model accounting for hepatocyte proliferation. Both infected and uninfected hepatocytes proliferate logistically with maximum rates r_T and r_I, respectively, until the total number of hepatocytes reaches T_max.

Under some specific parameter regimes the model can generate a triphasic viral decline, where a transient shoulder phase takes place between the initial and final phase of the viral decline, as observed in some patients treated with peg-IFN.16,17 Because the observation of this triphasic response requires frequent sampling measurements, both the prevalence and the duration of the shoulder phase (3 days to 1 month) are not known. A statistical comparison between the standard and the extended model on a large population of patients has never been performed and therefore the need for an extended model remains to be determined. Further, the origin of the triphasic decline could also be explained by other mechanisms than cell proliferation, such as pharmacokinetics or a progressive restoration of the immune system.17

Viral rebound and the notion of critical effectiveness

An important prediction of both the standard and the extended viral kinetic models is that a low level of antiviral effectiveness may lead to a rebound to a new steady-state level in spite of continuous therapy. This rebound is due to the fact that with less infection, more target cells become available, which increases the chance for virus to infect a cell and, therefore, to rekindle infection. This can be mathematically characterized by a threshold called the critical effectiveness, ɛ_c.18 If ɛ<ɛ_c, enough new infections continue to occur so that the viral load eventually stops declining and rebounds to a new set-point steady state. This critical effectiveness is related to the basic reproductive number, R₀, defined as the number of newly infected hepatocytes that arise from one infected cell, and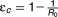. The expression of 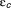for both the standard and the extended models can be found in the article of Dahari et al.18 By definition, in a patient with chronic infection R₀ is higher than 1. The goal of treatment is to achieve a sufficiently high effectiveness such that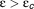, or, in other words, that the basic reproductive ratio under treatment, R_T = R₀(1-ɛ) is lower than 1. In that case the viral load declines as long as the treatment is administered. Of course, treatment cessation in a chronically infected patient immediately leads to a virological relapse. In order to predict a viral eradication or cure, the model needs to incorporate a so-called “cure boundary” (discussed below).

It is important to understand that this rebound caused by a suboptimal drug effectiveness can occur only in models with a nonconstant number of target cells. In the biphasic models, where the number of target cells is supposed to be constant, the viral load is assumed to decline continuously during treatment regardless of the value of ɛ.

Hepatocyte kinetics

A major limitation in using the viral kinetic models is that only the viral load data are available, making the parameters related to hepatocyte kinetics hardly identifiable (s, d, β in the standard model and parameters concerning hepatocytes proliferation in the extended model).19 Information on these parameters could be gained from other contexts, such as acute infection (where the rate of viral expansion is related to the viral infectivity, β), liver regeneration after resection. However, both the parameter values and their variability in the population may be very different from those in chronic infection. Because the value of these parameters are involved in the calculation of R₀18 and hence the value of the critical effectiveness, sensitivity analysis on these parameters may be needed to assess the robustness of model predictions. Recent efforts in modeling imagery data obtained after biopsy of chronic HCV patients may shed new light on the kinetics of uninfected and infected hepatocytes.20,21

Ribavirin modes of action

Ribavirin (RBV) monotherapy has only little impact on viral kinetics22–24 but its association with IFN is critical to achieve SVR.5,6 However its mechanism of action, its effect on viral kinetics, and the way to model it remain largely unclear.

For instance, by analyzing HCV-RNA levels from 34 patients receiving either peg-IFN alone, peg-IFN/RBV, or IFN/RBV, Herrmann et al. found that RBV was not associated with overall treatment effectiveness, ɛ, but increased the loss rate of infected cells, δ, by two-fold.17 In contrast, Layden-Almer et al. observed no significant effect of RBV on δ in patients receiving high daily doses of IFN.25 Importantly, the effectiveness of IFN was higher in the study of Layden-Almer et al. (mean ɛ = 0.89 and 0.98 in African-American and Caucasian-American patients, respectively) than in Herrmann et al. (mean ɛ < 0.7). Further, Layden-Almer et al. observed that δ was higher in African-American patients receiving IFN/RBV than in patients receiving IFN alone, but this difference did not reach statistical significance. In another study, Pawlotsky et al. showed that RBV did not impact viral kinetics in patients who received IFN daily dose (i.e., high ɛ) but reduced the relapse rate at the end of each IFN dose and was associated with an increased δ in patients who received IFN thrice a week (lower ɛ).22 Although these studies were done on a small number of patients with different combination regimens and/or baseline characteristics, they tended to support that RBV does not impact the first phase and may enhance the second phase decline, especially in patients where IFN had a modest antiviral effectiveness (i.e., low ɛ). Dixit et al. explained this feature by assuming that RBV exerts its effect through increased lethal mutagenesis, and thus renders a fraction of newly produced virions noninfectious, with effectiveness ρ.26 The authors found that ρ = 0.5 provided a reasonable description of the clinical trial outcome rate. This result was later corroborated by Snoeck et al. on a large population of patients treated with peg-IFN/RBV.27 However RBV's effectiveness is poorly identifiable19 and this estimate remains to be taken with caution. Besides the value of RBV antiviral effectiveness, it is still unclear whether the prediction of this model is correct. For instance, Feld et al. found that a higher second phase was found only in patients having an adequate first phase decline (≥0.5 log₁₀) but not in those with slow first phase decline (<0.5 log₁₀ IU/mL).28 Because RBV will continue to be part of several future drug combinations against HCV,29–31 it is critical to have a better understanding about RBV's mechanisms of action. Future models will probably need to consider its various mechanisms of action, such as enhancing IFN activity,23,28,32 reducing liver inflammation,23 or acting against mutant virus.

PARAMETER ESTIMATION IN VIRAL KINETIC MODELING

Viral kinetic data can be analyzed using nonlinear regression on each individual. However, this approach may lead to an overestimation of interindividual variability, risk of parameter nonidentifiability, and lack of statistical power to identify covariate effect, especially when the data are sparse.33 These limitations can be in part overcome by fitting data of all individuals together using nonlinear mixed effect models (NLMEM), also called the population approach. In this approach, each individual parameter θ_i is comprised of a fixed effect μ, representing the mean value of population and a random effect η_i with η_i∼N(0,ω²). Usually, constraints of positivity lead to assume a log-normal distribution for θ_i, i.e., θ_i = μ × exp(η_i), or a logit-normal distribution for parameters comprised between 0 and 1, such as treatment effectiveness. Lastly, an additive independent error e_ij on log₁₀ of viral load in patient i, time j is usually assumed, with e_ij ∼ N(0,σ²). Parameters can be estimated using a maximum likelihood or Bayesian approach. Several estimation methods have been developed to handle data below the quantification/detection limit (BQL/BDL) in parameter estimation in NLMEM and correct for the bias obtained by naïve approaches that omit or censor BQL/BDL data.34–36

CONSTANT EFFECTIVENESS, VARYING EFFECTIVENESS, AND PHARMACOKINETIC-RELATED EFFECTIVENESS

Pharmacokinetic-viral kinetic (PK-VK) model

The HCV kinetic models presented above were used with the assumption of a constant drug effectiveness (CE). However, the variation of drug concentration over time can lead to fluctuations/rebound in the virologic response. In such conditions, a model including available pharmacokinetic information may be more appropriate to describe the viral kinetics. The relation between the drug concentration and the antiviral effectiveness can be described by an E_max model 4:

Eq 4

where C(t) is the drug concentrations predicted at time t, EC₅₀ is the drug concentration needed to achieve an effectiveness of 50% of the maximum effect, E_max, and γ is the Hill coefficient, a parameter that determines the steepness of the drug concentration–effect curve. Theoretically, E_max can be estimated with a good sampling design and a sufficient range of drug concentrations. However, it is usually set at 1, which is a reasonable assumption, as a complete suppression of HCV RNA can be obtained at high concentrations in in vitro studies.37

It was shown by simulation that PK-VK models lead to more precise estimates of model parameters and provide better description of the viral kinetics during peg-IFN therapy.38,39 Likewise, Nguyen et al. analyzed the viral kinetics during treatments with alisporivir and/or peg-IFN40 and found that using the PK-VK model improved the fitting criterion (BIC) and reduced the residual errors by nearly 20%, compared to the CE model (unpublished result). Even when the pharmacokinetic data are sparse and cannot be used to fully characterize the drug exposure profile, the inclusion of only predose concentrations could capture a significant part of the interindividual variability.41

From a statistical point of view, the gold-standard estimation method for a PK-VK model is to simultaneously estimate pharmacokinetic and viral kinetic parameters. However, this approach may be time-consuming and can lead to numerical issues, such as a lack of convergence of estimation algorithms.42,43 These difficulties can be alleviated with a sequential approach that consists of fitting the pharmacokinetic model first to obtain individual pharmacokinetic predictions, which are then injected into the viral kinetic model to estimate the viral kinetic parameters. However, this approach is subject to biased estimates, especially with sparse pharmacokinetic sampling, where the individual predictions are susceptible to the problems of shrinkage.42,43 To avoid this issue, another sequential approach has been suggested, in which the second step consists of simultaneously estimating the individual pharmacokinetic parameters and the viral kinetic parameters with the population pharmacokinetic parameters fixed at values obtained in the first step.42,43

K-VK model

If no pharmacokinetic data are available the dose–effect relationship can be characterized using a K-VK model (absence of the letter P means absence of pharmacokinetic data).27,44 In this model, drug effectiveness is described using an E_max equation, where drug concentration is replaced by the given dose 4. Unlike the PK-VK model, the K-VK model assumes that drug effectiveness is constant over time for a given dose.

Varying effectiveness (VE) model

The change in drug effectiveness over time can also be described using an empirical model such as the exponential model45:

Eq 5

This model represents the variation (increase or decrease) of the treatment effectiveness from an initial level, ɛ₁, to a final level, ɛ₂, with k representing the changing rate of effectiveness. Other models, such as some variations of this exponential model or a sigmoidal function, have also been proposed.38,46,47 These models, called varying effectiveness (VE) models in the following, have been notably used to account for the decrease in drug effectiveness after injection of peg-IFN or treatment cessation38,46 or for the increase due to drug accumulation over the first intakes of an oral drug.46,47 For instance, a VE model has been used to explain the slow viral load decline observed with mericitabine monotherapy (a nucleoside analog) as a result of the time needed to build up high levels of active triphosphates.47 Interestingly, the build-up rate was higher in patients who received twice daily doses compared to four times a day, suggesting that the VE model can capture some pharmacokinetic information included in the viral kinetic data. In a subsequent study, another VE model was also found to perform better than the CE model to fit the viral kinetics under treatment with GS-0938 and sofosbuvir, two nucleotide analogs. The first phase observed with GS-0938 and sofosbuvir was much faster than with mericitabine, consistent with the fact that mericitabine needs three phosphate groups to be added, while GS-0938 and sofosbuvir only need two in order to have an antiviral effect and that adding the first phosphate group is a rate-limiting step among the three steps of tri-phosphorylation process.48

When to use PK-VK, VE, K-VK, or CE?

When it is possible, the best approach is to include all information available and therefore to use a PK-VK model. However, a PK-VK model may not add much value in some contexts, such as when the viral kinetics shows a consistent decline in viral load levels during treatment (indicating that there is no significant effect of drug fluctuation) or when plasma concentration is not a good proxy of active drug's concentration at the site of action. In these cases the use of a CE, K-VK, or VE may be sufficient to estimate the treatment effectiveness.38,49 Of note, the interpretation of the VE model's parameters may be complicated by the correlation between parameters related to the drug effectiveness and viruses.45 Therefore, to verify that a VE model is needed and that the parameters obtained are biologically reasonable, one can be recommended to systematically fit the data using both CE and VE models and to compare the viral kinetic parameters obtained with these two models. Because the VE model is a simple extension of the CE model, the need for a varying effectiveness can also be assessed using standard statistical tools such as F-test in individual data fitting or likelihood ratio test in mixed-effect models.

IN VITRO VIRAL KINETIC MODEL

A tool to characterize viral lifecycle and define potential targets for new drugs

With the development of subgenomic HCV replicons and quantitative analysis of intracellular RNA and proteins, several models have been developed to characterize HCV kinetics in replicon cell culture and to understand drugs' mechanisms of action. Dahari et al. developed the first mathematical model to characterize the different steps in HCV replication, in particular the translation of HCV polyproteins in cytoplasm and the RNA synthesis in the vesicular membrane structure.50 Binder et al. extended this model to describe HCV kinetics in the early hours after infection. The model identified the polyprotein translation and RNA polymerization of NS5B as the most influential steps of viral replication, i.e., the potentially most sensitive/effective targets of DAA.51

A tool to understand drugs' modes of action

A direct application of these models is to characterize more precisely the mode of action and the effectiveness of antiviral treatment. The use of in vitro data is indeed particularly appealing, as one can directly measure the drugs' effect on the site of action, i.e., intracellularly. This approach was successfully used for the first time by Dahari et al. to describe the kinetics of intracellular HCV RNA suppression under treatment with IFN-α52:

Eq 6

R is the intracellular positive single-strand RNA (replicon), α is the replicon production rate, μ is the replicon loss rate. IFN was supposed to block RNA production with an effectiveness ɛ_IFN. Fitting this model to the early replicon kinetics in response to different doses of IFN, Dahari et al. showed that blocking viral RNA (vRNA) production, and not enhancing RNA elimination, was the main effect of IFN-α, consistent with the prediction of the standard model. Although the experimental setting makes it more difficult to interpret long-term data (absence of infectious virus and immune response), a trend towards a continuous viral decline over time was observed at higher doses, which may be explained by the elimination of replication complexes over time. This was modeled by refining the previous model.52

Eq 7

where γ is the elimination rate of the replication units. Another model accounting for the complex processes of viral replication and resistant strains was also developed to investigate the intracellular HCV RNA kinetics under treatment with several potent antivirals.53 The increasing availability of an infectious system holds the promise that more comprehensive models integrating the treatment effect on both intracellular and extracellular viruses will be developed.

IN VIVO VIRAL KINETIC MODEL IN DRUG DEVELOPMENT

A tool to predict in vivo drug's antiviral effectiveness

In vitro data can also be used to anticipate in a quantitative manner the effect of drugs in vivo. Using the data of 10 nonnucleoside polymerase inhibitors and 14 protease inhibitors, Reddy et al. showed that combining the in vitro EC₅₀ of antivirals and their minimum plasma concentration in a viral kinetic model could provide good prediction for short-term (3-day) virologic response.54 However, depending on drugs' properties, such as drug distribution in the liver (site of action), several adjustments (e.g., using protein-shifted EC₅₀ to account for plasma protein binding, correction of drug concentration at site of action using liver-to-plasma ratio) are required. In spite of these limitations this approach is a first step towards using in vitro effectiveness (EC₅₀) obtained in animals and pharmacokinetic data in healthy volunteers to predict the early virological response in HCV-infected patients.

A tool to understand the emergence of resistance with DAA treatment

As DAAs target specific HCV proteins, they are more prone to mutations conferring resistance than IFN-based therapy. In fact, viral breakthrough due to resistance can occur as early as 2 days after initiation of some agents, such as telaprevir monotherapy.55 The rapid emergence of mutation is indeed favored by the high production rate of HCV,15 the high error rate during replication (μ = 10^-5 to 10^-4 per copied nucleotide per replication cycle),56,57 and the large size of the genome (9,600 nucleotides). In fact, with four types of nucleotides, the number of possible strains containing one or two substituted nucleotides are 2.9  ×  10⁴ and 4.1  ×  10⁸, respectively. If μ = 10^-5, the mutation rate per genome is 0.096 per replication. Hence, according to Poisson approximation, the probability for a new virion to contain none, one, or two mutant nucleotides are 91%, 8.7%, and 0.42%, respectively. As a consequence, there are about 8.7  ×  10¹⁰ and 4.2  ×  10⁹ viruses with one or two mutant nucleotides among about 10¹² newly produced viruses each day. These numbers are much higher than the number of possible mutant strains that can be generated, indicating that all the single and double mutant resistant viruses may exist before treatment and rapidly compete with the wildtype virus during therapy.55 This explains why only treatment with a high genetic barrier to resistance, typically requiring four or more mutations, can lead to SVR.58

Mathematical models can be used to explain the early emergence of resistance and its rapid amplification. The standard viral kinetic model was extended to consider two viral strains: drug-sensitive and drug-resistant virus (Figure 3).58 This two-strain model was able to provide good fits for the viral kinetics observed during 2-week treatment with telaprevir monotherapy or telaprevir/peg-IFN (by assuming the same peg-IFN effectiveness on the mutant and wildtype virus). The rapid increase in the mutant frequency under therapy was shown to be a consequence of the rapid and profound decline of the wildtype virus, which reveals the preexisting mutant virus.58 Both forward and backward mutations during treatment were shown to have only a minor impact on the kinetics of drug-resistant virus.58

Figure 3.

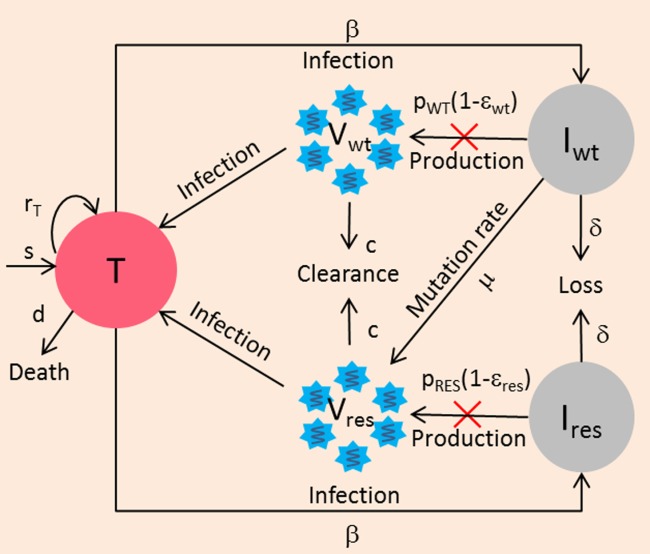
Two-strain model accounting for drug-sensitive (wildtype) and drug-resistant virus. I_wt, I_res are the two populations of hepatocytes infected with wildtype virus V_wt and drug-resistant virus V_res, respectively. The model assumes that V_res is generated from V_wt, with rate μ but no backward mutation. Mutant strain is produced with a lower production rate p_res compared to wildtype virus (p_wt) due to its lower relative fitness (f_i = p_res/p_wt). Each viral strain has different sensitivity to treatment, ε_wt and ε_res. The model predicts that resistant virus should already exist before treatment at frequency μ/(1 − p_res/p_wt).

Adiwijaya et al. extended the two-strain model to account for multiple resistant strains.59 The model fitted well both on-treatment and post-treatment viral kinetics in patients receiving telaprevir monotherapy as well as the variant prevalence observed after treatment. Later, Adiwijaya et al. analyzed the viral load and pharmacokinetic data obtained in various early clinical studies of telaprevir monotherapy or in combination with peg-IFN/RBV using the multistrain model and population approach. The model could provide good prediction for the SVR rates of several clinical studies of telaprevir.60

An important assumption of these models is that the rapid amplification of the mutant virus is supported by the rapid infection of newly produced hepatocytes. As explained above, this assumption remains to be validated, as no data are available on the hepatocyte kinetics. The origin of the viral expansion, also called the “replication space,” could be supported by other mechanisms, such as reinfection of cells previously infected with wildtype virus or the loss of an antiviral state due to lower levels of viral replication.58

A tool to predict treatment outcome and optimize treatment duration

Achieving a rapid virologic response (RVR, undetectable viral load at week 4 of treatment) has long been identified as one of the best early predictive markers of SVR.61,62 Stimulated by model prediction, several authors have reported an association between the magnitude and the rapidity of the phases of viral decline and the treatment outcome,63,64 suggesting that viral kinetic models could provide even earlier predictors of treatment outcome than RVR.

Because viral kinetic models are based on continuous ordinary differential equations (ODEs), they predict that HCV RNA will systematically relapse after treatment cessation. This is why Dixit et al. introduced a theoretical threshold, called here the cure boundary, under which viral eradication is considered as achieved and relapse cannot occur afterwards. This cure boundary is defined as having less than one viral particle in the whole extravascular fluid, i.e., 15L, and therefore corresponds to a theoretical concentration of 10^-4.22 IU/mL.26 Alternatively, one can define the cure boundary as having less than one infected cell, which is a slightly more conservative assumption and delays the predicted time to eradication by 2–3 weeks with standard parameter values.65

When using the biphasic model, a nice advantage of the cure boundary is that the treatment duration can easily be predicted by extrapolating the second slope of the viral decline. This approach was used in 2010 by Gane et al. to predict that between 8 and 12 weeks of treatment should be sufficient to cure patients treated with danoprevir (a protease inhibitor) and mericitabine.66 Similar results were made using a telaprevir VE-model.65 Although the predictions that in theory SVR could be achieved in a majority of patients in less than 12 weeks of treatment turned out to be correct,9–11 they were made by assuming that no resistance emerged and that the viral decline would continue at the same pace over time. This assumption, however, depends on many factors, in particular the genetic barrier to resistance. In fact SVR rates obtained after 12 or 24 weeks of treatment with danoprevir and mericitabine were low, and virologic breakthrough or relapse were associated with danoprevir-resistant virus in most cases.67

The combination of the cure boundary and a complex model could also be used to predict SVR rates retrospectively. Snoeck et al. developed a model from the extended viral kinetic model by incorporating this cure boundary and fitted this model to on- and post-treatment data in a large population of patients treated with peg-IFN with or without RBV.27 The model was able to reproduce all the observed patterns of virologic response such as nonresponse, relapse, or SVR and provided good prediction for SVR rates in other clinical studies.

Using a population viral kinetic model built from only on-treatment data in a large number of patients receiving telaprevir monotherapy or in combination with peg-IFN, Adiwijaya et al. predicted the SVR rates for several phase 2–3 clinical trials of telaprevir.60 Although telaprevir dosing regimen, treatment duration, and patient characteristics were different from the studied data, the prediction made with the cure boundary matched very well the observed SVR rates. Recently, Nguyen et al. showed that this approach could also be used using short-term data. For that purpose, they fitted the viral kinetics observed in patients treated for 4 weeks with alisporivir (a cyclophylin inhibitor) or alisporvir/peg-IFN using a PK-VK model and they used the model to accurately predict the SVR rate of a subsequent clinical study (VITAL-1) with long treatment duration (24 weeks) and a complex response-guided design.40 Although the results of the VITAL-1 study were known when the modeling was done, the data of this study were not used to construct the model, thereby showing that modeling of short-term data can be used to anticipate the outcome of a complex clinical trial.

New models to explore new modes of action of DAA

New characteristics of the viral kinetics in response to DAA-based treatment, compared to IFN-based treatment, have been repeatedly observed. In particular, protease inhibitors such as telaprevir, ciluprevir, and TMC-435 were shown to enhance the second phase, which, in some cases, was correlated with treatment effectiveness.65,68,69 Another remarkable observation was that NS5A inhibitors such as dataclasvir, ledipasvir, and, to a lesser extent, some protease inhibitors such as danoprevir, telaprevir, yield a much steeper first-phase decline.70–72 These observations cannot be explained with the standard model.

To explain the profound second phase in protease inhibitor therapy, Guedj and Neumann extended the standard model, which only focuses on the cellular infection (CI) level, to incorporate intracellular (IC) kinetics of vRNA.73 This ICCI model considers two additional populations: 1) the positive-strand RNA (R) available for transcription and translation, R, 2) the replication units (U), which are the negative-strand and double-stranded RNA available for vRNA synthesis. U are translated from R with a production rate π, limited by the number of U, and are lost with a rate γ. R are produced from U with a rate α and are lost, either by being released as free virus or cleared from the infected cells, with a rate σ:73

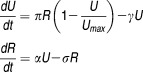Eq 8

In the ICCI model, the production rate p of free virus in the CI model is replaced by a second-order rate, ρ, depending on R and I. If the treatment blocks the synthesis of intracellular vRNA, with an effectiveness ɛ_α, the model defines two critical effectiveness, ɛ_ICCI and ɛ_IC with ɛ_ICCI<ɛ_IC: i) if ɛ_ICCI<ɛ_α< ɛ_IC, vRNA reaches a new lower steady state and, consistent with the standard model, HCV RNA is cleared due to a lower level of viral production and a progressive loss of infected cells; ii) if ɛ_α>ɛ_IC, vRNA is cleared from the infected cells and as a consequence, from the whole body. In that case, long-term viral load decline is a combined effect of the loss rate of infected cells and intracellular vRNA, i.e., δ+γ, as predicted by the in vitro model discussed above.52 Therefore, the model predicts that the more rapid second phase obtained with protease inhibitors could be due to the progressive eradication of intracellular viral content within infected cells. However, the correlation between the second phase and the treatment effectiveness predicted by the model remains to be validated.

Although this model provides a theoretical framework for the rapid second phase, several parameters cannot be identified if only HCV RNA are available, which limits its use in the clinical setting. Moreover, this model makes the mean-field approximation that all infected cells have the same (mean) intracellular kinetics, which clearly is not physiological. To overcome these limitations, another multiscale model with fewer parameters that introduces a relationship between vRNA and time since cell infection was developed:70,71

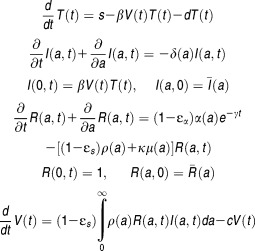Eq 9

where a is the infection age and α, ρ, μ are age-dependent rates of vRNA production, assembly/secretion, and degradation, respectively. The term e^-γt represents the loss of the replication units over time due to highly effective treatment.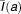, 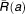are the pretreatment steady-state distribution of the infected cells and intracellular vRNA, respectively. In this model, drugs can have an antiviral effect via: a) blocking vRNA production with an effectiveness ɛ_α, b) blocking viral assembly/secretion with ɛ_s, c) enhancing intracellular vRNA degradation by κ-fold (Figure 4).

Figure 4.

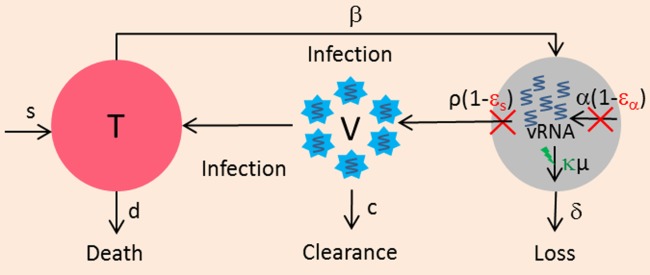
Multiscale model. The intracellular viral RNA is produced with a rate α, is assembled/released with rate ρ, and is degraded with rate μ. In this model, antiviral effect can be distinguished into the effect of blocking viral RNA production, ε_α, the effect of blocking viral assembly/secretion, ε_s, and the effect that enhances the degradation of intracellular viral RNA, κ.

By making the assumptions of constant effectiveness and by neglecting the number of new infection occurring after treatment initiation, an analytical approximation for the multiscale model can be obtained:

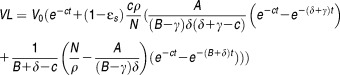Eq 10

where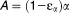, 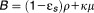and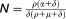

This analytical solution makes the interpretation of parameters easier. The model predicts that the viral load declines in three phases whose amplitude and duration depend on the values of parameters. If ɛ_s = 1 and ɛ_α ∼ 1, the viral load initially declines with the viral clearance rate c, as predicted by the standard model. The second phase represents the loss of intracellular vRNA by secretion and degradation (with rate ρ+κ × μ+δ), and eventually the terminal phase is due to the deficit in viral production by loss of infected cells and progressive eradication of replication units within remaining infected cells (with total rate δ+γ) (see figure 3 in Rong et al.71).

Using this model to fit the very rapid viral decline following one dose of daclatasvir, a NS5A inhibitor, Guedj et al. showed that daclatasvir had a dual mode of action and efficiently blocked not only vRNA production (like many drugs such as IFN) but also virus assembly/secretion. Further, the effectiveness in blocking assembly/secretion ɛ_s was higher than its effectiveness in blocking vRNA production ɛ_α (0.999 vs. 0.99).70 These predictions were consistent with in vitro experiments reported subsequently that NS5A inhibitors have a rapid and potent activity in blocking viral assembly but a slower build-up and lower activity on blocking vRNA production.37 In the framework of this model, the first phase of the viral decline is close to the viral clearance rate in serum, c, if and only if the drug efficiently blocks assembly/secretion. If the drug has a modest effectiveness in blocking viral assembly/secretion, then a large quantity of viruses continues to be secreted after treatment initiation and the first phase with rate c is not observed. Based on this new paradigm, the estimate of free virus clearance was reestimated to 22.3 day^-1, corresponding to a half-life of 45 minutes,70 i.e., approximately four times shorter than previous estimates obtained during IFN-based therapy (≈2.7 hours).

Of note, an effect, though smaller, of protease inhibitors (telaprevir and danoprevir) was also found on blocking assembly/secretion.71 These predictions are consistent with in vitro findings that protease inhibitors are also involved in the assembly of virus but their blockage activity is lower compared to NS5A inhibitors.37 Finally, the multiscale model also predicted that both protease inhibitors enhanced intracellular vRNA degradation by a factor of κ ≈ 4. One possible explanation is that protease inhibitors can restore the cellular antiviral capabilities. However, the mechanism for this mode of action remains unclear.

Although the multiscale model is more physiological, the assumptions needed to arrive at an analytical solution, i.e., constant drug effectiveness and no cell infection, may limit its use in the context where drug effectiveness may vary due to pharmacokinetics or emergence of resistance. Because only the extracellular viral loads are measured, the parameters of intracellular kinetics are nonidentifiable and have to be fixed at certain values to estimate other parameters. The choice of values for these nonidentifiables may influence the estimation of other parameters, for example, ɛ_s depends on the value of μ. With the growing knowledge from in vitro models for intracellular vRNA kinetics,51 more information about viral intracellular kinetic parameters is now available to refine this multiscale model. Further development can also be made to this model such as including several host proteins to account for the nonlinearity of the replication process and to better understand DAAs' new modes of action.

FUTURE CHALLENGES AND APPLICATIONS OF HCV MODELING

Cell–cell infection

All the HCV kinetic models presented above assume a well-mixed system where virus has the same chance to infect any cell. However, it has been recently shown that infected cells tend to be found in clusters20,21 and that cell-to-cell spreading is one of the routes for HCV transmission.74 Therefore, to better describe the infection step, HCV kinetic models should be extended to account for the spatial localization of infection and the two ways of virus spreading (virus-to-cell and cell-to-cell transmission).

Partial differential equation (PDE) and stochastic modeling

The HCV kinetic models described by ODEs make the mean-field approximation that all the uninfected cells have the same chance of being infected and that all the infected cells produce the same, constant amount of virus. These assumptions are not realistic and can be relaxed by using more physiological partial differential equations (PDEs) that can account for the heterogeneity in kinetics due to differences in infection age (time) and/or in distance to infection foci (space). However, the solution of PDEs requires computationally expensive and time-consuming processes. Thus, the development of efficient and fast PDE solving techniques for individual fitting and population approach will be needed to broaden the use of more complex models in HCV kinetic modeling.75

Although deterministic models are reasonable at the pretreatment steady state, as a large number of virus and infected cells are present they become less realistic when the number of virus and infected cells is small, such as a few days after infection or several weeks after efficient treatment. In these situations stochastic models might be needed to account for the stochastic nature of the infection, e.g., the randomness of events of cell infection, mutation, and apoptosis.76

Can we use models for individualized HCV treatment?

One appealing application of viral kinetic models is to use real-time data to predict treatment outcome and optimize treatment duration at the individual level. Using the first 3 weeks data of an experienced patient treated with silibinin/RBV, Dahari et al. successfully predicted that 34-week treatment would be sufficient to achieve SVR in this patient.77 However, this result has to be confirmed in a larger population before concluding about the usefulness of this approach, as it relies on several assumptions. First, the treatment outcome is predicted by extrapolating the second phase of viral load decline, i.e., by assuming that the slope of viral decline continues at the same pace. However, the rate of viral load decline could be affected by several mechanisms such as the emergence of drug-resistant viruses or the presence of reservoirs; on the other hand, recovery of immune system capabilities could also accelerate the final phase of viral decline (Figure 5).78 Second, the capability to predict individual parameters can be hampered by sparse sampling designs and/or poorly identifiable parameters. Individual parameter identifiability can be improved by using a Bayesian estimation of individual parameters, as long as BQL data are properly accounted for and correct a priori information is used for nonidentifiable parameters such as de novo infection rate β.79 Lastly, it is important to underline that the good match between the model prediction and SVR rate for a population in previous studies27,40,60 are not sufficient to prove either the existence or the value of the proposed cure boundary. In fact, the cure boundary may be too conservative and one could argue that the goal of treatment is not necessarily to totally eradicate the infection, but rather to bring it down to a sufficiently low level such that it can be handled by the immune system on its own (Figure 5). This functional cure can be reproduced using the extended model, however it requires using very specific and sometimes not realistic parameter values.80 If such a functional cure boundary exists, it may strongly depend on the immune response and thus be subject to a large interpatient variability. More discussion on the limits of this approach can be found in a recent editorial.78

Figure 5.

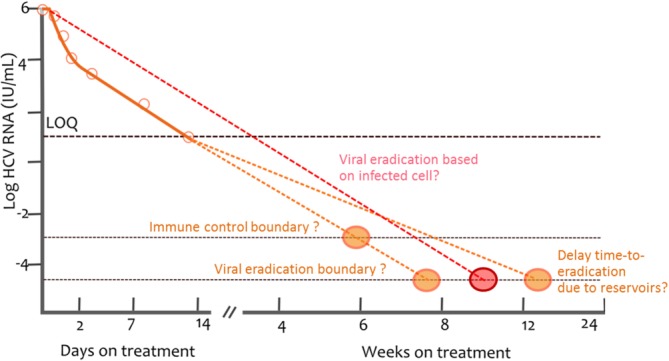
Illustration of the cure boundary (viral eradication). Viral eradication is considered as achieved once the predicted total HCV RNA is lower than one copy in the entire extracellular fluid volume, assumed to be 15L, which corresponds to a viral concentration of 6.7 x 10^-5 HCV RNA/mL. Once the viral load is predicted to cross this boundary, HCV is considered eradicated. The cure boundary can be based on the last infected cell instead of last virion. The cure boundary makes the assumption that the HCV RNA decline rate is the same before and after it crosses the assay limit of detection (orange dotted line). This may not be correct, for instance, when resistance or reservoirs lead to a slowing of the viral decline (red dotted line), or, on the other hand, if there are mechanisms leading to an acceleration of the viral decline (due, for instance, to restored immune capabilities).

Modeling combination therapy

We have essentially focused above on the modeling when only one drug was given. In order to assess the effect of drug combinations,81,82 two main models are used, the Bliss independence and the Loewe additivity.

The Bliss independence model assumes that the two drugs have independent mechanisms. Therefore, the fraction of virus production that escapes the action of one drug is then subject to the action of the other and the combined effect is given by:

Eq 11

This model has been used to describe the combined effect between peg-IFN and other antivirals.41,60,83 However, the underlying assumption about the independence of two drugs is a strong assumption in a highly integrated system such as an infected cell and is difficult to verify in vivo, even when the two drugs target different viral proteins.

On the other hand, if one assumes that two agents have similar modes of action, the Loewe additivity model can be employed, as was done for modeling the combination of two nucleotide analogs47:

Eq 12

Of note, the combined effect obtained with the Loewe additivity model is systematically lower than that obtained with the Bliss independence model. For instance, if two drugs have separated effectiveness of ɛ₁ = ɛ₂ = 0.9, the combined effect will be 0.99 with the Bliss independence model and 0.947 with the Loewe additivity model. An interesting property of the Loewe additivity model is the fact that it can be easily expanded to account for a synergistic or antagonistic effect:

Eq 13

where α is called the “combination index,” with α<1 indicative of synergism, α>1 indicative of antagonism. To our knowledge, this model has never been used in vivo to evaluate drug interaction in HCV therapy and the information needed to precisely estimate α (number of different doses of monotherapies, combinations, etc.) needs to be evaluated.

Of note, the interaction of drug effects can also be a reflection of pharmacokinetic interaction. For this reason, PK-VK modeling is useful to separate pharmacokinetic and pharmacodynamic interaction. Lastly, drug interaction can also increase the risk of toxicity. In that context, mathematical modeling can also be used to optimize the balance between safety and efficacy. This approach may encompass the retrospective analysis on large populations using appropriate statistical tools, such as the generalized additive logistic model proposed by Snoeck et al. to evaluate the optimal dose of RBV in peg-IFN/RBV-treated patients.84 It can also encompass a more physiological model to dynamically adapt dosing regimens at the individual level, such as proposed by Laouenan et al., who used individual predose concentrations of ribavirin and peg-IFN to predict the evolution of hemoglobin and platelet levels, respectively, in patients treated with peg-IFN/RBV and telaprevir or boceprevir.85

Towards new modeling paradigms to understand treatment outcome with new therapies

Recent results of short and extremely efficient therapies brought new questions about the reliability of HCV RNA to predict treatment outcome. In the SYNERGY trial, patients received 12 weeks of sofosbuvir and ledipasvir (an NS5A inhibitor) or 6 weeks of sofosbuvir, ledipasvir, and GS-9669 or GS-9451. Interestingly at the end of treatment N = 6/60 patients had quantifiable viral load and N = 29/60 patients had detectable viral load with the Abbott assay (LOD of 10 IU/mL) but only one of them failed to achieve SVR.86 Using the existing models, one would fail to predict SVR for these patients. To our knowledge, few isolated cases of detectable viremia at the end of treatment have been reported in patients having SVR after peg-IFN/RBV therapy with a highly sensitive assay.87–89 However, unlike in the SYNERGY trial, all detectable values at the end of treatment were preceded by undetectable measurements,87–89 which made them appear to be due to measurement errors. Whether this observation is specific to SYNERGY or will be observed elsewhere is unclear; in any case, it may reveal the importance of important features largely ignored until now, such as a high proportion of noninfectious virus or a strong restoration of the immune response, is not known.

CONCLUSION

HCV kinetic models have played an important role in deciphering the origin of viral decline, leading the US Food and Drug Administration (FDA) to recommend its use during drug development.90 In the new era of short and extremely effective treatment, modeling efforts will be particularly needed to anticipate and optimize drug combinations, both in terms of efficacy and safety, and to optimize individual treatment. These new developments will probably be focused on specific hard-to-treat populations, such as cirrhotic or patients who failed previous treatments. The development of more complex models will require the use of other biomarkers which, in complement to HCV RNA, will allow integrating important mechanisms involved in treatment outcome with new HCV therapies.

Abbreviations

BDL

Below detection limit

BQL

Below quantification limit

CE

Constant effectiveness

CI

Cell infection

DAA

Direct-acting antiviral

FDA

Food and Drug Administration

GT

Genotype

HCV

Hepatitis C virus

HIV

Human immunodeficiency virus

IC

Intracellular

ICCI

Intracellular-cell infection

IFN

Interferon

K-VK

Viral kinetic model using dosing information

NS5A

Nonstructural 5A protein

NLMEM

Nonlinear mixed effect model

ODE

Ordinary differential equation

PDE

Partial differential equation

peg-IFN

Pegylated interferon

PK

Pharmacokinetic(s)

PK-VK

Pharmacokinetic-viral kinetic

RBV

Ribavirin

SVR

Sustained virologic response

VE

Varying effectiveness

vRNA

Viral RNA

Conflict of Interest

The authors declare no conflicts of interest.