Quantifying and Communicating Uncertainty in Preclinical Human Dose-Prediction

Abstract

Human dose-prediction is fundamental for ranking lead-optimization compounds in drug discovery and to inform design of early clinical trials. This tutorial describes how uncertainty in such predictions can be quantified and efficiently communicated to facilitate decision-making. Using three drug-discovery case studies, we show how several uncertain pieces of input information can be integrated into one single uncomplicated plot with key predictions, including their uncertainties, for many compounds or for many scenarios, or both.

Human dose-prediction is pivotal in drug discovery to ensure the right exposure for safe and effective treatment.1 It is used for ranking lead-optimization compounds and judging feasibility of the target and of chemical series, and informing the design of phase I and IIa trials in early clinical development. It also provides important information to other functions involved in drug development, such as pharmaceutical development (formulations), process chemistry (how much compound to synthesize), and preclinical safety (exposure margins). Like all model-based predictions, human dose-predictions are associated with uncertainty. This tutorial describes how uncertainty in preclinical human dose-prediction can be quantified and efficiently communicated to decision-makers and scientists not trained in modeling. We anchor our discussion on effective communication of uncertainty in the science communication research. The calculation and communication methods we describe are applicable to translation in general; examples include veterinary medicine, dose-setting in investigatory preclinical experiments, and between patient groups (e.g., from healthy volunteers to a diseased population).

The human dose is predicted from a mathematical model based on the nature of the pharmacokinetic/pharmacodynamic (PK/PD) relationship and the pharmacokinetic (PK) parameters, such as clearance, bioavailability, and distribution properties. Uncertainty enters both in the choice of model structure and in the parameterization of the model as well as errors in actual data. This tutorial focuses on parameter uncertainty and how that can be propagated into dose prediction uncertainty, but also illustrates model structure uncertainty in one of the examples. For any translational prediction method, it is of importance to distinguish the prediction uncertainty of scaling from the population variability of a specific parameter. Variability is a property of the system (e.g., environmental or genetic variations) that does not decrease when larger samples of a population are observed.2 In contrast, uncertainty represents limited knowledge of the system (not a system property), and decreases as information accumulates. For example, assume that human clearance for a drug candidate is predicted to 1 mL/min/kg. This point estimate is uncertain and the true average human clearance may differ from the prediction. In a human population, clearance in different individuals will vary around the true average value, and this variability is generally unrelated to the uncertainty of scaling. The main concern in the scaling process is typically the inherent uncertainty in the scaling methodology and not primarily the variability in preclinical input data or the variability in the target population.

There are several ways to predict human PK parameters, and historically the most common methods used are based on allometric relationships, taking into account the difference in size between species.3,4 In recent years when access to human hepatocytes and liver microsomes has increased dramatically, in vitro-in vivo extrapolation or physiologically based pharmacokinetic modelling is often used (e.g., Jones et al.5). In general, taking physicochemical properties, metabolism, and excretion pathways into account leads to improved predictions (i.e., reduced uncertainty). Several publications have evaluated the accuracy of different scaling methods by comparing the predicted parameters (e.g., plasma or intrinsic clearance, volume of distribution, and bioavailability) to measured human parameters.6–22

The uncertainty in the pharmacodynamic (PD) effect and the PK/PD understanding varies depending on the biological system, the preclinical models used to establish the PK/PD relationship, as well as the design and evaluation of these studies. Clearly, species differences in the underlying biology constitute a potential big source of uncertainty. It is, however, difficult to generalize uncertainty in dynamics because it depends on the knowledge of the system investigated. Hence, uncertainty in PD typically varies between drug projects to a larger extent than uncertainty in PK.

There are several ways to reason about and present uncertainty; from simple dose-range tables or graphical illustrations of sensitivity, to more integrated probabilistic analyses. Tables are easy to generate but are limited to show uncertainty in two parameters and at discrete points. Sensitivity plots communicate uncertainty in only one dimension at a time (Figure 1a,b). This leads to a risk of information overload if all aspects are covered (i.e., many figures or tables), or lack of information if only selected instances are communicated. This tutorial focuses on the Monte-Carlo simulation, which is a method to quantify overall uncertainty by simultaneously integrating all sources of uncertainty.2,23–25 The main output from the Monte-Carlo simulation is a distribution of the predicted dose, and, in our examples, we will use such distributions to show the impact of uncertain inputs to the dose prediction (e.g., Figure 2a,b for case study 1). The simulation also outputs concentration-time data (exemplified in Figure 1c where uncertainty is indicated by percentiles), and such information may be a useful complement to the dose distributions.

Figure 1.

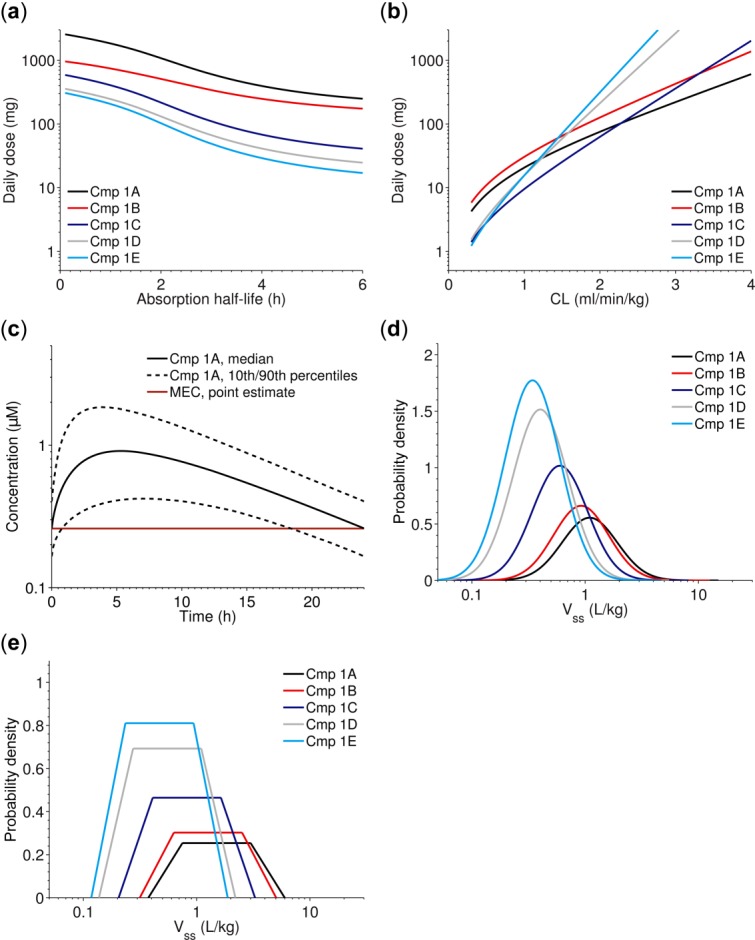
(a–b) Examples of sensitivity plots showing predicted human dose using the minimal effective concentration level as target (Eq. 3 in main text), vs. absorption half-life a or clearance (CL) b. (c) Example of how uncertainty in pharmacokinetic/pharmacodynamic (PK/PD) parameters influence the predicted human plasma concentration-time profile (data from case study 1). The plot was generated using the Monte-Carlo simulation. (d–e) For each parameter, the uncertainty in scaling can be represented by a distribution. Uncertainty in scaling the volume of distribution at steady state (V_ss) (from case study 1) using a log-normal distribution d, and a log-uniform distribution with truncated tails e, cf. Nestorov (2001)². In d, V_ss is assumed to be within threefold of the predicted point estimate with 95% probability. In e, V_ss is assumed to be within twofold of the predicted point estimate and otherwise within twofold to fourfold with probability decreasing toward both ends. Many possible shapes can be considered. Cmp, compound; MEC, minimum effective concentration.

Figure 2.

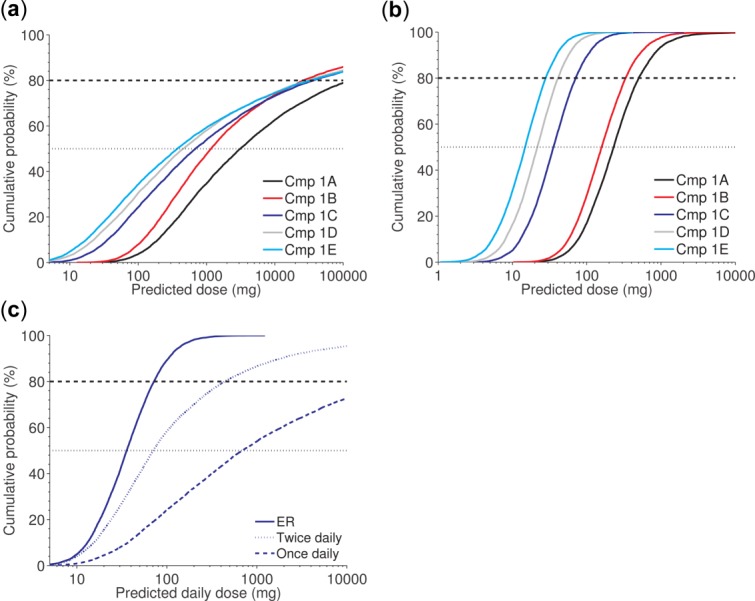
Case study 1. Given the proposed scaling approach and parameter ranges (Table 2), all compounds (Cmps) 1A–1E are unlikely to have a human dose below 100 mg once daily with an immediate release formulation (a); Cmps 1C, 1D, and 1E are likely to have a human dose below 100 mg once daily with a putative extended release (ER) formulation (b). Focusing on Cmp 1C shows it is very likely to be feasible for once daily administration using an ER formulation (solid line), has a medium likelihood of being feasible for twice daily administration (dotted line), but is unlikely to have an acceptable dose for once daily administration (dashed line), using an immediate release (IR) formulation (c).

Given a human dose-prediction calculated from a model with parameters obtained from a combination of the methods discussed above, one wishes to communicate the result adequately and effectively. Unfortunately, the underlying computational and translational science may not be easily accessible to decision-makers, and modelers may not understand decision-makers' information needs. Effective science communication bridges the gap between science and decision-making, and informs decision-makers about the benefits and risks, thereby allowing them to make the right decisions.26–28

Based on three drug-discovery examples, this tutorial demonstrates the usefulness of addressing uncertainty in scaling and presents a way of communicating scaling based on industrial experience and anchored in the science communication research.

Uncertainty quantification

The uncertainty quantification of PK parameters from preclinical experiments to clinical has been extensively investigated in the literature. Prediction methods for clearance is by far the most studied case because of its importance for systemic drug elimination and oral bioavailability. Clearance is defined as the volume of blood, from which the drug is removed, per unit of time. Reported evaluations of in vivo clearance prediction-methods are often based on relatively small datasets (up to 50 compounds), although a few investigations are based on larger datasets (up to 400 compounds).9,12,17,20 The main reason for evaluation-data scarcity is that many compounds are only administered by the oral route to humans, making unambiguous distinction of in vivo clearance and bioavailability impossible. It is therefore recommended to cautiously interpret ranking of different methods for clearance prediction.

Although some studies show that simple allometric prediction from a monkey performs best,12,17,21 there are typically cost and ethical reasons against using higher species in preclinical research. It has been suggested, albeit using smaller datasets, that the rat and dog data may perform equally well.6,13 Allometry may indeed work well for compounds excreted renally, or whose clearance is limited by liver blood flow, but may not be applicable for low-clearance compounds limited by cytochrome P450 enzyme activity.13,29 In some studies, methods using correction factors, such as the rule of exponents method or fraction (unbound) corrected intercept method have been shown to predict better than allometry or at least decrease the risk of overprediction.6,8,12 Including a correction for species differences in intrinsic clearance could also possibly decrease the prediction error of allometric methods.30 However, as reported by the publication using the largest dataset,12 the best allometric methods only predict approximately 60% of compounds within twofold of the human clearance.

In vitro-in vivo extrapolation methods (hepatocytes or microsomes) for hepatic clearance predictions have varying success rates reported in the literature, ranging from 20–90% of compounds predicted within twofold.6,13,14,22,31–34 The variation may be due to the differences in experimental setups and in experimental/empirical correction factors (see Fagerholm14 for an extensive review). It has been reported that in vitro-in vivo extrapolation, using a regression-line correction established in the utilized hepatocyte assays, may be the method of choice because it will correct for systematic errors in the experimental setup.31 Overall, it seems reasonable to suggest that the uncertainty in clearance predictions falls in the order of a factor three for high-performance methods (this can, for example, be approximated by a lognormal distribution with 95% chance of falling within threefold from the predicted point estimate).

Volume of distribution at steady state (V_ss) is defined as the proportionality factor between the total amount of drugs in the body at steady state and plasma (or blood) concentration. Similar to clearance, V_ss can be predicted using several different methods with allometry historically being most used. Indeed, allometry may be a reasonable method to predict V_ss because of the physiological aspects governing this parameter, such as organ weights and volumes. There is little consensus of the best method for predicting V_ss.7,11,13,15,18 Two publications7,11 suggest that the semimechanistic Oie-Tozer equation predicts relatively well if nonhuman in vivo data are available. To confidently predict V_ss, especially when in vivo data are scarce, it is important to consider the physicochemical properties of the compound and that they conform to the assumptions made in the model. One way to investigate the predictive power of a method is to apply the method between preclinical species.7 Similar to clearance, it seems reasonable to suggest that the V_ss predictions will fall within threefold of the true value.

The absorption of drugs from the gut into the systemic circulation is a complex dynamic process.35,36 The main determinants for the extent and kinetics of this process are dose, solubility/dissolution rate, and permeability. However, gut metabolism, stability of the drug in the intestine, fasted/fed state, and mass transfer may also affect the dynamics. Bioavailability (F) is defined as:

1

where F_a denotes fraction absorbed, F_g denotes fraction that escapes gut metabolism, and F_h denotes fraction that escapes hepatic metabolism. Absorption is often predicted using the Biopharmaceutics Classification System, which categorizes the candidate drugs on the basis of their solubility and permeability. Compounds with high solubility and high permeability (Biopharmaceutics Classification System I) have an almost complete and rapid absorption. However, for compounds with low permeability or low solubility, or both (Biopharmaceutics Classification System II–IV), it is more difficult to accurately predict the absorption process, and compounds in these classes may display a large variation in both extent and kinetics between patients and administrations.37,38 In vitro methods are routinely used to get a qualitative understanding of absorption properties.39–41 Translating F_a and F_g from animal to human is difficult because of interspecies differences in intestinal physiology as well as enzymatic activity.42,43 For example, bioavailability in dogs is often higher than in humans, possibly because of a more leaky intestine paracellular pathway,44,45 and monkeys often have lower bioavailability because of a higher enzymatic activity in the gut.46 Physiologically based pharmacokinetic models are reported to underpredict bioavailability, but the number of investigated compounds is limited (≤8 per Biopharmaceutics Classification System class).19

Most drug-discovery programs actively strive to develop compounds with sufficiently high solubility and permeability in order to reduce the uncertainty and risk of variation in exposure. For such compounds, it is reasonable to assume that absorption can be controlled by formulation. In the three case studies presented here, the working hypothesis has been that the compounds will have good absorption properties in humans. This has been based on in vitro (permeability, crystalline solubility) combined with in vivo animal PK studies. Naturally, if solubility and permeability properties are less favorable, or gut metabolism is suspected, one should account for uncertainty in absorption parameters (using the same principles as outlined for CL and V_ss).

As mentioned earlier, the uncertainty in PD can be considerable. In some cases, differences in PD effect can be attributed to differences in metabolism between species (i.e., active metabolites), leading to different pharmacological/toxicological responses.1,47 Another example is species differences in receptor distribution, which have been reported for the opioid receptors in the brain48 and in histamine receptor subtypes in bronchi.49 Differences in relative receptor density between species can be found both for serotonergic and dopaminergic receptors.50,51 Cardiac glycosides (e.g., digoxin and related compounds) are an example of compounds with a large difference in affinity between species, in the order of 100-fold lower affinity in rodents compared with humans.52 Further, translational modeling of disease progression is not straightforward, but can sometimes be scaled with the expected lifespan of the species.53 Taking all these factors into account, uncertainty in PD can influence the dose prediction significantly, especially for a first-in-class compound targeting an unprecedented class of target or pathway. On the other hand, confidence increases when clinical data on the same target/pathway have been generated, the preclinical disease model has been shown to translate to human, or the system pharmacology of the target is understood, or a combination of those.54–57

The human dose is often predicted using relatively simple models, which can be represented by closed-form expressions. As a base case, the dose prediction for a compound with assumed one-compartment kinetics, systemic clearance CL, a desired average steady-state concentration (C_ss), bioavailability F, and dosing interval τ is calculated as:

2

Alternatively, for a compound with a desired coverage above a minimum effective concentration (MEC), the predicted dose is calculated as:

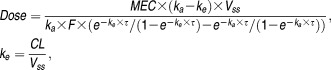3

where k_a denotes the absorption rate-constant. For nonlinear models with no closed-form expression for dose, simulation-based methods are needed.

To investigate the uncertainty of the dose prediction, PK and PD parameters can be represented by empirical distributions based on available information on translational performance. Specifically, for a PK parameter, the distribution around the point estimate reflects the uncertainty of each method, as well as potential variability in input data. The shape of the distribution can be chosen based on reasonable assumptions or inferred empirically from compounds tested in man. A log-normal distribution is useful to avoid negative values (exemplified in Figure 1d). Alternatives to log-normal distributions include fuzzy numbers or other interval analyses that are common in engineering applications58 and that have also been used in physiologically based pharmacokinetic applications2,23 (exemplified in Figure 1e). In those probabilistic frameworks, it is straightforward to include correlations between parameters. However, there is presently not much information in the literature on potential correlations of PK/PD parameter uncertainties. In the case studies, no correlations were incorporated in the Monte-Carlo simulations.

In the next step, the model and the parameter distributions are fed into a Monte-Carlo simulation to calculate the distribution of the dose prediction. Basically, random samples for each parameter are drawn from the chosen distribution (the number of samples depends on the problem, and is typically greater than 1,000). The dose is calculated for each set of parameters, resulting in an empirical dose distribution. Monte-Carlo simulations using closed-form dose expressions, like Eqs. 2 and 3, are computationally feasible and can typically be generated within milliseconds on a standard computer. For more complex PK/PD models, the calculation may be significantly slower, because each dose calculation involves an optimization (e.g., to assure that plasma concentration is above a certain threshold at a specific timepoint), and each evaluation step in the optimization requires numerical integration of the ordinary differential equations of the model. It is often expedient to present the resulting dose distribution as a cumulative probability plot (which describes on the y-axis the probability that the dose is less than or equal to the value on the x-axis, cf. Figure 2a).

Uncertainty communication

Science communication in general and uncertainty communication in particular are actively discussed in the environmental science,59–61 as well as in other areas, like radiotherapy.62,63 We mention the following main challenges in order to effectively communicate uncertainty in human dose-predictions:

• Communication of results based on modeling and simulation is hard and requires careful preparation. Such preparation is often performed iteratively and involves complete listing of modeling assumptions, translation of model equations into words or overview figures, choice of simulations and interpretation of results, and reflection on consequences of the modeling predictions. Note in particular that formulas and technical terms are easy to list but difficult to interpret for scientists without adequate training in mathematics.60

• Human dose-predictions tend to focus on PK properties of the drug, and not so much on PD properties. However, translating the PD model from animal pharmacology to the human situation is based on assumptions and associated with uncertainties.1,23,24 Therefore, no or low emphasis on PD uncertainty may underestimate overall uncertainty/risk and, hence, bias decision-makers.

• It is easy to mistake variability for uncertainty, and a consequent language is essential to avoid this problem.

Fundamental communication elements are words, numbers, and visualizations. Concerning words, it is important to be aware of variation in interpretation of phrases of likelihood (e.g., likely and probable).64,65 To elucidate the meaning of such words, it is recommended to define a consistent language according to numerical levels of confidence as exemplified by the verbal quantifiers in Table 1. The number of levels of such a table depends on the amount and quality of data, the type of research question, and the expected level of granularity of the response. It is also wise to strive for a simple language and avoid technical jargon.61 Concerning numbers, they can be directly used to communicate, for example, confidence levels, and there is empirical evidence that including both verbal and numerical characterization improves communication.59 Communication by visualization is central in science to convey causal relationships, temporal trends, data, etc.27

Table 1.

Probability words as quantitative subjective probability judgments

Term	Probability range
Virtually certain	>0.99
Very likely	0.90–0.99
Likely	0.66–0.90
Medium likelihood	0.33–0.66
Unlikely	0.10–0.33
Very unlikely	0.01–0.10
Exceptionally unlikely	<0.01

Mapping of probability words into quantitative subjective probability judgments, used by the Intergovernmental Panel on Climate Change Third Assessment59,65 based on recommendations developed by Moss & Schneider.69

Successful communication depends on several factors²⁸:

1. Identify the science relevant to decision-making; separate need-to-know science from nice-to-know science. Determine the decision-maker's background knowledge in the subject area.

2. Design communication to fill the critical gaps between what people know and need to know.

3. Collect systematic feedback provided by empirical evaluation, and use the information to evaluate the adequacy of the communication and to revise it accordingly.60

The case studies that we show in the next section represent the final outcome of this iterative approach (points 1–3 above). The feedback (step 3) was continuously collected from various industrial and academic stakeholders during approximately one year and is summarized in the Discussion section. We have chosen to communicate by visual means complemented with verbal quantifiers (exemplified in Table 1). Specifically, we have condensed complex information from multiple sources into a single uncomplicated plot that captures the uncertainty in human dose-prediction, and, in that way, pinpoints the need-to-know science.

CASE STUDIES

We present three case studies of how uncertainty in preclinical human dose-prediction can be quantified and communicated. In these case studies, clearance was estimated from in vitro and in vivo data using two different scaling methods. First, clearance was predicted from human hepatocyte data using a regression correction method based on 36 marketed drugs reflecting the same principles as in Sohlenius-Sternbeck et al.31 This study reports that 66% of compounds have a predicted intrinsic clearance within twofold. Second, clearance was also scaled from in vivo data obtained from rats and dogs using the liver blood flow method.17 Using a clinical dataset of 18 compounds, this method predicts in vivo clearance within twofold for 67% of the compounds and within threefold for 94% of the compounds.6 The uncertainty distribution for each clearance method was represented by a log-normal distribution with 95% of samples falling within threefold of the predicted point estimate. Variability in input data to the scaling methods was considered negligible in comparison to the translational uncertainty. If two predictions are available for the same parameter, it is common to take the average value of the predictions as the point estimate. For each iteration of the Monte-Carlo simulation, one sample is drawn from each of the two distributions, and the average value is used. In this way, two (similar) predictions of CL, for example, result in a consensus prediction with less uncertainty than each individual prediction. The approach generalizes to three or more predictions.

Volumes of distribution for all three case studies were predicted using the semi-mechanistic Oie-Tozer equation.66 For this method, 78% of the predictions were within twofold and 89% within threefold of the in vivo result using a dataset of 18 compounds.7 For a larger dataset of 400 compounds, 67% of the predictions were within twofold.11 Unbound V_ss for each series in the case studies was consistent across species (rat and dog; i.e., the slope of a simple unbound allometric plot fell between 0.8 and 1.2), which further adds confidence in prediction. V_ss was assumed log-normally distributed with 95% of samples falling within threefold of the predicted point estimate. Similar to clearance predictions, variability in input data to the scaling method was considered negligible in comparison to the translational uncertainty.

For all case studies, it was assumed that rate of absorption was rapid (k_a = 1h⁻¹), unless a scenario with an absorption-modifying formulation was simulated. In addition, the fraction of the dose absorbed was assumed high (F_a = 1) and gut metabolism negligible (F_g = 1). Hence, the major contributor to F was first-pass metabolism in the liver and F was calculated as:

4

where LBF is the liver blood flow and CL is the systemic blood clearance. Hence, the F distribution is consequential from the clearance distribution.

The target audiences for communication of the three case studies have been PK/PD-modelers, medicinal chemists, bioscientists, and governance bodies.

Case study 1

The first case study considers five compounds (Cmp 1A–1E), that were evaluated in the lead-optimization phase of a drug-discovery project. The aim was to support ranking of the compounds for subsequent progression into toxicological studies. For each compound, a dose resulting in 24-hour coverage above the MEC was predicted using Eq. 3. However, because of an estimated short half-life (3–4 hours) of the compounds, small changes in PK parameters had a large impact on the dose prediction, thereby increasing overall uncertainty. The project team was considering an extended release (ER) formulation in order to generate a flatter concentration-time profile and to decrease dependence on elimination half-life and thereby obtain a more clinically realistic dose level. During these discussions, it became apparent that understanding and efficiently communicating uncertainty in the dose predictions were pivotal to progress the project.

Parameters and distributions were generated as described in the “Uncertainty Quantification” section (Table 2; example in Figure 1d). Predictions for CL using methods based on in vitro data (in vitro-in vivo extrapolation from hepatocytes) and in vivo data (rat/dog liver blood flow17) were in a similar range and did not diverge more than twofold for any of the compounds. Naturally, the combination of information from two clearance prediction methods decreased uncertainty. The point estimate of MEC was derived from potency measures in a whole blood in vitro assay (Table 2). The same biomarker and assay were planned to be used in humans. The in vitro assay potency results fell within twofold of the potency seen ex vivo in human whole blood, for two reference compounds with reported clinical data, targeting the same pathway. Hence, the uncertainty in PD was set to let 95% of the samples fall within twofold of the point estimate. The absorption constant, k_a, was fixed because it is a parameter that can be largely controlled by formulation choices as long as the compounds are judged to show properties suitable for ER formulation. Specifically, k_a was kept fixed at 1 h⁻¹ and 0.1 h⁻¹ when simulating immediate release (IR) and ER formulations.

Table 2.

Parameters for case study 1

Compound	MEC (µM)	Vss (L/kg)	CL (heps) (L/h/kg)	CL (LBF) (L/h/kg)	t1/2 (h)
1A	0.26 (0.13–0.52)	1.5 (0.50–4.5)	0.43 (0.14–1.3)	0.20 (0.067–0.60)	3.3
1B	0.40 (0.20–0.80)	1.3 (0.42–3.8)	0.31 (0.10–0.93)	0.12 (0.040–0.36)	4.1
1C	0.079 (0.040–0.16)	0.82 (0.27–2.5)	0.23 (0.077–0.69)	0.14 (0.047–0.42)	3.1
1D	0.073 (0.037–0.14)	0.55 (0.18–1.7)	0.12 (0.040–0.36)	0.13 (0.043–0.39)	3.0
1E	0.056 (0.028–0.12)	0.47 (0.16–1.4)	0.09 (0.030–0.27)	0.14 (0.047–0.42)	2.8

CL, clearance; LBF, liver blood flow; MEC, minimum effective concentration; V_ss, volume of distribution at steady state; heps, hepatocytes.

Point estimates and 95% uncertainty ranges. The parameter t_1/2 is derived from CL and V_ss.

Overall uncertainty was calculated by Monte-Carlo simulation. For an IR formulation, ranking of the compounds was communicated by a cumulative probability distribution of the daily dose for each compound, all summarized into a single plot combined with verbal quantifiers (Figure 2a). This approach significantly facilitates comparison of dose predictions for multiple compounds.

We next investigated the effect of an ER formulation using the same communication layout (Figure 2b). As already pointed out, the uncertainty around the point estimate of the IR dose was large because of the short half-life of the compounds. For example, the 90% confidence interval for Cmp 1E ranges from 10 mg to more than 100,000 mg. The confidence interval for an ER preparation is significantly narrower and ranges from 4–50 mg. Cmp 1B was predicted to have a somewhat longer half-life compared with the others, and, consequently, this compound exhibits the steepest slope in Figure 2a. Along the same line of reasoning, the cumulative probability curves for the ER formulation generally show much steeper slopes, compared to the corresponding curves for the IR formulation. The tendency of the compounds to fall into two groups in the ER scenario illustrates a substantial difference in potency between the compounds and it was deemed likely that Cmp 1C–1E would have a daily dose below 100 mg.

Based on the information in Figure 2a,b and Table 2, the project team concluded that the point estimates for an IR dose were low enough to facilitate once daily dosing for the best compounds. However, the uncertainty in these dose estimates was relatively large and the lead-optimization program was planned to account for ER feasibility. Figure 2c efficiently communicated this rationale to decision-makers for one of the top compounds.

In summary, the first case study demonstrates how proper uncertainty quantification and communication support compound selection in the lead-optimization phase of a drug-discovery project. It also shows how different administration schedules and formulations can be analyzed within this framework.

Case study 2

The second case study considers five compounds (Cmp 2A–2E), that were evaluated in the lead-optimization phase of another drug-discovery project. The project team explored a first-in-class target, and, in the current phase of the project, it was not known if the C_ss (Eq. 2) or the MEC (Eq. 3) was most appropriate for human dose prediction. The goal was to select one compound for further toxicological and pharmacological profiling, taking both uncertainty in model and choice of dosing schedule into account. This case study illustrates how model structure uncertainty can be quantified and communicated.

PK parameters and their uncertainties were quantified as described in the “Uncertainty Quantification” section. For PD, limited information was available for human translation. Therefore, the MEC and C_ss for each compound were predicted from in vitro potency data, and threefold translational uncertainty was assumed around the predicted point estimates (Table 3). Dose predictions for the case of C_ss-driven effect show that Cmp 2A–2D are likely to have a human dose <500 mg (Figure 3a). However, taking the more conservative MEC prediction into account reveals a pronounced separation with Cmp 2A as the preferred compound because of its relatively long half-life (14 hours compared to 3–6 hours for the other compounds; Figure 3b). The plots in Figure 3a,b illustrated the effect of the long half-life on the predicted human dose, and facilitated decision-making in the project. Cmp 2A is likely to have a human dose <500 mg, whereas the other compounds have a medium likelihood of a dose >1,000 mg.

Table 3.

Parameters for case study 2

Compound	MEC (µM)	Vss (L/kg)	CL (heps) (L/h/kg)	t1/2 (h)
2A	1.2 (0.38–3.5)	1.2 (0.41–3.7)	0.060 (0.020–0.18)	14
2B	0.20 (0.067–0.6)	1.7 (0.55–5.1)	0.28 (0.093–0.84)	4.1
2C	0.28 (0.093–0.84)	1.5 (0.49–4.5)	0.29 (0.10–0.87)	3.6
2D	1.4 (0.47–4.3)	0.49 (0.16–1.5)	0.060 (0.020–0.18)	5.7
2E	0.38 (0.13–1.1)	1.1 (0.36–3.3)	0.32 (0.11–0.96)	2.4

CL, clearance; heps, hepatocytes; MEC, minimum effective concentration; V_ss, volume of distribution at steady state.

Point estimates and 95% uncertainty ranges for MEC, V_ss, and CL. The parameter t_1/2 is derived from CL and V_ss.

Figure 3.

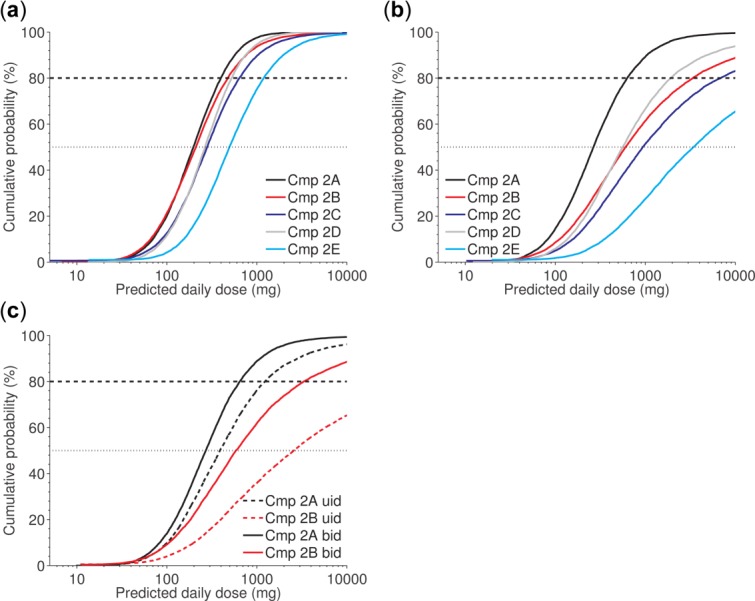
Case study 2. Given the proposed scaling approach and parameter ranges (Table 3), compounds (Cmps) 2A–2D are likely to have a human dose below 500 mg, and Cmp 2E is likely to have a dose below 1,000 mg for a model with steady-state concentration (C_ss)-driven effect (a). If the effect is driven by the minimal effective concentration, Cmp 2A is likely to have a human dose below 500 mg, whereas the others are not (b); and assuming this model is medium likelihood that Cmp 2A can be administered once daily (c).

In a subsequent step, taking also other factors than the human dose-prediction into account, the project team prioritized Cmp 2A and B and was interested in understanding the influence of once daily vs. twice daily dosing schedules. Simulations indicate that Cmp 2A may be feasible for once daily administration while Cmp 2B is not (Figure 3C). Hence, Cmp 2A stands out as superior to Cmp 2B based on the human dose-prediction. This compound was assumed to be least sensitive for different dosing approaches and was selected for further profiling.

In summary, the second case study adds to the first by demonstrating how model uncertainty (C_ss-driven vs. MEC-driven effect) influences dose quantification and uncertainty level for different dosing schedules, and how these aspects can be quantified and efficiently communicated.

Case study 3

The third case study applies a PK/PD-link model containing a one-compartment PK model (first order absorption, linear elimination) connected to a receptor-occupancy model with elementary kinetics defined as:

5

where C denotes drug plasma concentration, R_tot denotes the total receptor concentration, RC denotes the drug-receptor complex and k_on and k_off are kinetic parameters (the dissociation constant is derived as K_D = k_off/k_on). For this case study, the human dose was predicted by requiring a certain level of receptor occupancy (e.g., 50%) over a certain period of the day (e.g., 16 hours). The aim was to predict the required human dose and its uncertainty for a candidate drug, Cmp 3A, in order to assure a certain level of receptor occupancy. Human PK parameters were predicted from empirical scaling from both in vitro (hepatocytes) and in vivo (mouse/rat/dog) data (Table 4).

Table 4.

Parameters for case study 3

Predicted parameter	Cmp 3A
PK: Vss (L/kg)	4.0 (1.3–12)
PK: CL (heps) (mL/min/kg)	9.9 (3.3–30)
PK: CL (LBF) (mL/min/kg)	6.3 (2.1–19)
PD: minimum RO (%)	50 (37–63)
PD: required coverage (h)	16 (14–18)
PD: receptor KD (µM)	0.096 (0.032–0.29)
PD: receptor koff (h−1)	0.38 (0.13–1.1)

CL, clearance; Cmp, compound; heps, hepatocytes; LBF, liver blood flow; PK, pharmacokinetic; RO, receptor occupancy; V_ss, volume of distribution at steady state; PD, pharmacodynamic.

Point estimates and 95% uncertainty ranges for six parameters based on domain knowledge, data, and literature.

For PD parameters, the required receptor occupancy level was observed at 24 hours in rodents (rat 37%, mouse 63%) and translated to the same average level, 50%, but at 16 hours in humans. The difference in coverage (24 hours in rodents compared to 16 hours in humans) reflects well-established species differences in the particular disease area. The uncertainty for human translation was represented by a log-normal distribution with 95% chance of falling in the range of 37–63%. Furthermore, human point-estimates for receptor-occupancy parameters K_D and k_off were obtained from PK/PD analysis of mouse data (with K_D protein-binding corrected). Uncertainty in determination of K_D and k_off from mouse data was assumed negligible in comparison to uncertainty in translation. We assume that, with 95% confidence, K_D and k_off in humans independently varies by a factor of three to corresponding mouse parameters. In summary, uncertainty in six key PK and PD parameters influenced the human dose prediction (Table 4).

Using a PK/PD-link model, we algorithmically searched for the minimal required human dose for each combination of receptor-occupancy coverage and dosing schedule. This calculation was defined as an optimization problem: find the minimal predicted dose that ensures a certain level of receptor occupancy, given a certain number of doses per day, a certain coverage time, and the predicted human PK parameters. A simple half-interval search was used to find the minimal dose. Here, we took advantage of a flexible and efficient Matlab library to ensure computational feasibility.67

Then, the Monte-Carlo simulation was used to integrate uncertainty from all specified sources and to predict empirical distributions for dose and C_max (Figure 4). Data indicate that it is likely that the human dose is <200 mg when uncertainty in both PK and PD are integrated (Figure 4a). Understanding of human PK would significantly reduce the overall uncertainty; here simulated for the case with PK parameters fixed at the predicted point estimates (Figure 4a). In order to design preclinical safety studies and interpret in vitro safety screens, it is pivotal to have a good understanding of expected exposure levels in humans. The Monte-Carlo simulation outputs such predictions as well, and data indicate that it is likely that C_max is <0.4 µM taking PK/PD uncertainty into account (Figure 4b). Overall, data indicate that PD uncertainty is important to consider, in particular when key biomarkers are not accessible in at least one of the species, and when change in disease state is not well understood.

Figure 4.

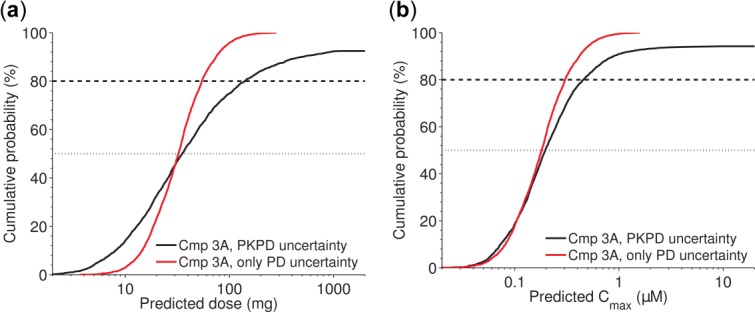
Case study 3. Given the proposed scaling approach and parameter ranges (Table 4), it is likely that the human dose of compound (Cmp) 3A is <150 mg (black solid line) (a); it is likely that C_max in humans is <0.5 µM (black solid line) (b). In both a and b, the red steeper curve illustrates the information gain if human pharmacokinetic (PK) was known (here assumed known at the predicted point estimate) and only uncertainty in pharmacodynamic (PD) contributed to overall uncertainty.

In summary, the third case study adds to the two others first by demonstrating how arbitrary (nonlinear) PK/PD model structures, as well as uncertainty in several PD parameters can be considered. The analysis can be connected to a dose optimization step and still be computationally feasible when no closed-form dose expression can be analytically derived. The third case study also shows how other parameters, like C_max, can be communicated in the same way as dose.

DISCUSSION

In the case studies, uncertainty in human dose-prediction is quantified by a systematic integration of information from various uncertain sources, and reported as a single uncomplicated plot complemented with verbal quantifiers that facilitates communication and enables informed decisions. The approach allows drug-project teams to evaluate various scaling scenarios or models, to identify the most influencing parameters, to rank compounds (e.g., compounds with similar predicted dose point-estimates but different uncertainty), and to properly assess the risk before the first time in humans. Other uncertainty considerations, such as safety aspects, commercial feasibility, cost of goods, and competitive landscape, can be directly connected to the framework as they often use the predicted human dose as one of the input parameters (cf. Thompson et al.68). The same reasoning can be applied to the predicted C_max or area under the curve distribution or other derived parameters. The empirical calculations can be performed efficiently, not only for closed-form expressions, but also for nonlinear ordinary differential equation systems. In this way, calculations can be instantly revised as soon as new data are generated, or a different scenario is to be tested. Taken together, the approach exemplified by the three case studies represents a useful way of quantifying and communicating uncertainty in human dose-predictions.

The most basic alternative to the proposed approach is to simply communicate point estimates. However, in our experience, such communications always raise questions (e.g., how is ranking influenced by variability/uncertainty, and what is the chance of having a dose less than a certain amount). In particular, this is the case when uncertainties differ between compounds (because of different types, amounts, or quality of input data), or a combination of those. A Monte-Carlo approach can address these and other questions.

There are several ways of communicating the result of a dose prediction based on a probabilistic approach. A concentration-time plot (Figure 1c) is one obvious alternative to the cumulative probability plot of dose advocated in this tutorial (Figure 2a). Our preference for the latter is based on two factors. First, we have experienced that many audiences misinterpret the uncertainty in the concentration-time plot as population variability. Second, the concentration-time plot gets crowded when more than one compound or scenario, or both, are compared (Figure 1c shows just one compound and would be hard to interpret if all compounds 1A–1E were included, as in Figure 2a). Nevertheless, the concentration-time plot remains a useful complement to the dose distribution.

In case study 1, the need to investigate ER feasibility of the compound series was successfully communicated by Figure 2. It was also apparent that an ER formulation was likely to generate a dose below 100 mg/day for any of the three compounds 1C–E. The plots were used to illustrate the risk with the IR once daily approach and gain confidence in the chosen mitigation plan using an ER preparation. In addition, Figure 2c efficiently communicates that an ER formulation would potentially be superior to twice daily administration for one of the compounds. Indeed, the high uncertainty associated with once daily IR formulation (Figure 2a) illustrates the importance of communicating uncertainties; only communicating point estimates gives a false sense of security. In this and the two other case studies, the compounds show good absorption properties and bioavailability was derived from CL only. However, we acknowledge that a more conservative approach with uncertainty in F_a can be argued. Generally, for low permeability compounds or compounds predicted to be highly metabolized in the gut, the bioavailability estimate should take F_a and F_g into consideration. Plausible uncertainty distributions for these parameters must then be proposed in the same way as for other parameters.

The method used for human dose-prediction is drug-project specific and should be chosen based on the pharmacological understanding of the target. Case study 2 shows the impact of model choice on the distribution of the predicted dose (C_ss vs. MEC-driven approach). Of course, model averaging can be considered in situations where information is lacking and a single model cannot be selected. Commonly, uncertainty in clearance and bioavailability, and sometimes volume of distribution and rate of absorption, strongly influences overall uncertainty in the prediction. Uncertainty in PD parameters can have a large impact on dose, as seen in case study 3, but is even more project-specific compared to PK parameters. Uncertainty in PD can be decreased by, for example, understanding the target and its biological pathway, using preclinical animal models with known translational properties, or taking advantage of published clinical data for compounds with the same target or compounds already approved for the indication. The same type of communication can be used to inform about remaining uncertainty in PD when PK is known from a clinical phase I study (cf. Figure 4). Furthermore, for early toxicological studies, the uncertainty in predicted exposure levels (C_max and area under the curve), can be used to better assess and communicate uncertainty in safety margins.

In order to quantify uncertainty in the dose prediction, it is useful to list the contributing parameters and then assess the uncertainty of each parameter, as well as correlations between those measures if independence cannot be assumed. Naturally, it is not uncommon that compounds in a series are supported by various amounts of data (e.g., clearance can be predicted from either hepatocyte data, or animal data, or both). However, such differences in input data can be directly incorporated in the uncertainty calculation. Notably, for cases where the predictions of a parameter vary substantially between two or more methods, it is advisable to further investigate the underlying reason because one of the methods may be more suitable for the compound series. However, in principle, the computational framework also works for this case.

In general, it is hard to determine the translational uncertainty in scaling methods and PD relationships, and to assign or infer reasonable distributions representing those uncertainties. There is a rich literature covering uncertainty of various methods for predicting PK parameters. However, there is lack of consensus in ranking these methods, partly because datasets are limited and differ in size. Different physicochemical properties for compounds may also influence which methods are best suited for a certain compound class. As a rule-of-thumb, literature data on translation of PK parameters indicate that good methods predict 80–90% of the compounds within threefold from the true parameter value.6–22 However, these evaluations of methods are based on data for compounds that have reached the clinical phase and have been reported in the literature; potential bias in any direction cannot be excluded. In our case studies, we have assumed log-normally distributed uncertainty with 95% probability to be within threefold from the point estimate. It is recommended to increase confidence in prediction by using different types of data (e.g., in vitro and in vivo, more than one scaling method, and information from other compounds with similar properties).

In our experience, decision-makers in drug discovery gain a lot from having a rough indication of the uncertainty levels. Integrating information in the way proposed here quantifies the overall uncertainty (although not being exact) in a manner that is easy to understand. Therefore, we believe it is worthwhile doing this analysis when uncertainty levels can be captured in at least the right order of magnitude.

Fundamental to science communication is to determine how much and what information the audience needs to make an informed decision²⁸; what is considered good communication for one audience may not suit another. Communicating modeling and simulation can often be difficult, especially when trying to describe the impact of assumptions and uncertainty to people not used to working with prediction models or translational aspects, or both. Also, it is challenging to find the right balance between communication of the point estimate and the uncertainty. Hence, finding the right communication strategy requires iterative trials with intermediate collection and analysis of feedback from the audience.

The proposed communication approach was developed in this iterative way. Generally, the reception of the communications has been very positive from various academic and industrial stakeholders from different scientific backgrounds. For example, medicinal chemists emphasize the value of rough uncertainty quantifications during the design-make-test-analyze process. Negative feedback during the process was mainly related to the three challenges in order to effectively communicate uncertainty in human dose-predictions listed in the “Uncertainty Communication” section. To overcome these challenges, we have strived to avoid technical jargon and minimize the usage of equations in our presentation. Furthermore, as pointed out by Pidgeon and Fischhoff,⁶⁰scientists from a different field can get an exaggerated sense of scientific uncertainty when uncertainties that are most difficult to understand or model are discussed in depth, whereas uncertainties of commonly accepted methods (e.g., a certain PK scaling method) are never brought up. The approach used in the case studies is designed to put the same emphasis on all contributing factors to the overall scaling uncertainty in order to avoid this problem. The hardest communication problem has been related to the distinction between variability for uncertainty (e.g., the uncertainty distribution of CL may be incorrectly interpreted as the population variability of CL). To overcome this problem, we have strived to use a consequent language (Table 1), focused on dose distribution plots and not concentration-time plots (as discussed above). Another important factor for successful communication is to allow the audience to take active part in the reasoning behind the prediction. By using efficient software, users can revisit and change the assumptions, or simulate a different scenario, and get an instant reply.

Communication should be designed specifically for the target audience (see point 1 in the numbered list in section “Uncertainty Communication”). In our experience, the cumulative probability plots are useful both for modelers and nonmodelers (e.g., decision-makers). However, the underlying assumptions and calculation steps should be motivated more rigorously for modelers compared to nonmodelers. In this way, we can balance the right to know and full disclosure with need-to-know. We believe it is hard to avoid the iterative phase when preparing a communication. However, the number of iterations can be reduced by a well chosen starting point. The approach outlined by three case studies in this tutorial can be such a useful starting point for communicating human dose-predictions in pharmaceutical research organizations. In summary, the three case studies have been communicated by three means (Figures 4; Tables2−4):

• A single plot showing the cumulative probability of predicted dose levels, allowing several compounds or scenarios, or both, to be simultaneously evaluated.

• A summary table of underlying assumptions, detailing which parameters were considered uncertain and to what extent.

• A headline interpreting the presented data and summarizing them into the key finding (e.g., “It is likely that the human dose is <100 mg”).

Together, these three pieces fit into a single slide in presentation format (e.g., PowerPoint).

The communication strategy is simple, efficient, and sound. Simple because the data is easily generated, revised, and summarized into a single slide, efficient because the audience is provided the information that they need in a form they can use, and sound because we have strived to transparently acknowledge main sources of scientific uncertainty.

CONFLICT OF INTEREST

The authors declared no conflict of interest.