Abstract
An adaptive P300 brain-computer interface (BCI) using a 12 × 7 matrix explored new paradigms to improve bit rate and accuracy. During online use, the system adaptively selects the number of flashes to average. Five different flash patterns were tested. The 19-flash paradigm represents the typical row/column presentation (i.e., 12 columns and 7 rows). The 9- and 14-flash A & B paradigms present all items of the 12 × 7 matrix three times using either nine or 14 flashes (instead of 19), decreasing the amount of time to present stimuli. Compared to 9-flash A, 9-flash B decreased the likelihood that neighboring items would flash when the target was not flashing, thereby reducing interference from items adjacent to targets. 14-flash A also reduced adjacent item interference and 14-flash B additionally eliminated successive (double) flashes of the same item. Results showed that accuracy and bit rate of the adaptive system were higher than the non-adaptive system. In addition, 9- and 14-flash B produced significantly higher performance than their respective A conditions. The results also show the trend that the 14-flash B paradigm was better than the 19-flash pattern for naïve users.
1. Introduction
Brain-computer interface systems (BCIs) provide a new channel for disabled patients to convey messages and commands. Some BCIs rely on voluntary changes in endogenous brain rhythms. Birbaumer et al. (1999) published the first BCI validated with severely disabled users, which was a spelling system using slow cortical potentials (SCPs). However, the SCP approach is slow, inaccurate, and requires extensive training. BCIs based on event-related (de)synchronization (ERD/ERS) have been widely used and validated with able-bodied and disabled subjects, who often attain satisfactory results even without extensive training (Pfurtscheller and Neuper, 2001; Neuper et al., 2003; Pfurtscheller and Müller-Putz, 2003; Scherer et al., 2004; Kübler et al., 2005; Vaughan et al., 2006; Blankertz et al., 2008).
Some BCI systems do not rely on voluntary changes in endogenous brain rhythms, but instead rely on voluntary changes in evoked potentials, usually visual evoked potentials (VEPs). Steady-state visual evoked potentials (SSVEP) and P300 potentials have been widely used in BCIs to spell. Untrained subjects have used BCIs based on SSVEPs in speller systems (Gao et al., 2003; Friman et al., 2007; Sugiarto et al., 2009). Unfortunately, SSVEP BCIs do not work for some subjects (Lalor et al., 2005; Müller-Putz et al., 2005; Allison et al., 2008; Müller-Putz and Pfurtscheller, 2008), and some users may find the flickering lights annoying (Allison et al., 2008).
P300-based BCIs work without training, and may work in subjects who are not successful with other approaches (Sellers and Donchin, 2006; Birbaumer and Cohen, 2007; Allison and Neuper, 2010). P300 BCIs have been validated with disabled users, with visual, auditory, and tactile stimuli (Allison and Pineda, 2003; Hoffmann et al., 2005; Sellers et al., 2006, Allison et al., 2006; Sellers and Donchin, 2006; Sellers et al., 2006, Allison et al., 2006; Hoffmann et al., 2008; Furdea et al., 2009; Kübler et al., 2009; Guger et al., 2009; Townsend et al., 2010, Sellers et al., 2010). Although P300 BCIs offer excellent information transfer rate (ITR) relative to other BCI approaches, there remain unexplored opportunities to further improve ITR.
There are several ways to improve the classification accuracy and bit rate (also known as information transfer rate, ITR) in a P300 BCI (Allison and Neuper, 2010). The most common approach is to apply improved signal processing and machine learning algorithms (Jung et al., 2001; Xu et al., 2004; Hill et al., 2008; Lenhardt et al., 2008; Krusienski et al., 2008; Guger et al., 2009). However, four other possibilities are:
Decreasing the number of trials per average (if the data collected from the first few trials could allow adequately accurate communication), since presenting flashes after effective classification increases the time for each character selection and decreases bit rate (Serby et al., 2005; Allison and Pineda, 2006; Lenhardt et al., 2008; Townsend et al., 2010). In our paper, one trial includes n flashes (i.e., sub-trials). Trials per average are the number of trials used for each average;
Decreasing the number of flashes per trial (including target and non-target flashes); that is, reducing the number of flashes necessary to identify a target;
Preventing items from flashing twice in succession, as the second flash might generate a small P300 or might not even be fully processed due to the “repetition blindness” (Fazel-Rezai, 2007; Koivisto and Revonsuo, 2008; Salvaris and Sepulveda, 2009);
Reducing interference that occurs when an item adjacent to the target flashes during a non-target sub-trial (Townsend et al., 2010). When this occurs, the subject might misclassify the nontarget flash as a target flash, which could evoke incorrect P300 responses or make the subjective flashing probability higher than the actual flash probability of the target for the participants. A high subjective flashing probability would lead to a reduction in P300 amplitude. Reducing interference from neighbor flashing characters can decrease this “attentional blink” (Fazel-Rezai, 2007; Kranczioch et al, 2007).
The first approach (fewer trials per average) is often suggested in P300 BCI articles, which often present figures or tables that show how classification accuracy could change with different numbers of trials per average. Indeed, this precedent was established in the first P300 BCI paper (Farwell and Donchin, 1988) and has since become commonplace (Lenhardt et al., 2008; Krusienski et al., 2008; Jin et al., 2010a). However, articles rarely capitalize on this information in an online BCI that varies the number of trials per average. Lenhardt et al. (2008) allowed the subjects to select the number of trials per average. Townsend et al. (2010) have taken a different approach. Using a calibration data set from each participant, they determined the optimal number of trials per average for each participant using a metric referred to as the written symbol rate (WSR) (Kübler et al., 2009). The fixed optimal value was then used online for classification feedback. Serby et al. (2005) instead used an automated method online to determine the optimal number of trials per average for each character, which allows the number of flashes to vary from one character to the next. The approach introduced here does so as well, but differs substantially in the method used to present and identify the characters.
The second approach (fewer flashes per trial) capitalizes on a potential weakness of the row/column (RC) approach. The RC approach is designed around the assumption that target flashes should be relatively infrequent, since P300 amplitude is directly related to the target to target interval (TTI) (Gonsalvez and Polich, 2002; Jin et al., 2010a). Therefore, the RC approach yields robust P300s, but requires numerous flashes to identify the target – specifically, one flash for each row and column. Allison and Pineda(2006) introduced the “multiple flash” approach, in which flashes were designed around binary decomposition of the available choices. That is, each flash illuminated half the characters on the screen, instead of only one row or column, and hence the minimum number of flashes necessary to identify a target was equal to log2(R)+log2(C) instead of R+C. Even though decreasing the TTI did indeed reduce P300 amplitude, the resulting reduction in the number of flashes per trial may result in an overall improvement to information throughout (Allison and Pineda, 2003, 2006; Sellers et al., 2006; Jin et al., 2010a). Similarly, Townsend et al. (2010) disassociated the rows and columns and presented stimuli in quasi-random flash groups. Here, we introduce a new method based on binomial coefficients that does not use rows and columns (Jin et al., 2010b). Each flash illuminated a subset of characters that we selected to avoid short TTIs and distracting nontarget flashes. We compared this new flashing approach, which requires fewer flashes per trial (nine or 14 as compared to 19 in the current paradigms) to a canonical RC flash pattern approach. This issue is important since increasing the probability that a target character flashes (that is, reducing TTI) decreases P300 amplitude (Sellers et al., 2006; Duncan-Johnson and Donchin, 1979; Sellers et al., 2006). Since the inter-stimulus interval did not change in this study, changing the probability has a proportionate effect on the TTI (Gonsalvez and Polich, 2002). Therefore, we sought to avoid a high target probability (or short TTI) because this could reduce P300 amplitude and thus impair classification accuracy (Allison and Pineda, 2003; Allison and Pineda, 2006; Sellers et al., 2006; Townsend et al., 2010).
The third approach (preventing items from flashing twice in succession) also involves the problem of short TTIs. In the standard RC P300 BCI, cases in which the target element flashes twice in succession are unavoidable. Since P300 amplitude is proportional to TTI, the second flash will produce a weak P300, which impairs classification accuracy. This may cause P300 habituation, which refers to the fact that the P300 may become smaller if the same stimulus is presented repeatedly (Ravden and Polich, 1998; Jin et al., 2010c). In addition, even if a P300 response is produced, overlapping target epochs would ensue, resulting in waveform distortion (Woldorff, 1993; Martens et al., 2009). Furthermore, the user might not see the second flash because of “repetition blindness” (Kanwisher, 1987). Therefore, P300 BCIs should be designed to reduce the likelihood that the same stimulus flashes twice in succession, since the resulting reduction in P300 amplitude could impair classification. This idea was suggested in Woldorff (1993), and Citi et al. (2009) capitalized on TTI variability to develop a model to improve classification accuracy by accounting for sequence effects. Townsend et al. (2010) used a paradigm that placed a minimum of six flashes between two flashes of any given matrix item (a minimum of 750 ms), thereby avoiding the repetition blindness window. The current study is the first to introduce, test, compare, and validate novel flash patterns specifically designed to reduce the repetition blindness in a BCI.
The fourth approach (reducing the interference from adjacent flashes when the target was not flashing) involves a different phenomenon called the near-target effect (Duncan-Johnson and Donchin, 1979). This refers to the fact that flashes that are adjacent to the target stimulus tend to produce a larger P300 than more distant flashes and/or make the subjective flashing probability higher than the actual flash probability of the target for the participants. If a non-target flash near the target attracts attention by flashing less than 500msec before the target is flashed, it will lead to “attentional blink”. Therefore, we introduce and validate a novel flash pattern approach that substantially reduces flashes of characters adjacent to the target during non-target sub-trials; see Townsend et al. (2010) for an alternative method achieving the same goal. We hereafter refer to these unwanted flashes as SAINSTs: Spatially Adjacent Illuminations during Non-target Sub-Trials.
In this paper, we simulated a keyboard with a 12 × 7 matrix. Our four goals correspond to the four possible methods for improvement presented above. Our first goal was to compare an automatic selection approach to a conventional approach that uses a fixed number of trials per average. The number of trials per average was selected automatically based on the classifier output while the user selected characters online. The fixed number of trials per average was obtained from the mean number of trials used for each selection in the adaptive system. The results of the fixed number of trials were obtained offline, using the data collected while the subjects used the adaptive online system. A canonical P300 BCI would flash each row and column, and hence a 12 × 7 matrix would require 19 flashes per trial to identify the target character. We explored different “flash patterns”, which refer to which characters were illuminated during each flash. One condition used 9 groups of items (9-flash A) in each trial, and the second condition used 14 groups of items (14-flash A) in each trial. In these two conditions, matrix items would flash without and effort to reduce the interference from adjacent flashing characters (9-flash A) and without avoiding flashes of the same item twice in succession (14-flash A). Our second goal was to evaluate a flash pattern approach that reduces the likelihood of the interference from neighbor flashing characters when the target was not flashing. To address the second goal, we compared two types of 9-flash patterns (i.e., 9-flash A and B). In 9-flash B, stimuli were chosen to reduce the likelihood of interference from flashes of neighboring characters when the target was not flashing. Our third goal was to evaluate a flash pattern approach that reduces the likelihood that the same character is flashed twice in succession. Both the 9- and 14-flash pattern approaches were designed to decrease the interference from cells adjacent to the target. However, to address the third goal, we compared two types of 14-flash patterns (i.e., 14-flash A and B). In 14-flash pattern B, stimuli were chosen to reduce the likelihood that the same character would be flashed twice in succession. A fourth goal was to determine whether these new flash patterns yield higher classification accuracies/bit rates than the RC method.
2. Methods and materials
2.1 The flash pattern design
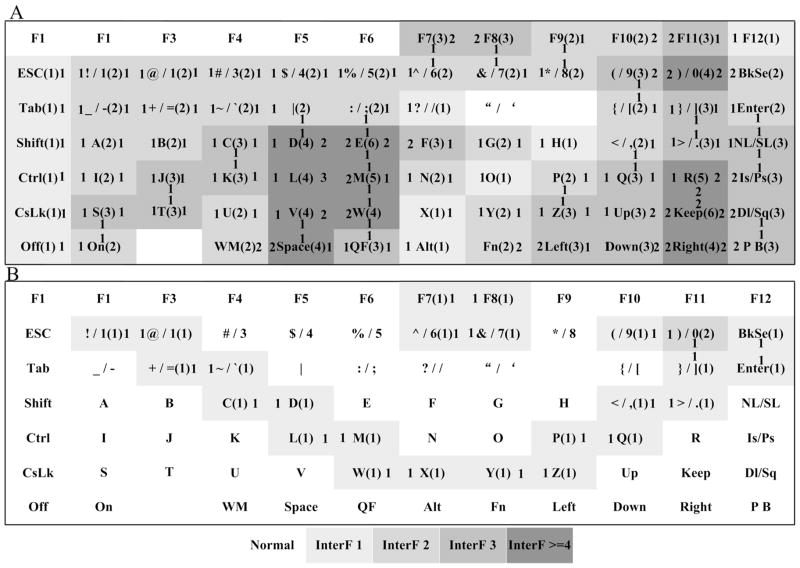
The flash pattern approaches presented here are based on binomial coefficients (excluding the 19-flash pattern, which is a control condition and is hence based on the canonical RC approach). The set of k combinations of a set with size n is denoted by C(n, k) = n!/(k!(n − k)!),0 ≤ k ≤ n. The number of flashes per trial is n, and k is the number of flashes per trial for each character. We used the set of k combinations ( k = {2,3} ) from sets with sizes n = {9,14}). C(9,3) and C(14,3) denote the 9- and 14-flash patterns respectively. A 12 × 7 matrix has 84 elements. C(9,3) contains 84 elements and is adequate to identify any element in such a matrix. C(14,3) contains more elements than C(9,3). Figure 1 shows the configuration of the different flash pattern combinations in this study, excluding the 19-flash pattern approach we used as a control condition. In the other four flash patterns, stimuli are not grouped in rows or columns during each flash. The flashes are named “flash1, flash2, …, flashn”. For the 9-flash pattern, n is 9; for the 14-flash pattern, n is 14. Flash1 highlights the elements in Figure 1 that contain “1”, flash2 highlights the elements in Figure 1 that contain “2”, and flashn highlights the elements in Figure 1 that contain “n”. The position of the elements in Figure 1 corresponds to the position in Figure 2.
Figure 1.
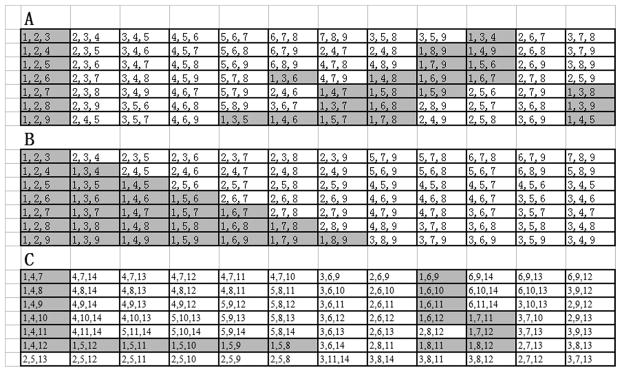
These three panels depict the configuration of different flash patterns: 9-flash A (panel A), 9-flash B (panel B) and 14-flash pattern (A&B) (panel C). The numbers indicate which of the n flashes would illuminate the target character. For example, the top right element of panel A would be illuminated during the third, seventh, and eighth of the nine flashes. The shaded cells provide an example of what the subject would see for flash1 of the sequence.
Figure 2.
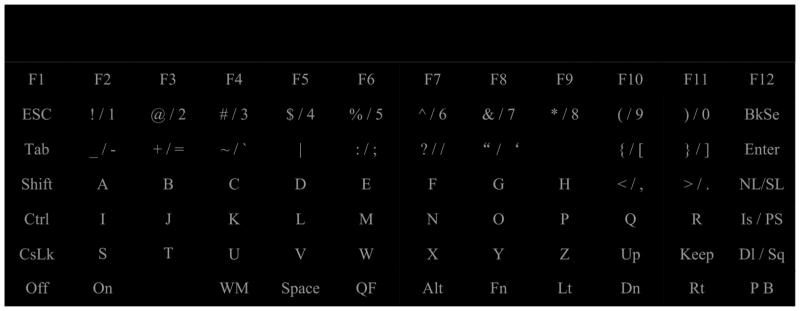
The stimulus screen for the online runs.
For example, the character “F1” would be selected if flash1, flash2, and flash3 evoked a P300 in the 9-flash pattern A condition (see Figures 1A and 2) or in a 9-flash pattern B condition (see Figures 1B and 2). However, in the 14-flash pattern condition, “F1” would be selected if flash1, flash4 and flash7 evoked a P300 (see Figures 1C and 2). In this study, values of k = {2, 3} were used. k=2 corresponds to the RC pattern used when two target sub-trials are presented in each trial. k=3 is selected to decrease the number of sub-trials (that is, individual flashes) in each trial. However, k cannot be very high because the number of characters that flash at the same time depends on k; increasing k will increase interference from characters neighboring the target when the target is not flashing. For the 9-flash pattern, if double flashes were not avoided, higher k values would increase the probability of a double flash, which would attenuate the P300 ERP (Duncan-Johnson and Donchin, 1979; Allison et al., 2003; Sellers et al., 2006).
9-flash pattern B and both 14-flash patterns were optimized to decrease the interference from adjacent characters (see Figures 3 and 4), and 14-flash pattern B was optimized to eliminate successive flashes of the same item. In Figures 3 and 4, each cell contains information arranged as follows: . U, D, L, and R refer to the number of SAINSTs per trial in the cell above (U), below (D), left (L), and right (R) of that cell. In this paper, if the number of SAINSTs from one side was less than or equal to one, SAINSTs on that side would count as zero. For example, if there is one SAINST per trial to the left of the target cell (L), and one SAINST per trial to the right of the target cell (R), and another SAINST per trial below the target cell (D), and three SAINSTs per trial above the target cell (U), then the total number of SAINSTs would be two (L+R+D+U=2, L=0, R=0, D=0, U=2), since the SAINSTs left, right and below the target would count as zero. Modified SAINSTs (or MSAINSTs) are the sum of these “SAINSTs” values from all sides. In other word, MSAINSTs is R+L+U+D. If there is no character on one side (for example, the right side of “on”, see figure 2), then the number of SAINSTs on that side equals zero. It is impossible to reduce the number of SAINSTs on one side to zero except when there is no character on that side, because this is only possible if the cells adjacent to the target cell always flash (or never flash) at the same time as the target cell, and it would then be impossible to determine which cell is the target without some other means of conveying information.
Figure 3.
Panel A shows the number of SAINSTs and MSAINSTs for each cell in 9-flash pattern A. Panel B shows the number of SAINSTS and MSAINSTs in 9-flash B (Panel B). “Normal” means that the number of MSAINSTs was zero. InterF 1, 2, 3, and >=4 means that MSAINSTs were 1, 2, 3, and >=4. Modified SAINSTs or MSAINSTs are the sum of these “SAINSTs” values from all sides.
Figure 4.

SAINSTs and MSAINSTs in the two 14-flash patterns (A&B). “Normal” means that the number of MSAINSTs was zero. InterF 1, 2, 3, and >=4 means that MSAINSTs were 1, 2, 3, and >=4. Modified SAINSTs or MSAINSTs are the sum of these “SAINSTs” values from all sides.
One goal in this paper is to decrease SAINSTs. For example, the top left cell in Figure 1B is illuminated during the first, second, and third flashes of each trial, indicated by “1, 2, 3”, which is just one number different from its neighbors, “2, 3, 4” and “1, 2, 4”. Thus, whenever the top left cell flashes, a neighboring cell also flashes. During the fourth flash of each trial, the top left cell does not flash, but the two adjacent cells do, and hence these adjacent cell flashes during the fourth trial are SAINSTs. In the 14-flash pattern conditions, SAINSTs could not be reduced to the same level as in 9-flash B, since the arrangement of 14-flash B was designed to avoid successive flashes of the same element. This constrained our flexibility in reducing SAINSTs in both 14-flash patterns, since they had to be identical except for the flash sequence. For the 14-flash pattern, when flashk flashed, the next flash would be flashk−1, flashk−2, flashk+1 or flashk+2, since flashk−1, flashk−2, flashk+1 and flashk+2 did not contain the characters of flashk.
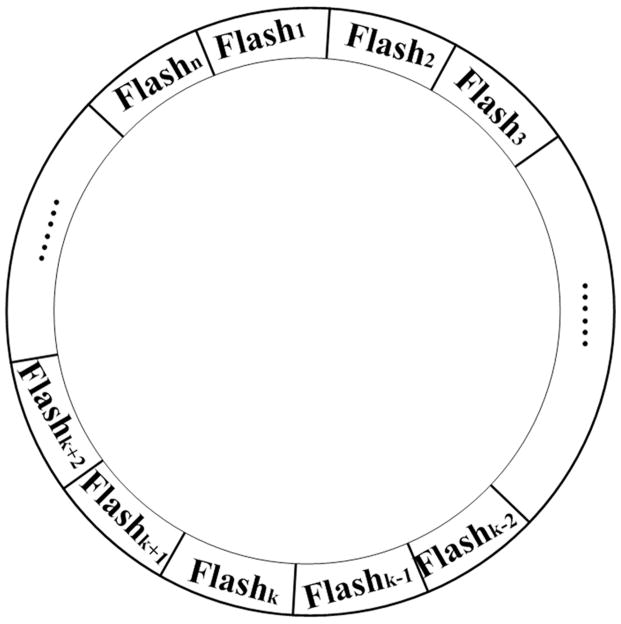
For example, “1, 4, 7” is the first element in Figure 1C. When flash1 highlighted this element, flash2 flash3, flash13 and flash14 would not highlight it, since this element did not contain 2, 3, 13 or 14. Figure 5 shows how the different flashes were arranged cyclically, such that flash1 is next to flashn (n=14). For example, if k was n (14), flashk+1 would be flash1, and if k was 1, flashk−1 would be flashn. The different flashes (aka sub-trials) in the 9A-, 9B- 14A-and 19- flash pattern conditions flash in random order.
Figure 5.
This figure depicts the method used to determine the flash sequence for the 14-flash pattern conditions.
2.2 Laptop Keyboard Design
Figure 2 shows the display used in this study. We simulated a keyboard using a 12 × 7 matrix. English letters were adjacent and alphabetical, and numbers were arranged similarly. Function keys were arranged on the four sides of the matrix, which is similar to some laptop keyboards. To decrease interference from adjacent characters, the names of the function keys were abbreviated to leave a large distance between two adjacent characters. “BkSe” is Backspace, “NL/SL” is Number Lock/Scroll Lock, “Is/Ps” is Insert/Print Screen, “Dl/Sq” is Delete/System Request, “P B” is Pause Break, “Lt” is left, “Dn” is down, “Rt” is right, “CsLk” is Caps Lock, “WM” is the shortcut key for start menu, and “QF” is the quick function (same as the right mouse button). “On” and “off” keys are used to open and close files, and “keep” is used to store the state of other keys for shortcut functions. The goal of this design is to make it easy for users to find target characters and control the laptop. These items in the keyboard can allow for full keyboard emulation in future studies; however, in the current study we focused on typing alphanumeric items.
2.3 The flash probabilities
In each trial, each flash occurs once (“flash1, flash2, …, flashn”). The probability that any flash illuminates the target character is calculated by dividing the number of character flashes per trial by the number of total flashes per trial; in other words, it is k/n. Therefore, the probability of flashing the target is 3/9=33.3% in the 9-flash pattern, and 3/14=21.4% in the 14-flash pattern. These probabilities are higher than conventional P300 BCIs. The canonical Donchin matrix uses a 6 × 6 matrix with single row and column flashes, and hence the probability of flashing the target is 1/6 or 16.7%.
2.4 Experimental set up and stimulation parameters
Ten healthy subjects (6 males and 4 females) participated in this study. Subjects were between 23 and 35 years old. Subjects 1–5 had used a P300 BCI prior to the study, and the other five subjects had never used any BCI. During data acquisition, subjects were asked to relax and avoid unnecessary movement.
EEG signals were recorded with a g.tec biosignal amplifier (Guger Technologies, Graz, Austria) and an EasyCap (Herrsching-Breitbrunn, Germany) with a sensitivity of 100μV, band pass filtered between 0.1Hz and 30Hz, and sampled at 200Hz. We recorded from EEG electrode positions Fz, Cz, Pz, Oz, C3, C4, P3, P4, P7, P8, O1, and O2 from the extended International 10–20 system. The left mastoid electrode was used as the reference, and the right mastoid electrode was used as a ground.
In the experimental paradigm, subjects are required to focus their attention on one of the characters and silently count each time the character flashed. The subject focuses on one of the characters from a predefined character sequence for 16 trials (called one run) in the offline experiment. There are 15 characters in the predefined character sequence. In the beginning of each run, a cue is presented for 1s to inform the subject which character to focus on. Each flash lasts for 100ms, then there is a 75ms delay with grey character matrix before the next flash begins. In the online experiment, the number of trials for average was selected by system adaptively and the characters identified as the targets are shown on the top of the screen (see Figure. 2). Figure 6 shows the timing of each run in the online experiment for copy spelling and free spelling. In copy spelling, subjects spelled 15 characters from a predefined character sequence. In free spelling part, subjects spelled five characters selected by themselves.
Figure 6.
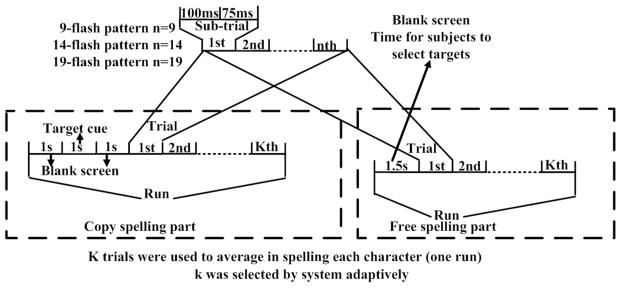
This figure shows the timing of each run in the online experimental for copy spelling and free spelling. Each run contained k trials, and each trial contained n sub-trials based on flash patterns. Each sub-trial contained one flash, followed by a brief delay.
Each subject participated in two experimental sessions on different days to reduce fatigue. The flash patterns were divided into three groups (9-flash A&B, 14-flash A&B and 19-flash pattern). These groups used in each session and patterns in each group were chosen randomly. The first session contained two groups, and the second session contained one group. Both sessions involved both offline and online experiments. Data acquired offline were used to train the classifier using Bayesian linear discriminant analysis (BLDA) and obtain the classifier model (see section 2.6). This model was then used in the online system.
2.5 Feature extraction procedure
A third order Butterworth band pass filter was used to filter the EEG between 0.1Hz and 12Hz. Although the P300 is primarily in the band 0.1–4Hz (Jansen et al., 2004), it can also be found in higher bands (Kolev et al., 1997). The EEG was downsampled from 200Hz to 40Hz by selecting every fifth sample from the filtered EEG. Single sub-trials lasting 500ms were extracted from the data, since Piccione et al. (2006) reported that P300 latency for healthy people is 445ms and ten healthy subjects participated in this study. The size of the feature vector was 12 × 20 (12 channels by 20 time points).
2.6 Classification scheme
BLDA is an extension of Fisher’s linear discriminant analysis (FLDA). The details of the algorithm can be found in (Hoffmann et al., 2008). Lei et al (2009) reported that BLDA classified more accurately than LDA and SVM when they were applied to motor imagery classification. Thus, BLDA was selected because of its demonstrated classification performance in P300 BCI applications (Hoffmann et al., 2008). Here, each trial yields 9, 14, or 19 classifier outputs, one output for one flash. The first and second (19-flash pattern) or first to third (9-and 14-flash pattern) maximum classifier outputs are selected to identify the target character.
2.7 Adaptive system settings
The number of trials per average was automatically selected by the system based on the classifier output. During online operation, it is necessary to adjust two parameters. The first parameter is the average trial length (t1). “t1” is the trial number that starts tracking the selected output of t2. “t2” is the criterion used to determine enough evidence is present to select a given character; t2 is the number of times the classifier must output the same character to stop flashing additional trials, and present feedback to the subject. For example, Subject 1 in condition 9-flash B (Table 1, top left) had values of t1=3 and t2=3; thus, after three trials the first three (t1) groups of classifier outputs would be averaged and a character would be tagged as the likely target. Since t2=3, it is necessary for the classifier to tag the same character three consecutive times for the classifier to reach the criterion and terminate the run block. Thus, after trial 3 (t1), t2 is computed for the first time using the average output of “flash1, flash2, …, flashn”. The average result of trials 1–3 or A–C is: (A+B+C)/3. For the classifier to terminate, the classifier output (t2) would need to be the same after trials 3–5, given that t2=3. Table 1 (top left) shows that the 9-flash B mean number of trials to termination was 8.4 (AVT) for S1. For 9-flash A and B, TTI is short and some subjects found it difficult to count the individual flashes because they were too fast. Hence, the first and second output was not correct for most subjects. Based on the analyses of the training data, the value of t1 was 1 or 3, and t2 was 2–3. In 9-flash, t1=1 was used for subjects that produced a very robust P300 response and t1=3 was used for subjects that produced less robust responses. Presumably because the target probability is lower for 14- and 19-flash patterns, the correct selection could be obtained with only one or two trials, and t1=1 was selected for all subjects. In the 9-flash pattern, analysis of the training data showed that t2=2 was not stable; therefore, t2=3 was used in this pattern. When t1=1 was used, subjects were tested by spelling five characters. If the output accuracy was greater than 80%, then t1=1 would be used. Otherwise, t1=3 would be used. We did not use t1=2 and t1>3 because t1=2 would not improve accuracy over t1=1 and t1>3 was not better than t1=3. In the 14- and 19-flash pattern, when we used t2=2, the subjects were also tested by spelling five characters. Again, if the output accuracy was greater than 80%, t2=2 would be used, otherwise t2=3 would be used. t2>3 was not used because it did not improve accuracy beyond t2=3. The maximum number of trials averaged was 16. When 16 trials were used to average, the output would be the result obtained from 16 average trials.
Table 1.
The classification accuracy and corresponding bit rate of adaptive system and non-adaptive system
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | Av | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-PBA | Acc | 80.0 | 86.7 | 93.3 | 100 | 80.0 | 80.0 | 73.3 | 73.3 | 73.3 | 73.3 | 81.3±9.3 |
| BR | 19.9 | 33.8 | 35.6 | 54.1 | 40.8 | 38.1 | 20.4 | 19.1 | 18.6 | 24.9 | 30.5±11.9 | |
| PBR | 11.9 | 24.8 | 30.9 | 54.1 | 24.5 | 22.8 | 9.5 | 8.9 | 8.6 | 11.6 | 20.8±14.2 | |
| Range | 8~11 | 5~8 | 5~8 | 3~9 | 3~6 | 3~7 | 5~15 | 3~11 | 5~15 | 5~9 | ||
| AVT | 8.4 | 5.6 | 6.0 | 4.5 | 4.1 | 4.4 | 7.2 | 7.7 | 7.9 | 5.9 | 6.2±1.6 | |
| t1—t2 | 3—3 | 3—3 | 3—3 | 1—3 | 1—3 | 1—3 | 3—3 | 1—3 | 3—3 | 3—3 | ||
|
| ||||||||||||
| 9-PBN | Acc | 73.3 | 86.7 | 93.3 | 86.7 | 80.0 | 66.7 | 73.3 | 60.0 | 66.7 | 73.3 | 76.0±10.5 |
| BR | 18.4 | 31.6 | 35.6 | 37.9 | 41.9 | 31.9 | 21.0 | 13.7 | 15.9 | 24.5 | 27.2±9.9 | |
| PBR | 8.6 | 23.2 | 30.9 | 27.8 | 25.1 | 10.6 | 9.8 | 2.7 | 5.4 | 11.4 | 15.5±10.1 | |
| FixT | 8 | 6 | 6 | 5 | 4 | 4 | 7 | 8 | 8 | 6 | 6.2±1.5 | |
|
| ||||||||||||
| 14-PBA | Acc | 100 | 100 | 100 | 100 | 93.3 | 100 | 100 | 100 | 86.7 | 100 | 98±4.5 |
| BR | 25.7 | 58.0 | 39.1 | 44.7 | 18.3 | 55.9 | 44.7 | 26.1 | 18.5 | 55.9 | 38.7±15.6 | |
| PBR | 25.7 | 58.0 | 39.1 | 44.7 | 15.9 | 55.9 | 44.7 | 26.1 | 13.5 | 55.9 | 37.8±16.7 | |
| Range | 4~9 | 2~4 | 2~12 | 2~9 | 3~15 | 2~5 | 2~6 | 2~12 | 2~13 | 2~5 | ||
| AVT | 6.1 | 2.7 | 4 | 3.5 | 7.5 | 2.8 | 3.5 | 6 | 6.6 | 2.8 | 4.6±1.8 | |
| t1—t2 | 1—3 | 1—2 | 1—2 | 1—2 | 1—3 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | ||
|
| ||||||||||||
| 14-PBN | Acc | 86.7 | 93.3 | 86.7 | 93.3 | 73.3 | 93.3 | 80.0 | 66.7 | 66.7 | 86.7 | 82.7±10.5 |
| BR | 20.3 | 45.8 | 30.5 | 34.4 | 11.8 | 45.8 | 26.9 | 13.7 | 11.7 | 40.6 | 28.2±13.5 | |
| PBR | 14.9 | 39.7 | 22.3 | 29.8 | 5.5 | 39.7 | 16.1 | 4.6 | 3.9 | 29.8 | 20.6±13.8 | |
| FixT | 6 | 3 | 4 | 4 | 8 | 3 | 4 | 6 | 7 | 3 | 4.7±1.9 | |
|
| ||||||||||||
| 19-PA | Acc | 93.3 | 100 | 100 | 100 | 100 | 100 | 93.3 | 93.3 | 86.7 | 86.7 | 95.3±5.5 |
| BR | 38.7 | 50.2 | 46.1 | 37.2 | 42.7 | 50.2 | 31.7 | 22.5 | 17.6 | 33.3 | 37.0±11.0 | |
| PBR | 33.8 | 50.2 | 46.1 | 37.2 | 42.7 | 50.2 | 27.4 | 19.5 | 12.9 | 24.4 | 34.4±13.1 | |
| Range | 2~4 | 2~3 | 2~4 | 2~5 | 2~4 | 2~3 | 2~6 | 2~8 | 3~13 | 2~4 | ||
| AVT | 2.6 | 2.3 | 2.5 | 3.1 | 2.7 | 2.3 | 3.2 | 4.5 | 5.1 | 2.7 | 3.1±1.0 | |
| t1—t2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | 1—2 | ||
|
| ||||||||||||
| 19-PN | Acc | 93.3 | 100 | 100 | 86.7 | 80.0 | 100 | 80.0 | 80.0 | 66.7 | 80.0 | 86.7±11.3 |
| BR | 33.8 | 57.7 | 38.5 | 29.9 | 26.4 | 57.7 | 26.4 | 15.9 | 12.1 | 26.4 | 32.5±15.3 | |
| PBR | 29.3 | 57.7 | 38.5 | 21.9 | 15.9 | 57.7 | 15.9 | 9.5 | 4.0 | 15.9 | 26.6±19.0 | |
| FixT | 3 | 2 | 3 | 3 | 3 | 2 | 3 | 5 | 5 | 3 | 3.2±1.0 | |
In this table, “AVT” is “trials per average,” “Acc” refers to classification accuracy, “n-PBA” (n={9, 14}) corresponds to the adaptive system of 9-and 14-flash pattern B, and 19-PA corresponds to the adaptive system of 19-flash pattern. And “n-PBN” (n={9, 14}) corresponds to the non-adaptive system of 9-and 14-flash B and 19-PN corresponds to the non-adaptive system of 19-flash pattern. “FixT” is fixed number of trials for average. “t1” is the starting counting trial and “t2” is the same times of the output. “Range” is the range of the trials used for average in spelling 15 characters. PBR is practical bit rate and BR is raw bit rate, all measured in bits/min.
3. Results
In this paper, we used two bit rate calculation methods called practical bit rate and raw bit rate. The practical bit rate is used to estimate the speed of the system in a reasonable real world setting. The analyses of this paper are based on practical bit rate; we only present raw bit rate to facilitate comparisons with other studies. Practical bit rate can estimate the actual experiment speed of the system, because it incorporates the fact that every error results in a penalty of two additional selections. The practical bit rate is calculated by BR*(1−2*P), where BR is the raw bit rate and P is the online error rate of the system (Townsend et al., 2010). If P >=50%, the classification accuracy is too low to correct mistakes and the practical bit rate is therefore zero. Thus, a high practical bit rate with very low classification accuracy is impossible. Furthermore, even an accuracy of 100% would not necessarily lead to high practical bit rates if the bit rate was slow for other reasons. For example, assume that the classification accuracy of system A is less than 100%. If system A could correct errors quickly and take less time to finish the task than system B (whose classification accuracy is 100%), system A would have a higher practical bit rate than system B.
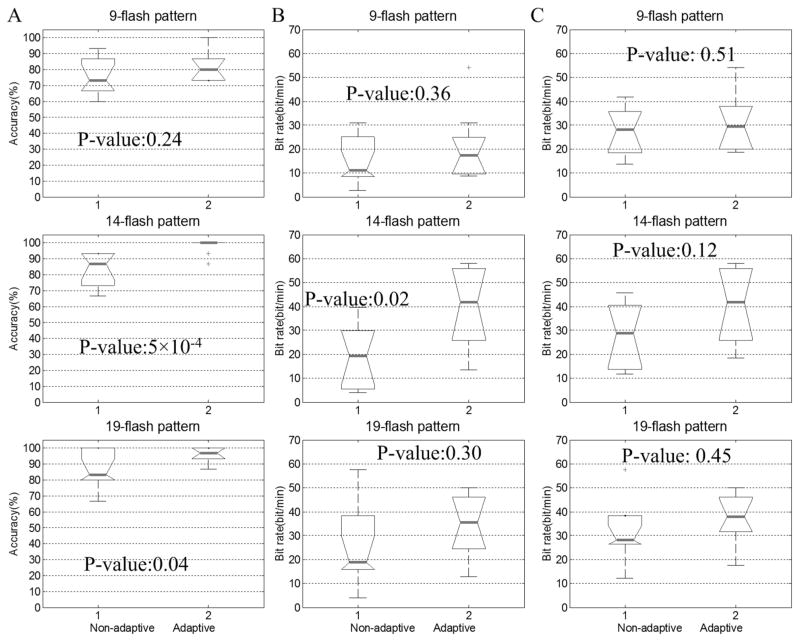
T-test analyses were used to test mean differences in Figure 7. Figure 7 (top panel) shows that the classification accuracy of 9-flash B are significantly higher than those of 9-flash A, (p<0.05). Figure 7 (lower panel) shows that 14-flash B yields a significantly higher bit rate than 14-flash A (p<0.05); however, accuracy is statistically similar (p=0.153).
Figure 7.
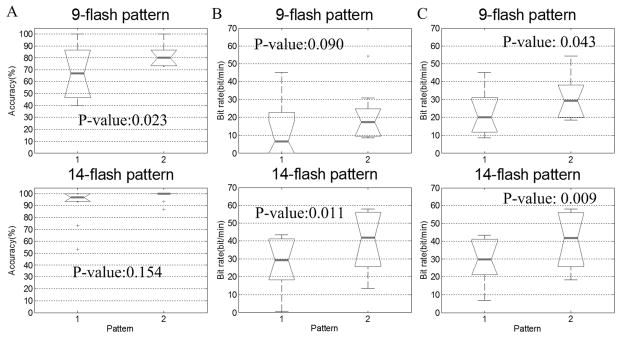
Box plots of classification accuracy and bit rate. In 9-flash pattern, pattern 1 is 9-flash pattern A, and pattern 2 is 9-flash pattern B. In 14-flash pattern, pattern 1 is 14-flash pattern A, and pattern 2 is 14-flash pattern B. Panel A is classification accuracy, Panel B is practical bit rate and panel C is raw bit rate.
Table 1 shows that the number of trials per average in the non-adaptive system was determined by rounding the average number of trials per average in the adaptive system. The results over all 15 characters were then re-calculated accordingly, based on the result of the adaptive system. The number of trials per average in the non-adaptive condition is t3, and the number of trials per average for one character in an adaptive system is N. If online classification is correct and N<=t3+t2−1, the result is a correct classification in the non-adaptive system. If the online classification result is correct and N>t3+t2−1, the result is an incorrect classification in the non-adaptive system. If the online classification result is wrong and N<t3, the result is uncertain; however, it is counted as correct in the non-adaptive system. Figure 8 and table 1 show that the adaptive system (which varies the number of trials per average for each character) is superior to the system using a fixed number of trials. ANOVA was used to test. Figure 8 shows the following results: for 14-flash B (comparing adaptive vs. non-adaptive), p<0.01 for classification accuracy and p<0.05 for practical bit rate; for 19-flash (comparing adaptive vs. non-adaptive), p<0.05 for classification accuracy; for 9-flash B (comparing adaptive vs. non-adaptive), although the difference is not statistically significant, 7 of 10 subjects obtained higher practical bit rate from adaptive Pattern in table 1, and the mean bit rate, practical bit rate and classification accuracy from adaptive pattern are higher than that from non-adaptive pattern.
Figure 8.
Box plot of classification accuracy and bit rate for non-adaptive versus adaptive versions of different flash patterns. Panel A is classification accuracy, Panel B is practical bit rate and panel C is raw bit rate.
Figure 9 compares results among 9-flash B, 14-flash B, and 19-flash. 14-flash B and 19-flash were both significantly higher than 9-flash B (p<0.01 (14-flash B), p<0.01 (19-flash)). For this multi-comparison, ANOVA was used to test (F=17.5 and p<0.01 for classification accuracy; F=3.78 and p<0.05 for practical bit rate).
Figure 9.
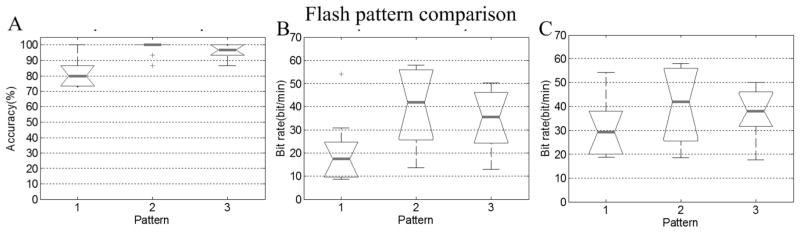
Box plots of classification accuracy and bit rate for 9-and 14-flash B and 19-flash pattern. Pattern 1 is 9-flash pattern B, pattern 2 is 14-flash pattern B, and pattern 3 is 19-flash pattern. Panel A is classification accuracy, Panel B is practical bit rate and panel C is raw bit rate.
Although the classification accuracy and practical bit rate difference between 19- and 14-flash B patterns are not statistically significant, Figure 9 shows that the classification accuracy of 14-flash B is more robust and higher than that of 19-flash pattern. Moreover, 14-flash B yields higher bit rates than 19-flash pattern for 7 out of 10 subjects. In this paper, subjects 6–10 are naïve. Subjects 1–5 had used a 19 flash pattern (RC pattern) P300 BCI prior to the study (three weeks before this experiment) and did not use 14-flash B before this experiment. Table 1 shows the trend that 14-flash B is better than 19 flash pattern for naïve subjects in practical bit rate (p<0.1) and in classification accuracy (p<0.1).
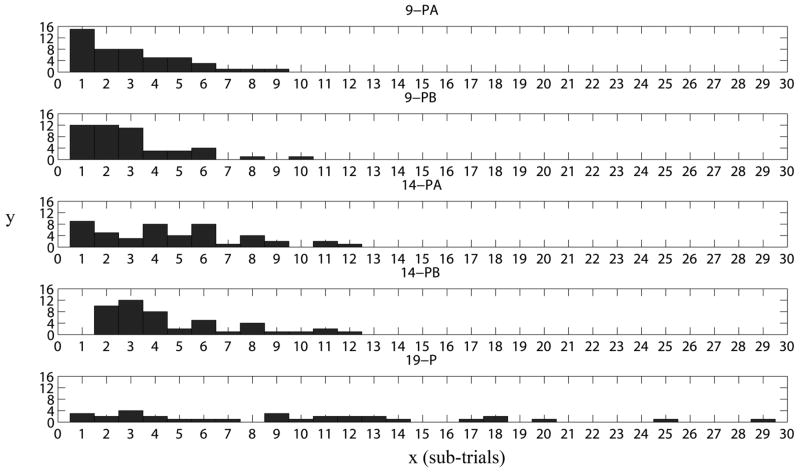
The flash sequence is random in each trial. In order to show the TTI distributions for five patterns in this paper, Figure 10 was used to show frequency of TTI of each pattern for one run of offline experiment. TTI is x*175ms.
Figure 10.
Frequency of TTI for one run. “y” is frequency of TTI and “x” is sub-trials used to calculate TTI (x*175ms). 9-PA is 9-flash pattern A, 9-PB is 9-flash pattern B, 14-PA is 14-flash pattern A, 14-PB is 14-flash pattern B and19-P is 19-flash pattern.
Figure 11 shows the grand averages of P300 amplitude for 9-flash A&B at the same TTI (350ms) on site Cz and Pz from subjects 1–10. Figure 11 shows that P300 amplitude of 9-flash pattern B is higher than that of 9-flash pattern A. This may occur because of interference from neighboring flashing characters in 9-flash pattern A, which make the flashing probability higher than the target stimuli probability. This also may occur because of the “attentional blink”. Table 1 and Figure 8 also show that 9-flash B is superior to 9-flash A.
Figure 11.
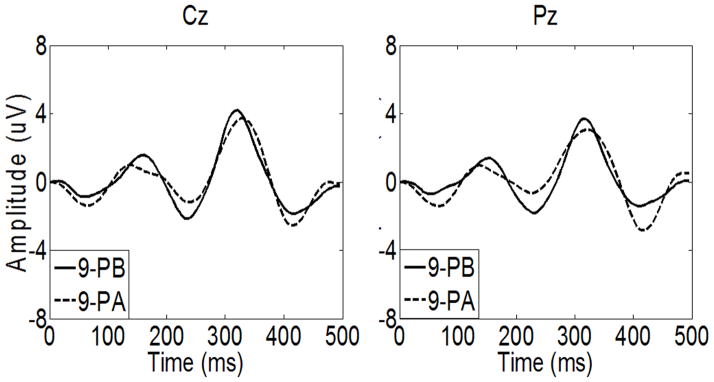
The grand averages of P300 amplitude for 9-flash A&B at the same TTI (350ms) over sites Cz and Pz from subjects 1–10. 9-PA is 9-flash A, 9-PB is 9-flash B pattern.
In Figure 12 shows the grand averages of P300 amplitude for 14-flash pattern A&B and 19-flash pattern on site Pz and Cz. P300 amplitude for 14-flash B is larger than that for 14-flash A. This result underscores the fact that 14-flash pattern B is superior to 14-flash A. The P300 amplitude for 19-flash is larger than that for 14-flash B on site Cz and the P300 amplitude for 14-flash B is larger than that for 19-flash on site Pz. If the P300 amplitude was large and could be detected by the classifier, the classification accuracy would be high (see Table 1 and Figure 9). Table 1 and Figure 9 show that 14-flash B exhibits superior classification accuracy and bit rate.
Figure 12.
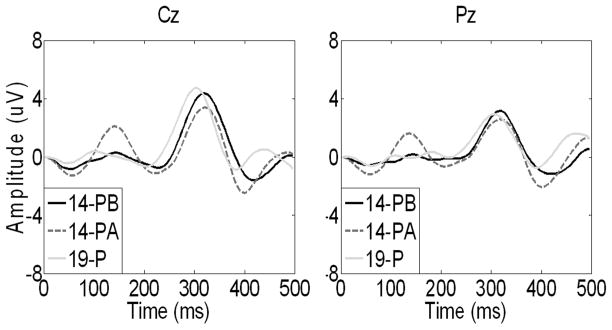
The grand averages of P300 amplitude for 14-falsh pattern A&B and 19-flash pattern over sites Pz and Cz from subject 1–10. 14-PA is 14-flash A, 14-PB is 9-flash B, 19-P is 19-flash pattern.
In these results, the bit rate was calculated without including the time between trials and characters. Table 2 shows the result of spelling another five characters (except the predefined 15 characters) selected by subjects, which were obtained by selecting the best pattern for each subject. The time between character selections was 1.5 s. In Table 2, practical bit rate is calculated including the time between characters and raw bit rate did not include the time between characters. Thus, practical bit rate shows the real online output speed of the system.
Table 2.
The classification accuracy and bit rate including selection time
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | Av | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Acc | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 80 | 100 | 98±6.3 |
| BR | 41.2 | 55.9 | 38.4 | 57.7 | 41.2 | 46.9 | 37.2 | 44.4 | 35.0 | 44.4 | 44.2±7.5 |
| PBR | 35.5 | 45.9 | 33.4 | 47.1 | 35.5 | 39.6 | 32.5 | 37.8 | 17.5 | 37.8 | 36.3±8.2 |
In this table, “Acc” refers to classification accuracy. PBR is practical bit rate and BR is raw bit rate, all measured in bits/min.
4. Discussion
This study addressed four potential approaches to improve P300 BCI performance. The first question was whether our real-time adaptive system, which automatically adjusts the number of trials per average for each character, could produce superior performance compared to a system that uses a fixed number of trials for each character selection. The answer is yes. Figure 8 and Table 1 shows that the adaptive system is better than the non-adaptive system in terms of classification accuracy, bit rate or both classification accuracy and bit rate. Table I also shows that the adaptive approach is better. Presumably, the P300s elicited during target vs. non-target flashes varied between characters; hence, a system that used the same number of trials per average would sometimes use too few trials per average (which impairs accuracy) or too many trials per average (which wastes time with unnecessary flashes). One might argue that the method used here does not provide definitive evidence that an adaptive system is superior because the fixed trial analysis was conducted offline. However, we argue that the method used to estimate the fixed trial accuracy is robust and provides results that may have more internal validity than an online comparison of the two methods because both analyses are being conducted on the same data set. As noted earlier, we could have used a fixed number of trials and estimated the potential adaptive performance offline. However, this option is less attractive; the ultimate goal is to maximize online performance.
A second question is whether we could improve performance with flash patterns that require fewer flashes to identify the target than the canonical RC approach. This paper presented four new flash patterns based on the binomial coefficient. All four flash patterns required fewer flashes to identify the target than the conventional row/column approach, which was represented by a fifth flash pattern used as a control, called 19-flash. Though the lack of statistical significance makes strong conclusions challenging, some results show trends that indicate improved performance with the novel flash patterns.
Also, the potential benefits of the new flash patterns may have been obscured by their shorter TTI, which can impair P300 amplitude. Jin et al. (2010b) reported that a paradigm based on binomial coefficients could be significantly better than a paradigm based on the RC pattern. In that work, the paradigm based on binomial coefficients and RC were similar in both interference and TTI (inter-stimulus interval=175ms and target flash probability=22.2% for paradigms based on binomial coefficients; inter-stimulus interval=175ms and target flash probability=16.7% for RC). The 9-flash approach, however, did not perform as well as the other approaches. 9-flash used the shortest TTI and the highest target probability, both of which can serve to reduce P300 amplitude and have a higher likelihood that subjects may miss a target flash. Hence, future work should further assess different flash patterns across different TTIs (Sellers et al., 2006; Allison and Pineda, 2006). Moreover, it is possible that a within subjects design may suffer from order effects, particularly if testing is conducted over a longer session where fatigue and distraction can alter attentional awareness. Or, if the sessions are performed on different days, within-subject individual differences may significantly alter performance. (Given that we were already testing two sessions (one session contain two groups and the other contain one group) on two different days, one of three groups (9-flash A&B, 14-flash A&B, and 19-flash pattern) was not tested on the same day, we may have already intruded some noise into the current data.) A between-subjects design is also not optimal because intra-subject variability is problematic, and we would need to collect data from many people to have enough power to draw meaningful conclusions.
Our third question was whether P300 BCIs might perform better if the target stimulus does not flash twice in succession as often. The answer is yes. 14-flash B, which was optimized to avoid double flashes, showed a significantly higher bit rate than 14-flash A, which was identical except that double flashes were possible. 14-flash B also showed a higher accuracy, but this effect was not significant, perhaps partly because accuracy was close to ceiling in both conditions. Furthermore, minimizing double flashes should make the system easier to use; the second of two consecutive flashes may be harder to detect because of the repetition blindness and it will distort the waveform (Woldorff et al., 1993; Martens et al., 2009). In this paper, high classification accuracy (i.e., 14-flash A condition) could be obtained by presenting more trials before averaging, and bit rate of 14-flash A was lower than that of the optimized 14-flash B pattern. However, it is necessary to use more flashes per trial to increase the minimum number of flashes between each flash of the same character may result in higher accuracy at the cost of lower bit rate (Townsend et al., 2010). Therefore, the minimum number of flashes needed between the same character should be studied in the future. In this paper, the minimum number of flashes between two flashes of the same character is one. The results show that the bit rate of 14-flash B was improved significantly compared to that of 14-flash A (which allows the same character to flash twice in succession).
Our results showed that 9-flash B resulted in significantly better classification accuracy than 9-flash pattern A. This result shows that SAINSTs do contribute to errors in P300 BCIs, and should be minimized. Given that combinations of C(9,3) and C(14,3) were used to identify the position of the item in the stimulus matrix, each item in the matrix flashed three times per trial. If all the three elements in one combination were different from the three elements of the neighbor combinations, its neighbor item would flash three times when it was not flashing. Thus, these flashes provide three opportunities to attract attention to the neighboring non-target character. The number of SAINSTs was dramatically reduced in 9-flash B as compared to 9-flash A. One important question for future research is: why was performance better in flash pattern 9B than 9A? That is, why did reducing SAINSTs improve accuracy and bit rate? We believe that the main reason is that SAINSTs could evoke P300s (and hence false positives) during non-target trials, and/or make the subjective flashing probability higher than the actual flash probability of the target for the participants, and/or “attentional blink”. A high subjective flashing probability would reduce P300 amplitude. However, another (noncompeting) explanation is that SAINSTs essentially create a divided attention task, since SAINSTS distract subjects from the task of attending to the target, which reduces the P300 elicited by the target. Isreal et al. (1980) showed that P300s are diminished if subjects must divide attention between visual stimuli in different regions (Isreal et al., 1980). However, we do not think this explanation is the main cause of our results, since SAINSTs are very close to targets, and subjects were never told to pay attention to SAINSTs. Hence, SAINSTs only divide attention involuntarily, in as much as subjects are unable to ignore them. A third and related possibility is that SAINSTs prevent subjects from “zoning in” on the target – that is, entering a state of highly focused attention that may lead to larger P300 amplitude (Lakey et al., 2010).
Although parametric analyses of subjective reports are not possible, some subjects did anecdotally report that flashes seemed to be too fast. Subjects seemed more likely to report this concern in the 9-flash conditions, and less likely to report this concern in the 14 flash B and 19 flash condition. Hence, the objectively verifiable benefits of our novel flash pattern approach may be offset somewhat by subjective factors – a BCI that works faster but annoys or fatigues subjects may be worse than a slower but more user friendly system. Future work should assess different flash patterns at different TTIs, evaluate possible benefits of training or alternate displays, and consider differences between subjects (younger subjects, and/or some types of gamers, may have less trouble with faster flashes).
Many articles present bit rates based only on the time needed to spell each character, ignoring the breaks between characters. However, these breaks between characters are necessary so subjects can select a new target, at least in untrained subjects and without a novel paradigm that somehow avoids these breaks. Therefore, omitting this selection time creates unrealistically high performance (Sellers and Donchin, 2006; Lenhardt et al., 2008; Townsend et al., 2010). In our current paper, all subjects spelled five characters that they chose. Table 2 presents practical bit rates that include the time between each character selection (1.5s).
5. Conclusion
This paper presented new flash pattern approaches that can lead to better classification accuracies and bit rates than the conventional row/column approach. Furthermore, an adaptive classifier performed better than the non-adaptive approach. Future work could address many topics, including SAINSTs with different displays, different TTIs, effects of training, differences across different populations, peripheral stimuli, and the underlying reasons why SAINSTs impair performance. Future work should also extend this speller to more real world tasks such as controlling a laptop, writing a letter, or chatting online. This approach should also be validated with persons with special needs, such as persons with severe motor disabilities or language disorders such as dyslexia and aphasia.
Acknowledgments
This work was supported in part by the Grant National Natural Science Foundation of China, under Grant No.61074113 and supported part by Shanghai Leading Academic Discipline Project, Project Number: B504, NIBIB & NINDS, NIH (EB00856 (EWS)), NIDCD, NIH (1 R21 DC010470-01 (EWS)), and NIDCD, NIH (1 R15 DC011002-01 (EWS)). This work was also supported by the Information and Communication Technologies Collaborative Project action “BrainAble” within the Seventh Framework of the European Commission, Project number ICT-2010-247447.
References
- Allison BZ, Pineda JA. ERPs evoked by different matrix sizes: Implications for a brain computer interface (BCI) system. IEEE Trans Neural Syst Rehabil Eng. 2003;11(2):110–3. doi: 10.1109/TNSRE.2003.814448. [DOI] [PubMed] [Google Scholar]
- Allison BZ, Pineda JA. Effects of SOA and flash pattern manipulations on ERPs, performance, and preference: Implications for a BCI system. Int J Psychophysiol. 2006;59(2):127–40. doi: 10.1016/j.ijpsycho.2005.02.007. [DOI] [PubMed] [Google Scholar]
- Allison BZ, Volosyak I, Luth T, Vabuena D, Sugiarto I, Spiegel MA, Teymourian A, Condro IS, Brindusescu A, Stenzel K, Cecotti H, Graser A. BCI demographics: How many (and what kinds of) people can use an SSVEP BCI?. Proc 4th Int Brain-Computer Interface Workshop and Training Course; Graz. 2008; pp. 333–8. [Google Scholar]
- Allison BZ, McFarland DJ, Schalk G, Zheng SD, Jackson MM, Wolpaw JR. Towards an independent brain–computer interface using steady state visual evoked potentials. Clin Neurophysiol. 2008;119(2):399–408. doi: 10.1016/j.clinph.2007.09.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison BZ, Neuper C. Could anyone use a BCI? (B+H)CI: The Human in Brain-Computer Interfaces and the Brain in Human-Computer Interaction. Springer; 2010. pp. 35–54. [Google Scholar]
- Birbaumer N, Ghanayim N, Hinterberger T, Iversen I, Kotchoubey B, Kuber A, Perelmouter J, Taub E, Flor H. A spelling device for the paralysed. Nature. 1999;388:297–8. doi: 10.1038/18581. [DOI] [PubMed] [Google Scholar]
- Birbaumer N, Cohen LG. Brain- computer interfaces: communication and restoration of movement in paralysis. J Physiol. 2007;579:621–36. doi: 10.1113/jphysiol.2006.125633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blankertz B, Losch F, Krauledat M, Dornhege G, Curio G, Müller KR. The Berlin brain–computer interface: Accurate performance from first-Session in BCI- naïve subjects. IEEE Trans Biomed Eng. 2008;55(10):2452–62. doi: 10.1109/TBME.2008.923152. [DOI] [PubMed] [Google Scholar]
- Citi L, Poli R, Cinel C. Exploiting P300 amplitude variations can improve classification Accuracy in Donchin’s BCI speller. 4th int conf IEEE/EMBS; Antalya. April 2009; pp. 478–81. [Google Scholar]
- Duncan-Johnson CC, Donchin E. The time constant in P300 recording. Psychophysiology. 1979;16(1):53–5. doi: 10.1111/j.1469-8986.1979.tb01440.x. [DOI] [PubMed] [Google Scholar]
- Farwell LA, Donchin E. Talking off the top of your head: toward a mental prosthesis utilizing event-related brain potentials. Electroencephalogr Clin Neurophysiol. 1988;70(6):510–523. doi: 10.1016/0013-4694(88)90149-6. [DOI] [PubMed] [Google Scholar]
- Fazel-Rezai R. Human error in P300 speller paradigm for brain-computer interface. 29th Annual Int Conf of the IEEE EMBS; 2007; pp. 2516–2519. [DOI] [PubMed] [Google Scholar]
- Friman O, Luth T, Volosyak I, Graser A. Spelling with Steady-State Visual Evoked Potentials. 3rd Int IEEE/EMBS Int Conf Neural Engineering; Kohala Coast. 2007; pp. 354–357. [Google Scholar]
- Furdea A, Halder S, Krusienski DJ, Bross D, Nijboer F, Birbaumer N, Kubler A. An auditory oddball (P300) spelling system for brain-computer interfaces. Psychophysiology. 2009;46(3):617–625. doi: 10.1111/j.1469-8986.2008.00783.x. [DOI] [PubMed] [Google Scholar]
- Gonsalvez CL, Polich J. P300 amplitude is determined by target-to-target interval. Psychophysiology. 2002;39(3):388–396. doi: 10.1017/s0048577201393137. [DOI] [PubMed] [Google Scholar]
- Gao X, Xu D, Cheng M, Gao S. A BCI-based environmental controller for the motion-disabled. IEEE Trans Neural Syst Rehabil Eng. 2003;11(2):137–40. doi: 10.1109/TNSRE.2003.814449. [DOI] [PubMed] [Google Scholar]
- Guger C, Daban S, Sellers EW, Holzner C, Krausz G, Carabalona R, Gramatica F, Edlinger G. How many people are able to control a P300-based brain-computer interface (BCI) Neurosci Lett. 2009;462(1):94–8. doi: 10.1016/j.neulet.2009.06.045. [DOI] [PubMed] [Google Scholar]
- Hoffmann U, Garcia G, Vesin JM, Diserens K, Ebrahimi T. A boosting approach to P300 detection with application to brain-computer interfaces. 2nd Int IEEE/EMBS Int. Conf. Neural Engineering; Arlington. 2005; pp. 97–100. [Google Scholar]
- Hoffmann U, Vesin JM, Ebrahimi T, Diserens K. An efficient P300-based brain–computer interface for disabled subjects. J Neurosci Meth. 2008;167(1):115–25. doi: 10.1016/j.jneumeth.2007.03.005. [DOI] [PubMed] [Google Scholar]
- Hill J, Farquhar J, Martens S, Bießmann F, Schölkopf B. Effects of stimulus Type and of Error-correcting code Design on BCI speller Performance. NIPS. 2008 on line http://books.nips.cc/papers/files/nips21/NIPS2008_0359.pdf.
- Isreal JB, Chesney G, Wickens CD, Donchin E. P300 and tracking difficulty: evidence for multiple resources in dual-task performance. Psychophysiology. 1980;17(3):259–273. doi: 10.1111/j.1469-8986.1980.tb00146.x. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Westerfield M, Townsend J, Courchesne E, Sejnowski TJ. Analysis and visualization of single-trial event-related potentials. Hum Brain Mapp. 2001;14(3):166–185. doi: 10.1002/hbm.1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen BH, Allam A, Kota P, Lachance K, Osho A, Sundarean K. An exploratory study of factors affecting single trial P300 detection. IEEE Trans Biomed Eng. 2004;51(6):975–978. doi: 10.1109/TBME.2004.826684. [DOI] [PubMed] [Google Scholar]
- Jin J, Allison BZ, Brunner C, Wang B, Wang XY, Zhang JH, Neuper C, Pfurtscheller G. P300 Chinese imput system based on bayesian LDA. Biomed Tech. 2010a;55(1):5–18. doi: 10.1515/BMT.2010.003. [DOI] [PubMed] [Google Scholar]
- Jin J, Horki P, Brunner C, Wang XY, Neuper C, Pfurtscheller G. A new P300 stimulus presentation pattern for EEG-based spelling systems. Biomed Tech. 2010b;55(4):203–210. doi: 10.1515/BMT.2010.029. [DOI] [PubMed] [Google Scholar]
- Jin J, Allison BZ, Sellers EW, Brunner C, Horki P, Wang XY, Neuper C. Optimized stimulus presentation patterns for an event-related potential EEG-based brain computer interface. Med & Bioll Eng & Comput. 2010c doi: 10.1007/s11517-010-0689-8. in press. [DOI] [PubMed] [Google Scholar]
- Kanwisher NG. Repetition blindness: type recognition without token individuation. Cognition. 1987;27(2):117–43. doi: 10.1016/0010-0277(87)90016-3. [DOI] [PubMed] [Google Scholar]
- Koivisto M, Revonsuo A. Comparison of event-related potentials in attentional blink and repetition blindness. Brain Research. 2008;1189:115–26. doi: 10.1016/j.brainres.2007.10.082. 2008. [DOI] [PubMed] [Google Scholar]
- Kolev V, Demiralp T, Yordanova J, Ademoglu A, Isoglu-Alkaç U. Time-frequency analysis reveals multiple functional components during oddball P300. Neuro Report. 1997;8(8):2061–2065. doi: 10.1097/00001756-199705260-00050. [DOI] [PubMed] [Google Scholar]
- Kubler A, Nijboer F, Mellinger J, Vaughan TM, Pawelzik H, Schalk G, Mcfarland DJ, Birbaumer N, Wolpaw JR. Patients with ALS can use sensorimotor rhythms to operate a brain-computer interface. Neurology. 2005;64(10):1175–7. doi: 10.1212/01.WNL.0000158616.43002.6D. [DOI] [PubMed] [Google Scholar]
- Kranczioch C, Debener S, Maye A, Engel AK. Temporal dynamics of access to consciousness in the attentional blink. Neurolimage. 2007;37(3):947–955. doi: 10.1016/j.neuroimage.2007.05.044. [DOI] [PubMed] [Google Scholar]
- Krusienski DJ, Sellers EW, McFarland DJ, Vaughan TM, Wolpaw JR. Toward enhanced P300 speller performance. J Neurosci Meth. 2008;167(1):15–21. doi: 10.1016/j.jneumeth.2007.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubler A, Furdea A, Halder S, Hammer EM, Nijboer F, Kotchoubey B. A brain-computer interface controlled auditory event-related potential (P300) spelling system for locked-in patients. Ann N Y Acad Sci. 2009;1157:90–100. doi: 10.1111/j.1749-6632.2008.04122.x. [DOI] [PubMed] [Google Scholar]
- Lalor EC, Kelly SP, Finucane C, Burke R, Smith R, Reilly RB, McDarby G. Steady-state VEP-based brain-computer interface control in an immersive 3D gaming environment. EURASIP Journal on applied signal processing. 2005;2005(19):3156–64. [Google Scholar]
- Lakey CE, Berry DR, Sellers EW. Attentional Manipulations Can Improve P300-based BCIs. J Neural Eng. 2010 doi: 10.1088/1741-2560/8/2/025019. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenhardt A, Kaper M, Ritter HJ. An adaptive P300-based online Brain-Computer Interface. IEEE Trans Neural Syst Rehabil Eng. 2008;16(2):121–130. doi: 10.1109/TNSRE.2007.912816. [DOI] [PubMed] [Google Scholar]
- Lei X, Yang P, Yao DZ. An empirical bayesian framework for brain computer interface. IEEE Trans Neural Syst Rehabil Eng. 2009;17(6):521–9. doi: 10.1109/TNSRE.2009.2027705. [DOI] [PubMed] [Google Scholar]
- Muller-Putz GR, Scherer R, Brauneis C, Pfurtscheller G. Steady-state visual evoked potential (SSVEP)-based communication: impact of harmonic frequency components. J Neural Eng. 2005;2(4):123–30. doi: 10.1088/1741-2560/2/4/008. [DOI] [PubMed] [Google Scholar]
- Muller-Putz GR, Pfurtscheller G. Control of an Electrical Prosthesis With an SSVEP-Based BCI. IEEE Trans Biomed Eng. 2008;55(1):361–364. doi: 10.1109/TBME.2007.897815. [DOI] [PubMed] [Google Scholar]
- Neuper C, Muller-Putz GR, Kubler A, Birbaumer N, Pfurtscheller G. Clinical application of an EEG-based brain-computer interface: a case study in a patient with severe motor impairment. Clin Neurophysiol. 2003;114(3):399–409. doi: 10.1016/s1388-2457(02)00387-5. [DOI] [PubMed] [Google Scholar]
- Martens SMM, Hill NJ, Farquhar J, Scholkopf B. Overlap and refractory effects in a brain-computer interface speller based on the visual P300 event-related potential. J Neural Eng. 2009;6(2):26–29. doi: 10.1088/1741-2560/6/2/026003. [DOI] [PubMed] [Google Scholar]
- Piccione F, Giorgi F, Tonin P, Priftis k, Giove S, Silvoni S, Palmas G, Beverina F. P300-based brain computer interface: Reliability and performance in healthy and paralysed participants. Clin Neurophysiol. 2006;117:531–37. doi: 10.1016/j.clinph.2005.07.024. [DOI] [PubMed] [Google Scholar]
- Pfurtscheller G, Neuper C. Motor imagery and direct brain-computer communication. Proc IEEE. 2001;89(7):1123–1134. [Google Scholar]
- Pfurtscheller G, Muller GR, Pfurtscheller J, Gerner HJ, Rupp R. Thought’—control of functional electrical stimulation to restore hand grasp in a patient with tetraplegia. Neurosci Lett. 2003;351(1):33–36. doi: 10.1016/s0304-3940(03)00947-9. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Luck SJ. Delayed working memory consolidation during the attentional blink. Psycho Bull Rev. 2002;9(4):739–743. doi: 10.3758/bf03196329. [DOI] [PubMed] [Google Scholar]
- Vaughan TM, McFarland DJ, Schalk G, Sarnacki WA, Krusienski DJ, Seller EW, Wolpow JR. The wadsworth BCI research and development program: at home with BCI. IEEE Trans Neural Syst Rehabil Eng. 2006;14(2):229–33. doi: 10.1109/TNSRE.2006.875577. [DOI] [PubMed] [Google Scholar]
- Ravden D, Polich J. Habituation of P300 from visual stimuli. Int J Psychophysiol. 1998;30(3):359–365. doi: 10.1016/s0167-8760(98)00039-7. [DOI] [PubMed] [Google Scholar]
- Raymond JE, Shapiro KL, Arnell KM. Temporary suppression of visual processing in a RVSP task: An attentional blink? Journal of Experimental Psychology: Human Perception and Performance. 1992;18:849–860. doi: 10.1037//0096-1523.18.3.849. [DOI] [PubMed] [Google Scholar]
- Salvaris M, Sepulveda F. Perceptual Errors in the Farwell and Donchin Matrix Speller. 4th international conference IEEE/EMBS; Antalya. April 2009; pp. 275–278. [Google Scholar]
- Schendan HE, Kanwisher NG, Kutas M. Early brain potemtials link repetition blindness, priming and novelty detection. Neuroreport. 1997;8(8):1943–1948. doi: 10.1097/00001756-199705260-00030. [DOI] [PubMed] [Google Scholar]
- Scherer R, Muller-Putz GR, Neuper C, Graimann B, Pfurtscheller G. An asynchronously controlled EEG-based virtual keyboard: improvement of the spelling rate. IEEE Trans Biomed Eng. 2004;51(6):979–84. doi: 10.1109/TBME.2004.827062. [DOI] [PubMed] [Google Scholar]
- Serby H, Yom-Tov E, Inbar GF. An improved P300-based brain-computer interface. IEEE Trans Neural Syst Rehabil Eng. 2005;13(1):89–98. doi: 10.1109/TNSRE.2004.841878. [DOI] [PubMed] [Google Scholar]
- Sellers EW, Donchin E. A P300-based brain-computer interface: initial tests by ALS patients. Clin Neurophysiol. 2006;117(3):538–548. doi: 10.1016/j.clinph.2005.06.027. [DOI] [PubMed] [Google Scholar]
- Sellers EW, Krusienski DJ, McFarland DJ, Vaughan TM, Wolpaw JR. A P300 event-related potential brain–computer interface (BCI):The effects of matrix size and inter stimulus interval on performance. Biol Psychol. 2006;73(3):242–52. doi: 10.1016/j.biopsycho.2006.04.007. [DOI] [PubMed] [Google Scholar]
- Sellers EW, Vaughan TM, Wolpaw JR. A brain-computer interface for long-term independent home use. Amyotrophic Lateral Sclerosis. 2010;11(5):449–455. doi: 10.3109/17482961003777470. [DOI] [PubMed] [Google Scholar]
- Sugiarto I, Allison BZ, Graser A. Optimization Strategy for SSVEP-Based BCI in Spelling Program Application. 2009 ICCET’08 Int Conf Computer Engineering and Technology; 2009; pp. 223–226. [Google Scholar]
- Townsend G, LaPallo BK, Boulay CB, Krusienski DJ, Frye GE, Hauser CK, Schwartz NE, Vaughan TM, Wolpaw JR, Sellers EW. A novel P300-based brain-computer interface stimulus presentation paradigm: moving beyond rows and columns. Clin Neurophysiol. 2010;121(7):1109–20. doi: 10.1016/j.clinph.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woldorff MG. Distortion of ERP averages due to overlap from temporally adjacent ERPs: analysis and correction. Psycholophysiology. 1993;30(1):98–119. doi: 10.1111/j.1469-8986.1993.tb03209.x. [DOI] [PubMed] [Google Scholar]
- Xu N, Gao XR, Hong B, Miao XB, Gao SK, Yang FH. BCI competition 2003 - Data Set IIb: Enhancing P300 wave detection using ICA based subspace projections for BCI applications. IEEE Trans Biomed Eng. 2004;51(6):1067–72. doi: 10.1109/TBME.2004.826699. [DOI] [PubMed] [Google Scholar]