AGENT-BASED MODELS IN EMPIRICAL SOCIAL RESEARCH

Abstract

Agent-based modeling has become increasingly popular in recent years, but there is still no codified set of recommendations or practices for how to use these models within a program of empirical research. This article provides ideas and practical guidelines drawn from sociology, biology, computer science, epidemiology, and statistics. We first discuss the motivations for using agent-based models in both basic science and policy-oriented social research. Next, we provide an overview of methods and strategies for incorporating data on behavior and populations into agent-based models, and review techniques for validating and testing the sensitivity of agent-based models. We close with suggested directions for future research.

1. INTRODUCTION

Agent-based models are computer programs in which artificial agents interact based on a set of rules and within an environment specified by the researcher (Miller and Page 2007). While these rules and constraints describe predictable behavior at the micro-level, the interactions among agents and their environment often aggregate to create unexpected social patterns. It is such emergent patterns that sociologists want to understand or policy-makers want to change (e.g., patterns of residential segregation, the intergenerational reproduction of inequality, or the origin and persistence of disease epidemics). Because agent-based models explicitly link individuals’ characteristics and behavior with their collective consequences, they provide a powerful tool for exploring the social consequences of individual behavior.

While agent-based modeling is not new to sociology (see Macy and Willer 2002 for a comprehensive review of early work), these models tend to be highly stylized and—with the exception of Schelling’s (1971, 1978) seminal work on neighborhood tipping and Axelrod’s model of cooperation (Axelrod and Hamilton 1981; Axelrod and Dion 1988; Axelrod 1997) —have had minimal impact on mainstream sociological research. One reason for this lack of impact is the absence of dialogue between agent-based modeling and data-driven social research within the discipline.¹ This is unfortunate, as agent-based models are very useful for sharpening one’s thinking about an empirical problem and identifying key explanatory mechanisms. Agent-based models help fill the gap between formal but restrictive models and rich but imprecise qualitative description (Holland and Miller 1991, cited in Page 2008). Moreover, agent-based models are especially amenable to incorporating detailed, multi-layered empirical data on human behavior and the social and physical environment, and can represent a granularity of information and faithfulness of detail that is not easily handled within statistical or mathematical models.

The goal of this paper is to provide a practical overview of how agent-based models can be used within a larger program of empirical research. We proceed as follows. First, we discuss reasons to use agent-based models in both basic science and more policy-driven research, and describe the kinds of substantive and methodological problems where agent-based models are particularly helpful. Next, we review the different ways in which agent-based models can be anchored to real-world information: “low-dimensional realism” in which there is empirical realism along one or two dimensions but the model remains simple and abstract; or “high dimensional realism” in which the goal is to accurately represent some phenomenon along many dimensions. We also provide concrete strategies for constructing agent-based models that correspond to real populations and incorporating empirical data on individual behavior into agent-based models. Finally, we discuss state-of-the-art techniques to assess both the goodness-of-fit of these models to data, and also their sensitivity to key assumptions. We close with some suggested directions for future research.

Modeling Interdependent Behavior

A key feature of agent-based modeling is that it explicitly links micro- and macro-levels of analysis. Sociology has a longstanding interest in the relationship between individuals’ motivations and decisions and large-scale patterns of social organization and change.² The “micro-macro problem” concerns how to explicitly account for the ways in which actions of individuals give rise to social organization and dynamics, rather than assuming that macro-level phenomena are simply aggregates of individual characteristics and behavior (Coleman 1994, p.197; Granovetter 1978 p.1421; Hedström and Bearman 2009, pp. 9-14). The connection between individuals’ actions and their collective consequences would be transparent if one could simply sum over individuals’ intentions or behavior to generate expected population-level attributes.³ The problem is that nearly all human behavior is interdependent; individuals’ actions are contingent on the past, present, and predicted future behavior of others.⁴

Contingent behavior can take on a number of different forms. For example, people have preferences for the composition of social groups (e.g., friendship circles, neighborhoods, or churches), but their own characteristics also contribute to group composition. Accordingly, any decision to join or leave the group is both responding to and changing its composition. More generally, individuals’ actions are constrained by the social context (e.g., network structure, social institutions, and demographic composition) that shapes available opportunities for action. But this social context is produced (and reproduced) from the accumulation of people acting in the past. Thus, interdependent behavior implies feedback between micro and macro levels of analysis. In the short run, individuals respond to their environments; in the longer run, the accumulation of individuals’ choices or behavior changes the environment. This feature makes standard statistical models that assume independence of observations or unidirectional causality inappropriate for analyzing the relationship between micro- and macro levels of analysis. Feedback also often implies a non-linear relationship between individual behavior and its macro consequences. Models that seek to explain the social consequences of interdependent behavior must explicitly represent feedback between individuals’ actions and their decision-making environments.⁵

The explicit representation of how micro-level processes generate largerscale social dynamics is a hallmark of mechanism-based explanations (cf. Hedström and Udehn 2009; Elster 2007; Hedström and Ylikoski 2010). In essence, mechanisms explain some social phenomenon in terms of a dynamic and robust process through which individual interactions compose some social aggregate (Hedström and Swedberg 1998). In addition to various forms of feedback (e.g., tipping, contagion, diffusion, self-fulfilling prophecy, tragedy of the commons), other mechanisms in sociological research include selection (Hedström and Bearman 2009), offsetting (Bruch 2013), vacancy chains (e.g., White 1970), and network externalities (Dimaggio and Garip 2011). A good explanation of a social phenomenon specifies the conditions necessary for the social phenomenon to arise and how those conditions depend on both individuals’ behavior and the distribution of salient social attributes within the population. Agent-based models allow researchers to explicitly investigate how and why a given set of interactions among individuals generates some collective result. One can also explore how alternative assumptions regarding population constraints (e.g., the sex ratio of students within a classroom, or number or proportion of minority groups in a city) affect observed dynamics. In addition, because the models are usually built from the ground up, they bring into sharp relief our “implicit models,” that is, latent assumptions regarding individual traits and behavior, the nature of interaction among individuals, and the environment in which the interaction takes place.

Finally, when used iteratively within an empirical research program, an agent-based model can be a powerful tool to help guide specification of statistical models and data collection efforts. In many empirical research problems, we face one of two related dilemmas. On the one hand, we may have large amounts of data, but we do not know which statistical models to run. We make model specification decisions not knowing which decisions are truly consequential. On the other hand, often our ideas about human behavior are much richer than available data. In both instances, agent-based models can help. In the first instance, we can experiment with simulated data to see what difference our assumptions about individual behavior make for aggregate outcomes. In the second instance, individual-level data, combined with alternative behavioral assumptions and aggregate data, may be used to simulate aggregate outcomes that can be compared to observed data.⁶

Feedback Effects & Public Policy

Beyond pure academic interest, there is a practical need for models that allow for contingent behavior of individuals and feedback between micro- and macro-levels of analysis. Within a number of fields, most notably epidemiology and public health, there is an increasing acknowledgement that our current methods of designing, evaluating, and implementing policy do not work and may potentially even make things worse (e.g., Fenichel et al. 2011; Sterman 2006; Homer and Hirsch 2006; Mabry et al. 2008; Deaton 2010). A major roadblock in the development of more effective policy is that most social problems exhibit a dynamic complexity that hinders our ability to identify underlying causal relationships. Dynamic complexity does not imply many moving parts so much as the interconnectedness among parts (Forrester 1971). This is apparent in both self-reinforcing cycles for individuals (e.g., perceived job insecurity is associated with poorer health, and poor health affects labor market performance [Burgard, Brand, and House 2009]) and in neighborhood “spillover effects” where disadvantage along one dimension of neighborhoods (e.g., high vacancy rates and low property values) exacerbates inequalities along other neighborhood dimensions (e.g., school funding and school quality) thus contributing to the cycle of poverty (Durlauf 1993, 1995). Poverty traps and other self-reinforcing cycles of disadvantage can make it difficult to identify the most effective points of intervention.

Moreover, people may change their behavior in response to an intervention, and failure to anticipate this can lead to undesirable and unexpected outcomes.⁷ Within public health, there is evidence that low-fat foods may have contributed to the obesity epidemic as people ate larger quantities than they would have otherwise (La Berge 2008). Within criminology and sociology, there is some controversial evidence that Section 8 housing programs led to an increase in neighborhood violence in some cities, as the program moved people from high-poverty neighborhoods into moderately poor areas. It is in these areas where the number of social problems (e.g., neighborhood violence) increases nonlinearly with the poverty rate (Galster 2005; Rosin 2008). By keeping the total number of high-poverty neighborhoods fixed, but increasing the poverty rate in medium-poverty areas, the vouchers may have inadvertently led to a net increase in violent crime across all poor neighborhoods.

Agent-based models and other methods such as system dynamics may be able to identify potentially self-reinforcing behaviors or feedback loops, and suggest better designs for policies based on identification of major flaws in existing ones. More modestly, these models can allow for a relaxation of unrealistic assumptions made in more traditional models. For example, classical epidemiology models assume random mixing and relatively homogenous populations. Agent-based models allow for heterogeneous agents with more realistic behavioral responses and varying risk profiles. A key advantage is that agent-based models can integrate data and theories from many different sources and at many levels of analysis. Finally, agent-based models can demonstrate tradeoffs, efficiencies, or links between policies and theoretical concepts.

The most successful policy-driven agent-based modeling projects to date have come from epidemiology and urban planning. Within epidemiology, the Models of Infectious Disease Agent Study (MIDAS) draws together multiple interdisciplinary teams of researchers at different sites to investigate how to use computational and mathematical models of disease transmission to understand infectious diseases.⁸ The network of researchers developed a number of agent-based models that incorporate detailed geographic, demographic, social, biological, and epidemiological information to model the spread of disease. These models have been particularly influential in exploring potential response scenarios for disease outbreaks during the H5N1 and H1N1 flu scares. For example, the Global Scale Agent Model developed at Brookings played a key role in analyzing both the H1N1 and avian flu outbreaks, modeling both the predicted spread of the disease, and also the potential costs and benefits of specific interventions (e.g., school closures or the allocation of scarce vaccines) See Epstein (2009) for more details.⁹

In the area of urban planning, the UrbanSim model developed by Paul Waddell and his collaborators (Waddell 2002) represents the state of the art in agent-based models of urban policy, transportation, and development. UrbanSim was designed to be an experimental laboratory for the analysis of policies related to city infrastructure and investment (Borning, Waddell, and Forster 2008). The model blends empirically grounded modules describing processes at the person level (e.g., individuals’ decisions regarding place of work and residence, job choice, and transportation), organization level (e.g., business birth and death, relocation, and development), infrastructure level, and housing market (e.g., real estate prices) with a highly realistic geographic landscape. It has been influential in guiding decisions regarding urban transportation investments such as light rail, freeway extension, and changes in land use zoning (Borning and Waddell 2006).

2. HIGH VERSUS LOW DIMENSIONAL REALISM IN AGENT-BASED MODELS

A key issue for the analyst is the appropriate level of model complexity and empirical realism. These are by no means the same; a model may be relatively simple, but its few dimensions can be firmly grounded in empirical data, or complex phenomena may be modeled with only anecdotal evidence. The appropriate levels depend on the research question and intended use of the model. Agent-based models range from abstract worlds where agents are defined by a single attribute, have simple deterministic rules for interaction, and exist in a highly stylized environment (e.g., a grid or torus) to simple worlds where agents have only one or two attributes and behaviors anchored to as many empirical features as possible to high dimensional worlds where agents have many attributes, the environment contains a great deal of information and may even have its own dynamics, and agents engage in a variety of different behaviors.

The degree of empirical realism desired in the model depends on its analytical and empirical goals. Models should be designed with a specific question in mind. At one extreme, empirically validated agent-based models may be used as a virtual “laboratory” to test the implications of a policy intervention or predict future population dynamics. For example, the MIDAS study enlisted a team of subject matter experts to develop an empirically rich model of disease spread, and this model is used to anticipate the spread of epidemics and explore alternative disaster response scenarios (Epstein 2009). Similarly, the Artificial Anasazi project marshaled substantial archeological, anthropological, and ecological data to explore the rise and fall of the Anasazi culture in the Long House Valley in northeastern Arizona between 1800 B.C. and 1300 A.D (Dean et al. 2000). Both models were subject to intensive validation and testing.

At the other extreme, simple, abstract models allow for the clarification or development of new theories or mechanisms. Schelling’s (1978) famous tipping model, which allowed for two groups to sort themselves across a grid in accordance with their preferences about the composition of their neighborhoods, demonstrated how even seemingly tolerant agents can generate highly segregated neighborhoods. Axelrod’s prisoners’ dilemma tournament model pitted different strategies against one another to show how cooperation can emerge and even thrive in a world of self-interested agents (Axelrod and Hamilton 1981). More recently, the research program spearheaded by Michael Macy (e.g., Willer, Kuwabara, and Macy 2009; Centola, Willer, and Macy 2005; Centola and Macy 2007) uses simple agent-based models to illuminate theoretical properties of game theoretic and network models. In these examples, the goal is not to reproduce existing patterns or even to anchor agents’ behavior, characteristics, or environment in empirical knowledge. Rather, the models are generative; they develop new ways of thinking about a problem and provide a great deal of theoretical stimulation for existing empirical research.

Between these two extremes are models that incorporate one or more dimensions of realism but keep other aspects of the model abstract. Often these “low dimensional realism” models are aimed at exploring the implications of empirical research or testing the assumptions of formal theories. For example, Epstein et al. (2008) uses a relatively simple model to demonstrate that when one takes the traditional epidemic model, which assumes perfect mixing and fixed behavior, and adds adaptive behavior, whereby agents may hide from disease or flee to a safer area, this changes the dynamics in ways that more closely approximate the dynamics observed in the Spanish flu and other historical epidemics. Todd and Billari (2003) explore how empirically plausible mate-search heuristics give rise to population-wide patterns of age-at-marriage distributions. Hedström and Åberg (2005) take a somewhat empirically richer approach, in which they assign agents the social and demographic characteristics of Swedish youth in the Stockholm metropolitan area, and explore how empirically grounded rates of leaving unemployment vary under alternative assumptions about social interactions. The goal of in all cases, however, is not to reproduce empirical patterns or incorporate all aspects of reality so much as understand the implications for social dynamics of one or more empirical observations or stylized facts.

Coming from a conventional social research background, the most seductive approach often is to create agent-based models that incorporate as much empirical data and knowledge as possible in an attempt to create a highly realistic laboratory in which to conduct experiments. However, this approach is rarely the most fruitful line of inquiry. For one thing, our data and knowledge of human behavior are almost never up to the task. While social scientists are good at collecting demographic, biological, and social characteristics of discrete units such as individuals, families, or other social groupings, we are often missing data on key mechanisms governing interaction among those units. As mentioned above, one advantage of agent-based modeling is that it allows researchers to hypothesize about the importance of mechanisms for which there are no data (and assess the potential value of collecting these data). Second, layering on many dimensions of realism can make the model cumbersome, and it can be difficult to get clear analytic results. A model’s success is determined not by how realistic it is but by how useful it is for helping understand the problem at hand.¹⁰

One useful heuristic for determine the appropriate level of model complexity and realism is to consider what motivated the agent-based model in the first place. Simulations are useful in three different circumstances. First, when some micro-level behavior is known or strongly assumed, and simulation explores its aggregate consequences. In this case, a simple abstract model or a “low-dimensional” realism model is often most effective. Second, when some aggregate phenomenon is observed empirically, and the simulation investigates alternative mechanistic explanations. In this case, a low dimensional model may be illuminating but cannot rule out all alternative explanations. Finally, simulations are useful when the analyst must explore the behavior of a social system under some hypothesized conditions for predictive purposes. In this case, a “high dimensional” realism model is usually necessary to ensure that the model predictions are not based on some reduced form account of the social process. In the balance of this article, we focus on empirically grounded models aimed at addressing questions of the second or third type.

3. EMPIRICALLY GROUNDED AGENT-BASED MODELS

Agent-based models can incorporate a wide range of empirical measures, including but not limited to rates such as age-specific mortality, fertility, and disease risk; population size and demographic composition; geographic boundaries and spatial relationships; inputs into dynamical processes (e.g., estimated payoffs to educational investments); granularity of time (e.g., how often agents make decisions, and to what extent to agents act simultaneously or asynchronously); individuals’ preferences, behavior, memory, and/or ability to perceive and detect environmental change; the organization of labor, marriage, or housing markets; and social network structure. Of course, some features of the model are easier to anchor in data than others. The primary constraint is the availability of high quality data at the appropriate unit of analysis. To illustrate how one might incorporate empirical data into an agent-based model, we focus on two features of agent-based models that have been most frequently grounded in past work: individual behavior and population characteristics.

Incorporating Population Characteristics

The actors that populate agent-based models are typically assigned some set of attributes such as a sex, age, education, income, life expectancy, disease risk, or network position. The analyst may assume an arbitrary distribution of agent attributes, or he or she can import the joint distribution of agents’ attributes from an empirical data source.¹¹ Survey data typically document the characteristics and attitudes of individuals, households, or families and thus it is relatively straightforward to assign agents characteristics from these data. However, survey data are a relatively small sample; more often scholars prefer to use population (Census) data to initialize agents. For U.S. populations one can initialize the agents using data from the United States Integrated Public Use Microdata Series (IPUMS), which is a five percent sample of all U.S. households. For United Kingdom populations, one can use the UK Sample of Anonymized Records (SAR) Census data. However, while these sources provide Census data at the individual, household, or family level, they do not contain detailed geographic identifiers. The smallest geographic identifier available for United States Census data is IPUMS’ Public Use Microdata Area (PUMA), which contains approximately 100,000 people each.

A key challenge in initializing agent-based models using Census data is adapting the aggregated or discrete nature of these data to a more finely grained context. Individual-level Census data are publicly available at smaller units of geography (i.e., blocks, block groups, tracts) only in the form of aggregated, multi-way tables. Thus, if the researcher wants to initialize her agent population with more than a single attribute (e.g., race/ethnicity or household income), these tables typically do not contain the full joint distribution of household or population traits.¹² Also, continuous attributes are often collapsed into discrete categories. The smaller the geographic unit identified, the less information is available and the more collapsed the variable categories are. For example, one might know the marginal distribution of categorical household size and the marginal distribution of categorical household income within identified Census tracts, but not the joint distribution of household size and household income.

Fortunately, there are well-developed methods for converting a set of incomplete marginal tables into a full table when the joint distribution of variables is known from a separate source. The most common method for generating individual-level data from incomplete tables on populations is table standardization using iterative proportional fitting (e.g., Agresti 2002: 345-6; Deming and Stephan 1940; Fienberg 1970; Ireland and Kullback 1968; Beckman, Baggerly, and McKay 1996). This approach was used in the NIH funded Models of Infectious Disease Agent Study (MIDAS) to generate an agent-based model with a population that included every household and individual in the U.S. population in 2000, as well as schools and workplaces generated to match counts at the Census block level area of geography (Wheaton et al. 2009; Wheaton 2009).¹³ The MIDAS micro- population data are available by request from RTI International. However, the data were constructed using specific criteria to assign households to block groups, and thus the fit is optimal for only a narrow subset of Census variables (Wheaton et al. 2009:7).

Finally, agents can be assigned social networks that correspond to some data source; for example the sexual or friendship networks collected in the National Longitudinal Study of Adolescent Health (Add Health). This network information may be read into the agent-based model the same way that population characteristics are initialized. While networks may correspond to some empirical social structure at the beginning of the model, they can also evolve over time based on subsequent agent interactions. Realistic data on social networks have been used in policy-driven agent-based models of disease transmission and epidemics (e.g., Ferguson et al.2005; Eubank et al. 2004; Cauchemez et al. 2011; Germann et al. 2006), and this represents a potentially fruitful direction for future work.

Specifying Agent Behavior

Another rich area of investigation within agent-based modeling research is to explore the population dynamics implied by a given set of empirical preferences or behaviors (e.g., Schelling 1978; Bruch and Mare 2006, 2009; Benenson and Torrens 2004). Thus a key challenge is specifying appropriate activities for the individual actor. If the goal of the modeling exercise is to explore the macro-level consequences of some theorized preference or behavior, the analyst may prefer to assume a set of behaviors that correspond to the underlying theory. However, if the goal is to understand the aggregate consequences of real world phenomena, it is critical to specify agents’ actions in a way that is empirically defensible (Hedström andÅberg 2005: 118-199). Agents typically gather information about their environment, assess that information according to some set of criteria or ranking system, and then make decisions based on their assessment. They may also learn from past experiences and update their behavior. Empirical information can potentially enter into each stage of this process.

One useful strategy is to assume that agents’ preferences, strategies, or likelihood of making a particular choice or state transition are based on a statistical model. If the agent-based model is aimed at modeling discrete changes in agents’ attributes—for example entering or exiting a state of unemployment, getting married or divorced, or having a child—these state transitions can be defined based on coefficients from a discrete-time event history model (Allison 1982; see also Hedström and Åberg 2005). If the agent-based model is aimed at capturing agents’ decision-making process, discrete choice models provide one flexible framework for estimating the parameters of choice behavior (McFadden 1973; Louviere, Hensher, and Swait 2000; Train 2009).These models have become increasingly sophisticated in recent years, and can allow for variation in individuals knowledge of available options, strategies for learning about or evaluating available options; reactions to change in environmental conditions; reactions to past experiences; and susceptibility to social influence. Estimation of relevant coefficients requires information on either on revealed preferences (observed choices) or stated preferences (survey responses to hypothetical choice scenarios) for some population of interest. These data may be obtained from surveys, observational data, or administrative records. Multiple sources of data on behavior or preferences may be combined in specifying agents’ behavior.

Given some defined set of alternatives, discrete choice models specify a ranked ordering of these choice outcomes, which can be converted into predicted probabilities. However, in order for agents to make a realized choice, these probabilities must be transformed into actual decisions. One method of doing this is to sample from a multinomial distribution with probabilities given by those computed by the agent. Sampling from predicted probabilities incorporates a random component into the choice process, consistent with the specification of discrete choice models. The random component maybe interpreted as the fact that agents may make mistakes or that the choice model does not reflect all dimensions of a choice that affect its desirability. Alternatively, one can assume that the probabilities computed from the choice model accurately reflect the underlying desirability of alternatives, and agents make decisions without error. In this case, one might specify that agents always “take the best” outcome, that is, they choose the outcome with the highest calculated utility.

A different strategy for modeling decision-making is to specify that agents’ behavior follow some set of rules, for example heuristics that update behavioral rules according to the accumulation of experience (Todd, Billari, and Simao 2005). Heuristics are “rules of thumb” for making decisions under conditions of uncertainty (Kahneman, Tversky, and Slovic 1982). Heuristics are used both in the information-gathering stage of decision-making, and also when making the final choice. Typically heuristic decision-making strategies must be used in conjunction with a set of assumed or revealed preferences for agents to rank order-outcomes by desirability. For example, in marriage market models one concern is how to best choose a marriage partner when potential mates can only be explored one at a time, and there is uncertainty about whether the next person down the pipeline will be better than what is currently available. One strategy is to use a “satisficing” heuristic; give agents only a preference for members of the opposite sex, and then let the initial period of interaction be one of learning about the market (e.g., treat the first dozen or so encounters or “dates” agents have with the opposite sex as a learning experience). Agents pick the next agent who comes along whose quality is equal to the best agent observed during the learning period (Todd 1997; Todd and Miller 1999).

Finally, agents may also be assigned beliefs, values, or world-views that correspond to observations from ethnographic or participant observation, or in accordance with stakeholders’ assessments. For example, agents in a model of the intergenerational reproduction of inequality may vary in their beliefs about the degree to which education can lead to social mobility, or their understanding of how to go about getting a job. In practice, these beliefs or worldviews would be programmed as a set of rules governing action. For example, an agent who believes that networks are most important for job seekers may spend its time attempting to develop ties with other agents whereas an agent that believes credentials are key to success may focus on education. Unlike in the statistical model of behavior based on quantitative data, the qualitative data is incorporated into the agent-based model loosely as a set of rules governing behavior, or alternatively as a set of rules for interpreting information. However, agent beliefs, world-views, or values may be coupled with a statistical or heuristic model of decision-making. For example, if qualitative data were available on how the time horizon an individual uses to make a decision varies with their degree of uncertainty about outcomes and perception that things are improving or deteriorating, the appropriate time horizon could be used to adjust the inputs to a statistical model of behavior. See Yang and Gilbert (2008) for more on qualitative data and agent-based models and Geller and Moss (2008) for an example of agent behavior that is empirically grounded using a stakeholder approach.

4. ASSESSING MODEL OUTPUT: UNCERTAINTY, VARIABILITY, & SENSITIVITY

After specifying an agent-based model and providing inputs, one needs to produce and make sense of the model outputs. At the lowest level of granularity, agent-based models can output the distribution of agents and their associated states at every time point. This is often an unwieldy amount of data and its granularity can outstrip the theoretical and empirical knowledge that was used to create the model.¹⁴ It is often more useful to summarize output as population level or sub-group statistics or as a modal experimental trajectory taken by an agent who fits a given profile. For example, the spatial distribution of agents can be summarized into a single measure of segregation (e.g., the index of dissimilarity) or a set of local neighborhood composition measures. Alternatively one could track the trajectory of neighborhoods a typical agent experiences over the duration of the model. In applications of crime dynamics, one might capture overall crime rates within a stylized city, or look at neighborhood specific rates. At the micro level, one might examine the modal criminal career for an agent. Regardless of what types of output one chooses, variability in those measures needs to be considered in light of uncertainty about model inputs. Empirical measures and knowledge of key parameters or processes are often vaguely defined, measured with error, or completely unknown. This uncertainty generates statistical variability in model outputs. In the remainder of the section, we discuss different forms of uncertainty in agent-based models, and how to assess them via uncertainty and sensitivity analyses.

There are two sources of uncertainty and variability in agent-based models: input uncertainty and model uncertainty (McKay, Morrison, and Upton 1999). Input uncertainty—also known as epistemic uncertainty (see Helton et al. 2006)—arises due to incomplete knowledge of model input parameters; for example, the parameter estimates from a behavioral model estimated from survey data will represent point estimates with associated standard errors. Alternatively, the data used to initialize the model may have some uncertainty due to sampling variability. Model uncertainty arises because the model typically requires some set of unverifiable assumptions about key parameters, processes, or social interactions. Thus, this source of uncertainty is associated with the architecture of the model. Model uncertainty and input uncertainty imply that there are a number of alternative specifications of the model possible, and these alternatives may generate variability in the outcome of interest (which may be one or more of the outputs discussed in the previous section). Agent-based models also have a third source of variability due to the stochastic elements of the model. Stochastic variability refers to the variation in model estimates that occurs from randomness within the model. For example, if agents’ choices are realized from probabilities, there will be fluctuation from model run to model run due to random sampling.

Input Uncertainty

There is a well-developed literature aimed at assessing the implications of input uncertainty (see Helton et al. 2006; Saltelli et al. 2004; Saltelli et al. 2008; Marino et al. 2008). The overarching goal is to assess what inputs and initial conditions are critical for the model results. This approach breaks down into two types of analyses. Uncertainty analyses examine the total variability in the model output that can be attributed to uncertainty in model inputs. Sensitivity analyses explore how uncertainty in the output of a model can be allocated across different sources of model input (Saltelli et al. 2004, 2008). The setup is the same for both and typically one first does an overall uncertainty analysis and then focuses on key parameters via sensitivity analyses.

Input uncertainty is most commonly assessed via Monte Carlo sampling procedures whereby the analyst varies input values systematically, re-runs the model, and then examines how the distribution of model outputs vary with model inputs. The first step is to specify the known or assumed joint distribution of parameters of interest. If nothing is known about the distribution, it is best to assume that each parameter follows a uniform distribution. If the analyst believes a parameter tends to take on a specific value, a normal distribution may be more appropriate (Marino et al. 2008). The actual sampling may be done via random sampling, importance sampling, or—as is most common—Latin Hypercube sampling (Helton and Davis 2003; Saltelli et al. 2008:76-78; Mease and Bingham 2006). Latin Hypercube sampling allows for an unbiased estimate of model output uncertainty, and requires fewer samples to accomplish this task than random sampling of input parameters (McKay, Beckman, and Conover 1979). Latin Hypercube sampling first requires the analyst to partition the distributions of relevant model parameters into s > 2 non-overlapping regions (where each region has the same density), and then sample one value from within each region without replacement. If k is the number of parameters, than s should be of value at least k + 1, but generally is much larger to allow the analyst to examine the influence of each parameter separately. Typically this method assumes that sampling is performed independently for each parameter, although there are methods for imposing correlations across the sampled values (Iman and Conover 1982; Iman and Davenport 1982, cited in Marino et al. 2008).

An illustrative example is interest shown in Figure 1. Let us say that we have three input parameters of interest, where a~N (μ_a, σ_a) and b~N (μ_b, σ_b) are parameter estimates from a discrete choice model, and c~Unif (c_min, c_max) is the assumed distribution of agents’ consumption thresholds. Let y be some model outcome of interest. Figure 1 shows the partitioning of the parameters into s = 5 regions, and we randomly sample a value from within each region. We then combine randomly sampled values to generate our s by k (in this example, a 5 × 3) input matrix X, where. X_j = {a_j,b_j, c_j}. We then run the agent-based model for j = 1,2, … 5, each time using a set of parameters X_j. We record the model outputs y_j for each of the five runs to generate y = {y₁, y₂, y₃, y₄, y₅}. This distribution of outputs reveals the impact of input uncertainty on model estimates because variation in the y_i‘s shows the model to be sensitive to which parameter combinations we are starting with. The simplest way to examine the distribution of output values is via a histogram, which provides an overall measure of model uncertainty, or scatterplots where the distribution of model output is plotted against the distributions for each of the input variables (which provides a qualitative assessment of model sensitivity to a particular input value). For a more rigorous quantitative assessment, a variety of statistical techniques can be used, including correlation coefficients and decomposition of model output variance. Details and discussion of these techniques can be found in Saltelli (2002); Saltelli et al. (2004, 2008); and Marino et al. (2008).

Figure 1. Latin Hypercube Sampling for Uniform and Normal PDFs*.

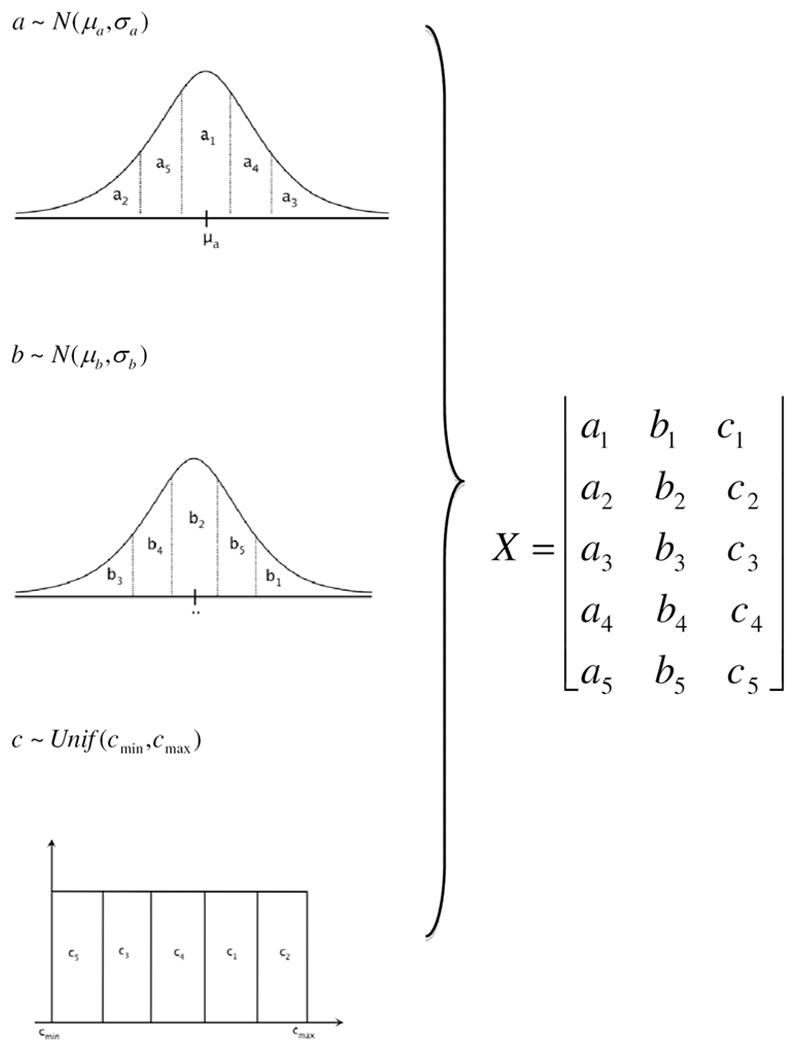
* Note: This figure is adapted from Marino et al. (2008).

Model Uncertainty

If the goal is to assess the degree to which uncertainty in the architecture of the model (e.g., assumptions about functional forms, sequencing of events, and definition of units of analysis like neighbors) generates uncertainty in model output, model uncertainty can be handled in ways similar to input uncertainty. However, rather than simply sampling values from a known or assumed distribution, the analyst will run the model under alternative assumptions about model architecture. For example, the analyst can run the model under varying assumptions about population size or the shape of neighborhoods to assess the extent to which these factors affect conclusions about residential segregation (Fossett and Dietrich 2009; Laurie and Jaggi 2003). An alternative approach is to use Bayesian model averaging (Raftery 1995; Hoeting et al. 1999) to average over all possible values of parameters and model specifications based on their likelihood of generating the data. Bayesian model averaging was originally developed as a method of accounting for uncertainty in statistical models, but it could be adapted to agent-based models by replacing the likelihood function with a comparison between simulated and observed data. This procedure is called approximate Bayesian computation. The technical details are beyond the scope of this essay, but more information can be found in Toni et al. (2009); also see Sisson, Fan, and Tanaka. (2007).

Stochastic Variability

Most uncertainty and sensitivity analysis techniques were developed for deterministic models. Because agent-based models often contain a stochastic element—for example, the initial distribution of agents across the landscape may vary over model runs, or probabilities may be sampled randomly from a multinomial distribution—there is often fluctuation in model output across model runs. Sometimes this fluctuation is a property of the phenomenon being studied; path dependence within the model may result in meaningful output variability and is interesting in its own right. In other instances, fluctuation is not meaningful and merely the result of stochastic elements of the model. In our experience, this fluctuation will be less apparent if the agent population size is sufficiently large and if the model output is summarized into aggregate summary measures. However, if the population is small or the analyst is interested in individual- or locally-based measures, this stochastic variation will lead to a distribution of output measures even with the same input values. The simplest way to account for this is to run each model setting multiple times and then analyze the resulting model trajectories. To reduce variability from random fluctuation, one can average over the distribution of estimated output values for a given set of input values (Marino et al. 2008).While it is common for agent-based modelers to explore how model output changes under a few alternative assumptions about key model inputs, only a handful of researchers have done rigorous sensitivity analyses. All of these are biological or epidemiological models. See Marino et al. (2008), Segovia-Juarez et al. (2004), Dancik, Jones, and Dorman (2010), and Riggs et al. (2008) for details.

6. MODEL VALIDATION IN HIGH AND LOW DIMENSIONAL AGENT-BASED MODELS

Agent-based models, like laboratory experiments, have strong internal validity. Since the modeler is aware of all aspects of model design, and since agent-based models make it easy to manipulate different parameters of the model, one can usually trace the causes of some observed aggregate process to one or more specific assumptions within the model. Insofar as one or more model parameters are grounded in empirical knowledge, this means that the analyst can rigorously explore how realistic assumptions about behavior, populations, or their environment affect an outcome of interest under highly controlled conditions. However, all these inferences are made internal to the model. External validity—the ability to generalize conclusions from the model to real- world processes—requires substantially more effort.

Of course, many agent-based models are not designed to reproduce real-world patterns. Indeed, in a world where theories are poorly developed and at best only weakly linked to empirical results and statistical models often stand in for analytic modeling, simple low-dimensional agent-based models can have substantial payoffs. However, if the aim of the agent-based model is to make some policy recommendation—even if the goal is just to identify one or two potentially useful mechanisms for manipulation and not make predictions—researchers need to trust that the inferences made from the model reflect actual mechanisms operating in the world. In the case of low dimensional, more abstract models, this may require conducting an analysis external to the agent-based model to assess whether there is empirical evidence for the mechanisms observed within the model. In the case of highly realistic models, the goal is typically to compare output from the model with empirical data to evaluate overall goodness of fit.

Evaluating Highly Realistic Models

A few requirements must be in place for an agent-based model to be feasibly evaluated by comparing model output to real world data. First, the model must be initialized with a population of agents that correspond to some known population. Second, the model output must be able to be mapped into real units of time. If spatial comparisons are desired, then the model environment must be linked to real space (e.g., using GIS data as discussed earlier). Finally, of course, the analyst must have access to field data at the appropriate level with which to do the evaluation. Typically some statistic is computed from the model and compared with its real world analogue. Highly aggregated summary statistics are the lowest bar of validation criteria. Because of the high level of data aggregation, a wide range of local conditions may give rise to the same aggregate statistic. One can compare either the final statistic after some specified time span or the evolution of that statistic over some time period. For validation at the micro level, the observed behavior of individual agents in the model can be compared with the behavior of individuals drawn from a comparable population. For example, if the researcher initialized the agents using a discrete choice model to describe their behavior, he could re-estimate this model from the agent decisions, and see if the coefficient estimates line up. Alternatively, one can look at trajectories for different types of agents to see if their average trajectory corresponds with observed human behavior.

Between the micro and macro levels of analysis, one can also compare information about local area statistics; for example, the proportion poor in a neighborhood or the average test scores in a school. The less stringent test would be to compare distributions from the agent-based model with data; for example, the number of high-poverty neighborhoods estimated in the model and the number of high-poverty neighborhoods observed in the data. Unfortunately, this ignores the spatial distribution of outcomes. The more stringent criterion would be to go area-by-area and compare the degree to which the agent-based model predicted outcomes consistent with the attributes of real places. Again, one can compare the trajectories of units over time, or merely record their start and end points. Maps may be useful to show geographic areas where the model did and did not perform well.¹⁵

Over the past five years, a number of simulation researchers have offered detailed, programmatic recommendations for data-based model evaluation (Richiardi et al. 2006; Troitzsch 2004; Windrum, Fagiolo, and Moneta 2007; an older discussion is available in Carley 1996). However, there is a fairly well developed methodology in the atmospheric and physical sciences aimed at evaluating the results of computer experiments (e.g., Sacks et al. 1989; Bayarri et al. 2007a, Bayarri et al. 2007b). This approach has been suggested for agent-based research (see Berk 2008), but is not widely known or utilized within the agent-based modeling community. It provides a solid statistical foundation for the validation exercise and represents the state of the art (Berk 2008: 294). We briefly summarize their suggested method below, and provide relevant references for readers who want to pursue more technical details. See Bayarri et al. (2007) and especially Berk (2008) for more details. Figure 2 provides a summary of the steps involved.

Figure 2. Process of Model Evaluation.

The first step of model evaluation is to specify model inputs and parameters with associated uncertainties or ranges. Ideally the modeler has already done a sensitivity analysis (see Section 7), so she is aware of how the model responds to fluctuations in key parameters. In particular, she knows the distribution of model results given the degree of empirical uncertainty in model inputs. (Note that model inputs can include parameter estimates as well as any key modeling decisions [for example, assumptions about the structure of the housing or labor markets or the extent to which an agent has incomplete information about its environment]). The sensitivity analysis will help determine which modeling decisions are most critical in explaining variation in model results. The model evaluation then takes into account uncertainty in inputs, and compares the distribution of model output to the observed data.

The second step is to determine the evaluation criteria. Researchers will generally want to include multiple measures of fit at multiple levels of granularity, and these measures will likely be adapted and refined as the evaluation process proceeds (Bayarri et al. 2007: 143). At least one measure will likely include an overall goodness-of-fit between the model and the data. Mean-squared error is one possible statistic, although it is sensitive to outliers (Berk 2008: 296). Summary measures are useful for assessing overall fit, but they do not provide detailed diagnostic information. For this, more detailed measures are useful. For example, residuals can be constructed from differences in expected versus observed characteristics of local areas, specific agents, or agent types. Note that these statistics may display substantial spatial or temporal autocorrelation, which can be handled via standard statistical techniques (Cressie 1991).

The third step is to identify real-world data suitable for the model evaluation. The data will preferably be at the same geographic level and time scale of the model output. Decennial Census data are one likely candidate for comparing populations, though these are only available at ten-year intervals. School enrollment data are available annually, but provide information only on children’s characteristics. However, these might be used to get some sense of population distributions within school districts. Other possible data sources include police reports and other crime data, hospital admissions records, births and deaths, and of course surveys on relevant populations. Ideally the data used to assess the model are not the same as those used to initialize it, but that is not always possible.

The fourth step is to generate the agent-based modeling estimates for comparison with real-world data. If the analyst has done a sensitivity analysis, he should already have collected data on how the distribution of model outcomes varies with uncertainty in model inputs. Note that obtaining this distribution of model outcomes may require a substantial number of model runs. When model runs are computationally expensive and the researcher lacks access to high performance computing, this approach may not be feasible. One option is to estimate Statistically Equivalent Models (SEMs) using nonparametric statistical techniques that reply on algorithms designed to link model inputs to model outputs without trying to represent the underlying causal mechanisms (Brieman 2001; see also Berk 2008: 304-5).Finally, the researcher compares the distribution of model output to the real world data. Of course, we would expect the model to do an imperfect job of predicting real world outcomes. However, the ways in which the model estimates depart from real world processes may be highly informative and useful for highlighting parts of the model that might be usefully revised, or point to data required to improve model fidelity. The process is iterative. The agent-based model and any associated empirical estimates may be refined based on conclusions from the evaluation, and the whole process repeats again.

Evaluating Low-Dimensional or Abstract Agent-based Models

While highly realistic models have been widely used in urban studies, epidemiology, and public health, this approach is less common in sociological research. Most agent-based models aimed at solving concrete empirical problems in sociology are not designed to replicate real-world situations, or predict expected outcomes under alternative policy scenarios. Rather, the goal is to explore the systems implications of behavioral mechanisms and the robustness of those mechanisms to changes in the key parameters. Even when much of the agent-based modeling architecture is informed by empirics, the purpose of the analysis is not to recreate the process of interest so much as identify key relationships among the parameters. In this case, one should resist the temptation to “validate” the model by comparing its output to empirical, aggregate patterns. Since multiple assumptions at the individual level can give rise to the same aggregate social dynamics, an agent-based model has not “explained” some process of interest merely by reproducing it (Grimm et al. 2005; Jones 2007).¹⁶ However, the model can show what might be expected under a set of empirically plausible assumptions. Rather than directly comparing model output to empirical data, researchers should try to determine whether the key relationships or mechanisms highlighted in the agent-based model seem to be plausible explanations of real-world phenomena. This often involves an analysis of empirical data that is completely separate from the agent-based model. In this case, the agent-based model is more of a theoretical tool used for the generation of hypotheses.

The trick is to figure out what empirical patterns would be consistent with a given mechanism. This is especially difficult when the focal mechanism is unobserved. For example, network externalities are rarely observed explicitly (e.g., Hedström and Åberg 2005; DiMaggio and Garip 2011). However, one can still specify hypotheses about what empirical relationships would be consistent with the observed mechanism. In quantitative models, fixed effects or statistical controls can help rule out alternative explanations. This strategy of model validation is useful in situations in which there is good aggregate data to test the theoretical relationships implied by the agent-based model. For example, Bruch (2013) uses both abstract and empirically grounded agent-based models to explore how between- and within-race income inequality shapes racial segregation dynamics. She finds that when there is a sufficiently high level of within-race income inequality, an increase in between-race income inequality has offsetting effects at the high and low ends of the income distribution. These offsetting effects attenuate the total change in segregation resulting from a decrease in between-race income inequality. To evaluate whether such offsetting effects are operating in real world settings, she uses fixed-effects models applied to three decades of decennial Census data to estimate the relationships among between-race income inequality, within-race income inequality, and the relative size of minority groups. While this approach shares the same drawbacks as any observational study, it does establish some empirical support for the underlying relationships observed in the agent-based model.

An alternative approach for testing the validity of mechanisms identified in the agent-based model is to design an experiment aimed at capturing the mechanism of interest. This is the strategy used by Todd and colleagues (Todd and Miller 1999; Lenton, Fasolo, and Todd 2009; Todd 2007) in their analyses of mate search strategies and marriage market outcomes. They first use an agent-based model to simulate outcomes under alternative assumptions about the degree of competition. They assume individuals update beliefs about their own marketability after sequential encounters with potential mates. They find that when there is greater indirect competition among same sex mate-seekers, individuals are quicker to make their choice, and shorten the initial learning period. To test whether this same result holds in the real world, they organize a series of speed-dating experiments to see how differences in levels of competition (e.g., the sex ratio and total number of participants) affects individuals’ mate choice behavior.

7. FUTURE DIRECTIONS AND CHALLENGES

Agent-based models are increasingly recognized as valuable tools within an empirical research program. However, there is no codified set of recommendations for or practices for using these models in empirical research programs. This paper offers a set of suggestions and practical guidelines for how to conceptualize, develop, and evaluate empirically grounded agent-based models. Our goal is to bring together literature across a wide range of fields—including transportation research, epidemiology, biology, atmospheric sciences, and statistics—representing “best practices” in this line of work.

There are several promising directions for future research. One is to make use of the emerging insights from behavioral economics and cognitive science on how people make collect, analyze, and act upon information to develop agents with more plausible and nuanced human behavior (c.f. Payne, Bettman, and Johnson 1993). Much of our work in sociology has focused solely on the role of preferences in individual choices and assumed people have infinite cognitive resources; we have not paid much attention to how people actually gather information and make decisions. For example, how do systematic biases in perception of things with near versus far time horizons affect choice behavior and to what extent do individuals learn from experience or past mistakes? One might specify agents that not only have tastes but also strategies for action under limited information or learning mechanisms, and then exploring how these features of human decision- making matter for social dynamics. Allowing for a more empirical realism in individual behavior would open up a whole set of interesting theoretical questions concerning how individuals’ cognitive biases and heuristic strategies for gathering information and making decisions shapes opportunity structure and the social environment. This topic is especially well suited to agent-based modeling given its natural ability to model the co-evolution of individual behavior and social environments.

Another promising application of empirical agent-based models is in studies aimed at understanding the development and evolution of social networks. Structural sociologists argue that the social environment formalized as networks constrains individual actions and defines the implications of those actions. Accordingly the majority of research treats an existing network as an independent variable, rather than an endogenous outcome of social interaction. However, agent-based models can be used to specify dynamic networks that explore how social outcomes and structure evolve given agents’ preferences and opportunities to create ties.¹⁷ To date, the most systematic and ambitious treatment of network change is work by Padgett and Powell (2012) that uses a simple agent-based model of autocatalysis and a multiple networks perspective to make sense of emergent phenomena ranging from partnership systems to high-tech clusters.

Another potential research direction is to couple detailed geographic data with quantitative and qualitative accounts of how people interact with space to better understand how physical proximity and the layout of cities and other social environments hinder or facilitate interaction and interdependence among individuals and groups, and how this process aggregates up to result in cooperation or conflict among communities. Space remains an under theorized aspect of social life: we often take spatial relationships as proxies for social relationships but we know very little about how individuals’ orientation to their physical environment affects social life. Geography may be especially relevant in applications where agents’ opportunities are constrained or defined by geography. This includes studies of residential mobility, but also marriage markets, employment opportunities, and school choice. Moreover there is evidence that geographic barriers such as freeways, train tracks, busy intersections, and other features play important roles in neighboring relationships, social networks, and community dynamics (e.g., Noonan 2005; Grannis 2009). Agent-based models historically have represented the agents’ environment as abstract and aspatial; a continuous space or a discrete space composed of cells arrayed on a grid. However, modelers are increasingly using explicit geography for a specific city or region (e.g., Crooks, Castle, and Batty 2008; Robinson et al.2007). In addition, detailed sensor data available from cell phones provides rich information on individuals’ movement in space, which can be also be incorporated into agent-based models (Osgood and Stanley 2012). Capturing how geographic barriers constrain or enhance interaction patterns may shed further light on how space conditions social life.

We close with a few words about software, documentation and replicable science. There are many software platforms and programming languages that support the construction of agent-based models. Well established platforms like Repast, Netlogo, MASON, and Swarm speed up development time by taking care of messy background details, but it is also relatively easy it is to construct a model in environments like R or Matlab. For empirically grounded models, especially those that realistic geography and populations, languages Python and R can make the handling and analysis of data easier. Regardless of what language one chooses, there are several practical introductions to the modeling process to consult before you begin (cf. Macal and North 2010, Railsback and Grimm 2011).

A key part of model development is documenting the code. Good documentation abstracts away from the code and makes the model’s structure and assumptions apparent. There have been calls for standardization of documentation (cf. Grimm et al. 2006, Richiardi et el. 2006), and one promising candidate is the Unified Model Language (UML). UML lays out a series of well-defined and standardized schematics—independent of any specific programming language—for representing the underlying logic of the model. This technique has become the gold standard for describing object oriented programming code (Fowler 2003), and agent-based modelers have begun to incorporate these diagrams into documentation and publications (Bersini 2012). In addition, the OpenABM repository is an excellent vehicle for sharing code and supporting documents.¹⁸ However, the adoption of these “best practices” has been slow and there remains great variation in how models are documented and shared. All methods would benefit from more peer validation of data and coding, but because agent-based models have more opportunities for coding error it is all the more important to allow others to explore and test models.¹⁹ Good practices around documenting and sharing models will help broaden the appeal and acceptance of agent-based models.

APPENDIX A

AGGREGATE VERSUS INDIVIDUAL-LEVEL MODELS

In this appendix, we provide an overview of how agent-based modeling compares to other methods for analyzing interdependent behavior, feedback effects, and social dynamics. These include systems dynamics and various forms of mathematical modeling. A full discussion of the relative advantages of these approaches is beyond the scope of this appendix (see Osgood 2008 for detailed discussions of model tradeoffs), but it is important to highlight the key methodological distinction between dynamic models that represent aggregated or expected behavior (e.g., general equilibrium models, interactive Markov models and other forms of population projection, and systems of differential equations) and models specified at the individual level, where each agent represents an autonomous actor (Osgood 2008; Bruch and Mare 2012; section 8).²⁰ In sociology, nearly all individual-based models are agent-based models, so we use the terms interchangeably.

Aggregate models typically represent the distribution of a population across some discrete set of “states” at time t, where states denote the proportion of the population with a given value of an attribute at a given time point. For example, in the classic “SIR” epidemiologic model, states reflect the number or proportion of people who are susceptible to, infected by, or recovered from some disease (Brauer,van den Driessche and Wu 2008). In a neighborhood dynamics model, states may reflect the population distribution across specific neighborhoods or areas (e.g. Mare and Bruch 2003). A matrix of transition values describes the probability of transitioning from one state to another, either as constants or as a function of the population distribution at time t, so that the probabilities are endogenous to the underlying population dynamics (Conlisk 1976). The observed dynamics or expected equilibrium can be computed by iteratively multiplying over matrices, or the system may be solved analytically.²¹

There are two key differences between aggregate and individual-level models: (1) their ability to handle population heterogeneity (which includes not just variation in individual attributes but also local interactions and network topology); and (2) whether decisions are represented as discrete choices or continuous transition probabilities or realized decisions. The former difference is due to the computational limits of aggregate models and the latter is the chief methodological innovation of agent-based modeling. First, agent-based models allow for a significantly more robust representation of population heterogeneity than do aggregate models because, as the analyst subdivides the population into detailed categories based on one or more key attributes, the complexity of the aggregate model grows geometrically whereas the complexity of the agent-based model grow only linearly (Osgood 2008). Thus, typically the number of subgroups represented in aggregate models is small even while there may still be considerable heterogeneity within subgroup categories. Furthermore, if there is heterogeneity within the population subgroups defined by the aggregate model, and those heterogeneous individuals have different transition probabilities, this can lead to a biased set of inferences regarding population dynamics due to selection effects (Vaupel and Yashin 1985)²²

The second difference between models at the aggregate and individual levels is that aggregate models simulate dynamics based on continuous or “smoothed” probabilities while agent-based models simulate the dynamics of realized decisions (that may be generated probabilistically). Simulating based on smoothed probabilities is tantamount to assuming an infinitely large population, as it implies that people can be subdivided into arbitrarily fractional units without changing the underlying dynamics. When the population under investigation is small or the units in which individuals influence one another is small (e.g., networks, neighborhoods, contact areas for disease), individual and aggregate models can generate different observed macro dynamics (Green, Kiss, and Kao 2006). For example, in residential mobility models an agent’s decision to move or stay will change neighborhood composition by 1 unit. Contrast this with an aggregate model of neighborhood change, in which probabilities may take on any value between 0 and 1. When neighborhoods are small, a 1-unit change may have very different implications for neighborhood desirability than a unit change for a given individual response behavior. Similarly, if total population size is small, agent-based models may generate different predictions about the emergence of pandemics than a model that assumes an infinite population (Keeling and Grenfell 2000).

In spite of these limitations, aggregate models do have certain advantages over agent-based models. They are more straightforward to construct and understand, they take less time and computational power to run,²³ and it may be easier to find empirical data for anchoring them. Also, if one wants to simulate the dynamics of a very large population (e.g., the population of the United States), agent- based models may become unwieldy. Accordingly, researchers have to weigh the tradeoffs. Both aggregate and individual models can incorporate feedback, stocks and flows, and other properties of dynamic systems. A few factors that can motivate using an agent-based model include the amount of individual heterogeneity desired in the model, the size of the population and relevant units, and the extent to which the problem at hand has the features outlined in the section below.