Abstract
A semicompeting risks problem involves two-types of events: a nonterminal and a terminal event (death). Typically, the nonterminal event is the focus of the study, but the terminal event can preclude the occurrence of the nonterminal event. Semicompeting risks are ubiquitous in studies of aging. Examples of semicompeting risk dyads include: dementia and death, frailty syndrome and death, disability and death, and nursing home placement and death. Semicompeting risk models can be divided into two broad classes: models based only on observables quantities (class ) and those based on potential (latent) failure times (class ). The classical illness-death model belongs to class . This model is a special case of the multistate models, which has been an active area of methodology development. During the past decade and a half, there has also been a flurry of methodological activity on semicompeting risks based on latent failure times ( models). These advances notwithstanding, the semi-competing risks methodology has not penetrated biomedical research, in general, and gerontological research, in particular. Some possible reasons for this lack of uptake are: the methods are relatively new and sophisticated, conceptual problems associated with potential failure time models are difficult to overcome, paucity of expository articles aimed at educating practitioners, and non-availability of readily usable software. The main goals of this review article are: (i) to describe the major types of semicompeting risks problems arising in aging research, (ii) to provide a brief survey of the semicompeting risks methods, (iii) to suggest appropriate methods for addressing the problems in aging research, (iv) to highlight areas where more work is needed, and (v) to suggest ways to facilitate the uptake of the semicompeting risks methodology by the broader biomedical research community.
Keywords: Competing risks, Semicompeting processes, Multi-state models, Informative censoring, Potential failure times, Causal inference
1 Introduction
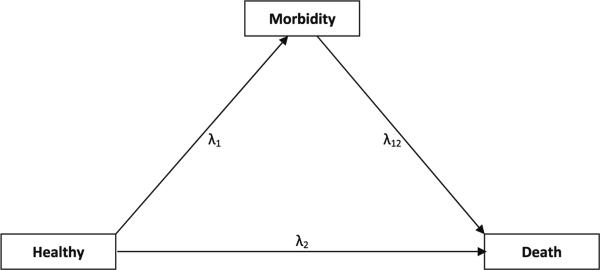
A main concern of gerontological research (i.e. the study of aging) is the understanding of the natural history and risk factors of age-related morbidity outcomes in order to predict, prevent or postpone the incidence of morbid outcomes. A major goal of this enterprise is to find ways to promote independent and active living in old age. This was termed “compression of morbidity” by Fries (1980). Death is a pervasive competing risk in studies of aging. It terminates the aging process. The occurrence of morbidity outcomes is precluded by death, but death itself can always be observed with sufficiently long followup. To distinguish this from the classical competing risks situations, the phrase semicompeting risks was coined by Fine et al. (2001). A semicompeting risks problem involves a dyad of events: a nonterminal and a terminal event (death). Typically, the nonterminal event is the focus of the study, but the terminal event can preclude the occurrence of the nonterminal event (Fig. 1). The semicompeting risks problem becomes a classical competing risks problem, if we restrict our focus to the first event, i.e. if we ignore the information after the nonterminal event. While competing risks have been extensively reviewed in statistical and biomedical research journals, there are no reviews on semicompeting risks models.
Fig. 1.
A semicompeting risks model of aging
Semicompeting risks are ubiquitous in studies of aging. Examples of semicompeting risk dyads include: dementia and death, frailty syndrome and death, disability and death, and nursing home placement and death. In these examples, we are typically interested in making inferences about the morbidity process that results in the nonterminal event. However, it is quite likely that the morbidity process is also correlated with the terminal event. It is common to temporally observe markers associated with the morbidity process. Such markers are useful in improving our understanding of the morbidity process and can also help in predicting the incidence of morbid outcomes. For example, hormones such as insulin-like growth factor I (IGF-1) play key roles in metabolic regulation and are tightly regulated to ensure normal function. The fact that data from young and healthy adults show wide variation between individuals suggests that individual set points exist. Scientists are now hypothesizing that the observed age-related change in hormones exemplifies that resilience is a dynamic process. Therefore, individual-level trajectories of change in hormones, more than the absolute levels, may be clinically meaningful for predicting health, function, and survival in old age. Death, in addition to truncating the nonterminal event, also truncates the marker process. This may be called semicompeting processes.
The semicompeting risks problem is equivalent to the classical illness-death model (Fix and Neyman 1951). The illness-death model is a special case of the multistate models (Hougaard 1999), which has been an active area of methodology development. During the past decade and a half, there has also been a flurry of methodological activity on semicompeting risks based on latent failure times (Robins 1995a,b; Lin et al. 1996; Fine et al. 2001; Peng and Fine 2006, 2007; Ding et al. 2009; Hsieh and Huang 2012; Chen 2012). These developments notwithstanding, the semicompeting risks methodology has not penetrated gerontological research. Likely reasons include: methods are relatively new and sophisticated, paucity of expository articles to provide guidance for practitioners, lack of collaboration between medical researchers and methodologists with expertise in this niche area, and lack of availability of ready-to-use software. The main goals of this review article are: (i) to describe the major types of semicompeting risks problems arising in aging research, (ii) to provide a brief survey of the semicompeting risks methods, (iii) to suggest appropriate methods for addressing the problems in aging research, (iv) to highlight areas where more work is needed, and (v) to suggest ways to facilitate the uptake of the semicompeting risks methodology by the broader biomedical research community.
Here is an outline of the paper. In Sect. 2, we present some motivating examples of the types of major research problems in aging where semicompeting risks play an important role. In Sect. 3, we provide a review of major methodological approaches for semicompeting risks, distinguishing between methods based only on observable data (Sect. 3.3) and those based on latent failure times (Sect. 3.4). In Sect. 4, we discuss semicompeting process models, which are an extension of the joint survival longitudinal models that deal with single time-to-event outcome to semicompeting risks problems. In Sect. 5, we use simulations to motivate the need for potential failure time models that can account for dependent censoring, and study one important type of model: the bivariate location-shift model. Using simulations, we evaluate the criticality of the assumptions made in this model and demonstrate that a major assumption can be relaxed. We, then, address the practical question of which methods are appropriate for answering different research questions in aging (Sect. 6). In Sect. 7, we discuss the open methodological problems in semicompeting risks and identify some areas where work is needed. In particular, we emphasize causal inference in semicompeting risks as an under-studied area and suggest some interesting ideas for further exploration. We also suggest some practical strategies for faciltating the uptake of semicompeting risks methodology by practitioners in biomedical research.
2 Some motivating problems in aging research
2.1 Risk factor etiology in older adults
With the fast growing older population, there is great interest in identifying risk factors for diseases and conditions and their related morbidity outcomes such as frailty and disability. Information on risk factor-outcome association is critical for optimal risk management and diagnosis. Compared to younger adults, studying risk factor-outcome association in older adults faces unique challenges including competing risks, age-related physiological changes, imperfect measurement of risk factors and outcomes, selective survival, confounding by comorbidity, shifting attitudes and changing perceptions of outcomes, and altered disease manifestations and/or presentations affecting diagnosis and detection of outcomes (Kaplan et al. 1999). There is mounting evidence that many if not all the complexities mentioned above may have contributed to the reports of weakened risk factor-outcome associations with advancing age (Kaplan et al. 1999). For example, a systematic review found that the effect of cigarette smoking on the risk of Alzheimer disease (AD) and dementia varies dramatically across studies with relative hazard ranging from 0.27 to 2.72 for AD and from 0.38 to 1.42 for dementia (Hernan et al. 2008). It turns out that this heterogeneity could be largely accounted for by the between-study differences in the minimum age at study entry. The effect of cigarette smoking on the risk of dementia is modified by age: smoking was harmful at younger ages, but beneficial at older ages. One explanation is selection bias due to age-dependent change in smokers’ susceptibility to AD and dementia. Alternatively, the selection bias could be the result of censoring by death, i.e., selective dropout of susceptible smokers due to death prior to onset or clinical diagnosis of AD. While factors such as age-related alteration in physiology, manifestations, and presentations of diseases or conditions may be real biological phenomena driving the change in risk factor-outcome association, other challenges including competing risks (e.g., AD-free death) should be and can be dealt with analytically such that scientific discovery is not impeded by our failure to account for the clinical complexity and population heterogeneity.
2.2 Studying association of marker processes with morbidity outcomes
Risk factor-outcome association studies in gerontology have primarily focused on risk factors measured at a single time point. For many physiologic measures (e.g., anabolic hormones), variation in levels between people greatly exceeds the changes within a single person, even among healthy younger adults. This suggests that individual set-points exist (Cappola et al. 2009). From a single measurement, an individual's usual normal level or setpoint cannot be determined nor whether the set-point is being successfully maintained. Repeated measurements from the same person taken over time can overcome these limitations. A major advantage of longitudinal trajectory analysis is the capacity to separate change over time within individuals (i.e., aging effect) from differences among people with different ages in their baseline levels (i.e., cohort effect), thus providing better control for unmeasured confounding. Moreover, studying the association of risk factor (or marker) processes and outcomes may provide a unique opportunity to understand the natural history of risk factors as time-evolving processes and their relationships with outcomes. For example, muscle weakness defined based on a single measurement of handgrip strength correlates well with subsequent adverse health outcomes, even when measured in mid-life to predict physical disability decades later (Rantanen et al. 1999). Recently, studies have shown that a decline in grip strength over time is a stronger predictor than a single observation of grip strength of a variety of subsequent adverse outcomes including falls, disability and death, suggesting that “becoming weaker” is important in addition to “being weak” (Xue et al. 2010, 2011). Studies like this and others have contributed to the growing interest in relating longitudinal processes of biomarkers or risk factors to health outcomes in older adults. It is important to note that the concept of semicompeting risk equally applies to this setting with added complexity that the terminal event not only precludes the primary event of interest but it also censors the marker process, leading to biased inference of the relationship between covariates, marker process, and the nonterminal event.
2.3 Multimorbidity in older adults
A hallmark of geriatric medicine is that chronic conditions rarely occur in isolation in older adults. The co-occurrence of two or more chronic conditions, or “multimorbidity,” is thought to heighten the risk of adverse outcomes beyond that associated with the individual conditions (Boyd and Fortin 2010). For example, among the older women participating in the United States nationally representative survey NHANES, examining five major chronic diseases—coronary heart disease, stroke, diabetes, arthritis or chronic respiratory disease, fewer than 20% who had any one of these diseases had it in isolation (except arthritis which had an isolated prevalence of 47%) (Boyd and Fortin 2010). Among the pressing issues for gerontological research is to elucidate shared etiology underlying such multimorbidity as well as sentinel clusters and combinations of multimorbid disease (Marengoni et al. 2011). Statistically, the first issue is informed by—and the second issue requires—the study of association among multiple dependent failure times, each subject to the substantial semi-competing risk of death. Of additional interest is clustered occurrence of an index chronic disease among multiple related individuals, so that heritability and other sources of shared risk can be studied. The study of time to onset of dementia in families is a well-known example in the statistical literature on multivariate failure times subject to competing risks. Collectively these examples highlight multivariate failure-time analysis accounting for competing risks as a potentially important tool in gerontological research.
2.4 Assessing the impact of interventions in older adults
Randomized controlled trials (RCTs) can provide valid estimates of treatment efficacy. Efficacy measures the ideal, biological effect of a treatment. In contrast, the effectiveness of an intervention is measured in terms of the actual benefit obtained in the real world, where complications including competing risks, adverse events related to treatment, and non-adherence to treatment are present. An effective intervention should reduce the absolute risk of the nonterminal event of interest, as well as not exceed acceptable levels of harm. When the risk of terminal event is high, even an efficacious intervention may not substantially reduce the absolute risk of the nonterminal event. An intervention that is efficacious in relatively healthy older adults may not be effective in the larger at-risk population of older adults with two or more coexisting conditions (multimorbidity) because of the greater risk of competing terminal events and increased susceptibility to treatment related adverse events (Welch et al. 1996). Therefore, it is important to consider competing risks and risk of adverse events when applying trial evidence to older adults with multimorbidity (Weiss et al. 2012).
2.5 Routine screening in older adults
A main goal of routine, population-wide screening is to detect asymptomatic disease at a stage where the disease can be detected reliably (i.e. with minimal false positives) and once detected it can be treated effectively. For middle-aged adults, the starting age and frequency of screening are the important issues. In older adults, however, there has been a lot of debate about when to stop screening, i.e. when it is not beneficial to screen. For example, most screening guidelines do not recommend prostate-specific antigen (PSA) screening in older men with limited remaining life expectancy because the potential benefits, which are not expected to occur until several years in the future, are thought to be outweighed by the potential harms of screening, which occur immediately (Walter et al. 2006). For cancer screening in older adults, Walter and Covinsky (2001) present a framework for making individualized decisions. They consider the baseline risk of dying of a screen-detectable cancer, the length of time that must elapse for screening to yield a survival benefit, and the probability of dying from causes unrelated to the cancer. They argue that cancer screening will be ineffective for older adults with severe disabilities due to their limited remaining life expectancy (less than 10-years). For example, the American Cancer Society and the American Urological Association recommend annual PSA screening for average-risk men over 50 years of age, if they have greater than 10-year remaining life expectancy. The US Preventive Services Task Force (USPSTF) concluded that evidence is insufficient (“Grade I”) to recommend routine PSA screening, and men with a low probability of surviving 10 years are unlikely to benefit from screening even under favorable assumptions (Walter et al. 2006). Similar finding of reduced effectiveness has also been reported for colorectal cancer screening in adults older than 80 years of age (Lin et al. 2006).
3 A brief review of existing modeling approaches
3.1 Notation and terminology for semicompeting risks
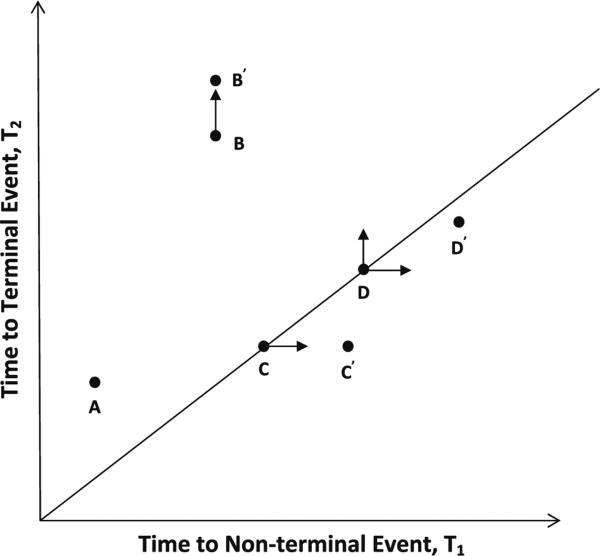
A main goal in semicompeting risks problems is to make inference on the distribution of the failure time of the nonterminal event, T1. Ideally, we would like to observe {T1i} for each individual i = 1, · · · , n. Then, we can readily make inferences on T1. In reality, however, we only get to observe n i.i.d. copies of {Y1i, Y2i, δ1i, δ2i, Xi, Vi(t)}. See Fig. 2 for a representation of the semicompeting risks data. Subject A experienced the nonterminal event and later died, so we observe both T1 and T2. Subject B had the nonterminal event, but did not die before end of study, so we observe T1 and censoring time C. The potential unobserved death time T2 is given by point B′. Subject C died, but did not experience the nonterminal event, so we only observe T2. The potential unobserved nonterminal event time T1 is denoted by point C′. Finally, subject D experienced neither event, so both T1 and T2 are unobserved, but depicted as point D′.
Fig. 2.
Basic semicompeting risks data structure
3.2 Two types of semicompeting risks models
Semicompeting risk models can be divided into two broad classes: models based only on observables quantities and those based on potential (latent) failure times. Observables models are based on the observed data: O = {Y1i, Y2i, δ1i, δ2i, Xi, Vi(t); i = 1, . . . , N}. Models for the cause-specific hazards (CSH) and the cumulative incidence functions (CIF) are identifiable with observed data, O (Prentice et al. 1978). We might call such models as forming the class . Models for potential (or latent) failure times go beyond the observable data and attempt to model the joint distribution of {T1, T2} or the marginal distributions of T1 and T2. We might call such models as forming the class .
3.3 Models based on observables ( models)
3.3.1 Cause-specific models
One approach to treating the semicompeting risks problem is to ignore the information available after the nonterminal event by only considering the time and type of the first event that occurs to an individual. This becomes a classical competing risks problem. The two main quantities in classical competing risks are: cause-specific hazard (CSH) and the cumulative incidence function (CIF). The CSH and CIF for the non-terminal (k = 1) and terminal (k = 2) cause of failure are defined as:
| (1) |
| (2) |
where Y is time elapsed since a well-defined origin, ε ∈ {1, 2} indicates the cause of failure, and dt denotes an infinitesimal increment of time. These functions can depend on covariates. While it is easy to evaluate the impact of a covariate X on the CSH of event k, it is more difficult to evaluate the effect of X on the corresponding CIF, Fk. This is because the cumulative incidence Fk(t) depends on λk, as well as λj , j ≠ k. Therefore, regression methods that directly estimate the impact of X on Fk have been developed. The subdistribution hazard model (Fine and Gray 1999) is becoming increasingly popular in biomedical research. Flexible regression modeling techniques, which can incorporate various transformations of CIF and accommodate time-varying effects, have been developed recently (Scheike and Zhang 2008). These models assume the form:
| (3) |
where h and g are specifed link functions and β(t) and γ are vector of time-varying and fixed coefficents, respectively. The model (3) includes the subdistribution hazard model and several other models as special cases.
An important issue is determining which estimand to use, CSH or CIF, for the competing risks problem at hand. This was addressed by Varadhan et al. (2010).
3.3.2 Shared frailty models
A major difference between classical competing and semicompeting risks is that in semicompeting risks problems we can estimate the association parameter that represents the dependence between the nonterminal and terminal event times (Fine et al. 2001). Xu et al. (2010) developed an extension of the classical illness-death model for semicompeting risks. They defined the hazards as follows (Fig. 1):
| (4) |
| (5) |
| (6) |
where 0 < t1 < t2. Equations 4 and 5 are the usual CSH functions for the competing risks part of the model in which either the terminal or nonterminal event occurs first. The hazard (6) is special to the semicompeting risks situation. It is the rate of the terminal event following the occurrence of the nonterminal event at time T1 = t1. Generally, λ12 can depend on both t1 and t2, but in a Markov model, it only depends on t2, and in a semi-Markov model it depends only on t2 − t1. With a Markov model, the ratio λ12(t)/λ2(t) is known as the explanatory or predictive hazard ratio, and it characterizes the dependence between T1 and T2. When this ratio is equal to 1, the occurrence of nonterminal event at time t1 has no impact on the rate of occurrence of terminal event after that. Xu et al. (2010) modeled the dependence structure between T1 and T2 using a Markov shared frailty model as follows:
| (7) |
where γ is a positive random variable denoting frailty or random effect with E(γ) = 1. Conditional on γ , this is a standard Markov illness-death model. The assumption=that λ03(t2) = λ02(t2) is of special interest. Under this assumption,the shared frailty model can be shown to be the same as the semicompeting risks models of class discussed in Sect. 3.4.2. In this restricted model, the dependence between T1 and T2 is fully captured by γ . Xu et al. (2010) assumed that the frailty variable γ has a gamma distribution with mean 1 and variance θ. They showed how to estimate the two baseline hazard functions and the frailty parameter using the maximum likelihood approach. They also showed how to incorporate covariates into the model (7). Other distributions than gamma may also be used for the frailty variable such as log-normal or positive stable distributions. A limitation of the shared frailty models is that they can only capture the positive correlation between T1 and T2.
3.4 Models for potential failure times ( models)
Cause-specific models of class are straightforward to model and do not invoke untestable assumptions. However, models are not satisfactory from a causal perspective. They do not target the distribution of marginal failure times, unless when nonterminal and terminal failure times are assumed to be independent. Furthermore, CSH are conditional quantities (i.e. hazard of failure at a particular instant of time having survived up to that time), and hence susceptible to survival bias due to dependent censoring (as demonstrated in Sect. 5.1). Therefore, it is of interest to consider models and estimate the marginal distribution of nonterminal event time and its dependence on covariates.
3.4.1 Bounds for marginal distribution of nonterminal event
The joint distribution of potential failure times cannot be identified nonparametrically (Tsiatis 1975). Identifiable bounds (i.e., bounds in terms of observable quantities) can be derived for FT1, the marginal distribution of nonterminal event (Peterson 1976).
| (8) |
In other words, the distribution of nonterminal event is bounded from below by the CIF of nonterminal event and from above by the distribution of first event (including censoring). The Petersen bounds on FT1 apply without any restrictions, but they are too wide, even in the presence of moderate censoring, to be practically useful. Sharper bounds are possible for FT1, but with additional stipulations on the joint distribution of T1 and T2. For example, Slud and Rubinstein (1983) derive sharper bounds by postulating a simple, yet general, quantification of the degree of dependence between T1 and T2. They define the ratio of the conditional hazard function for T1 at time t, given T2 < t to the conditional hazard function for T1 at time t given T2 ≥ t (“the rho-function”). They produce bounds for FT1 by assuming reasonable bounds on the unknowable rho function.
3.4.2 One sample estimation of the joint distribution
The semicompeting risks data is denoted by: O = {Y1i, Y2i, δ1i, δ2i; i 1, . . . , N}. The joint distribution of T1 and T2 can be estimated by postulating parametric or semiparametric models for how the unobserved failure times, T1 and T2 are related to observed data O. The joint distribution (T1, T2) is identifiable in the upper wedge where T1 < T2, but the marginal distribution of the nonterminal event T1 is not identifiable. The joint distribution can be modeled as:
| (9) |
where S1 and S2 are the marginal survival functions for the nonterminal and terminal events, respectively, and Cθ is a copula representing the dependence between T1 and T2, and θ is the indexing parameter for the copula family that characterizes the dependency between the two failure times. Day et al. (1997) and Fine et al. (2001) proposed the Clayton copula for modeling the dependence:
| (10) |
for θ ≥ 1. This model for S(t1, t2) does not hold on the lower wedge T1 > T2, which is why the function S(t1) cannot be interpreted as the marginal survival function for the nonterminal event. Fine et al. (2001) proposed an estimator for θ based on a concordance estimating function, and a plug-in estimator for S(t1). Wang (2003) used a more general Archimedean copula for Cθ to represent the joint distribution (T1, T2):
| (11) |
where φθ is a decreasing convex function defined on (0, 1] with φθ(0) = 1. Wang proposed two types of estimating functions for the dependence parameter θ, which, under the Archimedean copula, can vary over time, in contrast to the Clayton copula model where it is constant. Lakhal et al. (2008) presented a general approach for estimating the dependency parameter θ in the Archimedean copula.
3.4.3 Bivariate location-shift models for marginal distributions
For estimating the effect of treatment on the failure time of nonterminal events, in the presence of dependent censoring, in two-arm RCTs, Robins (1987) showed that treatment group specific marginal distribution of time to nonterminal event is identified if (i) data are available on a time-varying marker process, and (ii) the CSH of terminal event does not depend on the potential time to nonterminal event conditional on the history of marker process. When data on such a marker process is not available, Robins (1995a,b) and Lin et al. (1996) (hereafter referred to as LRW) developed a semipara-metric bivariate location shift model to describe the joint effect of a binary treatment variable on nonterminal event and death in two-arm RCTs. They used a bivariate accelerated failure time (AFT) regression model for the effect of a binary treatment group indicator X on T1 and T2, when T1 and T2 are not necessarily independent, given X:
| (12) |
LRW first estimate parameter η for the terminal event T2 using standard rank procedures, and then use an artificial censoring technique for constructing unbiased rank-based estimation of parameters θ of nonterminal event T1. They transform the observed variables Y1 and δ1 to new variables Ỹ1 and and base their estimation on these transformed variables. Under this transformation, some of the uncensored observations may become censored, which is denoted as articificial censoring. The articifical censoring occurs in only one of the two groups of X, and which group it occurs depends on the ordering of parameters θ and η. It is not required that T1 and T2 be independent conditional on X. The error ε = {ε1, ε2} is left unspecified, but a key assumption is that does not depend on X. Robins (1995a) called this the “non-interaction” assumption.
Peng and Fine (2006) (hereafter referred to as PF) extended the two-sample bivariate location shift model to regression settings, and also improved upon the artificial censoring idea of LRW by using pairwise ranking to obtain a rank-based estimator that achieves large reductions in artificial censoring compared to LRW. The PF estimator also provides large efficiency gains over LRW and it even evinced moderate efficiency gains, under independent censoring, over a rank estimator that is semipara-metric efficient. PF method is also broadly applicable for estimation in regression settings, whereas LRW is limited to two-sample comparisons. The bivariate location-shift regression model considered by PF is:
| (13) |
where X′ denotes the transpose of the design matrix X of baseline covariates. The error ε = {ε1, ε2} is left unspecified, but a key assumption, as in LRW, is the “non interaction” assumption that ε does not depend on X. The PF method represents an important development in semicompeting risks methodology.
3.4.4 Recent developments
Ding et al. (2009) extended the bivariate AFT location-shift models where the transformation of failure time for nonterminal event can be different from that of the terminal event. Note that the LRW, PF and Ding et al. (2009) model only the marginal distributions. They do not provide any information on the dependence between nonterminal and terminal events. If dependence itself is of interest (which is not common), either copulas or shared frailty models can be used. Peng and Fine (2007) and Hsieh and Huang (2012) developed copula-based models for time-varying effects of a treatment on the marginal distribution of nonterminal event. In Peng and Fine (2007), the copula parameter is allowed to be time-varying. In Hsieh and Huang (2012), the copula parameter is constant over time, but it can depend on discrete covariates. Chen (2012) provided a nonparametric maximum likelihood estimation (NPMLE) approach for the semiparametric transformational models for marginal regressions, where dependence between nonterminal and terminal events is modeled using a copula. These recent developments extend the seminal works of LRW and PF, and, together, provide a wide array of class methods for semicompeting risks.
4 Semicompeting process models
We define semicompeting process model as a joint model of a marker, V , assessed repeatedly over time (termed “marker process V (t) henceforth) and a possibly censored time-to-event outcome comprised of a dyad of a nonterminal and a terminal event such as death as in the semicompeting risks model setting. The primary interest here is in evaluating the relation between the marker process and the non-terminal event. When the non-terminal event (e.g., dementia) is subject to censoring by the terminal event (e.g., dementia-related dropout), both characterization of the marker process and the assessment of the association between the marker process and the non- terminal event are known to be biased if the conventional joint model of Henderson et al. (2000) is applied (Elashoff et al. 2007). To address this, Elashoff et al. has extended the joint model of Henderson et al. (2000) to handle competing risks data (Elashoff et al. 2007, 2008). By defining non-terminal event and terminal event in the absence of non-terminal event as mutually exclusive competing events, the model of Elashoff et al. can be applied to semicompeting process data. To illustrate, following the same notation as in Sect. 3.1, let (Y1i, Y2i, δ1i, δ2i, Xi, Vi(t)) be the competing risks data on subject i, where Xi = (X1i, X2i, X3i, X4i) represents a collection of covariate vectors with non-overlapping or overlapping components. The joint model consists of two submodels:
Longitudinal submodel for marker process V (t):
| (14) |
where β are population mean effects (i.e., fixed effects); are subject-specific deviations from the mean effects (i.e., random effects) withU mean zero and variance-covariance matrix of D. The submodel (14) is the classical linear random effects model, which assumes that is independent of εi and Vi = (Vi(t), t = 1, . . . , ni) are independent conditioned on .
Survival submodel for (Y1i , Y2i, δ1i, δ2i):
| (15) |
| (16) |
Model (15) is logistic regression relating the marginal probability of subject i experiencing the primary event of interest (i.e., nonterminal event). Model (16) defines the conditional CSH λk for event type k (k=1 if non-terminal event, and 2 if terminal event; Larson and Dinse 1985; Ng and McLachlan 2003), with λ0k(t) being the baseline hazard function for event type k. X3i and X4i are vectors of covariates associated with π1 and λk(t), respectively; and α and γ are corresponding regression coefficients (Elashoff et al. 2007). and are random effects that are typically linked to by either assuming a multivariate normal distribution for (Elashoff et al. 2008) or using linear models such as and (Elashoff et al. 2007). In the former case, exp(θ then can be interpreted as the odds ratio of experiencing the non-terminal event versus terminal event in the absence of non-terminal event associated with one unit change in , and exp(ζk) the hazard ratio of experiencing event type k associated with one unit change in . Model (16) can be alternatively formulated as a mixture model of event-type-specific parametric survival function (e.g., Weibull model) with π1 and (1 − π1) being the mixing parameters (Yu and Ghosh 2010). The joint model assumes that the marker process is independent of the competing risks failure time data, conditional on all the covariates and random effects. The survival submodel can be seen as an extension of Larson and Dinse and Ng and McLachlans mixture model for competing risks data by incorporating the random effects (Larson and Dinse 1985; Ng and McLachlan 2003). Elashoff et al. used an EM-based algorithm to estimate model parameters, with their standard errors estimated via a profile likelihood approach (Elashoff et al. 2007). A Bayesian method was also proposed for parameter estimation that has been shown to be computationally more tractable for high-dimensional random effects (Hu et al. 2009). In cases where the effects of covariates on the marginal probabilities of occurrence of competing events are not of explicit interest, a simpler model can be formulated by removing model (15) and replacing the conditional CSH in model (16) with the standard CSH (Elashoff et al. 2008). For risk factor markers measured on an ordinal scale, Li et al. (2010) recently proposed a partial proportional odds model for the longitudinal submodel, which is an extension of the partial proportional odds model proposed by Peterson and Harrell (1990) by incorporating random effects to account for the within-person correlation of the longitudinal outcome.
5 Simulations for bivariate location shift models
As discussed in Sect. 3.2, semicompeting risks data can be analyzed using the CSH or using models for the potential failure times of nonterminal and terminal events. The two approaches can produce different results if the nonterminal event times are dependently censored by the terminal event. This becomes intuitively clear when we note that the CSH is a conditional quantity where the conditioning event, the set of units at risk for the terminal event at a given time, changes over time in a selective manner due to the terminal event. This is well known as survival bias or selection bias (Vaupel and Yashin 1985; Aalen 1994; Hernan 2010). Thus, CSH models can be misleading for assessing treatment effects or risk factor associations in the presence of dependent censoring that is quite likely in studies of aging. Analysis of potential failure times can be useful for assessing the impact of the treatment or a risk factor.
In all the following simulation studies, we use the Cox PH model for estimating the impact of a binary covariate (e.g., treatment) on the CSH for nonterminal and terminal events, and the PF method for estimating the impact of treatment on the marginal distribution of potential failure times.
5.1 Simulation I: impact of dependent censoring
We consider a single binary covariate, treatment group indicator, which affects the time to death, but has no impact on the time to nonterminal event. We conduct simulations for the standard CSH models and the semicompeting risk model, Eq. 12 or 13. The CSH model does not account for dependent censoring, wheras the semicompeting risk model does. We considered the following simulations parameters: N = 1000, X1 ~ Binomial(N, prob = 0.5), θ = 0 and η = −0.8. This means that the treatment has effect on the nonterminal event, but increases the rate of terminal event. The error distribution was assumed to be normal: ε = N(0, Σ), where .
We considered 3 different correlations between death and nonterminal event times, ρ = {−0.5, 0, 0.5} . There was no censoring. We ran 1000 simulations. Results are show in Table 1. For ρ = −0.5 and 0.5, the CSH model estimated log(hazard ratio) of −0.22 and 0.32, respectively. This means that the treatment decreases or increases the hazard of the nonterminal event, depending on whether the death and nonterminal events are negatively or positively correlated, respectively. When the events are independent (ρ = 0), there is no effect of treatment on CSH of the nonterminal event. The PF semicompeting risks model correctly estimates that the treatment does not have any impact on the nonterminal event regardless of the nature of the correlation between the events. This simple simulation shows why the standard CSH analysis cannot be used to estimate the effects when there is the possibility of dependent censoring due to death.
Table 1.
Simulation I: Impact of dependent censoring on the effect of treatment on the nonterminal event
| ρ | CSH log(HR) (se) | PF |
|---|---|---|
| –0.5 | –0.22 (0.10) | 0.00 (0.09) |
| 0 | 0.00 (0.11) | 0.00 (0.09) |
| 0.5 | 0.32 (0.11) | 0.00 (0.9) |
Mean and standard error of the estimates from 1,000 simulations, where the truth was θ = 0(and n = –0.8)
5.2 Simulation II: impact of the non-interaction assumption
Here we demonstrate the impact of the non-interaction modeling assumption of the LRW/PF model (13), i.e. the error is independent of covariates X. In particular, we examine the bias in the treatment effect when the error distribution depends on covariates. We consider two situations:
Simulation II.1. There is a single covariate: a treatment group indicator, X1. The error depends on X1.
Simulation II.2. There are two binary covariates: a treatment group indicator, X1, and a prognostic variable, X2. The error is marginally dependent on X1, but conditionally independent of X1 given X2.
For simulation II.1, we had the following settings: N = 1000, X1 ~ Binomial(N, prob = 0.5), η = −0.1, θ = 0.5. The error ε = N(0, (X1)) where . Correlation was fixed in the untreated group, ρ(0) = ρ0 = 0.5, but was varied in the treated group: ρ(1) ρ1 {−0.5, −0.3, −0.1, 0.1, 0.3, 0.5}. There was no censoring. We ran 1,000 simulations. Results are shown in Table 2.
Table 2.
Simulation II.1. Impact of non-interaction assumption on the estimate of treatment effect on the nonterminal event in the bivariate location-shift model, Eq. 12
| ρ1 (ρ0 = 0.5) | PF |
|---|---|
| –0.5 | 0.13 (0.067) |
| –0.3 | 0.18 (0.070) |
| –0.l | 0.24 (0.075) |
| 0.1 | 0.30 (0.078) |
| 0.3 | 0.40 (0.079) |
| 0.5 | 0.50 (0.082) |
Mean and standard error of the estimates from 1,000 simulations, where the truth was θ = 0.5 (and η = –0.1)
The true θ is 0.5. The bias in increases as the difference in the error distribution between two treatment groups becomes larger. Thus, the “non-interaction” assumption is critical in the bivariate location-shift model of LRW and PF.
In simulation II.2, we demonstrate that the “non-interaction” condition can be relaxed. Suppose that we are only interested in estimating the treatment effect θ. We demonstrate that we can get an unbiased estimate for treatment X1 under the weaker assumption that is independent of X1 conditional on X2. We call this “conditional non-interaction” assumption. We used the following settings:
N = 1000, X1 ~ Binomial(N, prob = 0.5), X2 ~ Binomial(N, prob = p(X1)), θ = (0.5, −0.2) and η = (0, −0.2). The first components of θ and η are the effect of X1 on the nonterminal and terminal events, respectively, and the second components are the effect of X2 on the terminal and nonterminal events. The error was assumed to be normal, ε = N(0, Σ(X2)), where . Correlation between the 2 failure times in the control group was fixed at ρ(0) = ρ0 = 0.5, but in the treated group the correlation ρ(1) = ρ1 took on 3 different values: −0.5, 0, and 0.5. We chose p(X1)= Prob(X2 = 1|X1) = logit−1(α0 + α1X1) such that the correlation between X1 and X2 was close to 0.5. This construction ensures that ε is conditionally independent of X1 given X2, but depends on X1 marginally. Approximately 400 nontermminal events were observed on average with these setitngs. Death was uncensored. We ran 1,000 simulations. Results are shown in Table 3.
Table 3.
Simulation II.2. Impact of conditional non-interaction assumption on the estimate of treatment effect on the nonterminal event in the bivariate location-shift model with 2 covariates, Eq. 13
| ρ1 (ρ0 = 0.5) | PF |
|
|---|---|---|
| –0.5 | 0.52 (0.096) | –0.58 (0.10) |
| 0.0 | 0.51 (0.097) | –0.41 (0.10) |
| 0.5 | 0.50 (0.094) | –0.20 (0.097) |
Mean and standard error of the estimates from 1,000 simulations, where the truth was θ1 = 0.5, θ2 = –0.2) (and η1 = 0, η2 = –0.2)
We observe that the estimate is unbiased even when the error distribution depends marginally on X1, because it is conditionally independent of X1 given X2, i.e. we have conditional non-interaction. However, the estimate is biased, as expected. When ρ0 = ρ1 = 0.5, we have non-interaction and hence, both and are unbiased. While this is not a mathematical proof, these simulation studies suggest that the noninteraction condition may be relaxed in favor of conditional non-interaction.
6 Appropriate semicompeting risks methods for aging research questions
In Sect. 2, we discussed some of the major research problems in aging where semi-competing risks play a role. In Sects. 3.3 and 3.4, we reviewed the statistical methods for semicompeting risks. Now, we return to the examples in Sect. 2 to illustrate how the different methods discussed so far can be used for addressing different questions. More general recommendations are summarized in Table 4.
Table 4.
Commonly used analytic approaches for competing risks problems: match the analysis method to research questions
| Problem | Research questions | Estimand | Methods | Remarks |
|---|---|---|---|---|
| Risk factor etiology | 1. What is the effect of risk factor X on the relative risk of developing disease Y? | Cause-specific hazard Eq.(1) | Separate Cox model for Y and Y-free death | Pros: based on observed data; appropriate for studying impact of X on the rate of Y amongst those still alive |
| Cons: susceptible to survival bias due to dependent censoring; does not quantify the cumulative impact of X on the whole population | ||||
| 2a. What is the effect of risk factor X on the risk of transition from being healthy to disease Y or death without disease or disease to death? | Cause-specific hazards Eqs. (4)-(6) | Illness-Death Model (Putter 2011) | Pros: based on observed data; characterization of dependence between Y and death in terms of λ12(t) and λ2(t) is easier to interpret | |
| Cons: susceptible to survival bias; lack of guidance on selecting appropriate Markovian assumptions in a given problem | ||||
| 2b. What is the dependence between death and disease Y? | Hazard Ratio λ12(t)/λ2(t), where λ12(t) and λ2(t) are respectively the hazard of death given that Y has or has not previously occurred; Eqs. (4)-(6) | Xu et al. (2010) | Pros: characterization of dependence between Y and death in terms of λ12(t) and λ2(t) is easier to interpret | |
| Cons: shared gamma frailty may not be appropriate | ||||
| Copula parameter in semicompeting risks models | Peng and Fine (2007), Hsieh and Huang (2012) | Cons: joint distribution is only defined in the upper wedge; interpretation of marginal distribution is problematic | ||
| 3. What is the effect of risk factor X on the absolute risk of developing disease Y in T years after accounting for the competing risk of disease-free death? | Cumulative Incidence Function Eq. (2) | Direct CIF regression Models (Fine and Gray 1999; Scheike and Zhang 2008) | Pros: based on observed data; being absolute risk, is easier to interpret and more relevant to policy making | |
| Cons: result of aggregate effects of X on Y and Y-free death; less relevant to the underlying biology of Y | ||||
| 4. What is the 'net' effect of risk factor X on the time to onset of disease Y in the absence of competing risk of death | Marginal survival function Sect. 3.4 | Semi-competing risks model (Peng and Fine 2006; Peng and Fine 2007) | Pros: best suited for studying disease etiology | |
| Cons: unrealistic to imagine situations where competing risk of death does not exist (Prentice et al. 1978); assumptions about potential failure times cannot be verified based on observed data | ||||
| Biomarker process | 1. What is the effect of rate of decline in biomarker X on the relative risk of developing disease Y? | Random effects of time trajectories of X; Cause-specific hazards | Semicompeting process models (Elashoff et al. 2007, 2008; Yu and Ghosh 2010) | Pros: accounts for non-ignorable missing data due to death; accounts for informative censoring of Y by death |
| Cons: assumptions on random effects are non-identifiable; convergence issues in model fitting in the case of highdimension parameter space | ||||
| 2. What is the effect of rate of decline in biomarker X on the probability of occurrence of Y versus Y-free death | Random effects of time trajectories of X; conditional cause-specific hazards; marginal probabilities of experiencing Y and Y-free death Eq. (15), (16) | Semicompeting process models (Elashoff et al. 2007; Yu and Ghosh 2010) | Pros: Same as above | |
| Cons: assumptions on random effects are non-identifiable | ||||
| Impact of interventions | 1. What is the efficacy of intervention X on disease Y? | Cause-specific hazard Eq. (1) | Separate Cox Model for Y and competing events (e.g., death, adverse events related to treatment) | Pros: Better suited for studying biological effect of X |
| Cons: Efficacy ≠ effectiveness; an efficacious intervention may not reduce the absolute risk of Y | ||||
| Marginal survival function Sect. (3.4) | Semi-competing risks model (Fine and Gray 1999; Peng and Fine 2007) | Cons: interpretation of marginal distribution is problematic | ||
| 2. How effective is the intervention X on disease Y in the real world | Cumulative incidence function Eq. (2) | Direct CIF regression Models (Fine and Gray 1999; Scheike and Zhang 2008) | Pros: allows to assess the balance between absolute risk of Y and accompanying levels of harm, particularly in vulnerable populations | |
| Cons: less relevant to biological effect of intervention X | ||||
| Routine screening | 1. When to stop routine screening of older adults for asymptomatic disease? | Based on prediction models of cumulative incidence with and without screening | Remark: This is a difficult problem that needs accurate predictions models for CIF, as well as decision-theoretic methods for individualization. |
6.1 Smoking as a risk factor for Alzheimer's disease (AD)
To evaluate whether smoking increases the risk of AD, both CSH and CIF can be used. Although the CSH analysis ignores the dependent censoring of AD by death, the resulting estimate of the effect of smoking can be validly interpreted as the ratio of instantaneous rate of developing AD among smokers compared to that of non-smokers at time t conditonal upon being alive at time t. It may, however, be argued that CSH, being instantaneous risk, does not quantify the cumulative impact of a risk factor on the population as a whole. The proportion of smokers who would develop AD by time t (i.e., CIF) cannot be estimated from the CSH without also estimating the CSH of AD-free mortality. The effect of smoking on the CIF of AD can be estimated using the methods of Fine and Gray (1999) or Scheike and Zhang (2008). The CIF is easier to interpret and may also be more relevant to policy decisions. However, CIF is not appropriate for studying the etiology of AD since it integrates the effects of smoking on both AD and mortality (Varadhan et al. 2010). Smoking could have a statistically significant effect on the CIF of AD even though it has no biological effect on AD, provided that smoking is a risk factor for mortality. To address this, the latent failure time models (i.e., models) of semicompeting risks data can be used to directly model the marginal survival distribution of AD as well as the dependence structure between AD and death via a copula. Although models have the advantage of directly informing the net risk for developing AD that would accrue if the possibility of AD-free death were removed, their usage in practice is still being debated because the estimation of net risk requires the conceptualization of latent failure times beyond observed data and, in turn unverifiable statistical assumptions about their distribution.
6.2 Aging-related change in muscle strength and mobility disability
The analysis of the impact of aging-related change in muscle strength on the development of mobility disability has to address two challenges: (1) non-ignorable missing data on strength due to disability-related informative dropout or mortality censoring and (2) dependent censoring of disability onset by death. To address both, the model of Elashoff in Sect. 4 can be applied. By modeling the random effects of and in Eqs. 15 and 16 as a linear function of the random effects from the longitudinal model (e.g., individual-specific rate of decline in strength), i.e., and , we could assess the relative impact of change in strength on the marginal probabilities of disability onset and disability-free death based on exp(θ), e.g., the odds ratio of experiencing mobility disability versus death associated with one unit decrease in the rate of decline in strength. The effects of change in strength on the risk of mobility disability, given that disability is destined to occur in ones lifetime, can be assessed by exp(ζk), the hazard ratio of experiencing event type k (i.e., mobility disability) associated with one unit decrease in the rate of decline in strength.
6.3 Multimorbidity in older adults
Whether considering clustering of multimorbid diseases within individuals or multiple occurrences of a single index disease among family members, multivariate failure time analysis with accounting for competing risks can be useful as an analytic tool. The associated literature offers a number of measures by which to describe disease-onset-time associations. One such measure is the cause-specific conditional hazard ratio which is interpreted as the factor of increase in one's hazard for (say) dementia onset at time s if one's relative has been diagnosed at time t as compared to one's relative remaining alive and dementia-free at t (Bandeen-Roche and Liang 2002; Cheng and Fine 2008; Shih and Albert 2010). Alternatively, Cheng et al. (2007) proposed measures comparing bivariate cumulative CSH to the product of the marginal counterparts, or doing likewise for the bivariate and marginal cumulative incidence functions. Methods accommodating regression of the component disease onset time distribution on covariates also have been proposed (e.g. Scheike et al. 2010). However, these methods have only been used to study index chronic disease in familial setting. The methods have not been targeted to the issue of multimorbidity in individuals, and regression models to describe the strength of association for multivariate failure times subject to competing risks are largely lacking. Thus, there remain fertile areas of inquiry on how best to analyze times to onset of multimorbid conditions in older adults.
6.4 Assessing the impact of interventions in older adults
The impact of an intervention can be assessed in two ways: its efficacy and its effectiveness (Sect. 2.4). Efficacy measures the ideal, biological effect of a treatment. To estimate treatment efficacy, it seems that we would want to isolate the effect of treatment on the nonterminal event of interest by hypothesizing in an ideal world where competing risks have been eliminated and where adherence to treatment is perfect. In other words, we would like to estimate the effect of the treatment on the marginal distribution of potential failure time of nonterminal event. The methods discussed in Sect. 3.4 can be useful here. However, we need to think carefully about the conceptual problems raised by Prentice et al. (1978) in the use of potential failure times. We consider this in more detail in Sect. 7.
The“real-world” effectiveness of interventions should be assessed in terms of their impact on the CIF. In other words, does the intervention reduce the absolute risk of the nonterminal event? Furthermore, an effective intervention should have a favorable benefit versus harm trade-off. It should not increase the rate of competing events. Therefore, it is also important to consider the impact of the intervention on all the CSH (Varadhan et al. 2010).
6.5 Routine screening in older adults
In Sect. 2.5, we briefly discussed a decision-making framework proposed by Walter and Covinsky (2001) to evaluate whether it is appropriate to screen an older adult for cancer. Their approach considers the baseline risk of dying of a screen-detectable cancer, the length of time that must elapse for screening to yield a survival benefit, and the probability of dying from causes unrelated to the cancer before realizing the intended benefit of screening. They suggest that older adults with severe disabilities due to their limited remaining life expectancy (less than 10-years) should not be screened for cancer. This framework has some shortcomings. First, it is based on the incorrect reasoning that the individual is highly unlikely to benefit if the remaining life expectancy is smaller than average time to benefit from screening. Second, it is predicated on the assumptions that the time to benefit from screening and the remaining life expectancy can be reliably estimated for the individual. Valid individual-level prediction models for the CIF of specific cancers (e.g., prostate cancer, colorectal cancer) need to be developed, with and without screening (Gulati 2011). The model predictions can then be incorporated into a decision-making framework to compare the expected utility of screening and not screening. There is plenty of scope for more work on this challenging problem.
7 Discussion
We highlight some of the important methodological needs and then suggest some strategies to facilitate the uptake of semicompeting risks methods by practitioners.
Causal interpretation of potential failure time models (class models) deserves more attention. Robins (1995a) addressed this for the bivariate location-shift model of LRW. He discussed two sufficient, but untestable, conditions required for the identification and causal interpretation of the treatment effect on the marginal distribution of nonterminal event. He called these conditions non-interaction and rank preservation assumptions. The non-interaction assumption is that the error distribution is the same across treatment groups; the rank preservation assumption is that for any two individuals i and j, if i dies before j under treatment A then i also dies before j under treatment B. Since Robins’ seminal paper, little attention has been paid to this conceptual issue. There are many interesting questions here. For instance, how biologically plausible is the rank preservation condition? Are there examples or situations where this assumption is not reasonable? Are there other, possibly less stringent, conditions than rank preservation that can provide a causal interpretation for the effect on the marginal distribution of nonterminal event?
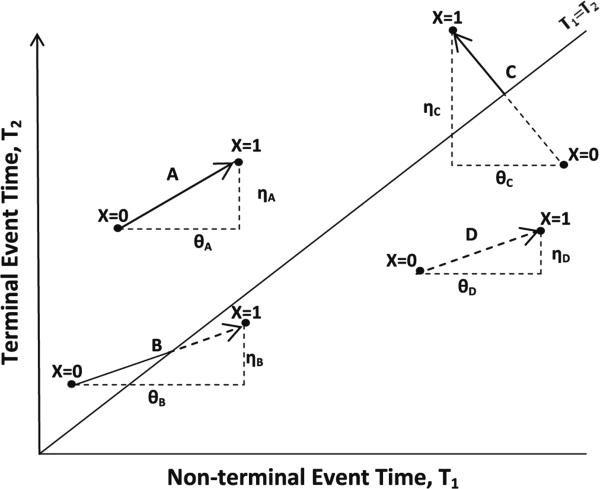
When can a treatment effect on the potential nonterminal event time be meaningfully defined in the presence of death? Is it meaningful to consider nonterminal event time after death? Considering different potential outcomes under different treatments might help clarify this (see Fig. 3). Suppose that a treatment (binary) has an effect on both nonterminal (T1) and terminal (T2) event times, with effects being θ and η, respectively. We assume that T2 can always be observed under the actual treatment received by an individual. We define 4 types of individuals on the basis of their potential failure times under two different values of treatment variable: type A individual who will experience the nonterminal event under both treatments (i.e. T1(X = j) ≤ T2(X = j), j = 0, 1); type B individual who will experience the nonterminal event only under treatment X = 0; type C individual who will experience the nonterminal event only under treatment X 1; and, type D individual who will not experience the nonterminal event under= either treatment (i.e. T1(X = j) > T2(X = j), j = 0, 1). It may be argued that treatment effect is meaningfully defined only for type A individuals, since it is impossible to observe the potential outcome T1(X = 1) for type B and type D individuals, and T1(X = 0) for type C individuals. There is some initial work on this general topic (Zhang and Rubin 2003; Frangakis et al. 2007). More theoretical work as well as demonstration in real applications is warranted.
Critical reviews evaluating the strengths and limitations of various and models can be useful. Comparative evaluations of different modeling approaches can be useful to practitioners in highlighting the relative strengths and weaknesses of the methods. Methods that attempt to answer the same scientific question can be compared and evaluated. The summary in Table 4 may be a useful starting point.
Tutorials demonstrating applications of semicompeting risks models (both and models) would also be valuable to practitioners.
Finally, we encourage the developers of competing risks methodology to write usable software. This would accelerate the translation and uptake of the novel methods by practitioners. A good model of such translation is the recent special issue on competing risks in the Journal of Statistical Software (Putter 2011).
Fig. 3.
Treatment effects in semicompeting risks
Acknowledgements
Ravi Varadhan is a Brookdale Leadership in Aging Fellow and would like to thank the Brookdale Foundation for their support. The authors would also like to thank the support from the Johns Hopkins Older Americans Independence Center under the NIA/NIH contract P30-AG02133 and the Johns Hopkins Alzheimer's Disease Research Center, NIA P50 AG005146.
Footnotes
Publisher's Disclaimer: Your article is protected by copyright and all rights are held exclusively by Springer Science +Business Media New York. This e-offprint is for personal use only and shall not be self-archived in electronic repositories. If you wish to self-archive your article, please use the accepted manuscript version for posting on your own website. You may further deposit the accepted manuscript version in any repository, provided it is only made publicly available 12 months after official publication or later and provided acknowledgement is given to the original source of publication and a link is inserted to the published article on Springer's website. The link must be accompanied by the following text: “The final publication is available at link.springer.com”.
Contributor Information
Ravi Varadhan, Division of Geriatric Medicine and Gerontology, The Center on Aging and Health, Johns Hopkins University, Baltimore, MD, USA.
Qian-Li Xue, Division of Geriatric Medicine and Gerontology, The Center on Aging and Health, Johns Hopkins University, Baltimore, MD, USA.
Karen Bandeen-Roche, Department of Biostatistics, Bloomberg School of Public Health, Johns Hopkins University, Baltimore, MD, USA.
References
- Aalen OO. Effects of frailty in survival analysis. Stat Methods Med Res. 1994;3:227–243. doi: 10.1177/096228029400300303. [DOI] [PubMed] [Google Scholar]
- Bandeen-Roche K, Liang KY. Modelling multivariate failure time associations in the presence of a competing risk. Biometrika. 2002;89:299–314. doi: 10.1093/biomet/asm091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd CM, Fortin M. Future of multimorbidity research: how should understanding of multimorbidity inform health system design? Public Health Rev. 2010;32:451–474. [Google Scholar]
- Cappola AR, O'Meara ES, Guo W, Bartz TM, Fried LP, Newman AB. Trajectories of dehydroepiandrosterone sulfate predict mortality in older adults: the cardiovascular health study. J Gerontol Med Sci. 2009;64:1268–1274. doi: 10.1093/gerona/glp129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y-H. Maximum likelihood analysis of semicompeting risks data with semiparametric regression models. Lifetime Data Anal. 2012;18:36–57. doi: 10.1007/s10985-011-9202-4. [DOI] [PubMed] [Google Scholar]
- Cheng Y, Fine JP. Nonparametric estimation of cause-specific cross hazard ratio with bivariate competing risks data. Biometrika. 2008;95:233–40. [Google Scholar]
- Cheng Y, Fine JP, Kosorok MR. Nonparametric association analysis of bivariate competing-risks data. J Am Stat Assoc. 2007;102:1407–1415. [Google Scholar]
- Day R, Bryant J, Lefkopoulou M. Adaptation of bivariate frailty models for prediction, with application to biological markers as prognostic indicators. Biometrika. 1997;84:45–56. [Google Scholar]
- Ding AA, Shi G, Wang W, Hsieh J-J. Marginal regression analysis for semi-competing risks data under dependent censoring. Scand J Stat. 2009;36:481–500. [Google Scholar]
- Elashoff RM, Li G, Li N. An approach to joint analysis of longitudinal measurements and competing risks failure time data. Stat Med. 2007;26:2813–2835. doi: 10.1002/sim.2749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elashoff RM, Li G, Li N. A joint model for longitudinal measurements and survival data in the presence of multiple failure types. Biometrics. 2008;64:762–771. doi: 10.1111/j.1541-0420.2007.00952.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fine JP, Gray RJ. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc. 1999;94:496–509. [Google Scholar]
- Fine JP, Jiang H, Chappell R. On semi-competing risks data. Biometrika. 2001;88:907–919. [Google Scholar]
- Fix E, Neyman J. A simple stochastic model to recovery, relapse, death and loss of patients. Hum Biol. 1951;23:204–241. [PubMed] [Google Scholar]
- Frangakis CE, Rubin DB, An M-W, Mackenzie E. Principal stratification designs to estimate input data missing due to death. Biometrics. 2007;63:641–662. doi: 10.1111/j.1541-0420.2007.00847_1.x. [DOI] [PubMed] [Google Scholar]
- Fries JF. Aging, natural death, and the compression of morbidity. N Engl J Med. 1980;303:1369–1370. doi: 10.1056/NEJM198007173030304. [DOI] [PubMed] [Google Scholar]
- Gulati R. what if i don't treat my psa-detected prostate cancer? Answers from three natural history models. Cancer Epidemiol Biomark Prev. 2011;55:3–24. doi: 10.1158/1055-9965.EPI-10-0718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson R, Diggle P, Dobson A. Joint modelling of longitudinal measurements and event time data. Biostatistics. 2000;1:465–480. doi: 10.1093/biostatistics/1.4.465. [DOI] [PubMed] [Google Scholar]
- Hernan MA, Alonso A, Logroscino G. Cigarette smoking and dementia: potential selection bias in the elderly. Epidemiology. 2008;19:448–450. doi: 10.1097/EDE.0b013e31816bbe14. [DOI] [PubMed] [Google Scholar]
- Hernan MA. The hazards of hazard ratios. Epidemiology. 2010;21:13–15. doi: 10.1097/EDE.0b013e3181c1ea43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hougaard P. Multi-state models: a review. Lifetime Data Anal. 1999;5:239–264. doi: 10.1023/a:1009672031531. [DOI] [PubMed] [Google Scholar]
- Hsieh J-J, Huang Y-T. Regression analysis based on conditional likelihood approach under semi-competing risks data. Lifetime Data Anal. 2012;103:302320. doi: 10.1007/s10985-012-9219-3. [DOI] [PubMed] [Google Scholar]
- Hu W, Li G, Li N. A bayesian approach to joint analysis of longitudinal measurements and competing risks failure time data. Stat Med. 2009;28:1601–1619. doi: 10.1002/sim.3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan GA, Haan MN, Wallace RB. Understanding changing risk factor associations with increasing age in adults. Annu Rev Public Health. 1999;20:89–108. doi: 10.1146/annurev.publhealth.20.1.89. [DOI] [PubMed] [Google Scholar]
- Lakhal L, Rivest LP, Abdous B. Estimating survival and association in a semicompeting risks model. Biometrics. 2008;64:180–188. doi: 10.1111/j.1541-0420.2007.00872.x. [DOI] [PubMed] [Google Scholar]
- Larson MG, Dinse GE. A mixture model for the regression-analysis of competing risks data. Appl Stat J R Stat Soc Ser C. 1985;34:201–211. [Google Scholar]
- Li N, Elashoff RM, Li G, Saver J. Joint modeling of longitudinal ordinal data and competing risks survival times and analysis of the ninds rt-pa stroke trial. Stat Med. 2010;29:546–557. doi: 10.1002/sim.3798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Robins JM, Wei LJ. Comparing two failure time distributions in the presence of dependent censoring. Biometrika. 1996;83:381–393. [Google Scholar]
- Lin OS, Kozarek RA, Schembre DB, et al. Screening colnoscopy in very elderly patients: prevalence of neoplasia and estimated impact on life expectancy. JAMA. 2006;295:2357–2365. doi: 10.1001/jama.295.20.2357. [DOI] [PubMed] [Google Scholar]
- Marengoni A, Angleman S, Melis R, et al. Aging with multimorbidity: a systematic review of the literature. Aging Res Rev. 2011;10:430–439. doi: 10.1016/j.arr.2011.03.003. [DOI] [PubMed] [Google Scholar]
- Ng SK, McLachlan GJ. An em-based semi-parametric mixture model approach to the regression analysis of competing-risks data. Stat Med. 2003;22:1097–1111. doi: 10.1002/sim.1371. [DOI] [PubMed] [Google Scholar]
- Peng L, Fine JP. Rank estimation of accelerated lifetime models with dependent censoring. J Am Stat Assoc. 2006;101:1085–1093. [Google Scholar]
- Peng L, Fine JP. Regression modeling of semicompeting risks data. Biometrics. 2007;63:96–108. doi: 10.1111/j.1541-0420.2006.00621.x. [DOI] [PubMed] [Google Scholar]
- Peterson AV., Jr Bounds for a joint distribution function with fixed sub-distribution functions: application to competing risks. Proc Natl Acad Sci. 1976;73:11–13. doi: 10.1073/pnas.73.1.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson B, Harrell FE. Partial proportional odds models for ordinal response variables. Appl Stat J R Stat Soc Ser C. 1990;39:205–217. [Google Scholar]
- Prentice RL, Kalbfleisch JD, Peterson AV, Jr, Flournoy N, Farewell VT, Breslow NE. The analysis of failure times in the presence of competing risks. Biometrics. 1978;34:541–554. [PubMed] [Google Scholar]
- Putter H. Special issue about competing risks and multi-state models. J Stat Softw. 2011;38:1–4. [Google Scholar]
- Rantanen T, Guralnik JM, Foley D, Masaki K, Leveille S, Curb JD, White L. Midlife hand grip strength as a predictor of old age disability. JAMA. 1999;281:558–560. doi: 10.1001/jama.281.6.558. [DOI] [PubMed] [Google Scholar]
- Robins JM. A new approach to causal inference in mortality studies with sustained exposure periods— application to control of the healthy worker survivor effect. Comput Mathl Appl. 1987;14:923–945. [Google Scholar]
- Robins JM. An analytic method for randomized trials with informative censoring: part i. Lifetime Data Anal. 1995a;1:241–254. doi: 10.1007/BF00985759. [DOI] [PubMed] [Google Scholar]
- Robins JM. An analytic method for randomized trials with informative censoring: part ii. Lifetime Data Anal. 1995b;1:417–434. doi: 10.1007/BF00985453. [DOI] [PubMed] [Google Scholar]
- Scheike TH, Zhang M-J. Flexible competing risks regression modeling and goodness-of-fit. Lifetime Data Anal. 2008;14:464–483. doi: 10.1007/s10985-008-9094-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheike TH, Sun Y, Zhang MJ, Jensen TK. A semiparametric random effects model for multivariate competing risks data. Biometrika. 2010;97:133–145. doi: 10.1093/biomet/asp082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih JH, Albert PS. Modeling familial association of ages at onset of disease in the presence of competing risk. Biometrics. 2010;66:1012–1023. doi: 10.1111/j.1541-0420.2009.01372.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slud EV, Rubinstein LV. Dependent competing risks and summary survival curves. Biometrika. 1983;70:643–649. [Google Scholar]
- Tsiatis A. A nonidentifiability aspect of the problem of competing risks. Proc Natl Acad Sci. 1975;72:20–22. doi: 10.1073/pnas.72.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varadhan R, Weiss CO, Segal JB, Wu AW, Scharfstein D, Boyd C. Evaluating health outcomes in the presence of competing risks: a review of statistical methods and clinical applications. Med Care. 2010;48:96–105. doi: 10.1097/MLR.0b013e3181d99107. [DOI] [PubMed] [Google Scholar]
- Vaupel JW, Yashin AI. Heterogeneitys ruses: some surprising effects of selection on population dynamics. Am Stat. 1985;39:176–185. [PubMed] [Google Scholar]
- Walter LC, Bertenthal D, Lindquist K, Konety BR. Psa screening among elderly men with limited life expectancies. J Am Med Assoc. 2006;296:2336–2342. doi: 10.1001/jama.296.19.2336. [DOI] [PubMed] [Google Scholar]
- Walter LC, Covinsky KE. Cancer screening in elderly patients: a framework for individualized decision making. J Am Med Assoc. 2001;285:2750–2756. doi: 10.1001/jama.285.21.2750. [DOI] [PubMed] [Google Scholar]
- Wang W. Estimating the association parameter for copula models under dependent censoring. J R Stat Soc. 2003;65:257–274. [Google Scholar]
- Weiss CO, Segal JB, Varadhan R. Assessing the applicability of trial evidence to a target sample in the presence of heterogeneity of treatment effect. Pharmacoepidemiol Drug Saf. 2012;21:121–129. doi: 10.1002/pds.3242. [DOI] [PubMed] [Google Scholar]
- Welch HG, Albertsen PC, Nease RF, Bubolz TA, Wasson JH. Estimating treatment benefits for the elderly: the effect of competing risks. Ann Intern Med. 1996;124:577–584. doi: 10.7326/0003-4819-124-6-199603150-00007. [DOI] [PubMed] [Google Scholar]
- Xu J, Kalbfeisch JD, Tai B. Statistical analysis of illness-death processes and semicompeting risks data. Biometrics. 2010;66:716–725. doi: 10.1111/j.1541-0420.2009.01340.x. [DOI] [PubMed] [Google Scholar]
- Xue QL, Walston JD, Fried LP, Beamer BA. Rate of decline in grip strength predicts the risk of falling, physical disability, and frailty: the womens health and aging study. Arch Intern Med. 2011;171:1119–1121. doi: 10.1001/archinternmed.2011.252. [DOI] [PubMed] [Google Scholar]
- Xue QL, Beamer BA, Chaves PHM, Guralnik JM, Fried LP. Heterogeneity in rate of decline in grip, hip, and knee strength and the risk of all-cause mortality: the women's health and aging study ii. J Am Geriatr Soc. 2010;58:2076–2084. doi: 10.1111/j.1532-5415.2010.03154.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu B, Ghosh P. Joint modeling for cognitive trajectory and risk of dementia in the presence of death. Biometrics. 2010;66:294–300. doi: 10.1111/j.1541-0420.2009.01261.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang JL, Rubin DB. Estimation of causal effects via principal stratification when some outcomes are truncated by death. J Educ Behav Stat. 2003;28:353–368. [Google Scholar]