Abstract
Purpose
A projection onto convex sets reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE) is developed to reduce motion-related artifacts, including respiration artifacts in abdominal imaging and aliasing artifacts in interleaved diffusion weighted imaging (DWI).
Theory
Images with reduced artifacts are reconstructed with an iterative POCS procedure that uses the coil sensitivity profile as a constraint. This method can be applied to data obtained with different pulse sequences and k-space trajectories. In addition, various constraints can be incorporated to stabilize the reconstruction of ill-conditioned matrices.
Methods
The POCSMUSE technique was applied to abdominal fast spin-echo imaging data, and its effectiveness in respiratory-triggered scans was evaluated. The POCSMUSE method was also applied to reduce aliasing artifacts due to shot-to-shot phase variations in interleaved DWI data corresponding to different k-space trajectories and matrix condition numbers.
Results
Experimental results show that the POCSMUSE technique can effectively reduce motion-related artifacts in data obtained with different pulse sequences, k-space trajectories and contrasts.
Conclusion
POCSMUSE is a general post-processing algorithm for reduction of motion-related artifacts. It is compatible with different pulse sequences, and can also be used to further reduce residual artifacts in data produced by existing motion artifact reduction methods.
Keywords: motion artifacts, projection onto convex sets, multiplexed sensitivity encoding, artifact correction
Introduction
Patient motion is the most common source of inconsistencies among different portions of MRI k-space data. Motion-induced k-space data inconsistencies are particularly pronounced in time-consuming acquisition protocols such as spin warp imaging, and the resultant artifacts may significantly reduce the accuracy and diagnostic value of the reconstructed images.
In the past two decades, numerous techniques have been investigated to improve the motion tolerance of MRI. For example, the ’periodically rotated overlapping parallel lines with enhanced reconstruction’ (PROPELLER) technique is designed to reduce motion-related artifacts in many applications, including neuroimaging in the presence of head motion and free-breathing body MRI [1]. A number of other strategies are available for reducing motion-related artifacts originating from specific sources: First, the respiration-induced artifacts in abdominal MRI can usually be reduced with respiratory-triggered scans. However, the residual artifacts may still be significant when the respiratory frequency changes over time, particularly in data obtained from older adults and seriously ill patients. Second, single-shot echo-planar imaging (EPI) can be used to reduce motion-induced phase variations compared with multi-shot methods; this is particularly useful in diffusion-weighted imaging (DWI), where phase variations are significantly amplified by the diffusion-sensitizing gradients. However, the spatial resolution of single-shot EPI based DWI is limited, even when the parallel imaging method is incorporated [2, 3]. Recent papers show that high-resolution DWI can be achieved with multi-shot EPI or multi-shot spiral imaging, after correcting motion-induced phase inconsistencies among multiple EPI or spiral k-space segments [4–18]. In these techniques, the phase inconsistencies among multiple segments are first measured either from navigator echoes [5, 6, 7, 8, 11, 16] or by comparing complex-domain images reconstructed from different segments using a parallel MRI algorithm, as in the recently reported multiplexed sensitivity encoding (MUSE) algorithm [18]. However, (1) the inclusion of navigator echoes reduces the scan throughput; (2) the existing MUSE-DWI implementation can only be applied to data obtained with regular Cartesian trajectories.
Although motion-related artifacts in MRI data can be largely reduced with existing technologies, there is still a strong need for further developing and improving motion artifact correction algorithms for the following reasons. First, the residual artifacts in MRI data corrected with conventional procedures may still degrade clinical MRI quality (e.g., in respiratory-triggered scans), and it would be ideal if those residual artifacts can be further reduced with an additional post-processing procedure. Second, many existing artifact reduction methods rely on specific pulse sequences (e.g., PROPELLER; multi-shot DWI with navigator echoes), and it would be beneficial for both the clinical and research communities if algorithms that are independent of specific pulse sequences become available.
To address this need, we report a general post-processing algorithm, which uses the RF coil sensitivity profile as a constraint to minimize motion-induced inconsistencies among different portions of the k-space data. This algorithm has the following strengths. First, it is capable of further reducing residual motion-related artifacts in MRI data produced by existing motion artifact reduction procedures. Second, the new algorithm is generally compatible with MRI data obtained with different pulse sequences (e.g., fast spin-echo (FSE); multi-shot EPI; spin-warp imaging) and k-space filling trajectories (e.g., Cartesian and non-Cartesian scans), addressing a limitation of the previously reported MUSE method that is compatible only with regularly sampled Cartesian k-space data. Third, this algorithm can be used to suppress motion-related artifacts of different patterns (e.g., artifacts resulting from nonlinear motion in abdominal FSE; artifacts resulting from shot-to-shot phase variations in multi-shot EPI based DWI).
Theory
This section describes the principles of reducing artifacts due to k-space data inconsistency, using the RF coil sensitivity profile as a constraint, through either the existing MUSE or the new POCSMUSE methods.
SENSE reconstruction of undersampled data versus MUSE reconstruction of fully sampled data
Using the sensitivity encoding (SENSE) technique [2], a full-FOV image can be reconstructed from regularly undersampled k-space data acquired with multi-channel coils. Here, we briefly review the SENSE algorithm using a 4× undersampled scan as an example, with the k-space scan trajectory and the corresponding point spread function (PSF) shown in Figures 1a (solid lines) and 1b, respectively. The aliased image reconstructed from the undersampled and zero-filled k-space data set can be represented by Equation 1, where uj represents the aliased signal obtained by the j-th coil (j = 1 to Nc; with Nc being the total number of coil elements); Sj is the coil sensitivity profile for the j-th coil; and p is the un-aliased full-FOV image to be reconstructed.
Figure 1.
(a) An example of regular sub-sampling in k-space (usually achieved with 4-shot segmented MRI). (b) The PSF corresponding to the first segment of (a). (c) The true (unaliased) image-domain signals. (d) The aliased image-domain signal resulting from the k-space undersampling (e.g., the first segment only of (a)) with the aliasing pattern predictable by the PSF. (e) An example of irregular sub-sampling in k-space. (f) The complicated PSF corresponding to the first segment of (e).
| (1) |
With known coil sensitivity profiles, the full-FOV image p can be reconstructed by solving Equation 1 through matrix inversion.
Although the SENSE algorithm was originally designed for image reconstruction of undersampled k-space data, the mathematical framework can be extended to perform multiplexed sensitivity encoding of fully sampled k-space data, comprising multiple segments of subsampled k-space data (e.g., solid and dashed ky lines in Figure 1a). For example, Equation 1 can be modified to jointly incorporate all four segments of the k-space data shown in Figure 1a, considering a case where the unaliased source image p remains consistent across all four segments, as shown in Equation 2.
| (2) |
where uj,k represents the aliased signal detected by the j-th coil in the k-th segment (k = 1 to 4), and the phase term reflects the relative k-space trajectory shift among the four segments. It can be seen that the unaliased source signals in pixels p(x, y + r × FOVy/4) (with r = 0 to 3) can be jointly calculated from full k-space data through matrix inversion.
As compared with a direct 2D Fourier transform of the full k-space data, the image reconstruction through solving Equation 2 imposes a constraint (i.e., the coil sensitivity profile) during the reconstruction so that the reconstructed full-FOV image corresponds to a solution with the shortest Euclidean distance from data in all four segments, even in the presence of inconsistencies across the four segments in Figure 1a. This reconstruction algorithm is termed multiplexed sensitivity encoding (MUSE), which can be used to reduce artifacts in images reconstructed with 2D Fourier transform.
It should be noted that the conventional SENSE algorithm has a major limitation in that the number of coil elements should be greater than the acceleration factor (e.g., 4 in our example). In contrast, the MUSE matrix inversion (e.g., Equation 2) is designed for processing full or near-full k-space data, and is applicable even when the number of coil elements is smaller than the number of k-space segments. For example, for a 4-segment data set (e.g., 4-shot FSE; 4-shot EPI) obtained with a 3-channel coil, the matrix inversion of Equation 2 solves 4 unknowns from 12 equations.
Challenges in performing MUSE reconstruction with irregularly sampled Cartesian or non-Cartesian k-space data
Here we generalize Equation 2 to a matrix form, so that the concept of MUSE can be applied to k-space data obtained with either regularly or irregularly sub-sampled patterns in Cartesian k-space (e.g., as shown in Figures 1a and 1e, respectively). Generally, the MUSE reconstruction of a full-FOV image (of matrix size N × N) from multiple segments (1 to Ns) of sub-sampled Cartesian k-space data can be achieved by solving Equation 3.
| (3) |
where u is a vector of length N2Nc containing the complex signals obtained from all segments and all coils (1 to Nc); p is a vector of length N2 denoting the pixel-wise complex values of the un-aliased full-FOV image to be reconstructed; S is a matrix of size N2Nc × N2 describing the coil sensitivity profiles; Φ is a matrix of size N2NcNs × N2Nc representing the phase variation among segments; and E is a matrix of size N2Nc × N2NcNs representing the PSF corresponding to the chosen sampling pattern. In many applications (e.g., multi-shot T2-weighted FSE), the phase variation among k-space segments is insignificant and thus Φ becomes a matrix comprising Ns identity matrices of size N2Nc × N2Nc.
For multi-shot MRI comprising multiple segments of regularly sub-sampled k-space data (e.g., solid and dashed ky lines in Figure 1a), the corresponding PSF are a set of sharp peaks (Figure 1b). In this case, E in Equation 3 contains the weightings of the PSF in a relatively simple form (e.g., as illustrated by Figures 1c and 1d), and many of the matrix elements are zeros. Therefore, Equation 3 can be decomposed into multiple equations of a small matrix size (e.g., Equation 2) that can be solved with matrix inversion. However, as will be described in the Methods section, in some pulse sequences the sampling patterns may not always be as regular as that shown in Figure 1a. When a more complicated sampling pattern is chosen (e.g., Figure 1e), the corresponding PSF are no longer a set of sharp peaks (e.g., Figure 1f). In this case, Equation 3 of a very large matrix size cannot be decomposed into multiple equations, and the matrix inversion based MUSE reconstruction would be highly numerically challenging and computationally expensive [3]. Similarly, the MUSE reconstruction for data obtained with non-Cartesian sampling patterns may not be easily achievable with matrix inversion. To address this limitation, we describe a new POCSMUSE algorithm below.
The POCSMUSE reconstruction
The POCS algorithm has been successfully used in various MRI applications [19, 20, 21, 22, 23]. For example, Samsonov et al. have integrated POCS and SENSE into a framework, termed POCSENSE [24], to perform parallel MRI reconstruction for irregularly undersampled k-space data. Inspired by the POCSENSE method, here we integrate POCS and multiplexed sensitivity encoding, performing iterative MUSE reconstruction of full k-space data comprising multiple segments of regularly or irregularly sub-sampled data.
The POCSMUSE framework is schematically illustrated in Figure 2a, comprising the following steps. Step 1: An initial guess of the unaliased source image Pi (i = 0 at first iteration) is used as the input, which is then multiplied with the sensitivity profiles of coils Sj (j = 1 ~ Nc) and the segment-specific phase term vk (k = 1 ~ Ns) that can be ignored (i.e., vk = 1) when phase variations among k-space segments are insignificant (e.g., in multishot T2-weighted FSE). Step 2: Images of all coils and segments generated by step 1 are transformed (with inverse 2D Fourier transform) to k-space signals, which are then projected to (j = 1 ~ Nc and k = 1 ~ Ns). As shown in Figure 2a, the data projection to is achieved by replacing certain ky lines of the calculated signals with the experimentally acquired signals. Step 3: The projected k-space signals are transformed (with 2D Fourier transform) to image-domain complex signals , which are then averaged to generate an unaliased source image Pi+1 for the subsequent iteration, as shown in Equation 4.
Figure 2.
A schematic diagram of the Cartesian (a) and non-Cartesian (b) POCSMUSE implementations.
| (4) |
where
| (5) |
and is the complex conjugate of the sensitivity profiles. In data acquired with certain pulse sequences (e.g., interleaved EPI based DWI), the phase variations among k-space segments may be significant, as described by the segment-specific phase term vk that will be discussed later (Equation 8). Step 4: The procedures described above are iterated until the unaliased source image converges, i.e., when the absolute variation of an iteration (i.e., ei+1 in Equation 6) falls below a predefined tolerance.
| (6) |
As compared with the original MUSE implementation, the POCSMUSE method is a more general approach and can be used to process data obtained with arbitrary k-space trajectories and complicated PSF.
MUSE and POCSMUSE reconstruction of fully-sampled data in the presence of significant phase variations among k-space segments
When the phase variation among k-space segments is insignificant, the RF coil sensitivity profile is the only constraint for both MUSE (Equation 2) and POCSMUSE (Figure 2 with vk = 1) reconstruction procedures. In certain applications (e.g., multi-shot EPI based DWI), the significant shot-to-shot phase variation should be included in both MUSE and POCSMUSE as an additional constraint, in addition to the coil sensitivity profile. In this case, Equation 2 should be replaced with Equation 7 [18].
| (7) |
| (8) |
where p represents the un-aliased image that is expected to be consistent across segments, and ϕk is the motion-induced phase error across the four shots. It should be noted that the background phase independent of motion is included in p for simplicity.
Segment-specific phase variation terms vk should be known, before the unknown p can be calculated with matrix inversion. As used in the MUSE algorithm [18], segment-specific phase variations can be estimated from the SENSE reconstruction of an individual k-space segment (Equation 9):
| (9) |
where qk are the full-FOV images estimated by the SENSE method from individual k-space segments, and Hann represents the Hanning window based smoothing operation.
Since the SENSE method must first be used to estimate significant shot-to-shot phase variations (Equation 9), the number of segments cannot be larger than the number of receiving coil elements in the MUSE reconstruction that takes shot-to-shot phase variations into consideration. To address this limitation, we propose to use an additional phase smoothness constraint in the POCSMUSE reconstruction procedure. Specifically, since the phase terms are expected to be smooth spatially, we use a Hanning kernel to smooth the phase terms of the POCSMUSE produced images from individual segments. The POCSMUSE algorithm with phase smoothness constraint is similar to that shown in Figure 2, except that the averaging of image-domain complex signals (i.e. Avg module in Figure 2) comprises three steps: 1) (j = 1 ~ Nc and k = 1 ~ Ns) are first averaged to produce (Equation 10), eliminating the modulation of coil sensitivity profiles in individual segments.
| (10) |
where
| (11) |
2) Segment-specific phase variations vk+1 for the subsequent iteration are computed with Equation 12.
| (12) |
3) Images from individual segments are averaged to generate an unaliased source image Pi+1 for the subsequent iteration using Equation 13.
| (13) |
where
| (14) |
This phase smoothness constraint can mitigate the noise amplification from an ill-conditioned problem when estimating phase variations among multiple k-space segments.
Non-Cartesian POCSMUSE
The POCSMUSE algorithm can be applied to non-Cartesian k-space data, after making two modifications to the procedure shown in Figure 2a. First, a k-space data regridding operation [27, 28] is included in the algorithm. Second, the data projection for non-Cartesian POCSMUSE is implemented in image domain rather than k-space domain. As schematically illustrated in Figure 2b, the non-Cartesian POCSMUSE comprises the following steps. Step 1: An initial guess of the unaliased source image Pi (i = 0 at first iteration) in Cartesian grid is used as the input, which is then multiplied with coil sensitivity profiles Sj (j = 1 ~ Nc) and segment-specific phase terms vk (k = 1 ~ Ns). Step 2: The images of all coils and segments generated by step 1 are zero-padded and their matrix size is doubled. Step 3: The double-size images are transformed (with an inverse regridding operation) to non-Cartesian k-space signals (i.e., along the original non-Cartesian trajectory). Step 4: The differences between the original and updated k-space values (from step 3) are calculated, and then transformed (with regridding operation and 2D FFT) to images in Cartesian grid. Step 5: The difference images generated by step 4 are trimmed and subtracted from to produce the projected image-domain complex signals . Step 5: are then averaged to generate an unaliased source image Pi+1 for the subsequent iteration, as shown in Equation 4. Note that steps 2 to 4 represent the ’data projection’ for non-Cartesian data.
Methods
The developed POCSMUSE technique was evaluated with human MRI experiments, using a 3 Tesla system (General Electric, Waukesha WI, USA), by testing its effectiveness in removing motion-related artifacts. The experiments on human subjects were compliant with the standards established by the Institutional Review Boards of Duke University Medical Center.
Artifact removal for abdominal T2-weighted FSE imaging: respiratory-triggered acquisition
Motion-related artifacts in abdominal imaging are often not completely removed with respiratory triggering, particularly when the respiratory frequency changes during scans. To evaluate the feasibility of using POCSMUSE to further reduce residual motion artifacts in respiratory-triggered data, we conducted abdominal T2-weighted FSE imaging with respiratory triggering.
FSE data were acquired from three healthy volunteers, using an 8-channel receiving coil, with the following scan parameters: effective TR = 6667 ms, TE = 101 ms, slice thickness = 8 mm, number of slices = 9, FOV = 40×40 cm2, in-plane matrix size = 256 × 256, and echo train length = 16. Table 1 lists the ky lines obtained from each FSE segment in our experiments. In order to simultaneously achieve both high scan efficiency and smooth point spread function in multi-shot T2-weighted FSE imaging, an irregular k-space sampling scheme needs to be chosen, as shown in Table 1.
Table 1.
The acquired ky lines in each segment of 16-shot FSE
| Segment # | The acquired ky lines (ETL = 16) |
|---|---|
| 1 | 221,213,205,197…125,117,109,101 |
| 2 | 222,214,206,198…126,118,110,102 |
| 3 | 223,215,207,199…127,119,111,103 |
| 4 | 224,216,208,200…128,120,112,104 |
| 5 | 225,217,209,201…129,121,113,105 |
| 6 | 226,218,210,202…130,122,114,106 |
| 7 | 227,219,211,203…131,123,115,107 |
| 8 | 228,220,212,204…132,124,116,108 |
| 9 | 229,237,245,253,5,13,21,29…93 |
| 10 | 230,238,246,254,6,14,22,30…94 |
| 11 | 231,239,247,255,7,15,23,31…95 |
| 12 | 232,240,248,256,8,16,24,32…96 |
| 13 | 233,241,249,1,9,17,25,33,…97 |
| 14 | 234,242,250,2,10,18,26,34…98 |
| 15 | 235,243,251,3,11,19,27,35…99 |
| 16 | 236,244,252,4,12,20,28,36…100 |
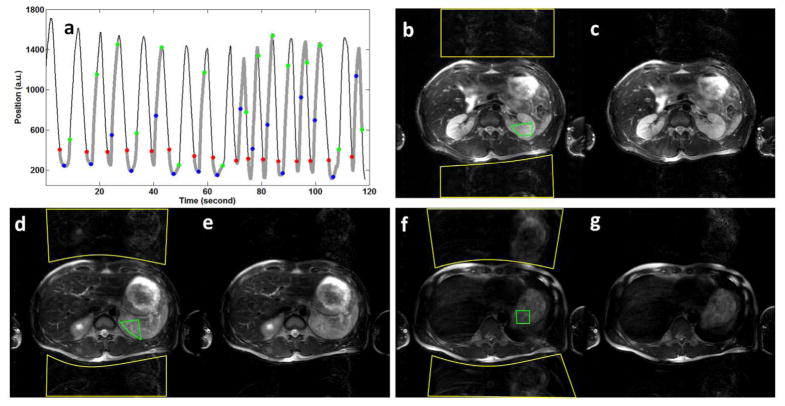
The respiratory waveforms and the scan trigger point were recorded, and the k-space data inconsistency in each individual slice was quantified based on its standard deviation (STD) in the corresponding respiratory phases. For example, Figure 3a shows the respiratory waveforms (thin line), the scan trigger point (red) in each respiratory phase, and the MRI acquisition window (thick line) for one of the subjects. It can be seen that the k-space data of the first slice (red dots) were acquired at time points corresponding to approximately the same respiratory phase (i.e., with a low STD in the corresponding respiratory phase: indicative of less k-space data inconsistency). Because of the changes in respiratory frequency during scans, the k-space data of other slices (e.g., the 4th slice: blue dots; the 9th slice: green dots) were acquired at time points corresponding to different respiratory phases (i.e., with a higher STD in the corresponding respiratory phases: indicative of more k-space data inconsistency).
Figure 3.
Experimental results of respiratory-triggered abdominal FSE imaging: (a) shows the respiratory waveforms, with red, blue and green dots representing trigger points of the 1st, 4th, and 9th slices, respectively. (b), (d) and (f) are images of the 1st, 4th, and 9th slices, respectively, reconstructed with 2D Fourier transform; (c), (e) and (g) are images of the 1st, 4th, and 9th slices, respectively, reconstructed with the POCSMUSE method.
The acquired respiratory-triggered FSE data were reconstructed with two approaches: 1) 2D Fourier transform and 2) the POCSMUSE algorithm. Since the shot-to-shot phase variation is expected to be insignificant in T2-weighted FSE data, the segment-specific phase term vk in Figure 2 was set to 1 in the POCSMUSE reconstruction of FSE data. The ghost-to-signal ratios (GSRs) of all reconstructed images were calculated.
Artifact removal for abdominal T2-weighted FSE imaging: a hybrid simulation study
Ideally, the performance of the POCSMUSE technique in removing motion-related artifacts of respiratory-triggered abdominal MRI data corresponding to different breathing patterns and frequencies should be evaluated in a large patient population. As an initial proof of concept study, we used a hybrid simulation to assess the POCSMUSE technique in the presence of different k-space data inconsistency levels.
We acquired four consecutive sets of free-breathing abdominal FSE imaging data from a healthy volunteer, using the same coil and scan parameters as in the respiratory-triggered acquisition. The respiratory waveforms and the scan trigger point were recorded.
Ten sets of k-space data corresponding to different levels of inconsistencies were produced from the acquired free-breathing FSE data with the following steps. First, we randomly selected 10000 patterns from all 416 possible grouping patterns that could be used to produce a single full k-space data from the acquired four data sets. Second, the STD values of the corresponding respiratory phases, indicative of the k-space data inconsistency level, were calculated from each of those 10000 data sets. Third, the 10000 data sets were ranked based on the levels of the k-space data inconsistency, and 10 final data sets with different levels of inconsistency (corresponding to 5%, 15%… to 95% of the ranked STD values) were identified. Fourth, images were reconstructed from these 10 selected data sets using either 2D Fourier transform or POCSMUSE, and the artifact levels of the reconstructed images were quantitatively assessed.
Artifact removal for interleaved EPI based DWI
Baseline T2-weighted and diffusion-weighted imaging data were acquired with a 4-shot interleaved EPI pulse sequence from 3 healthy volunteers using an 8-channel coil. The scan parameters included TR = 5 s, TE = 65 ms, slice thickness = 5 mm, FOV = 240×240 mm2, in-plane matrix size = 256×256 after partial-Fourier reconstruction, number of partial-Fourier over-scan ky lines = 24, b-factor = 800 s/mm2, number of diffusion weighting directions = 15, and number of baseline (b = 0) images = 4. Two pre-processing procedures were carried out. First, phase errors due to odd-even-echo inconsistency were measured from the baseline T2-weighted EPI using the phase-cycled reconstruction procedure [25]. The measured phase error information was then used to remove Nyquist artifacts in both baseline T2-weighted and diffusion-weighted images. Second, the coil sensitivity profiles were estimated from the baseline T2-weighted images. A series of assessments were then performed:
To test the performance of POCSMUSE on well-conditioned data (i.e., 4-shot EPI based DWI data from an 8-channel coil), we processed Nyquist-corrected DWI data with the following steps. First, using the POCSENSE reconstruction procedure, four full-FOV images were reconstructed from four segments respectively. Second, intersegment phase variations were estimated using Equation 9. Third, similar to the recently reported Homodyne-MUSE reconstruction of partial-Fourier DWI data [26], the partial-Fourier k-space data were multiplied by a ramp weighting function in preparation for the subsequent POCSMUSE reconstruction. Fourth, using the Homodyne-POCSMUSE algorithm (which is identical to POCSMUSE except that the input partial-Fourier k-space data are multiplied by a ramp weighting function), aliasing-free DWI images were produced from the smoothed phase variation maps and the coil sensitivity profiles. In addition, the Nyquist-corrected DWI data were processed with the original Homodyne-MUSE method to produce another set of aliasing-free images for comparison. The initial image for the POCSMUSE iterative process was a zero matrix, and the stopping tolerance (Equation 6) was set to 0.0005.
To assess the performance of POCSMUSE on data with ill-conditioned reconstruction matrices (e.g., 4-shot EPI based DWI data from a 3-channel coil), we selected DWI k-space data randomly from three of the coil elements for image reconstruction with the following steps. First, using the POCSENSE reconstruction procedure, four full-FOV images were reconstructed from four segments respectively. Second, the inter-segment phase variations were calculated using Equation 9. Third, the partial-Fourier k-space data were multiplied by a ramp weighting function in preparation for the subsequent Homodyne-POCSMUSE reconstruction. Fourth, using the Homodyne-POCSMUSE algorithm with an additional phase smoothness constraint, aliasing-free DWI images were produced from the smoothed phase variation maps and the coil sensitivity profiles. In addition, the Nyquist-corrected DWI data (from 3 of the coil elements) were processed with the original Homodyne-POCSMUSE method to produce another set of images for comparison. The initial image for the POCSMUSE iterative process was a zero matrix, and the stopping tolerance was set to 0.001. We chose a higher stopping tolerance for ill-condition reconstruction (in which more POCS iterations were needed), in order to reduce the computation time.
Artifact removal for brain DWI with spiral k-space trajectory
Multishot spiral DTI data from a healthy volunteer were acquired in ten contiguous axial slices at the top of the brain with a single spin-echo spiral sequence and a 32-channel phased-array head coil (Nova Medical, Wilmington, MA). The scan parameters included TR = 2 s, TE = 51 ms, FOV = 160×160 mm2, matrix size = 256×256 (for both the acquisition and reconstruction), in-plane resolution = 0.625×0.625 mm2, slice thickness = 3 mm, b-factor = 800 s/mm2, number of diffusion weighting directions = 10, and number of baseline (b = 0) images = 1. A spatial spectral pulse was used for fat suppression and the k-space trajectory was a six-shot constant-density spiral-out trajectory with 10,892 data points per interleaf and a readout duration of 44 ms. The coil sensitivity profiles were estimated from the baseline T2-weighted images.
To assess the feasibility of using the POCSMUSE method to reconstruct DWI images from k-space data obtained with non-Cartesian trajectories, we processed the interleaved spiral DWI data with the following steps. First, using the POCSENSE reconstruction procedure, six full-FOV images were reconstructed from six segments respectively. Second, the intersegment phase variations were estimated using Equation 9. Third, using the non-Cartesian POCSMUSE algorithm, images were produced from interleaved spiral DWI data, smoothed phase variation maps and the coil sensitivity profiles. The regridding and inverse regridding operations were implemented with a Kaiser-Bessel kernel (with kernel size L = 3 and sidelobe suppression parameter B = 14.1372) for convolution and an over-sampling factor of 2. The initial image for the POCSMUSE iterative process was a zero matrix, and the stopping tolerance was set to 0.0005.
The signal-to-noise ratios (SNRs) of brain DWI data were quantified by measuring the ratio of the mean value to the standard deviation of signals within chosen ROIs. All data reconstruction and analysis procedures were implemented with Matlab (The MathWorks, Natick, MA) running on a Windows computer equipped with an Intel Core i5 CPU (1.6 GHz) and a 6GB memory.
Results
Artifact removal for abdominal T2-weighted FSE imaging: respiratory-triggered acquisition
Figure 3 shows the results of our respiratory-triggered FSE scans. As described in the Methods section, Figure 3a shows that the k-space data of the first slice (red dots) were acquired at time points corresponding to approximately the same respiratory phase (with STD = 54.4 a.u.), and the k-space data of other slices (e.g., the 4th slice: blue dots; the 9th slice: green dots) were acquired at time points corresponding to more different respiratory phases (with STD = 326.7 and 495.5 a.u. for the 4th and 9th slices, respectively).
Figures 3b, 3d, and 3f show images of the 1st, 4th and 9th slices, respectively, reconstructed with 2D Fourier transform. It can be seen that there are substantial aliasing artifacts despite respiratory triggering, and the GSRs in these 3 slices are 0.38, 0.45 and 0.61, respectively. The ROIs for ghost and parent-image-signal measurements are outlined by yellow and green lines, respectively. Figures 3c, 3e, and 3g show that the aliasing artifacts can be significantly reduced with the POCSMUSE algorithm, and the GSRs in these 3 slices are 0.22, 0.23 and 0.32, respectively. The ratios of the artifact reduction are 43.1%, 45.1% and 46.2% for the three selected slices, after applying the POCSMUSE technique.
The number of POCSMUSE iterations for image reconstruction was 76, and the total POCSMUSE computation time was 273.1 seconds per slice.
Artifact removal for abdominal T2-weighted FSE imaging: a hybrid simulation study
Figure 4a shows the recorded respiratory waveform of four consecutive free-breathing FSE data. The blue dots indicate the time points when the re-grouped k-space data set with the minimal data inconsistency (i.e., the one with the lowest STD among 10 re-grouped data sets) were acquired, and the red dots indicate the time points when the re-grouped k-space data set with the maximal data inconsistency were acquired.
Figure 4.
Results of the hybrid simulation study: (a) shows the respiratory waveforms of four consecutive free-breathing FSE scans, with blue dots representing the k-space trigger points for the hybrid-simulated data set with the lowest data inconsistency level, and red dots representing the k-space trigger points for the hybrid-simulated data set with the highest data inconsistency level. (b) shows the GSR values in images reconstructed with 2D Fourier transform (black bars) and POCSMUSE (yellow bars) corresponding to different data inconsistency levels.
Figure 4b quantitatively compares the artifact levels (measured by GSR) in images reconstructed with 2D Fourier transform (black bars) and POCSMUSE (yellow bars) from 10 re-grouped data sets with different levels of data inconsistency. The STDs values are 130.8 (data of blue dots in Figure 4a), 399.4, 423.3, 441.4, 455.2, 470.1, 485.0, 516.6, 540.2 and 632.9 (data of red dots in Figure 4a). It can be seen that POCSMUSE can significantly reduce aliasing artifacts regardless of the level of k-space data inconsistency. The artifact reduction ratios are 46.1%, 45.9%, 33.0%, 32.6%, 30.9%, 34.5%, 32.1%, 36.1%, 34.6% and 35.5%.
The number of POCSMUSE iterations for POCSMUSE reconstruction was 78, and the total POCSMUSE computation time was 283.8 seconds per image.
Artifact removal for interleaved EPI based DWI
Figure 5a shows 4-shot DWI images (8-channel coil) of two selected slices reconstructed with 2D Fourier transform. Because of shot-to-shot phase variations, these images are severely corrupted by aliasing artifacts. As shown in Figure 5b, the aliasing artifacts can be effectively removed using the previously reported Homodyne-MUSE method. Using the new Homodyne-POCSMUSE reconstruction procedure (Figure 5c), the reconstructed images have comparable quality as that produced with the Homodyne-MUSE method. The SNRs of Homodyne-MUSE produced images are 9.16 (upper image: measured from the indicated ROI) and 12.68 (lower image: measured from the indicated ROI), and the SNRs of Homodyne-POCSMUSE produced images are 9.17 (upper image) and 12.68 (lower image). The number of POCSMUSE iterations was 98, and the POCSMUSE computation time was 290.1 seconds per slice (Figure 5c). The MUSE computation time was 8 seconds per slice (Figure 5b). The condition number (i.e., the ratio of the largest to the smallest singular value of the inversion matrix) of the data shown in Figure 5 was 29639.
Figure 5.
Reconstruction of well-conditioned brain DWI data (4-shot DWI; 8-channel coil) with (a) 2D Fourier transform, (b) Homodyne-MUSE, and (c) Homodyne-POCSMUSE.
Figure 6 compares images of two selected slices reconstructed with (a) 2D Fourier transform, (b) the Homodyne-POCSMUSE, and (c) the new Homodyne-POCSMUSE method with phase smoothness constraint from data with ill-conditioned reconstruction matrices (4-shot DWI; 3-channel coil). As expected, images reconstructed with 2D Fourier transform are corrupted by aliasing artifacts (Figure 6a). Although the aliasing artifacts can be reduced with Homodyne-POCSMUSE (Figure 6b), the residual artifacts are pronounced because the initial POCSENSE-based estimation of shot-to-shot phase variations is not accurate due to ill-conditioning. Figure 7a shows the shot-to-shot phase variations (from 4 segments of a DWI data set) estimated by an ill-conditioned POCSENSE reconstruction (4 unknowns; 3 equations). After a simple Hanning filtering, the produced phase maps are smooth but still degraded by aliasing artifacts (indicated by arrows in Figure 7b). The inaccuracy in phase estimation results in artifacts in the POCSMUSE-produced images shown in Figure 6b.
Figure 6.
Reconstruction of brain DWI data with ill-conditioned reconstruction matrices (4-shot DWI; 3-channel coil) with (a) 2D Fourier transform, (b) Homodyne-POCSMUSE, and (c) Homodyne-POCSMUSE with phase smoothness constraint.
Figure 7.
(a) shows shot-to-shot phase variations (from 4 segments of a DWI data set) estimated by an ill-conditioned POCSENSE reconstruction (4 unknowns; 3 equations). (b) shows that the phase maps produced by a simple Hanning filtering are affected by aliasing artifacts. (c) shows shot-to-shot phase variations obtained from the last POCSMUSE iteration with phase smoothness constraint. (d) shows shot-to-shot phase maps estimated from a POCSENSE reconstruction of all 8 coil elements (4 unknowns; 8 equations).
Using the Homodyne-POCSMUSE with phase smoothness constraint, the reconstructed images have significantly improved quality (Figure 6c). Figure 7c shows shot-to-shot phase variations obtained from the last iteration of the POCSMUSE with phase smoothness constraint. It can be seen that the aliasing artifact in the phase maps is significantly reduced (as compared with Figure 7b), and the estimated phase values are closer to those obtained from a POCSENSE reconstruction of all 8 coil elements (Figure 7d: 4 unknowns and 8 equations).
The SNRs of Homodyne-POCSMUSE produced images are 6.88 (upper image) and 4.22 (lower image); and the SNRs of POCSMUSE with phase smoothness constraint produced images are 8.69 (upper image) and 8.97 (lower image). The number of POCSMUSE iterations was 89, and the POCSMUSE computation time was 340.3 seconds per slice. The condition number of the data shown in Figure 6 was 51772.
Artifact removal for brain DWI with spiral k-space trajectory
Figure 8 compares (a) uncorrected interleaved spiral DWI images and (b) POCSMUSE-produced spiral DWI images, for three of the diffusion directions (the top three rows) and the mean DWI (the bottom row: mean of 10 diffusion directions). It can be seen that the aliasing artifacts in interleaved spiral DWI can be effectively removed by non-Cartesian POCSMUSE. The number of non-Cartesian POCSMUSE iterations was 51, and the POCSMUSE computation time was 514.2 seconds per slice. These results demonstrate that the new non-Cartesian POCSMUSE algorithm addresses the limitation of the original MUSE, which is only applicable to data obtained with regular sampling pattern in Cartesian space.
Figure 8.
Interleaved spiral DWI reconstructed with (a) conventional regridding and inverse regridding operations and 2D Fourier transform, and (b) the developed POCSMUSE algorithm.
Discussion
POCSMUSE is a post-processing algorithm capable of reducing motion-related artifacts of various patterns, using the RF coil sensitivity profile as a constraint. This method has several strengths:
First, POCSMUSE is complementary to existing motion artifact reduction strategies, and can be used to further reduce residual artifacts in data produced from existing methods. As demonstrated with our respiratory-triggered scans (Figure 3) and hybrid simulation (Figure 4), residual artifacts in abdominal FSE imaging data can be further reduced with the developed POCSMUSE method. We expect that the capability of POCSMUSE in reducing artifacts in respiratory-triggered abdominal imaging data should prove highly valuable for clinical uses, particularly for patients whose respiratory frequencies change significantly during scans. We expect that the POCSMUSE method can also be applied to reduce residual artifacts in cardiac MRI with breath-holding and cardiac-gating, particularly in patients who cannot hold their breath well for an extended period of time and those with irregular heart rates.
Second, as compared with the MUSE method originally designed for interleaved DWI data obtained with regular Cartesian sampling patterns, the new POCSMUSE method is more generally compatible with data obtained with different k-space sampling trajectories, pulse sequences, and contrasts. Instead of relying on matrix inversion used in the original MUSE implementation, the POCSMUSE method reconstructs images through an iterative procedure. As demonstrated in Figure 8, the iterative POCSMUSE algorithm is capable of producing interleaved spiral DWI images of high-quality. We expect that the developed algorithm can be generally applied to k-space data obtained with different types of non-Cartesian scan trajectories (e.g., radial sampling).
Third, various constraints can be easily incorporated into the POCSMUSE method to further improve the robustness of the reconstruction. For example, through constraining the phase terms, high-quality images can be obtained even from ill-conditioned POCSMUSE reconstruction of 4-shot interleaved DWI data of 3 coil elements. Since the image-domain phase terms are spatially smooth in nature, phase smoothness constraint is an appropriate choice for denoising and stabilizing the POCSMUSE reconstruction.
The compatibility of the POCSMUSE method with both full k-space and under-sampled k-space data provides a unique flexibility to further optimize the reconstruction scheme for challenging cases. For example, as shown in Figure 3a, 16 k-space segments of slice #9 (green dots) were acquired at very different respiratory phases, and thus the reconstructed images (Figures 3f and 3g) had more pronounced artifacts as compared with data of slice # 1 (red dots in Figure 3a; Figures 3b and 3c). In this case, we may choose to reconstruct images from subsets of the k-space data that correspond to similar respiratory phases (e.g., the 2nd, 3rd, 5th, 7th, 10th, 11th, 12th, 13th, 14th segments: shown by green dots in Figure 3a), and the produced images have a lower level of aliasing artifact (with GSR = 0.24, instead of 0.32 in the full k-space produced image shown in Figure 3g).
When reconstructing the abdominal FSE data with the POCSMUSE algorithm, we assumed that the shot-to-shot phase variation was insignificant (i.e., with vk = 1 in Figure 2). For applications where shot-to-shot phase variations are significant, a navigator echo should be used to measure segment-specific phase terms and included in the POCSMUSE reconstruction to further improve the reconstructed image quality. Alternatively, when 1) the parallel imaging capability is supported by the RF coil geometry and 2) the number of segments is smaller than the number of RF coil elements (e.g., data in Figure 5), shot-to-shot phase variations can be estimated from the initial SENSE or POCSENSE based reconstruction of data from individual segments, and used in the subsequent POCSMUSE reconstruction.
When the shot-to-shot phase variations in interleaved DWI scans are known (either from navigator echoes or a SENSE-based estimation), they can be used to reduce interleaved DWI artifacts with different approaches. The first approach, termed ‘direct phase subtraction’, removes phase errors directly from each individual segment, and then combines the phase-corrected segments to produce full-FOV images [15]. However, because the complicated segment-specific signal overlapping patterns (in reduced FOV) are not taken into consideration in this simple phase subtraction procedure, the residual artifacts are usually noticeable [29]. The second approach incorporates the segment-specific phase terms when reconstructing full-FOV images through a matrix inversion that takes segment-specific signal overlapping patterns into consideration, and can more effectively reduce aliasing artifacts in various applications ranging from interleaved DWI to EPI Nyquist artifact removal [30]. However, when the estimated shot-to-shot phase errors are noisy or inaccurate, the reconstructed images are prone to undesirable artifacts [31]. The third approach further incorporates the coil sensitivity profiles, as additional constraints [29, 31, 8, 18, 32], into the matrix inversion based reconstruction used in the second approach, and is capable of effectively and reliably removing artifacts in interleaved DWI. The POCSMUSE algorithm reported in this paper inherits all the advantages of the POCS framework and the third approach described above.
Figures 5 and 6 show that, in the absence of large-scale motions, the aliasing artifacts resulting from shot-to-shot phase variations of interleaved DWI data can be effectively removed by the MUSE and POCSMUSE methods. As shown in our recent work [33], it is possible to incorporate additional transformation matrices (reflecting rigid-body intra-scan rotation and translation) into the MUSE reconstruction, so that high-quality interleaved DWI can be achieved even in the presence of intra-scan rigid-body motion. However, the artifacts resulting from intra-scan nonlinear motions (e.g., in free-breathing abdominal imaging) may not be effectively removed with the above-mentioned procedure. Therefore, in this study, we used respiratory triggering to reduce k-space data inconsistency during abdominal MRI acquisition, and then simply applied the POCSMUSE algorithm to further lower the artifact level. In the future, we plan to further take the intra-scan nonlinear motion into consideration in the MUSE and POCSMUSE reconstructions, so that the motion-related artifacts can be minimized in free-breathing abdominal MRI.
In our abdominal MRI studies, the sensitivity maps were measured from low-resolution FSE data (128×128) that were acquired while the subjects held their breath (~ 30 sec). We extrapolated the coil sensitivity maps (based on Biot-Savart law), so that the MUSE and POCSMUSE reconstruction could be performed even in the presence of large-scale motion. We have also evaluated the abdominal MRI quality reconstructed with sensitivity maps of lower resolution (64×64: that could be acquired in 15 sec), and found that the POCSMUSE images reconstructed with sensitivity maps of different matrix sizes (128×128: 30 sec acquisition; and 64×64: 15 sec acquisition) have the same quality.
Like the majority of existing iterative reconstruction methods, a limitation of the POCSMUSE algorithm is its relatively long computation time (e.g., about 5 min per 2D image with Matlab). In our current POCSMUSE implementation, the reconstruction speed is determined by a pre-defined tolerance level of the inter-iteration signal variation. The POCSMUSE reconstruction time may be further reduced either by choosing a more loose tolerance level or by using alternative stopping criteria (e.g., terminating the iterative processes when the aliasing artifact level in a pre-defined background ROI is lower than a certain threshold). It is also possible to increase the convergence speed by adding a relaxation term to the iterative process [24].
Another limitation of the current study is that the POCSMUSE has only been evaluated with two MRI applications in a small number of volunteers. The performance and reliability of the POCSMUSE method in different clinical applications need to be further assessed in future studies.
In conclusion, POCSMUSE is a general post-processing algorithm capable of reducing motion-related artifacts in MRI data, using the RF coil sensitivity profile as a constraint. It can be applied to reduce artifacts of various patterns, ranging from breathing-induced artifacts in abdominal FSE imaging to aliasing artifacts due to shot-to-shot phase variations in interleaved DWI. POCSMUSE is compatible with existing motion artifact correction schemes, and can be used to further improve the image quality in data produced from existing artifact correction procedures.
Acknowledgments
This research was supported by NIH R01 NS-074045 and R21 EB-018419.
References
- 1.Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magn Reson Med. 1999;42:963–969. doi: 10.1002/(sici)1522-2594(199911)42:5<963::aid-mrm17>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 2.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42:952–962. [PubMed] [Google Scholar]
- 3.Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46:638–651. doi: 10.1002/mrm.1241. [DOI] [PubMed] [Google Scholar]
- 4.Atkinson D, Porter DA, Hill DL, Calamante F, Connelly A. Sampling and reconstruction effects due to motion in diffusion-weighted interleaved echo planar imaging. Magnetic resonance in medicine. 2000;44(1):101–109. doi: 10.1002/1522-2594(200007)44:1<101::aid-mrm15>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 5.Atkinson D, Counsell S, Hajnal JV, Batchelor PG, Hill DL, Larkman DJ. Non-linear phase correction of navigated multi-coil diffusion images. Magn Reson Med. 2006;56:1135–1139. doi: 10.1002/mrm.21046. [DOI] [PubMed] [Google Scholar]
- 6.Bammer R, Stollberger R, Augustin M, Simbrunner J, Offenbacher H, Kooijman H, Ropele S, Kapeller P, Wach P, Ebner F, Fazekas F. Diffusion-weighted Imaging with Navigated Interleaved Echo-planar Imaging and a Conventional Gradient System. Radiology. 1999;211:799–806. doi: 10.1148/radiology.211.3.r99jn15799. [DOI] [PubMed] [Google Scholar]
- 7.Butts K, deCrespigny AJ, Pauly JM, Moseley ME. Diffusion-weighted interleaved echo-planar imaging with a pair of orthogonal navigator echoes. Magn Reson Med. 1996;35:763–770. doi: 10.1002/mrm.1910350518. [DOI] [PubMed] [Google Scholar]
- 8.Jeong HK, Gore JC, Anderson AW. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med. 2013;69:793–802. doi: 10.1002/mrm.24320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li Z, Pipe JG, Lee CY, Debbins JP, Karis JP, Huo D. X-PROP: A fast and robust diffusion-weighted propeller technique. Magn Reson Med. 2011;66:341–347. doi: 10.1002/mrm.23033. [DOI] [PubMed] [Google Scholar]
- 10.Pipe JG, Farthing VG, Forbes KP. Multishot diffusion-weighted FSE using PROPELLER MRI. Magn Reson Med. 2002;47:42–52. doi: 10.1002/mrm.10014. [DOI] [PubMed] [Google Scholar]
- 11.Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn Reson Med. 2009;62:468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
- 12.Skare S, Newbould RD, Clayton DB, Bammer R. Propeller EPI in the other direction. Magn Reson Med. 2006;55:1298–1307. doi: 10.1002/mrm.20890. [DOI] [PubMed] [Google Scholar]
- 13.Wang F-N, Huang T-Y, Lin F-H, Chuang T-C, Chen N-K, Chung H-W, Chen C-Y, Kwong KK. PROPELLER EPI: an MRI technique suitable for diffusion tensor imaging at high field strength with reduced geometric distortions. Magn Reson Med. 2005;54:1232–1240. doi: 10.1002/mrm.20677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Frank LR, Jung Y, Inati S, Tyszka JM, Wong EC. High efficiency, low distortion 3D diffusion tensor imaging with variable density spiral fast spin echoes (3D DW VDS RARE) Neuroimage. 2010;49:1510–1523. doi: 10.1016/j.neuroimage.2009.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): Application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 16.Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med. 2003;50:343–353. doi: 10.1002/mrm.10531. [DOI] [PubMed] [Google Scholar]
- 17.Robson MD, Anderson AW, Gore JC. Diffusion-weighted multiple shot echo planar imaging of humans without navigation. Magn Reson Med. 1997;38:82–88. doi: 10.1002/mrm.1910380113. [DOI] [PubMed] [Google Scholar]
- 18.Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE) Neuro Image. 2013;72:41–47. doi: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gubin LG, Polyak BT, Raik EV. The method of projections for finding the common point in convex sets. USSR Comput Math Phys. 1967;7:1–24. [Google Scholar]
- 20.Youla DC, Webb H. Image restoration by the method of convex projections: Part 1, Theory. IEEE Trans Med Imaging. 1982;1:81–94. doi: 10.1109/TMI.1982.4307555. [DOI] [PubMed] [Google Scholar]
- 21.Haacke EM, Lindskog ED, Lin W. A fast, iterative, partial-Fourier technique capable of local phase recovery. J Magn Reson. 1991;92:126–145. [Google Scholar]
- 22.Liang ZP, Boada FE, Constable RT, Haacke EM, Lauterbur PC, Smith MR. Constrained reconstruction methods in MR imaging. Rev Magn Reson Med. 1992;4:67–185. [Google Scholar]
- 23.McGibney G, Smith MR, Nichols ST, Crawley A. Quantitative evaluation of several partial Fourier reconstruction algorithms used in MRI. Magn Reson Med. 1993;30:51–59. doi: 10.1002/mrm.1910300109. [DOI] [PubMed] [Google Scholar]
- 24.Samsonov AA, Kholmovski EG, Parker DL, Johnson CR. POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging. Magn Reson Med. 2004;52:1397–1406. doi: 10.1002/mrm.20285. [DOI] [PubMed] [Google Scholar]
- 25.Chen NK, Avram AV, Song AW. Two-dimensional phase cycled reconstruction for inherent correction of echo-planar imaging Nyquist artifacts. Magn Reson Med. 2011;66:1057–1066. doi: 10.1002/mrm.22896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chang HC, Guhaniyogi S, Chen NK. Interleaved Diffusion-Weighted EPI Improved by Adaptive Partial-Fourier and Multiband Multiplexed Sensitivity-Encoding Reconstruction. Magn Reson Med. 2014 doi: 10.1002/mrm.25318. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rasche V, Proksa R, Sinkus R, Börnert P, Eggers H. Resampling of data between arbitrary grids using convolution interpolation. IEEE Trans Med Imaging. 1999;18:385–392. doi: 10.1109/42.774166. [DOI] [PubMed] [Google Scholar]
- 28.Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding. IEEE Trans Med Imaging. 1991;MI-10:473–478. doi: 10.1109/42.97598. [DOI] [PubMed] [Google Scholar]
- 29.Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn Reson Med. 2005;54:1412–1422. doi: 10.1002/mrm.20706. [DOI] [PubMed] [Google Scholar]
- 30.Chen NK, Wyrwicz AM. Removal of EPI Nyquist ghost artifacts with two-dimensional phase correction. Magn Reson Med. 2004;51:1247–1253. doi: 10.1002/mrm.20097. [DOI] [PubMed] [Google Scholar]
- 31.Xu D, King KF, Zur Y, Hinks RS. Robust 2D phase correction for echo planar imaging under a tight field-of-view. Magn Reson Med. 2010;64:1800–1813. doi: 10.1002/mrm.22577. [DOI] [PubMed] [Google Scholar]
- 32.Truong TK, Guidon A. High-resolution multishot spiral diffusion tensor imaging with inherent correction of motion-induced phase errors. Magn Reson Med. 2014;71:790–796. doi: 10.1002/mrm.24709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Guhaniyogi S, Chu ML, Chang HC, Song AW, Chen NK. Simultaneous Correction of Motion-Induced Artifacts and Diffusion-Encoding Corruption in Multishot Diffusion Tensor EPI. Proceedings of the 22th Annual Meeting of ISMRM; 2014. p. 4351. [Google Scholar]