Towards an Automated Acoustic Detection System for Free Ranging Elephants

Abstract

The human-elephant conflict is one of the most serious conservation problems in Asia and Africa today. The involuntary confrontation of humans and elephants claims the lives of many animals and humans every year. A promising approach to alleviate this conflict is the development of an acoustic early warning system. Such a system requires the robust automated detection of elephant vocalizations under unconstrained field conditions. Today, no system exists that fulfills these requirements. In this paper, we present a method for the automated detection of elephant vocalizations that is robust to the diverse noise sources present in the field. We evaluate the method on a dataset recorded under natural field conditions to simulate a real-world scenario. The proposed method outperformed existing approaches and robustly and accurately detected elephants. It thus can form the basis for a future automated early warning system for elephants. Furthermore, the method may be a useful tool for scientists in bioacoustics for the study of wildlife recordings.

Introduction

Asian (Elephas maximus) and African (Loxodonta africana and Loxodonta cyclotis) elephants are the largest terrestrial herbivores. Today, however, elephants remain under threat from poaching (Douglas-Hamilton 2009; Lemieux & Clarke 2009), habitat loss, and the resulting human-elephant conflict, which refers to the problem that elephants destroy crops, damage houses, and occasionally even kill people. Farmers, in return, react by shooting, wounding and killing elephants (Hoare & Toit 1999; Santiapillai et al. 2010).

Elephants require relatively large areas and diversity of environments to forage (Santialillai et al. 2010; von Aarde et al. 2008). Therefore ranges are complex and not confined to officially designated protected areas. In Kenya, elephants have distinct home sectors linked by travel corridors that typically cross unprotected range (Hamilton et al. 2005). In Southern Africa, landscape fragmentation forces elephants into clustered conservation areas across several countries (van Aarde & Jackson 2007), which leads to local overpopulation and perceived adverse consequences for vegetation (Pienaar 1966, Hanks, 1979).

Progressive conservation approaches aim at providing corridors between core areas to facilitate elephant’s natural movements (van Aarde & Jackson 2007). Such corridors require autonomous systems that detect elephants area-wide and continuously monitor their migration patterns. In addition, elephants approaching human settlements need to be detected in real-time so that actions can be set in a timely manner.

Elephants make extensive use of powerful low-frequency vocalizations commonly termed “rumbles” (Poole et al. 1988; Langbauer 2000; Soltis 2010), which travel distances of up to several kilometers (Garstang et al. 2004). This qualifies the elephant as a perfect model species for acoustic observation since it is possible to detect elephants by their rumbles even if they are out of sight (Seneviratne et al. 2004; Payne et al. 2003).

The automated analysis of animal vocalizations recently received increasing research attention as a method to study and monitor wild animals without interfering with their lives or habitat (Blumstein et al. 2011). Thompson et al. (2009a, b) showed that the calling rate of low-frequency elephant vocalizations is a useful index of elephant numbers, demonstrating that acoustic surveying is a valuable tool for estimating elephant abundance, as well as for detecting other vocal species and anthropogenic noises that may be associated with poaching (Thompson et al. 2009a, b; Payne et al. 2003).

Most research on acoustic (and partly automated) analysis of elephant vocalizations addresses highly selective tasks such as the vocal identification of individual elephants (McComb et al. 2003; Soltis et al. 2005, Clemins et al. 2006) and the analysis of particular call types (Berg 1987; Leong et al. 2003; Stoeger-Horwath et al. 2007) and intra-call variations (Wood et al. 2005; Stoeger et al. 2011). The automated detection of elephant vocalizations has rarely been investigated so far.

Acoustic detection of elephants has been performed by Venter and Hanekom (2010). The authors detect elephants from their rumbles in wildlife recordings by extracting the characteristic fundamental frequency of rumbles using a subband pitch estimator. They decompose the spectrum by 32 logarithmically scaled bandpass filters and compute the normalized autocorrelation for each frequency channel. The peaks in the autocorrelation function of each channel give an indication of the fundamental frequency. The autocorrelation functions of those channels that show significant peaks are summed up. From the location of the largest peak in the summed autocorrelation function the fundamental frequency is estimated. Next, pitch tracking is performed to find audio segments where the estimate of the fundamental frequency is stable over time. Such segments are declared to be rumbles. The approach has several shortcomings. First, pitch detection, as pointed out by the authors, is difficult and often fails in noisy situations. Second, engine sounds of cars and airplanes exhibit harmonic characteristics similar to those of rumbles and thus are confused easily by the detector. Third, the detector is not able to learn a robust model (classifier) of rumbles from the data directly. Instead, the detector requires the tuning and specification of numerous thresholds (one for fundamental frequency estimation and four for pitch tracking). As a result the method is not expected to generalize well to novel (previously unseen) data. Additionally, the data used in the experiments has been recorded exclusively early during the day (in the morning) which adds an additional bias to the detector and the evaluation.

Wijayakulasooriya (2011) proposes a detector which exploits the shape of formant frequency tracks of rumbles to detect elephants. The author extracts formant frequencies from the transfer function of the all-pole filter given by Linear Predictive Coding (LPC). The basic assumption of the approach is that the first and second formants are nearly stationary during a rumble. The author applies the standard deviation of the first and second formant as features to detect rumbles. A Hidden Markov Model (HMM) is then trained on these features to automatically detect rumbles. The limitations of the approach are twofold. First, the assumption that the formants are stationary during a rumble does not hold in practice which could be shown in experiments with our data (Zeppelzauer et al. 2013). Rumbles exhibit partly strong temporal modulations (frequency changes) which are clearly reflected in the formant frequency tracks. Second, the dataset on which the detector has been evaluated contains only a few minutes of recordings and is thus not representative for a real-world scenario. As a result the reported performance has limited expressiveness.

Existing approaches for acoustic elephant detection strongly rely on highly specific sound attributes (fundamental frequency and formants) that are difficult to estimate in noisy wildlife recordings. This requirement limits the applicability of these approaches in a real-world scenario. Therefore, although research is in progress, no system exists that fulfils the requirements for the reliable automated detection of elephant vocalizations under natural field conditions.

In this work we present a robust method for automated detection of elephant rumbles. The proposed method does not require the detection of specific sound attributes and trains a detector for rumbles directly from a small number of sound samples. This first makes parameter tuning obsolete and second allows the method to adapt autonomously to the present environment. The detector uses a novel method for signal enhancement to improve the signal-to-noise ratio in the wildlife recordings (Zeppelzauer et al. 2013). Signal enhancement emphasizes spectro-temporal structures of rumbles and attenuates noise sources from the environment such as wind and rain. We evaluate the detector on a large set of wildlife recordings of African elephants captured within a natural habitat in South Africa. The evaluation shows that sound enhancement strongly improves the signal-to-noise ratio of the recordings and facilitates the robust detection of rumbles. The proposed detector yields high performance on unconstrained wildlife material and represents a first important step towards an automated detection system for elephant presence. In addition to that the detector may serve as a tool for the semi-automatic annotation and support the study of wildlife recordings by domain experts.

Methods

Study population and data acquisition

Acoustic recordings were collected from three female and two male African elephants (Loxodonta africana) aged between 9 and 17 years located at Adventures with Elephants, Bela Bela, South Africa. The elephants were fully habituated to human presence and free to roam around in a savannah reserve of 300 ha. This enabled us to capture data under well-controlled recording settings within the natural habitat of African elephants.

Stereo recordings were conducted on a 722 Sound Devices HDD recorder at 44.1 kHz, a directional AKG C480 B CK 69-ULS microphone (frequency response 8Hz-20kHz ± 0.9 dB) and a customized omni-directional Neumann microphone (optimized for low-frequency recordings from 5 Hz on). The signal captured by the Neumann microphone is well-suited as input to the developed elephant detector because it enables the detection of elephant calls coming from all directions.

Vocalizations were recorded during two social contexts: spatial separation and subsequent bondings. Recording distances between the elephant and the microphone ranged from 10 to several hundreds of meters. For a detailed description of the recording context see Stoeger et al. (2012). In a total amount of 359 minutes (~6 hours) of recordings, we annotated 635 rumbles by manually tagging the beginning and the end of each rumble. Rumbles were found by visual inspection of the spectrograms. The annotations further include information about the individual, its gender and age, the quality of the recording and whether noise was evident within the annotated call.

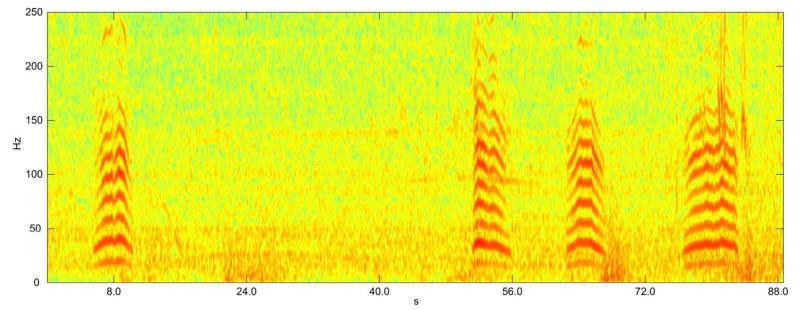
The rumble is a harmonic sound with a fundamental frequency in the range of about 15-35Hz and a strongly varying duration (from 0.5s to more than 10s in our data). Depending on the distance of the caller, rumbles exhibit a varying number of harmonics (McComb et al. 2003). The spectrogram of a series of four rumbles with high signal-to-noise ratio is shown in Figure 1. The fundamental frequency at approximately 20Hz and numerous higher harmonics are clearly recognizable. The figure further shows that the second harmonic is significantly stronger than the fundamental frequency which makes the fundamental frequency a weak indicator for the detection of rumbles compared to its higher harmonics.

Figure 1.

A series of four “clean” elephant rumbles with high signal-to-noise. Only the higher harmonics of the fourth rumble are slightly masked by noise.

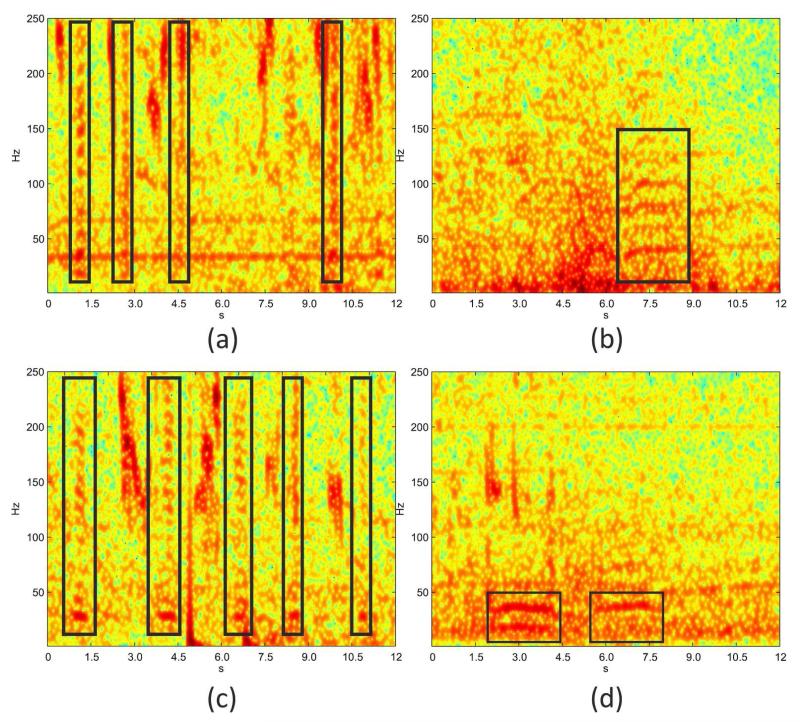
From the captured wildlife recordings we observe that many noise sources corrupt the frequency band where rumbles reside. As a result the fundamental frequency and the harmonic structure are masked to a high degree. The most interfering noise sources are wind and rain, as well as engine sounds of cars and airplanes (see Figure 2). Figure 2(a) shows rumbles in the presence of narrow-band noise introduced by a car engine. The engine sound has a fundamental frequency at 30Hz, which is particularly misleading for detectors that rely on pitch detection (Venter & Hanekom 2010). Figure 2(b) shows a rumble superimposed by broadband noise where the harmonic structure is hardly visible. The harmonic structure for short rumbles (Figure 2(a) and 2(c)) is less salient than for rumbles with a longer duration. Sound of higher frequency is limited in range by atmospheric attenuation (Garstang et al. 1995). As a consequence the number of harmonics decreases with the distance of the caller to the microphone. Figure 2(d) shows a far-distant rumble (>100m) where the higher harmonics are missing. The missing of higher harmonics impedes the detection of rumbles as reported by Venter and Hanekom (2010).

Figure 2.

Rumbles in the presence of different noise sources, at different distances to the microphone, and with different durations. (a) A series of short rumbles (1 to 1.5s duration) and a concurrent engine sound with a fundamental frequency around 30Hz and a second harmonic at 60Hz. (b) A rumble of approx. 2.5s which is heavily masked by broadband noise. (c) Short rumbles with low signal-to-noise ratio, especially in the channel between 50Hz and 100Hz. (d) Far distant rumbles where most of the harmonics are missing.

Robust Detection of Rumbles

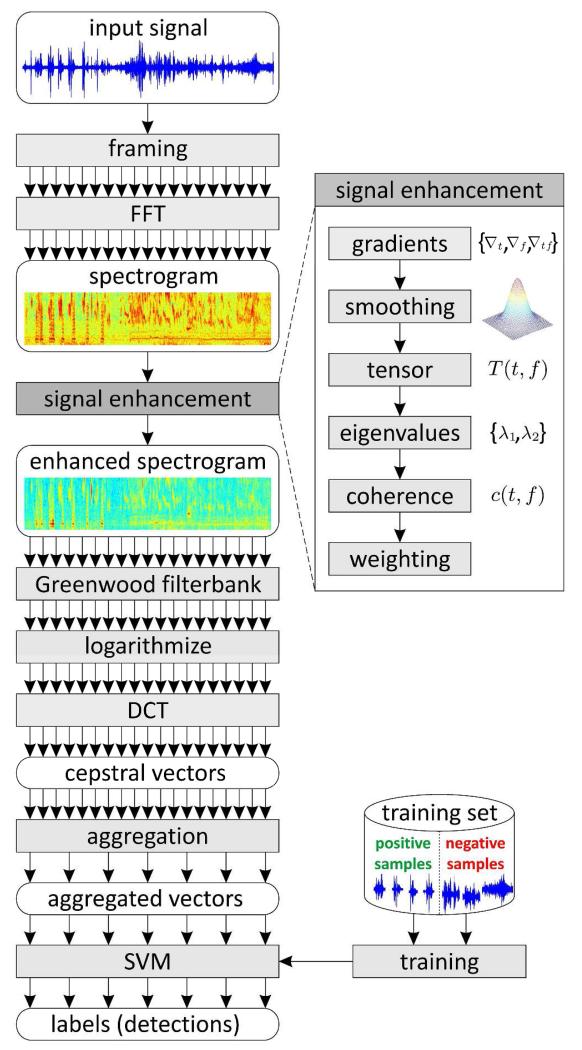
We propose a robust method for the detection of elephant rumbles that first emphasizes the harmonic structure of rumbles and then extracts the spectral envelope, to obtain a compact and robust spectral representation for the detection of rumbles. Figure 3 provides an overview of the entire approach.

Figure 3.

The entire workflow of the proposed method. First, the input signal is framed and a spectrogram is computed by applying FFT on each frame. Next signal enhancement is performed on the spectrogram. The enhanced spectrogram is filtered with a Greenwood filter bank, logarithmized, and mapped to the cepstral domain by DCT. Finally, the cepstral feature vectors are temporally aggregated and input to a trained classifier (SVM). The SVM outputs labels (“rumble” / “background”) for each aggregated vector.

The harmonics together with the fundamental frequency appear as horizontally running frequency tracks (contours) in the spectrogram, see Figure 1. The basic idea behind our approach is to enhance (emphasize) these contours prior to feature extraction to better separate them from noise and thus to facilitate the automated detection of rumbles. Next, we extract robust features that represent the coarse spectral envelope of short audio frames. The short-term features are temporally aggregated and input to a classifier. The classifier is trained on a small training set that contains rumbles as well as background (ambient) sound. Ultimately, the learned classifier is applied to the captured wildlife recordings to automatically detect rumbles.

Signal Enhancement

The first processing step is the enhancement of the input signals. We emphasize the contours by applying a two-dimensional (spectro-temporal) structure enhancement on the spectrogram (Zeppelzauer et al. 2013). For this purpose, we consider the spectrogram as an image and compute a two-dimensional structure tensor across time and frequency.

The structure tensor (Fernández et al. 2009) is constructed from the gradients (partial derivates) of the spectrogram along time and frequency. At each position (t, f) in the spectrogram S where t is time and f frequency, the tensor T(t, f) is defined as:

$$T(t,f)=\left(\begin{array}{cc}\hfill {\nabla }_t^2\hfill & \hfill {\nabla }_{tf}\hfill \\ \hfill {\nabla }_{tf}\hfill & \hfill {\nabla }_f^2\hfill \end{array}\right),$$ (1)

where ∇_t and ∇_f are the partial derivates along time and frequency, respectively and ∇_tf is the product of ∇_t and ∇_f. The tensor characterizes the structure of the intensity distribution in its local neighborhood. Prior to the computation of the tensor the gradients are smoothed along the time and frequency axes by a two-dimensional Gaussian filter. This makes the tensor more robust and representative for a larger neighborhood. From the tensor, we extract the eigenvalues λ₁ and λ₂ by:

$${\lambda }_{1,2}=\frac{1}{2}\left(({\nabla }_t^2+{\nabla }_f^2)\pm \sqrt{{({\nabla }_t^2-{\nabla }_f^2)}^2+4{\nabla }_{tf}^2}\right).$$ (2)

The eigenvalues characterize the local gradient structure in the neighborhood of position (t, f) and can be interpreted as follows. If there is an edge-like structure (e.g. a frequency contour) in the neighborhood, the condition λ₁ > λ₂ is fulfilled. For a perfect edge (a sharp contour) λ₂ becomes 0 while λ₁ > λ₂ is still fulfilled. If λ₁ equals λ₂, the underlying structure is rotationally symmetric (e.g. an isolated spectral peak). If both eigenvalues become zero, the underlying structure is homogeneous (e.g. broadband noise). From the eigenvalues we compute the coherence c which is a combined measure that provides the amount and type of structure at a given position:

$$c=\frac{{\lambda }_1-{\lambda }_2}{{\lambda }_1+{\lambda }_2}.$$ (3)

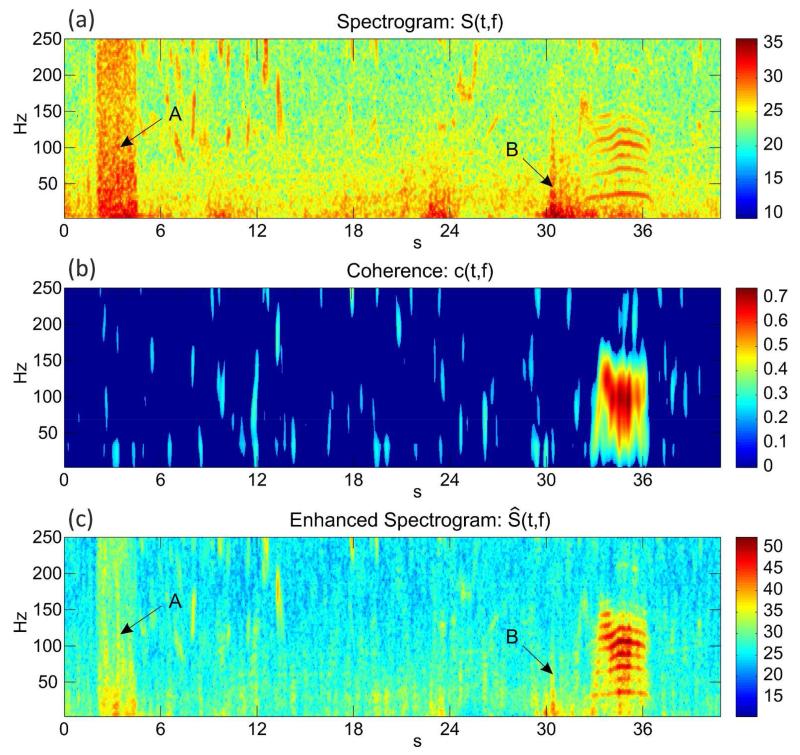
The higher the coherence at position (t, f), the stronger the edge-like structures observed in the neighborhood of (t, f). Thus, coherence is a well-suited indicator for spectro-temporal structures, such as frequency contours. To enhance frequency contours (and at the same time to attenuate noise) we apply the coherence as a weighting function to the spectrogram. The enhanced spectrogram Ŝ(t, f) is computed as Ŝ(t, f) = S(t, f) · (c(t, f)+1). Figure 4 illustrates the effect of the spectral weighting. The coherence in Figure 4(b) for the input spectrogram in 4(a) gives strong weights to the frequency contours produced by the rumble at 35s and lower weights to nearly homogeneous and isotropic structures originating from noise. The coherence for the broadband noise, for example, at 4s (label “A”) becomes nearly zero. Consequently, the broadband noise is attenuated in the enhanced spectrogram in Figure 4(c). Other noise sources, such as the low-frequency spike at 30s (label “B”) are attenuated as well.

Figure 4.

The effect of sound enhancement. (a) The input spectrogram with a rumble at 35s and several noise sources, e.g. broadband noise (label “A” and label “B”); (b) The coherence obtained for each location in the spectrogram. The highest values are obtained in the area of the rumble; (c) The enhanced spectrogram after weighting with the coherence. The signal-to-noise ratio of the rumble is clearly improved and the noise sources are attenuated.

Acoustic Feature Extraction

After spectral enhancement, we extract acoustic features from the spectrogram as a basis for the automated detector. Related approaches on the detection of elephant rumbles rely on highly specific acoustic attributes, such as pitch and formants, which are difficult to extract automatically (Venter & Hanekom 2010; Wijayakulasooriya 2011). Instead of trying to detect such specific acoustic attributes, we compute robust features that compactly represent the spectral energy distribution of short audio frames. This representation can be computed independently of the amount of noise present.

Each audio frame is 300ms wide and subsequent frames have an overlap of 90%. The spectral range is limited to the frequency band of 0Hz to 500Hz where rumbles mostly reside. First, we apply a Greenwood-scaled filterbank to the spectrogram. The Greenwood-scale models the logarithmic spacing of the critical bands of mammals (Greenwood 1961). For an adequate modeling the Greenwood scale requires the specification of the hearing range of the investigated species and a parameter k which is set to 0.88 for mammals according to LePage (2003). Similarly to Clemins et al. (2006) we set the hearing range to 10Hz to 10.000Hz and apply a Greenwood-scaled filterbank of 30 bands. After the application of the filter bank, the filter energies are logarithmically scaled and a discrete Cosine transform (DCT) is applied to the logarithmized filter energies to obtain cepstral coefficients. We select the first 18 cepstral coefficients as features to represent the coarse spectral envelope of each 300ms audio frame.

For automated detection, we temporally aggregate the cepstral coefficients of successive audio frames by taking their mean and variance. The result is a more robust and long-time numeric representation (aggregated feature vectors) that can be used directly as input to the automated detector.

Detector Training and Classification

For the detection of elephant rumbles, we train a classifier on the aggregated feature vectors. For this purpose, we split the available set of wildlife recordings into a training set and disjoint test set. The training set contains rumbles (the positive class) as well as background sounds (the negative class). The number of background sounds is significantly larger than the number of rumbles, to account for real-world conditions.

As a detector for elephant vocalizations we employ a Support Vector Machine (SVM) classifier. The SVM is a non-probabilistic discriminative classifier introduced by Vladimir Vapnik and colleagues (Vapnik and Lerner 1963, Cortes and Vapnik 1995, Vapnik 1995). We have chosen the SVM as detector for the following reasons: (i) the application of an already trained SVM no novel (unseen) data is computationally efficient. In the context of an automatic detection system, runtime is an important factor since the continuously captured audio data has to be processed in real-time; (ii) SVMs can generate robust models even from few training data. The number of parameters required by an SVM is independent of the size of the training set. This prevents overfitting and improves the generalization ability of the classifier; (iii) In the context of automated elephant detection the number of positive examples in the training set is significantly lower than the number of negative examples. SVMs can cope well with such asymmetric class cardinalities by the use of asymmetric loss functions.

The idea of SVMs is to find a function in feature space with a preferably low number of parameters (e.g. a linear or quadratic function) that separates the classes represented by the training samples as best as possible. For the training of an SVM we are given n training samples X = (x₁, … , x_n) in ${ℝ}^d$. The vector of corresponding class labels y = (y₁, … , y_n) contains values y_i ∈ {−1, +1} corresponding to the two classes ω₁ and ω₂. The objective of SVM training is to find a function g(x) such that:

$$sign\left(g\right({\mathit{x}}_i\left)\right)=-1\text{if}{\mathit{x}}_i\in {\omega }_1\text{and}$$ (4)

$$sign\left(g\right({\mathit{x}}_i\left)\right)=+1\text{if}{\mathit{x}}_i\in {\omega }_2.$$ (5)

The function g(x) is called discriminant function. In the case of SVMs g(x) is linear and represents a hyperplane in ${ℝ}^d:g\left(\mathit{x}\right)=\mathit{w}\cdot \mathit{x}+b$, where w (weight vector) is the d-dimensional normal vector of the hyperplane and b (bias) is the translation of the hyperplane along w. For b = 0 the hyperplane goes through the origin. The dot operator “·” denotes the inner product of two vectors.

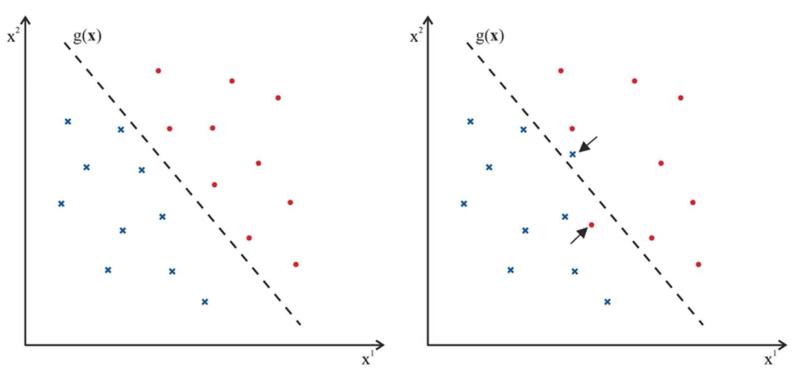
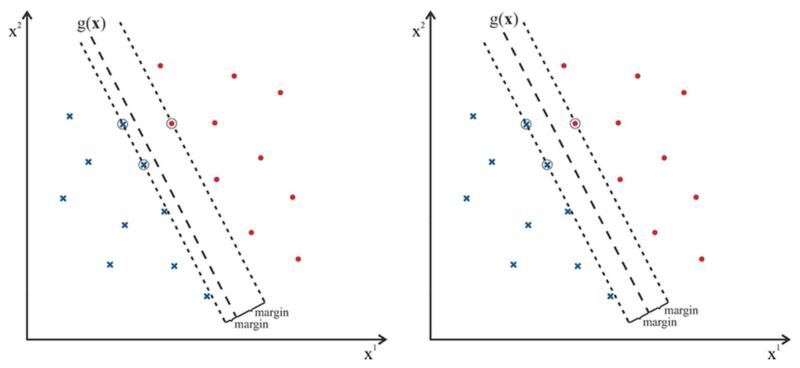
Two classes ω₁ and ω2 are linearly separable if there exists a weight vector w and a bias b such that sign(w · x_i + b) = y_i for all samples x_i in X, i.e. all samples can be correctly classified. Figure 5 gives examples for linearly separable and non-separable classes in two-dimensional feature space. If the training samples of the two classes are linearly separable, then the SVM constructs an optimal separating hyperplane w · x + b = 0 between both classes that maximizes the distance between the hyperplane and the nearest data points of each class. The data points that determine the hyperplane are the support vectors. The distance between the support vectors and the hyperplane is called margin. Figure 6 depicts the difference between a suboptimal and an optimal separating hyperplane. For an optimal separating hyperplane the margin to both sides is maximized. The larger the margin the higher is the robustness of the classifier.

Figure 5.

Linear separability of classes: (a) the classes are not linearly separable. There is no linear function that is able to separate the two classes without errors (b) the classes are linearly separable.

Figure 6.

Optimal separating hyperplanes: (a) the margin of the hyperplane g(X) is not optimal. (b) shows a hyperplane with maximized margin. The support vectors are encircled.

From Figure 6 we observe that the separating hyperplane is defined by a few support vectors only which all have the same distance to the hyperplane. Not all training samples contribute to the hyperplane. Instead the SVM emphasizes are those samples only that are most difficult to separate (the support vectors) and which in turn are the most important samples for the classification task (Duda et al. 2001). Due to the low number of support vectors the generalization ability and the robustness of SVMs tends to be high (Cortes and Vapnik 1995).

According to Cortes and Vapnik (1995) the optimal hyperplane that maximizes the margin can be computed by estimating the saddle point of the following Lagrange functional:

$$L(\mathit{w},b,\alpha )=\frac{1}{2}\mathit{w}\cdot \mathit{w}-{\Sigma }_{i=1}^n{\alpha }_i\left[y_i\right(\mathit{w}\cdot \mathit{x}+b)-1],$$ (6)

where α_i with 1 ≤ i ≤ n are the Lagrange multipliers. The optimal parameters for the hyperplane are obtained by finding the saddle point where w and b are minimized and α is maximized. The functional can be reformulated into a maximization problem in α (see Fletcher (2009) for details):

$$L\left(\alpha \right)={\Sigma }_{i=1}^n{\alpha }_i-\frac{1}{2}{\Sigma }_{i,j}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathit{x}}_i\cdot {\mathit{x}}_j,$$ (7)

subject to the conditions:

$${\alpha }_i\ge 0,{\Sigma }_{i=1}^n{\alpha }_i{y}_i=0,1\le i\le n.$$ (8)

This representation is the dual form of Equation (6). It is noteworthy that Equation (7) only requires the computation of inner products between feature vectors x_i and x_j. This is an important property for the integration of kernels to enable non-linear discriminant functions.

In practice, two classes are often not linearly separable. For this reason, Cortes and Vapnik introduced slack variables which represent penalties for samples that cannot be correctly classified by the linear discriminant function (Cortes and Vapnik, 1995). For each sample a slack variable ζ_i is introduced with ζ_i = 0 for correctly classified samples and ζ_i > 0 for misclassified samples. During optimization the sum of all slack variables ${\Sigma }_{i=1}^n{\zeta }_i$ is minimized. The separating hyperplane is constructed in such a manner that an optimal tradeoff is found between a maximum margin and a minimum number of misclassified samples.

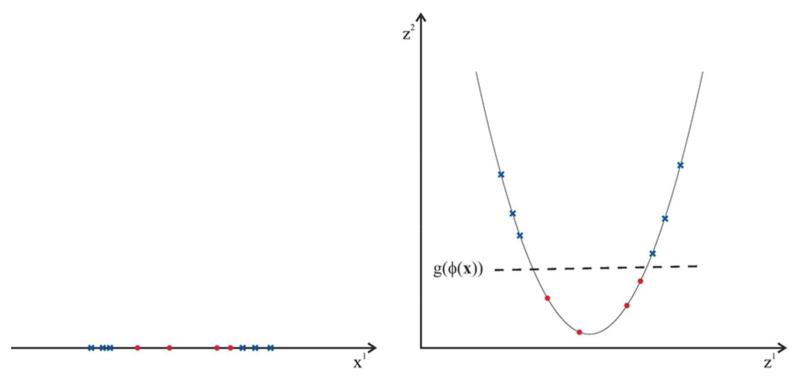
For some data sets linear separation is generally suboptimal, see for example the data set in Figure 7. For such data sets non-linear classification is more suitable. However, the complexity of estimating non-linear discriminant functions is higher than that of linear functions. Fortunately, SVMs allow the integration of non-linear discriminant functions in an efficient way. Instead of estimating a non-linear discrimination function in feature space, the feature vectors are mapped non-linearly from the original feature space ${ℝ}^d$ into a higher dimensional space, the target space ${ℝ}^{d\prime }$, by a function $\varphi :{ℝ}^d\to {ℝ}^{d\prime }$ with d < d′. In the higher dimensional target space the feature points move apart from each other which facilitates linear separability. Given an adequate mapping ϕ the data set becomes separable by a linear discrimination function g(ϕ(x)) in the target space. This linear function in the target space is in turn a non-linear discrimination function in the original feature space. Figure 7 illustrates the effect of a non-linear transformation that maps the feature space into a higher-dimensional target space where the samples of the two classes become linearly separable.

Figure 7.

A non-linear mapping from ${ℝ}^1$ to ${ℝ}^2$: (a) the samples in the original feature space are not linearly separable. In the higher dimensional space (b) the samples become linearly separable.

The transform ϕ and the computations in the high-dimensional target space are complex and can be avoided by the kernel trick (Aizerman et al. 1964). Instead of transforming the feature vectors and comparing the feature vectors in the target space, an appropriate nonlinear comparison function (the kernel) can be applied in the original space. From Equation (7), we observe that the samples (feature vectors) contribute to the optimization problem only in terms of inner products. The inner product x_i · xj in Equation (7) can be replaced by a kernel function K with K(x_i, x_j) = ϕ(x_i) · ϕ(x_j) that represents an inner product in the target space obtained by the mapping function ϕ.

By the use of kernels the computation of the mapping ϕ and the computations in the target space become implicit and can thus be avoided. This property makes nonlinear classification with SVMs efficient. Any continuous symmetric semi-positive definite function (Mercer’s Theorem) is a valid kernel function (Mercer 1909). This means, that each function that represents an inner product in the target space is a valid kernel (Cortes and Vapnik 1995). The simplest kernel is the linear kernel: K(x_i, x_j) = x_i · x_j. In this work, we employ a non-linear Gaussian radial basis function kernel (RBF) kernel to account for the complexity of the training data: K(x_i, x_j) = e^{(−||x_i−x_j||2/2σ2}.

Once the SVM has been trained on the training data, we can use it as a detector for elephant vocalizations on the test data. First, for a given recording we apply signal enhancement, feature extraction and temporal aggregation (as described above) for successive audio frames. Next, the trained SVM is applied on the temporally aggregated features and assigns each audio frame either to the class of rumbles (ω₁ or to the class of background sounds (ω₂). Figure 3 gives an overview of the complete algorithm.

Evaluation and Results

The training set in our experiments contains 63 randomly chosen rumbles from the recordings (10% of all rumbles in the dataset). 30 randomly chosen sound segments that contain only background sound are used as negative training set. The remaining data (93% of all recordings) are used for testing the detector.

For performance evaluation, we compare the proposed approach with two alternative approaches. The first approach is a method for sound detection recently introduced by Hao et al. (2012). The approach autonomously extracts a representative and discriminative template for rumbles from the training data and detects rumbles in the test set by template matching using the CK distance measure (Campana & Keogh 2010). The second alternative approach uses the same cepstral features (Clemins et al. 2006) as the proposed approach but without applying signal enhancement. All methods are evaluated on the same training and test data.

The results for all three evaluated methods are summarized in Table 1. The approach by Hao et al. (2012) autonomously selects a representative template for rumbles from the training data, which shows that template selection works satisfactorily. Detection is performed by sliding the selected template over the test data and performing template matching. The method yields a detection rate of 78.6% and a false positive rate of 78.2%. The second evaluated approach using cepstral features but without signal enhancement outperforms Hao et al. (2012) in both detection rate (88.2%) and false positive rate (24.4%). The proposed approach using signal enhancement yields a detection rate of 88.2% and a false positive rate of 13.7%. The proposed approach reduces the false positive rate by 10.7% by means of signal enhancement.

Table 1.

Overall detection results of the proposed method and two compared methods in terms of detection rate and false positive rate.

Method	Detection Rate	False Positive Rate
Hao et al. (2012)	78.6%	78.6%
Clemins et al. (2006)	88.2%	24.4%
Proposed approach	88.2%	13.7%

Discussion

From the results we observe that template matching often fails in noisy situations. Since the template is not able to model the different noise sources, template matching yields low similarities when noise corrupts a rumble. A single template is a too simple model for the detection of elephant rumbles in wildlife recordings. Furthermore, rumbles have highly varying duration and fundamental frequency. Template matching is not able to take such intra-call variations into account.

The second approach clearly outperforms template matching. The high detection rate of 88.2% shows that the cepstral features and the model generated by the SVM are well-suited for the given task. However, due to noise still many false positive detections are generated (24.4%). As a result, nearly every fourth detection is a false detection.

The proposed approach with spectro-temporal signal enhancement yields a similar detection rate as the detector without signal enhancement. However, the false positive rate almost halves to only 13.7%. Signal enhancement strongly improves the signal-to-noise ratio in the recordings by emphasizing rumble-like structures and at the same time by attenuating narrow- and broadband noise sources. The comparison with the second evaluated approach shows that signal enhancement enables the cepstral features to better model the spectral characteristics of rumbles which ultimately results in a more accurate detection.

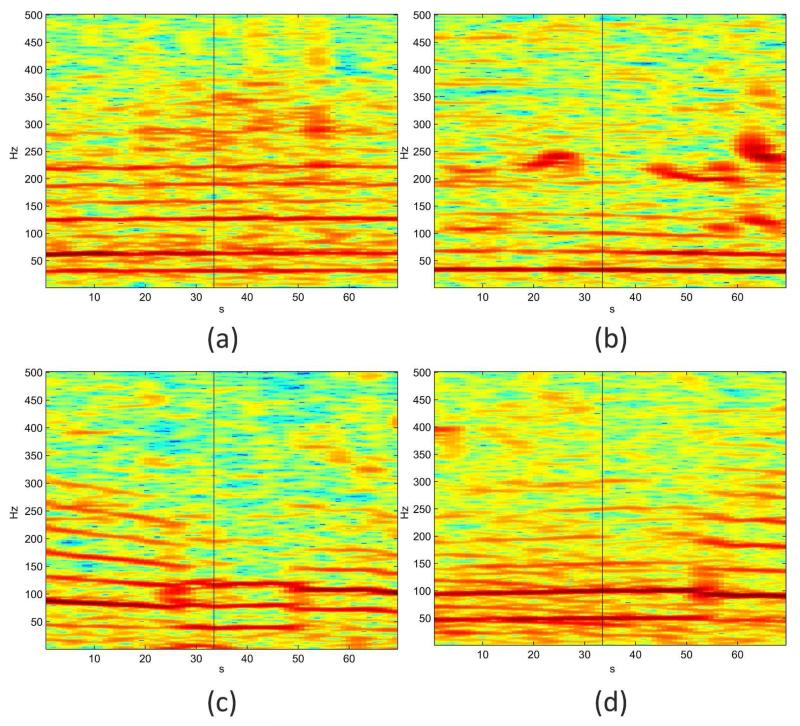
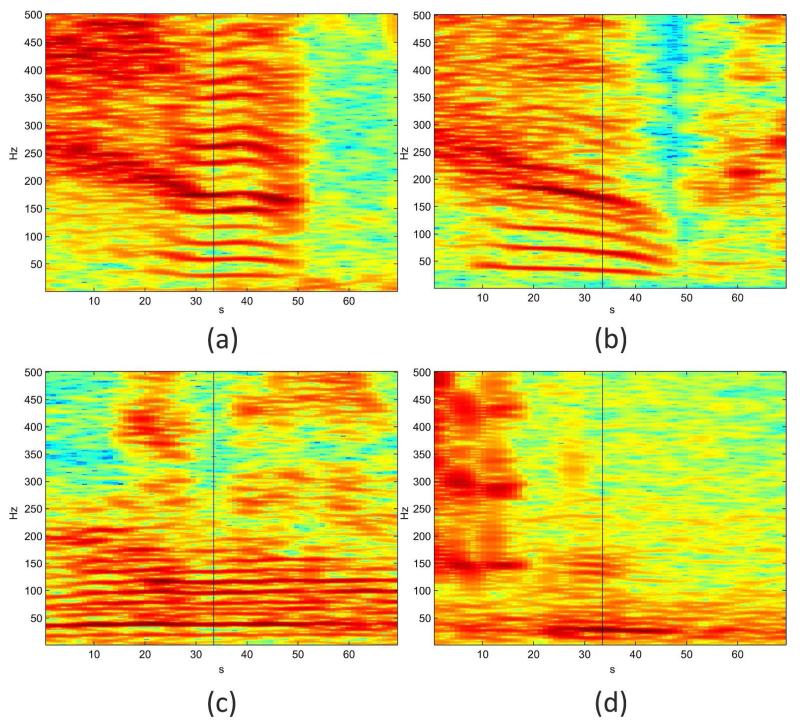
We further investigate the false detections generated by the detector. We observe that false detections were introduced by engine sounds of airplanes and cars which have partly similar fundamental frequencies and harmonic structure to rumbles. Figure 8 shows spectrograms of different false detections that originate from engine noises. Figure 8(a) shows the spectral distribution of the engine sound of an airplane. The fundamental frequency as well as the higher harmonics resemble those of rumbles. Figures 8(b) to 8(d) show engine sounds of cars. Again the fundamental frequency is in the range of 30Hz – 50Hz and thus can easily be confused with that of elephant rumbles. The engine sound in Figure 8(d) even resembles the typical temporal modulation of rumbles (a slight increase of frequency in the middle of the call). From our experiments, we conclude that engine sounds cannot be separated reliably from elephant rumbles by an acoustic short-time analysis. The most significant difference between rumbles and engine sounds is their duration. While most rumbles have durations between 0.5s and 10s, engine sounds have a much larger duration. Thus, the distinction of rumbles from engine sounds requires a longer-time analysis. A combination of our detector with a long-time acoustic analysis is one direction of research that will be followed in future to further improve the detector’s performance.

Figure 8.

False detections due to engine sounds of cars and airplanes. The detection occurs exactly in the middle of each spectrogram (black vertical line). (a) an airplane; (b) a car engine; (c) a mixture of car engine sounds; (d) a car engine with a similar temporal modulation as frequently exhibited by rumbles.

Further inspection of false positives reveals that our method is able to discover rumbles that where for some reason not annotated, for example, because they were combined or partly masked by other calls). Figure 9 shows spectrograms of such rumbles. The black vertical line marks the exact position of the detection. In Figure 9(a) a rumble is detected correctly, which directly follows a roar vocalization. Similarly, in Figure 9(b) a roar transitions into a rumble. Both rumbles were not included in the annotation. Figure 9(c) shows the detection of a non-annotated rumble which is superimposed by snorts and trumpets of other elephants. Ultimately, Figure 9(d) shows a rumble that has been overlooked during annotation. However, the rumble could be discovered by our detector.

Figure 9.

Detections of rumbles that were not discovered during annotation. (a) a rumble that follows a roar vocalization; (b) a roar that transitions into a rumble; (c) a rumble superimposed by snorts and trumpets of other elephants; (d) an isolated rumble recovered by our method.

These results show that the proposed detector is not only a first step towards an automatic elephant monitoring and early warning system but further a helpful tool for experts in the annotation of large amounts of monitoring data. The detector enables to support the annotation process in a semi-automatic way. In semi-automatic annotation the automated detector provides the annotator locations of special interest in the recorded data where the searched for sound occurs with high probability. This is of great value, especially because our experiments show that the detector has the potential to discover rumbles which are difficult to find manually. Additionally, semi-automatic annotation accelerates the tedious process of annotation significantly.

There is currently no public benchmark data set for the evaluation of elephant detectors. However, we can compare the results of the proposed approach with that of related approaches, such as that of Venter and Hanekom (2010). The authors obtain a detection rate of 85.7% and a false positive rate of 14.2% on a dataset comprising 4 hours with, however, only 28 rumbles in total. Our dataset comprises 6 hours, contains 635 rumbles, and outperforms the method of Venter and Hanekom (2010) in detection rate as well as false positive rate. An objective comparison with the results of Wijayakulasooriya (2011) is not appropriate, since the author uses a dataset of only a few minutes for evaluation.

To the best of our knowledge, the employed dataset in this work is the most comprehensive dataset employed for automated elephant detection so far. In order to establish a common benchmark dataset, we make the employed dataset publicly available to researchers also working on elephant detection. This will enable objective comparisons between different approaches and foster research in this field in future.

In summary, it can be stated that the proposed method for elephant detection is a further step towards an autonomous early warning system for elephant presence, which is crucial to alleviate the human-elephant conflict. Our experiments demonstrate that signal enhancement is essential for the detection of elephant calls in noisy wildlife recordings and that local spectro-temporal structure analysis is well-suited for this purpose. Future work comprises the explicit integration of further call types into the detector to enable a more comprehensive detection of elephant presence. Furthermore, additional short- and long-time features are currently investigated to further improve the robustness of the detector.