The co-development of looking dynamics and discrimination performance

Abstract

The study of looking dynamics and discrimination form the backbone of developmental science and are central processes in theories of infant cognition. Looking dynamics and discrimination change dramatically across the first year of life. Surprisingly, developmental changes in looking and discrimination have not been studied together. Recent simulations of a dynamic neural field (DNF) model of infant looking and memory suggest that looking and discrimination do change together over development and arise from a single neurodevelopmental mechanism. We probe this claim by measuring looking dynamics and discrimination along continuous, metrically organized dimensions in 5-, 7, and 10-month-old infants (N = 119). The results showed that looking dynamics and discrimination changed together over development and are linked within individuals. Quantitative simulations of a DNF model provide insights into the processes that underlie developmental change in looking dynamics and discrimination. Simulation results support the view that these changes might arise from a single neurodevelopmental mechanism.

Looking is one of the few reliable behaviors that infants engage in. It is not surprising, then, that much of our scientific understanding of infant cognitive development comes from looking measures. They have been used to acquire a basic understanding of how infants form categories (Quinn, Eimas, & Rosenkrantz, 1993), detect statistical regularities (Saffran, Aslin, & Newport, 1996), perceive objects (Needham, 2000), and learn words (Rost & McMurray, 2009). This reliance on looking measures builds upon seminal theories of infant habituation which described well how looking changes as infants become familiar with a stimulus and discriminate familiar from novel stimuli (Cohen, 1972). Despite this rich history, there remains a poor understanding of how looking dynamics and visual discrimination processes are linked on the real and developmental time scales. A recent theory of infant looking and memory formation posits that looking dynamics and discrimination processes share a common mechanistic source (Perone & Spencer, 2013). We probe this theoretical claim here.

Looking dynamics change in predictable ways during the first year. Much of the literature on this topic comes from the Visual Paired Comparison (VPC) procedure. In this task, infants explore pairs of identical items during a familiarization phase. Then, during a test phase, they view the familiar item paired with a novel item. Infants' recognition of the familiar item can be inferred from a reliable familiarity preference (longer looking to the familiar item relative to total looking time) or a reliable novelty preference (longer looking to the novel item relative to total looking time). Historically, familiarity preferences have been interpreted as reflecting a point early in learning in which a stimulus is becoming familiar to infants and their memory is weak. Novelty preferences have been interpreted as reflecting a point later in learning in which one stimulus has become familiar to infants and they are beginning to encode properties of a novel stimulus (for a review, see Hunter & Ames, 1988).

In the VPC, shift rate (rate of gaze switching between pairs of stimuli relative to total looking time), look duration (average look length), and peak look (longest look) have emerged as reliable indices of learning. With age, infants exhibit higher shift rates, shorter look durations, and shorter peak looks. Individual and developmental differences in these looking dynamics are associated infants' recognition performance (Rose, Feldman, & Jankowski, 2001; Rose, Feldman, & Jankowski, 2001). Critically, in studies on visual recognition infants are typically presented with high-dimensional stimuli such as geometrical patterns and faces. For stimuli such as these, the basis of infants' recognition and discrimination is unclear. Thus, these studies leave unanswered whether looking dynamics and discrimination change together over development and how looking and discrimination might be related within individuals.

A second literature has examined developmental changes in visual discrimination directly using stimuli with well-controlled similarity relations between familiar and novel items. Evidence indicates that infants' discrimination improves over the first year. For example, Brannon, Sumarga, and Libertus (2007) found that infants' made more precise discriminations of visual temporal duration between 6 and 10 months of age. They suggested that these results reflect increasingly precise representations over development (see also Lipton & Spelke, 2003). Much like the visual recognition literature, this literature has not examined the link between looking dynamics and discrimination.

Theories of infant looking have also treated developmental changes in looking dynamics and discrimination as separate issues. Conceptual and neural network models have largely focused on explaining the linkage between the time course of memory formation and infants' familiarity and novelty preferences (Cohen, 1972; Hunter & Ames, 1988; Sirois & Mareschal, 2004). Other, different neural network models have focused on developmental changes in the precision with which infants' represent features (Westermann & Mareschal, 2004). Importantly, none of these theories specify how looking and the cognitive dynamics that underlie discrimination are linked on the task or developmental time scale.

Our goal is to investigate how looking dynamics and visual discrimination are related. This investigation was inspired by simulations of a Dynamic Neural Field (DNF) model of infant looking and memory formation which showed that looking and discrimination changed together over development in a single presentation habituation context (Perone & Spencer, 2013). The provocative claim of the model is that changes in looking and discrimination arise from a single neurodevelopmental mechanism.

In the present report, we tested this claim using a combination of empirical and theoretical methods. The empirical component involved examining whether looking and discrimination change together over development and are linked within individuals in the VPC. We chose to test this claim with 5-, 7-, and 10-month-old infants because there are marked changes in looking dynamics (Rose et al., 2001) and infants' ability to discriminate stimuli along continuous, metrically organized magnitude dimensions (Brannon et al., 2007) during this period. We used the VPC procedure to probe infants' discrimination of items from a new stimulus set with well-controlled metric properties along continuous color (hue) and shape (aspect-ratio) dimensions. We examined whether looking dynamics and discrimination change together in a consistent fashion, and whether individual differences in looking dynamics predict discrimination performance.

The theoretical component involved two steps. First, we tested whether the same DNF model used to establish a link between looking and neurocognitive processes in the single presentation habituation task is also capable of producing the richer set of looking dynamics, recognition, and discrimination performance measured in the VPC. Second, we evaluated whether developmental changes in looking and discrimination performance can arise from a common mechanistic source by testing whether a single neurodevelopmental change in the DNF model could quantitatively simulate developmental changes in infants' looking dynamics and discrimination performance.

Experiment

Method

Participants

Forty-five 5-month-old infants (M=170.31 days, SD=13.28 days), 39 7-month-old infants (M=230.31 days, SD=7.74 days), and 35 10-month-old infants (M=303.11 days, SD=11.43 days) participated in this study.

Stimuli

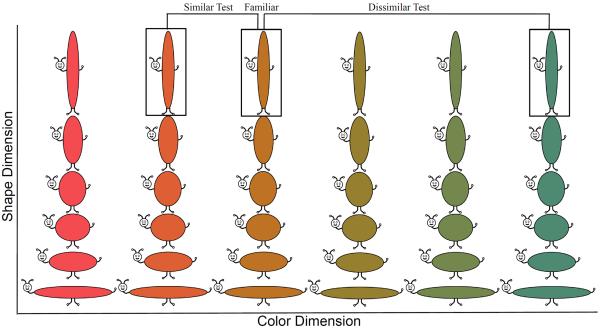
The stimuli were “buggles” (see Figure 1). Each buggle consisted of a value along continuous shape and color dimensions. Shape was defined by an aspect-ratio. Each metric step was defined by a proportional change in height and width, generating six equidistant metric steps with the total area of each stimulus held constant. Aspect-ratio is a relevant dimension along which categories can be discriminated. For example, Spivey (2007) found that adults parsed cups and bowls into categories based on aspect-ratio rather than width or height alone (see also Oden, 1981). Twelve equidistant colors were sampled from a 360° continuous color space (CIE*Lab, 1976). The entire stimulus set consisted of 72 unique items.

Figure 1.

Shows stimulus set of “buggles.” Each buggle consisted of one value along a continuous shape (aspect ratio) and color (hue) dimension. The shape dimension consisted of six equidistant metric steps and the color dimension consisted of 12 equidistant metric steps sampled from a continuous 360° color space (from right to left, ° 91 – 271° in 30° increments shown). Figure also shows experimental design. One of the central 5 shapes and one of the 12 colors was selected as the familiar item. The novel item on the similar test was novel by one metric step and the novel item on the dissimilar test was novel by three metric steps. The similar and dissimilar test were always on the same dimension and in opposite directions from the familiar item on the dimension.

Design and Procedure

Infants were familiarized with pairs of identical items across 6 10 s trials. Following the familiarization phase, there were 2 20 s test trials (location of familiar and novel items were reversed after 10 s). No previous study has probed infants' discrimination with the metric organization of the color and shape dimensions that constitute the buggles. Thus, it was unclear how dissimilar the familiar and novel items needed to be to observe a robust preference. We therefore presented two test trials where we manipulated the metric similarity between the familiar and novel item, presenting a difficult discrimination first and an easier discrimination second. In infant looking paradigms, it is common to present stimuli highly dissimilar to the familiarization stimulus last in a series of intervening discrimination tests (e.g., Oakes et al., 1996). This maximizes the likelihood of observing a robust preference for the more difficult discrimination which is presented first. There are disadvantages as well. Most critically, the order with which stimuli with different properties are presented can influence the duration with which infants gaze on subsequent trials during familiarization (Bashinski, Werner, & Rudy, 1985) and test (Schöner & Thelen, 2006) phases.

In our design, the first test was the similar test, in which the familiar item was paired with an item that was novel by one metric step on a single dimension. The second test was the dissimilar test, in which the familiar item was paired with an item that was novel by three metric steps on the same dimension as the similar test. The direction of the similar and dissimilar tests was in opposite directions on the continuous dimension (see Figure 1). This was done to reduce interference on the dissimilar test that might arise from exposure to a novel item situated in between the familiar and dissimilar novel item. As a consequence of our design, the first and sixth shape that mark the beginning and end of the dimension were reserved as novel items, leaving shapes 2–5 as familiar items.

We created 12 different familiar objects by pairing each of the 12 different colors with one randomly selected shape reserved for the familiarization item. Discrimination for each object could be probed on the shape or color dimension. The familiar object and discrimination dimension was probed was randomly assigned across infants. For the 12 familiar objects, the color dimension was probed at least once for all 12 at 5 months of age, 11 at 7 months of age, and all 12 at 10 months of age. The shape dimension was probed for 11 of the familiar objects at 5 months of age, 11 of the familiar objects at 7 months of age, and 12 of the familiar objects at 10 months of age. Thus, infants within each age group were exposed to discriminations across the entire stimulus set.

Stimuli were presented on a gray background on a 37” LCD monitor. Pairs of stimuli were centered equidistantly on the left and right portions of the monitor. Infants were tested in a dimly lit experimental room in which a black curtain divided the room. The curtain revealed the monitor and a low-light TV camera lens used to view infants' looking behavior. During the experimental session, infants sat on their parents' lap 100 cm in front of the monitor. Parents wore opaque glasses to prevent parental bias. A trained observer sat behind the curtain and presented stimuli on the monitor and also recorded infants' looking time on a computer while watching them on a black and white TV. At the beginning of each trial, a looming white circle appeared that periodically produced a chirping sound. Once the observer determined that the infant was looking at this attention-getting stimulus, the observer pressed one computer key to present the stimuli, one key when the infant was looking left, and one key when the infant was looking right. Looking time to locations other than left or right was not recorded. A second trained observer recorded the looking of 25% of the infants offline. Interobserver reliability was high: looking time on each trial, r ≥ .90, shift rate, r ≥ .93, and look duration, r ≥ .87. The mean absolute difference between observers was low: looking time on each trial, M ≤ .62 s, shift rate, M ≤ .06, and look duration, M ≤ .15 s.

Results

Analyses are presented across three sections: familiarization, test, and individual differences in looking and discrimination performance.

Familiarization

The goal of our first analysis was to characterize developmental change in infants' total looking time during familiarization, which typically decreases with age as infants more quickly form memories for visual stimuli (Colombo & Mitchell, 1990). A one-way Analysis of Variance (ANOVA) revealed that total looking time differed across age, F(2,116)=4.35, p<.05, η_p² = .07. Post-hoc comparisons revealed total looking time was less at 10 months of age (M=34.90 s, SD=7.35) than at 5 months of age (M=39.82 s, SD=8.66), p<.05, d = .61. Total looking time was also less at 7 months of age (M=35.15 s, SD=9.52) than at 5 months of age, p<.05, d = .51. Thus, 5-month-old infants accumulated more total looking time than 7- and 10-month-old infants.

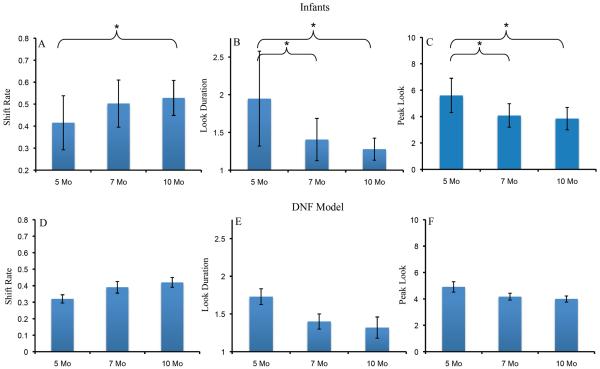
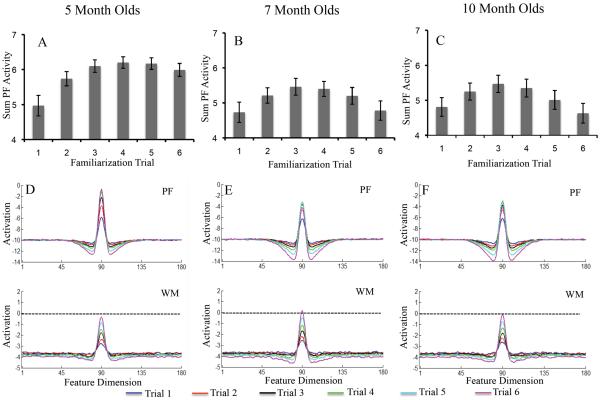
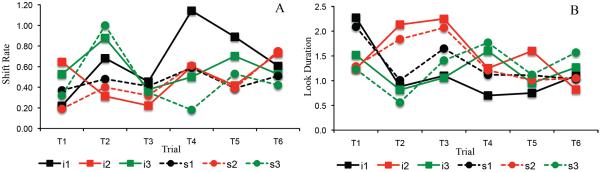
Figure 2A–C shows developmental change in three measures of looking dynamics – shift rate (A), look duration (B), and peak look (C). We evaluated developmental change in these looking measures using one-way ANOVA. The test for shift rate revealed a significant effect of age, F(2,116)=3.16, p<.05, η_p² = .05. Post-hoc comparisons revealed that shift rate at 10 months of age (M=.53, SD=.16) was higher than at 5 months of age, (M=.42, SD=.25), p=.05, d = .52. The ANOVA for look duration also revealed a significant age effect, F(2,116)=7.19, p<.001, η_p² = .11. Post-hoc comparisons revealed that look durations were shorter at 10 months of age (M=1.28 s, SD=.29) than at 5 months of age (M=1.95 s, SD=1.26), p<.01, d = .73, and shorter at 7 months of age (M=1.41 s, SD=.56) than at 5 months of age, p<.05, d = .55. Finally, the ANOVA for peak look revealed a significant age effect, F(2,116)=8.43, p<.0001, η_p² = .13. Post-hoc comparisons revealed that peak looks were shorter at 10 months of age (M=3.85 s, SD=1.70) than at 5 months of age (M=5.6 s, SD=2.61), p<.001, d = .79, and shorter at 7 months of age (M=4.08 s, SD=1.78) than at 5 months of age, p<.01, d = .68. Thus, duration measures decreased between 5 and 7 months of age, and shift rate increased between 5 and 10 months of age.

Figure 2.

Panels A–C show developmental changes in shift rate (A), look duration (B), and peak look (C) for infants. Panels D–F show developmental changes in shift rate (D), look duration (E), and peak look (F) for the DNF model. Shift rate is the frequency of gaze shifting relative to total looking time, look duration is the average length of each look, and peak look is the length of the longest look. Error bars show +/− .5 SD.

Test

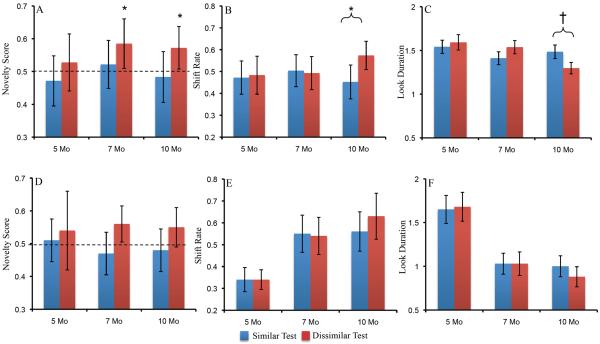
To determine whether discrimination performance interacted with test dimension over development, we conducted a repeated measures ANOVA with novelty score (similar, dissimilar) as a within subjects factor and age (5, 7, 10) and dimension (shape, color) as between subjects factors. There were no significant effects of dimension (all ps > .1). For our primary analyses, we collapsed across test dimension. We conducted two sets of analyses on infants' looking behavior during the test phase. The first set of analyses centered on infants' discrimination performance on the similar and dissimilar tests. Infants' novelty scores are shown in Figure 3A. To determine whether infants' novelty scores were significantly different than chance on the similar and dissimilar tests, we conducted a series of two-tailed, one-sample t-tests. Infants' preference on the similar test was not reliable at 5 months of age, t(44)=−1.26, p>.1, d = .28, 7 months of age, t(38)=.92, p>.1, d = .19, or 10 months of age, t(35)=−.64, p>.1, d = .19. On the dissimilar test, 5-month-olds' preference was not reliable, t(44)=1.06, p>.1, d = .25. However, infants' novelty preference was reliable on the dissimilar test at 7 months of age, t(38)=3.50, p<.001, d = .75, and 10 months of age, t(34)=3.29, p<.01, d = .76. Thus, infants' novelty preference on the dissimilar test were significantly different from chance at 7 and 10 months of age but not 5 months of age.

Figure 3.

Panels A–C show developmental changes in novelty scores (A), shift rate (B), and look duration (C) for infants on the similar (blue bars) and dissimilar (red bars) tests. Panels D–F show developmental changes in novelty scores (D), shift rate (E), and look duration (F) on the similar and dissimilar tests. Error bars show +/− .5 SD. *p<.05 †p<.10

We also assessed whether there were any differences in test performance across development using a repeated measures ANOVA. Test type (similar, dissimilar) was a within-subjects factor and age (5, 7, 10) was a between-subjects factor. Results revealed a main effect of test type, F(1,116)=11.35, p<.001, η_p² = .09, with higher novelty scores on the dissimilar test than similar test (see Figure 3A). There was also a marginal main effect of age, F(2,116)=.2.78, p=.07, η_p² = .05. Post-hoc comparisons revealed that novelty scores were higher at 7 months of age (M=.55, SD=.10) than at 5 months of age (M=.5, SD=.011), p=.05, d = .70.

The next set of analyses examined whether shift rate and look duration during the test trials differed as a function of discrimination and/or over development. Previous studies have shown that stimulus differences influence how infants distribute their looks. For example, Ruff (1975) found that infants' shift rates were higher when looking at similar items than dissimilar items. One might expect, then, that infants' shift rates would be higher during the similar test than dissimilar test. No previous study has examined this possibility when infants are looking at stimuli with well-controlled metric properties.

Figure 3 shows shift rate (B) and look duration (C) on the similar and dissimilar tests across development. To evaluate shift rate, we conducted a repeated measures ANOVA with test (similar, dissimilar) as a within-subjects factor and age (5, 7, 10) as a between-subjects factor. There was a significant test x age interaction, F(2,116)=3.43, p<.05, η_p² = .06. Tests of simple effects revealed that infants' shift rate was higher on the dissimilar test than the similar test at 10 months of age, F(1,116)=9.48, p<.01, η_p² = .08, but infants' shift rate did not differ across test trials at 5 months of age, F(1,116)=.11, η_p² = <.001, p>.1, or 7 months of age, F(1,116)=.07, p>.1, η_p² = <.001. Interestingly, older infants more frequently shifted gaze when looking at dissimilar familiar and novel items.

We evaluated look duration using the same method. The test revealed a marginal age x test interaction, F(2,116)=2.36, p=.10, η_p² = .04. Tests of simple effects revealed that infants' look durations were marginally shorter on the dissimilar test than on the similar test at 10 months of age, F(1,116)=2.95, p<.10, η_p² = .02, but infants' look durations did not differ across test trials at 5 months of age, F(1,116)=.29 p>.1, η_p² = <.01, or 7 months of age, F(1,116)=1.50, p>.1, η_p² = .01. The pattern of infants' look durations across the similar and dissimilar tests followed the same pattern of their shift rate on the test trials, that is, as 10-month-old infants more frequently switched gaze on the dissimilar test relative to the similar test, their look durations became shorter.

Individual Differences

Previous studies have shown that individual differences in looking dynamics are predictive of novelty scores (Rose et al., 2001), indicating a mechanistic link between looking and recognition performance. Here, we used hierarchical regression to probe whether individual differences in looking are predictive of infants' discrimination performance on the similar and dissimilar tests.

All regression analyses are presented in tables with the same structure. On the left, the step and predictor variables entered on each step are presented. The tables present summary statistics including proportion of variance accounted for (R²), change in R² from one step to the next, F statistic change from one step to the next, and the probability value associated with the change in the F statistic. These summary statistics indicate the proportion of variance in the dependent measure accounted for and, in steps after the first step, whether that proportion was above and beyond the proportion accounted for in previous steps. On the right side of the table are the unstandardized beta weights (ß) and standardized beta weights (beta). The weight is the unique contribution of each predictor. The sign of the weight indicates the direction of the relationship between a predictor variable and the dependent measure. The size of the weight indicates the slope, where steeper slopes indicate that the dependent measure changes more for each unit change in the predictor. The significance value of each predictor in the context of the other predictors entered on the step is also included.

The first analysis examined whether looking measures predict performance on the similar test after the contribution of age was controlled for. Age was entered as a predictor on the first step and novelty score on the similar test as the dependent measure. Results are shown in Table 1. Age did not account for a significant proportion of variance in novelty scores. In the second step, we entered shift rate, look duration, and peak look. These looking dynamics together did account for a significant proportion of variance in novelty scores, R²=.08. Evaluating the beta weights indicates that shift rate is the strongest predictor in the context of the others (for similar results, see Rose et al., 2001). It is notable that the slope of the beta weight is negative, indicating that lower novelty scores (familiarity preferences) were associated with higher shift rates. Peak look was also a significant predictor. The negative beta weight suggests that longer peak looks were associated with lower novelty scores on the similar test. These results are somewhat counterintuitive. The association between long peak looks and lower novelty scores fits the general observation that long peak looks and familiarity preferences are signatures of slow processing (for a discussion, see Colombo & Mitchell, 1990; Rose, Feldman, & Jankowski, 2007). However, the association between high shift rates and lower novelty scores does not fit previous observations; high shift rates are typically a signature of efficient comparison and strong novelty preferences (Rose et al., 2002).

Table 1.

Infants Similar Test

Step	Predictors	R 2	R2 Change	F Change	p	β	beta	p
1	Age	.001	.001	.08	.78	.002	.03	.78
	Shift Rate					−.26	−.37	.01
2	Look Duration	.083	.083	3.42	.02	−.04	−.21	.14
	Peak Look					−.02	−.30	.05

In the next analysis, we conducted the same regressions on data from the dissimilar test. Results are shown in Table 2. The model was not significant on any step. Neither age nor looking measures were predictive of performance on the dissimilar test.

Table 2.

Infants Dissimilar Test

Step	Predictors	R 2	R2 Change	F Change	p	β	beta	p
1	Age	.013	.013	1.49	.23	.009	.11	.23
	Shift Rate					−.05	−.07	.65
2	Look Duration	.03	.017	.67	.57	.01	.04	.77
	Peak Look					−.01	−.2	.20

Discussion

Shift rate and look duration measures of looking dynamics changed between 5 and 7 months of age. Simultaneously, discrimination between items distributed along the continuous, metrically organized dimensions of color and shape that constitute the buggle objects emerged. These findings are consistent with the possibility that developmental change in looking dynamics and discrimination share a mechanistic source as suggested by the DNF model (see Perone & Spencer, 2013). To probe whether looking dynamics and discrimination were related within individuals, we used hierarchical regression. Individual differences in looking dynamics were predictive of discrimination performance on the similar, but not the dissimilar, test. This raises the possibility that how infants distribute their looks while learning is mechanistically linked to discrimination performance. In the next section, we test whether a single neurodevelopmental mechanism implemented in the DNF model can quantitatively capture the empirical pattern of results reported here.

A DNF Model of Infant Looking and Memory

DNF models provide an effective set of concepts for thinking about the linkage between brain and behavioral dynamics (for a review, see Spencer, Perone, & Johnson, 2009). The DNF model used here is derived from a model of adult visual working memory and change detection performance (Johnson, Spencer, Luck, & Schöner, 2009; Johnson, Spencer, & Schöner, 2009). The same architecture used here has been used to provide an account of developmental change in infant habituation (Perone & Spencer, 2013), visual working memory capacity in infants (Perone, Simmering, & Spencer, 2011) and children (Simmering & Patterson, 2012), and spatial recall performance in children (Schutte & Spencer, 2009). Below, we first describe the model's architecture. Next, we illustrate how looking and neurocognitive dynamics are linked in the model. Finally, we present simulations of developmental change in looking dynamics and discrimination in the VPC task. Model equations and parameter settings are presented in the Appendix.

Model Architecture

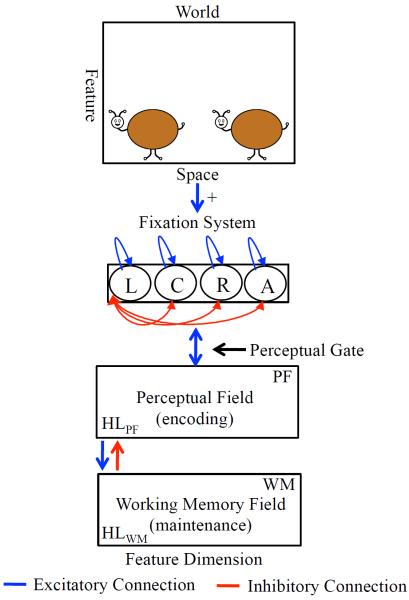
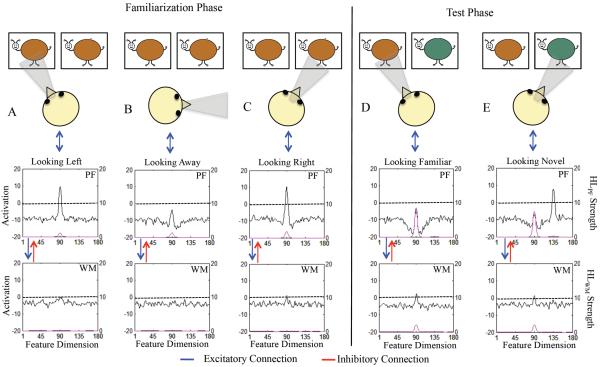
Figure 4 shows the DNF model architecture. The model consists of a fixation and a neurocognitive system that is situated in a virtual world where task-relevant stimuli appear at left and right locations, attention-getting stimuli appear at a center location, and task-irrelevant stimulation appear at away locations. The fixation system consists of a collection of nodes that fixate the left (L), right (R), center (C), and away (A) locations in a winner-take-all fashion.

Figure 4.

DNF model architecture. At the top is the virtual world at which the model looks. The presence of “buggles” biases the fixation system to look left (L) or right (R) (see blue arrow from space to fixation system). Fixating one location acts like a perceptual gate and allows the stimulus from space to be input to the cognitive system, which consists of a perceptual field (PF) and working memory (WM) field. PF and WM are reciprocally coupled to a shared layer of inhibitory interneurons (Inhib, not shown). Strong activity in PF supports fixation (blue bi-directional arrow between PF and fixation system). Strong WM activity suppresses PF activity via a strongly tuned connection from WM to Inhib (see red bi-directional arrow between PF and WM). PF and WM activity are also influenced by a Hebbian layer, HL_PF and HL_WM, respectively, which accumulates slowly over learning and facilitates encoding in PF and memory formation in WM.

The presence of stimuli at left and right locations biases the fixation system to look to the displays (blue arrow from space to fixation system in Figure 4). Fixating left or right opens a perceptual gate into a perceptual field (PF) that consists of a population of neurons with receptive fields tuned to continuous dimensions (e.g., color)¹. PF encodes items. Encoding has two functions. First, encoding supports continued fixation via an excitatory connection between PF and the fixation system (see blue bi-directional arrow). Second, encoding passes excitatory activation to a working memory (WM) layer which can maintain neural activity associated with an item in the absence of input from PF.

The next critical aspect of neural interactions in the model is reflected in the pattern of connectivity from WM to PF. Interactions between PF and WM are set such that strong activation in WM inhibits similarly-tuned neurons in PF via a strongly tuned connection to a shared inhibitory layer (not shown for simplicity; see red arrow from WM to PF). This inhibition suppresses encoding of fixated inputs that match remembered items, weakening PF support for fixation. This, in turn, leads to the release from the current fixation state. PF and WM are also reciprocally coupled to Hebbian layers (not shown; see HL) that instantiate a form of Hebbian learning to capture changes that occur with repeated presentation of items across trials. These layers strengthen encoding of previously-encoded items in PF and facilitate the maintenance of items in WM.

Looking and Neurocognitive Dynamics

Figure 5 illustrates the mechanisms underlying memory formation, recognition, and novelty preferences in the model. The left portion shows the state of PF and WM while looking at pairs of identical items early in familiarization. Initially, the model is looking left (A; the infant head indicates gaze direction) and the brown color excites selectively tuned neurons in PF. Local excitatory / lateral inhibitory interactions within PF create an activation peak (black line, left y-axis), which estimates the specific feature value of the stimulus, supports continued fixation, and feeds into WM. Peaks in PF enable Hebbian learning to occur at active sites, priming previously-excited neurons to respond more robustly (pink line, right y-axis).

Figure 5.

Illustrates the linkage between looking and learning during familiarization (A–C) and the basis for discrimination during the test phase (D–E) in the DNF model. The left y-axis shows the strength of activation in PF / WM (black line) and the right y-axis shows the strength of activation HL_PF (top panel) / HL_WM (pink line). Initially, in panel A the model is fixating the left location and the brown stimulus is being encoding (see activation peak centered at site 90 in PF). Notice that activity in HL_PF has already begun to accumulate. In panel B, the model spontaneously switches gaze to an away location at which no task relevant stimulus is present. Activity in PF subsides. In panel C, the model reacquires fixation and is looking at an identical brown stimulus at the right location. This stimulus is again input into PF and encoding is strengthened due to the accumulated activity in HL_PF (see pink line, right y-axis). Activity in WM is also starting to emerge (see black line in lower panel).

After the familiarization phase, the model enters the test phase and, like infants, is presented with the familiar stimulus and a novel stimulus. In this example, the novel stimulus is dissimilar on the color dimension. Panel D shows the state of PF and WM when the model looks at the familiar stimulus. Here, HL_WM (pink line, right y-axis) has accumulated across the familiarization phase and WM is actively maintaining a peak associated with the familiar item (black line). Consequently, PF activity generated by the familiar stimulus is strongly inhibited by WM and support for looking low. Panel E shows the state of PF and WM when the model looks at the novel stimulus. Here, the sustained WM peak associated with the familiar item continues to suppress PF activity at the familiar site. However, inhibition at sites tuned to the dissimilar novel item is minimal, PF activity strong, and support for looking is high.

Stochastic forces within the fixation system enable it to spontaneously switch gaze. In this example, the model happens to look “away” where no task-relevant stimulation appears and PF activity subsides (B). We refer to this stimulus-dependent activity in PF as encoding. After looking away, the model switches gaze again. This time the model looks right, the location at which an identical item is present (C). The stimulus is again input to PF and activity in WM is beginning to emerge (see bottom panel in C).

Across a series of fixations and stimulus presentations, WM activity and Hebbian learning associated with WM increases. This is evident in the state of PF and WM during the test phase, illustrated in the right portion of Figure 5. During the test phase, the model, like infants, is presented with the familiar item paired with a novel item. In this example, the familiar and novel item are dissimilar. Initially, the model looks left (D) and the familiar, brown item is input to PF. Importantly, WM activity is robust and is creating strong inhibition in PF (see trough around peak in PF) which suppresses encoding. This is the neural mechanism of recognition in the model. This, in turn, leads to weak support from PF to continue fixation and the model tends to switch gaze away from the familiar item, the behavioral signature of recognition in the VPC task.

PF activity is very different when the model looks to the dissimilar novel item (Figure 5E). Here, PF activity associated with the green item is robust and provides support for continued fixation. Notice that PF activity at sites associated with the familiar item remains suppressed by the maintenance of the item's color in WM. Consequently, when the model switches gaze to look again at the familiar item, support for fixation is weak and look durations are short. The duration fixation to left and right locations in the model, like infants, can be measured (see Appendix). This enables us to calculate a novelty score, shift rate, look duration, and peak look for each simulation of the model.

The final issue we tackle here is whether changes in looking dynamics and discrimination arise from a single neurodevelopmental mechanism. Previous simulations of the DNF model in a single presentation habituation task have shown that the model produces canonical developmental changes in habituation curves and discrimination between familiar and novel items that vary in their metric similarity (Perone & Spencer, 2013). Importantly, both of these changes emerged from a single mechanism - the spatial precision hypothesis (SPH) - which posits that excitatory and inhibitory interactions become stronger over development as children accumulate experience across diverse contexts (Perone et al., 2011; see also Schutte & Spencer, 2009). Below, we describe the SPH in greater detail in the context of our simulation method.

Model Simulations

Method

The goal of the model simulations was to elucidate the neurocognitive processes that might underlie looking dynamics, learning, and discrimination performance on the task and developmental time scales. To test whether a single mechanism might underlie developmental changes in looking and discrimination, we created 5-, 7-, and 10-month-old models by implementing the SPH. This involved manipulating the strength of excitatory and inhibitory interactions within PF and WM such that these interactions were stronger over development (Perone et al., 2011; Perone & Spencer, 2013; Schutte & Spencer, 2009; Simmering & Patterson, 2012). Table 3 shows the strength of these parameters over development. As can be seen, the strength of excitation within PF (a_uu) and WM (a_ww) increased most strongly between 5 and 7 months, the strength of inhibition from Inhib to PF (a_uv) increased most strongly between 7 and 10 months, and the strength of inhibition from Inhib to WM steadily increased over development (a_wv).

Table 3.

Spatial Precision Hypothesis Parameter Manipulations

Parameter	5 Mo	7 Mo	10 Mo
auu	0.1041	0.2028	0.2867
aww	0.7741	0.9676	0.972
auv	1.106	1.1642	1.4553
awv	0.1781	0.1875	0.2037

We situated each model in the same procedure as infants. The model was familiarized with pairs of identical items across 6 10 s trials (1 time step = 5 ms). Stimuli were Gaussian inputs centered over a specific site (e.g., a specific hue value) in a field consisting of 180 neurons (so each unit in the field equaled, for instance, 2° in color space). Recognition of the familiar item was assessed across 2 20 s test trials, the similar and dissimilar tests. On the similar test, the model was presented with the familiar item paired with a novel item that differed by 15 units (e.g., 30°) in one direction. On the dissimilar test, the model was presented with the familiar item paired with a novel item that differed by 45 units in the opposite direction as the similar test.

We ran 200 simulations with each parameter set (i.e., at each age). Perone & Spencer (2013) showed that this number of simulations produces means for looking behavior that were quantitatively close across repeated batches of simulations. This is important because it ensures that the model's behavior can be attributed to the parameter settings and not simulation-to-simulation variation that arises from stochastic fluctuations in the fixation and cognitive systems. Moreover, large batches of simulations for a single parameter setting enable us to pull out structure across simulations and examine how the neurocognitive dynamics of the DNF model specified by the parameter settings give rise to the developmental changes in behavior that we aimed to reproduce.

Parameters were fit by hand to capture the behavior of the 5-month-old infants. The four SPH parameters were then increased to capture the behavior of 7- and 10-month-old infants until a parameter set that produced a good quantitative fit across a wide range of looking behaviors over development was achieved. To evaluate the fit between the model and infant data, we calculated the Root Mean Squared Error (RMSE) for means and standard deviations across all ages for three categories of measures: shift rate (shift rate during familiarization, similar test, and dissimilar test), looking lengths (peak look as well as look duration during familiarization, similar test, and dissimilar test), and novelty scores (novelty score on similar test and dissimilar test). We also computed the RMSE for a second batch of 200 simulations at each age to ensure that the model produces quantitatively similar means in looking measures across simulation batches.

A summary of the RMSE for the original and replication simulation batches is shown in Table 4. The RMSE was comparable for the original simulations and the replication simulations. The model fit for means and standard deviations was good across the board. In particular, for the original batch of simulations the mean shift rate ratio for the model was within .10 of empirical values, mean look durations within .31 s of the empirical values, and mean novelty scores were within 3% of the empirical values. The model simulations also quantitatively fit the empirically-measured standard deviations for novelty preferences quite well. The standard deviation fits for shift rate and duration measures were not as close because the model produced less variable behavior in these measures during familiarization when the model looked back in forth at identical items than it did during the test phase when it looked back and forth at different items.

Table 4.

Root Mean Squared Error Model Fit

	Shift Rate		Duration		Novelty Score
Simulations	M	SD	M	SD	M	SD
Origina	0.10	0.12	0.31	0.50	0.03	0.04
Replication	0.10	0.12	0.32	0.50	0.03	0.03

Results

We examined the model's performance in three sets of analyses that parallel the empirical results reported previously. We begin with analyses of the model's performance during familiarization, followed by test, and finally individual differences in looking dynamics and discrimination performance.

Familiarization

The DNF model captured developmental change in looking dynamics quite well. Figure 2D–F shows the looking dynamics of the 5-, 7-, and 10-month-old parameter sets. As the strength of neural interactions increased, the model exhibited a higher shift rate (D), shorter look durations (E), and shorter peak looks (F). The model captured the developmental pattern in some detail – the decline in look duration from 5 to 7 months, for instance, was steeper than from 7 to 10 months.

Figure 6 illustrates the neurocognitive dynamics underlying these behavioral changes. The top portion of the figure shows the sum of PF activity when the model looked at the familiar stimulus on each trial. By trial 3, PF activity was robust for the 5-month-old model (A). This led to strong support for fixation, which, in turn, led to long look durations. Consequently, shift rates were low and peak looks were long. By contrast, PF activity shows a clear decline during later trials for the 7- and 10-month-old models. This led to weaker support for fixation, which, in turn, led to shorter look durations. Consequently, shift rates were higher and peak looks shorter.

Figure 6.

Shows neural dynamics in DNF model underlying looking behavior during familiarization phase. Top row shows sum of PF activity while looking on each trial across the familiarization phase for the 5-month-old model (A), 7-month-old model (B), and 10-month-old model (C). PF activity was stronger for the 5-month-old model than the 7- or 10-month-old models. Error bars show +/− .5 SD.

Bottom row shows the state of PF and WM during the inter-stimulus interval after each familiarization trial, averaged across simulations. Neural interactions were weaker in the 5-month-old model (D), leading to stronger PF activity than in the 7- (E) and 10-month-old models (F) with stronger neural interactions. The stronger neural interactions of the older models gave rise to less total looking, higher shift rates, shorter look durations, and shorter peak looks relative to the weaker neural interactions in the younger model.

This difference in PF activity is a consequence of the SPH. This can be seen in Figure 6D–F, which shows the state of PF and WM averaged across the ISI after each familiarization trial. PF activity is more robust and WM activity weaker for the 5-month-old model than the 7- and 10-month-old models. For the older models, stronger neural interactions gave rise to more robust WM activity and suppression of PF activity after a few trials, that is, the SPH led to speeded encoding and memory formation. For the older models, WM activity is also near threshold (i.e., 0) toward the end of the familiarization phase. This strongly influences test performance, which we describe below. Note that although the dynamics appear very similar at 7 and 10 months, the strength with which the neurons interact is different which leads to the small behavioral changes seen. Below, we discuss how these subtle differences impact looking dynamics at test.

Test

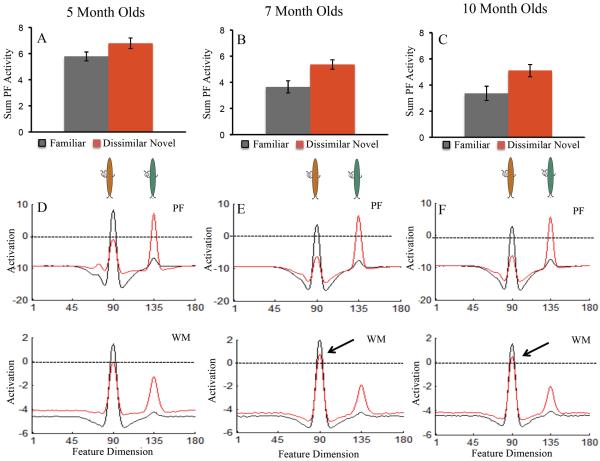
The SPH can capture developmental changes in infants' looking dynamics during familiarization. Does the same neurodevelopmental mechanism also capture infants' discrimination performance? As can be seen in Figure 3D, like infants, only the 7- and 10-month-old models exhibited a robust novelty preference on the dissimilar test. These developmental differences arise from a shift in the contribution of PF activity when the models look at the familiar and novel stimuli. Figure 7A–C shows the sum of PF activity while the model is looking at the familiar (black bar) and novel (red bar) items across development. For the 5-month-old model (A), PF activity was comparable while looking at the familiar and novel items. This led to equal support for looking at each item and a null preference. For the 7- (B) and 10-month-old (C) models, PF activity associated with the novel item was stronger than the familiar item. This led to more fixation support while looking at the novel item and, consequently, a novelty preference.

Figure 7.

Shows neural dynamics in the DNF model that underlie developmental change in discrimination on the dissimilar test. Top row shows the sum of PF activity while looking at the familiar item (black bars) and novel dissimilar item (red bars) for the 5-month-old (A), 7-month-old (B), and 10-month-old (C) models. PF activity associated with the familiar item decreased over development. This led the older models to preferentially look at the novel item relative to the familiar item. Error bars show +/− .5 SD.

The bottom row shows the state of PF and WM while looking at the familiar item (black line) and novel dissimilar item (red line). That is, the black line shows the activity of neurons at sites tuned to the familiar item and the novel item while looking at the familiar item. Similarly, the red line shows the activity of the neurons at sites tuned to the familiar item and novel item while looking at the novel item. For illustrative purposes, the brown buggle is the familiar item and green buggle the dissimilar novel item. Their relative similarity is represented on the feature dimension (x-axis).

For the 5-month-old model, activation was comparable while looking at the familiar and novel item (D), leading to a null preference. For the 7-month-old (E) and 10-month-old (F) models, activation was stronger while looking at the novel item than while looking at the familiar item. This arises from suprathreshold activity associated with the familiar item in WM (see arrows), which produces strong inhibition in PF. Importantly, WM activity associated with the familiar item remains suprathreshold even when the model is looking at the dissimilar novel item (see red line at familiar site in 7- and 10-month-old models relative to red line 5-month-old model).

The shift in the contribution of PF activity associated with the familiar and novel items over development arises from changes in the interaction between PF and WM. This can be seen in the bottom portion of Figure 7, which shows the state of PF and WM while looking at the familiar (black line) and novel (red line) stimulus on the dissimilar test across development.² For illustrative purposes, the familiar stimulus is brown and the novel stimulus is green (see buggles in the figure). When the 5-month-old model looks at the familiar brown item and dissimilar novel green item (D), activation associated with each stimulus is quite similar and the model looks equally at the two items. For the 7- (E) and 10-month-old (F) models, however, activation is stronger while looking at the dissimilar novel green item than while looking at the familiar brown item. This leads the model to look longer to the dissimilar novel green item than the familiar brown item.

Where does this developmental change come from? The older models are able to maintain a working memory of the familiar brown item even while exploring the dissimilar novel green item. This is reflected in the activity of the WM layer shown in panels E–F (see red line at site 90 = the brown item). Importantly, the red line shows the state of WM while the model is looking at the novel stimulus. In other words, when the model is looking at the dissimilar green novel item, it is maintaining a working memory representation of the familiar brown item. This has an important consequence – WM produces inhibition in PF at the site associated with the familiar item, even when the model is looking at the novel item. Thus, when the model re-fixates the familiar item, support for fixation is weak, and the model looks away.

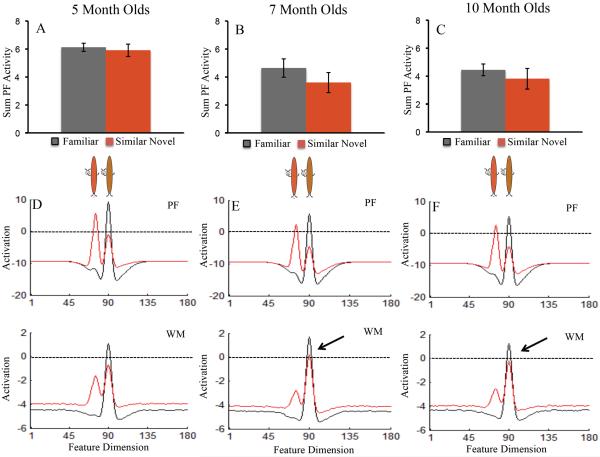
The same analysis of the model's performance on the preceding test, the similar test, is shown in Figure 8. Again, for illustrative purposes the familiar item is brown and the similar novel item is orange (see buggles in Figure 8). Here, activation in PF associated with the familiar brown item and the similar novel orange item was comparable, which led to a null preference for the 5-, 7-, and 10-month-old models.

Figure 8.

Neural dynamics in the DNF model that underlie performance on the similar test. Top row shows the sum of PF activity while looking at the familiar item (black bars) and novel similar item (red bars) for the 5-month-old (A), 7-month-old (B), and 10-month-old (C) models. PF activity associated with the familiar and novel item was comparable across development, leading to null preferences on the similar test for each model. Error bars show +/− .5 SD.

The bottom row shows the state of PF and WM while looking at the familiar item (black line) and novel similar item (red line). That is, the black line shows the activity of neurons at sites tuned to the familiar item and the novel item while looking at the familiar item. Similarly, the red line shows the activity of the neurons at sites tuned to the familiar item and novel item while looking at the novel item. For illustrative purposes, the brown buggle is the familiar item and orange buggle the similar novel item. Their relative similarity is represented on the feature dimension (x-axis).

Activation associated with the familiar and novel item were comparable for the 5-month-old (D), 7-month-old (E), and 10-month-old (F) models. However, in the older models activation associated with the familiar item was on the cusp of suprathreshold activity, which surfaced during the subsequent dissimilar test trial (see Figure 6).

It is notable that across the test phase, activation in PF associated with the familiar item decreased for the older models (compare 7B–C to 8B–C). This decrease in activation in PF associated with the familiar item and relatively stronger neural dynamics of the 10-month-old model led this model to release fixation from the familiar item more quickly on the dissimilar test. This, in turn, enabled the model to capture the critical empirical finding that 10-month-old infants exhibited a higher shift rate (3E) and shorter look durations (3F) on the dissimilar test than the similar test.

Individual Differences in Looking and Discrimination

A unique feature of the DNF model is that it produces looks that can be directly measured. This enabled us to quantitatively capture developmental change in an unprecedented array of looking measures and provide an account of the linkage between neurocognitive and behavioral dynamics. But are looking dynamics in the DNF model meaningfully linked to discrimination performance, as they are in infants? To explore this possibility, we conducted the same regressions on the model data as with infants. Note that the only source of simulation-to-simulation variation in the model data is stochastic fluctuations in the fixation and neurocognitive systems. Put differently, we did not manipulate any parameters to make some simulations exhibit different patterns of looking. Rather, the model spontaneously generated patterns of looking and learning over trials in the task, and we asked whether this produced patterns of covariation between looking and discrimination performance that mimic our sample of infants.

Table 5 shows results of the first hierarchical regression predicting novelty score on the similar test. On the first step, age was entered as a predictor. Age accounted for a significant proportion of variance in novelty scores on the similar test. On the second step, shift rate, look duration, and peak look were entered. Consistent with the empirical results, looking dynamics together accounted for a significant proportion of variance in novelty scores on the similar test above and beyond the effects of age (change in R²=.02). The regression results for the dissimilar test are shown in Table 6. As in the infant analyses, the model was not significant on any step.

Table 5.

Model Similar Test

Step	Predictors	R 2	R2 Change	F Change	p	β	beta	p
1	Age	.007	.007	4.22	.04	−.005	−.08	.04
2	Shift Rate					−.13	−.08	.20
	Look Duration	.022	.015	2.98	.03	.04	.09	.21
	Peak Look					.002	.01	.83

Table 6.

Model Dissimilar Test

Step	Predictors	R 2	R2 Change	F Change	P	β	beta	p
1	Age	.001	.001	.51	.48	.002	.71	.48
2	Shift Rate					−.05	−.03	.58
	Look Duration	.002	.001	.25	.86	−.01	−.02	.75
	Peak Look					.01	.03	.58

In summary, individual differences in looking dynamics in the model across simulations were predictive of discrimination in ways comparable to analyses of infants' performance. It is notable that the proportion of variance in novelty scores accounted for by looking measures was comparable for infants and for the model. Thus, the DNF model captures a realistic magnitude of the relationship between looking and discrimination. We discuss these results in greater detail below.

General Discussion

Over the past several decades, a rich empirical database has shown that looking dynamics and recognition change together over development and are linked within individuals (e.g., Rose et al., 2001). During this same developmental period, infants' discrimination abilities improve for stimuli with well-controlled similarity properties (Brannon et al., 2006). Simulations of a recent DNF model of infant looking and memory formation (Perone & Spencer, 2013) posits that developmental changes in looking dynamics and discrimination performance in a single presentation task can arise from a common mechanistic source. Here, we probed this claim by testing whether looking dynamics and discrimination change together over development and are linked within individuals. Further, we tested whether a single mechanism in the DNF model - the SPH - could capture developmental changes in infants' behavior.

Empirical results from our study revealed that looking dynamics and discrimination change together over development. As with previous studies, with age infants' shift rates were higher, look durations shorter, and peak looks shorter. With age, infants' also began to discriminate along the metrically organized color and shape dimensions that constitute the buggle objects. These findings are consistent with the possibility that developmental changes in looking dynamics and discrimination share a common mechanism. The regression analyses supported this view. Results showed that looking dynamics predicted discrimination performance on the similar test. This indicates that looking dynamics and discrimination are meaningfully linked within individuals.

The DNF model simulations also support the view that developmental changes in looking dynamics and discrimination share a common mechanism. We implemented the SPH by increasing the strength with which excitatory and inhibitory neurons governing encoding and working memory formation interact. This led to quick encoding and robust memory formation, enabling the model to detect novelty along continuous dimensions. Behaviorally, the SPH led to a quicker release of fixation for remembered items, giving rise to higher shift rates, shorter look durations, and shorter peak looks over development.

The SPH might capture a confluence of neurodevelopmental processes happening during infancy that influence visual memory. For example, the SPH might reflect changes in the visual processing pathways projecting to primary visual cortical areas involved in processing visual information such as color. In fact, in adults strong neural activity in primary visual cortical areas is associated with working memory performance (Sligte, Scholte, & Lamme, 2009). The SPH might also reflect decreases in neuronal noise during the first year of life. Skoczenski and Norcia (1998) proposed that noise in neural transduction processes early in development limits infants contrast sensitivity. They found that neuronal responsivity was similar for visual contrasts with and without external noise, which they attributed to internal noise sources. This difference decreased with age and was associated with improvements in contrast sensitivity from 6 to 30 weeks of age. Perone and Spencer (2013) similarly found that high levels of neural noise in the DNF model was required to capture developmental change in infants' looking behavior from 6 to 12 weeks of age. Interestingly, an emergent consequence of the SPH is resistance to interference from noise, as the SPH leads to increasingly stable neuronal states. We are currently probing how experience-dependent changes in neural connectivity within DNFs influences basic perceptual and memory processes as well as the stability of neuronal states underlying working memory formation.

The DNF model also produced patterns of covariation between looking dynamics and discrimination performance. Individual differences in looking have long been interpreted as reflecting variation in neurocognitive ability (for reviews, see Colombo, 1995; Colombo & Mitchell, 1990; Rose et al., 2007). In the simulations of the DNF model, there were no individual differences of this sort. However, the DNF model is a historical system and, critically, each simulation of the model creates a unique trial-to-trial pattern of behavior (see Perone & Spencer, 2013). For example, when the model spontaneously exhibits a long look, encoding is sustained and robust memory formation ensues. This, in turn, impacts the state of perceptual and working memory processes in the model upon entering the test phase and, ultimately, can influence relative dwell time to familiar, remembered items and novel items. We probed whether this type of variation was predictive of discrimination performance. Remarkably, the DNF model produced comparable patterns of covariation between looking and discrimination as infants. Looking measures in the model, like infants, were predictive of discrimination performance on the similar but not dissimilar test.

Why might looking dynamics be predictive of discrimination performance only on the similar test? In the DNF model, looking between the familiar and novel items on the similar and dissimilar tests are influenced by neural dynamics within PF and WM very differently. Figure 8D–F shows the state of PF and WM while looking at the familiar and similar novel items. The state of PF and WM are both influenced by looking and learning across the familiarization phase. If PF and WM activity associated with the familiar item are robust, Hebbian learning in PF can support brief looking to the familiar item. If WM is also robust, inhibition surrounding the familiar item will be strong. This, in turn, leads to quick suppression of PF activity associated with the similar novel item and release of fixation. Indeed, Figure 8A–C shows that activation in PF associated with the familiar item is slightly stronger than activation in PF associated with the similar novel item. In other words, subtle differences in looking and learning across the familiarization phase that lead to robust encoding and memory formation impact the neural dynamics that influence looking between highly similar familiar and novel items.

An emerging challenge in developmental psychology is to map the rich set of behavioral dynamics we observe in the laboratory to cognitive dynamics at the level of the individual. The scope of this challenge has become increasingly salient as technological advances have enabled researchers to obtain massive quantities of data on the temporal dynamics of behavior from individual infants (Adolph, Robinson, Young, & Gill-Alvarez, 2008; Franchak, Kretch, Soska, & Adolph, 2011). Here, we provided an account of the neurocognitive sources of looking measures that are aggregated across a series of trials. Can the DNF model also account for the linkage between ongoing behavioral and cognitive dynamics at the level of the individual? Like infants, the model does produce complex patterns of looking through time. Figure 9 shows the shift rate (A) and look duration (B) of three individual infants (solid squares) and three hand-selected simulations (dashed circles) from those reported here. As can be seen, the DNF model produces patterns of looking that mirror that of infants. These individual differences stem from stochastic fluctuations in the DNF model, which was sufficient to produce a pattern of covariance between looking and discrimination that resembles the pattern of infants.

Figure 9.

Shows shift rate (A) and look duration (B) of three individual infants (solid squares) and three individual DNF model simulations (dashed circles) across the 6 familiarization trials.

Given that all three simulation trajectories in Figure 9 were generated from the same model in the same paradigm with the same parameters, are variations in these individual trajectories simply the result of noise and therefore not meaningful or indicative of `real' individual differences? This is an oversimplified interpretation for several reasons. First, stochastic variations have a role in how infants distribute their looks (Robertson, Bacher, & Huntington, 2001) and may have an important role in visual foraging more broadly (Mobus & Fisher, 1999). Thus, fluctuations in performance are interesting in their own right. Second, the individual patterns in Figure 9 are a result of a complex looking and memory formation system at work. Consequently, these individual patterns do not just reflect the effects of noise; rather, they reflect the effects of noise on the operation of a real-time system and how real-time variations create differential patterns of looking and learning over time. Third, several studies have shown that individual differences in looking and memory formation processes are robust over development (for a review, see Rose et al., 2007). In this context, the question is not whether individual differences in looking performance are meaningful; the question is which aspects of individual differences are meaningful.

The DNF model can be a useful tool on this front because we can probe the full range of possible trajectories that could arise for a given parameter setting. This allows us test specific hypotheses about the origin of individual differences in infants' performance. For instance, we could hypothesize that the variation in infants' performance shown in Figure 9 comes from real-time stochastic fluctuations in looking and not from substantive individual differences across these infants. This predicts that if we run these same infants and the same DNF model in, for instance, the single presentation habituation paradigm used by Perone and Spencer (2013), we should find that the individual trajectories of both the infants and (some of) the simulations once again align. If they do not, then we clearly failed to capture a critical source of individual differences in the DNF model.

What might we be missing? One missing source of individual differences in the model is a long-term learning history. Infants' familiarity with a stimulus influences how they look and what they remember (Bahrick & Pickens, 1995; Martin, 1975; Quinn, Yahr, Kun, Slater, & Pascalis, 2002). A simulation study by Perone and Spencer (2013) showed that the DNF model can capture this source of individual differences. They observed that high levels of familiarity with a stimulus in the model was associated with low levels of initial looking, fast memory formation, and low levels of looking across trials in a single presentation task.

The second source of individual differences is parametric differences across infants that reflect variations in each infant's neurodevelopmental state. This form of individual differences most closely resembles what individual and population differences in looking are attributed to in the literature (see, e.g., Rose et al., 2001; 2002). This view stems from the observation that individual differences in looking resemble developmental differences in looking. For instance, individual infants who exhibit relatively higher shift rates than similarly aged peers also exhibit higher novelty scores, much like older infants exhibit higher shift rates and higher novelty scores than younger infants. Gilmore and Thomas (2002) probed this type of individual difference, fitting exponentially decreasing functions to individual infants' habituation rates across trials and identifying clusters of fast and slow habituators. This work is promising but has some limitations. For example, this work does not specify the neurocognitive processes that underlie habituation rate or looking as an active dynamical behavior distributed in time and space. The DNF model overcomes these limitations, and may shed light parametric differences between individuals. For instance, Perone and Spencer (2013) showed that the parameters modified according to the SPH can capture individual differences in looking that resemble developmental differences. They simulated a series of fine-grained changes in the SPH parameters. This yielded individual differences in models that generated looking and discrimination behaviors ranging from relatively less to relatively more mature.

We contend that the DNF model can be a powerful tool to shed new light on the origin of individual differences in performance, teasing apart how real-time stochastic forces impact learning trajectories, how longer-term learning about individual stimuli and stimulus dimensions impacts performance, and how parametric differences in infants' neurodevelopmental state impact performance. Understanding individual differences at this level will clearly require a substantive empirical and theoretical effort. On the empirical front, we must observe infants' behavior across multiple contexts and at multiple points over development. On the theoretical front, we must develop ways to differentiate how classes of learning trajectories generated by the DNF model are influenced by the multiple factors that can create individual differences.

To summarize, measures of infant looking form the basis of our scientific understanding of infant cognition. A large literature has accumulated describing individual, developmental, and population differences in infants' looking dynamics, recognition performance, and discrimination abilities. Here, we observed that looking dynamics and discrimination change together over development and are linked within individuals. Simulations of a DNF model of infant looking and memory support the view that developmental changes in looking and discrimination share a common mechanistic source. The DNF model simulations also provide new insights into how looking is linked to neurocognitive processes in real time, over learning, and over development. Finally, our simulations raise the exciting possibility that a richer theoretical account of how individual infants create their own development is within reach.

Appendix

Dynamic Neural Fields

DNFs belong to a larger class of bi-stable attractor networks (for a review, see Spencer, Perone, & Johnson, 2009) and consist of layers of neurons that are organized by functional topography along continuous, metrically organized dimensions (e.g., color). In DNFs, neighboring neurons mutually excite each other. Active excitatory neurons also stimulate similarly tuned inhibitory neurons, which implements a form of surround inhibition. This creates a local excitatory / lateral inhibitory activation profile. The state of each neuronal layer depends on its intrinsic dynamics (e.g., the strength with which neighboring neurons mutually excite each other) and the inputs impinging on them (e.g., stimulation from other neural populations or environmental stimuli).

DNFs can enter qualitatively different states. Our use of DNFs has focused on transitions from a resting state (i.e., baseline neural activity) to a self-stabilized, input-driven state where suprathreshold activity depends on the continued presence of a stimulus. We have also focused on transitions from a resting state to a self-sustaining, working memory state where intrinsic interactions within a field are sufficient to maintain suprathreshold activity. These attractor states can be used to implement different cognitive functions. We have used the self-stabilized, input-driven state to implement a form of perceptual encoding and the self-sustaining state to implement the maintenance of information in working memory. These states constrain the parameter values within the model because, for instance, strong excitation and inhibition are required to move the network into the self-sustaining state.

The DNF model used here consists of a fixation and neurocognitive system. The fixation system consists of a collection of nodes that stochastically look among left, right, center, and away locations. The fixation system acts as a perceptual gate into the neurocognitive system by allowing the stimulus at the fixated location to stimulate the neurocognitive system. The neurocognitive system consists of a perceptual field (PF) in which stimuli are encoded, a working memory (WM) field in which information about a stimulus can be maintained in the absence of input, and a layer of inhibitory interneuron's (Inhib) through which PF and WM interact. PF and WM are also reciprocally coupled to Hebbian layers (HL), which, in PF, strengthens the neuronal response to the representation of a stimulus and, in WM, helps neurons sustain suprathreshold activity in the absence of input (i.e., enter a working memory state). Each neuronal layer is specified by a differential equation numerically integrated using the Euler method. The notation used in the equations is presented in Table A1.

Model Equations

Perceptual Field (PF)

PF consists of reciprocally coupled excitatory, PF(u), and inhibitory, Inhib(v), layers, for dimensions color (x) and shape (y). The equations for each dimension are identical. For simplicity, only the equations for color are shown. The excitatory layer of PF is given by the following equation:

$$\begin{array}{cc}\hfill {\tau }_e\stackrel{.}{u}(x,t)=& -u(x,t)+h_u\hfill \\ \hfill & +a_{ul}\sum _{i=1}^{n}g\left(l_i\right)+\sum _{i=1}^n{s}_i(x,t)g\left(l_i\right)\hfill \\ \hfill & +\int c_{uu}(x-x^{\prime })g\left(u\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & -\int c_{uv}(x-x^{\prime })g\left(v\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & -{\alpha }_{uv\_\mathit{global}}\int g\left(v\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_{um}(x-x^{\prime })m(x^{\prime },t)d{x}^{\prime }\hfill \\ \hfill & +\int c_r(x-x^{\prime })\xi (x^{\prime },t)d{x}^{\prime }\hfill \end{array}$$

where $\stackrel{.}{u}(x,t)$ is the rate of change of activation in the excitatory layer of PF across the continuous behavioral dimension, x, as a function of time, t. τ_e is the time constant along which excitatory activation evolves. Activation within PF is influenced by its current state, u(x,t), and its negative neuronal resting level, h_u. PF receives a global boost from the fixation system, $a_{ul}{\sum }_{i=1}^{n}g\left(l_i\right)$, which is dictated by the gating function, g(l_i), and weighted by the amplitude or “strength” parameter, a_ul. This means that when a task-relevant location is fixated. PF receives a boost of activation. PF also receives stimulus input at the suprathreshold fixated location, ${\sum }_{i=1}^n{s}_i(x,t)g\left(l_i\right)$, where s_i(x,t) is a Gaussian input (see below) distributed across the behavioral dimension, x. Note that for these inputs n = 2 because only looking nodes associated with the left and right locations are associated with task-relevant stimuli in the task space (see “Fixation System” below).

The gating function is given by the following equation which takes a sigmoidal shape over the activation variable, u:

$$g\left(u\right)=\left[\frac{1}{1+\exp [-\beta (u\left(t\right)-u_0\left)\right]}\right],$$

where β is the slope of the sigmoid function and u₀ is the threshold (0).

The stimulus input takes the form of a Gaussian distributed over the behavioral dimension, x:

$$s(x,t)=\alpha \exp \left[-\frac{{(x-\mu )}^2}{2{\sigma }^2}\right]\chi \left(t\right)$$

with stimulus position centered at μ, strength α (set to 20), and width σ (set to 3). The gating function, χ(t), is set to 1 when the stimulus is present and 0 otherwise.

PF dynamics are also influenced by local excitatory within-layer interactions, ∫c_uu(x − x′)g(u(x′,t))dx′. These interactions are specified by the convolution of a Gaussian profile, c_uu(x − x′), which determines the neighborhood across which excitatory interactions propagate and a nonlinear gating function, g(u(x′,t))dx′, dictating that only neurons with above threshold activation (>0) participate in the interactions.

The Gaussian convolution was defined by:

$$c(x-x^{\prime })=\alpha \exp \left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }^2}\right]$$

where a sets the amplitude and σ sets the width (i.e., standard deviation) of the connection matrix function.

PF dynamics are also influenced by two inhibitory components. The first is a local inhibitory component, ∫c_uv(x − x′)g(v(x′,t))dx′. Inhibitory interactions are projected across a neural neighborhood specified by a Gaussian, c_uv(x − x′), and only above threshold activity in the inhibitory layer contribute to interactions. The second is a global inhibitory component, a_{uv_global} ∫ g(v(x′,t))dx′, where the sum of suprathreshold activity within the inhibitory layer across the behavioral dimension, x, at time, t, is weighted by a_{uv_global}.

The last contribution to PF dynamics is spatially correlated noise, which is presented to PF by convolving a field of white noise with a Gaussian kernel, ∫ c_r(x − x′)ξ(x′,t)dx′, with strength, a_r, set to .12 and width, σ_r, set to 3.

Inhibitory Field (Inhib)

The excitatory layers PF(u) and WM(w) are reciprocally coupled to an inhibitory layer, Inhib(v). The equation for Inhib is:

$$\begin{array}{cc}\hfill {\tau }_i\stackrel{.}{v}(x,t)=& -v(x,t)+h_v\hfill \\ \hfill & +\int c_{vu}(x-x^{\prime })g\left(u\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_{vw}(x-x^{\prime })g\left(w\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_r(x-x^{\prime })\xi (x^{\prime },t)d{x}^{\prime }\hfill \end{array}$$

where $\stackrel{.}{v}(x,t)$ specifies the rate of change of activation for each neuron along the behavioral dimension, x, as a function of time, t. τ_i is the time constant along which inhibitory activation evolves. Activation in Inhib is influenced by its current state, v(x,t), and its resting level, h_v. Inhib receives excitatory inputs from PF, ∫c_vu(x − x′)g(u(x′,t))dx′, and WM, ∫c_vw(x − x′)g(w(x′,t))dx′. These inputs are projected across a neural neighborhood specified by a Gaussian projection, c(x − x′), to which only suprathreshold neurons in PF and WM contribute as dictated by the gating function, g. An independent source of spatially correlated noise is also added to the inhibitory layer, ∫c_r(x − x′)ξ(x′, t)dx′.

Working Memory Field (WM)

The WM(w) field is given by the following equation:

$$\begin{array}{cc}\hfill {\tau }_e\stackrel{.}{w}(x,t)=-& w(x,t)+h_w\hfill \\ \hfill & +a_{ws}\sum _{i=1}^n{s}_i(x,t)g\left(l_i\right)\hfill \\ \hfill & +\int c_{wu}(x-x^{\prime })g\left(u\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_{ww}(x-x^{\prime })g\left(w\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_{wv}(x-x^{\prime })g\left(v\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & -a_{\mathrm{wv}\_\mathrm{global}}\int g\left(v\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +\int c_{wm}(x-x^{\prime })m(x^{\prime },t)d{x}^{\prime }\hfill \\ \hfill & +\int c_r(x-x^{\prime })\xi (x^{\prime },t))d{x}^{\prime }\hfill \end{array}$$

The equation for WM is identical to the equation for PF with two exceptions. First, the input from the fixation system differs: there is no global boost in activation from the fixation system into WM, and the stimulus input to WM, $a_{ws}{\sum }_{i=1}^n{s}_i(x,t)g\left(l_i\right)$, is weighted by a strength parameter, a_ws, which was set to .05. Second, WM receives an excitatory input from PF, ∫c_wu(x − x′)g(u(x′, t))dx′.

Memory/Hebbian Layers (HL)

Activation in PF and WM is influenced by traces in associated memory (m) or Hebbian layer (HL), which implement a form of Hebbian learning (see text). The equations for each HL are identical. The equation for the HL associated with PF is:

$${\stackrel{.}{m}}_u(x,t)=\{\begin{array}{cc}(-m_u(x,t)+g(u(x,t))∕{\tau }_{m\_\mathrm{build}}\hfill & \mathrm{if}u(x,t)>0\hfill \\ (-m_u(x,t\left)\right)∕{\tau }_{m\_\mathrm{decay}}\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$

where ${\stackrel{.}{m}}_u(x,t)$ is the rate of change of activation for each site, x, in HL as a function of time, t. The constants τ_{m_build} and τ_{m_decay} set the time scale along which activation traces accrue and decay, respectively. Activation in HL only accrues when there is suprathreshold activation in PF. Otherwise, activation in HL decays.

Fixation System

The fixation system consists of four nodes that stochastically look at left and right locations (at which stimuli can appear) and center and away locations (at which no task-relevant stimuli appear). The nodes interact in a mutually inhibitory, winner-takes-all fashion. The equation for the fixation system is:

$$\begin{array}{cc}\hfill {\tau }_e{\stackrel{.}{l}}_i\left(t\right)=& -l_i+h_i\left(t\right)+s_i\left(t\right)\hfill \\ \hfill & +a_{ii}g\left(l_i\right)\hfill \\ \hfill & +a_{lu}g\left(l_i\right)\int g\left(u\right(x^{\prime },t\left)\right)d{x}^{\prime }\hfill \\ \hfill & +a_{lu}g\left(l_i\right)\int g\left(u\right(y^{\prime },t\left)\right)y^{\prime }\hfill \\ \hfill & -a_{l\_\mathrm{global}}\sum _{j\ne l}g\left(l_i\right)\hfill \end{array}$$

where the activation variable, l, is set by the excitatory time scale, τ_e. Activation of each looking node is influenced by its current state, l, and its dynamic negative resting level, h_i(t) (described below). Activation of each looking node is also influenced by a stimulus input given by:

$$s_i\left(t\right)=a_{i\_\mathrm{tonic}}\left(t\right)(a_i+\xi (t\left)\right)+a_{i\_\mathrm{transient}}\left(t\right)$$

The stimulus associated with each node is different (see “Fixation System Parameters” below) to reflect the different stimulus properties of the attention-getter at the central location, the buggle objects at the left and right locations, and non-task-relevant input at all “away” locations. The left and right nodes are presented with a noisy input at each time step when a stimulus is present, a_{i_tonic}(t)(a_i + ξ(t)), and a transient input to signify the appearance of a stimulus, a_{i_transient}(t), present for the initial 75 time steps of each stimulus presentation. The away node is continuously presented with a noisy input to signify the “tonic” presence of stimuli in the task space. The center node is presented only with a transient input to reflect attention-getting stimuli briefly present at the onset of a trial (in our simulations, 50 time steps), effectively driving the fixation system to switch gaze from the away location to the center location.

The gating function, g, dictates the presence of a self-excitatory component to each looking node, a_iig(l_i), and the passing of a negative, inhibitory input to all other nodes, $a_{l\_\mathit{global}}{\sum }_{j\ne i}g\left(l_j\right)$, with weight a_{l_global}. The gating function also regulates the presence of input to the fixation system from the perceptual fields across both the color, x and shape, y, dimensions, a_lug(l_i) ∫ g(u(x′, t))dx′ and a_lug(l_i) ∫ g(u(y′, t))dy′, respectively, with weight a_lu. Note that these inputs are set to 0 for the looking nodes associated with the center and away locations because there are no color and shape stimuli presented at these sites (within the range of stimulus values probed in the experiment).

The resting level of each looking node is dynamic and is governed by the following equation:

$${\tau }_h{\stackrel{.}{h}}_i\left(t\right)=-h_i\left(t\right)+a_{h\_\mathrm{rest}}+a_{h\_\mathrm{low}}g\left(l_i\right)$$

where τ_h sets the time scale along which the resting level of each node, h_i, evolves. When the current level of activation of a looking node is above threshold (determined by the gating function, g(l_i)) the resting level decreases toward a low attractor, the sum of a_{h_rest} and a_{h_low}(which are both negative values). When the current level of activation of a looking node is below threshold, the resting level returns to baseline, a_{h_rest}.

Model Parameters

Table A2 shows the parameters for the neurocognitive system and Table A3 shows the parameters for the fixation system used to simulate the looking behavior of 5-, 7-, and 10-month-old infants. To quantitatively stimulate looking behavior over development, we implemented the Spatial Precision Hypothesis (SPH) using the method used by Schutte and Spencer (2009; see also Perone & Spencer, 2012; Perone, Simmering, & Spencer, 2011; Simmering, 2012). This method involved increasing the strength of within-layer excitatory connections in PF (a_uu) and WM (a_ww) and across layer inhibitory connections from inhib to PF (a_uv) and to WM (a_wv). The SPH parameters are shown in bold. All other parameters were fixed for all ages simulated.

The core three-layer architecture of the model used here has been instantiated in other models and applied to visuo-spatial cognition. Across six different instantiations, the core architecture has been applied to visual working memory and change detection in adults (Johonson, Spencer, Luck, & Schöner, 2009), supervised learning (Linpinski, Spencer, & Samuelson, 2010), spatial recall (Schutte & Spencer, 2009), Piagetian A-not-B task (Simmering, Schutte, & Spencer, 2008), infant habituation (Perone & Spencer, 2012), and infant visual working memory capacity (Perone, Simmering, & Spencer, 2011). Across these instantiations, there are five relations among parameters that constrained the parameter values here. First, the time constant, t, was smaller for the inhibitory layer than the excitatory layer. Second, the resting level of the inhibitory layer was lower than the excitatory layer. Third, the inhibitory projection to WM was broader than the inhibitory projection to PF (identical in Perone & Spencer, 2012). Fourth, the strength of local excitation was stronger in WM than PF. Fifth, the time scale of activation build was shorter than decay. The diverse contexts in which these relations have been applied suggest a pervasive commonality in how neuronal layers must evolve through time and interact to simulate visuo-spatial cognitive dynamics.

Table A1.

Notation

Letter	Meaning
a	amplitude / strength parameter
x,y	dimension (x = color, y = shape)
li	looking nodes (i = index of the node)
u	activation variable for PF
v	activation variable for Inhib
w	activation variable for WM
m	activation variable for memory / Hebbian layer
g	stimulus input (Gaussian for fields)
c	connection weight function
S	gating function
t	time
τ	time scale parameter
h	resting level (static or dynamic)
n	number of nodes
r	random contribution
ξ	noise parameter
e	excitatory
i	inhibitory

Table A2.

Neurocognitive System Parameters

PF(u)				WM(w)				Inhib(v)				Time Scales (τ)		Memory Layers (M)
	5 Mo	7 Mo	10 Mo		5 Mo	7 Mo	10 Mo		5 Mo	7 Mo	10 Mo	AIL Ages		All Ages
hu	−10.20	-	-	hw	−3.57	-	-	hv	−10.20	-	-	τe	80	cum	2.40
auu	0.1041	0.2082	0.3867	aww	0.7741	0.9676	0.9720	auv	1.1060	1.1642	1.4553	τi	10	σum	3.00
σuu	3.00	-	-	σww	3.00	-	-	σuv	15.00	-	-	τbuild	5000	cwm	0.70
				awu	0.40	-	-	avu	0.80	-	-	τdecay	50000	σwm	3.00
				σwu	5.00	-	-	σvu	5.00	-	-	τh	100
				avw	3.00	-	-	awv	0.1781	0.1875	0.2037
				σvw	5.00	-	-	σwv	15.00	-	-
								avw	3.00	-	-
								σvw	5.00	-	-
								awv_global	0.1250
								auv_global	0

Table A3.

Fixation System Parameters

Location
	Left	Right	Center	Away
al_global	3.25	-	-	-
aii	1.20	-	-	-
aiu	0.35	-	-	-
aui	1.00	-	-	-
ai_transient	1.00	1.00	5.5	0
ai_tonic	8.00	8.00	8.00	8.00
ai	0.75	0.75	0	0.875
ah_rest	−5.00	-	-	-
ah_down	−6.00	-	-	-