Assessing the effectiveness of a cancer screening test in the presence of another screening modality

Abstract

Objectives

Analysis of cancer screening effectiveness is challenging in part because of competing tests, which are additional screening tests that identify the condition of interest. For example, studies investigating screening with fecal occult blood tests to prevent colorectal cancer mortality need to consider the occurrence of screening colonoscopy. This paper compares analytic approaches to accounting for competing tests in analyses of cancer screening data.

Methods

We used simulations to compare bias and efficiency across approaches in different scenarios, quantify bias, and make recommendations for analyzing the effectiveness of a screening test in the presence of competing tests.

Results

Under all scenarios, the best performing approach for accommodating competing screening tests was censoring at the time of the competing screening test (range in bias across scenarios: -7.6% to 1.6%). Bias from other approaches ranged from 23.9% to 652.1%.

Conclusions

Censoring at the competing screening exam is the recommended approach for studying cancer screening effectiveness in the presence of competing tests. Censoring avoids confounding by prior competing test results and selection bias resulting from analyzing data on participants after they received a competing screening exam. Results from this study are broadly applicable to screening studies for other conditions, including other types of cancer screening.

INTRODUCTION

Much of what we know about cancer screening effectiveness comes from retrospective observational studies. Yet important methodological questions remain about how to use observational data to assess the effect of screening on cancer mortality. One particular analytic challenge is created by the availability of multiple screening modalities for most screen-detectable cancers. For example, colorectal cancer (CRC) is detectable by flexible sigmoidoscopy, fecal occult blood test (FOBT), or colonoscopy, and national clinical guidelines endorse all these preventive methods (1). Breast cancer can be detected by digital and film mammography and magnetic resonance imaging (MRI). Cervical cancer screening methods include human papillomavirus (HPV) and cytology testing. Many other conditions including hearing loss and mild cognitive impairment can be identified using more than one screening modality.

When multiple screening modalities are available for a particular cancer, the different tests are considered to be “competing” because once a person has been screened with one modality, they are unlikely to be screened with another, at least for a period of time. Another factor that complicates the study of screening effectiveness is that certain test results (e.g., cancer diagnosis) may be available in administrative databases while others (e.g., FOBT results, high-risk adenomas detected on colonoscopy) may not. This is a noted challenge in large population-based studies of screening (2). Thus, analytic strategies need to be tailored to this limited set of data.

This paper examines observational data analysis approaches that account for competing screening tests and can be used with datasets that contain limited test results. We use CRC screening with the competing tests of FOBT and colonoscopy as an example to quantify and compare bias among approaches. This work adds to our understanding of the benefits and drawbacks of different analytic approaches to analyzing screening tests as they are used in real-world healthcare settings.

METHODS

Our approach was to define several realistic but simple screening patterns and several possible analytic approaches for estimating the effectiveness of a screening test for reducing cancer mortality. More complex patterns can be extrapolated as combinations of the simple patterns we have investigated. We evaluated the bias and precision of the different approaches using a simulation study.

Screening patterns

Our example was a CRC screening study on FOBT effectiveness that considered colonoscopy to be a competing screening examination. We identified five possible simple screening patterns (Figure 1): (A) no screening at all; (B) receipt of only FOBT; (C) receipt of only screening colonoscopy; and (D) receipt of FOBT and then screening colonoscopy, or (E) receipt of screening colonoscopy and then FOBT.

Figure 1.

Possible screening patterns for two competing screening modalities. FOBT, fecal occult blood test; T_i1 is the observed time of FOBT, the screening test of interest, and T_i2 the observed time of colonoscopy (a competing screening test for the same disease). X_i describes the observed screening pattern for person i, with X_i = (1(observed to use FOBT), 1(observed to use screening colonoscopy)) where 1() is the indicator function which takes a value of 1 if the condition is satisfied.

Analytic approaches

We compared five analytic options for studying the effectiveness of screening FOBT for reducing the rate of cancer mortality in the presence of competing screening colonoscopy when screening test results are unknown. Table 1 shows these options and how they could be implemented in cohort and case-control studies.

Table 1.

Approaches for Studying the Effectiveness of Screening FOBT in the Presence of Screening Colonoscopy

Approach	Description	Implementation in cohort study	Implementation in case-control study
Pool	Ignore use of screening colonoscopy	Do not collect or incorporate screening colonoscopy information
Censor	Exclude person-time after screening colonoscopy	Censor at screening colonoscopy	Exclude person from pool of cases and controls after occurrence of screening colonoscopy
Stratify	Estimate effectiveness of FOBT stratified by prior screening colonoscopy	Compute effectiveness estimates stratified by prior screening colonoscopy or include covariate for prior screening colonoscopy with an interaction between FOBT and screening colonoscopy in model
Adjust	Weighting or regression adjustment for screening colonoscopy	Compute effectiveness estimates stratified by prior screening colonoscopy use and combine weighted estimates or include covariate for screening colonoscopy in analytic model
Exclude	Exclude for any screening colonoscopy	Exclude person for any screening colonoscopy	Exclude person from pool of cases and controls for any screening colonoscopy

Abbreviation: FOBT, fecal occult blood test

The first analytic decision is whether to account for the competing screening test at all. Not accounting for the competing test results in pooling people with and without screening colonoscopy when estimating FOBT effectiveness. Accounting for the competing screening test requires an approach for handling screening colonoscopy. In one approach, person-time following exposure to screening colonoscopy is excluded from estimates of FOBT effectiveness. In this approach, individuals are censored at the time of receipt of screening colonoscopy. In another approach, individuals are stratified by prior receipt of screening colonoscopy and data on the effectiveness of FOBT in the presence of competing screening colonoscopy is reported separately. Alternatively, standardized estimates are used to adjust for prior receipt of screening colonoscopy. Standardization is achieved by weighting the estimates of FOBT effectiveness in the presence and absence of screening colonoscopy by the proportion of people who receive and do not receive screening colonoscopy. A final approach is excluding data on people with screening colonoscopy.

To illustrate how the five analytic options could be implemented in practice, we describe estimators for the effectiveness of screening FOBT to reduce CRC mortality, assuming constant mortality rates within the effectiveness window (Appendix 1). Effectiveness was defined as the additive difference in mortality rate for screened compared to unscreened individuals. We defined the effectiveness window to be the period of person-time when a screening test might reduce mortality from the cancer of interest; this period might differ among tests for the same condition. We made the simplifying assumption that the effectiveness window was approximately equal to the time until a person was next due for screening (i.e., the recommended screening interval), although this assumption likely resulted in an underestimate of the length of the effectiveness window. A longer interval would have increased the frequency with which competing tests could occur during the effectiveness window. The estimators illustrate how the approaches differ in events (the numerators) and persons or periods of person-time (the denominators). All approaches correspond to maximum likelihood estimators (MLEs) for the rates of exponentially distributed random variables over some period of person-time, except for the “exclude” approach (Table 1). This approach excluded both person-time and events using future information on use of the competing screening test and does not correspond to an MLE. The exclude approach is therefore not necessarily a consistent estimator for the event rate. Moreover, although all other approaches corresponded to MLEs for event rates, these rates were not necessarily the rates in the general population—the target of inference—and thus may lead to biased effectiveness estimates.

Simulation study

Simulation study design

We conducted a simulation study to compare the bias and efficiency of alternative estimators of screening test effectiveness in the presence of a competing screening test. In simulations, the objective was to estimate the effectiveness of FOBT relative to no FOBT. Our measure of effectiveness was the difference in risk of cancer mortality for unscreened versus screened individuals during the effectiveness window. We simulated screening data over a period of 10 years assuming the time to the first use of screening FOBT and colonoscopy were exponentially distributed.

Simulations varied the rates of initial uptake of screening colonoscopy and uptake following FOBT to determine the performance of different analytic approaches for different rates of occurrence of a competing test (Table 2). For each of four scenarios, we simulated 1,000 cohorts of size 100,000. The four scenarios were: (1) low initial rate of screening colonoscopy uptake, high rate of screening colonoscopy after FOBT; (2) high initial rate of screening colonoscopy uptake, high rate of screening colonoscopy after FOBT; (3) low initial rate of screening colonoscopy uptake, low rate of screening colonoscopy after FOBT; and (4) high initial rate of screening colonoscopy uptake, low rate of screening colonoscopy after FOBT.

Table 2.

Colonoscopy Screening Rates in Simulated Data

Scenario	Screening colonoscopy uptake rate (exams/year) among unscreened	Screening colonoscopy uptake rate (exams/year) within effectiveness window of FOBT
Scenario 1	0.036 (low)	0.036 (high)
Scenario 2	0.16 (high)	0.036 (high)
Scenario 3	0.036 (low)	0.005 (low)
Scenario 4	0.16 (high)	0.005 (low)

Abbreviations: FOBT, fecal occult blood test

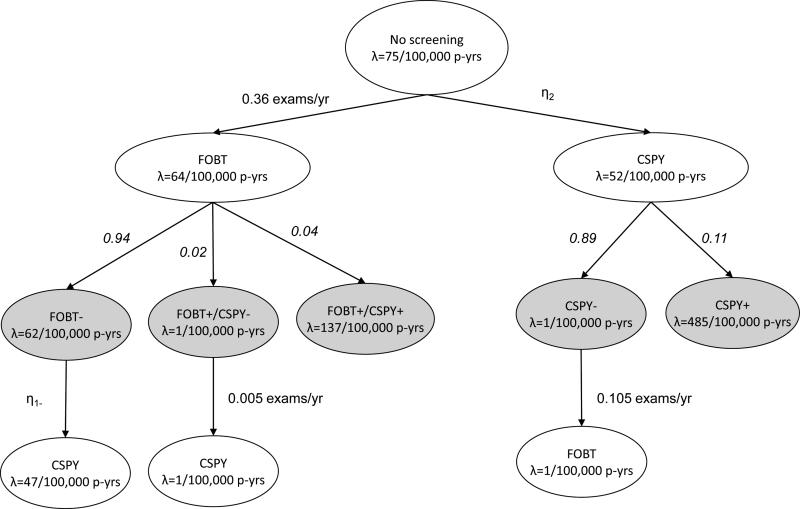
The flow of simulated participants through the screening process is in Figure 2. Each oval represents a subset of the population with its CRC mortality rate indicated by λ. Arrows indicate the movement from one subgroup of the population into another, with rates of transition specified in exams per year or denoted by η. The entire population starts unscreened. Mortality from CRC in the absence of any screening was assumed to be 75 per 100,000 person-years for age ≥50 years based on Surveillance, Epidemiology, and End Results program (SEER) data from 1973 to 1993 (3). Our assumptions for screening test utilization rates (4-6), mortality rates (7-11), and probabilities for screening test results (12,13) are in Figure 2. We assumed that in the absence of other screening tests, biennial FOBT reduced mortality by 15% annually and colonoscopy reduced the risk of CRC mortality by 31% annually. Mortality rates used in simulations were chosen to correspond to these mortality reductions, assuming exponentially distributed times to event. The CRC mortality rate in the population with negative colonoscopies was assumed to be very low based on reported CRC incidence following negative exams (10,11).

Figure 2.

Simulation of colorectal cancer screening and mortality outcomes. FOBT, fecal occult blood test; CSPY, colonoscopy; p-yrs, person-years; λ, mortality rate; η, rate of transition in exams per year ; numbers in italics, probability; +, positive test findings (CRC or high risk adenoma); −, negative findings (no CRC or high risk adenoma); gray, information used to generate the simulated data but assumed unavailable when conducting analysis using observational administrative data.

We assumed screening and choice of test were unrelated to CRC risk (i.e., no confounding). For colonoscopy, screening test results were assumed to be definitive and were therefore simulated as positive (CRC or high risk adenoma) or negative (no CRC or high risk adenoma) from a Bernoulli distribution. For FOBT, we assumed false-positive screening test results were possible and hence, simulated results (true positive, false positive, negative) from a multinomial distribution. Negative results were assumed to contain both true negatives and false negatives. We simulated subsequent mortality conditional on screening test results. Screening tests were assumed to reduce risk by lowering the mortality rate among individuals with true-positive test results. We computed overall mortality rates following a screening test by averaging the mortality rate across individuals with differing screening test results, weighted by the frequency of screening test results. The conferred decrease in mortality risk was assumed to persist for 2 years following FOBT and 10 years following colonoscopy. All patients with false-positive FOBT results were assumed to receive diagnostic colonoscopy and experience a lower mortality rate associated with negative colonoscopy for 10 years following the examination. We assumed no further screening following a positive colonoscopy. Following negative colonoscopy, negative FOBT, or false-positive FOBT, we assumed that people could be screened with the other screening modality before being due again for screening. Time to death and time to uptake of the competing screening test were assumed to be exponentially distributed.

Simulated life histories were followed until the earliest of death, 10 years of follow-up, or two years after receipt of FOBT. This ensured that the data resembled what would be available in a cohort study in which participants were followed until death, for 10 years, or through the effective interval following a screening FOBT (i.e., until the next recommended screening), whichever occurred first. Our simulation study thus focused on the effect of a single round of FOBT screening and not the effect of repeated screening.

Measures of comparison: bias and standard errors

For each simulated dataset generated under the scenarios and using the assumptions described above we estimated the FOBT effectiveness using the five analytic approaches described above and in Table 1. We computed absolute risk (AR) reduction as the difference between estimated mortality rates with and without FOBT screening. For each approach we summarized our findings using the average and standard error of the AR across all 1,000 simulated datasets; bias was estimated by taking the difference between the average AR and the true value (-11 per 100,000 person-years). Percent bias was computed as 100 times the ratio of bias divided by the true AR. Empirical standard errors were computed as the standard deviation of the estimated AR across the simulated datasets to estimate the variability of each approach.

RESULTS

We examined five approaches—pooling, censoring, stratifying, adjusting, or excluding data—for estimating the effectiveness of a screening method (FOBT) in the presence of a competing screening method (colonoscopy). Bias, empirical standard errors, and percent bias were different for each of the approaches (Table 3). The censoring approach had the lowest bias. Of the other methods, the pooled approach was the least biased, particularly when the initial rate of screening colonoscopy uptake was low (scenarios 1 and 3). The other approaches overestimated the effectiveness of FOBT, particularly when the initial rate of screening colonoscopy was high (scenarios 2 and 4). The magnitude of the bias was similar to or larger than the empirical standard errors. Bias of this magnitude makes erroneous inference particularly likely because the true value will often not be covered by confidence intervals. Variability of all estimates was similar with the exception of the stratification approach, which computed estimates within restricted subsets of the data.

Table 3.

Bias, Empirical Standard Errors, and Percent Bias of Estimates for Attributable Risk of Mortality per 100,000 Person-years for Individuals Screened by FOBT Compared to Unscreened Individuals Based on Four Simulated Scenarios, Assuming a True Attributable Risk of -11 per 100,000 Person-years

	Scenario 1a		Scenario 2a		Scenario 3a		Scenario 4a
Analytic approach	Bias (SE)	% biasb	Bias (SE)	% biasb	Bias (SE)	% biasb	Bias (SE)	% biasb
Pool	−3.75 (7.87)	34.1	−11.06 (7.05)	100.6	−2.63 (7.69)	23.9	−9.45 (7.07)	85.9
Censor	0.60 (8.64)	−5.5	0.44 (9.27)	−4.0	−0.17 (8.20)	1.6	0.84 (9.06)	−7.6
Stratifyc	−60.79 (12.90)	552.6	−60.53 (6.69)	550.3	−60.03 (13.43)	545.7	−60.64 (6.87)	551.3
Stratify (Test 1 before Test 2)	−60.89 (13.25)	553.6	−60.37 (8.22)	548.8	−59.55 (18.22)	541.4	−60.38 (15.31)	548.9
Stratify (Test 2 before Test 1)	−71.73 (13.09)	652.1	−71.55 (6.71)	650.5	−71.08 (13.44)	646.2	−71.65 (6.87)	651.4
Adjust	−8.36 (7.55)	76.0	−21.08 (6.38)	191.6	−6.01 (7.51)	54.6	−18.55 (6.54)	168.6
Adjust (Accounting for test order)	−8.37 (7.55)	76.1	−21.08 (6.38)	191.6	−6.00 (7.51)	54.6	−18.55 (6.54)	168.6
Exclude	−8.92 (9.42)	81.1	−36.74 (11.88)	334.0	−7.41 (8.60)	67.4	−32.09 (11.13)	291.7

Abbreviations: FOBT, fecal occult blood test; SE, standard error

^aScenario 1: Low initial rate of colonoscopy uptake; high rate of colonoscopy after FOBT; Scenario 2: High initial rate of colonoscopy uptake; high rate of colonoscopy after FOBT; Scenario 3: Low initial rate of colonoscopy uptake; low rate of colonoscopy after FOBT; Scenario 4: High initial rate of colonoscopy uptake; low rate of colonoscopy after FOBT.

^bPositive % bias indicates overestimation of the benefit of FOBT relative to true AR of -11 per 100,000 person-years.

^cResults are for FOBT in the stratum with colonoscopy; results in the stratum without colonoscopy are equal to those in the Censor row

DISCUSSION

We explored analytic approaches for evaluating the effectiveness of a screening test when a competing screening modality might be used during the test's effectiveness window. The best-performing approach for analyzing screening test effectiveness in the presence of a competing test was censoring at the time of the competing test. Simulation studies demonstrated that substantial bias occurs when other approaches were used. Based on our findings, we recommend censoring at the time of the competing screening test. In case-control studies, the censoring approach is equivalent to risk-set sampling in which people are eligible to be cases or controls until they have a competing screening exam. While stratification by the competing screening exam may be intuitively appealing, for the reasons described below it produces biased estimates.

Results of a prior competing screening test act as a confounder because people who have a positive screening test are not eligible to be screened again, so only those with a prior negative screening test go on to receive the screening test of interest. If results of the prior competing screening test are available, traditional methods for handling confounding (e.g., stratification or adjustment by prior test results) should be sufficient to eliminate bias. We focused on identifying the best analytic approach when data sources contain the occurrence of a competing screening test but not results. For instance, in administrative data, information on cancer incidence and cancer mortality but not individual test results may be available. This is often the case in studies of CRC screening, where colonoscopy results are not available in administrative data (2). In this scenario, stratification by the true confounder (results of a prior competing screening test) is impossible.

The occurrence of a competing screening test after the exam of interest (and during the effectiveness window of the test of interest) causes selection bias. This is because receipt of the competing test during the effectiveness window of the test of interest is related to the results of the test of interest. Only individuals with a negative result on the screening test of interest can subsequently receive the competing test. So for example, FOBT will clearly look beneficial when comparison is made between individuals with a negative FOBT (low risk) and unscreened (average risk) individuals. Because this bias arises from stratification based on results of the test of interest, it is not remediable even if results of the competing screening test (e.g., colonoscopy) are known. In summary, biases that result from competing screening tests before and after the exam of interest occur because the only people screened with both tests are those whose first screening test was negative; these people are at lower risk of mortality.

We note that our findings apply to competing screening tests, not diagnostic tests that are performed in response to signs or symptoms of disease. Censoring at diagnostic exams is not recommended because these exams are often events along a causal pathway in which people are diagnosed with cancer before dying from it. Administrative data algorithms can help identify test indication (14). We also note that the question of how to study people who change screening regimens when they become due again for screening is different and not considered in this paper, which focuses on single rounds of screening.

Estimates of bias and precision are based on simulations to investigate five straightforward screening scenarios with simplifying assumptions. This approach has several limitations. First, we investigated only two tests with five screening strategies. Real-world applications involve more complex combinations of tests. However, by considering only the test of interest and the first competing test to occur, more complicated strategies can be reduced to fit into our scenarios. Second, mortality rates were assumed to be constant and the effect of screening tests was assumed to act on mortality via a step function with risk immediately decreased following screening, then returning to its pre-screening value at the end of the effectiveness window. In reality, mortality rates and the effect of screening over the course of the effectiveness window are likely to be nonconstant. Bias in situations with more complex mortality rates and screening effects might differ in magnitude from our findings. However, the basic pattern of bias and efficiency is expected to be the same across the five approaches. A different set of assumptions about ARs due to FOBT and colonoscopy may have resulted in slightly different estimates of bias but would not affect overall conclusions about the different approaches. Changing the length of follow-up in our simulations would have similar effects. In spite of the simplicity of our simulations, our results provide guidance to researchers for estimating the comparative effectiveness of screening tests in the presence of competing screening tests by describing the type of bias that may arise in different analytic approaches.

Our findings are broadly relevant to screening studies. However, understanding how to analyze real-world screening data is especially important for CRC studies because multiple screening modalities are common and the comparative effectiveness of alternative regimens has primarily been examined using modeling (15,16). Nonetheless, similar issues are arising for studies of breast cancer screening with screening MRI, ultrasound and mammography all competing. The issue of analyzing data in the presence of competing screening tests is likely to become increasingly important with new emerging technologies and an emphasis on real-world comparative effectiveness studies using observational data. Our recommended analytic approach of censoring at the time of the competing screening test is straightforward, can be employed in both cohort and case-control studies, and is applicable to a variety of conditions that are detected by multiple screening modalities.

Appendix 1: Overview of estimators for effectiveness

Let D_i represent the time of death for participant i and let C_i represent the censoring time for this subject. Let Y_i = min(D_i, C_i) and Δ_i = 1(D_i < C_i), where 1() is the indicator function, which takes the value 1 when its condition is satisfied and 0 when it is not. We define a vector of screening times, T_i* = (T_i1*, T_i2*) with T_i1* the time of the screening test of interest (Test 1) and T_i2* the time of a competing screening or diagnostic test for the same disease (Test 2). T_i* is observed only if screening occurs prior to death or censoring. Its observable analog is T_i = (min(T_i1*, Y_i), min(T_i2*, Y_i)). Finally, we define an indicator for the sequence of screening tests observed, X_i = (1(T_i1 < Y_i), 1(T_i2 < Y_i)). We assume that screening is effective only during a limited period of time following receipt of a screening test (the effectiveness window) and therefore evaluate only the association between a test and cancer mortality in this window of time. If X_i1 = 1, data are censored at T_i1 + d, where d is the length of the effectiveness window for Test 1.

Below we present maximum likelihood estimators (MLEs) for the mortality rate among screened and unscreened individuals, assuming D_i is exponentially distributed with rate λ. In general, we can define the MLE for the rate of an exponentially distributed random variable conditional on the length of time T that an individual was observed to be at risk, with Δ indicating whether an event was observed. Specifically, the likelihood for λ based on a sample of n observations is given by

$$L\left(\lambda \right)=\prod _{i=1}^n{\lambda }^{{\Delta }_i}\exp (-\lambda T_i)={\lambda }^{\sum _{i=1}^n{\Delta }_i}\exp (-\lambda \sum _{i=1}^n{T}_i).$$

By differentiating the log-likelihood we obtain the MLE, $\widehat{\lambda }={\sum }_{i=1}^n{\Delta }_i∕{\sum }_{i=1}^n{T}_i$. The alternative methods described below are distinguished by the subset of events included in ${\sum }_{i=1}^n{\Delta }_i$ and the relevant time-frame for observation of person-time included in ${\sum }_{i=1}^n{T}_i$. Estimators for the five approaches in Table 1 are presented below, with the choice of numerator and denominator for each. Each numerator and denominator implies a different choice of persons and person-times to include in the likelihood above.

1. Pool

Under this approach the mortality rate in unscreened subjects is estimated as

$${\widehat{\lambda }}_0^P=\frac{\sum _i{\Delta }_i(1-X_{i1})}{\sum _i{T}_{i1}},$$

and in screened subjects as

$${\widehat{\lambda }}_1^P=\frac{\sum _i{\Delta }_i{X}_{i1}}{\sum _i(Y_i-T_{i1})}.$$

This approach combines events and person-time for subjects screened with the competing test and for subjects not exposed to the competing test.

2. Censor

In this approach, time at risk is included only until the occurrence of the competing screening test. Events prior to this test are included in estimators, while both events and time subsequent to the competing test are ignored. Under this approach, the mortality rate during the unscreened person-time is estimated as

$${\widehat{\lambda }}_0^C=\frac{\sum _i{\Delta }_i(1-X_{i1})(1-X_{i2})}{\sum _i{T}_{i1}(1-X_{i2})+T_{i2}{X}_{i2}1(T_{i2}<T_{i1})+T_{i1}{X}_{i2}1(T_{i1}<T_{i2})}$$

and during person-time following screening as

$${\widehat{\lambda }}_1^C=\frac{\sum _i{\Delta }_i{X}_{i1}(1-X_{i2})}{\sum _i(Y_i-T_{i1})X_{i1}(1-X_{i2})+(T_{i2}-T_{i1})X_{i1}{X}_{i2}1(T_{i1}<T_{i2})}.$$

3. Stratify

An alternative to excluding person-time and events following use of Test 2 is to compute separate effectiveness estimates for Test 1 before and after use of the competing test. The effectiveness estimator for person-time prior to screening with the competing test is the censored estimator given above. The stratified estimator for Test 1 following Test 2 is below. In this stratum, the referent “unscreened” group thus consists of person-time following screening with the competing test only. If we assume that when both screening tests are performed, the effect of the two tests does not depend on the order in which they were performed, then the mortality estimator during person-time following screening with Test 2 but not Test 1 is

$${\widehat{\lambda }}_0^S=\frac{\sum _i{\Delta }_i(1-X_{i1})X_{i2}}{\sum _i(Y_i-T_{i2})(1-X_{i1})X_{i2}+(T_{i1}-T_{i2})X_{i1}{X}_{i2}1(T_{i2}<T_{i1})},$$

and for person-time following screening with both Test 1 and Test 2 is

$${\widehat{\lambda }}_1^S\frac{\sum _i{\Delta }_i{X}_{i1}{X}_{i2}}{\sum _i(Y_i-T_{i2})X_{i1}{X}_{i2}1(T_{i1}<T_{i2})+(Y_i-T_{i1})X_{i1}{X}_{i2}1(T_{i2}<T_{i1})}.$$

The stratified estimator can be further refined for subjects exposed to Test 2 by stratifying by the ordering of the two tests to allow the effectiveness of the test of interest to depend upon this ordering. The estimator during person-time not exposed to Test 1 is the same as above, ${\widehat{\lambda }}_0^{S1}={\widehat{\lambda }}_0^S$, while for person-time following exposure to both tests, with Test 1 preceding Test 2 (stratum S1), is

$${\widehat{\lambda }}_1^{S1}=\frac{\sum _i{\Delta }_i{X}_{i1}{X}_{i2}1(T_{i1}<T_{i2})}{\sum _i(Y_i-T_{i2})X_{i1}{X}_{i2}1(T_{i1}<T_{i2})}.$$

We can construct a similar stratified estimator for the combined effect of both screening tests when the test of interest follows the competing test (stratum S2). As above, the estimator for person-time exposed to Test 2 is unchanged, ${\widehat{\lambda }}_0^{S2}={\widehat{\lambda }}_0^S$. The estimator for person-time following exposure to both tests, with Test 2 preceding Test 1, is

$${\widehat{\lambda }}_1^{S2}=\frac{\sum _i{\Delta }_i{X}_{i1}{X}_{i2}1(T_{i2}<T_{i1})}{\sum _i(Y_i-T_{i1})X_{i1}{X}_{i2}1(T_{i2}<T_{i1})}.$$

4. Adjust

An adjusted estimator can be constructed by taking a weighted average of stratified estimators, weighted by the probability of observing each combination of tests. This estimator weights mortality estimators from the strata described above, person-time exposed and unexposed to the competing test, by the probability of being exposed to the competing test. The estimator for subjects not exposed to the test of interests is

$${\widehat{\lambda }}_0^A={\widehat{\lambda }}_0^C\sum _i(1-X_{i2})∕N+{\widehat{\lambda }}_0^S\sum _i{X}_{i2}∕N,$$

and for subjects exposed to Test 1 is

$${\widehat{\lambda }}_1^A={\widehat{\lambda }}_1^C\sum _i(1-X_{i2})∕N+{\widehat{\lambda }}_1^S\sum _i{X}_{i2}∕N.$$

Alternatively, if the ordering of the two tests is believed to be important, then we can compute weighted averages further stratified by order. This estimator takes a weighted average of estimators for participants screened with the competing test and those unscreened by the competing test. However, in this version, we further allow for stratification by order of the test of interest and the competing test. The estimator for subjects exposed to only Test 2 is the same as above, ${\widehat{\lambda }}_0^{A1}={\widehat{\lambda }}_0^A$, while the estimator for subjects exposed to both tests is

$${\widehat{\lambda }}_1^{A1}={\widehat{\lambda }}_1^C\sum _i(1-X_{i2})∕N+{\widehat{\lambda }}_1^{S1}\sum _i{X}_{i2}1(T_{i1}<T_{i2})∕N+{\widehat{\lambda }}_1^{S2}\sum _i{X}_{i2}1(T_{i2}<T_{i1})∕N.$$

While it is possible to derive an adjusted estimator, we note that if Test 2 modifies the effect of Test 1, it is generally preferable to present stratum-specific estimates and not to adjust.

5. Exclude

Finally, we can construct an estimator that ignores all information from subjects observed to be screened with the competing test at any time. In this case, the estimator for subjects who are unscreened is

$${\widehat{\lambda }}_0^E=\frac{\sum _i{\Delta }_i(1-X_{i1})(1-X_{i2})}{\sum _i{T}_{i1}(1-X_{i2})},$$

and the estimator for subjects screened by Test 1 only is

$${\widehat{\lambda }}_1^E=\frac{\sum _i{\Delta }_i{X}_{i1}(1-X_{i2})}{\sum _i(Y_i-T_{i1})X_{i1}(1-X_{i2})}.$$

Note that the numerator of these expressions is the same as the numerator of the censored estimator. However, the denominators omit person-time prior to the competing screening test, suggesting that this estimator will be upwardly biased because it excludes person-time at risk for participants who subsequently experience the competing test. This estimator cannot be derived from the exponential likelihood because it uses information from the future in determining the persons and person-time to include in analysis.