Characteristics of Unintentional Movements by a Multi-Joint Effector

Abstract

We explored the phenomenon of unintentional changes in the equilibrium state of a multi-joint effector produced by transient changes in the external force. The subjects performed a position-holding task against a constant force produced by a robot and were instructed not to intervene voluntarily with movements produced by changes in the robot force. The robot produced a smooth force increase leading to a hand movement, followed by a dwell time. Then, the force dropped to its initial value leading to hand movement towards the initial position, but the hand stopped short of the initial position. The undershoot magnitude increased linearly with the peak hand displacement and exponentially with dwell time (time constant of about 1 s). For long dwell times, the hand stopped at about half the total distance to the initial position. We interpret the results as consequences of a drift of the referent hand coordinate. Our results provide support for back-coupling between the referent and actual body configurations during multi-joint actions and produce the first quantitative analysis of this phenomenon. This mechanism can also explain the phenomena of “slacking” and force drop after turning visual feedback off during accurate force production task.

Introduction

The equilibrium-point hypothesis (Feldman, 1966, 1986) and its recent development as the referent coordination (RC) hypothesis (Feldman, 2009) have been highly influential and controversial in the field of motor control. According to these hypotheses, the central nervous system (CNS) uses neurophysiological signals to set referent values for salient variables. The control of a natural movement can be described as based on a hierarchy of RCs with few-to-many mapping between consecutive levels (Latash, 2010): At the highest level, RC specifies referent values for a handful of task-related variables, while at the lowest level RC defines a body configuration at which all the muscles are at the threshold of activation via the tonic stretch reflex.

One of the predictions of the RC hypothesis is movement equifinality in response to transient perturbations. Equifinality is a property of a neuromotor system to come to an originally planned final state in the space of task-related performance variables despite possible transient force perturbations. Note that equifinality is not an obligatory signature of the control with RCs, although it may be expected under certain conditions including, in particular, no corrective action by the CNS and no changes in the muscle force-generating properties (Feldman & Latash, 2005). Several studies (Bizzi, Polit, & Moraaso, 1976; Kelso & Holt, 1980; Schmidt & McGown, 1980; Latash & Gottlieb, 1990) confirmed equifinality under transient perturbations, while other papers reported violations of equifinality under special conditions such as the action of the Coriolis force and “negative damping” (Lackner & DiZio, 1994; DiZio & Lackner, 1995; Hinder & Milner, 2003).

Equifinality in a redundant system may be considered at the level of task-related variables or at the level of redundant elemental variables. A few recent studies have shown that a smooth, transient perturbation leads to equifinality at the task-related level but not at the level of elemental variables (Wilhelm, Zatsiorsky, & Latash 2013; Zhou, Solnik, Wu, & Latash, 2014). Recently, a few studies have also reported violations of equifinality at the level of task-related variables under longer-lasting transient perturbations (Ambike, Paclet, Zatsiorsky, & Latash, 2014; Zhou, Solnik, Wu, & Latash, in press). These effects have been interpreted as consequences of an unintentional drift in the corresponding RC. Assuming a possibility of such a drift offers an interpretation for a few other findings, such as a drop in force in isometric force production tasks without visual feedback (Slifkin, Vaillancourt, & Newell, 2000; Vaillancourt & Russell, 2002; Shapkova, Shapkova, Goodman, Zatsiorsky, & Latash, 2008) and the phenomenon of “slacking” representing a decrease in muscle activation during repetitive movements (Scheidt, Reinkensmeyer, Conditt, Rymer, & Mussa-Ivaldi, 2000; Emken et al. 2007).

Within the scheme of hierarchical control with RCs, the few-to-many mappings are organized in a way that ensures stability of task-related salient variables with the help of back-coupling loops (Latash, Shim, Smilga, & Zatsiorsky, 2005; Martin, Scholz, & Schöner, 2009) that channel variance at the level of elemental variables primarily into a space where task-related variables show no changes, i.e., into the uncontrolled manifold (UCM) for those variables (Scholz & Schöner, 1999; reviewed in Latash, Scholz & Schöner, 2007). The mentioned observations of violations of equifinality suggest another kind of back-coupling. Changes in RC for a salient variable in the hierarchical scheme attract this variable to a new value specified by the RC and lead to movement (direct coupling). However, if actual configuration is prevented from moving to the corresponding RC for a relatively long time, the RC starts to be attracted to the actual configuration (we will address this hypothetical process as RC-back-coupling to distinguish it from the back-coupling postulated in the cited earlier papers). This RC-back-coupling leads to an unintentional movement.

The main purpose of this study has been to explore the spatial and timing characteristics of RC-back-coupling using transient perturbations of varying duration applied during a static position-holding task against a constant force vector. We tested the following hypotheses: (1) Brief, smooth perturbations (changes in the force vector) will lead to relative equifinality in the space of task-related variables (relatively small deviations of the final hand position from the initial position), while longer perturbations will lead to larger violations of equifinality; (2) The magnitude of violations of equifinality will be an exponential function of the duration of the perturbation (Zhou et al. in press); (3) For very long-lasting perturbations, removal of the perturbation will not lead to motion towards the initial state (RC moves all the way to the actual configuration); and (4) Perturbations of a larger magnitude will produce proportionally larger violations of equifinality.

To test these hypotheses, subjects performed a position holding task against a baseline force generated by a robot (HapticMaster). During the baseline force application, subjects were required to resist it and maintain the initial joint configuration. After that, a smooth, transient change in the external force, increasing to a new level over 500 ms in a ramp fashion, was applied to the handle held by the subjects. The subjects were always instructed not to interfere with possible motion of the handle induced by this force change (“allow the robot to move your arm”). The force change was followed by a dwell time of varying duration (up to 8 s) and then the force returned to the initial level.

Methods

Participants

Seven male subjects (all self-reported right-handers) took part in this study (age: 28.8 ± 0.8 years, height: 1.69 ± 0.04 m, and mass: 65.5 ± 4.2 kg). All subjects were healthy and had no history of hand injury. All subjects provided informed consent in accordance with the procedures approved by the Office for Research Protection of the Pennsylvania State University.

Apparatus and Procedure

Experimental setup

The HapticMaster (Moog, The Netherlands) is an admittance-controlled robot with an arm that possesses three degrees of freedom (DOFs). A handle with three kinematic DOFs - pitch, roll and yaw - was attached to the end of the robot arm. The robot arm was used to generate both baseline force (F_BASE) and perturbation force (F_PERT) (details in Procedures). Visual feedback was presented with a 20-inch monitor placed 0.8 m from the subject.

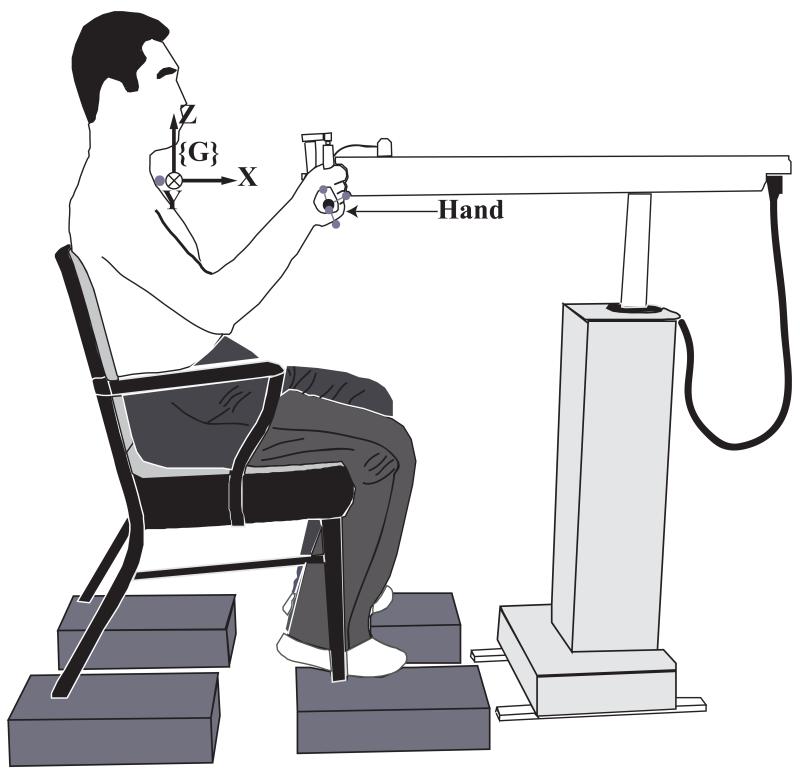
Each subject sat upright in the chair and held the handle attached to the robot arm with the right hand. One reflective marker was placed on the suprasternal notch (SN). Three-dimensional coordinates of the suprasternal notch (SN) marker were used as the origin of the XYZ global coordinate system {G}. The X-axis was a horizontal axis in a sagittal plane pointing in the anterior direction, the Y-axis was a horizontal axis in a frontal plane pointing to left side of the subject, and the Z-axis pointed vertically upward. The robot arm was aligned such that the subject’s hand moved primarily in a parasagittal plane. The subject selected a comfortable hand position, from which the hand could move 30 cm freely along positive (X+) direction in the global coordinate system. The marker locations from one camera were drawn on a transparent sheet attached to the monitor and used to guide the subject to the initial joint configuration in all trials. The 3D position of the handle of the robot arm was set as the initial position of the robot by the robot control program. The global coordinate systems, as well as the initial joint configuration of the subject, are illustrated in Figure 1.

Figure 1.

An illustration of the initial posture. The subject sits in a chair, using the right arm to hold the handle in an initial position. The robot arm is aligned such that the subject’s hand moves primarily in a parasagittal plane. The hand marker cluster and additional marker are shown. {G} designates the Global Coordinate System.

Kinematic data collection

A Qualisys Motion Capture System (Qualisys AB, Sweden), consisting of five ProReflex MCU240 infrared light emitting cameras, was used to record three-dimensional (3D) kinematic data at 120 Hz. The five cameras were mounted on tripods positioned around the experimental space. Calibration was considered to be successful if the standard deviation of the wand length was less than 1 mm. The 3D tracking maximum residual of the camera system was set as 5mm. A Marker cluster (four markers per cluster, see Mattos et al. 2011) was used to track the position of right hand. The cluster was placed at the dorsal surface of the hand. Surgical tape (Transpore™, 3M) was used to fasten the cluster.

Experimental procedure

Subjects started with sitting in the chair and holding the handle with the right arm. The robot generated a constant baseline force (F_BASE = 10 N, same for all subjects) along positive X+ axis. The subject was instructed to resist the baseline force and maintain the initial joint configuration and position (Figure 1). No visible hand displacement was seen during this initial phase.

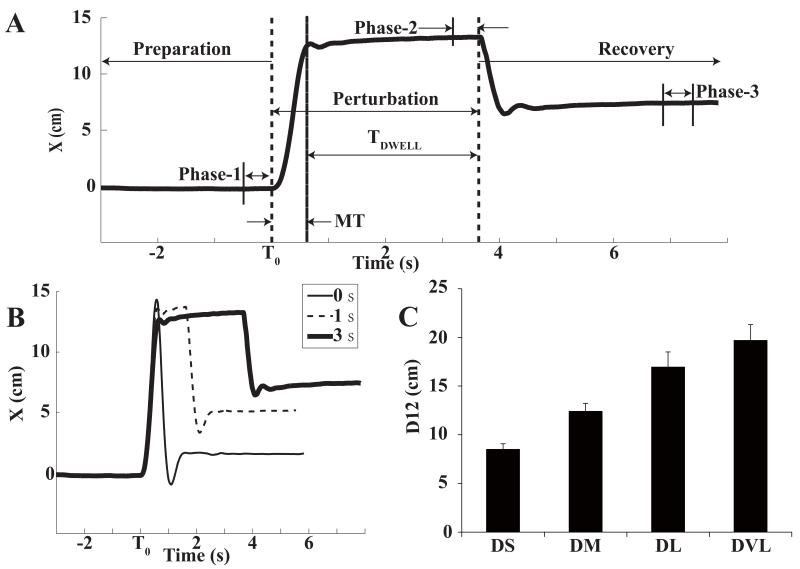
Each trial consisted of three parts. The first part, Preparation, was a steady state until the perturbation onset (T₀, Figure 2A). During the second part, Perturbation, the force along positive X+ axis produced by the robot increased to a certain value and stayed at that value for a certain dwell time; the final part was Recovery, in which the robot force returned to F_BASE and the subject’s arm came to a new steady state.

Figure 2.

A: A typical hand trajectory along X direction in the global coordinate system with dwell time of 3 s for the medium perturbation distance. The two vertical dashed lines show the start (T₀) and the end of the perturbation force. The time intervals of data analysis (Phase-1, Phase-2, and Phase-3) are shown. B: Three typical hand trajectories along X direction with different T_DWELL (0, 1, and 3 s) for the medium perturbation distance. Note the scaling of the undershoot with T_DWELL. C: The hand displacements produced by the perturbation (D12): DS (short distance), DM (medium distance), DL (long distance), DVL (very long distance). Averages across subjects with standard error bars are shown.

During Preparation, the subject was required to hold the handle against F_BASE. This part lasted for 2 – 4 s. During the next two parts, the subject was instructed not to interfere voluntarily (“allow the robot to move your arm, do not relax and do not resist”) (Feldman, 1966; Latash, 1994). After T₀, the robot force increased in the same direction as F_BASE and the subject’s hand was pulled away from the subject. During the perturbation, robot velocity was recorded online and peak velocity (V_PEAK) of the handle was updated based on the robot velocity by the robot control program. The perturbation force increased to a new level over 500 ms and was kept at that level until the handle velocity dropped under 10% V_PEAK, which was used as the criterion for the pause in the force change. Movement time (MT) was defined as time elapsed from the initiation of the perturbation to the time when the movement paused. The perturbation distance from initial position to the position where the movement paused depended on the force level set in the robot control program. Before experiment, the subject performed a few trials for practice. During those practice trials, subjects familiarized with the experiment and appropriate magnitudes of F_PERT were defined, which moved the handle about 8 cm (short distance), 12 cm (medium distance), 16 cm (long distance) and 20 cm (very-long distance) away from its initial position by the time when the movement paused (Figure 2C). As a result, the handle excursion was approximately matched across subjects while F_PERT magnitude varied from subject to subject; F_PERT was always larger than F_BASE even for the short distance perturbation.

After the handle velocity dropped under 10% V_PEAK, the program started to count dwell time, the total amount of time during which F_PERT was applied after V < 10% of Vpeak. Nominal dwell time (T_DWELL) could be any integer between 0 s and 8 s. If T_DWELL was 0 s, F_PERT was immediately removed after the velocity dropped under 10% V_PEAK. For the largest T_DWELL, the robot paused for 8 s. Perturbation time was defined as the sum of movement time and T_DWELL. During Recovery, the subject kept the final position for 2 - 3 s and then released the handle. The handle returned to the initial position, the subject grasped it, and the system was ready for the next trial.

Given different combinations of perturbation distance (D_PERT) and T_DWELL, there were 36 conditions: 4 D_PERT (short, medium, long, and very-long) × 9 T_DWELL (0–8 s). Trials consisted of 4 blocks with different perturbation distances, and within each block, 9 T_DWELL conditions were also block randomized. Subjects performed each condition 3 times in a row (108 trials in total). Short rest intervals were offered between trials within a condition (about 5 s), while 1-min rest was given between conditions.

Data Processing

The data were analyzed with a customized MATLAB program (Mathworks Inc, MA, USA). Marker coordinates were low-pass filtered at 5 Hz with a zero-phase 4^th-order Butterworth filter. The coordinates of the suprasternal notch (SN) marker were subtracted from the coordinates of all markers. To obtain the hand coordinates, one marker of the hand marker cluster was selected to represent the hand. The hand coordinates were averaged over each of the three phases in each trial and the Euclidean distance of the hand was calculated between Phase-1 and Phase-2 (D12, peak hand displacement produced by the robot), and between Phase-1 and Phase-3 (D13, the amount of undershoot).

Three time intervals (phases) were extracted from the three parts of each trial for further analysis (Figure 1A). During Preparation, the 0.5 s time interval prior to T₀ was defined as Phase-1. During Perturbation, for T_DWELL = 0 s, Phase-2 was defined as the 0.1 s time interval prior to the drop of F_PERT; for other T_DWELL, Phase-2 was defined as the final 0.5 s time interval of the perturbation time. For T_DWELL ≠ 0, a plateau of hand position along the X direction was seen in Phase-2. When T_DWELL = 0, no such plateau was available because of the fast changes in force/position. Thus, we selected a smaller time interval for T_DWELL = 0 to represent the state in-between the application and removal of F_PERT. During Recovery, Phase-3 was defined as the 0.5 s time interval that ended 0.5 s before the trial end.

We further explored the dependence of D13 and D13/D12 Ratio (D-ratio) on perturbation time (PT = MT + T_DWELL) using regression analysis. The data suggested exponential relations (see Results), and hence, exponential functions D13 = a × (1 − e^{−b × PT}) and D-ratio = A × (1 − e^{−B × PT}) were used to fit the data.

Statistics

All descriptive statistics are reported in the text and figures as means and standard errors unless stated otherwise. One-way repeated-measures ANOVA was used to test effect of D_PERT(short, medium, long, and very-long) on the coefficient a, b, A and B in the regression equations. Two-way repeated-measures ANOVAs were used to test effect of D_PERT and T_DWELL on D13 across subjects. Within this analysis, the number of levels of T_DWELL was limited to three because for very long T_DWELL no major change in the outcome variables was observed. To fulfill the assumption of normality, dependent variables were log-transformed when needed. Pairwise comparisons with Bonferroni corrections were used to explore significant effects, while post-hoc ANOVAs were performed to explore interaction effects in the two-way analysis. The statistical tests were performed with SPSS 20.0 (IBM Corporation, USA) and MATLAB (Mathworks Inc., MA, USA).

Results

The application of the perturbation force (F_PERT) resulted in hand motion from the initial position to a new position. When F_PERT was removed and the robot force returned to F_BASE, the hand moved back towards the initial position but typically stopped short of the initial position. The amount by which the subject undershot the initial position changed in a consistent way with both the magnitude of F_PERT and T_DWELL. With T_DWELL = 0, relatively small difference was observed between the hand positions in Phase-1 and in Phase-3 (on the order of 20% of the total hand displacement caused by F_PERT). However, with an increase of T_DWELL, this difference became larger and saturated for T_DWELL values of about 2 s (Figure 2B and Figure 3).

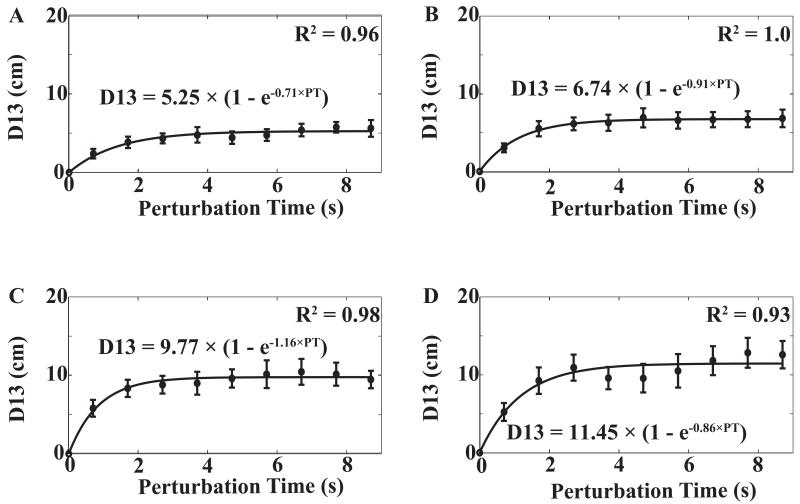
Figure 3.

The distance from the initial to the final hand position (D13) averaged across subjects with standard error bars for the short (A), medium (B), long (C), and very long (D) distances produced by the perturbation. The data (including perturbation times) were averaged across the three trials with the same combinations of distance and dwell time within each subject. Further, the data were averaged across subjects. The data points correspond to the nine perturbation times (the sum of movement time and T_DWELL). For zero perturbation time, we assume D13 = 0. An exponential regression D13 = a × (1 − e^{−b × PT}) was fitted to the data points. The corresponding R² are provided.

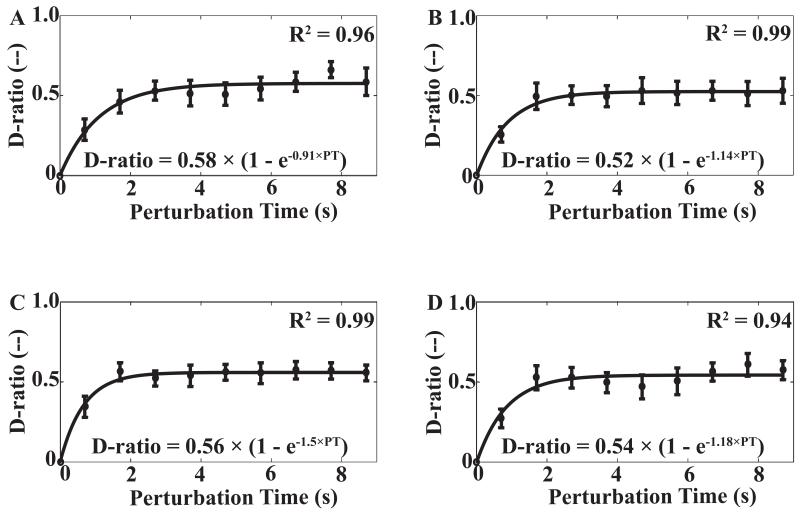
Figure 3 illustrates the average D13 across subjects for different combination of perturbation time, T_PERT (9 levels) and perturbation distance, D_PERT (4 levels). The perturbation time varied slightly across trials; however, the standard error of perturbation time was small (less than 10 ms) for each combination of T_DWELL and D_PERT. Thus, we averaged the data across subjects for the same nominal T_DWELL values. Since no handle position drift was observed in the initial steady state when the subjects held the handle against a constant F_BASE, we assumed that the difference of hand position between Phase-1 and Phase-3 was zero when no perturbation was applied. We used exponential regression lines, D13 = a × (1 − e^{−b × PT}), to fit both average across subjects data (illustrated in Figures 3 and 4) and individual data. For the relative amount of the undershot, quantified as the D-ratio (D13/D12), exponential regressions, D-ratio = A × (1 − e^{−B × PT}), were also fitted using individual subject’s data. Across all subjects and conditions, the exponential regression produced R² with median values ranging between 0.85 and 0.94. Further statistical analysis was performed on the regression coefficients, a, b, A, and B.

Figure 4.

The D-ratio (D13/D12) averaged across subjects with standard error bars for the short (A), medium (B), long (C), and very long (D) distances produced by the perturbation. The data points correspond to the nine perturbation times. For zero perturbation time, we assume D13 = 0. An exponential regression D-ratio = A × (1 − e^{−B × PT}) was fitted to the ten data points. The corresponding R² are provided.

When perturbation distance increased, a became progressively larger, while b did not show any consistent pattern. Similar regression analyses were run on D13 computed based on the data for individual subjects averaged across repeated trials for each condition. Averaged across subjects a coefficient values for the four perturbation distances (from short to very-long) were 5.6 ± 0.8 cm, 7.0 ± 1.0 cm, 10.1 ± 1.5 cm and 12.0 ± 1.7 cm. The significant effect of D_PERT was confirmed by a one-way repeated-measure ANOVA [F_{(3, 18)} = 26.98; p < 0.01]. Post hoc comparisons confirmed that a for short < medium < long < very-long (p < 0.01). No significant effect on b was observed.

D-ratio showed similar results across the four distance conditions. Figure 4 illustrates the average D-ratio across subjects for different combination of perturbation time and perturbation distance. There were no consistent patterns for either of the regression coefficients, A and B. Similar regressions were performed on the individual subject’s data averaged across trials for each condition. One way repeated-measure ANOVA failed to show significant effects on A [F_(3,18) = 1.56; p = 0.23] and B [F_(3,18) = 2.07; p = 0.14]. The D-ratio increased with T_DWELL from T_DWELL = 0 s (0.29 ± 0.03) to T_DWELL = 1 s (0.51 ± 0.03) and T_DWELL = 2 s (0.52 ± 0.03). The result was confirmed by the main effect of T_DWELL [0, 1, 2 s] in a two-way repeated-measures ANOVA [F_{(1, 6)} = 142.197; p < 0.01]. Pairwise comparisons confirmed that D-ratio for 0 s < 1 s and 2 s (p < 0.01), while the difference between 1 s and 2 s was non-significant.

Discussion

The experiments provided support for three of the four specific hypotheses formulated in the Introduction and evidence against the third specific hypothesis. Indeed, brief transient perturbations led to relatively small deviations of the final handle coordinate from its initial position (on the order of 20% of the total hand displacement caused by the perturbation, cf. Zhou et al. in press), which may be interpreted as a relatively minor violation of equifinality (Bizzi et al., 1976; Kelso & Holt, 1980; Latash & Gottlieb, 1990; Schmidt & McGown, 1980) in support of Hypothesis-1. The non-zero deviations of the final handle coordinate from its initial position in the condition with no dwell time could be interpreted as consequences of the non-zero duration of the perturbation itself, which allowed the hypothetical RC-back-coupling process to run for a short time. Transient perturbations with longer T_DWELL led to larger violations of equifinality (the hand stopped short of the initial position), and exponential functions were able to provide a good fit for the magnitude of the distance between the initial and final handle coordinate across subjects and magnitudes of the perturbation as predicted by Hypothesis-2. Larger perturbations led to proportionally larger violations of equifinality thus supporting Hypothesis-4. However, even for the longest T_DWELL values, when an increase in T_DWELL led to no further change in the distance between the initial and final coordinates of the handle, the handle still showed movement towards its initial coordinate after the perturbation was removed. The motion back towards the initial position was typically not smaller than 40% of the hand displacement caused by the perturbation. These observations provide evidence against Hypothesis-3.

Equifinality and its violations

Biological movements can be produced by changes in external forces and/or by neural processes leading to changes in muscle activation. According to the referent configuration (RC) hypothesis (Feldman, 2009), intentional movements are generated by discrepancies between the actual and referent configurations of the body. The actual configuration was manipulated in our study by changes in the external force, whereas the RC was expected to be unchanged under the “do not intervene voluntarily” instruction (Feldman, 1966; Latash, 1994). Within this simplified scheme, a transient perturbation is not expected to change the final equilibrium state of the system (i.e., lead to equifinality). Indeed, equifinality has been demonstrated in many studies.

In fact, violations of equifinality have also been reported in experiments with relatively fast voluntary movements performed in the presence of a destabilizing force field (; Lackner & DiZio 1994; DiZio & Lackner, 1995; Hinder & Milner, 2003). Further (Feldman & Latash, 2005), a hypothesis has been offered that, even under the “do not intervene voluntarily” instruction, subjects could be unable to ignore destabilizing perturbations, such as those experienced in a rotating environment and under “negative damping” conditions, and modify their neural command to the involved effectors unintentionally leading to changes in the RC.

Our study offers an example of large unintentional changes in the equilibrium state of the human hand in the absence of destabilizing force fields (also see Ambike et al., 2014). An important feature of our experiment that makes it different from similar earlier studies is the relatively long dwell time, during which the handle was kept at a new position. This allowed observing unintentional drift in RC leading to the observed violations of equifinality. Clearly, in experiments with fast, transient force changes, effects of this slow process could not be observed.

Current observations complement recent studies (Wilhelm et al., 2013; Zhou et al., 2014) that analyzed the phenomenon of equifinality at two levels, those of task-related performance variables (e.g., hand position and orientation in multi-joint tasks and total force in multi-finger tasks) and of a redundant set of elemental variables (joint angles and finger forces, respectively). In those studies, the application of a quick, transient perturbation led to relative equifinality (reflected in the low inter-trial variance) at the level of task-related variables, but not at the level of elemental variables. Those observations have been discussed as reflecting different, task-specific stability properties (cf. Schöner, 1995) in different directions of the redundant space of elemental variables. Overall, the phenomena of equifinality and its violations during natural movements happen to be much more complex in their appearance as compared to how they were viewed earlier (reviewed in Feldman & Latash, 2005). They seem to be intimately tied to physical and physiological processes within the body related to ensuring stability of action with respect to salient performance variables.

Back-coupling in motor control schemes

Negative feedback loops are common within the human body; in particular, most reflexes from proprioceptors are negative feedback loops (reviewed in Latash, 2008). The idea of task-specific, adjustable loops both from peripheral receptors and within the central nervous system has been developed recently to account for the typical structure of inter-trial variance observed experimentally in multi-element tasks (Todorov & Jordan, 2002; Latash et al., 2005; Martin et al., 2000). In particular, these schemes channel most inter-trial variance into a subspace (uncontrolled manifold, Scholz & Schöner, 1999) compatible with an unchanged value of a task-specific performance variable. One of the schemes assumes a computational process implementing optimal feedback control (Todorov & Jordan, 2002; see also Diedrichsen, Shadmehr, & Ivry, 2010). The other two schemes act as physical feedback loops with adjustable gains; these schemes have been addressed as back-coupling loops. They have been assumed to act at very small time delays, from a few milliseconds for central back-coupling loops (Latash et al., 2005) to a few tens of milliseconds for back-coupling loops from peripheral receptors (Martin et al., 2009). To interpret our results, we are going to use a different notion of back-coupling acting at much longer characteristic times; we will address it as RC-back-coupling to avoid confusion with the earlier terms.

Within the RC hypothesis, shifts in RC lead to changes in muscle activations and in the actual body configuration; this may be addressed as direct coupling from RC to actual configuration acting at relatively short time delays that are typical of reflex feedback loops and electromechanical delays (tens of milliseconds). Our results, as well as those of a few recent studies (Wilhelm et al., 2013; Ambike et al., 2014) suggest the existence of a relatively slow drift in RC towards the actual one (RC-back-coupling) if the actual body configuration is kept away from the RC for a few seconds. We observed time constants of the RC drift on the order of 1 s in our experiment, while longer time constants were observed in a recent experiment with perturbations of the grip aperture during static prehensile tasks (~ 10 s; Ambike et al., 2014).

Our observations are not the first to report unintentional movements that were likely consequences of slow RC shifts. It has been known for many years that, when a person produces constant force against a stop, turning visual feedback off leads to a slow decline in the force (Slifkin et al., 2000; Vaillancourt & Russell, 2002; Shapkova et al., 2008). Vaillancourt and Russell (2002) used an exponential function to model the force decline; their time constants were on the order of 10 s. Another example is the phenomenon of “slacking”, which reflects a reduction in the subject’s motor output when the kinematic error is small (Emken et al., 2007). Slacking was observed, in particular, while practicing arm and gait movements with robotic assistance after neurologic injury: Subjects sometimes reduced their effort in response to external assistance. Another example of unintentional hand force changes has been presented is a recent study that used a slowly expanding and contracting handle held by the subjects (Ambike et al. 2014). In that study, grip force dropped by about 25% over a 10-s period of the handle expansion and contraction despite the instruction to the subjects not to react to possible force changes induced by the changes in the handle size.

In all the mentioned studies, the participants could become tired physically or mentally (become “lazy”). Within the current study, we tried to design the task and the protocol to minimize chances of fatigue and “laziness”. In particular, the involved forces were relatively low and regular rest intervals were offered between trials and between conditions. Note that we saw the violations of equifinality after only 1 second of dwell time (Figure 4), which is too short for effects of fatigue at such low forces. Also, the violations of equifinality were observed starting from the very first trials when the subjects were fresh, and we saw no signs of an increase of these effects with the progression of the experiment.

Our interpretation of the results within the framework of the RC hypothesis may be viewed as limited. Unfortunately, we are unaware of other approaches to motor control that would not require assuming that the subjects’ brains performed some kind of computations with forces and coordinates. Such approaches can account for any experimental observations assuming appropriate changes in internal models (cf. Kawato, 1999; Shadmehr & Wise, 2005). This assumption, however, is unattractive to us because we see our goal as finding laws of nature that lead to certain behaviors, not possible computational ways of solving apparent mechanical problems associated with those behaviors.

Consequences of RC drift for the apparent stiffness

One feature of the RC-back-coupling observed in our study is that the RC did not move all the way to the actual configuration. Depending on the dwell time, RC moved over up to 50% of the total hand excursion. These observations are illustrated in a simplified way in Figure 5. The initial equilibrium position of the hand is shown as point 1 on the force-coordinate plane. An increase in force ΔF led to the hand motion to a new coordinate, point 2. After a dwell time, the force returned back to its initial value, and the hand moved to a new, intermediate position, point 3 (open circle). One can approximate motion of the hand using the notion of apparent stiffness (cf. Latash & Zatsiorsky, 1993). Under the application of the force, the hand showed apparent stiffness k₁ = ΔF/ΔX₁. After the force removal, the apparent stiffness changes to k₂ = ΔF/ΔX₂. Clearly k₂ > k₁. This simple analysis suggests that the apparent stiffness of the hand had to increase to lead to the observed results. If k remained constant during the drift of RC, the actual hand coordinate would have to show a drift, which was not observed in the experiment.

Figure 5.

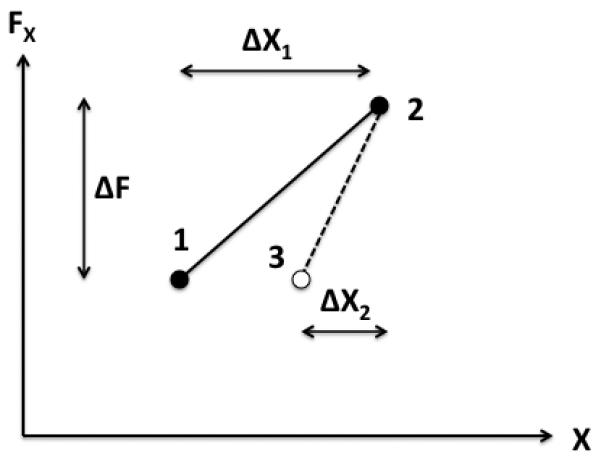
The initial equilibrium position of the hand is shown as point 1 on the force-coordinate (F_X vs. X) plane. An increase in force ΔF led to the hand motion to a new coordinate, point 2. After a dwell time, the force returned back to its initial value, and the hand moved to a new, intermediate position, point 3 (open circle). The slope of the straight line represents the apparent stiffness of the end-effector. After the dwell time, the apparent stiffness increases as shown by the steeper line.

Two findings support the scheme in Figure 5. First, even at the longest dwell times, there was no visible deviation of the hand from the final position. This means that any changes in the apparent stiffness and referent coordinate had to be coupled. For example, a drop in apparent stiffness would have to be accompanied by a shift in the RC further away from the actual hand position. Second, the unloading after the dwell time led to a hand displacement that allowed estimating the hand apparent stiffness. The smaller displacement under the force change of the same magnitude suggests a larger magnitude of apparent stiffness. Combining the two main findings leads to the conclusion on an increase in the apparent stiffness and simultaneous drift of the RC towards the hand position during the dwell time. If the apparent stiffness dropped, the hand would be expected to move over a larger distance after the unloading thus overshooting the initial position.

In a recent study of multi-finger force production (Wilhelm et al., 2013), a slow decline of the total force was observed after the visual feedback had been turned off, which was seen in both control trials (without perturbations) and in trials with transient positional perturbations applied to one of the fingers. The perturbation consisted of smoothly raising the finger and then lowering it to its initial position. The drift in total force was observed during the dwell time; actually, the rate of the drift increased. These observations suggest that a drift of RC may be associated with an observable drift in the performance variable. Why was this drift not observed in our study?

A major difference between the two experiments is the absence of visual feedback in the finger force production trial and the presence of visual feedback in the current study. Note that a difference in the force change magnitude between the open-eyes and closed-eyes conditions was observed (Ambike et al., 2014). Besides, visual distraction has been found to aggregate “slacking” (Secol, Milot, Rosati, & Reinkensmeyer, 2011). Different from the observed slacking phenomenon, hand movement during dwell time was not observed in this experiment. The instruction of our experiment (“let the robot move your arm”) in combination with visual feedback could inadvertently bias our subjects. They were prepared that hand movement would occur under robot force changes (which they could perceive), but were biased to think that no hand movement was allowed when the robot force remained constant, as during the dwell time. So, it is possible that the subjects co-adjusted the apparent stiffness with the RC drift to keep the hand motionless. This required increasing k, possibly by changing the level of muscle co-contraction (Franklin & Miller, 2003; Darainy, Malfait, Gribble, Towhidkhah, & Ostry, 2004; Patel, O’Neill, & Artemiadis, 2014). We did not record muscle activation levels, which may be viewed as a drawback of the study.

Concluding Comments

There are several issues that remain unresolved as a result of this study. First, the interpretation of the major violations of equifinality in the trials with non-zero dwell time suggests a relatively fast process associated with unintentional RC shifts. The estimated time constant was on the order of one second. Earlier studies that also suggest an unintentional RC drift (Vaillancourt and Russell 2002; Secol et al. 2011; Ambike et al. 2014) described considerably slower processes with typical times on the order of 10 s or so. There seems to be two major differences between the cited studies and the current one. First, it is potentially important that the slow drift has been observed in kinetic tasks (a drop in force), not in kinematic (position drift) tasks. Second, the external force perturbations were relatively fast in the current study but not in the earlier studies. Can external perturbations accelerate the hypothetical RC drift? We have no answer to this question, which may be the focus of a future study.

The offered interpretation suggests coupled changes in the referent coordinate and apparent stiffness. This is another prediction that can be studied experimentally, for example using small perturbations at different times during the dwell time. Such an experiment could also fix one of the drawbacks of the current study, namely the suboptimal set of T_DWELL values, which had only a couple of points on the rising part of the exponential curve (cf. Fig. 4); only one of these points showed value significantly different from those on the following plateau. Using more values of T_DWELL within the first two seconds would be preferred.

Earlier studies invoked the notions of fatigue and limited visuo-motor memory (e.g., Vaillancourt and Russell 2002) as potential contributors to the observed unintended force changes. In our study, violation of equifinality took effect in about one second, which is very short for any effects of fatigue and/or memory decay. Nevertheless, these issues could be studied experimentally using trials with fatigue and with longer-lasting time intervals in the absence of perturbations moving the end-point away from the initial position.