A Torque Balance Measurement of Anisotropy of the Magnetic Susceptibility in White Matter

Abstract

Purpose

Recent MRI studies have suggested that the magnetic susceptibility of white matter (WM) in the human brain is anisotropic, providing a new contrast mechanism for the visualization of fiber bundles and allowing the extraction of cellular compartment-specific information. This study provides an independent confirmation and quantification of this anisotropy.

Methods

Anisotropic magnetic susceptibility results in a torque exerted on WM when placed in a uniform magnetic field, tending to align the WM fibers with the field. To quantify the effect, excised spinal cord samples were placed in a torque balance inside the magnet of a 7 T MRI system and the magnetic torque was measured as function of orientation.

Results

All tissue samples (n=5) showed orienting effects, confirming the presence of anisotropic susceptibility. Analysis of the magnetic torque resulted in reproducible values for the WM volume anisotropy that ranged from 13.6 to 19.2 ppb.

Conclusion

The independently determined anisotropy values confirm estimates inferred from MRI experiments and validate the use of anisotropy to extract novel information about brain fiber structure and myelination.

INTRODUCTION

Human tissue placed in the strong magnetic field of an MRI scanner becomes slightly magnetized to a level that is dependent on its composition and molecular structure. This tendency to become magnetized, known as magnetic susceptibility, affects the MRI signal through changes in the Larmor resonance frequency, providing contrast for various applications including functional MRI (1), MRI venography (2), and the study of tissue iron accumulation (for reviews see references (3) and (4)).

Recent MRI studies at high field (3.0–9.4 T) have demonstrated a significant magnetic susceptibility contrast in the brain’s white matter (WM) with dependencies on fiber myelination (5,6) and fiber bundle orientation relative to the magnetic field (7,8); in addition, the MRI resonance frequency may be sensitive to the cellular geometry (9,10). These phenomena offer unique opportunities to study the intricate geometry of the brain’s fiber structure on a microscopic level, to characterize myelination levels, and to detect changes that may occur in demyelinating diseases such as multiple sclerosis (10) and amyotrophic lateral sclerosis (11).

A remaining difficulty with the interpretation of MRI susceptibility contrast relates to the fact that the magnetic susceptibility of white matter is likely to be anisotropic, a phenomenon recently demonstrated (12,13). This is attributed to myelin’s lipid bilayers, the diamagnetic susceptibility of which may be dependent on bilayer orientation relative to the magnetic field (12–17). Although this may offer unique opportunities to extract cellular-compartment specific information (18–20), it significantly complicates interpretation of resonance frequency shifts in terms of changes in WM myelination or integrity (10). Confirmation and quantitative measurement of this putative anisotropy is therefore critical for the interpretation of magnetic susceptibility contrast in WM.

Several attempts have been made to study and estimate the anisotropy of the magnetic susceptibility in WM by measuring resonance frequency distributions in and around large WM fiber bundles (13,21). Unfortunately, the accuracy of such estimates is limited due to the small effect size and the difficulty in disentangling the contributions to the MRI frequency that originate at various (sub and supra voxel) spatial scales (9,19). Here we propose an alternative, MRI independent approach to demonstrate and quantify an object’s anisotropic susceptibility that is based on its orienting behavior in a homogeneous magnetic field. Such behavior has been observed in samples with certain molecular ordering including proteins (22), viruses (23), lecithin vesicles (14), red blood cells (24), retinal rods (15), and muscle fibers (25), and its dynamics have been studied to derive quantitative susceptibility values (14,15,24,25). In the following, we explore whether this approach can be used to confirm and quantify the anisotropic susceptibility of white matter.

METHODS

Torque balance approach

In a homogeneous magnetic field B̄, a non-ferromagnetic object with anisotropic magnetic susceptibility experiences a torque that tends to orient it in a direction that maximizes its magnetization. For an object with cylindrically symmetric magnetic structure the magnitude of this magnetic torque T_mag is dependent on the orientation angle θ of the object’s magnetic symmetry axis with the direction of B̄ according to (see (25) and Appendix 3):

$$T_{\mathit{mag}}=-\frac{V{B}^2}{2{\mu }_0}\left({\chi }_{\left|\right|}-{\chi }_{\perp }\right)sin(2\theta ),$$ [1]

with χ_|| and χ_⊥ representing the object’s magnetic susceptibility parallel and perpendicular to the axis of symmetry, V the volume of the object, and μ₀ a constant representing the permeability of free space (the relative permeability of air is assumed 1.0).

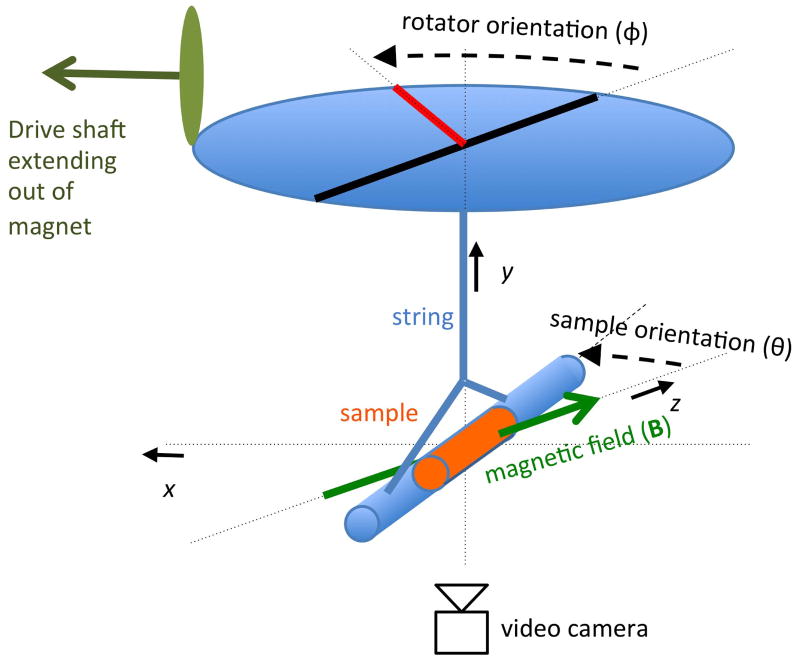
The susceptibility anisotropy Δχ = χ_|| − χ_⊥ can be calculated based on measurements of the magnetic torque performed with a torque balance (25), in which a sample is suspended from a string inside a (static) homogeneous magnetic field (Fig. 1). In this setup, the magnetic torque T_mag is counterbalanced by a mechanical torque T_mech exerted by the suspension string attached to a remotely controlled rotator wheel.

Figure 1.

Magnetic torque balance for the measurement of anisotropic susceptibility. The mechanical torque exerted by a string on a sample suspended from it is changed in a stepwise fashion by turning the rotator wheel. The resulting dynamic reorientation of the sample in the magnetic field B is observed and recorded with a video camera place below the sample.

To measure T_mag and infer Δχ in WM, sectioned human spinal cord samples (n=5) were placed in a custom built torque balance positioned in the magnet of a 7 T MRI system.

Torque balance experiments

A torque balance was constructed from non-magnetic components and included a rig with a plastic rotator wheel, a nylon suspension string, and a cylindrical glass sample holder of 90 mm length and 15 mm diameter (Fig. 1). On one end, the string was glued in place at the center of the rotator wheel, while the other end was tied to a string section that was looped through an empty glass holder tube. For the string, a section of monofilament fishing line was used (4 lb test line, 0.2 mm diameter, ‘Trilene’ brand, by Berkley, Spirit Lake, IA, USA), the vertical free standing section was 116 mm. Glass was selected for the sample holder as it was found several other material choices (paper, various plastics) showed an anisotropy effect themselves. The rotator could be advanced remotely (i.e. from outside the magnet) to exert torque on the holder tube. This was accomplished using a fiberglass drive shaft connected to the rotator wheel through a gear mechanism. Spinal cord and control (water) samples were contained in glass tubes that were placed into the holder tube. The spinal cord samples were sectioned from the thoracic part of formalin-fixed spinal cords from patients that died from non-neurological diseases (n=5). Measurements were performed at room temperature (18.7–22.3°C) over a period of 54 days.

The rotator wheel was turned in 15–20 steps of ~30° each. After every step, a time of 3–5 minutes was allowed for the sample orientation to equilibrate. Rotations in opposing directions were also performed to check for possible hysteresis effects (none were found). On each day of measurement, a calibration measurement was performed to determine the torsion constant of the string. This was accomplished by measuring the oscillatory response to changes in rotator position, which was changed in a few steps of ~90° each (see Appendix 1 for equations). For this purpose, the sample was replaced by a polycarbonate calibration rod (length 128.2 mm diameter 10 mm diameter, weight 0.0109 kg), of which the moment of inertia could be accurately calculated. These calibration measurements were performed outside of the magnet, at the same temperature as the sample measurements. The orientations of sample holder and rotator wheel were recorded with an MR-compatible camera (MRC Systems GmbH, Heidelberg, Germany) placed below the sample holder. To simplify image processing, sample holder and rotator wheel were marked with infrared reflecting tape and illuminated with an infrared LED in a dark environment. The camera output was digitized at 10 frames per second and 320×240 resolution. The sample tube orientation and rotator angle were extracted from each movie frame by an image processing procedure developed in MATLAB. In short, it involved a threshold on image intensity and cluster size to produce separate binary masks of the largest bright objects, the wheel and tube markers. Gaussian smoothing (FWHM= 11 pixel) of the marker mask and an additional Radon transform of the elongated tube marker mask produced maps with intensity maxima that correspond to the position of the rotator wheel markers and the angle of the sample tube respectively. In order to convert rotator wheel marker positions into orientation angles, the exact center of rotation was estimated from multiple positions of the markers traveling on a circular path around it,.

Measurement of white matter fraction and fiber alignment

The volume of the spinal cord samples was estimated from their weight and assumed density (1.038 kg/m³ (26)). The fraction of white matter within this volume was estimated from gradient echo MRI (14T vertical bore Bruker scanner, 120μm isotropic resolution) by segmenting each transaxial slice into grey matter (GM) and WM areas and then averaging the volume fractions across slices. A few images of poor quality (at either end of the sample) were simply assumed to have the same white matter fraction as the central area.

From one of the samples, diffusion tensor images were also acquired to confirm the assumed highly uniform orientation of the nerve fibers in the section (200 μm isotropic resolution, six gradient directions and a single reference without gradients, diffusion b-values of 2020–2095 s/mm²). Fiber orientation was determined by fitting a cylindrical model of restricted diffusion to the tensor data, resulting in two angles representing fiber orientation in each voxel. The root-mean-square (RMS) deviation in this orientation was averaged within a WM mask as a measure of orientational uniformity.

Calculation of anisotropy

The oscillatory response of the sample orientation after each rotator step was fitted with a damped sinusoid plus a constant offset in a non-linear least squares optimization. For the spinal cord measurements, only the tail end (about 100 seconds long) of the oscillation was used, in order to avoid amplitudes larger than 10° that may introduce nonlinearities in the sin(2θ) relationship between orientation and torque. As the oscillations would take several minutes to die down, fitting a sinusoid rather than waiting was a faster and more practical way to determine the equilibrium position in an already time-consuming experiment.

To calculate the torque originating from anisotropic susceptibility of the sample, the equilibrium orientations derived above and their corresponding rotator orientations were fitted to a model equation (Eq. [4], below) again using a nonlinear least squares optimization. Using the Euclidian distance between fit and measurement (taking each measurement pair as a point in a 2D plane) allowed for errors in both orientation angles. Extracted parameters included the angular offset of the neutral rotator position (φ₀) and the amplitude of the sin(2θ) term. The latter was then used to derive Δχ. Inhomogeneities in the main field or induced by the sample itself could potentially add to the torque on the sample, but these effects are estimated to be orders of magnitude lower than the expected torque stemming for the anisotropy and therefore ignored (see Appendix 2 and (25)).

Relating orienting behavior to anisotropy

In the torque balance used in this study (see Fig. 1), the mechanical torque T̄_mech exerted by the rotator (through the suspension string) on the sample is given by:

$${\overline{T}}_{\mathit{mech}}=k(\phi -{\phi }_0-\theta )\widehat{y}$$ [2]

where k is the string’s torsion constant, θ the orientation of the sample, φ the orientation of the rotator wheel, φ₀ the neutral (zero torque) position of the rotator, and ŷ the unit vector along the y-axis (all angles are relative to magnetic field orientation, here along the z-axis). The φ₀ term accounts for the difference between the (unknown) neutral wheel orientation and the location of the markers used to track the wheel orientation. The mechanical torque is equilibrated by an opposing magnetic torque T̄_mag leading to:

$${\overline{T}}_{\mathit{mech}}=-{\overline{T}}_{\mathit{mag}}=\frac{V{B}_z^2}{2{\mu }_0}sin(2\theta )({\chi }_{\left|\right|}-{\chi }_{\perp })\widehat{y}$$ [3]

and thus:

$$\phi ={\phi }_0+\theta +\frac{1}{k}\frac{V{B}_z^2}{2{\mu }_0}sin(2\theta )({\chi }_{\left|\right|}-{\chi }_{\perp })$$ [4]

Eq. [4] relates the equilibrium sample orientation to the orientation of the rotator wheel, and thus fitting this model to the measurement data allows estimation of the anisotropy Δχ = χ_|| − χ_⊥. The fitting was performed in form of Eq. [4], fitting φ as function of θ rather than the perhaps more natural dependence of θ on φ, because there are potentially multiple solutions for θ at a given φ. As the fitting procedure allowed for measurement errors in both angles, the results were not influenced by the choice of which variable was taken to be independent.

RESULTS

Sample Composition

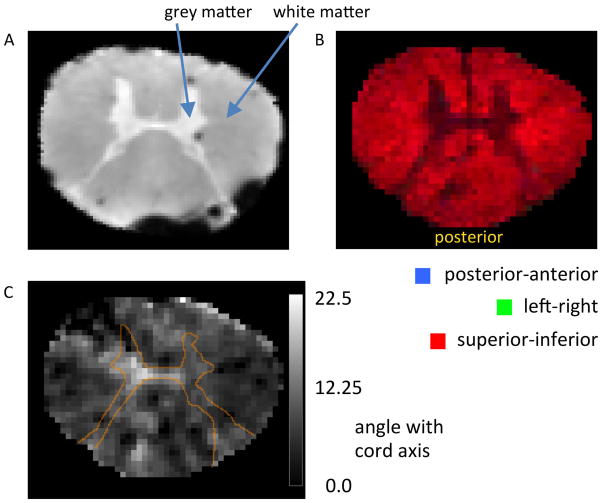
The WM content of these samples (see Fig. 2a for typical cross-section) ranged from 85 to 88% as determined from anatomical MRI, and the fiber directions within the samples (Fig. 2b–c) were highly uniform (<5% standard deviation (SD)) as determined from diffusion-weighted MRI.

Figure 2.

Axial images of a human spinal cord sample, showing white and grey matter distribution and microstructural fiber alignment as assessed by MRI. (A) Grey matter occupies a relatively small tissue fraction centrally located in the sample. The dark spots result from magnetic susceptibility effects caused by small air bubbles. (B and C) Diffusion-weighted MRI demonstrating consistent fiber alignment along spinal cord. (B) Diffusion anisotropy, with composite color indicating the direction of the dominant diffusion eigenvector (37), primary colors represent orientations along (red), and perpendicular to (green and blue) the cord axis. (C) Deviation of the angle of the dominant eigenvector with respect to the cord axis, in degrees. The thin orange line represents outline of grey matter (based on the FA map, see Methods). The low values seen in white matter confirm consistent alignment with cord axis (SD=4.8°).

Torsion constant

The torsion constant of the suscepnsion string was determined from the rotation frequency with a calibration rod inserted in the sample holder on each day of measurement. The resulting values varied from 3.7 to 9.6 10⁻⁷ Nm. Repeated measurements on the same day showed a SD of less than 1%, suggesting that the large day-to-day variation was due to external factors (e.g. temperature, humidity)rather than measurement error. This indicated that daily calibration was necessary and sufficient.

Confirmation of anisotropy

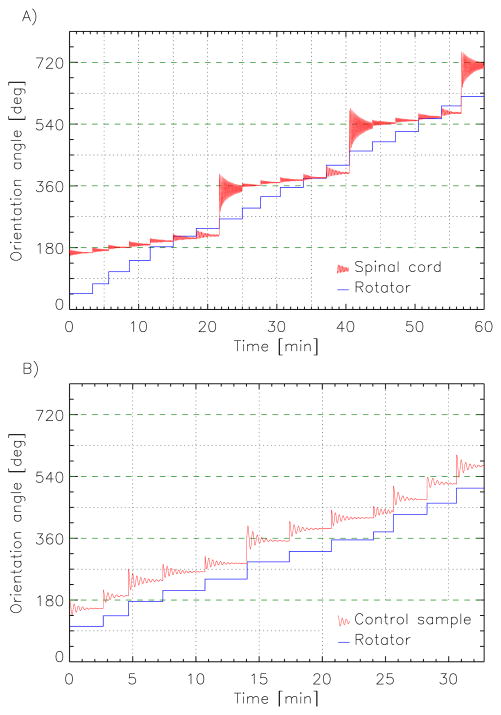
All spinal cord samples showed a clear orienting behavior consistent with their putative anisotropic susceptibility. With each step change in rotator orientation, the samples appeared to resist the imposed torque. After an initial, small orientation change in the direction of the rotator orientation change, the sample’s orientation oscillated towards a new equilibrium that tended to be approximately parallel with the magnetic field (Fig. 3a). With subsequent step changes in rotator orientation, this behavior repeated, until the mechanical torque exceeded the maximum magnetic torque (at θ =45°) and the sample rotated a half turn to realign with the field in the opposite direction. This tendency to align parallel to the magnetic field was absent in control experiments, in which the spinal cord was replaced by water (Fig. 3b); see also the online supporting information (SI) for two movies demonstrating these effects. These observations are consistent with an anisotropic susceptibility of white matter, confirming earlier indications from MRI experiments.

Figure 3.

Examples of spinal cord (A) and control (B) sample orienting behavior in response to step changes in mechanical torque effectuated by turning the rotator wheel. Samples responded with an oscillatory realignment to a new equilibrium orientation. (A) For the spinal cord this tended to be parallel with the magnetic field, i.e. orientation angles that are multiples of 180⁰, indicated by the dashed green lines. (B) No such tendency was observed for the control sample.

Quantification of anisotropy

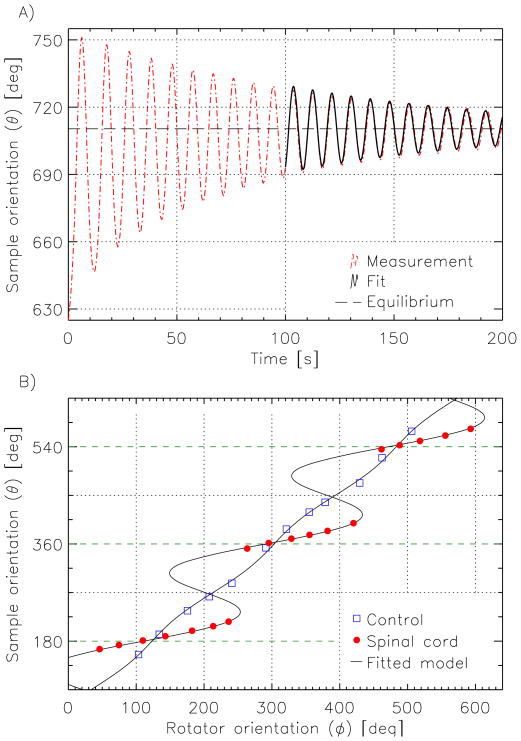
The models fitted the data well, both for the oscillatory response (cf. Fig. 4a, average residue after fitting was less than 1°), as well as for the relationship between rotator and equilibrium sample orientation (Fig. 4b). The results clearly demonstrate the tendency of spinal cord samples to align with the magnetic field, and a virtual absence of this behavior in control samples.

Figure 4.

Extraction of equilibrium orientations and anisotropic susceptibility values. (A) The new equilibrium position of the sample after a change in rotator wheel position was estimated by fitting a damped sinusoid (solid black line) to the tail end of the oscillatory sample motion (dashed red line). (B) A plot of each equilibrium position of the sample against the position of the rotator wheel reveals the markedly different behavior of the spinal cord tissue (red dots) compared to the water reference (blue squares). The curves show the results of fitting Eq. [4] to these data; regions with negative slopes represent unstable orientations. The horizontal green dashed lines indicate orientations parallel to the magnetic field.

The multiplicity of solutions of the model equation (Eq [4]) is reflected in the orienting behavior seen in Fig. 4b, where for an example rotator orientation of 200°, there are 3 solutions to the model (i.e. sample orientations 203°, 270° and 337°); and increasing the rotator orientation from 236° upward resulted in a jump from 216° to 351° in the sample orientation. This jump in orientation stems from the fact that the intermediate solutions, where the slope of the curve (in Fig. 4b) is negative, correspond to an instable equilibrium, a condition where the total torque (T̄_mech + T̄_mag) can be zero but has a positive derivative with respect to $\theta (\frac{d\overline{T}}{d\theta }>0)$.

The results of the model fitting showed that the spinal cord samples experienced magnetic torques on the order of 2×10⁻⁷ N·m. Correction for partial volume effects (assuming an isotropic magnetic susceptibility for grey matter) led to estimates of WM anisotropy ranging from 13.6 to 19.2 ppb, as presented in Table 1. Although significant variability was seen across samples, highly reproducible (< 3% difference) estimates were found for repeat measurements on the same sample, confirming the robustness of the torque balance approach.

Table 1.

WM anisotropy values for the magnetic susceptibility of spinal cord samples (n=5). Multiple entries indicate values from repeat experiments.

Sample	Mass [gr]	WM fraction	Δχ [ppb]	error* [ppb]	Avg. Δχ †[ppb]
1	2.91	0.85	13.5, 13.7	0.3, 0.3	13.6
2	3.96	0.86	13.9	0.3	13.9
3	5.07	0.85	19.1, 19.3, 19.1	0.5, 0.4, 0.3	19.2
4	2.76	0.89	15.1, 14.9, 14.2	0.3, 0.3, 0.4	14.7
5	2.51	0.87	15.3	0.5	15.3

^*estimated error (in ppb) in Δχ combines the errors derived from residuals of fitting the orientation data with the estimated errors in the torsion constant and volume measurements.

^†Average over repeats.

DISCUSSION

The experiments presented here establish that the magnetic susceptibility of WM in the central nervous system is indeed dependent on fiber orientation relative to the magnetic field, confirming earlier indications from MRI measurements (12,13). This anisotropy results in a minute magnetic torque, that is proportional to fiber bundle volume. For large fiber bundles such as the spinal cord, this torque is sufficiently large to allow its precise measurement with a torque balance. Since this torque is almost entirely caused by anisotropy of the susceptibility (see Appendix 2), it allows accurate inference of WM anisotropy values. Because of the similarity in the molecular composition of myelin in the brain and the spinal cord (27–29), these values are expected to be applicable to WM in the brain.

The quantitative results suggest WM susceptibility anisotropy ranges from 14 to 19 ppb. The sizable range is attributed to the substantial variability across samples, possibly originating from differences in their myelin content, and possibly their structural integrity. For example, factors such as biological variability and normal aging (29) affect brain myelin content, and this may be reflected in the anisotropy.

Quantitative comparison with anisotropy inferred from MRI

Analysis of macroscopic field effects observed in MRI in and around major fiber bundles of mouse and human brain have suggested a WM anisotropy from 12 to 22 ppb (12,13), a range consistent with the values found with the torque balance approach presented here. Somewhat higher values can be deduced from the comparison of modeled and measured NMR transverse relation characteristics in WM in-vivo (18,19), which have estimated the susceptibility anisotropy of the myelin sheath to be in the range of −180 to −220 ppb. Assuming a 30% volume of myelin sheath (including intra-laminar water) in WM, and using a factor of −0.5 to convert the anisotropy of a sheath to that of a fiber (due to the cylindrical arrangements of the sheath around a fiber, see Appendix 3 and supporting information in (19)), these values convert to a 27 to 33 ppb range for the anisotropy of WM, somewhat higher than the values found in this study. It is possible that some of this disparity is caused by differences in experimental methods or conditions; in addition, tissue constituents other than myelin could contribute to the anisotropy, a possibility not accounted for in the modeling studies (18,19).

While the MRI- and torque balance-based studies all indicate the presence of significant anisotropy of WM susceptibility, care should be exercised with interpreting the quantitative estimates of the anisotropy. First, the MRI-derived measures rely on the local resonance frequency to estimate magnetic field shifts, an indirect approach that suffers from confounds, including the effects of water compartmentalization (9,30). Second, tissue temperature may affect the anisotropy values, as it is known to affect membrane fluidity and thus molecular ordering (31,32). Difference between in-vivo temperatures and the room temperature (~20⁰C) conditions employed here and the fact that fixed tissue samples where used may thus lead to significant differences in anisotropy.

Molecular origin of anisotropic magnetic susceptibility

The orientation dependence of the magnetic susceptibility of WM has been attributed to the highly ordered molecular structure of the myelin sheath, combined with the highly ordered cellular structure of WM fiber bundles (12,13,18,19). This ordered structure leads to an orientation preference of specific molecular bonds, which in turn leads to an orientation dependence of the magnetic susceptibility. One of the prime candidate molecules underlying this anisotropy is phospholipid (18) which occupies almost 10% of WM volume (27). In fact, previous studies of model membrane systems containing phospholipids have found a significantly anisotropic susceptibility (17,33). This is likely to be caused by the hydrocarbon chains of phospholipids, which have a high orientational order within the lipid bilayer. Fully saturated chains, which lack double (C=C) bonds have an anisotropy of about −1 ppm (difference of susceptibility parallel and perpendicular to bond alignment) (34). Assuming a 6% volume fraction of phospholipid hydrocarbon chains in WM (and again using a factor of −0.5 assuming a perfect radial arrangement of these chains around each axon, Appendix 3), this could contribute up to 30 ppb to WM anisotropy, more than enough to explain the experimental values. Some of this anisotropy may be cancelled out by the C=C bonds (which have positive anisotropy) that are present in phospholipids. Nevertheless, it should be realized that other bonds and molecules in bilayers could contribute to their anisotropy with candidates including carboxyl, cholesterol, and even hydration water. Thus, there remains substantial uncertainty about the molecular origin of WM anisotropy.

Implications for MRI studies of white matter

The present findings support the notion that orientation dependent NMR frequency shifts in and around white matter fiber bundles originate in part from anisotropy of their magnetic susceptibility. They further validate emerging MRI applications such as susceptibility tensor imaging (21) for mapping the brain’s fiber bundles, and myelin water imaging based on cellular-compartment specific frequency shifts (18,35).

The cellular compartment specific frequency shifts that result from an anisotropic susceptibility of the myelin sheath, or possibly other tissue constituents, pose a challenge for methods geared toward deriving myelin content from quantification of local tissue susceptibility. Specifically, methods such as susceptibility tensor imaging (21) and quantitative susceptibility mapping (36) will need to take these effects into account in order to avoid systematic errors originating from the effects of anisotropic susceptibility on the local frequency. This may require the collection of additional reference data incorporating local fiber orientation (19).

An interesting, and potentially concerning implication of the current findings is that the brains of humans placed in the strong magnetic fields of an MRI system will also be susceptible to the observed magnetic torque. Fortunately, even on the scale of the entire brain (with a WM volume on the order of (0.1 m)³), the estimated magnetic torque would not exceed 10⁻⁴ Nm, and the spread in fiber orientations further reduces these effects. It appears such forces are sufficiently small (relative to those experienced during daily life) to not adversely affect brain physiology and function.

APPENDIX

1: Calibration of string torsion constant

The torsion constant k of the suspension string was determined from the oscillation frequency of the torsion pendulum composed of the sample holder filled with a polycarbonate rod. Denoting their combined moment of inertia I (for cylindrical objects $I=\frac{1}{12}m{L}^2$, where m=mass, L=length), the equation of motion for this oscillation becomes:

$$T_{\mathit{mech}}=I\alpha =I\frac{d^2}{d{t}^2}=k(\phi -{\phi }_0-\theta )$$ [1]

resulting in an angular velocity of:

$$\omega =\sqrt{k/I}$$ [2]

2: Possible confounding effects from magnetic field inhomogeneity

The force F̄ on an object placed in a magnetic field is given by:

$$\overline{F}=\overline{M}·\nabla \overline{B}V=\frac{\chi \overline{B}·\nabla \overline{B}V}{{\mu }_0}$$ [3]

Consequently, the torque on an object (of isotropic susceptibility) due to field inhomogeneity is the difference in this force over the length L of the object times the average lever (L/4), resulting in:

$${\overline{T}}_{\mathit{mag}}\approx \frac{\chi B·{\nabla }^{2}BV{L}^2}{4{\mu }_0}$$ [4]

On the scale of the samples used in this experiment (centimeters), the second order inhomogeneity (B ∇² BL²) of the MRI magnet used here is below 10⁻⁶ T², resulting in a torque orders of magnitude below (~10⁻¹⁴ Nm)the anisotropy contributions of interest (~10⁻⁷ Nm). Likewise, the field inhomogeneity caused by the object itself is of the order:

$$\nabla B\approx \chi B/L$$ [5]

resulting in a torque of:

$${\overline{T}}_{\mathit{mag}}\approx \frac{\chi B·\chi BV}{2{\mu }_0}=\frac{{\chi }^2{B}^{2}V}{2{\mu }_0}$$ [6]

again resulting in a contribution orders of magnitude below (~10⁻¹⁴ Nm) the torque associated with anisotropy susceptibility. Note that these equations represent coarse estimates, as the actual contribution of field inhomogeneities depends on their spatial distribution as well as the precise shape of the object.

3: Orientational averaging of molecular-scale magnetic torque

In the following it is shown how the magnetic torque on individual molecules combines to a total torque on a myelinated axon.

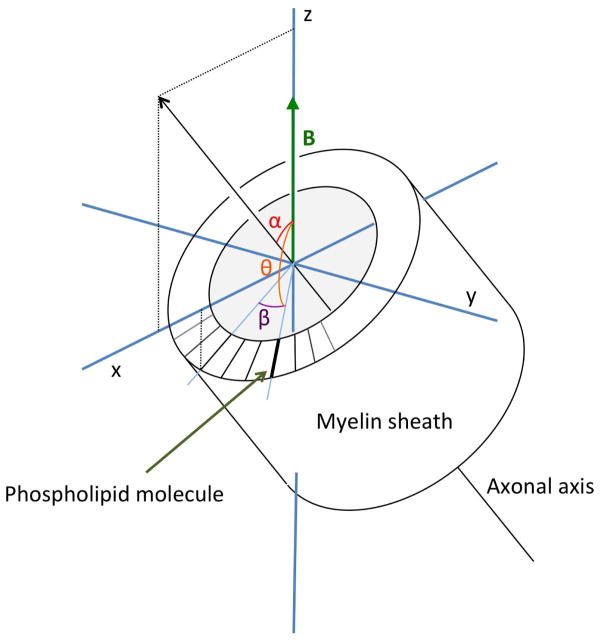
We assume that the magnetic susceptibility is different along the long axis of a phospholipid molecule (χ_a) as compared to perpendicular to that (χ_p) (34). Here the symbols χ_a and χ_p refer to the molecular susceptibilities to distinguish these from the macroscopic values, notated as χ_|| and χ_⊥, which refer to the macroscopic susceptibility of the nerve fiber as a whole, parallel and perpendicular to the nerve fiber axis. Myelin’s phospholipid bilayer ensheaths a nerve fiber’s axon in a cylindrical fashion, resulting in a high orientational ordering of its phospholipid molecules (38), and a possibility of a net magnetic torque on the fiber. For a molecule with azimuthal angle β in a cylinder oriented with its axis in the xz-plane at angle α with respect to the z -axis (Fig. A1), its orientation relative to the z-axis (direction of the magnetic field) can be described as being the result of two rotations:

$$\begin{array}{l}\overline{r}=R_{y,\alpha }{R}_{z,\beta }\widehat{x}=\left(\begin{array}{ccc}cos(\alpha )& 0& sin(\alpha )\\ 0& 1& 0\\ -sin(\alpha )& 0& cos(\alpha )\end{array}\right)\left(\begin{array}{ccc}cos(\beta )& -sin(\beta )& 0\\ sin(\beta )& cos(\beta )& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)\\ =\left(\begin{array}{c}cos(\alpha )cos(\beta )\\ sin(\beta )\\ -sin(\alpha )cos(\beta )\end{array}\right)\end{array}$$ [7]

Figure A1.

Illustration of the relation between macroscopic-, and molecular-scale anisotropy as calculated in Appendix 3. β is the angle of myelin phospholipid molecule with the x-axis in a plane perpendicular to the axis of rotational symmetry, α is the angle of this axis with B̄₀, and θ the angle of the molecular axis with B̄₀. The macroscopic anisotropy, related to α, is the average of the molecular orientation effects, characterized by θ, which in turn is a function of α and β.

Compared to standard polar coordinates (which can be taken as R_z,ψR_y,θẐ), the following relations can be derived:

$$\overline{r}=\left(\begin{array}{c}cos(\psi )sin(\theta )\\ sin(\psi )sin(\theta )\\ cos(\theta )\end{array}\right)=\left(\begin{array}{c}cos(\alpha )cos(\beta )\\ sin(\beta )\\ -sin(\alpha )cos(\beta )\end{array}\right)\to [\begin{array}{c}cos(\psi )=cos(\alpha )cos(\beta )/sin(\theta )\\ sin(\psi )=sin(\beta )/sin(\theta )\\ cos(\theta )=-sin(\alpha )cos(\beta )\end{array}$$ [8]

The magnetic moment of a molecule at angle θ with the main field, at azimuthal angle ψ (from the x-axis), follows from the components of the magnetic field along and perpendicular to its orientation. This can be calculated as a series of rotations:

$$\overline{M}=\frac{1}{{\mu }_0}{R}_{z,\psi }{R}_{y,\theta }\overline{\overline{\chi }}{R}_{y,\theta }^{-1}{R}_{z,\psi }^{-1}\overline{B}=R_{z,\psi }{R}_{y,\theta }\overline{\overline{\chi }}{R}_{y,-\theta }{R}_{z,-\psi }\left(\begin{array}{c}0\\ 0\\ B_z\end{array}\right)$$ [9]

Multiplying the expression in Eq. [9] in steps:

$$\begin{array}{c}\overline{M}=\frac{1}{{\mu }_0}{R}_{z,\psi }{R}_{y,\theta }\overline{\overline{\chi }}{R}_{y,-\theta }{R}_{z,-\psi }\left(\begin{array}{c}0\\ 0\\ B_z\end{array}\right)=\\ \frac{1}{{\mu }_0}{R}_{z,\psi }{R}_{y,\theta }\overline{\overline{\chi }}{R}_{y,-\theta }\left(\begin{array}{c}0\\ 0\\ B_z\end{array}\right)=\\ \frac{1}{{\mu }_0}{R}_{z,\psi }{R}_{y,\theta }\overline{\overline{\chi }}\left(\begin{array}{c}-sin(\theta )\\ 0\\ cos(\theta )\end{array}\right)B_z=\\ \frac{1}{{\mu }_0}{R}_{z,\psi }{R}_{y,\theta }\left(\begin{array}{c}-{\chi }_{p}sin(\theta )\\ 0\\ {\chi }_{a}cos(\theta )\end{array}\right)B_z=\\ \frac{1}{{\mu }_0}{R}_{z,\psi }\left(\begin{array}{c}{\chi }_{a}sin(\theta )cos(\theta )-{\chi }_{p}sin(\theta )cos(\theta )\\ 0\\ {\chi }_p{sin}^2(\theta )+{\chi }_a{cos}^2(\theta )\end{array}\right)B_z=\\ \frac{1}{{\mu }_0}{R}_{z,\psi }\left(\begin{array}{c}\frac{1}{2}({\chi }_a-{\chi }_p)sin(2\theta )\\ 0\\ {\chi }_p{sin}^2(\theta )+{\chi }_a{cos}^2(\theta )\end{array}\right)B_z=\\ \left(\begin{array}{c}sin(2\theta )cos(\psi )({\chi }_a-{\chi }_p)\\ sin(2\theta )sin(\psi )({\chi }_a-{\chi }_p)\\ 2({\chi }_p{sin}^2(\theta )+{\chi }_a{cos}^2(\theta ))\end{array}\right)\frac{B_z}{2{\mu }_0}\end{array}$$ [10]

The magnetic torque becomes:

$${\overline{T}}_{\mathit{mag}}=\overline{M}\times \overline{B}=\frac{B_z^2}{2{\mu }_0}\left(\begin{array}{c}sin(\psi )sin(2\theta )({\chi }_a-{\chi }_p)\\ -cos(\psi )sin(2\theta )({\chi }_a-{\chi }_p)\\ 0\end{array}\right)$$ [11]

This torque results in an alignment with the field if (χ_|| − χ_⊥)>0, i.e. when the parallel susceptibility is higher than the perpendicular value. In terms of α and β, substituting the relations given in Eq.[8], this becomes:

$${\overline{T}}_{\mathit{mag}}=\overline{M}\times \overline{B}=\frac{B_z^2}{2{\mu }_0}\left(\begin{array}{c}-sin(2\beta )sin(\alpha )({\chi }_a-{\chi }_p)\\ {cos}^2(\beta )sin(2\alpha )({\chi }_a-{\chi }_p)\\ 0\end{array}\right)$$ [12]

The integral over all orientations in a cylinder (β =0…2π) results in:

$${\overline{T}}_{\mathit{mag}}=\overline{M}\times \overline{B}=\frac{B_z^2}{4{\mu }_0}\left(\begin{array}{c}0\\ sin(2\alpha )({\chi }_a-{\chi }_p)\\ 0\end{array}\right)$$ [13]

For situations where χ_a > χ_p, the macroscopic magnetic torque T̄_mag tends to turn the cylinder towards an orientation in which its axis is perpendicular to the magnetic field, whereas for χ_a < χ_p, the cylinder axis will tend to orient parallel to the magnetic field. In both cases the strength of this torque is half of that resulting from a uniform (rather than radial) alignment of phospholipid molecules. For comparison, recalculating the torque on a fiber bundle in terms of its macroscopic (averaged) susceptibity results in:

$$\begin{array}{c}{\overline{T}}_{\mathit{mag}}=\overline{M}\times \overline{B}=\overline{\overline{\chi }}\frac{\overline{B}}{{\mu }_0}\times \overline{B}=R_{y,\alpha }\left(\begin{array}{ccc}{\chi }_{\perp }& 0& 0\\ 0& {\chi }_{\perp }& 0\\ 0& 0& {\chi }_{\left|\right|}\end{array}\right)R_{y,-\alpha }\frac{\overline{B}}{{\mu }_0}\times \overline{B}=\\ \frac{B_z}{{\mu }_0}\left(\begin{array}{c}{\chi }_{\left|\right|}sin(\alpha )cos(\alpha )-{\chi }_{\perp }sin(\alpha )cos(\alpha )\\ 0\\ {\chi }_{\left|\right|}{cos}^2(\alpha )+{\chi }_{\perp }{sin}^2(\alpha )\end{array}\right)\times \overline{B}=\\ -\frac{B_z^2}{2{\mu }_0}\left(\begin{array}{c}0\\ sin(2\alpha )({\chi }_{\left|\right|}-{\chi }_{\perp })\\ 0\end{array}\right)\end{array}$$ [14]

When comparing Eq. 13 to Eq. 14, the conversion of molecular anisotropy to macroscopy fiber anisotropy required multiplying by a factor of −0.5:

$$({\chi }_{\left|\right|}-{\chi }_{\perp })=-0.5({\chi }_a-{\chi }_p)$$ [15]

A further reduction in torque may occur with imperfections in orientational order of the molecules, deviations from the cylindrical model of the myelin sheath, or nonuniform fiber alignment in the sample.