RECONSTRUCTION OF DYNAMIC IMAGE SERIES FROM UNDERSAMPLED MRI DATA USING DATA-DRIVEN MODEL CONSISTENCY CONDITION (MOCCO)

Abstract

Purpose

To accelerate dynamic MR imaging through development of a novel image reconstruction technique using low-rank temporal signal models pre-estimated from training data.

Theory

We introduce the MOdel Consistency COndition (MOCCO) technique that utilizes temporal models to regularize the reconstruction without constraining the solution to be low-rank as performed in related techniques. This is achieved by using a data-driven model to design a transform for compressed sensing-type regularization. The enforcement of general compliance with the model without excessively penalizing deviating signal allows recovery of a full-rank solution.

Methods

Our method was compared to standard low-rank approach utilizing model-based dimensionality reduction in phantoms and patient examinations for time-resolved contrast-enhanced angiography (CE MRA) and cardiac CINE imaging. We studied sensitivity of all methods to rank-reduction and temporal subspace modeling errors.

Results

MOCCO demonstrated reduced sensitivity to modeling errors compared to the standard approach. Full-rank MOCCO solutions showed significantly improved preservation of temporal fidelity and aliasing/noise suppression in highly accelerated CE MRA (acceleration up to 27) and cardiac CINE (acceleration up to 15) data.

Conclusions

MOCCO overcomes several important deficiencies of previously proposed methods based on pre-estimated temporal models and allows high quality image restoration from highly undersampled CE-MRA and cardiac CINE data.

INTRODUCTION

MRI often has to contend with inherent acquisition speed limits to depict time-varying processes at the desired spatial resolution and coverage. Hence, incomplete sampling followed by application of specialized image reconstruction algorithms has long been a popular strategy to increase effectual MRI speed (1–8). In dynamic MRI, such dedicated image reconstruction approaches often rely on various kinds of prior information in spatial and/or temporal dimensions to enhance reconstruction fidelity in these domains (9–12). Prior knowledge-based reconstruction approaches have shown utility in applications with complex temporal dynamics, such as contrast-enhanced MR angiography (CE-MRA) (13,14), cardiac imaging (15,16), and perfusion imaging (17–19).

One popular acceleration strategy is to explore spatio-temporal correlations in MR image series for reformulation of the reconstruction problem in a lower dimensional subspace (20,21). Such techniques assume that temporal progression of each pixel is a linear combination of several pre-learned temporal basis functions. The resulting dimensionality reduction improves conditioning of the reconstruction problem and yields high quality, albeit low-rank image series. In such techniques (20,21), a low-dimensional model space is pre-estimated by performing principal component (PC) analysis on a training dataset taken as a low resolution image series from fully-sampled k-space center, and selecting several PCs to form this space’s basis. The described approach is at the foundation of many reconstruction techniques, which were demonstrated to be efficient in cardiovascular (22) and perfusion (23,24) imaging and phase contrast velocimetry (25). Alternatively, low-rank solutions may be recovered without pre-estimating temporal basis using low-rank matrix recovery approaches (26,27).

A low-rank solution can provide an accurate estimate only if the underlying image series admits a low-dimensional representation. Hence, loss of reconstruction fidelity may be expected in the cases when temporal dynamics is too complex to be described by a model of low rank (21). Selecting more PCs in the model (increasing model order) improves its approximation power, but simultaneously reduces the constraining efficiency of the model leading to increased noise and undersampling artifacts (28). The latter may be partially mollified by invoking an additional set of assumptions about the image series such as sparsity in some domains (21,28). However, it does not solve the important problem of reconstruction through dimensionality reduction, namely, its high sensitivity to errors due to low-rank modeling of complex temporal behaviors. As we demonstrate in the paper, this problem may be further complicated by existence of additional errors in the temporal models learned from a (low-resolution) subset of data, which reduces the model’s ability to represent the image series at full resolution.

In this paper, we propose a novel method to reconstruct undersampled dynamic MRI data using pre-learned temporal representation systems. Unlike related techniques (20,21), our method avoids the strict assumption that true object dynamics is an exact linear combination of a set of predetermined basis functions. Instead, we utilize these basis functions to create a transform which is embedded into the minimization problem as a regularization term with robust l₁ norm. This allows enforcing consistency with the pre-estimated model while permitting deviations from it, and results in solutions of a higher rank than implied by the chosen temporal model. As we demonstrate in the paper, our approach reduces sensitivity to errors in the representation system caused by rank reduction and temporal model estimation from low-resolution data and thus allows efficient utilization of low-order models, and promotes an accurate restoration of temporal dynamics in highly accelerated regimes.

THEORY

Reconstruction through Dimensionality Reduction

For a discrete model of an image series s(t, x), we use both matrix S = (s(t_k, x_n)) ∈ 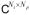and vector s = vec (S) = (s(t_k, x_n)) ∈ 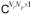representations, where (t_k) correspond to N_t sampled time instances and (x_n) correspond to N_p spatial grid locations (image pixels). MRI signal measurements may be modeled in the matrix form as

$$\mathbf{m}=\mathbf{Es},$$ [1]

where m ∈ 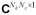is the vector of k-space measurements from N_c coil elements contaminated by additive identically independently distributed (i.i.d.) Gaussian noise, and E is the encoding matrix consisting of the Fourier encoding and, if N_c > 1, coil sensitivity terms (6). As the data undersampling typically creates a poorly conditioned encoding matrix, a straightforward inversion of Eq. [1] is unstable and may result in unresolved aliasing and significant noise increase in the images. Availability of a sparse representation with a known sparsity pattern may help obtain a feasible solution to Eq. [1]. Indeed, if s admits a P-sparse representation (i.e., has no more than P non-zero entries), it can be written as an image of a P-dimensional vector c under action of transformation R ∈ ,

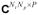$$\mathbf{s}=\mathbf{Rc},$$ [2]

and the problem can be reformulated in the lower-dimensional space:

$${\mathbf{E}}^{\prime }\mathbf{c}=\mathbf{m},{\mathbf{E}}^{\prime }=\mathbf{ER}\in {\mathbf{C}}^{N_k{N}_c\times P}.$$ [3]

As the dimensionality reduction typically improves condition number of the encoding matrix, solving Eq. [3] may resolve undersampling artifacts and mitigate noise amplification compared to the solution of the original problem (Eq. [1]).

Transition from Eq. [1] to Eq. [3] using a sparsity-based rank-reducing transformation (Eq. [2]) is equivalent to the change of basis for the image series S, which is originally represented in the full basis of delta functions for both spatial and temporal dimensions. Generally, an image series cannot be expected to possess a truly sparse representation. However, if there are significant correlations in the image series, there may exist rank-reducing transformations that closely approximate Eq. [2]. In particular, rank reduction may be often done efficiently in temporal dimension (20). Intuitively, this can be explained by existence of spatio-temporal correlations in the image series, i.e. having different spatial locations follow related time courses (waveforms). Following terminology of (20), application of singular value decomposition (SVD) to S allows creating a partially separable representation of the image series:

$$\mathbf{S}(t,x)=\mathbf{U}(t)\mathbf{\sum }{\mathbf{V}}^{\ast }(x)=\sum _{l=1}^L{\sigma }_l{u}_l(t)v_l^{\ast }(x),$$ [4]

where σ_l are non-zero singular values of the matrix S of rank L, U = (u_l) ∈ 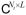and V = (v_l) ∈ 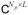are unitary matrices of left and right singular vectors or principal components (PCs), which provide separate temporal and spatial bases for the image series, respectively. Note that Eq. [4] attains form of Eq. [2] by assigning c = vec(ΣV*) and R = I_p ⊗ U, where I_p ∈ 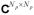is the identity operator and ⊗ is the Kronecker product. Although, as mentioned before, generally L cannot be expected to be less than N_t, the presence of temporal correlations in the image series implies that most energy is concentrated in several singular values. Truncating matrices in Eq. [4] to the first K columns (keeping the summands corresponding to the K largest singular values) provides the best rank K approximation S_K to S in Frobenius (ℓ₂) norm (29):

$${\mathbf{S}}_K(t,x)={\mathbf{U}}_K(t){\mathbf{C}}_K(x),{\mathbf{C}}_K={\mathbf{\sum }}_K{\mathbf{V}}_K^{\ast },$$ [5]

We will refer to the number of retained PCs K as the model order. If an estimate Ũ_K(t) of the target PCs U_K(t) is available (e.g., from low-resolution images), an image series can be obtained in the form

$${\stackrel{\sim }{\mathbf{S}}}_K(x,t)={\stackrel{\sim }{\mathbf{U}}}_K(t){\stackrel{\sim }{\mathbf{C}}}_K(x)$$ [6]

with C̃_K determined by solving a quadratic minimization problem

$${\stackrel{\sim }{\mathbf{C}}}_K=arg\underset{\mathbf{C}}{min}\left({\Vert \mathbf{E}{\stackrel{\sim }{\mathbf{U}}}_K\mathbf{C}-\mathbf{m}\Vert }_2\right)$$ [7]

We should note here that since the Fourier transform is a unitary operator, PCs for x-t space can be equivalently replaced by PCs for x-f space, where f denotes temporal frequency domain, as done in (21).

We introduce several error measures associated with the aforementioned approximations. Rank reduction error e_K is defined as the relative error of approximating the image series S by the first K PCs U_K(t) learned from the ground truth data. On account of Eq. [5],

$$e_K=\frac{{\Vert \mathbf{S}-{\mathbf{U}}_K(t){\mathbf{C}}_K(x)\Vert }_2}{{\Vert \mathbf{S}\Vert }_2}$$ [8]

As U_K(t) can be estimated only from fully-sampled data, we also refer to e_K as error of approximation by High-Resolution-Learned (HRL) model. Similarly, by ẽ_K we denote the relative error of approximating S by an estimate Ũ_K (t) of U_K (t). This measure is affected by both rank reduction error and errors in the temporal subspace caused by Low-Resolution Learning (LRL). We refer to it as the total model approximation error or, equivalently, LRL model error. The relative contribution of the temporal subspace errors to the total error will be calculated as

$${\epsilon }_K=\frac{|{\stackrel{\sim }{e}}_K-e_K|}{e_K}$$ [9]

In this paper, we will refer to the methods based on Eqs. [6],[7] as a PC-basis (PCB) approach (20,21). As the PCB approach constrains the solution to a pre-estimated K-dimensional temporal subspace, the error of PCB-reconstructed image series is bounded from below by the total model approximation error, which depends on the model order K and parameters of LR-learning. However, the PCB reconstruction error may exceed the lower bound depending on the acceleration potential of the model (i.e., its ability to resolve undersampling artifacts with minimized noise amplification), which in turns affects the conditioning of the final reconstruction problem in Eq. [7]). Thus, the choice of K is faced with a tradeoff between representation accuracy and acceleration potential of the model. Indeed, approximation error monotonically decreases to zero as K increases since spans of U_K, K = 1, …, L, form a nested sequence of subspaces with span (U_L) span(S). On the other hand, a lower model order may be preferred, as for larger K spans of U_K may expand well beyond the waveforms of S, increasing probability of fitting aliasing artifacts and noise by the model (28). Moreover, as we will demonstrate in Results section, in some cases higher order temporal basis elements may incur more errors than lower order ones due to low-resolution learning. Therefore, it is desirable to formulate a reconstruction procedure that would be robust to errors in the representation system caused by either rank reduction or low-resolution learning.

Model Consistency Condition

We propose to condition the original problem by requiring consistency with the model rather than hard-constraining the solution to the associated subspace as performed in the PCB approach. Namely, we assume that most pixels generally adhere to a chosen temporal model but some pixels can have deviating behavior. More precisely, let (d_k), k = 1, …, K, be the chosen temporal representation system. In this paper, we consider the representation system (d_k) formed by the first K pre-estimated PCs, though, in general, it does not have to be orthogonal and may be obtained using other techniques (e.g., K-SVD-based dictionary compression (30)). We say that an arbitrary temporal waveform w ∈ satisfies the model exactly, if it can be written as a linear combination Σc_kd_k with some coefficients c_k. We also assume that (d_k) is such that energy of any waveform is preserved by the inner product coefficients with respect to this system (i.e., it forms a tight frame (31)). Then, for any waveform that satisfies the model

$$\mathbf{w}=\sum _k\langle \mathbf{w},{\overline{\mathbf{d}}}_k\rangle {\mathbf{d}}_k,$$ [10]

where 〈 w, d̄_k 〉 is the inner product of w and complex conjugate of d_k. Let D denote the synthesis operator constructing a linear combination from the given coefficient vector (c_k):

$$\mathbf{D}:(c_k)\mapsto \sum _k{c}_k{\mathbf{d}}_k$$ [11]

and D^* denote the analysis operator mapping any waveform w to the vector of its coefficients with respect to the system (d_k):

$${\mathbf{D}}^{\ast }:\mathbf{w}\mapsto \left(\langle \mathbf{w},{\overline{\mathbf{d}}}_k\rangle \right)$$ [12]

Then, the condition in Eq. [10] may be expressed as:

$$\mathbf{\Psi }\mathbf{w}=\left({\mathbf{DD}}^{\ast }-{\mathbf{I}}_t\right)\mathbf{w}=0,$$ [13]

where I_t ∈ is the identity matrix, and DD* defines a projector on the K-dimensional linear subspace spanned by (d_k). Note that when (d_k) is an orthonormal system (e.g., formed by learned PCs), then D is the matrix with (d_k) as its columns and D^* is its Hermitian conjugate.

The operator Ψ introduced in Eq. [13] measures the “closeness” of the sought waveforms to the model and may be used to penalize solutions deviating from the null-space of this operator. An image series satisfying both this assumption (referred to as the MOdel Consistency COndition or MOCCO) and the data consistency condition may be obtained as follows:

$$\mathbf{s}=arg\underset{\mathbf{s}}{min}\left({\Vert \mathbf{Es}-\mathbf{m}\Vert }_2+\lambda {\Vert \left({\mathbf{I}}_p\otimes \mathbf{\Psi }\right)\mathbf{s}\Vert }_X\right)$$ [14]

where X is a chosen norm, and the Kronecker product constructs a block-diagonal matrix with operator Ψ on the main diagonal to apply the transform to temporal waveforms of each pixel individually. Quadratic (ℓ₂) norm is a natural choice if the image series can be expected to satisfy the pre-estimated temporal model. However, if temporal waveforms for some pixels are not consistent with the chosen model (due to model errors), the resulting deviations will be excessively penalized by l₂ norm, which may bias the solution. The proposed formulation (Eq. [14]) allows utilization of norms which are less sensitive to the mismatches between the model and actual temporal dynamics, such as l₁ norm. As we demonstrate in the Results section, this promotes solutions which are not constrained to a K-dimensional subspace but rather have full rank. In what follows, MOCCO by default will refer to Eq. [14] with l₁ norm, with MOCCO (X), where X is a norm of choice, reserved for the cases where there is a possibility of confusion.

METHODS

To ensure equivalency of assumptions (availability of a pre-estimated temporal model), we compared the basic versions of PCB (Eq. [7]) and MOCCO (Eq. [14]), although both methods may be enhanced by regularization terms exploiting other sources of prior knowledge (21,28). We used the following sampling schemes with fully sampled k-space center for LR learning: 1) Randomized variable density (VD) 2D Cartesian sampling (fully sampled 11×11 central area (21), density decreasing linearly towards the edges of k-space), and 2) Temporally interleaved radial k-space sampling with bit-reversed scheduling (32). To ensure consistency between the learned model and output of the optimization procedure in cases of multicoil data reconstruction, the training image series was created from low-resolution coil images via sensitivity-weighted coil combination as used in iterative reconstruction algorithm (33). The performance of the methods was compared using normalized root-mean-square error nRMSE = ||s − s_ref||₂/||s_ref||₂. Regularization parameter in MOCCO was manually adjusted to minimize nRMSE.

Implementation

All algorithms were implemented in Matlab (MathWorks, Inc., Natick, MA, USA). MOCCO (Eq. [14]) was applied with both quadratic (X = l₂) and robust (X = l₁) norms. The l₁ problem was solved using a standard iteratively reweighted least squares (IRLS) algorithm which alternates between inversion of a weighted least squares problem and update of the weighting matrix (34). We employed a practical (differentiable) variant of l₁ norm defined by

$$\Vert \mathbf{x}\Vert =\sum _i\varphi (x_i),\varphi (x)=\sqrt{1+{(x/\sigma )}^2}-1$$ [15]

with σ = 0.6·std(x) as suggested in (35). The conjugate gradient algorithm was applied to perform the least squares inversion step of the algorithm as well as to solve quadratic problems (PCB and MOCCO with l₂). The iterations were continued until relative norm of k-space residual fell below a preset tolerance (τ) or maximal number of iterations (N) was reached (noisy data: τ/N=1e-7/200; noise-free data τ/N=1e-16 (numerical precision)/2000) (36).

Digital Phantom Simulations

Contrast agent propagation in CE-MRA was modeled by a numerical phantom (matrix size 128 × 128 × 32) consisting of several circles with decreasing radii on a non-zero background (Fig. 1a). Temporal waveforms of the structures were modeled by a gamma-variate function (37) (Fig. 1b). Undersampled radial data (acceleration factor R=6) were generated to simulate a single coil acquisition both without and with noise (standard deviation of 5% of the maximal signal value).

Figure 1.

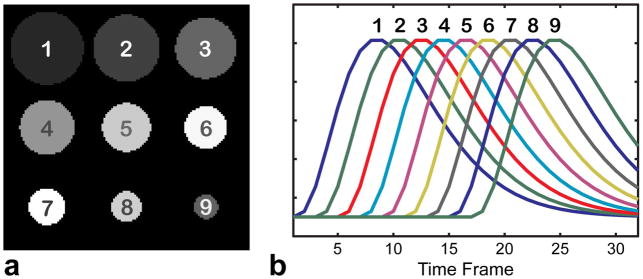
Digital CE MRA phantom. Circular structures of decreasing radii (a) are assigned distinct temporal waveforms simulating contrast propagation dynamics (b).

Physical Phantom

A carotid bifurcation physical phantom was scanned on a 3.0 T clinical scanner (Discovery ^™ MR750, GE Healthcare, Waukesha, WI) using a single channel head coil. The data were acquired after injection of gadolinium contrast agent followed by saline flush (fast gradient echo Cartesian sequence, matrix size 256×72, 4 slices, 2 s/frame, 48 time frames, TE/TR=1.8/6.7 ms). Fully sampled images were retrospectively undersampled onto a 2D VD Cartesian trajectory (net R=4.2).

In Vivo Experiments

An informed consent was obtained from all human subjects. The methods were first studied in a time-resolved contrast-enhanced exam from an intracranial aneurysms patient. The patient was scanned on a 3.0 T clinical scanner (Discovery ^™ MR750, GE Healthcare, Waukesha, WI) with an 8-channel head coil using a hybrid radial (in-plane)/Cartesian (through-plane) acquisition during a contrast injection (TE/TR=1.5/4 ms, FA=25°, BW=125 kHz, 20 slices, 256×256 matrix, 0.86×0.86×2 mm³ voxel). Coil sensitivities were estimated using fully sampled pre-contrast images (6). The images were reconstructed from 15 projections/slice (R=27, 1.2 s/frame).

Performance of MOCCO and PCB was further studied in cardiac CINE exams from two patients. Human subjects were scanned on a Siemens Aera 1.5T scanner (Siemens AG, Healthcare Sector, Erlangen, Germany) using a prospectively triggered bSSFP breath-held segmented acquisition with a 32-channel cardiac array (360×210 matrix size, FOV 360×360 mm, TE/TR=1.56/3.1 ms, 26 and 30 cardiac phases). In the first dataset, all coil channels were combined into a single-channel time series using the method of Walsh et al (38) to study sensitivity of the model-based methods to model errors independently of parallel MRI. A 2D VD Cartesian data were simulated from the data in each case (net acceleration factor R=4.2 in the first case, R=15 in the second case); its central fully-sampled square was used for low-resolution (LR) learning. True (HRL) model was obtained by applying PCA to the fully sampled data.

Analysis of Model Errors

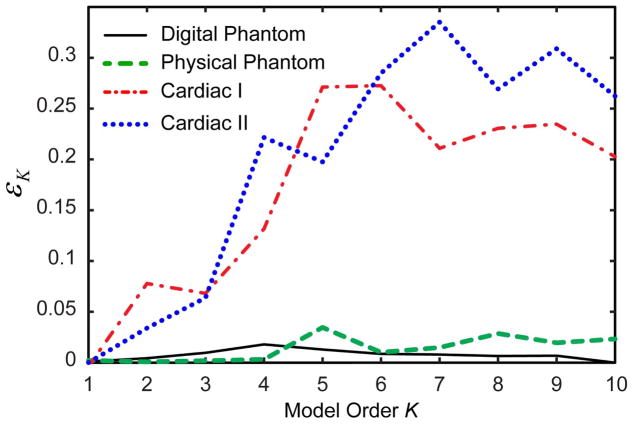
Figure 2 compares the relative contribution of the temporal subspace error ε_K (Eq. [9]) to the total model approximation error for the test datasets with available ground truth (digital and physical phantom CE MRA and cardiac CINE datasets). For the prototype CE MRA data, model error is dominated by rank reduction error. In contrast, model error for cardiac datasets is significantly affected by temporal subspace errors due to LR learning. Hence, cardiac data were used to study sensitivity of methods to both rank-reduction and temporal subspace errors, while methods’ performance on the digital and physical phantom datasets reflected primarily sensitivity to rank reduction errors.

Figure 2.

Comparison of the relative contribution of the temporal subspace errors to the total model approximation error for the test datasets.

RESULTS

Digital Phantom Simulations

Figure 3 illustrates performance of the dimensionality reduction by PCA for the digital phantom. Each one of ten linearly independent waveforms (including non-zero background) can be represented exactly as a linear combination of ten PCs. However, since the PCs are ordered to reflect the best l₂ approximation for a fixed model order K, more prevailing temporal behaviors (as determined by l₂ norm of the corresponding region) can be approximated by a smaller number of PCs. Therefore, as illustrated in Fig. 3, the ability to represent a particular waveform with a given model (K=2,5,8) decreases with the circle area. While the dominating waveform is represented well by 5 and 8 PCs, more deviations are seen for the intermediate waveform. The trend of providing a better approximation to more prevailing temporal dynamics is especially obvious for the waveform of the smallest circle, which encounters a visible error even with 8 PCs and necessitates the use of higher order models.

Figure 3.

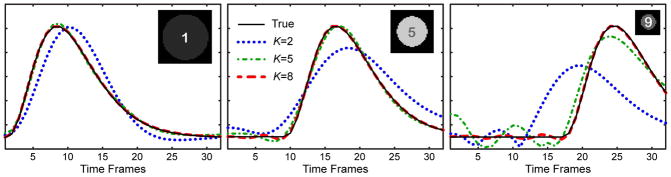
Approximation of three representative waveforms from the digital phantom data (Fig. 1) by models of different orders K. Note that higher model orders are needed to approximate less represented waveforms (as determined by the object energy).

Figure 4 shows dependence of the model and MOCCO/PCB reconstruction errors on the model order K in the digital phantom simulations. For noiseless data (Fig. 4a), model approximation error decreases monotonically reaching zero only for the full range of PCs (K=10). In this example, model approximation error ẽ_K (Figs. 4a,b) is predominantly due to the rank reduction (Fig. 2, ε_K < 0.018 for all values of K). It sets a lower bound for PCB reconstruction error, which follows it closely for K ≤ 5, but deviates for larger K and increases for K>8. This behavior juxtaposes inherent representation error of lower order models and diminished utility of higher order models for accelerated imaging. While MOCCO demonstrates a similar performance for larger K, it attains better approximation for K ≤ 6 due to its reduced sensitivity to model approximation errors. The usefulness of models of lower order is further illustrated in simulations with noise (Fig. 4b), where the error grows rapidly for K > 5 due to additional noise amplification (see next paragraph). Using MOCCO with lower model order (K=5) results in minimized errors from noisy data as well.

Figure 4.

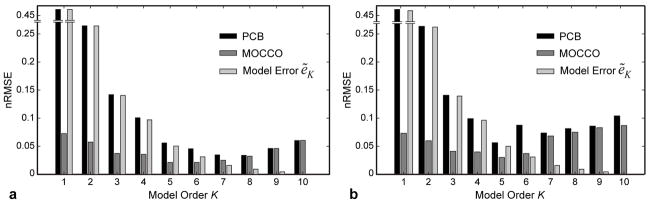
Dependence of PCB and MOCCO reconstruction errors and model approximation errors on the model order in digital phantom simulations for noiseless (a) and noisy (b) cases.

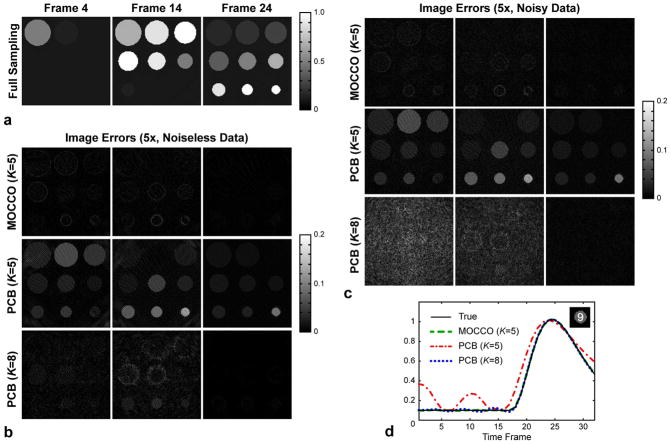
Figure 5 shows image errors for several model orders, which correspond to minimized nRMSE including K = 5 (MOCCO for both noisy and noise-free and, PCB for noisy data) and K = 8 (PCB for noise-free data) (Figs. 4a,b)). Enforcing the model consistency using l₁ norm produces a good estimate of the images (top rows in Fig. 5b,c) although model of order K = 5 cannot fully describe all temporal dynamics (Fig. 3). The latter translates into a larger PCB error. A higher order model (K = 8) improves representation of temporal waveforms (decreases lower bound for PCB error), but still leads to elevated PCB reconstruction errors (Fig. 5b,c) due to poorer problem conditioning. Plots in Fig. 5d compare the least represented waveform (calculated by averaging over the circular ROI #9) reconstructed from the noisy data by the three approaches. For K = 5, MOCCO estimates the waveforms accurately, while PCB attains similar restoration (with the exception of early time frames) only with K = 8 at the expense of higher noise levels (Fig. 5c).

Figure 5.

Performance of PCB and MOCCO reconstruction approaches in digital phantom simulations. a: Ground truth time frames. b: Image errors for noiseless simulations. c: Image errors for noisy simulations. d: Recovery of the least represented waveform.

Physical Phantom Simulations

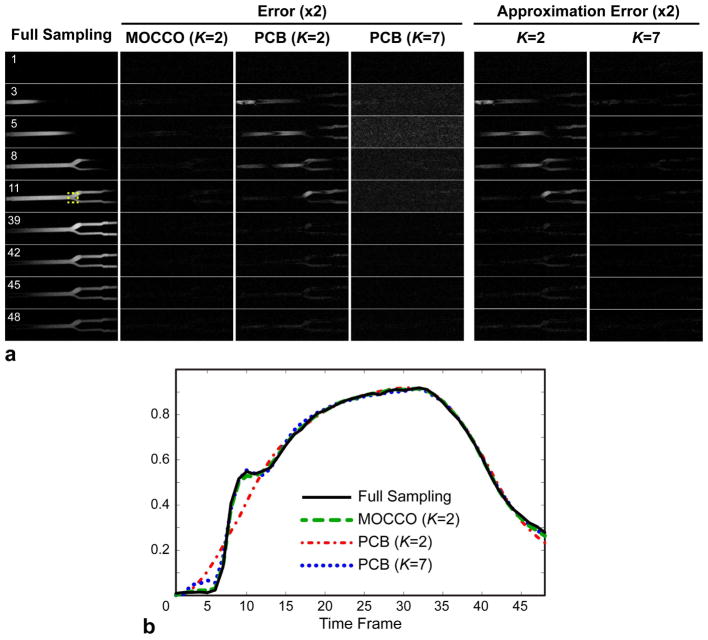
Results of experiments with the carotid phantom data exhibit trends similar to the digital simulations (Fig. 6). As in the digital phantom case, model approximation error is primarily due to rank reduction (Fig. 2, ε_K < 0.035 for all K). MOCCO provides an accurate image series estimate with minimized nRMSE (5.8%) for K = 2, even though the dynamics of contrast propagation cannot be closely approximated by only two PCs (approximation error image for K = 2 in Fig. 5a, nRMSE=11.1%). These errors are visible in the PCB results (K = 2, nRMSE=11.4%). The smallest model order, for which model approximation error reaches the level of the MOCCO reconstruction error is K = 7 (nRMSE=5.6%, rightmost column in Fig. 6a). While model error sets a lower bound for the PCB reconstruction error, the latter shows a much higher nRMSE (13.7%) due to noise amplification (Fig. 5a, also manifesting itself as a noise floor effect distortion in Fig. 6b). Models with K > 7 give rise to higher PCB reconstruction errors (results not shown here). Figure 6b further confirms higher accuracy of MOCCO compared to PCB in representation of temporal waveforms.

Figure 6.

Results of reconstruction of contrast agent bolus propagation in carotid bifurcation phantom. a: Fully sampled images, image errors of MOCCO and PCB for different model orders for several representative time frames capturing contrast arrival and washout, and errors of approximation of fully sampled dataset by the model. b: Waveforms measured in the bifurcation ROI shown in (a).

In-Vivo Experiments

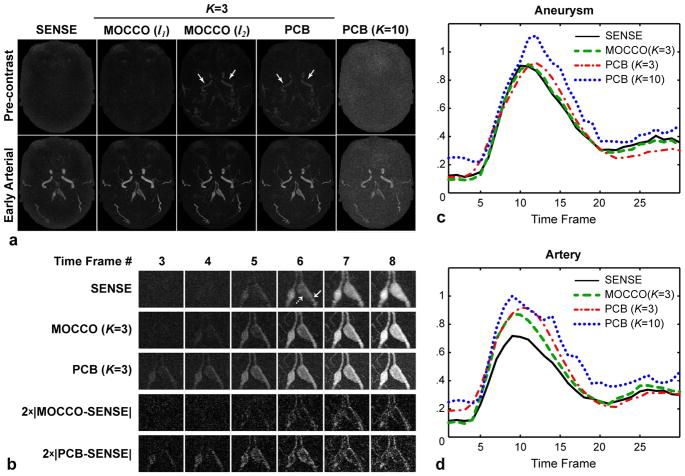
Figure 7 illustrates performance of the methods in intracranial time-resolved CE-MRA. The iterative SENSE images exhibit reduced spatial resolution due to inability of parallel imaging to restore high spatial frequencies at high accelerations (Fig. 7a). At the same time, these images represent a low-resolution estimate of temporal ground truth and may be used to gain initial insights about the bolus propagation dynamics. PCB with low model order (K = 3) erroneously produces an early enhancement of a pre-contrast frame compared to SENSE estimate (Fig. 7a, white arrows), while reconstruction with ten principal components (as suggested in (21)) leads to excessive noise amplification. MOCCO with quadratic norm (l₂) results in a similar enhancement of the pre-contrast time frame as the quadratic norm penalizes heavily deviations from the model (outliers). At the same time, MOCCO (l₁) preserves the filling pattern seen in the SENSE images while improving spatial resolution and keeping noise low. These effects may be further appreciated in Fig. 7b. The image differences show that, compared to SENSE (low-resolution ground truth), MOCCO primarily restores missing high spatial frequency content. At the same time, PCB causes error in larger structures (lower spatial frequency) indicating loss of temporal fidelity. Figure 7c compares waveforms in artery and adjacent aneurysm. The large size of the aneurysm allowed placing ROI away from its edges thereby minimizing the effect of resolution loss in SENSE on the estimation of reference temporal waveform. The aneurysm erroneously enhances earlier and reaches enhancement peak later in PCB (K = 3) than in the reference and MOCCO waveforms, which coincide almost exactly. Although using a higher model order theoretically should improve approximation accuracy, PCB waveform for K = 10 suffers from a distorted shape due to increased noise. A similar situation can be observed for arterial ROI (Fig. 7d), except now the loss of spatial resolution in SENSE causes underestimation of its waveform in the narrowly shaped artery.

Figure 7.

Reconstruction results for intracranial CE MRA exam. a: A pre-contrast (top) and early arterial (bottom) time frames. b: Magnified ROI in the time series reconstructed by SENSE, MOCCO, and PCB (K=3), and corresponding image differences. c,d: Contrast enhancement waveforms measured in the aneurysm and its feeding artery indicated by dashed and solid arrows in (b), respectively.

Figure 8 compares the effects of using HRL model (containing rank reduction error only) vs. LRL model (comprising both rank reduction and temporal subspace errors) on a single coil cardiac CINE dataset. LRL model error significantly exceeds that of HRL model (Fig. 8a), thereby increasing a lower bound for PCB reconstruction error. Figure 8b shows error of approximating each HRL basis function by the subspace spanned by the first six LRL PCs vs. the size of calibration area. These errors characterize the mismatch between the ranges of the LRL- and HRL-estimated subspaces. (This approach gives a more adequate estimation of LRL model error than comparison of individual PCs since PCA does not produce a unique basis for each subspace.) As expected, the difference between LRL and HRL models reduces as the size of the calibration area (resolution of the training images) increases. However, for lower order PCs (K ≤ 3) the error is smaller and decreases at a much faster rate than for higher order PCs (K ≥ 4), which supports observations of Fig. 2 that the range of basis functions describing prevailing temporal behavior is more likely to be preserved in LR learning, while higher order PCs incur larger error.

Figure 8.

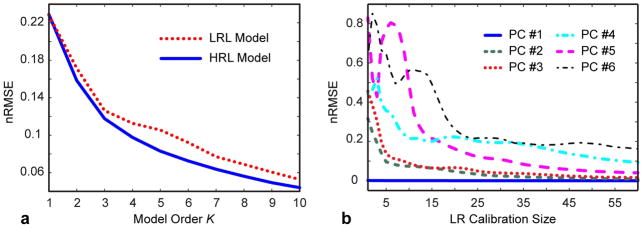
Comparison of representation powers of low-resolution learned (LRL) and high-resolution learned (HRL) temporal models (single-coil cardiac CINE dataset). a: Dependence of the model approximation error on the model order; b: Error of approximation of a given HR-learned temporal basis function (PC #1–6) by LR-learned models (K=6) for varying calibration area.

Propagation of LRL model errors into reconstructed images can be visually appreciated in Fig. 9. For K = 3, both LRL and HRL models cannot provide an accurate representation of temporal dynamics, therefore corresponding model errors and, consequently, error of PCB reconstruction is high in these regimes. As MOCCO is more robust to errors in both representations, it reconstructs image series with significantly higher accuracy. A notable contribution of temporal subspace errors to the total model approximation errors for K = 6 may be appreciated comparing corresponding LRL and HRL model errors. In this case, HRL model diminishes rank-reduction errors and improves representation of the image series. Nevertheless, PCB error is elevated due to noise amplification and aliasing artifacts, which are further exacerbated by temporal subspace errors still present in the LRL model. These drawbacks are mitigated in MOCCO reconstruction, although one can also note a slightly elevated noise in the high model order regime.

Figure 9.

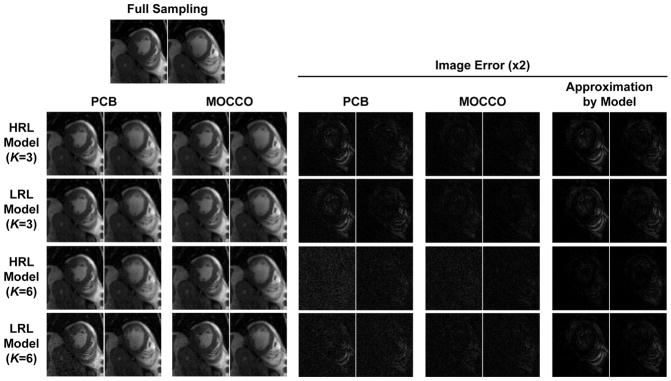
Illustration of sensitivity of PCB and MOCCO to representation errors caused by rank reduction both without (HRL model) and with temporal subspace estimation (LRL model) errors on the example of systolic (left) and diastolic (right) frames of a single coil cardiac CINE data.

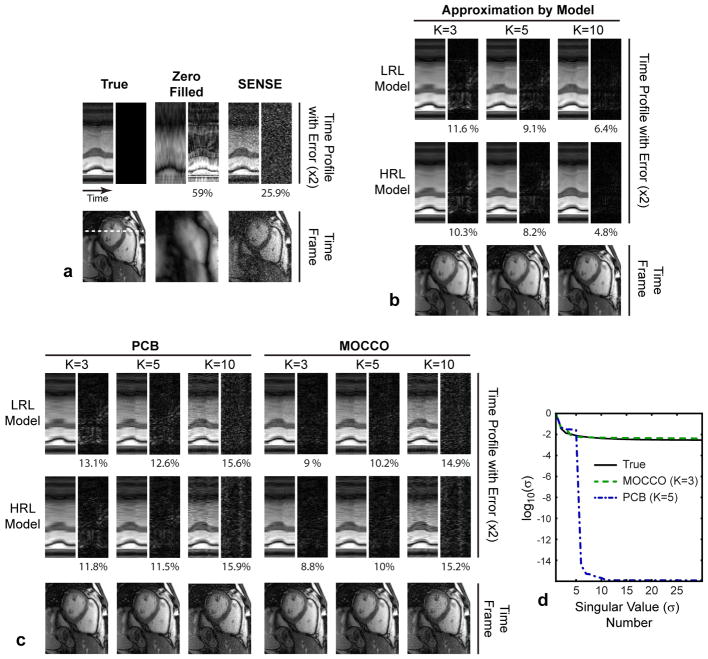
Figure 10 compares the methods in highly undersampled (R = 15) multi-coil cardiac CINE dataset. Zero-filled reconstruction and, to lesser degree, SENSE parallel imaging result in deteriorated image quality (Fig. 10a). The results are shown for the model orders minimizing nRMSE of MOCCO (K = 3) and PCB (K = 5), and the value suggested in (21) for PCB reconstruction of cardiac CINE data (K = 10). The PCB errors (Fig. 10c) for both LRL and HRL models exceed the lower bound set by the corresponding model approximation errors (Fig. 10b). Remarkably, MOCCO errors are much smaller than the model approximation errors. NRMSE-optimized PCB results (K = 5) show a visible loss of temporal fidelity and increased error compared to nRMSE-optimized MOCCO (K = 3). Although PCB with K = 10 improves temporal profiles, its application at such high acceleration increases noise and residual aliasing (Fig. 10c) leading to elevated nRMSE. Singular value plots in Fig. 10d show that best PCB and MOCCO solutions are of low- and full-rank, respectively.

Figure 10.

Illustration of the methods’ performance on 15×-accelerated multi-coil cardiac CINE dataset. Each sub-figure contains images of a representative time frame, temporal profiles with 2× magnified errors, and corresponding value of nRMSE (in %). a: Ground truth images and reconstructions by standard zero-filling and SENSE. b: Results of approximation of the full dataset by the models. c: PCB and MOCCO reconstruction results. d: Plots of singular values for ground truth images series and reconstructed with PCB and MOCCO.

DISCUSSION

In this paper, we proposed a novel method for accelerated dynamic MRI, termed MOCCO, which utilizes pre-estimated (data-driven) models of temporal signal evolution. The use of such models in the context of standard dimensionality reduction approaches may face several challenges when high undersampling factors are targeted. First, as demonstrated here and in (28), constraining the solution to a lower-dimensional subspace may create a dilemma of choosing between representation and acceleration capabilities of the model (i.e., the model order). Second, such solution may be sensitive to errors in the model caused by pre-estimation from low-resolution images, especially for higher order models (Figs. 2,8). Instead of hard constraining through dimensionality reduction, MOCCO uses temporal models to regularize the solution search in the native (full-dimensional) image space, which results in full-rank solutions. While performance of MOCCO also depends on the availability of an adequate representation system, its application with robust (l₁) norm is more forgiving to model shortcomings caused by its low rank and/or temporal subspace errors from low-resolution learning. MOCCO decreases image noise due to the use of low order models, while still recovering dynamic features accurately described only by higher order models. The reduced sensitivity to inaccuracies of low-resolution learning may relax requirements on the minimum size of calibration areas facilitating higher overall acceleration.

It may be noted that if randomized trajectories are used, MOCCO with l₁ norm (Eq. [14]) may be considered a compressed sensing (CS)-type technique (39) in which the pre-estimated model is used not to constrain the solution but to design a sparsifying transform given by (I_p ⊗ Ψ) in Eq. [14]. Thus, MOCCO combines advantages of both PCB and CS theories for an accurate reconstruction. Although MOCCO achieves a more accurate reconstruction and stable performance without invoking additional assumptions about sparsity of the solution in domains other than the model space, it may further benefit from augmenting its minimization problem with k-t SENSE (9) or k-t FOCUSS (11) regularizations often used with PCB approaches (21,28), and/or spatial-temporal differences (40).

An automated selection of model order remains an open problem for both PCB and MOCCO approaches. At the same time, MOCCO is less sensitive to model order selection for lower model orders (the preferred regime for MOCCO) while approaching the performance of PCB for higher order models (Fig. 4). One standard approach is to base model order selection on the analysis of l₂ approximation error (given by the energy of truncated singular values). However, it may not always be optimal for both PCB and MOCCO approaches given the significant differences between optimal (HR) and LR learning, especially in cardiac CINE imaging, though these differences are less pronounced in lower-order model regime preferred by MOCCO (Figs. 2,8). Another limitation of the l₂ norm-based metric is its well-known mismatch with visual image quality perception (41,42).

Full-rank solutions of MOCCO showed significant advantages over low-rank PCB reconstruction for time-resolved CE MRA and cardiac CINE imaging. The major improvement with MOCCO was attained in high acceleration regimes with lower model orders (e.g., Fig. 10), which reduce ill-conditioning of the problem. However, further multi-patient studies are warranted for a detailed comparison of these techniques in clinical settings for each particular application and desired acceleration factors. For example, MOCCO is expected to be less advantageous in applications with simpler temporal dynamics, which can be accurately approximated by a low-rank solution. In such cases, higher constraining power of PCB reconstruction is expected to improve image quality without inducing model-associated bias. Another scenario is adhering to lower accelerations where the high constraining power of lower order models is not required.

While MOCCO is robust to rank reduction and subspace estimation errors, theoretically it cannot be efficient in handling errors caused by a global mismatch with the pre-estimated model. Such mismatch may be generated by systematic measurement errors, for example, due to trajectory errors in non-Cartesian imaging. In this case, a separate measurement and modeling of these processes would be an important pre-requisite for a stable performance of the algorithm. Another limitation of MOCCO, as with any data-driven model pre-estimation technique, is the availability of a fully sampled area for model learning, which may not exist in certain types of undersampled trajectories such as uniformly undersampled spirals (43). In such cases, the trajectory should be modified to allow low-resolution learning (e.g., by utilizing variable density sampling (44)). As MOCCO accepts any (e.g., nonorthogonal or linearly dependent) model, it opens up a possibility to incorporate other types of learning (30,45). MOCCO may be potentially appealing for accelerated model-based parameter mapping (46,47), with preliminary results reported in (48).

CONCLUSIONS

We proposed a new method (MOCCO) for model-based reconstruction of undersampled dynamic MRI data, which overcomes deficiencies of techniques based on pre-estimated temporal models. MOCCO was shown to be robust to common sources of errors for such techniques associated with both rank reduction and low-resolution learning. MOCCO demonstrated significant image quality and temporal fidelity improvements in several dynamic MRI applications such as time-resolved CE MRA and cardiac CINE imaging. We conclude that MOCCO is a preferred way to utilize temporal models for reconstruction of highly accelerated dynamic MRI data in applications with complex temporal dynamics.