Population Pharmacokinetics of Benznidazole in Adult Patients with Chagas Disease

Abstract

The aim of the present study was to build a population pharmacokinetic (popPK) model to characterize benznidazole (BNZ) pharmacokinetics in adults with chronic Chagas disease. This study was a prospective, open-label, single-center clinical trial approved by the local ethics committee. Patients received BNZ at 2.5 mg/kg of body weight/12 h (Abarax, Elea Laboratory, Argentina) for 60 days. Plasma BNZ samples were taken several times during the study and analyzed by high-performance liquid chromatography with UV-visible detection (HPLC-UV). The popPK analysis was done with NONMEMv.7.3. Demographic and biological data were tested as covariates. Intraindividual, interoccasion, and residual variabilities were modeled. Internal and external validations were completed to assess the robustness of the model. Later on, simulations were performed to generate BNZ concentration-time course profiles for different dosage regimens. A total of 358 plasma BNZ concentrations from 39 patients were included in the analysis. A one-compartment PK model characterized by clearance (CL/F) and the apparent volume of distribution (V/F), with first-order absorption (K_a) and elimination, adequately described the data (CL/F, 1.73 liters/h; V/F, 89.6 liters; and K_a, 1.15 h⁻¹). No covariates were found to be significant for CL/F and V/F. Internal and external validations of the final model showed adequate results. Data from simulations revealed that a dose of 2.5 mg/kg/12 h might lead to overexposure in most patients. A lower dose (2.5 mg/kg/24 h) was able to achieve trough BNZ plasma concentrations within the accepted therapeutic range of 3 to 6 mg/liter. In summary, we developed a population PK model for BNZ in adults with chronic Chagas disease. Dosing simulations showed that a BNZ dose of 2.5 mg/kg/24 h will adequately keep BNZ trough plasma concentrations within the recommended target range for the majority of patients. (This study has been registered at EudraCT under number 2011-002900-34 and at ClinicalTrials.gov under number NCT01755403.)

INTRODUCTION

Chagas disease is a zoonotic disease endemic to Latin America, particularly to poor rural areas of Mexico, Central America, and South America (1). In recent years, the disease and its transmission have no longer been limited to areas of endemicity, and the disease has turned into an emerging global public health problem, mainly due to migratory flows (2). Its etiological agent is Trypanosoma cruzi, a hemoflagellate protozoan (family Trypanosomatidae, order Kinetoplastida) whose life cycle involves obligatory passage through vertebrate hosts (mammals, including humans) and invertebrate hosts (hematophagous triatomine bugs) in a series of stages (3).

The disease has two phases: an initial acute phase, which is usually asymptomatic, and a lifelong chronic phase, which in 60 to 70% of patients is clinically silent but in 30 to 40% of them will develop in years or decades into heart problems (20 to 30%), digestive problems, or a combination of both (10 to 15%). Acute Chagas disease treatment is highly effective, whereas the effectiveness of antiparasitic treatment of chronically infected patients has been a subject of controversy for years. Nevertheless, lately, the evidence supporting trypanocidal treatment during the chronic stage of the disease has increased considerably (4–6).

So far, two compounds are available for etiological treatment of Chagas disease, namely, benznidazole (BNZ) and nifurtimox, though BNZ is the most commonly used one globally. To date, limited data on benznidazole pharmacokinetics (PK) are available (7–9). Previous studies showed that BNZ has good oral bioavailability, an apparent volume of distribution (V/F) of 0.56 liter/kg of body weight, and an elimination half-life of 12 to 15 h (7, 8). Based on these investigations, the current recommended dosage of BNZ for the treatment of T. cruzi infection in humans is 5 mg/kg/day, divided into two doses (2.5 mg/kg/12 h), for 60 days. The trypanocidal concentrations of BNZ used in in vitro studies range from 3 to 6 mg/liter (8), and concentrations close to 20 mg/liter have been described as possibly related to a higher risk of toxicity, although in a recent study no relationship was found between the BNZ serum concentration and adverse drug reactions (10).

Giving the limited available data on human benznidazole pharmacokinetics (7, 8), population pharmacokinetic (popPK) modeling may play an important role in assessing the effects of demographic and physiological factors on drug exposure. With the knowledge of the population mean and interindividual variability of PK parameters, it is feasible to (i) simulate credible responses to different drug dosing schemes and (ii) customize dosage regimens to satisfy specific criteria (11, 12).

The main goals of this study were to characterize the pharmacokinetics of benznidazole in adult patients with Chagas disease by using a model-based approach and to identify the factors that contribute to its PK variability to establish new drug dosing schemes.

MATERIALS AND METHODS

Patients.

The CINEBENZ study is a prospective, open-label, single-center clinical trial conducted in the Tropical Medicine Unit in the Hospital Clinic of Barcelona and sponsored by CRESIB (Barcelona Centre for International Health Research). The protocol was approved by the ethics committee of the Hospital Clinic of Barcelona and AEMPS (the Spanish Agency of Medicines and Medical Devices), was registered in the European Clinical Trials Database (EudraCT number 2011-002900-34) and at the ClinicalTrials.gov website (number NCT01755403), and was conducted in accordance with the Declaration of Helsinki and national and institutional standards. Before inclusion in the study, all patients provided written informed consent.

Subjects eligible to participate in the study needed to be at least 18 years old, to be diagnosed with Chagas disease by two different T. cruzi serologic tests, and to not have received treatment before. Exclusion criteria were hypersensitivity to BNZ, close follow-up impossibility, immunodeficiency (HIV infection, cancer, prolonged corticoid treatments, or any other primary or secondary immunodeficiency), hepatic or renal impairment, pregnancy, or lactation. Enrolled subjects received treatment with BNZ at 2.5 mg/kg/12 h for 8 weeks, with a maximum dosage of 400 mg/day (Abarax, Elea Laboratory, Argentina).

Data.

Demographic characteristics, such as age, gender, total body weight, height, and body mass index (total body weight/height²), were recorded in the first evaluation. Clinical laboratory measurements, such as serum creatinine, creatinine clearance (CL_CR) (estimated according to the Cockcroft-Gault formula) (13), hematocrit, total serum proteins, and total bilirubin, were documented at every visit during treatment. Drug adherence was recorded every follow-up visit during treatment by drug pill counting by the investigator.

Blood BNZ samples were taken at different times. They were collected (i) 1 h, (ii) between 3 and 6 h, and (iii) between 6 and 12 h after the oral morning dose (observed by an investigator) on treatment days +1 (first dose) and +15 (steady-state conditions). After the last treatment dose, several other samples were also drawn, at (i) one point between 3 and 12 h, (ii) one point between 12 and 24 h, and (iii) an extra point between 24 and 36 h. Additional trough samples were collected at days +30 and +45 or at unscheduled visits during routine clinical follow-up, mainly for control of drug adherence. Time and dose deviations were recorded and taken into account in the PK analysis.

All blood samples were centrifuged at 5,000 × g for 10 min. Plasmas were separated and stored at −40°C until analysis by high-performance liquid chromatography with UV-visible detection (HPLC-UV) according to a previously published methodology developed in our research laboratory (14). Linearity was found in the range of 1.6 to 100 mg/liter. The analytical error between replicates was <6%. The quantitation and detection limits of the assay were 1.6 and 0.8 mg/liter, respectively.

Pharmacokinetic modeling.

Nonlinear effects modeling was performed using NONMEM v.7.3 (Icon Development Solutions) (15), following a three-step strategy: (i) basic population model selection, (ii) covariate selection, and (iii) model validation. The first-order conditional estimation with interaction (FOCE-I) method was used for parameter estimation.

Models of one and two open compartments with first-order absorption and first-order elimination were evaluated. Interindividual (IIV) and interoccasion (IOV) (16) variabilities were assumed to be log-normally distributed. Regarding IOV, each sampling day was defined as one occasion.

Consider for a generic PK parameter the following model: P = θ_P × exp(η_P + κ_P), where θ_P is the population mean of P (P = CL, V) and η_P and κ_P are random effects capturing the IIV and IOV of P, respectively. Additive, proportional, and combined error models were tested for residual variability (RV) (which comprises measurement and model errors) on drug concentrations.

Goodness of fit for a given model was assessed by (i) changes in the NONMEM minimum objective function value (OFV) (−2 log likelihood), (ii) plots of population and individual Bayesian predicted concentrations versus observed BNZ concentrations and of weighted residuals and conditional weighted residuals (CWRES) versus observed concentrations and time (17, 18), and (iii) changes in the standard error of parameter estimates (precision). The difference in −2 log likelihood between two hierarchical models (log likelihood ratio test) is asymptotically χ² distributed, with degrees of freedom equal to the difference in the number of model parameters. Significance levels of 0.05% and 0.01% denoted significant improvements of fit (drop in the OFV of >3.841 and >6.64, respectively) for a one-parameter difference. R v3.1.1 (R Foundation for Statistical Computing, Vienna, Austria) and the package Xpose v4.5.0 (19) were used to guide the model building process. Pearl-speaks-NONMEM (PsN) v.3.7.3 was used for automation throughout the modeling process (20).

In the second step, all reasonable demographic and biological factors were tested for inclusion as covariates in the basic population PK model to explain IIV. They were tested in NONMEM by using the “scm” approach. Continuous covariates were generally assessed as follows: ${\mathit{P}}_{\mathit{j}}={\mathit{P}}_{\text{POP}}\hspace{0.17em}\times \hspace{0.17em}{({\text{Cov}}_{\mathit{j}}/{\text{Cov}}_{\text{MEAN}})}^{{\theta }_{\mathrm{cov}}\hspace{0.17em}}$, where P_j is the PK parameter for the jth patient and a given covariate value, P_POP is the typical value of a PK parameter corresponding to the mean value of the covariate of interest in the population, Cov_j is the value of that covariate for the jth patient, Cov_MEAN is the mean of the covariate in the population, and θ_COV represents the scaling factor for the influence of that covariate. Categorical variables were included in the model as follows: P_j = P_POP + θ_COV(1 − Cov_i), where P_j is the PK parameter for the jth patient, Cov_i is a numeric index value (1 for the reference category and 0 for the comparative category), P_POP is the typical value of a PK parameter for the reference covariate values (i.e., Cov_i equals 1), and θ_COV is the multiplicative factor for the influence of this covariate on the PK parameter.

Covariates were first entered one by one into the population model and then entered by the cumulative forward inclusion/backward elimination procedures. Each covariate investigated in NONMEM was retained if it led to a significantly improved fit. Improvements to the model were evaluated by (i) biological plausibility of the covariate, (ii) graphical displays based on the agreement between the observed (OBS) and predicted drug concentrations, (iii) the uniformity of the distribution of the residuals, and (iv) the log likelihood ratio test between two nested models. Covariates were kept in the model if they yielded a significance level of 5% (reduction in the log likelihood ratio test of 3.841 points). A significance level of 1% (increase in the log likelihood ratio test of 6.635 points) was employed during the backward elimination step. A decrease of at least 10% in the IIV associated with a specific pharmacokinetic parameter was considered clinically relevant for the inclusion of that specific covariate. The extent of Bayesian shrinkage in the PK parameters was evaluated for each parameter in the final model (21).

Model evaluation.

The internal validation of the PK model was assessed by graphical and statistical methods, including visual predictive checks (vpc) (22). The bootstrap resampling technique (with replacement) was used to build confidence intervals (CIs) of pharmacokinetic parameters to assess their stability and evaluate the robustness of the final model (23). This was performed in PsN v.3.7.3 (University of Uppsala, Sweden) (20). The final model was fitted to the replicate data sets (200 data sets), and parameter estimates were obtained for each of them. The mean values (and the lower and upper limits of the 95% CIs) of the parameters obtained were compared with those estimated from the original data.

The external predictive performance of the PK model was assessed by analyzing data from new individuals (validation data set) treated with BNZ under conditions similar to those for the study population (index data set) (24). Individual predicted BNZ concentrations for all sampling times were obtained by Bayesian estimation (“post hoc” subroutine of NONMEM without the estimation step), with population PK parameter values (mean PK parameters and interindividual and residual variabilities) set to population values previously obtained in the index data set. The performance of the Bayesian analysis was evaluated by comparison of the observed (OBS) concentrations and the population predicted (PRED) and individual predicted (IPRED) concentrations. Bias and precision were calculated and expressed in terms of percentage prediction error (IPE% and PPE% for IPRED and PRED, respectively) and absolute percentage prediction error (IAPE% and PAPE% for IPRED and PRED, respectively) (25).

Dosage regimen simulations.

Monte Carlo simulations (1,000 simulations) were performed using the final model for BNZ to investigate the presumed steady-state drug concentrations for new dosing regimens. Following the presumption that the effectiveness of BNZ depends on sustaining a concentration within the trypanocidal range (3 to 6 mg/liter) (8), the recommended dose regimen of 2.5 mg/kg/12 h and once-daily doses of 2.5 mg/kg and 5 mg/kg were evaluated.

However, considering the recent finding of Bustamante et al. (26) that T. cruzi infection in mice can be cured by using 13 doses of BNZ at 5-day intervals and the knowledge of the T. cruzi life cycle duration (1, 26), a dose regimen of 5 mg/kg of BNZ given 5 days apart was also tested by simulation of 1,000 patients from our final population PK model.

Influence of body weight on dosage.

Based on the theory-based PK modeling approach, some relationships may be included in the popPK model even without being statistically significant. In this context, the inclusion of allometric scaling on the PK parameters may help to give an idea of the connection between body size and drug PK, particularly the influence of body weight on optimal dosing. BNZ is dosed on a per-kilogram basis, and this may have a certain impact on drug exposure. With the intention of understanding the influence of total body weight on BNZ PK, we decided to include this effect in the model to assess the fractions of patients over- and underexposed at extreme weights (43 kg and 100 kg). These values correspond to the minimum and maximum total body weights in our cohort of patients.

Hence, 1,000 additional simulations were done using a new popPK model (WT-popPK model) including allometric scaling of the PK parameters, as follows: CL_i/F = TVCL × (WT_i/WT_mean)^0.75 and V_i/F = TVV × (WT_i/WT_mean)¹, where CL_i/F and V_i/F are the individual total BNZ clearance and apparent volume of distribution for the ith individual, TVCL and TVV are the “typical” population values of the drug clearance and apparent volume of distribution, WT_i is the weight of the ith individual, and WT_mean is the average weight of all patients included in the study. The allometric exponents were fixed to the values obtained from the literature (27, 28).

Statistical analysis.

Statistical analysis was performed using S-Plus 6.1 (S-Plus 6.1 for Windows; Insightful Corporation, Seattle WA). Means, medians, standard deviations (SD), 90% confidence intervals (90% CIs), and quartiles (q) were calculated for continuous variables. The Student t test was used for comparisons of normally distributed variables, and the Mann-Whitney U test was used for comparisons of non-normally distributed variables.

Results are expressed as absolute and relative frequencies for categorical variables, and the chi-square test was used to compare them. The significance level for all analyses was defined by a P value of <0.05.

RESULTS

Subjects and samples.

Fifty-two subjects met the enrollment criteria and gave their informed consent. One subject withdrew the consent before treatment was started. Two subjects were excluded from the PK analysis due to early treatment discontinuation because of adverse reactions. In total, 49 subjects' samples were analyzed. The majority of patients were from Bolivia (96%) and were women (71%), and the median age was 36 years (range, 19 to 55 years).

Data from 39 subjects were use in the model construction (Table 1, index data set), and those from 10 subjects were used for validation (Table 1, validation data set). A total of 358 plasma BNZ concentrations, ranging from 0.56 to 28.94 mg/liter, were used during the analysis (index data set). On average, 9.1 samples were collected per patient during the whole study. Patients' ages and body weights (index data set) ranged from 19 to 55 years (mean, 37.15 years) and from 43 to 100 kg (mean, 70.55 kg), respectively. Mean values (± SD) for this group were as follows: CL_CR, 124.4 ± 25.1 ml/min; hematocrit, 0.40% ± 0.04%; and total serum proteins, 72.9 ± 4.2 mg/dl. The median global adherence (index data set + validation data set) was 99.2%, with only two cases of adherence of <85%.

TABLE 1.

Blood sample and patient characteristics for both groups of patients

Parameter	Value (mean ± SD)a
	Index data set	Validation data set
Total no. of plasma samples	358	96
Plasma concn range (mg/liter)	0.56–28.9	0.57–13.21
No. of subjects (no. of females/no. of males)	39 (26/13)	10 (9/1)
Mean no. of plasma samples/subject	9.1	9.6
Age (yr)	37.1 ± 7.5	38.8 ± 8.6
Weight (kg)	70.5 ± 14.5	68.4 ± 11.3
Body mass index (kg/m2)	27.8 ± 4.4	26.9 ± 4.4
Hematocrit (%)	0.40 ± 0.04	0.38 ± 0.03
Serum creatinine concn (mg/dl)	0.70 ± 0.14	0.67 ± 0.10
CLCR (ml/min)	124.4 ± 25.1	125.7 ± 23.1
Total serum proteins (mg/dl)	72.9 ± 4.2	70.5 ± 1.8
Total bilirubin (mg/dl)	0.6 ± 0.2	0.6 ± 0.3

^aUnless noted otherwise.

Population pharmacokinetic model.

The pharmacokinetics of BNZ was best described by a one-compartment open linear model with first-order absorption and first-order elimination, typified by the apparent clearance (CL/F), apparent volume of distribution (V/F), and population absorption rate constant (K_a). A second distribution compartment did not improve the model fit. BNZ was administered as an oral tablet, and the bioavailability of the drug could not be estimated. Hence, the model estimates are the values for apparent clearance (CL/F) and volume of distribution (V/F), where F represents oral bioavailability. The available data did not support the estimation of K_a, and thus it was set to a fixed value obtained from the literature (8). Interindividual variability (IIV) was incorporated into the CL/F and V/F values. Interoccasion variability (IOV) in CL/F significantly reduced the OFV ratio test (by 97 points; P > 0.001). Residual variability (RV) was characterized by a combined error model with a proportional part of 19.1% (expressed as the coefficient of variation [CV%]) and an additive part of 0.57 mg/liter (expressed as the standard deviation [SD]).

During covariate model selection, we tested the effects of age, gender, total body weight, body mass index, CL_CR, total serum proteins, and total bilirubin on the relevant pharmacokinetic parameters (CL/F and V/F). The results showed that none of the covariates (age, gender, total body weight, body mass index, total bilirubin, total serum proteins, hematocrit, and CL_CR) significantly influenced the BNZ CL/F (reduction of the NONMEM objective function value [P < 0.05]). Inclusion of covariates in V/F failed to cause a significant drop in the OFV ratio test as well.

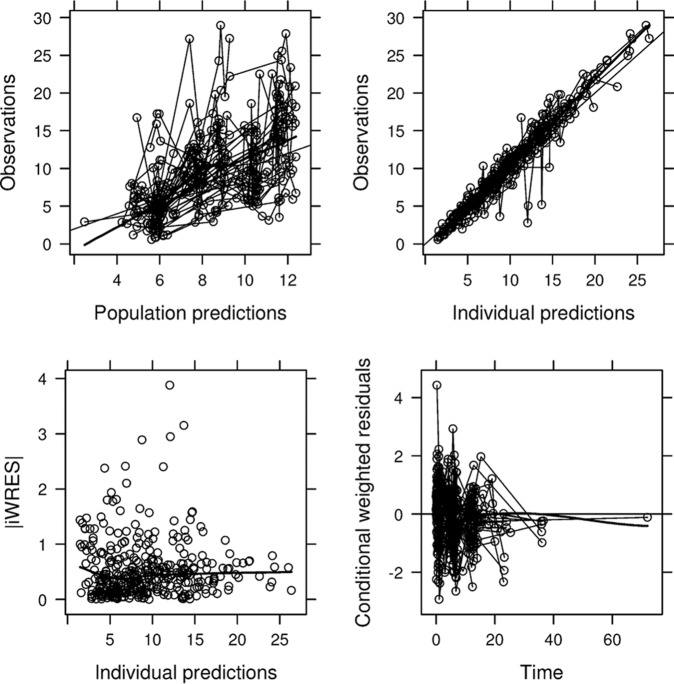
An overview of goodness-of-fit plots for the final PK model is given in Fig. 1. A good accordance between observed and population/individual predicted concentrations was observed. Residual error plots showed no systematic deviation over time (Fig. 1). The mean of the CWRES was 0.085, or close to zero, indicating the ability of the estimation method to fit the model to the data. The model parameters had reasonable levels of η-shrinkage for CL/F (13.1%) and V/F (34.7%). The magnitude of the ε-shrinkage was 27.7%.

FIG 1.

Goodness-of-fit plots for the final population PK model. (Top left) Plot of population predictions (PRED) versus observed BNZ concentrations (OBS); (top right) plot of individual population predictions (IPRED) versus OBS; (bottom left) individual weighted population residuals (IWRES) versus IPRED; (bottom right) conditional weighted residuals (CWRES) versus time. Dashed line, line of identity (upper panels) or target line (lower panels); thick line, line indicating the general data trend. Concentrations (OBS, PRED, and IPRED) are given in milligrams per liter, and times are given in hours.

An overview of the PK parameter estimates from the final population PK model is presented in Table 2.

TABLE 2.

Benznidazole popPK parameter estimates for the base and final models and bootstrap results for the final model

Parameter	Base/final popPK model estimate	Mean (95% CI) bootstrap resulta
Pharmacokinetic parameters
CL/F (liters/h)	1.73	1.73 (1.54–1.92)
V/F (liters)	89.6	92.54 (45.56–133.64)
Ka (h−1)	1.15 (fixed)
IIVb in:
CL/F	33.4	33.1 (17.3–44.0)
V/F	68.8	72.3 (25–94.2)
IOVb in:
CL/F	29.5	29.9 (20.4–36.4)
RVc
σ21 (mg/liter)	0.57 ± 0.19	0.56 (0.12–1.27)
σ22 (CV%)	19.53	17.1 (24.1–57.1)

^aDerived from 200 successful bootstrap sample runs.

^bEstimates of interindividual/interoccasion variability are expressed as coefficients of variation of variance (CVω²).

^cσ²₁, standard deviation of the additive component of residual variability; σ²₂, variance of the proportional component of residual variability.

Model validation.

As shown in Fig. 2, results from the visual predictive check showed that practically all observations fell within the 95% confidence intervals (CIs). The statistical distributions of the parameter estimates obtained from the bootstrap analysis are shown in Table 2. The median values of the parameters estimated from the bootstrap analysis were in good agreement with the NONMEM point estimates, and the 95% CIs were reasonably narrow, demonstrating satisfactory precision. Visual and numerical predictive checks demonstrated good predictive performance of the final pharmacokinetic model.

FIG 2.

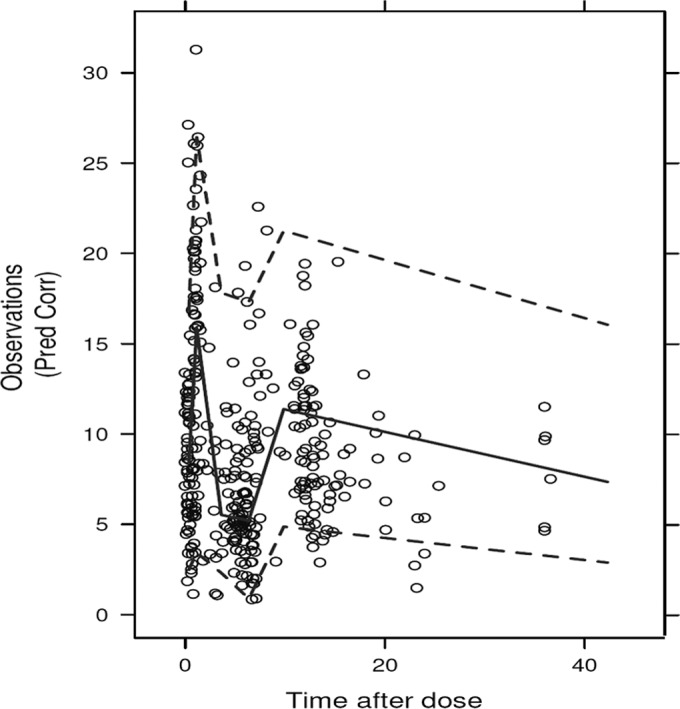
Visual predictive check. Comparisons were performed between the 5th, 95th (dashed lines), and 50th (solid line) percentiles obtained from 1,000 simulations and the observed BNZ plasma concentrations (open circles) for adult Chagas disease patients.

Regarding the predictive performance of the model, the validation data set included 10 new patients, whose demographic and clinical characteristics are displayed in Table 1. A total of 96 plasma BNZ concentrations, ranging from 0.57 to 13.21 mg/liter, were used for external validation of the full model. On average, 9.6 samples were collected per patient. Patients' ages and body weights ranged from 26 to 52 years (mean, 38.8 years) and from 51 to 91 kg (mean, 68.4 kg), respectively. Mean values (± SD) for this group were as follows: CL_CR, 125.7 ± 23.1 ml/min; hematocrit, 0.38% ± 0.03%; and total serum proteins, 70.5 ± 1.8 mg/dl. The median bias and precision for the MAP Bayesian estimates (IPRED) were 0.76% and 9.04%, respectively, which were much more desirable than those obtained from the population PK model-based estimates (PRED), which were −32.73% and 36.19%, respectively (Fig. 3).

FIG 3.

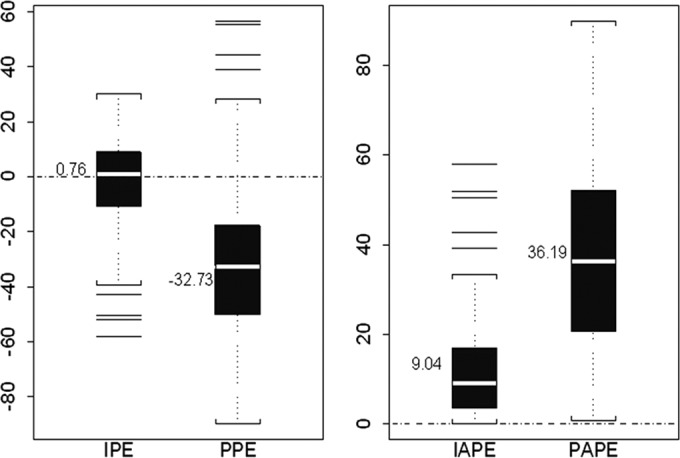
Box plots of percentage error (PE) and absolute percentage error (APE) for the validation data set as measures of bias and precision, respectively. The ordinates show percentages. The white band in each error box marks the 50th percentile; the box boundaries are at the 25th and 75th percentiles, and the limits of the whiskers are at the 10th and 90th percentiles. Other horizontal lines are “outliers,” i.e., values outside the 10th to 90th percentile range. IPE, percentage error for the individual predictions; PPE, percentage error for the population predictions; IAPE, absolute percentage error for the individual predictions; PAPE, absolute percentage error for the population predictions. Dashed line indicates target line.

Dosage regimen simulation under steady-state conditions.

Results from simulations are displayed in Table 3. The usual dose regimen of 2.5 mg/kg/12 h for an average patient of 70 kg would be enough to attain the target trypanocidal concentration during the whole interdose interval (12 h) in almost all treated subjects (95% of the patients; 5th quartile [q₅], 3.02 mg/liter at 10 h), since the simulated trough median (90% CI) at steady state was 7.53 (2.81 to 17.48) mg/liter.

TABLE 3.

Trough BNZ plasma concentrations under steady-state conditions and percentages of patients with trough BNZ concentrations of >6 mg/liter or <3 mg/liter after simulating 1,000 PK profiles for different dosing schemes and total body weights

Dose regimen and parametera	Value for body weight
	43 kg	70 kg	100 kg
2.5 mg/kg/12 h
Median (90% CI)	7.73 (2.88–17.61)	7.53 (2.81–17.48)	10.05 (4.06–23.33)
% of patients with [BNZ] at 12 h
>6 mg/liter	69.5	67.7	81.8
<3 mg/liter	5.3	5.5	1.6
2.5 mg/kg/24 h
Median (90% CI)	3.78 (0.88–9.51)	4.27 (1.20–10.19)	4.64 (1.52–12.1)
% of patients with [BNZ] at 24 h
>6 mg/liter	22.5	27.5	34.2
<3 mg/liter	33.6	25.5	23.5
5 mg/kg/24 h
Median (90% CI)	7.87 (2.20–19.07)	9.59 (2.90–23.81)	9.32 (2.81–22.90)
% of patients with [BNZ] at 24 h
>6 mg/liter	70.2	80	79.2
<3 mg/liter	7.8	4.5	5.8
5 mg/kg/5 days
Median (90% CI)	0.61 (0.08–2.34)	0.69 (0.067–2.61)	0.69 (0.062–2.80)
% of patients with [BNZ] at 168 h
>6 mg/liter	0	0	0.4
<3 mg/liter	97.7	96.6	94.2

^a[BNZ], BNZ concentration.

Simulations considering other dose regimens, such as (i) 2.5 mg/kg/day once a day (q.d.), (ii) 5 mg/kg/day q.d., and (iii) an extended dosing interval of 5 mg/kg of BNZ given 5 days apart, were also performed. The median (90% CI) trough BNZ plasma concentrations at the last day of treatment (steady-state conditions) for 1,000 simulated profiles are shown in Table 3. For an average patient of 70 kg, the results indicated that once-daily dose regimens (2.5 mg/kg/day q.d. and 5 mg/kg/day q.d.) were able to attain the target trypanocidal concentration during the whole interdose interval of 24 h. In contrast, for the extended dosing interval of 5 mg/kg of BNZ given 5 days apart, the drug levels fell below the minimum trypanocidal level after 48 h (median [90% CI], 2.83 [0.54 to 6.36] mg/liter). With this extended regimen, the median (90% CI) peak BNZ concentrations 2 h after dosing were 7.49 (2.81 to 20.36) mg/liter.

Influence of body weight on dosage.

The final popPK model including the allometric relationship between body weight and PK parameters (WT-popPK) did not improve the fit. The population PK estimates were very similar to the original final popPK model (without considering weight as an influential covariate). In the WT-popPK model, the final estimates of fixed-effects parameters were as follows: CL/F = 1.75 liters/h and V/F = 95.3 liters. K_a was fixed to 1.15. Log-normal IIV in CL/F and V/F resulted in values of 34.1% and 77.3%, respectively. Interoccasion variability was retained only for CL/F (30%), as in the original model.

Results of simulations after considering the influence of body weight on BNZ dosing and drug exposure are presented in Table 3.

DISCUSSION

The most widely available drug for treating Chagas disease is benznidazole, but little information exists on its pharmacokinetics. Recently, a study on the population PK of benznidazole in children was published (29), but to our knowledge, the present population PK study is the first to examine benznidazole plasma concentrations in adult subjects with Chagas disease.

In this study, we used NONMEM v.7.3 (15) to characterize the PK of the drug and to investigate quantitative relationships between the pharmacokinetic parameters and physiological and/or demographic features of subjects with Chagas disease who were treated with benznidazole. The data collected in this study were best described by an open one-compartment PK model with first-order absorption and elimination, characterized by CL/F, V/F, and K_a, in accordance with previous data (7, 8). The population estimates for CL/F and V/F were 1.73 liters/h and 89.6 liters, respectively, again in line with previously published results. IIV was incorporated into CL/F and V/F, and IOV in CL/F significantly reduced the OFV (P = 0.01). Our work showed high interindividual variabilities for PK parameters, i.e., 33.4% for CL/F and 68.8% for V/F (values are CV%). However, neither CL/F nor V/F was significantly influenced by the studied demographic or physiopathological factors. Goodness-of-fit plots and simulation-based diagnostics showed that the model described the data adequately.

Previous BNZ PK studies were conducted in healthy volunteers (7) or patients with chronic Chagas disease (8) and were analyzed (post hoc analysis) on a population approach basis by Altcheh et al. (29). In these studies, combined data from healthy subjects (single dose) and patients (multiple doses) led to a CL/F value of 0.0301 liter/h/kg (2.17 liters/h for a patient of 70 kg) and a typical half-life of 12.77 h. In the present study, performed under steady-state conditions in 39 adults with chronic Chagas disease, the estimated terminal drug half-life was about 36 h, which is quite longer than the previous estimates. We presume that this is related to the different characteristics of the study populations, mainly patients versus healthy subjects and adults versus children.

Regarding the inclusion of IOV in CL/F after repeated oral BNZ administration, and taking into account the excellent adherence to treatment seen in our cohort of patients throughout the study, with a mean (± SD) drug adherence of 98.12% ± 7.53%, it is possible to hypothesize that variability might be attributed to differences in either CL or bioavailability (F). Unfortunately, intravenous BNZ is not commercially available; hence, it is not possible to use it as a reference to estimate the “true clearance.” Thus, it was not feasible to discriminate in our model if IOV was related to CL or F, since CL and systemic availability are intermingled after oral drug administration (16).

A major goal of population PK studies is to identify covariates which explain the variation in the between-patient variance component (30). However, none of the covariates tested in this study showed a significant impact on oral BNZ pharmacokinetics in our sample. In addition, another valuable feature of population PK studies is the opportunity to perform Monte Carlo simulations (11). This is a very powerful method to forecast therapeutic outcomes and design adequate (effective and safe) dosing regimens (12). Therefore, we applied this methodology to theoretically determine the suitability of several potential BNZ dosage regimens which can be tested further in clinical trials (31). However, before carrying out any simulation to assist in selecting an optimal initial dosage regimen, it should previously be established that the described population PK model is predictive (24). External validation was conducted by assessing the ability of the population model to predict concentrations in a separate group of 10 patients with chronic Chagas disease. The model was evaluated by means of bias and precision, which showed mean values within acceptable limits (0.76% and 9.04%, respectively), supporting the validity and further utility of this population PK model.

To date, no pharmacokinetic/pharmacodynamic relationship or target exposure values, other than keeping BNZ trough concentrations within or above the in vitro trypanosomicidal range (3 to 6 mg/liter) (8), have been established for optimizing treatment of Chagas disease. However, it must be noted that several studies in the last 25 years (32–35) have shown that, in many cases, there is no correlation between the in vitro susceptibility of a given T. cruzi strain to benznidazole or nifurtimox and the efficacy of antiparasitic treatment with these drugs in experimental animals or human patients. This lack of correlation is explained by the multiple physicochemical and biochemical barriers to access of any drug to its potential cellular targets in an intact organism, a fact that may contribute to the known variability of the outcome of etiological treatment (36).

Data from the initial study (popPK) showed that the standard regimen of 5 mg/kg/day of BNZ divided into two doses (2.5 mg/kg/12 h) leads to a median (90% CI) trough BNZ concentration of 7.53 (2.81 to 17.48) mg/liter for an average patient of 70 kg. As expected, for 2.5 mg/kg/12 h, the simulated trough concentration of BNZ was below 3 mg/liter at 12 h in only 5% of patients, consistent with the observed data in this study. Looking deeper into our data set, we noted that only 5.4% of the observed (real) BNZ trough concentrations were below 3 mg/liter; 20% of them were within the optimal range (3 to 6 mg/liter), but most of them (74.54%) were above 6 mg/liter. These results support the views of other authors (26, 29) suggesting that standard treatment protocols using BNZ might be significantly overdosing patients and therefore that studies with lower doses in adults might be justified.

Therefore, by means of Monte Carlo simulations, a new, 50%-reduced-total-dose regimen of 2.5 mg/kg once daily was tested. Results from this test showed that this new proposed dose could keep median BNZ concentrations above 3 mg/liter for the whole interval of 24 h. It should be noted that for this dose regimen, subtherapeutic trough concentrations (<3 mg/liter) were reached 18 h after BNZ administration in only 15% of patients. In regard to the once-daily dose regimen of 5 mg/kg/24 h, median trough concentrations were always above the upper limit of the therapeutic range (>6 mg/liter), and only in 4 to 5% of cases did BNZ concentrations fall below 3 mg/liter during the last 4 h of a dose regimen of 24 h. With this dosing regimen, the most distressing point would be the BNZ concentrations achieved at earlier times after drug administration (median value for the maximum concentration of drug in serum [C_max] [90% CI], 7.49 [2.87 to 20.36] mg/liter), just 2 to 3 h after dosing, since in 5% of patients they could reach values close to the toxic level of 20 mg/liter. Even though our previous work (37) showed that BNZ concentrations might not be related to the appearance of serious drug effects, we believe that such high drug concentrations are neither desirable nor needed in patients with Chagas disease. Finally, simulations for the regimen of 5 mg/kg/5 days showed median trough concentrations far below the recommended target of 3 mg/liter (Table 3). As stated before, we chose this dose schedule by imitating the dosage regimen used by Bustamante et al. (26) in their study of mice. However, the effectiveness of regimens in which minimum BNZ concentrations remain below the suggested goal are still controversial. They are based on the fact that drug efficacy is related to the maximum BNZ concentration (C_max). Until now, this assumption has not been proved in humans, making it difficult to recommend extended intervals (>24 h) for Chagas disease treatment.

In our final popPK model, total body weight (WT) did not have a significant influence on any PK parameter. In order to investigate a possible weakness due to this fact, we conducted additional simulations, taking into account the theoretical relationship between WT and PK based on the allometric scaling described in many references in the literature (27, 28). Results from simulations showed that the usual dose regimen of 2.5 mg/kg/12 h would allow achievement of the target of 3 mg/liter during the whole interdose interval in almost all of the treated subjects. Taking into account the influence of total body weight on the administered dose, the median (90% CI) simulated trough BNZ concentrations at steady state for average patients of 43 kg and 100 kg of total body weight were 7.73 (2.88 to 17.61) mg/liter and 10.05 (4.06 to 23.33) mg/liter, respectively (Table 3). However, what is probably more important is the fraction of patients over- and underexposed to BNZ based on weight-based dosing, since these are the at-risk patients. These data are displayed in Table 3. Simulations with 2.5 mg/kg/12 h and 5 mg/kg/24 h of BNZ showed that the percentages of patients with trough BNZ concentrations of >6 mg/liter were between 70 and 80%. No significant differences within groups with different total body weights were seen. These high concentrations are probably excessive and might be toxic (in 5% of patients; the upper limit of the CI is 20 mg/liter). From this point of view, a reduction in the total BNZ daily dose might be considered. The fraction of overexposed patients decreased to 25 to 34% for a dosage regimen of 2.5 mg/kg/24 h, with no risk of achieving toxic concentrations. Nonetheless, with this dose regimen, the risk of BNZ underexposure (median trough concentrations below 3 mg/liter at 24 h) increased to around 30% of patients. Interestingly, and regardless of the total body weight, only 15% of patients would show subtherapeutic trough BNZ concentrations at 18 h of BNZ administration. Total body weight had no impact on the fraction of underexposed patients, since no significant differences were seen between groups (P > 0.05) (Fig. 4).

FIG 4.

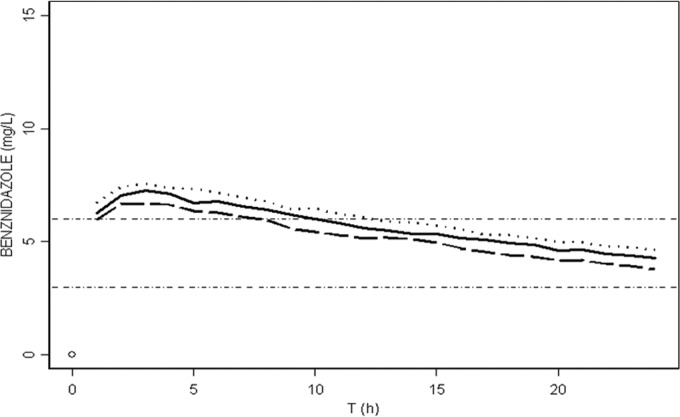
Median BNZ concentrations versus time at steady state (from 1,000 simulated profiles) for a dose regimen of 2.5 mg/kg/24 h and different total body weights: 43 kg (dashed line), 70 kg (solid line), and 100 kg (dotted line). Trypanosomicidal concentrations range from 3 to 6 mg/liter. The median trough concentration at 24 h for 43 kg (dashed line) was 3.78 mg/liter, that for 70 kg (solid line) was 4.27 mg/liter, and that for 100 kg (dotted line) was 4.64 mg/liter (P > 0.05).

A potential limitation of any population PK study is a lack of treatment adherence in some patients. Nonetheless, this limitation does not affect our results, because the median global adherence in our cohort of patients was 99.2%, with only two cases with values of <85%. Another drawback to consider is the impossibility of determining the absolute BNZ bioavailability and the influence of the IOV on it, since there is no intravenous formulation to use as a comparator for the oral one.

The current study represents a first step toward developing optimal oral BNZ dosing schedules for the treatment of Chagas disease patients on the basis of a better knowledge of BNZ pharmacokinetics in adults.

In conclusion, this is the first population PK study in adults demonstrating that the standard dose of oral BNZ (2.5 mg/kg/12 h) may be significantly overdosing patients. In addition, the results from this study might assist in the optimization of BNZ dosing regimens and highlight the rationale of proposing a lower BNZ dose (2.5 mg/kg/24 h). Additional clinical trials in adults with this lower BNZ dose, looking for safety and, mainly, efficacy, might be warranted before recommending its use in Chagas disease treatment.