Abstract
3D fluoroscopic images represent volumetric patient anatomy during treatment with high spatial and temporal resolution. 3D fluoroscopic images estimated using motion models built using 4DCT images, taken days or weeks prior to treatment, do not reliably represent patient anatomy during treatment. In this study we develop and perform initial evaluation of techniques to develop patient-specific motion models from 4D cone-beam CT (4DCBCT) images, taken immediately before treatment, and use these models to estimate 3D fluoroscopic images based on 2D kV projections captured during treatment. We evaluate the accuracy of 3D fluoroscopic images by comparing to ground truth digital and physical phantom images. The performance of 4DCBCT- and 4DCT- based motion models are compared in simulated clinical situations representing tumor baseline shift or initial patient positioning errors. The results of this study demonstrate the ability for 4DCBCT imaging to generate motion models that can account for changes that cannot be accounted for with 4DCT-based motion models. When simulating tumor baseline shift and patient positioning errors of up to 5 mm, the average tumor localization error and the 95th percentile error in six datasets were 1.20 and 2.2 mm, respectively, for 4DCBCT-based motion models. 4DCT-based motion models applied to the same six datasets resulted in average tumor localization error and the 95th percentile error of 4.18 and 5.4 mm, respectively. Analysis of voxel-wise intensity differences was also conducted for all experiments. In summary, this study demonstrates the feasibility of 4DCBCT-based 3D fluoroscopic image generation in digital and physical phantoms, and shows the potential advantage of 4DCBCT-based 3D fluoroscopic image estimation when there are changes in anatomy between the time of 4DCT imaging and the time of treatment delivery.
1 Introduction
Organ motion is a major source of tumor localization uncertainty for radiotherapy of cancers in the thorax and upper abdomen. 3D non-rigid organ motion may introduce large deviations between planned and delivered dose distributions, i.e. underdosage of the tumor and/or increased dose to adjacent normal tissues (Vedam et al. 2003). Image-based patient-specific motion modeling has the potential to accurately quantify anatomical deformations during treatment delivery and could therefore help to eliminate uncertainties associated with organ motion. Four-dimensional computed tomography (4DCT) has become a standard method to account for organ motion in radiation therapy planning. However, 4DCT images acquired at the time of simulation (prior to treatment), do not reliably represent patient anatomy or motion patterns on the days of treatment delivery.
Volumetric image guidance techniques available in the treatment room, such as 4D cone-beam CT (4DCBCT), have been recently used for verifying the tumor position during treatment delivery (Li et al. 2006). 4DCBCT uses a respiratory signal to group projections into bins representing different respiratory phases (Li et al. 2006). External surrogates (Vedam et al. 2003; Li et al. 2006) as well as image-based methods (Zijp et al. 2004; Rit et al. 2005; Van Herk et al. 2007; Dhou et al. 2013; Yan et al. 2013) have been used to generate the required respiratory signal.
Substantial developments in 3D lung motion modeling have made 3D information on tumor and normal structure position readily available (Sohn et al. 2005; Zhang et al. 2007; Li et al. 2010; Zhang et al. 2010; Fassi et al. 2014). 3D “fluoroscopic” imaging is a method that can generate 3D time-varying images from patient specific motion models and 2D projection images captured during treatment delivery. Generally, estimation of “fluoroscopic 3D images” is performed in two steps. First, a patient-specific lung motion-model is created based on information available prior to radiotherapy treatment (e.g. 4DCT) (Low et al. 2005; Sohn et al. 2005; Li et al. 2011; Hertanto et al. 2012). Second, 2D x-ray projection images are used to optimize the parameters defining the patient-specific motion mode, such that a DRR generated from the motion model matches the measured 2D x-ray projection image. This is accomplished via an iterative optimization procedure.
However, the 4DCT-based patient-specific motion modeling has some shortcomings. It cannot reliably represent organ motion and/or patient anatomy at the time of treatment delivery because it is usually performed several days before the treatment (Mishra et al. 2013). The initial patient positioning, tumor baseline position shift, or macroscopic anatomical changes may cause the spatial correlations used to generate the motion model to change. Onboard 4DCBCT, has the potential to resolve these problems since the motion model is generated from images with the patient already in treatment position, immediately before treatment. The major challenge of a 4DCBCT-based motion model is that it depends on the quality of the 4DCBCT images being used to build the model and the phase sorting (binning) used to bin the projections into phases. 4DCBCT images may contain severe streaking artifacts due to the small number of projections used for the image reconstruction at each respiratory phase. The advantages and the challenges of the 3D fluoroscopic image generation using 4DCBCT-based motion models are well-discussed in this study.
2 Methods and Materials
In this study, we develop a method to estimate 3D fluoroscopic treatment images from patient-specific 4DCBCT-based motion models and evaluate their quality compared to those estimated from 4DCT-based motion models. The 3D fluoroscopic images were evaluated based on the geometrical and global voxel intensity accuracy.
2.1 Datasets
Two kinds of datasets were used in this study to evaluate the method: 1) digital phantoms reproducing measured patient motion trajectories; and 2) and anthropomorphic physical phantom with both sinusoidal regular motion and patient-measured breathing patterns.
2.1.1 Digital modified XCAT phantom with recorded patients’ trajectories
The XCAT phantom, originally developed by (Segars et al. 2010), is used in this study to evaluate the method. The XCAT phantom has been modified in (Mishra et al. 2012) to include irregular 3D tumor motion measured from human lung cancer (Berbeco et al. 2005; Williams et al. 2013). Eight datasets were generated featuring different tumor locations and breathing signals. 4DCT images were approximated by 5 seconds of XCAT phantom output, similar to the clinical 4DCT protocol used in our clinic, and in other studies on 4DCT with the XCAT phantom (Li et al. 2011; Mishra et al. 2013; Mishra et al. 2014). The 4DCBCT data is estimated from the XCAT phantom by first generating 2D cone-beam CT projections from phantom and then reconstructing the 4DCBCT from these projections using an FDK back-projection approach (Feldkamp et al. 1984). We used the Reconstruction Toolkit (RTK) (Rit et al. 2013) for this purpose. Figure 1 shows sagittal and coronal slices from the 4DCT and 4DCBCT for one of the XCAT phantoms.
Figure 1.
XCAT phantom images: Sagittal slices of (a) 4DCT (b) 4DCBCT, and coronal slices of (c) 4DCT and (d) 4DCBCT. All images are in the end of exhale phase.
2.1.2 Physical anthropomorphic phantom
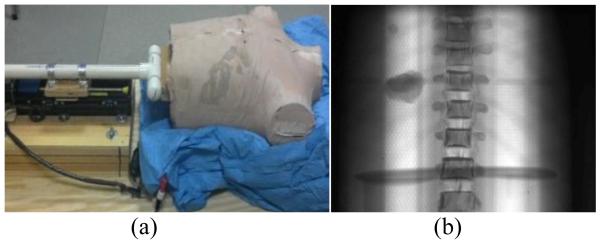
The physical phantom used in this study was a modified version of the Alderson Lung/Chest Phantom (Radiology Support Devices, Inc., Long Beach, CA). The phantom has skin and an anatomically realistic skeletal structure. Inserted foam slices, molded to fit snug into phantom’s rib cage were used to simulate lung tissue as well as to hold a tumor model. A wooden platform that can be moved by a programmable translation stage in superior-inferior (SI) direction is used to simulate diaphragm motion. A tumor model made of a tissue-equivalent resin created with a 3D printer was embedded in the foam slices in the rib cage (Court et al. 2010). The tumor has an irregular shape derived from a tumor contoured on a patient CT image set. The maximum diameter is 5 cm, and the volume is approximately 20 cm3. The tumor moves in the superior-inferior direction similar to the diaphragm motion. Figure 2 shows a photograph of the physical phantom setup used in this study and a selected CBCT projection taken at projection angles of 0 degrees.
Figure 2.
A photograph of the physical phantom setup (a) and an example 2D cone beam projection at 0 degrees.
CBCT images of the physical phantom were captured using a Varian TrueBeam LINAC operated in developer mode (Varian Medical Systems Inc., Palo Alto, CA). Two datasets were captured by rotating the gantry slowly (4 minutes) while acquiring projection images at a frame rate of 11 frames per second and a resolution of 1024 × 768 pixels. The total number of projections was 2692 projections for each dataset. In the first dataset, the phantom was moving according to a regular (sinusoidal) motion in a frequency of 15 cycles per minute. The diaphragm was moved in the superior-inferior direction with a 30 mm peak-to-peak amplitude, resulting in an approximately 15 mm peak-to-peak motion of the tumor. In the second dataset, a recorded patient’s breathing trajectory was applied with an average frequency, cycle time, and motion range similar to those for the first dataset. To generate the 4DCBCT each dataset’s projections were sorted based on their respective respiratory signals using the Amsterdam Shroud method (Zijp et al. 2004; Van Herk et al. 2007). The resulting ten phase bins were reconstructed independently using Varian iTools Reconstruction version 2.0.15.0, which includes the same preprocessing, reconstruction, and postprocessing procedures as the standard clinical software (Varian Medical Systems Inc., Palo Alto, CA).
For the purpose of 3D fluoroscopic image generation, each CBCT projection was downsampled by a factor of 4, resulting in a resolution of 256 × 192. It has been shown in (Li et al. 2011) that this downsampling factor achieves a reasonable balance between computational time and tumor localization accuracy in the generated fluoroscopic images.
The ground truth for the physical phantom was defined by manually contouring the tumor location in each measured cone-beam projection image using a simple graphical user interface programmed in MATLAB. The datasets used in this study both had tumors that were visible in cone-beam projections. These identified coordinates were compared to the estimated 3D fluoroscopic images by projecting the position of the tumor in the 3D fluoroscopic images onto the position of the flat panel detector, then comparing the error between the two tumor positions in 2D space. This error was then scaled down to an approximate error inside the phantom by using the tumor position to eliminate the magnification of error in the 2D projections (approximately the source to isocenter distance divided by the source to imager distance, with a correction for the tumor’s displacement from isocenter). This process was used in previous publications (Lewis et al. 2010; Li et al. 2011).
2.2 3D fluoroscopic image estimation
Principal component analysis (PCA)-based lung motion model
Each image in the 4DCBCT training set is registered to a reference image chosen from the same training set via deformable image registration (DIR). DIR results in displacement vector fields (DVFs) describing the voxel-wise translation between each image of 4DCBCT and the reference image. A patient-specific motion model is created by performing PCA on the resulting DVFs “condensing” the DVFs into a (smaller) subspace spanned by the set of basis eigenvectors that capture the largest modes of variation in the DVFs. The DVFs can be represented by a linear combination of only a few (2-3) basis eigenvectors and weighting parameters (known as PCA coefficients) (Zeng et al. 2007; Zhang et al. 2007; Ionascu 2008; Li et al. 2010).
| (1) |
where is the mean DVF, un are the basis eigenvectors which are defined in space, wn (t) are the PCA coefficients which are defined in time and N is the number of coefficients used. Thus, a small set of the temporal components of the DVFs wn (t) is used along with a reference image to compactly estimate a large set of 3D fluoroscopic images. Three coefficients are used for the lung motion model (N = 3). Details of the DIR code used can be found in (Gu et al. 2010). Using the definitions described in that paper, we implemented the double force variation of the demons algorithm with α fixed to 2.0. Ten images at different respiratory phases were used (t = 10). The peak exhale image is chosen as the reference image and the other images are registered to it. The accuracy of the optimization method is limited by the accuracy of DIR. So, the DIR accuracy needs to be at least as good as the goal for tumor or normal tissue localization.
Optimization-based 3D fluoroscopic image estimation
3D fluoroscopic images can be estimated by iteratively optimizing the coefficients wn (t) obtained from the PCA lung motion model. Let f0 be the reference image to which all other images were deformed when creating the patient-specific motion model. Let f be the estimated fluoroscopic image, P f its projection and × the projection image acquired during treatment delivery. Our goal is to optimize the PCA coefficients wn (t) so that a similarity measure comparing P.f with × is minimized:
| (2) |
where w is a vector of the PCA coefficients to be optimized and J(w) is cost function representing squared L2-norm of the error between the projection of the estimated image f and the 2D image × acquired during treatment delivery. The DVF (w) is the parameterized DVF and defined by the PCA basis vectors U and the PCA coefficients w. P is the projection matrix used to compute the projection from the 3D image f. λ is the relative pixel intensity between the optimization projected image and the projection treatment image ×. A version of gradient descent is used to minimize equation (2). A detailed description of the optimization of the cost function can be found in the appendix in (Li et al. 2011). Using the formalism defined in that paper, the parameters used in our implementation were set as follows. The initial step size μ0 was set to 2.0, and λ, defined as α in (Li et al. 2011), was set to 0.2 for digital phantom experiments and to 0.1 for physical phantom experiments. These values generally lead to fast convergence and were used for all experiments in this study. The algorithm stops whenever the step size for current iteration is sufficiently small (fixed at 0.01 for digital phantom experiments and 0.1 for physical phantom experiment). In both cases, increasing the number of iterations did not affect the results.
The projection images used to optimize the PCA coefficients were generated at an angle of 105 degrees for all digital phantom experiments (i.e., 15 degrees away from a lateral projection). Previous studies have explored the dependence of 3D fluoroscopic image accuracy on the imaging angle (Li et al. 2010; Mishra et al. 2013), but the relationship is not explored in this study.
2.3 Evaluation criteria
3D fluoroscopic image estimation is evaluated using the following two criteria:
-
a)
Tumor localization error is measured by computing the RMSE of the tumor centroid location in the estimated images compared to its location in the corresponding ground truth images. It is estimated in the LR (left – right), AP (anterior – posterior), and SI (superior – inferior) directions and in 3D. This provides a geometric measure of the accuracy. The 95th percentile error in tumor localization is also discussed in this study, which is the error value higher than 95% of the other error values in the same dataset.
-
b)3D fluoroscopic image intensity error is measured by computing the normalized root mean square error (NRMSE) from the voxel-wise intensity difference between the estimated image and ground truth image:
where fi is the estimated 3D fluoroscopic image, fi* is the ground truth image and i represents the voxel index. The NRMSE provides a global metric for evaluating the 3D images. Two variations of this metric are discussed and computed in the experiments: 1) “final” NRMSE which is evaluated by comparing the estimated 3D fluoroscopic images to the ground truth images, and 2) the “initial” NRMSE is evaluated between the ground truth reference image and the ground truth images at different phases.(3)
2.4 Experimental Design
Three experiments were carried out to evaluate the proposed 4DCBCT-based 3D fluoroscopic image estimation method using the datasets listed in section 2.1:
-
a)
Using the modified XCAT phantom with patient trajectories, we compare estimated 3D fluoroscopic images based on 4DCBCT motion models with the ones estimated based on 4DCT motion models. The estimated 3D fluoroscopic images are evaluated based on the evaluation criteria discussed in 2.3. Using the digital XCAT phantom, the tumor centroid is defined in the software when generating the phantom images.
-
b)The same scenario as in (a) but with added positioning/setup disparities or tumor baseline shifts to simulate positioning uncertainties resulting from building motion models using 4DCT images days or weeks before treatment starts:
- We simulate patient setup and positioning disparities found at treatment time by shifting both ground truth and 4DCBCT data by 4 mm in the LR or AP direction or 5 mm in the SI direction. The intent is to simulate situations where registration of planning images and setup images have resulted in patient positioning errors of the magnitudes stated. 4DCBCT is assumed to be able to captures the shift because it is acquired while the patient is in treatment position.
- We simulate a tumor baseline shift by shifting the tumor in both ground truth and 4DCBCT data by 4 mm in the LR or AP direction or 5 mm in the SI direction while the rest of the volume remains unchanged. Tumor baseline position shifts are observed frequently in the clinic (Berbeco et al. 2005; Keall et al. 2006).
-
c)
Using the physical phantom datasets we estimated 3D fluoroscopic images based on 4DCBCT motion models. The SI tumor centroid position in the estimated images was compared to the ground truth position which was manually determined in the ground truth 2D cone-beam CT projections captured during treatment time.
3 Experimental Results
3.1 Results for the modified XCAT phantom with patient motion
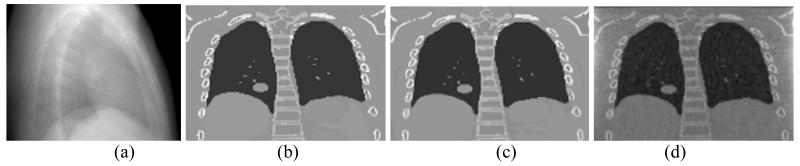
3D fluoroscopic images estimated using a 4DCBCT based motion model are compared to those estimated using a 4DCT based motion model. Figure 3 shows a sample x-ray projection used in estimation and coronal slices of the corresponding estimated fluoroscopic images based on the 4DCT-based and 4DCBCT-based motion models of dataset 1.
Figure 3.
(a) The x ray projection at angle 105° used to estimate the fluoroscopic images, and the coronal slices of: (b) the original ground truth image, (c) 4DCT-based estimated fluoroscopic image, and (d) 4DCBCT-based estimated fluoroscopic image.
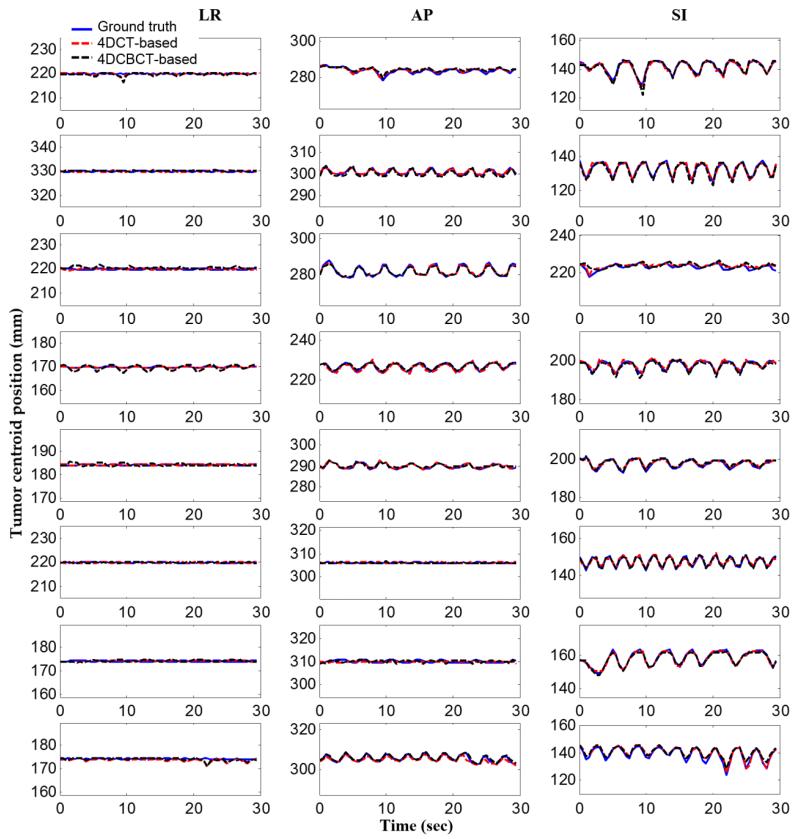
Figure 4 shows tumor centroid positions in the estimated 3D fluoroscopic images of eight datasets based on the 4DCT motion model and the 4DCBCT motion model compared to the ground truth images. It can be observed that tumor centroid positions matches the ground truth positions relatively well in all investigated datasets.
Figure 4.
Tumor centroid positions for eight datasets in the LR (left – right), AP (anterior – posterior), and SI (superior – inferior) directions
Table 1 shows the quantitative tumor centroid localization error in millimeters for all investigated datasets and using both 4DCT and 4DCBCT based motion models. The average 3D tumor localization error did not exceed 2 mm using either 4DCT or 4DCBCT motion models. The 3D tumor localization errors for 4DCT-based models are smaller than those for 4DCBCT-based models in most of the cases.
Table 1.
Tumor localization error and 95th percentile error (in mm) in the estimated images using 4DCT and 4DCBCT motion models for eight datasets in three directions; LR, AP and SI, and in 3D.
| Dataset no. | Tumor localization error (95th percentile) in mm |
|||||||
|---|---|---|---|---|---|---|---|---|
| LR | AP | SI | 3D | |||||
|
| ||||||||
| 4DCT | 4DCBCT | 4DCT | 4DCBCT | 4DCT | 4DCBCT | 4DCT | 4DCBCT | |
|
| ||||||||
| 1 | 0.29 (0.6) | 0.63 (1.1) | 0.56 (1.3) | 0.88 (1.4) | 0.98 (2.1) | 1.28 (2.0) | 1.28 (2.3) | 1.76 (2.6) |
| 2 | 0.28 (0.6) | 0.24 (0.5) | 0.26 (0.5) | 0.86 (1.3) | 0.92 (1.9) | 1.05 (1.8) | 0.85 (1.8) | 1.47 (3.0) |
| 3 | 0.15 (0.3) | 0.72 (1.5) | 0.53 (1.0) | 0.67 (1.4) | 0.91 (1.8) | 1.37 (3.0) | 0.82 (1.6) | 1.30 (2.5) |
| 4 | 0.12 (0.2) | 0.55 (0.8) | 0.36 (0.6) | 1.13 (2.2) | 0.75 (1.3) | 0.67 (1.1) | 0.74 (1.3) | 1.25 (2.4) |
| 5 | 0.04 (0.1) | 0.58 (1.1) | 0.19 (0.4) | 0.49 (0.9) | 0.68 (1.4) | 0.65 (1.4) | 0.67 (1.3) | 0.79 (1.4) |
| 6 | 0.14 (0.3) | 0.12 (0.3) | 0.33 (0.7) | 0.16 (0.3) | 0.77 (1.3) | 0.64 (1.1) | 0.70 (1.3) | 0.64 (1.2) |
| 7 | 0.13 (0.2) | 0.36 (0.6) | 0.17 (1.1) | 0.78 (1.2) | 0.76 (1.4) | 0.92 (1.6) | 0.91 (1.9) | 1.00 (2.0) |
| 8 | 0.73 (1.7) | 0.63 (1.3) | 0.88 (1.6) | 0.46 (0.9) | 1.40 (2.9) | 1.85 (4.1) | 1.39 (4.1) | 1.77 (3.9) |
|
| ||||||||
| Average | 0.24 (0.5) | 0.48 (0.9) | 0.48 (0.9) | 0.68 (1.2) | 0.90 (1.8) | 1.05 (2.0) | 0.92 (1.9) | 1.25 (2.4) |
Table 2 shows the NRMSE of the image intensity for 3D fluoroscopic images estimated based on a 4DCBCT motion model compared to those based on a 4DCT motion model. In this evaluation, the estimated images based on 4DCT motion models are compared to the 4DCT ground truth images, while the estimated images based on 4DCBCT motion models are compared to the 4DCBCT ground truth images. The final NRMSE from fluoroscopic image estimation appears to be in all investigated cases smaller than the initial NRMSE. This means that compared to any phase in the planning 4DCT or 4DCBCT, the estimated 3D fluoroscopic images are better approximations of the ground truth in treatment.
Table 2.
NRMSE for estimated 3D fluoroscopic images based on 4DCT motion models and 4DCBCT motion models, respectively for eight patients’ datasets. The initial NRMSE is the normalized RMSE of the ground truth images at different phases and the reference image. The final NRMSE is between the 3D fluoroscopic image and ground truth.
| Dataset no. |
4DCT | 4DCBCT | ||
|---|---|---|---|---|
|
| ||||
| Initial NRMSE |
Final NRMSE |
Initial NRMSE |
Final NRMSE |
|
|
| ||||
| 1 | 0.17 | 0.10 | 0.14 | 0.10 |
| 2 | 0.13 | 0.09 | 0.11 | 0.08 |
| 3 | 0.22 | 0.15 | 0.17 | 0.17 |
| 4 | 0.13 | 0.09 | 0.10 | 0.08 |
| 5 | 0.15 | 0.09 | 0.12 | 0.09 |
| 6 | 0.09 | 0.07 | 0.07 | 0.06 |
| 7 | 0.14 | 0.09 | 0.11 | 0.09 |
| 8 | 0.17 | 0.09 | 0.13 | 0.10 |
|
| ||||
| Average | 0.15 | 0.10 | 0.12 | 0.10 |
3.2 Results for the modified XCAT phantom with setup and tumor baseline shift
We simulated setup/positioning disparities or tumor baseline shifts occurring at the time of treatment. In the first three datasets, we simulated a patient positioning difference by shifting both ground truth and 4DCBCT images by 4 mm in the LR direction (dataset 1), 4 mm in the AP direction (dataset 2), and 5 mm in the SI direction (dataset 3). The 4DCBCT would be able to capture the shift because it is acquired while the patient is in treatment position. In the last three datasets, only the tumor has been shifted to simulate the scenario of tumor baseline shifts. Again, the tumor has been shifted in both ground truth images and 4DCBCT by 4 mm in the LR direction (dataset 4), 4 mm in the AP direction (dataset 5), and 5 mm in the SI direction (dataset 6), while the rest of the image remains unchanged. Figure 5 shows tumor centroid positions for the situations described above.
Figure 5.
Tumor centroid positions in LR, AP, and SI directions for six datasets. In the top three rows, setup/positioning errors are simulated in the LR, AP and SI direction, respectively. In the bottom three rows, tumor position is shifted in the LR, AP and SI directions, respectively.
As seen in Figure 5, setup and tumor position shifts caused errors in the tumor position when the 4DCT-based motion model was used. In the first three datasets, the anatomy in the estimated image was also affected by the simulated disparities since the whole image was shifted. In the last three datasets, the tumor centroid was shifted in the estimated images in the corresponding direction of the tumor baseline shift simulated in the original 4DCT images.
Table 3 shows the quantitative average tumor centroid error for each dataset. As observed, tumor localization error has increased when the 4DCT-based motion model was used. In the first three datasets, the tumor localization error has increased in all three directions and in 3D. This shows that setup/positioning disparities disturb the correspondence between the motions in different directions on which the model was trained. In the last three datasets, the tumor localization error has mainly increased in the direction where the tumor was shifted and in 3D.
Table 3.
Tumor localization and 95th percentile error (in mm) in the estimated images using 4DCT and 4DCBCT motion models for six datasets in three directions; LR, AP and SI, and in 3D. It is assumed that setup/positioning disparities are simulated in the LR, AP and SI direction, respectively in the top three rows. Tumor position is shifted in the LR, AP and SI directions, respectively in the bottom three rows.
| Dataset no. |
Tumor localization error (95th percentile) mm |
|||||||
|---|---|---|---|---|---|---|---|---|
| LR | AP | SI | 3D | |||||
|
| ||||||||
| 4DCT | 4DCBCT | 4DCT | 4DCBCT | 4DCT | 4DCBCT | 4DCT | 4DCBCT | |
|
| ||||||||
| 1 | 4.18 (4.6) | 0.63 (1.1) | 0.44 (0.8) | 0.88 (1.4) | 1.19 (2.7) | 1.28 (2.0) | 4.92 (6.8) | 1.76 (2.6) |
| 2 | 0.40 (0.8) | 0.24 (0.5) | 3.26 (4.1) | 0.86 (1.3) | 1.78 (3.4) | 1.05 (1.8) | 1.92 (3.1) | 1.47 (3.0) |
| 3 | 0.16 (0.2) | 0.72 (1.5) | 1.67 (2.8) | 0.67 (1.4) | 3.57 (4.6) | 1.37 (3.0) | 4.99 (6.1) | 1.30 (2.5) |
| 4 | 3.88 (4.0) | 0.55 (0.8) | 0.35 (0.7) | 1.13 (2.2) | 0.65 (1.2) | 0.67 (1.1) | 4.05 (5.2) | 1.25 (2.4) |
| 5 | 0.07 (0.1) | 0.58 (1.1) | 3.86 (4.1) | 0.49 (0.9) | 0.58 (1.2) | 0.65 (1.4) | 3.73 (4.7) | 0.79 (1.4) |
| 6 | 0.10 (0.2) | 0.12 (0.3) | 0.33 (0.7) | 0.16 (0.3) | 5.24 (6.6) | 0.64 (1.1) | 5.48 (6.7) | 0.64 (1.2) |
|
| ||||||||
| Average | 1.46 (1.6) | 0.47 (0.9) | 1.65 (2.2) | 0.70 (1.3) | 2.17 (3.3) | 0.94 (1.7) | 4.18 (5.4) | 1.20 (2.2) |
Table 4 shows the 3D fluoroscopic image intensity error based on 4DCT and 4DCBCT motion models. In the first three datasets of the 4DCT images, the whole original images used to build the motion model were shifted so the anatomy in the estimated images was affected. This effect manifests in the high final NRMSE. In the last three datasets, the tumor centroid has a slight shift in the original 4DCT images in one direction which resulted in a tumor shift in that direction in the estimated images, but the anatomy has not been affected. The final NRMSE for the last three datasets is approximately the same as that without having tumor positioning errors as shown in Table 2. On the other hand, the estimated images based on 4DCBCT motion models have the same NRMSE values as those shown in Table 2, because the 4DCBCTs are not affected by the positioning disparities and tumor baseline shift.
Table 4.
NRMSE for the estimated 3D fluoroscopic images based on 4DCT motion models and 4DCBCT motion models in six patient-based XCAT datasets. Setup/positioning disparities are simulated in the LR, AP and SI direction, respectively in the top three rows. Tumor position is shifted in the LR, AP and SI directions, respectively in the bottom three rows.
| Dataset no. |
4DCT | 4DCBCT | ||
|---|---|---|---|---|
|
| ||||
| Initial NRMSE | Final NRMSE | Initial NRMSE | Final NRMSE | |
|
| ||||
| 1 | 0.17 | 0.21 | 0.14 | 0.10 |
| 2 | 0.13 | 0.22 | 0.11 | 0.08 |
| 3 | 0.22 | 0.19 | 0.17 | 0.17 |
| 4 | 0.13 | 0.09 | 0.10 | 0.08 |
| 5 | 0.15 | 0.09 | 0.12 | 0.09 |
| 6 | 0.09 | 0.07 | 0.07 | 0.06 |
|
| ||||
| Average | 0.15 | 0.15 | 0.12 | 0.10 |
3.3 Results for the physical respiratory phantom
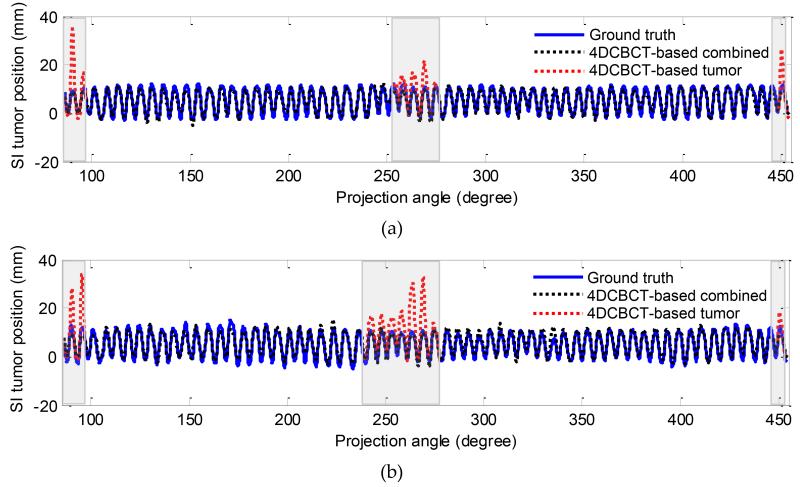
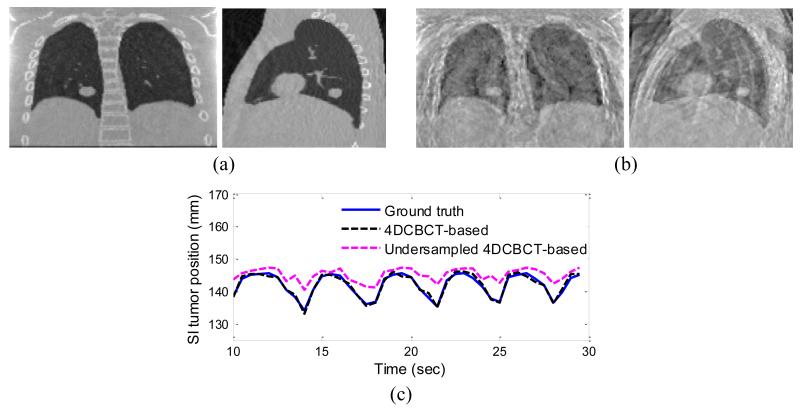
In this section, the estimated 3D fluoroscopic images of the physical phantom using a 4DCBCT-based motion model are evaluated. Figure 6 shows the SI tumor position in the estimated images and the ground truth projections in two datasets. In dataset #1 shown in Figure 6 (a), the average tumor localization and 95th percentile error in SI tumor position in all generated fluoroscopic images was 1.06 mm and 2.61 mm, respectively. In dataset #2, shown in Figure 6 (b), it was 1.21 mm and 2.95 mm respectively.
Figure 6.
SI tumor position in the estimated fluoroscopic images using 4DCBCT-based motion models in dataset #1 (a) and in dataset #2 (b). The shaded grey area shows the region in which diaphragm-based tracking was used. The black dashed line shows SI tumor position using combined tracking (i.e., alternating based on tumor and diaphragm tracking). The red dashed line in the shaded grey areas shows SI tumor position when tumor-based tracking was used.
As stated earlier, the tumor moves in the SI direction only. We assume the ground truth motion in the LR and AP directions to be zero and we calculated the tumor localization error in the LR and AP directions based on the tumor location estimated using our method. In dataset #1, the average tumor localization and 95th percentile error in LR-AP tumor position in all generated fluoroscopic images was 0.9 mm and 2.3 mm respectively. In dataset #2, it was 0.9 mm and 2.5 mm, respectively.
In these dataset, image processing techniques have been used to preprocess the measured cone-beam projections before using them in the 3D-2D mapping algorithm. Background subtraction is the first step applied to the measured projections to eliminate the background noise and make background illumination more uniform. We make the background uniform by creating an approximation of the background as a separate image and then subtract this approximation from the original image. Moreover, a region of interest (ROI) is chosen from both the computed and the measured projection in the optimization algorithm instead of using the whole projection images to reduce the effect of the noise and artifacts. In most projections, the ROI was chosen to surround the tumor. In some of the projections, the shoulder overlaps with the tumor which reduces the accuracy of the optimization. Thus, we have chosen to use the diaphragm as a surrogate in these projections. More details on this approach can be found in (Lewis 2010). The shaded grey area in Figure 6 shows the region in which diaphragm-based tracking was used.
Figure 7 shows coronal slices of the estimated 3D fluoroscopic images in two different respiratory phases (exhale and inhale) in the first dataset. It can be seen that the estimation method was able to capture anatomical variation caused by respiration. This experiment demonstrates the feasibility of implementing 4DCBCT-based 3D fluoroscopic image generation on clinical equipment.
Figure 7.
Coronal slices of the estimated 3D fluoroscopic images of physical phantom from dataset 1 in: (a) exhale and (b) inhale phases.
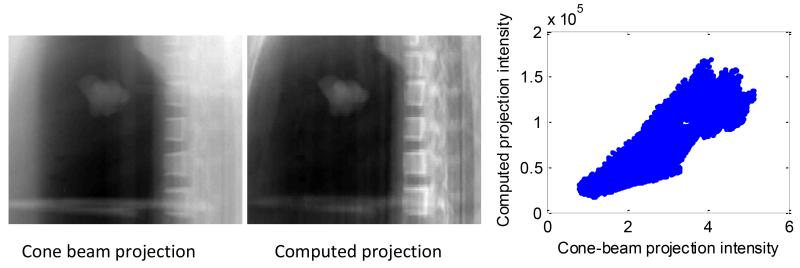
Figure 8 shows the scatter plots between the image intensities of a cone-beam projection and of a computed projection generated at the same projection angle for the physical phantom dataset #1. The figure shows the roughly linear relationship in pixel values between the two images. More than 90% of the variance can be explained by a simple linear model.
Figure 8.
Measured cone-beam projection after preprocessing of the image intensities (logarithm transform followed by reversion of the sign) (left), computed projection (middle), and scatter plots between the intensities of the two images. A linear model between the two image intensities is able to explain 91% of the variance in the two images.
Figure 8 demonstrates that the linear relationship assumed in this study between the measured cone-beam projections and the DRRs generated from the 3D fluoroscopic images is reasonable. This relationship is discussed further in the following section.
4 Discussion
In this paper, we have shown the feasibility of estimating 3D fluoroscopic images from a patient-specific 4DCBCT-based motion model and a set of 2D x-ray projection images captured at the time of treatment delivery. The method was evaluated on both a digital phantom and an anthropomorphic physical respiratory phantom driven by two patient breathing trajectories. A particular advantage of the proposed 4DCBCT-based method is the potential to capture both inter- and intra- fractional anatomical changes over the course of treatment which may be difficult when using models based on 4DCT images acquired during patient simulation as shown in the experiments in section 3.2.
Using the XCAT phantom and assuming there are no positioning/tumor baseline shift uncertainties, the 3D tumor localization errors for 4DCT-based models were smaller than those for 4DCBCT-based models in most of the datasets. This may be due to the superior quality of the 4DCT images. The streaking artifacts caused by CBCT reconstruction degrade the quality of the images, which may cause the DIR and the optimization algorithm to lose some accuracy.
We also simulated 4DCT images with different positioning/setup or tumor baseline locations relative to ground truth and 4DCBCT (assumed to be taken at the time of treatment). With the simulated setup and/or tumor baseline shift, we observed an average tumor localization error of about 4.2 mm when using a 4DCT-based motion model versus only about 1.2 mm when using a 4DCBCT-based motion model in these cases. This demonstrates the potential for a 4DCBCT-based motion model to remain robust in the presence of patient setup uncertainties. One scenario not investigated is a tumor baseline shift that has been accounted for by registration with CBCT. This would cause the tumor to be in the correct position, but the rest of the anatomy to be shifted. This could cause errors in estimated positions of normal tissues, and will be investigated in future work.
Finally, an anthropomorphic physical phantom was used to simulate the process of 4DCBCT-based 3D fluoroscopic image estimation using clinical equipment. The average SI tumor localization error was ≤ 1.0 mm in both datasets tested. This demonstrates the feasibility of implementing 4DCBCT-based 3D fluoroscopic image generation on clinical equipment.
Previous studies have explored causes of error that can be attributed either to the motion modeling or the iterative cost function optimization steps of 3D fluoroscopic image generation. (Li et al. 2011) showed in their study on 3D fluoroscopic image estimation from 4DCT images that errors can be mainly attributed to optimization-based part of the procedure, specifically the 2D to 3D registration between the projection image and the reference image, while the error introduced by DIR to build the motion model is negligible (for the datasets used). As stated earlier, DIR accuracy is an upper limit on the accuracy of this method. In some clinical situations, the demons algorithm approach might perform poorly. If DIR performs poorly, this fluoroscopic image estimation algorithm will likewise perform poorly. If another DIR algorithm is able to handle the situation, it would be straightforward to substitute it for the DIR method we chose. DIR algorithm development continues to be an active field, and alternative DIR methods can be considered in the future if necessary, such as (Coselmon et al. 2004; Li et al. 2013).
Using the algorithm discussed in this paper, we assume a linear relationship between the measured cone-beam projections and the DRRs generated from the 3D fluoroscopic images. While DRRs simulate the creation of 2D x-ray projection images, reconstruction artifacts, noise, voxel size, detector noise and other processes can cause non-linear relationships. Despite these limitations, the method has been shown to perform well in previous studies based on 4DCT motion models (Lewis et al. 2010; Li et al. 2011; Mishra et al. 2013) and a preliminary study based on 4DCBCT (Dhou et al. 2015). Likewise, the method performed well for the data used in this study, despite the expectation that CBCT reconstruction artifacts create an even less linear relationship. The use of other cost functions is an interesting topic, and it would be worth investigating the use of other similarity metrics in the future, such as normalized cross correlation.
The algorithm was implemented and run efficiently on GPU (GeForce GTX 670). The algorithm needs an average of 1.6 seconds to estimate a 3D fluoroscopic image for the digital phantom datasets and an average of 2.8 seconds for the physical phantom datasets. This processing time includes estimating the image and the tumor location. The DIR takes an average of 27.5 seconds to register a 4DCBCT image to the reference image for the digital phantom datasets and 17.7 seconds for the physical phantom dataset.
3D fluoroscopic image estimation can be applied to verify the position of the tumor and normal structures during radiotherapy treatment delivery. The resultant images could be used either for geometric verification, or for the estimation of delivered dose distributions. The estimated 3D fluoroscopic images using a 4DCBCT-based motion model may be more accurate than using the planning 4DCT images for dose calculation purposes, especially when there are uncertainties in the setup, tumor position or respiratory motion pattern, between simulation and treatment, or changes in the patient anatomy. However, there are other challenges associated with 4DCBCT imaging (discussed in the following paragraph) that make dose calculation difficult. These challenges need to be investigated in a future study on delivered dose verification.
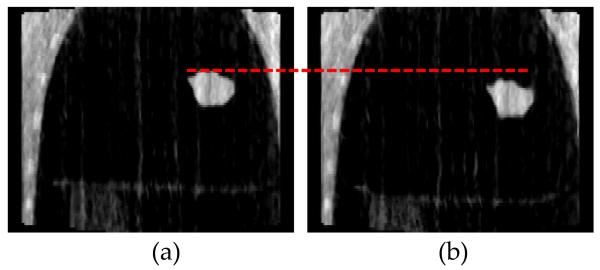
The accuracy of the proposed method can depend on the quality of the 4DCBCT images used in building the motion model. One cause of poor image quality in 4DCBCT volumes is having too few projections for image reconstruction. We explored the relationship between 4DCBCT image quality and the performance of 3D fluoroscopic image generation in the following example. Two motion models were constructed; one using 4DCBCT images reconstructed from 1000 evenly spaced projections (well-sampled), and the other reconstructed using 150 evenly spaced projections (under-sampled). Figure 9 shows the 3D fluoroscopic images of the digital phantom #1 used in this study generated using each acquisition type, and the decrease in tumor localization accuracy caused by the poor quality image of the 4DCBCT reconstructed from an under-sampled set of projections. Tumor localization error and the 95th percentile error were significantly increased when using the under-sampled 4DCBCT-based motion model: from 1.28 and 2.0 to 4.02 and 7.00 mm in the SI direction, and from 1.76 and 2.6 to 5.57 and 9.5 in 3D. The final NRMSE error of the under-sampled 4DCBCT-based 3D fluoroscopic images has also increased from 0.10 to 0.25.
Figure 9.
The estimated 3D fluoroscopic images of digital phantom #1 based on: (a) 4DCBCT reconstructed from a well-sampled projection set and (b) a 4DCBCT reconstructed from an under-sampled projection set. (c) Shows the SI tumor position in the estimated images derived from each type of 4DCBCT, illustrating that the tumor centroid position has changed when using the under-sampled 4DCBCT-based motion model.
In the digital phantom simulation, each dataset has 1000 projections which were sorted into 10 bins so each 4D image is reconstructed from 100 projections (high quality reconstructions are possible with the idealized XCAT phantom with relatively few projections compared to real physical measurements). In the physical phantom, for each dataset we have 2693 projections which where sorted into 10 bins so each image is reconstructed from about 2693/10 projections. The number of projections typically available in a clinical setting varies between manufactures and imaging modes/settings.
Various methods have been proposed to address the under-sampling problem and improve image quality in 4DCBCT, such as compressed sensing (Chen et al. 2008; Sidky and Pan 2008; Sidky et al. 2011; Gao et al. 2012; Choi et al. 2013), motion compensated reconstruction (Li et al. 2006; Li et al. 2007; Rit et al. 2008; Rit et al. 2009), intermediate frame interpolation (Weiss et al. 1982; Lehmann et al. 2001; Schreibmann et al. 2006; Bertram et al. 2009; Dhou et al. 2014), and other recent advanced methods (Jia et al. 2012; Wang and Gu 2013).
This study showed the applicability of estimating 3D fluoroscopic images using 4CBCT motion models on a preliminary basis. The digital and physical phantoms used in this study do not reliably represent a complete realistic human patient anatomy or respiration. Future studies will be needed utilizing 4DCBCT patient datasets to further validate the proposed algorithm.
5 Conclusion
This study showed the feasibility of estimating 3D fluoroscopic images using a 4DCBCT-based motion model and x-ray projections captured at treatment time. The estimated 3D fluoroscopic images using 4DCBCT-based motion model have been evaluated and compared to those estimated using 4DCT-based in terms of their global voxel intensity error and tumor localization error. Assuming positioning disparities and tumor baseline shift of magnitudes at the time of treatment delivery commonly seen in clinical settings (Berbeco et al. 2005; Keall et al. 2006), 4DCBCT-based motion models generated improved 3D fluoroscopic images compared to existing 4DCT-based methods. Experiments performed with a physical phantom verified the feasibility of implementing these methods on clinical equipment. Studies on the performance of these methods on patient images should be performed before these methods can be used clinically.
Acknowledgement
The authors would like to thank Dr. Seiko Nishioka of the Department of Radiology, NTT Hospital, Sapporo, Japan and Dr. Hiroki Shirato of the Department of Radiation Medicine, Hokkaido University School of Medicine, Sapporo, Japan for sharing the patient tumor motion dataset with us. This project was supported, in part, through a Master Research Agreement with Varian Medical Systems, Inc., Palo Alto, CA. The project was also supported, in part, by Award Number R21CA156068 from the National Cancer Institute. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
References
- Berbeco RI, Mostafavi H, Sharp GC, Jiang SB. Towards fluoroscopic respiratory gating for lung tumours without radiopaque markers. Phys Med Biol. 2005;50(19):4481–90. doi: 10.1088/0031-9155/50/19/004. [DOI] [PubMed] [Google Scholar]
- Bertram M, Wiegert J, Schafer D, Aach T, Rose G. Directional view interpolation for compensation of sparse angular sampling in cone-beam CT. IEEE Trans Med Imaging. 2009;28(7):1011–22. doi: 10.1109/TMI.2008.2011550. [DOI] [PubMed] [Google Scholar]
- Chen GH, Tang J, Leng S. Prior image constrained compressed sensing (PICCS): a method to accurately reconstruct dynamic CT images from highly undersampled projection data sets. Med Phys. 2008;35(2):660–3. doi: 10.1118/1.2836423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi K, Xing L, Koong A, Li R. First study of on-treatment volumetric imaging during respiratory gated VMAT. Med Phys. 2013;40(4):040701. doi: 10.1118/1.4794925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coselmon MM, Balter JM, McShan DL, Kessler ML. Mutual information based CT registration of the lung at exhale and inhale breathing states using thin-plate splines. Med Phys. 2004;31(11):2942–8. doi: 10.1118/1.1803671. [DOI] [PubMed] [Google Scholar]
- Court LE, Seco J, Lu XQ, Ebe K, Mayo C, Ionascu D, Winey B, Giakoumakis N, Aristophanous M, Berbeco R, Rottman J, Bogdanov M, Schofield D, Lingos T. Use of a realistic breathing lung phantom to evaluate dose delivery errors. Med Phys. 2010;37(11):5850–7. doi: 10.1118/1.3496356. [DOI] [PubMed] [Google Scholar]
- Dhou S, Hugo GD, Docef A. Motion-based projection generation for 4D-CT reconstruction; Proceedings of the IEEE International Conference on Image Processing (ICIP); Paris, France. 2014. [Google Scholar]
- Dhou S, Hurwitz M, Mishra P, Berbeco R, Lewis JH. SPIE Medical Imaging. Orlando, Florida, USA: 2015. 4DCBCT-based motion modeling and 3D fluoroscopic image generation for lung cancer radiotherapy. In press. [Google Scholar]
- Dhou S, Motai Y, Hugo GD. Local intensity feature tracking and motion modeling for respiratory signal extraction in cone beam CT projections. IEEE Trans Biomed Eng. 2013;60(2):332–42. doi: 10.1109/TBME.2012.2226883. [DOI] [PubMed] [Google Scholar]
- Fassi A, Schaerer J, Fernandes M, Riboldi M, Sarrut D, Baroni G. Tumor tracking method based on a deformable 4D CT breathing motion model driven by an external surface surrogate. Int J Radiat Oncol Biol Phys. 2014;88(1):182–8. doi: 10.1016/j.ijrobp.2013.09.026. [DOI] [PubMed] [Google Scholar]
- Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. Journal of the Optical Society of America A: Optics, Image Science, and Vision. 1984;1(6):612–619. [Google Scholar]
- Gao H, Li R, Lin Y, Xing L. 4D cone beam CT via spatiotemporal tensor framelet. Med Phys. 2012;39(11):6943–6. doi: 10.1118/1.4762288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu X, Pan H, Liang Y, Castillo R, Yang D, Choi D, Castillo E, Majumdar A, Guerrero T, Jiang SB. Implementation and evaluation of various demons deformable image registration algorithms on a GPU. Phys Med Biol. 2010;55(1):207–19. doi: 10.1088/0031-9155/55/1/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hertanto A, Zhang Q, Hu YC, Dzyubak O, Rimner A, Mageras GS. Reduction of irregular breathing artifacts in respiration-correlated CT images using a respiratory motion model. Med Phys. 2012;39(6):3070–9. doi: 10.1118/1.4711802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ionascu D, Park SJ, Killoran JH, Allen AM, Berbeco RI. Application of Prinicipal Component Analysis for Marker-Less Lung Tumor Tracking with Beam’s-Eye-View Epid Images. Medical Physics. 2008;35(6):2893. [Google Scholar]
- Jia X, Tian Z, Lou Y, Sonke JJ, Jiang SB. Four-dimensional cone beam CT reconstruction and enhancement using a temporal nonlocal means method. Med Phys. 2012;39(9):5592–602. doi: 10.1118/1.4745559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keall PJ, Mageras GS, Balter JM, Emery RS, Forster KM, Jiang SB, Kapatoes JM, Low DA, Murphy MJ, Murray BR, Ramsey CR, Van Herk MB, Vedam SS, Wong JW, Yorke E. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys. 2006;33(10):3874–900. doi: 10.1118/1.2349696. [DOI] [PubMed] [Google Scholar]
- Lehmann TM, Gonner C, Spitzer K. Addendum: B-spline interpolation in medical image processing. IEEE Trans Med Imaging. 2001;20(7):660–5. doi: 10.1109/42.932749. [DOI] [PubMed] [Google Scholar]
- Lewis JH. Physics. University of California; San Diego: 2010. Lung tumor tracking, trajectory reconstruction, and motion artifact removal using rotational cone-beam projections. PhD. [DOI] [PubMed] [Google Scholar]
- Lewis JH, Li R, Watkins WT, Lawson JD, Segars WP, Cervino LI, Song WY, Jiang SB. Markerless lung tumor tracking and trajectory reconstruction using rotational cone-beam projections: a feasibility study. Phys Med Biol. 2010;55(9):2505–22. doi: 10.1088/0031-9155/55/9/006. [DOI] [PubMed] [Google Scholar]
- Li M, Castillo E, Zheng XL, Luo HY, Castillo R, Wu Y, Guerrero T. Modeling lung deformation: a combined deformable image registration method with spatially varying Young’s modulus estimates. Med Phys. 2013;40(8):081902. doi: 10.1118/1.4812419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Jia X, Lewis JH, Gu X, Folkerts M, Men C, Jiang SB. Real-time volumetric image reconstruction and 3D tumor localization based on a single x-ray projection image for lung cancer radiotherapy. Med Phys. 2010;37(6):2822–6. doi: 10.1118/1.3426002. [DOI] [PubMed] [Google Scholar]
- Li R, Lewis JH, Jia X, Gu X, Folkerts M, Men C, Song WY, Jiang SB. 3D tumor localization through real-time volumetric x-ray imaging for lung cancer radiotherapy. Med Phys. 2011;38(5):2783–94. doi: 10.1118/1.3582693. [DOI] [PubMed] [Google Scholar]
- Li R, Lewis JH, Jia X, Zhao T, Liu W, Wuenschel S, Lamb J, Yang D, Low DA, Jiang SB. On a PCA-based lung motion model. Phys Med Biol. 2011;56(18):6009–30. doi: 10.1088/0031-9155/56/18/015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li T, Koong A, Xing L. Enhanced 4D cone-beam CT with inter-phase motion model. Med Phys. 2007;34(9):3688–95. doi: 10.1118/1.2767144. [DOI] [PubMed] [Google Scholar]
- Li T, Schreibmann E, Yang Y, Xing L. Motion correction for improved target localization with on-board cone-beam computed tomography. Phys Med Biol. 2006;51(2):253–67. doi: 10.1088/0031-9155/51/2/005. [DOI] [PubMed] [Google Scholar]
- Li T, Xing L, Munro P, McGuinness C, Chao M, Yang Y, Loo B, Koong A. Four-dimensional cone-beam computed tomography using an on-board imager. Med Phys. 2006;33(10):3825–33. doi: 10.1118/1.2349692. [DOI] [PubMed] [Google Scholar]
- Low DA, Parikh PJ, Lu W, Dempsey JF, Wahab SH, Hubenschmidt JP, Nystrom MM, Handoko M, Bradley JD. Novel breathing motion model for radiotherapy. Int J Radiat Oncol Biol Phys. 2005;63(3):921–9. doi: 10.1016/j.ijrobp.2005.03.070. [DOI] [PubMed] [Google Scholar]
- Mishra P, Li R, James SS, Mak RH, Williams CL, Yue Y, Berbeco RI, Lewis JH. Evaluation of 3D fluoroscopic image generation from a single planar treatment image on patient data with a modified XCAT phantom. Phys Med Biol. 2013;58(4):841–58. doi: 10.1088/0031-9155/58/4/841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra P, Li R, Mak RH, Rottmann J, Bryant JH, Williams CL, Berbeco RI, Lewis JH. An initial study on the estimation of time-varying volumetric treatment images and 3D tumor localization from single MV cine EPID images. Med Phys. 2014;41(8):081713. doi: 10.1118/1.4889779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra P, St James S, Segars WP, Berbeco RI, Lewis JH. Adaptation and applications of a realistic digital phantom based on patient lung tumor trajectories. Phys Med Biol. 2012;57(11):3597–608. doi: 10.1088/0031-9155/57/11/3597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rit S, Sarrut D, Desbat L. Comparison of analytic and algebraic methods for motion-compensated cone-beam CT reconstruction of the thorax. IEEE Trans Med Imaging. 2009;28(10):1513–25. doi: 10.1109/TMI.2008.2008962. [DOI] [PubMed] [Google Scholar]
- Rit S, Sarrut D, Ginestet C. Respiratory signal extraction for 4D CT imaging of the thorax from cone-beam CT projections. Med Image Comput Comput Assist Interv. 2005;8(Pt 1):556–63. doi: 10.1007/11566465_69. [DOI] [PubMed] [Google Scholar]
- Rit S, Vila Oliva M, Brousmiche S, Labarbe R, Sarrut D, Sharp GC. The Reconstruction Toolkit (RTK), an open-source cone-beam CT reconstruction toolkit based on the Insight Toolkit (ITK); International Conference on the Use of Computers in Radiation Therapy (ICCR’13); 2013. [Google Scholar]
- Rit S, Wolthaus J, van Herk M, Sonke JJ. On-the-fly motion-compensated cone-beam CT using an a priori motion model. Med Image Comput Comput Assist Interv. 2008;11(Pt 1):729–36. doi: 10.1007/978-3-540-85988-8_87. [DOI] [PubMed] [Google Scholar]
- Schreibmann E, Chen GT, Xing L. Image interpolation in 4D CT using a BSpline deformable registration model. Int J Radiat Oncol Biol Phys. 2006;64(5):1537–50. doi: 10.1016/j.ijrobp.2005.11.018. [DOI] [PubMed] [Google Scholar]
- Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BM. 4D XCAT phantom for multimodality imaging research. Med Phys. 2010;37(9):4902–15. doi: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky EY, Duchin Y, Pan X, Ullberg C. A constrained, total-variation minimization algorithm for low-intensity x-ray CT. Med Phys. 2011;38(Suppl 1):S117. doi: 10.1118/1.3560887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol. 2008;53(17):4777–807. doi: 10.1088/0031-9155/53/17/021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohn M, Birkner M, Yan D, Alber M. Modelling individual geometric variation based on dominant eigenmodes of organ deformation: implementation and evaluation. Phys Med Biol. 2005;50(24):5893–908. doi: 10.1088/0031-9155/50/24/009. [DOI] [PubMed] [Google Scholar]
- Van Herk M, Zijp L, Remeijer P, Wolthaus J, Sonke J. On-line 4D cone beam CT for daily correction of lung tumour position during hypofractionated radiotherapy. ICCR; Toronto, Canada: 2007. [Google Scholar]
- Vedam SS, Keall PJ, Kini VR, Mostafavi H, Shukla HP, Mohan R. Acquiring a four-dimensional computed tomography dataset using an external respiratory signal. Phys Med Biol. 2003;48(1):45–62. doi: 10.1088/0031-9155/48/1/304. [DOI] [PubMed] [Google Scholar]
- Wang J, Gu X. High-quality four-dimensional cone-beam CT by deforming prior images. Phys Med Biol. 2013;58(2):231–46. doi: 10.1088/0031-9155/58/2/231. [DOI] [PubMed] [Google Scholar]
- Weiss GH, Talbert AJ, Brooks RA. The use of phantom views to reduce CT streaks due to insufficient angular sampling. Phys Med Biol. 1982;27(9):1151–62. doi: 10.1088/0031-9155/27/9/005. [DOI] [PubMed] [Google Scholar]
- Williams CL, Mishra P, Seco J, St James S, Mak RH, Berbeco RI, Lewis JH. A mass-conserving 4D XCAT phantom for dose calculation and accumulation. Med Phys. 2013;40(7):071728. doi: 10.1118/1.4811102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan H, Wang X, Yin W, Pan T, Ahmad M, Mou X, Cervino L, Jia X, Jiang SB. Extracting respiratory signals from thoracic cone beam CT projections. Phys Med Biol. 2013;58(5):1447–64. doi: 10.1088/0031-9155/58/5/1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng R, Fessler JA, Balter JM. Estimating 3-D respiratory motion from orbiting views by tomographic image registration. IEEE Trans Med Imaging. 2007;26(2):153–63. doi: 10.1109/TMI.2006.889719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Hu YC, Liu F, Goodman K, Rosenzweig KE, Mageras GS. Correction of motion artifacts in cone-beam CT using a patient-specific respiratory motion model. Med Phys. 2010;37(6):2901–9. doi: 10.1118/1.3397460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, Pevsner A, Hertanto A, Hu YC, Rosenzweig KE, Ling CC, Mageras GS. A patient-specific respiratory model of anatomical motion for radiation treatment planning. Med Phys. 2007;34(12):4772–81. doi: 10.1118/1.2804576. [DOI] [PubMed] [Google Scholar]
- Zijp L, Sonke J-J, van Herk M. Extraction of the respiratory signal from sequential thorax cone-beam X-ray images; International Conference on the Use of Computers in Radiation Therapy; 2004. [Google Scholar]