Robust Biometrics Based Authentication and Key Agreement Scheme for Multi-Server Environments Using Smart Cards

Abstract

Biometrics authenticated schemes using smart cards have attracted much attention in multi-server environments. Several schemes of this type where proposed in the past. However, many of them were found to have some design flaws. This paper concentrates on the security weaknesses of the three-factor authentication scheme by Mishra et al. After careful analysis, we find their scheme does not really resist replay attack while failing to provide an efficient password change phase. We further propose an improvement of Mishra et al.’s scheme with the purpose of preventing the security threats of their scheme. We demonstrate the proposed scheme is given to strong authentication against several attacks including attacks shown in the original scheme. In addition, we compare the performance and functionality with other multi-server authenticated key schemes.

Introduction

With the swift development of wireless communications and network technologies, more and more people use wireless handheld devices (e.g.PDA, notebook and mobile phone, etc) to enjoy mobile services almost anytime and anywhere. However, open nature of networks demands for security concern of paid and protected resources available over the network [1–5]. Authentication mechanism becomes an essential need before a remote user can access the services. Since then Lamport [6] proposed the first authentication scheme, a number of authentication schemes have been put forward for different applications [7–13].

However, most of the existing password authentication schemes are based on a single-server environment which are unfit for the multi-server environments. Recently, a large number of smart cards based remote user authentication schemes for multi-server environments have been proposed. In addition, compared with other authentication schemes, schemes that only use random numbers and a hash function were getting much more attention because of their low computation costs. In 2008, Tsai [14] proposed an efficient multi-server authentication scheme using the random number and one-way hash function. After that, numerous authenticated key agreement schemes were presented for multi-server environments one after another [15–17]. In 2012, Li et al. [18] proposed a novel authenticated key exchange scheme for multi-server environments. Unfortunately, Xue et al.[19] showed that Li et al.’s scheme did not resist some types of known attacks, such as vulnerability to verifier stolen, off-line password guess, replay, denial of service and forgery attacks. Then, Xue et al. proposed an improved scheme to remedy the weaknesses of Li et al.’s scheme. Nevertheless, Lu et al.[20] observed that Xue et al.’s scheme was not only really insecure against masquerade and insider attacks but also was vulnerable to off-line password guessing attack. To improve the shortcomings of Xue et al.’s scheme, Lu et al. proposed a slight modified authentication scheme for multi-server environments.

All above mentioned authentication schemes are based on password and smart cards. Note that the password cannot be considered as a unique identity identifier and it’s needed to be remembered. Moreover, possibility of password guessing attack is also a concern. Compared with cryptographic keys and passwords, biometric keys (e.g.fingerprint, face, iris, hand geometry and palm-print, etc.) have many advantages [21], for example, they are difficult to lose or forget; they are difficult to copy or share; they are difficult to forge or distribute biometrics; they are difficult to guess; they are more difficult to break biometric keys. Recently, Chuang et al.[22] presented an efficient biometrics based authentication scheme using smart cards for multi-server environments, which was previously considered to be have more security properties. However, Mishra et al. [23] showed that Chuang et al.’s scheme was vulnerable to stolen smart card attack, server spoofing attack and impersonation attack. In addition, they proposed an improved biometrics-based multi-server authenticated key agreement scheme using smart cards and they claimed that their scheme satisfied all desirable security requirements. Unfortunately, this paper will demonstrate that the scheme cannot really resist replay attack and cannot provide an efficient password change phase.

In this paper, we concentrate on the security weaknesses of the three-factor authentication scheme by Mishra et al. After carefully analysis, we find their scheme does not really resist replay attack while fails to provide an efficient password change phase. We further propose an improvement of Mishra et al.’s scheme with the purpose of preventing the security threats of their scheme. We demonstrate the proposed scheme is given to strong authentication against several attacks including attacks showed in the original scheme. In addition, we compare the performance and functionality with other related schemes.

The rest of paper is organized as follows: In Section 2 and Section 3, we review and analyze the Mishra et al.’s scheme. In Section 4, we propose an enhancement authentication scheme for multi-sever environments. In Section 5, we present a security analysis of our scheme. Section 6 shows security and performance analyses by comparing our scheme with previous schemes. We conclude in Section 7.

Review of Mishra et al.’s scheme

There are three phases relating to Mishra et al.’s scheme which consists of the registration, login and authentication and password updating. Table 1 lists the notations used in this paper.

Table 1. Notations.

U i, S j	User, server
RC	The registration center
ID i, SID j	Identity of U i, S j
PW i, BIO i	Password and biometrics of U i
x, y	Master secret key of U i and RC
PSK	Secure key shared by RC and S j
h(⋅)	Hash function
H(⋅)	Biohash function
⊕, ∣∣	Exclusive-or operation and concatenation operation

Registration

Suppose RC is the trusted third party responsible for registration of U _i and S _j.

Server registration

1. S _j sends the registration request to RC;

2. After receiving the request, RC sends the key PSK to S _j through a secure channel;

3. Upon receiving the secret key PSK, S _j stores it with aim to authorize a legitimate user.

User registration

1. U _i selects his identity ID _i, password PW _i and keys his biometrics BIO _i. Then, U _i generates a random number N _i, computes W ₁ = h(PW _i∣∣N _i), W ₂ = h(ID _i⊕N _i) and sends the registration message {ID _i, W ₁, W ₂} to RC via a secure channel.

2. RC computes A _i = h(ID _i∣∣x∣∣T _r), B _i = h(A _i), X _i = W _i⊕B _i, Y _i = h(PSK)⊕W ₂ and Z _i = PSK⊕A _i, where T _r is the registration time. Then, RC issues the smart card SC _i to U _i which contains {X _i, Y _i, Z _i, h(⋅)} over a secure channel.

3. Upon receiving SC _i, U _i enters his personal biometric BIO _i at the sensor and computes N = N _i⊕H(BIO _i), V = h(ID _i∣∣N _i∣∣PW _i). Finally, U _i stores {X _i, Y _i, Z _i, N, V, h(⋅)} into SC _i.

Login and authentication

1. U _i inserts SC _i into the terminal and inputs his identity ID _i, password PW _i and imprints his biometrics BIO _i at the sensor.

2. SC _i computes N _i = N⊕h(BIO _i) and checks $h(I{D}_i\mid \mid N_i\mid \mid P{W}_i)\stackrel{?}{=}V$. If it holds, SC _i continues to compute W ₁ = h(PW _i∣∣N _i), W ₂ = h(ID _i⊕N _i), B _i = X _i⊕W _i and h(PSK) = Y _i⊕W ₂. Then, SC _i generates a random number n ₁ and computes M ₁ = h(PSK)⊕n ₁, M ₂ = ID _i⊕h(n ₁∣∣B _i) and M ₃ = h(ID _i∣∣n ₁∣∣B _i). Finally, U _i sends {Z _i, M ₁, M ₂, M ₃} to S _j.

3. When receiving the message from SC _i, S _j immediately computes A _i = Z _i⊕PSK, n ₁ = M ₁⊕h(PSK), ID _i = M ₂⊕h(n ₁∣∣h(A _i)) and checks whether $h(n_1\mid \mid B_i\mid \mid I{D}_i)\stackrel{?}{=}{M}_3$. If it is equal, S _j generates a random number n ₂ and computes SK _ji = h(ID _i∣∣SID _j∣∣B _i∣∣n ₁∣∣n ₂), M ₄ = n ₂⊕h(ID _i∣∣n ₁), M ₅ = h(SK _ji∣∣n ₁∣∣n ₂). Then, S _j sends {SID _j, M ₄, M ₅} to SC _i.

4. SC _i first computes n ₂ = M ₄⊕h(ID _i∣∣n ₁), SK _ij = h(ID _i∣∣SID _j∣∣B _i∣∣n ₁∣∣n ₂) and then checks whether h(SK _ij∣∣n ₁∣∣n ₂) is consistent with M ₅. If it is true, SC _i computes M ₆ = h(SK _ij∣∣n ₁∣∣n ₂) and delivers it to S _j.

5. S _j verifies the verification condition $M_6\stackrel{?}{=}h(S{K}_{ji}\mid \mid n_1\mid \mid n_2)$. If this verification holds, S _j can now use the keys SK _ji to communicate with U _i securely.

Password updating

U _i inputs his ID _i, PW _i and imprints his biometrics BIO _i at the sensor. SC _i computes N _i = N⊕h(BIO _i) and checks $h(I{D}_i\mid \mid N_i\mid \mid P{W}_i)\stackrel{?}{=}V$. If SC _i determines that they are equal, then U _i can key the new password $P{W}_i^{new}$. Subsequently, SC _i computes $W_1^{new}=h(P{W}_i^{new}\mid \mid N_i),X_i^{new}=X_i\oplus W_1\oplus W_1^{new},V_i^{new}=h(I{D}_i\mid \mid N_i\mid \mid P{W}_i^{new})$ and replaces X _i and V _i with $X_i^{new}$ and $V_i^{new}$, respectively.

Security analysis of Mishra et al.’s scheme

This section presents a cryptanalysis of a recently scheme proposed by Mishra et al. We show their scheme does not satisfy the key security attribute such as vulnerability to replay attack and incorrect password change phase. We assume that a malicious adversary 𝓐 has totally supervised the communication channel in login and session key establishment phases. In other words, 𝓐 has the capacity to intercept, insert, delete, refresh or update any information delivered between U _i and S _j [6].

Not withstanding the replay attack

Suppose an adversary 𝓐 has intercepted a past login message {Z _i, M ₁, M ₂, M ₃}. He is able to launch a replay attack and login to the server by resending the eavesdropped message {Z _i, M ₁, M ₂, M ₃} to S _j. In other words, the adversary without running the “Login phase”, sends the eavesdropped message {Z _i, M ₁, M ₂, M ₃} to S _j. In the “Login and authentication”, upon receiving the message {Z _i, M ₁, M ₂, M ₃}, S _j computes A _i = Z _i⊕PSK, n ₁ = M ₁⊕h(PSK), ID _i = M ₂⊕h(n ₁∣∣h(A _i)), $M_3^{\prime }=h(n_1\mid \mid B_i\mid \mid I{D}_i)$ and checks whether $M_3^{\prime }$ is equal to the received M ₃ or not. Since M ₃ and $M_3^{\prime }$ are equal, S _j will authenticate 𝓐 and 𝓐 will be able to login to S _j. Thus, 𝓐 can easily login to S _j by re-sending an old login message. Since S _j does not check the freshness of the received login message {Z _i, M ₁, M ₂, M ₃} and authenticate U _i in (3) of the “Login and authentication”, S _j will not be able to discover replay attack.

Incorrect password change phase

The user U _i inserts his smart card into a card reader and enters his identity ID _i, password PW _i and imprints his personal biometric BIO _i at the sensor corresponding to his smart card. Then smart card computes N _i = N⊕h(BIO _i), $V_i^{\prime }=h(I{D}_i\mid \mid N_i\mid \mid P{W}_i)$ and compares $V_i^{\prime }$ with the stored value of V in its memory to verify the legitimacy of U _i. Once the authenticity of cardholder is verified then U _i can instruct smart card to change his password. Afterwards, smart card asks the cardholder to resubmit a new password $P{W}_i^{new}$, then X _i = B _i⊕h(PW _i∣∣N _i) and V = h(ID _i∣∣N _i∣∣PW _i) stored in the smart card can be updated with $X_i^{new}=X_i\oplus W_1\oplus W_1^{new}$ and $V_i^{new}=h(I{D}_i\mid \mid N_i\mid \mid P{W}_i^{new})$, where $W_1^{new}=h(P{W}_i^{new}\mid \mid N_i)$. The $X_i^{new}$ value contains older password PW _i in h(PW _i∣∣N _i). Therefore, the modified $X_i^{new}$ is not correct.

The proposed scheme

In this section, we will present our robust biometrics based authentication scheme using smart cards for multi-sever environments. In our scheme, there are also three participants, the user U _i, the server S _j and the registration center RC. RC chooses the secret key PSK and a secret number x and shares them with S _j via a secure channel. We will describe all the phases relating to our scheme in the subsections, i.e. registration, login and authentication, and password update, where registration and login and authentication phases are shown in Fig 1.

Fig 1. Registration and authentication phases.

Registration

1. U _i keys his biometrics BIO _i, identity ID _i and password PW _i. Then, U _i sends {ID _i, h(PW _i∣∣H(BIO _i))} to RC.

2. Upon receiving the message from U _i, RC computes X _i = h(ID _i∣∣x), V = h(ID _i∣∣h(PW _i∣∣H(BIO _i))). Then, RC stores {X _i, V _i, h(PSK)} into a smart card and submits them to U _i.

3. U _i computes Y _i = h(PSK)⊕y, and replaces h(PSK) with Y _i. Finally, the smart card stores the values of {X _i, Y _i, V _i, h(⋅)}.

Login and authentication

1. U _i inserts his smart card into device and enters his identity ID _i, password PW _i and biometrics BIO _i. Then, the smart card validates whether V _i = h(ID _i∣∣h(PW _i∣∣H(BIO _i))) is equal to the stored V. If it holds, the smart card generates a random number n ₁ and computes K = h((y⊕Y _i)∣∣SID _j), M ₁ = K⊕ID _i, M ₂ = n ₁⊕K, M ₃ = h(PW _i∣∣H(BIO _i))⊕K, Z _i = h(B _i∣∣n ₁∣∣h(PW _i∣∣H(BIO _i))∣∣T ₁). Finally, U _i submits {Z _i, M ₁, M ₂, M ₃, T ₁} to S _j, where T ₁ is the current timestamp.

2. Upon receiving the message from U _i, S _j first checks whether T _c−T ₁ ≤ ΔT and then computes K = h(SID _j∣∣h(PSK)) by using a secure pre-shared key PSK. Then, S _j retrieves ID _i = M ₁⊕K, n ₁ = M ₂⊕K, h(PW _i∣∣BIO _i) = M ₃⊕K. Now, S _j computes X _i = h(ID _i∣∣x) and verifies whether $h(X_i\mid \mid n_1\mid \mid h(P{W}_i\mid \mid H(BI{O}_i)))\stackrel{?}{=}{Z}_i$. If it holds, S _j generates a random number n ₂ and computes SK _ji = h(n ₁∣∣n ₂∣∣K∣∣X _i), M ₄ = n ₂⊕h(n ₁∣∣h(PW _i∣∣H(BIO _i))∣∣X _i), M ₅ = h(ID _i∣∣n ₁∣∣n ₂∣∣K∣∣T ₂). Then, S _j sends back authentication message {M ₄, M ₅, T ₂} to U _i, where T ₂ is the current timestamp.

3. After checking the freshness of T ₂, U _i first computes n ₂ = M ₄⊕h(n ₁∣∣h(PW _i∣∣H(BIO _i))∣∣X _i) and then verifies whether h(ID _i∣∣n ₁∣∣n ₂∣∣K) is equal to the received M ₅. If they are equal, U _i computes the common session key SK _ij = h(n ₁∣∣n ₂∣∣K∣∣X _i) and sends {M ₆ = h(SK _ij∣∣ID _i∣∣n ₂∣∣T ₃), T ₃} to S _j, where T ₃ is the current timestamp.

4. S _j verifies the freshness T ₃ and the correctness of M ₆ by using SK _ji. If they do not hold, S _j stops the execution; Otherwise, S _j confirms the common session key SK _ji with U _i.

Password updating

U _i first inputs his smart card into the device and provides his identity ID _i, password PW _i and biometrics BIO _i. Then, the smart card validates whether V _i = h(ID _i∣∣h(PW _i∣∣H(BIO _i))) is equal to the stored V _i. If they are not equal, the smart card refuses the request; Otherwise, U _i keys in the new password $P{W}_i^{new}$. Finally, the smart card computes $V_i^{new}=h(I{D}_i\mid \mid h(P{W}_i^{new}\mid \mid H(BI{O}_i)))$ and replaces V _i by $V_i^{new}$.

Security analysis of the proposed scheme

In this section, we first adopt Burrows-Abadi-Needham (BAN)Logic [24] to demonstrate the completeness of the proposed scheme. Then, we conduct discussion and a cryptanalysis of the proposed scheme through both the informal and formal analyses.

Verifying the proposed scheme with BAN logic

BAN logic [24] is a set of rules for defining and analyzing information exchange schemes. It helps its users determine whether exchanged information is trustworthy, secured against eavesdropping, or both. It has been highly successful in analyzing the security of authentication schemes. First, we introduce some notations and logical postulates of BAN logic in Table 2.

1. BAN logical postulates

   1. Message-meaning rule: $\frac{A\mid \equiv A\stackrel{K}{\leftrightarrow }B,A⊲<X{>}_K}{A\mid \equiv \mid B\sim X}$: if A believes that the key K is shared by A and B, and sees X encrypted with K, then A believes that B once said X.
   2. Fresh conjuncatenation rule: $\frac{A\mid \equiv \#(X)}{A\mid \equiv \#(X,Y)}$: if A believes freshness of X, then A believes freshness of the (X, Y).
   3. Belief rule: $\frac{A\mid \equiv X,A\mid \equiv Y}{A\mid \equiv (X,Y)}$: if A believes X and Y, then A believes (X, Y).
   4. Nonce-verification rule: $\frac{A\mid \equiv \#(X),A\mid \equiv B\mid \sim X}{A\mid \equiv B\mid \equiv X}$: if A believes that X could have been uttered only recently and that B once said X, then A believes that B believes X.
   5. Jurisdiction rule: $\frac{A\mid \equiv B\Rightarrow X,A\mid \equiv B\mid \sim X}{A\mid \equiv X}$: if A believes that B has jurisdiction over X and A trusts B on the truth of X, then A believes X.

2. Establishment of security goals

   $g_1.S_j\mid \equiv U_i\mid \equiv U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j$

   $g_2.S_j\mid \equiv U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j$

   $g_3.U_i\mid \equiv S_j\mid \equiv U_i\stackrel{S{K}_{ji}}{\leftrightarrow }{S}_j$

   $g_4.U_i\mid \equiv U_i\stackrel{S{K}_{ji}}{\leftrightarrow }{S}_j$

3. Idealized scheme

   $U_i:<n_1,I{D}_i,h(P{W}_i\Vert H(BI{O}_i)){>}_K,{(n_1,X_i,T_1)}_{h(P{W}_i\Vert H(BI{O}_i))},{(n_2,U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j,T_3)}_{I{D}_i}$

   S _j: < n ₁, X _i, h(PW _i∣∣H(BIO _i)) > n ₂, (ID _i, n ₁, n ₂, T ₂)_K

4. Initiative premises

   p ₁. U _i∣ ≡ #n ₁ p ₂. U _i∣ ≡ S _j ⇒ #n ₂ p ₃. S _j∣ ≡ #n ₁ p ₄. S _j∣ ≡ #n ₂

   $p_5.S_j\mid \equiv U_i\stackrel{K}{\leftrightarrow }{S}_j{p}_6.U_i\mid \equiv U_i\stackrel{K}{\leftrightarrow }{S}_j$

   p ₇. U _i∣ ≡ ID _i p ₈. S _j∣ ≡ U _i ⇒ h(PW _i∣∣BIO _i)

   p ₉. S _j∣ ≡ U _i ⇒ ID _i p ₁₀. U _i∣ ≡ S _j ⇒ X _i

   p ₁₁. $S_j\mid \equiv U_i\Rightarrow U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j{p}_{12}$. $U_i\mid \equiv S_j\Rightarrow U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j$

5. Scheme analysis

   a ₁. By p ₅ and S _j⊲ < n ₁, ID _i, h(PW _i∣∣BIO _i) > K, we apply the message-meaning rule to derive: S _j∣ ≡ U _i∣ ∼ (n ₁, ID _i, h(PW _i∣∣H(BIO _i)))

   a ₂. By a ₁ and p ₃, we apply the fresh conjuncatenation rule and the nonce-verification rule to derive: S _j∣ ≡ U _i∣ ≡ (n ₁, ID _i, h(PW _i∣∣H(BIO _i)))

   a ₃. By a ₂, p ₃ and p ₈, we apply the belief rule and the jurisdiction rule to derive: S _j∣ ≡ ID _i

   a ₄. By a ₃ and $S_j⊲{(n_2,U_i\stackrel{S{K}_{ij},}{\leftrightarrow }{S}_j,T_3)}_{I{D}_i}$, we apply the message-meaning rule to derive: $S_j\mid \equiv U_i\mid \sim (n_2,U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j,T_3)$

   a ₅. By p ₄ and a ₄, we apply the fresh conjuncatennation rule and the nonce-verification rule to derive: $S_j\mid \equiv U_i\mid \equiv (n_2,U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j,T_3)$

   g ₁. By a ₅, we apply the belief rule to derive: $S_j\mid \equiv U_i\mid \equiv U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j$

   g ₂. By g ₁ and p ₁₁, we apply the jurisdiction rule to derive: $S_j\mid \equiv U_i\stackrel{S{K}_{ij}}{\leftrightarrow }{S}_j$

   a ₆. By p ₆ and U _i⊲(ID _i, n ₁, n ₂, T ₂)_K, we apply the message-meaning rule to derive: U _i∣ ≡ S _j∣ ∼ (ID _i, n ₁, n ₂, T ₂)

   a ₇. By p ₂ and a ₉, we apply the fresh conjuncatenation rule and the nonce-verification rule to derive: U _i∣ ≡ S _j∣ ≡ (ID _i, n ₁, n ₂, T ₂)

   a ₈. By a ₇, we apply the belief rule to derive: U _i∣ ≡ S _j∣ ≡ n ₂

   a ₉. By p ₂ and a ₈, we apply the jurisdiction rule to derive: U _i∣ ≡ n ₂

   a ₁₀. By a ₉ and U _i⊲ < n ₁, X _i, h(PW _i∣∣BIO _i) > n ₂, we apply the message-meaning rule to derive: U _i∣ ≡ S _j∣ ∼ (n ₁, X _i, h(PW _i∣∣BIO _i))

   a ₁₁. By a ₁₀ and p ₁, we apply the fresh conjuncatennation rule and the nonce-verification rule to derive: U _i∣ ≡ S _j∣ ≡ (n ₁, X _i, h(PW _i∣∣BIO _i))

   g ₃. By p ₁, p ₃, p ₄, p ₆, a ₁₁ and SK _ji = h(n ₁∣∣n ₂∣∣K∣∣X _i), we apply the fresh conjuncatennation rule and the nonce-verification rule to derive: $U_i\mid \equiv S_j\mid \equiv U_i\stackrel{S{K}_{ji}}{\leftrightarrow }{S}_j$

   g ₄. By g ₃ and p ₁₂, we apply the jurisdiction rule to derive: $U_i\mid \equiv U_i\stackrel{S{K}_{ji}}{\leftrightarrow }{S}_j$

Table 2. BAN logic notations.

A∣ ≡ X	A believes a statement X
$A\stackrel{K}{\leftrightarrow }B$	Share a key K between A and B
#X	X is fresh
A⊲X	A sees X
A ⇒ X	A controls X
A∣ ∼ X	A said X
(X)K	The formula X is hashed by K
< X, Y > K	X and Y are encrypted with the key K
(X, Y)	The formula X or Y is one part of the formula (X, Y)

Informal security analysis

This subsection verifies whether the proposed scheme is secure against various kinds of known attacks. We assume that a malicious adversary 𝓐 has totally supervised the communication channel in login and session key establishment phases. In other words, 𝓐 has the capacity to intercept, insert, delete, refresh or update any information delivered between U _i and S _j [6].

Anonymity

U _i’s identity ID _i is well protected by the shared secret parameter K as a substitute for real ones, 𝓐 can not get users’ real identities. In addition, the unauthorized server cannot get ID _i without knowing K since K is protected by the secret key PSK only known by the authorized server and is not exposed in the open channel. Thus, our scheme provides user anonymity, which can prevent the leakage of private user identities to malicious attackers.

Mutual authentication

In order to authenticate U _i, S _j has to verify validity of the evidence Z _i = h(X _i∣∣n ₁∣∣h(PW _i∣∣H(BIO _i))). The evidence is computed with the common secret parameter K only known U _i and S _j. In other words, (n ₁, ID _i, h(PW _i∣∣H(BIO _i))) are derived from the valid login message {Z _i, M ₁, M ₂, M ₃, T ₁} through K, no one can counterfeit the evidence. In addition, to compute X _i, secret key x is needed but only known by S _j. Moreover, checking h(SK _ij∣∣ID _i∣∣n ₂) to further assist S _j in authenticating U _i because the session key is only known by U _i and S _j. To authenticate S _j, U _i needs to verify whether $M_5\stackrel{?}{=}h(I{D}_i\mid \mid n_1\mid \mid n_2\mid \mid K)$. Because ID _i and K are only known by U _i and S _j, no one can forge a valid {M ₄, M ₅, T ₂} without them. Hence, mutual authentication between U _i and S _j is achieved.

Resist stolen smart card attack

Even if 𝓐 has gathered [25] the information {X _i, Y _i, V _i, h(⋅)} stored in the smart card, 𝓐 cannot figure out the login request message {Z _i, M ₁, M ₂, M ₃, T ₁} without the secret key y. Moreover, 𝓐 cannot get the identity ID _i and PW _i since they are protected by hash functions with the U _i’s biometrics BIO _i. Hence, 𝓐 still cannot succeed if he steals the smart card.

Session key agreement

We provide the session key SK = h(n ₁∣∣n ₂∣∣K∣∣X _i) to protect the message communication between U _i and S _j, where (n ₁, n ₂, K, X _i) are known to anybody but U _i and S _j. In addition, SK is different in each session, 𝓐 has obtained a known session key cannot be used to calculate the value of the next session key.

Resist replay attack

Assume 𝓐 has intercepted all the communication message {Z _i, M ₁, M ₂, M ₃, T ₁, M ₄, M ₅, T ₂, M ₆, T ₃,} and tried to replay them to U _i or S _j to obtain authentication. However, it is impossible to come true since all the authenticated messages imply the timesstamp which is also exposed in public channel. If 𝓐 resends the transmitted messages, the receiver will immediately detect the attack through the authenticated message. Hence, our scheme can withstand replay attack.

Resist stolen verifier and insider attacks

In the registration phase, RC does not directly get the U _i’s password PW _i and biometrics information BIO _i. Hence, 𝓐 performs a stolen verifier attack or insider attack will be hard.

Resist off-line guessing attack

In our proposed scheme, trying to launch an off-line passsword guessing attack with the information stored in the smart card and the eavesdropped messages is trying to solve the input from the given hash value. Since the identity ID _i and the random number N _i are required with the purposed of knowing PW _i, both the secrets are protected by the hash function and known by the user himself.

Formal security analysis of the proposed scheme

This subsection presents the formal security analysis of our scheme and shows that it is secure. For this, we first define the following hash function [26].

Definition 1. A secure one-way hash function h:{0, 1}* → {0, 1}ⁿ, which takes an input as an arbitrary length binary string x ∈ {0,1}* and outputs a binary string h(x) ∈ {0,1}ⁿ and satisfies the following requirements: a. Given y ∈ Y, it is computationally infeasible to find an x ∈ X such that y = h(x); b. Given x ∈ X, it is computationally infeasible to find another x′ ≠ x ∈ X, such that h(x′) = h(x); c. It is computationally infeasible to find a pair (x′, x) ∈ X′ × X, with x′ ≠ x, such that h(x′) = h(x).

Theorem 1. Under the assumption that the one-way hash function h(⋅) closely behaves like an oracle, then our scheme is provably secure against an attacker 𝓐 for protecting user’s personal information including identity ID _i, password PW _i and biometrics BIO _i, sever’s private key x and PSK.

Proof. The formal security proof of our scheme is similar to that as in [27–28]. Using the following oracle to construct 𝓐 who will have the ability to derive the user’s ID _i, password PW _i, biometrics BIO _i, sever’s private key x and PSK.

Reveal: This random oracle will unconditionally output the input x from the given hash value y = h(x).

𝓐 runs the experimental algorithm showed in Table 3, $EX{P}_{HASH,𝓐}^{BAKASSCMSE}$ for our biometrics based authentication and key agreement scheme using smart cards for multi-server environments, say BAKASSCMSE.

Table 3. Algorithm .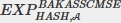

1.	Eavesdrop login message {Z i, M 1, M 2, M 3, T 1}
2.	Call the Reveal oracle. Let $(X_i^{\prime },n_1^{\prime },p^{\prime })\leftarrow Reveal(Z_i)$
3.	Eavesdrop authentication message {M 4, M 5, T 2}
4.	Call the Reveal oracle. Let $(I{D}_i^{\prime },n_1^{\prime \prime },n_2^{\prime },K^{\prime },T_2)\leftarrow Reveal(M_5)$
5.	if $(n_1^{\prime }=n_1^{\prime \prime })$ then
6.	Call the Reveal oracle. Let $(P{W}_i^{\prime },BI{O}_i^{\prime })\leftarrow Reveal(p^{\prime })$
7.	Call the Reveal oracle. Let $(I{D}_i^{\prime },x^{\prime })\leftarrow Reveal(X_i^{\prime })$
8.	Compute $K^{\prime \prime }=M_2\oplus n_1^{\prime }$
9.	if (K′ = K′′) then
10.	Call the Reveal oracle. Let (q′, SID j) ← Reveal(K)
11.	Compute $n_2^{\prime \prime }=M_4\oplus h(n_1^{\prime }\mid \mid X_i\mid \mid h^{\prime }(P{W}_i\mid \mid BI{O}_i))$
12.	if $(n_2^{\prime }=n_2^{\prime \prime })$ then
13.	Call the Reveal oracle. Let (PSK′) ← Reveal(q′)
14.	Accept $I{D}_i^{\prime },P{W}_i^{\prime },BI{O}_i^{\prime }$ as the correct ID i, PW i and BIO i of U i x′ and PSK′ as the correct private key of S j
15.	return 1
16.	else
17.	return 0
18.	end if
19.	else
20.	return 0
21.	end if
22.	else
23.	return 0
24.	end if

Define the success probability for $EX{P}_{HASH,𝓐}^{BAKASSCMSE}$ is $Suc{c}_{HASH,𝓐}^{BAKASSCMSE}=\mid Pr[EX{P}_{HASH,𝓐}^{BAKASSCMSE}=1]-1\mid$ and the advantage function for this experiment then becomes $Ad{v}_{HASH,𝓐}^{BAKASSCMSE}(t,q_R)=ma{x}_{𝓐}\backslash Suc{c}_{HASH,𝓐}^{BAKASSCMSE}$, where the maximum is taken over all 𝓐 with execution time t and the number of queries q _R made to the Reveal oracle. Consider the experiment showed in Table 3 for 𝓐. If 𝓐 has the ability to solve the hash function problem provided in Definition 1, then he can directly derive U _i’s identity ID _i, password PW _i, biometrics BIO _i, and S _j’s private key x and PSK. In this case, 𝓐 will discover the complete connections between U _i and S _j. However, it is a computationally infeasible problem to invert the input from a given hash value, i.e., $Ad{v}_{HASH,𝓐}^{BAKASSCMSE}(t)\le ϵ$, ∀ϵ > 0. Hence, we have $Ad{v}_{HASH,𝓐}^{BAKASSCMSE}(t,q_R)\le ϵ$, since $Ad{v}_{HASH,𝓐}^{BAKASSCMSE}(t,q_R)$ depends on $Ad{v}_{HASH,𝓐}^{BAKASSCMSE}(t)$. As a result, there is no way for 𝓐 to discover the complete connections between U _i and S _j and our scheme is provably secure against an adversary for deriving (ID _i, PW _i, BIO _i, x, PSK).

Performance and functionality analysis

In this section, we compare our scheme with other existing multi-server authenticated schemes ([18–20], [22–23]) regarding security and performance. Table 4 lists the functionality comparisons of our proposed scheme with other related schemes. It can be seen that the proposed scheme achieves all security and functionality requirements and is more secure than other related schemes.

Table 4. Functionality comparison.

	Ours	Mishra et al. [23]	Chuang et al. [22]	Lu et al. [20]	Xue et al. [19]	Li et al. [18]
Provide mutual authentication	Yes	Yes	No	Yes	Yes	Yes
User anonymity	Yes	Yes	Yes	Yes	Yes	Yes
Resist insider attack	Yes	Yes	Yes	Yes	No	Yes
Resist off-line guessing attack	Yes	Yes	Yes	Yes	No	No
Resist stolen smart card attack	Yes	Yes	No	-	Yes	Yes
Resist replay attack	Yes	No	No	No	No	No
Resist verifier attack	Yes	Yes	Yes	-	No	Yes
Session key agreement	Yes	Yes	Yes	Yes	Yes	Yes
Efficient password change phase	Yes	No	No	Yes	No	No

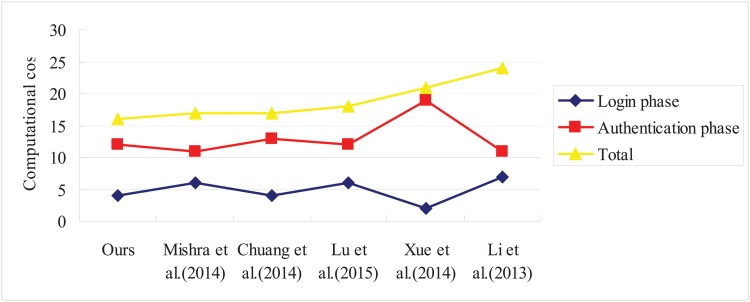
For performance analysis, we compare the computational primitives involved in login and authentication phases of our scheme and other related schemes. To analyze the computational complexity of the schemes, we use hashing operation as the time complexity since XOR operations require very little computations. Fig 2 shows comparison regarding the performance. From this comparison, we can see that our proposed scheme has better efficiency in comparison with other schemes.

Fig 2. Performance comparison.

Conclusion and future work

In this paper, we presented a cryptanalysis of a recently proposed Mishra et al.’scheme and showed that their scheme was susceptible to replay attack while failed to provide an efficient password change phase. An improved scheme is proposed that inherits the merits of Mishra et al.’s scheme and resists different possible attacks. The proposed scheme is practical and efficient compared with other related schemes. Comprehensive security analysis proves that the robustness of our scheme is more secure than other related schemes. Among the open problems to be faced in the near future we can mention the study of specific applications and practical limitations of our scheme for mutual authentication using smart cards based on biometrics and their large-scale implementation in real multi-sever environments.

Data Availability

All relevant data are within the paper.

Funding Statement

This work was supported by National Natural Science Foundation of China (grant no. 61121061), the Beijing Natural Science Foundation (grant no. 4142016), and the Asia Foresight Program under NSFC Grant (grant no. 61411146001). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.