Abstract
Objective To propose a new approach to privacy preserving data selection, which helps the data users access human genomic datasets efficiently without undermining patients’ privacy.
Methods Our idea is to let each data owner publish a set of differentially-private pilot data, on which a data user can test-run arbitrary association-test algorithms, including those not known to the data owner a priori. We developed a suite of new techniques, including a pilot-data generation approach that leverages the linkage disequilibrium in the human genome to preserve both the utility of the data and the privacy of the patients, and a utility evaluation method that helps the user assess the value of the real data from its pilot version with high confidence.
Results We evaluated our approach on real human genomic data using four popular association tests. Our study shows that the proposed approach can help data users make the right choices in most cases.
Conclusions Even though the pilot data cannot be directly used for scientific discovery, it provides a useful indication of which datasets are more likely to be useful to data users, who can therefore approach the appropriate data owners to gain access to the data.
Keywords: Privacy-preserving techniques, Genome-wide association studies, Differential Privacy, Test statistics, Single nucleotide polymorphisms (SNPs), Haplotype blocks
BACKGROUND AND SIGNIFICANCE
With the phenomenal advance in DNA sequencing technologies, the patients’ genome is becoming increasingly affordable to get and is expected to be integrated into healthcare systems. This development also presents an unprecedented opportunity to biomedical researchers, who can potentially leverage clinic data to discover genetic markers for various diseases using genome-wide association studies (GWAS).1 A critical step for GWAS is selection of appropriate datasets, as genetic markers associated with a disease can only be captured from the dataset where the case and control populations have certain structures. Some disease-associated genetic mutations only occur in in some populations,2 for example the presence of Tay–Sachs disease in Ashkenazi Jews,3 and cystic fibrosis in individuals with European ancestry.4 Also, even for the same disease, different ethnic groups may contain different genetic mutations (markers), for example β-thalassemia.5 The appropriate population compositions for discoveries of disease markers are not known a priori, while association tests only work under some circumstances depending on their assumptions. As a result, researchers often have to try out many different case/control datasets in GWAS.
However, most genomic datasets today, particularly those from clinical genome sequencing, are not publicly accessible, due to privacy concerns. Patients’ genomic data contain identifiable markers and can therefore be used to determine the presence of an individual in a dataset, even in the absence of explicit personal information (name, social security number, etc). Prior research shows that such identification can happen even when genomic data has been aggregated.6,7 To protect patients, nearly all the data owners today impose an application and evaluation procedure. At the end of it, an agreement needs to be signed before data use is permitted. This process often takes months to complete,8 which significantly limits the researchers’ capability to conduct timely researches on a large number of datasets. On the other hand, for a vast majority of the datasets that turn out to be less useful to a study, releasing them to the researchers increases the chance of information leaks.
Alternatively, we can simply have the data owners run the association algorithms submitted by the researchers and only release the outcomes of the computation. The problem is that even such outcomes (p values, for example) leak out identifiable information according to a prior study.9 Given the fact that the design of effective association algorithms itself is an active research topic,10,11 it is unrealistic for the owners to come up with optimized protection schemes for each existing and newly invented algorithm; furthermore, many of them are actually proprietary and their inventors are often reluctant to disclose them prematurely. Nor can this data access dilemma be directly addressed by existing security technologies. Cryptographic solutions such as secure multi-party computation do not protect information leaks from the outcomes of a computation. Techniques that directly add noise to published data to achieve differential privacy12–14 may result in unacceptable error rate.
Our solution to the problem is to let each data owner publish a set of pilot data to help data users choose the right datasets for their needs. Such pilot data comes from adding noise to the original genomic data to ensure that individuals’ information is protected to the level of differential privacy. It does not offer any utility guarantee in disease marker discovery. However, a data user can run arbitrary association tests on it, evaluate some indicators, and compare the outcomes with other pilot data to get a very good idea about which datasets are more likely to be useful to their research. We further developed a new technique to help a data user understand how confident the judgments made by their association test on the pilot data can be. We evaluated our approach on real human genomic data, using four popular association tests, from which many variations have been derived and extensively used in GWAS.10 Our study shows that the proposed approach can help data users make the right choices in most cases, performing much better than alternative solutions.
MATERIALS AND METHODS
Differential privacy
Clinical genomic data, even aggregated data, is known to be sensitive. Many statistical approaches have been confirmed on public data,6,7,15–17 which utilize the small signal leaked by each single nucleotide polymorphism's (SNP's) exact allele frequency about an individual to re-identify their presence. To protect an individual's information, we need to limit the impact of their SNP values on aggregated data, making their presence or absence less observable from allele frequencies. This can be achieved by adding noise to published data to ensure that they are differentially private18 (see online supplementary methods). In this case, an individual patient's presence or absence in the dataset will not make a big difference to these frequencies. This helps mitigate the threats of Homer's attack and related re-identification approaches.6,7
Instead of letting a data owner devote substantial computing resource for running users’ tests and returning safe results,14 we let them release only the processed (pilot) data, including perturbed allele frequencies for individual SNP sites and the information regarding the distribution of noise (added to SNPs), which data users can evaluate using any tests, including those unknown to the owner. Note that the release of the noise parameters does not violate differential privacy.18
Pilot data generation
Consider a clinical genomic dataset including the alleles for 
SNPs from 
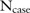case participants and 
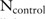control individuals. Denote the major and minor allele counts of these individuals by 
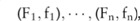, where 
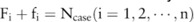. A pilot dataset constructed over the data is represented by a vector 
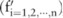, where 
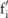is a pseudo-minor allele count randomly drawn from a certain noise distribution imposed on 
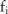, such that any change to a single participant's alleles at these SNP sites does not alter the distribution of the whole vector 
by more than a multiplicative factor of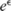 
. Notably, we consider 
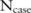to be public, and attempt to protect only the allele counts 
.
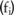SNP-based approach
A straightforward noise-adding approach is to treat each allele count pair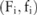 
as a histogram and directly add Laplacian noise there based on 
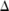and 
(see online supplementary methods).
A problem of this approach is that it essentially breaks down the privacy budget 
into 
pieces and allocates them across all 
SNPs. Naturally, when 
becomes large, the total sensitivity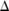 
also grows quickly while the budgets allocated for individual SNPs, which are no more than 
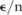, get small. As a result, we need to add a lot of noise to the counts of these SNPs in order to keep the level of information leaks below the overall budget; that is, the variance of the probability distribution from which 
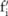is drawn, which is quadratic to 
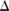, becomes large, making 
very likely to be far away from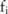 
. This can completely destroy the utility of the data.14
Dimension reduction using haplotypes
Differential privacy is hard to achieve without significantly undermining data utility on a high-dimensional dataset.14 From the point of view of SNP, genomic data have significantly high dimensions (hundreds for one locus) and the problem becomes intractable. Our solution is to leverage the correlation among SNPs, a unique feature of the genome,19 to reduce dimensions (see online supplementary methods).
Here we describe a new noise-adding approach that works on haploblocks haplotype blocks (haploblocks for short) from a partitioning algorithm.20 Consider the sequences with 
SNPs in a GWAS dataset that can be partitioned into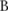 
haploblocks, with lengths of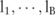 
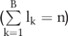. In the 
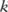th haploblock, there are 
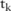haplotypes (
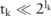). Each haplotype 
has 
major or minor alleles at each SNP site in the case group (so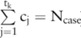 
). Assuming that the SNP site 
is located within a haploblock, and there are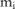 
haplotypes (denoted by 
) in this block containing the minor allele at the SNP site 
, we can derive the minor allele counts on each SNP site 
from the haplotype counts: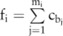 
. For example, assuming there are two haplotypes, 1100 and 0101, whose counts are 3 and 5, respectively, the minor allele counts on these four SNP sites are 3, 8, 0, and 5, respectively.
Our idea here is to add noise to individual haploblocks and release the SNP allele counts computed from perturbed haplotype counts as pilot data (see online supplementary methods). These allele counts are used in an association test for evaluating the utility of the original dataset. Note that here, differential privacy is achieved on haplotype counts and therefore trivially holds on the allele counts derived from the haplotypes.
This approach can be further improved by allocating an unequal budget to each haploblock: a haploblock taking many haplotypes tends to have a more complex distribution and therefore needs to receive less noise to preserve its utility; on the other hand, those with fewer haplotypes can accommodate more noise and still stay useful. Based on this intuition, we allocate larger budgets to more complex blocks and smaller budgets for simpler ones (see online supplementary methods). Note that this will not undermine the privacy protection for the sequence, simply because the total privacy budget, across all SNPs, remains the same.
Utility estimation
A user who intends to run arbitrary association tests (including newly-invented tests that are unknown to the data owner) on pilot datasets has little idea to what extent the results of these tests are reliable over different datasets during a data selection procedure. In this section, we describe our utility estimation technique designed to address these issues.
Preliminaries
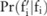(ie, the Laplacian distribution from which noises were drawn) can be released besides pilot data, because this will not undermine the privacy: an adversary cannot infer any information about original data from the public knowledge of the Laplacian mechanism of noise-adding, as well as the amount of added noise determined by the privacy budget. Assume a data user has an association test 
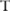: for a given minor allele count 
in a case group on SNP i,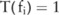 
if the test reports a p value below a threshold (
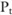), indicating that the SNP is significantly correlated with the disease; otherwise, 
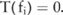. What we want to do is to estimate a confidence level 
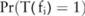for each SNP 
, based on the allele count of that SNP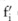 
disclosed from the pilot data and the knowledge of 
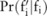(which will be used to identify the distribution of 
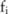given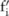 
), and only use SNPs with high confidence for data selection, as compared to the straightforward approach, which is based on the total number of significant SNPs measured from the pilot data. To this end, we need to find a way to estimate the confidence for each SNP, given 
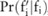, which indicates how the noise is added, and the association test 
.
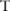Utility estimation for an arbitrary association test
Using the noise-adding technique and parameters, and the pilot data published by the data owner, a data user can infer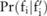 
, the distribution of the raw data, using Bayes’ rule (see online supplementary methods). For example, when the SNP-based noise adding approach is used in which additive Laplacian noise is directly added to allele frequencies, we can derive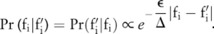 
Based on the pilot allele counts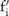 
(
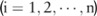), a data user can estimate the utility of the data by first inferring the distribution of their corresponding real counts 
and then computing the distribution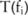 
for their test statistic 
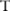. In this way, they can obtain a confidence level for each SNP, even though they cannot directly run the test on real data. The confidence here is the probability that the test on the real allele count of a SNP outputs a p value below a threshold 
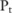for 
, that is,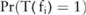 
, which can be computed numerically from the probability distribution of 
(
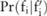). Here, 
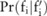is actually a discrete distribution: given a case group of 
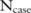participants, the minor allele count can only be one of 
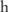values: 
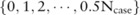, where 
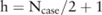; therefore, 
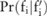becomes a distribution over these values: 
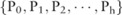, with 
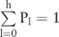. From this distribution, we can compute the confidence for 
as follows: 
.
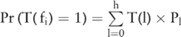This probability distribution can be easily determined if we have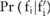 
: the complexity for getting this confidence level is just 
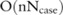for a case dataset with 
SNPs and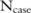 
participants. For the SNP-based approach, 
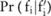can be directly inferred from the Laplacian distribution. For the haploblock-based approach, because 
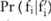becomes complicated, we have to sample the distribution to compute the confidence numerically. The allele frequency at SNP site 
can be computed from the haplotype counts in the haploblock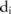 
that contains the SNP site: 
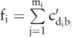, where 
are the haplotypes (totally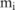 
of them) in this block containing the minor allele at the SNP site 
, and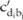 
represents the pilot counts for the haplotype 
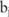in the block 
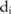, which has been sampled from a Laplacian distribution.
To compute the confidence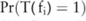 
, we adopt a Monte Carlo sampling algorithm. We first collect a sufficient number (
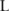) of samples of allele counts, denoted by 
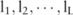(eg,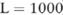 
), from the distribution of raw data 
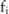, that is, 
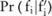, and then estimate the confidence by counting the number of times in which the association test function 
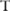reports a p value lower than the confidence threshold
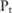among all these 
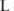samples: 
.
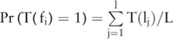This sampling of allele counts follows the procedure as described in the section ‘Dimension reduction using haplotypes’, which samples and normalizes perturbed haplotype counts first, and then computes allele counts from the haplotype, except that the mean of the Laplacian distribution of the haplotype count is now the published haplotype counts (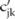
) instead of the original ones (
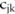). This sampling procedure is repeated 
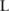times, generating a pool of allele counts for the estimation of the confidence.
RESULTS
We evaluated our techniques over real human genomic datasets, including the Wellcome Trust dataset19 on which we constructed significant SNPs, and real clinical genomic data from Kawasaki disease (KD) patients, and will report the results here.
Setting
The data
To understand how effective our new noise-adding technique and confidence-level based approach in selecting the appropriate datasets are, in comparison with the standard approach that adds noise to SNPs, we put both approaches to the test over a mock dataset (see online supplementary methods) based on a real human genomic dataset that contains 180 SNP sites (within a genomic locus on human chromosome 7) in 1000 individuals. This scale of the test, in terms of the number of SNPs, is in line with a typical validation study of predetermined disease-susceptible SNPs.21,22 The dataset we used is a part of the human genotyping data collected by the Wellcome Trust Case Control Consortium (WTCCC).23 We also test our methods over a real, unmodified clinical genomic dataset on KD,24,25 which is from 690 Caucasian KD cases (genotyped at the University of California, San Diego) with 130 SNPs on human chromosome 20. In our study, all control data was considered to be public, and only the case data was protected.
Specifically, our experiment repeatedly released pilot data for 1000 rounds. In each round, three sets of the pilot data were generated, using the three noise-adding methods (ie, SNP-based, equal-haploblock, unequal-haploblock), for each of the three constructed datasets (containing different numbers of significant SNPs).
Association tests
We utilized four common association tests in our evaluation study, including the χ2 test, G-test, Fisher exact test, and Cochran–Armitage test for trend. Note that even though there are many other association algorithms (including proprietary ones) in the wild, the diversity of the tests considered here makes them good representatives for understanding the efficacy of our technique.
On the allele counts, we ran association tests to detect the SNPs that have an unbalanced distribution between cases and controls, each of which output a binary value indicating the association (1) between the SNP and the disease or not (0). When the p value of the test is below a threshold (eg,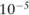 
), the SNP is considered to be strongly associated with the disease. After noise has been added to the allele counts in the case group, the p value of an SNP reported by a statistical test can deviate from its accurate value; however, the binary output of the test function may stay the same. Therefore, the utility of a test function can be evaluated by comparing the outputs of the test over the real dataset and the pilot data, particularly the relations between the numbers of significant SNPs detected under both settings.
Confidence-based selection
After a set of pilot data was generated in each of the 1000 rounds of data release, we then chose the best dataset based on the number of significant SNPs obtained either directly from association tests on the pilot data or estimating the utility of the data at different confidence levels based on the 1000 rounds of releases. This was measured by the number of rounds (among the 1000 rounds of data release) in which the order of the three constructed datasets was correctly identified (‘correct-order’) or the most relevant dataset for a test was successfully picked out (‘best-pick’), through analyzing the pilot data only.
We also measure the confidence levels for the selected dataset: that is, the probability that the one we choose is indeed the most useful one. Specifically, running the utility evaluation method on the three constructed datasets A, B, and C, we find that there are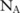 
, 
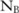, and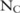 
significant SNPs (
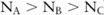) in these datasets, respectively, with their confidence higher than a threshold (eg, 0.95). Based on such confidence, which can be interpreted as the probability that an SNP is indeed significant, we can roughly estimate the confidence of selecting dataset A over B by computing the probability of the dataset having more significant SNPs than B, which can be approximated by a cumulative binomial distribution: 
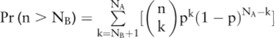, where p is a confidence threshold (eg, 0.95 in the above case).
Performances
Privacy risks
We first evaluated the privacy risks of releasing pilot data. Under the privacy budget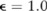 
, we show that the attack based on the optimal log likelihood ratio test,7 the most powerful known re-identification attack (see online supplementary methods), fails to identify any participant in the case group from the pilot data of the mock dataset. Similar results were obtained for the KD dataset (data not shown).
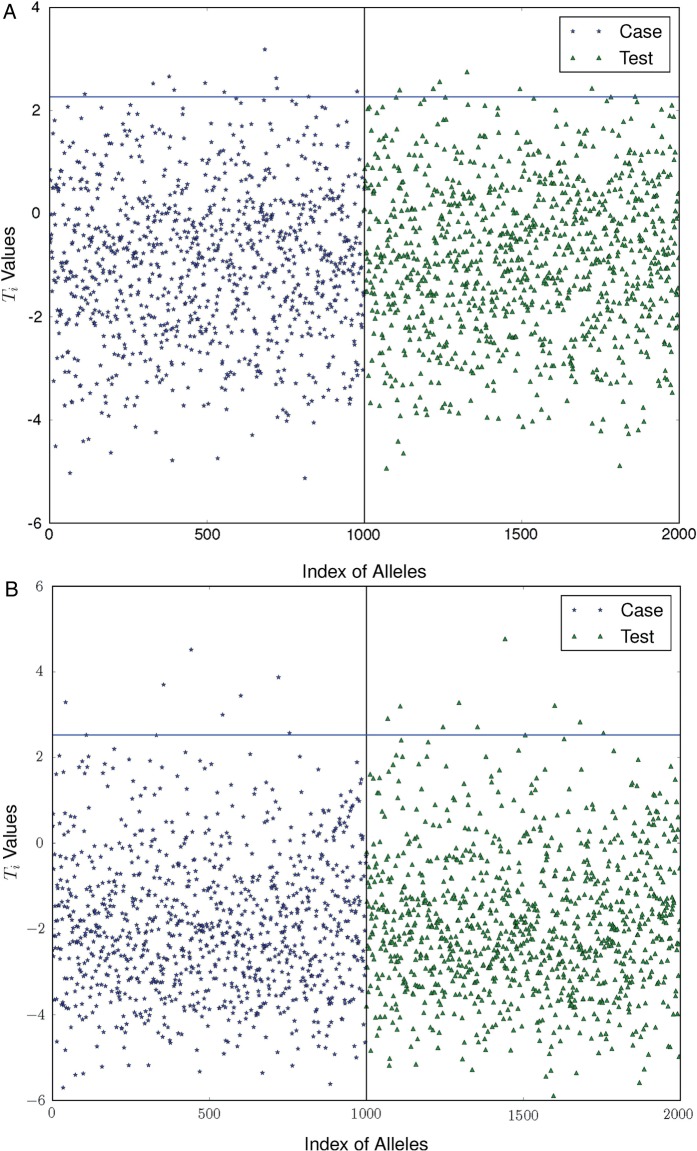
From figure 1, we can see that the distributions of the statistical values are similar between the case and test individuals: 11 and 7 case individuals received higher statistical values than 99% of test individuals (indicating a 1% false positive rate) from the two pilot datasets generated by using equal-haploblock and unequal-haploblock methods, respectively, both comparative to the number (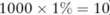
) of test individuals receiving the statistical values above the value. This implies that the optimal log likelihood ratio test cannot re-identify the case individuals from the published pilot datasets when an appropriate privacy budget (
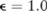) is used.
Figure 1:
The privacy risks of the pilot data built from the first dataset are low in the noised-added data by using the equal (A) and unequal (B) haplotype-based approaches. Each dot represents the test value (Ti) of a specific individual in the case (left) or test (right) group. The solid line indicates the 0.99 confidence level for re-identification of case individuals that are estimated based on the test statistic values of test individuals.
Utility comparison
Table 1 compares the utilities of the pilot data constructed by the three noise-adding techniques (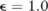
) from the mock dataset, when the χ2 test was in use. Over the three original datasets, the test identified 27, 13, and 9 significant SNPs (p value 
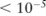), respectively. The utilities after noise-adding were measured by the number of rounds with the ‘correct order’ and those achieving the ‘best pick’ among a total of 1000 experiments. We can see from the table that the utility of the pilot data under the SNP-based noise adding is poor; both results are close to random guesses: 
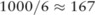for correct orders and 
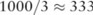for best picks. In contrast, the haploblock-based methods drastically improved the utility of the pilot data: the equal-haploblock approach identified the best dataset in about two-thirds of experiments, and preserved the correct order in about 40% of experiments. The unequal-haploblock approach further improved the utility, keeping the correct order in over half of the experiments and making the right picks in over 80% of the cases. Notably, all these noise-adding approaches introduce many false positive SNPs and therefore cannot be directly used for scientific discovery. However, a data user can still utilize these results to find good case datasets using their own association test, before requesting full access to the raw data by signing a user agreement with relevant data owners.
Table 1:
Selection of pilot datasets generated by using three noise-adding approaches
| Noise adding approaches | SNP-based | Equal-haploblock | Unequal-haploblock |
|---|---|---|---|
| Correct-order | 187 | 390 | 536 |
| Best-pick | 347 | 666 | 822 |
Outcomes of dataset selection
Table 2 shows the outcomes of data selection. For comparison purposes, the results of data selection through direct analysis of the pilot data are listed alongside those of the confidence-based method (with different confidence levels), across the pilot data generated by the three noise-adding approaches (shown in three separate sections). In the table, the first row in each section (whose ‘confidence’ is marked with ‘–’) shows the number of release rounds in which the correct order is preserved or the best dataset is picked out (shown in parentheses) under different association tests when the datasets are selected by directly running those tests on the pilot data; the subsequent rows present the results of the utility estimation based on different confidence levels (0.5, 0.8, 0.9, and 0.95, respectively). In general, using confidence-based utility estimation over the pilot data generated by the unequal-haploblock noising adding gives the best results in all association tests. Particularly, when the confidence threshold of 0.95 is used, in almost all cases (>950 out of 1000 experiments) the order of the three datasets can be correctly determined, compared with the close-to-random-selection results when Laplacian noise is directly added to individual SNPs and datasets are just chosen by running association tests on such data. This indicates that our technique (unequal-haploblock + confidence-based utility estimation) can be practically applied to the pilot release of human genomic data.
Table 2:
Dataset selection based on utility evaluation
| Noise adding | Confidence | Number of successes: correct order (best-pick) |
|||
|---|---|---|---|---|---|
| χ2 | Fisher's | G-test | Trends test | ||
| SNP-based | – | 187 (347) | 196 (387) | 170 (383) | 168 (348) |
| 0.5 | 63 (219) | 96 (283) | 18 (115) | 0 (40) | |
| 0.8 | 135 (320) | 174 (361) | 144 (330) | 153 (333) | |
| 0.9 | 153 (310) | 175 (376) | 143 (343) | 145 (336) | |
| 0.95 | 222 (430) | 215 (461) | 210 (441) | 185 (399) | |
| e-h* | – | 390 (666) | 560 (797) | 436 (683) | 401 (685) |
| 0.5 | 398 (669) | 564 (809) | 429 (713) | 385 (653) | |
| 0.8 | 599 (819) | 792 (942) | 645 (832) | 614 (845) | |
| 0.9 | 751 (899) | 813 (988) | 798 (920) | 770 (924) | |
| 0.95 | 846 (976) | 738 (1000) | 858 (974) | 836 (968) | |
| un-h† | – | 536 (822) | 639 (896) | 532 (833) | 538 (817) |
| 0.5 | 578 (883) | 786 (951) | 612 (897) | 625 (909) | |
| 0.8 | 716 (969) | 913 (971) | 745 (966) | 695 (949) | |
| 0.9 | 852 (981) | 983 (991) | 888 (986) | 837 (995) | |
| 0.95 | 967 (995) | 993 (994) | 980 (1000) | 958 (1000) | |
*Equal-haploblock.
†Unequal-haploblock.
We note that the utility evaluation procedure requires a data user to run the association test many (eg, 1000) times to sample the distribution of real allele frequencies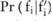 
. This turns out to be quite efficient for all the association tests used in our study: for the χ2 test, G-test, and the test for trends, it takes about 20 s to complete the sampling on a single Xeon CPU at 2.93 GHz, whereas for Fisher's exact test, it takes about 10 min because Fisher's test itself is about 30 times slower than the other tests.
Table 3 shows the number of experiments in which we can select the best dataset based on the pilot data with high confidence (eg, higher than 0.9, 0.95, or 0.99). When the unequal-haploblock noise adding approach is used, in more than 80% of times we can select the best dataset with a very high confidence (≥0.99), and in most other cases (over 90% of times), we can find the best dataset with moderate confidence (≥0.9).
Table 3:
Number of experiments with high confidence of selecting the best dataset
| Confidence level | Noise adding | Number of successes with high confidence |
|||
|---|---|---|---|---|---|
| χ2 | Fisher's | G-test | Trends test | ||
| ≥0.9 | e-h* | 724 | 714 | 778 | 733 |
| un-h† | 918 | 978 | 959 | 909 | |
| ≥0.95 | e-h | 694 | 576 | 743 | 710 |
| un-h | 892 | 971 | 924 | 875 | |
| ≥0.99 | e-h | 611 | 550 | 663 | 635 |
| un-h | 836 | 931 | 883 | 833 | |
*Equal-haploblock.
†Unequal-haploblock.
Table 4 shows the results on the second dataset on KD. Similar to the experiments on the WTCCC data, the haplotype-based approaches outperform the SNP-based approach on preserving the pilot data utility. When a confidence threshold of 0.5 or higher is used, in most cases the best dataset (ie, dataset A) is clearly the right choice. In contrast, when the SNP-based noise-adding approach is used, in more than half of the experiments (even worse than random guesses sometimes), the pilot data misleads the user to choose an inferior dataset. We note that the success rate of dataset selection is slightly lower on the clinical genomic dataset (ie, ∼80−85% as shown in table 4) than that on the WTCCC data (ie, ∼95%, as shown in table 2). This is because the locus studied here (on chromosome 20) shows weaker linkage disequilibrium among SNPs than the locus (on human chromosome 7) used for the study on the WTCCC data, which leads to higher dimensions for the clinical dataset and thus the count perturbation has a larger impact under the same privacy budget. In addition, fewer significant SNPs (4, 1, and 0) exist in these datasets; and a high confidence threshold (eg, 0.95) did not work well compared to a moderate threshold (0.8) on picking up the best dataset.
Table 4:
Data selection on a real clinical genomic dataset
| Noise adding | Confidence | Number of successes: correct order (best-pick) |
|||
|---|---|---|---|---|---|
| χ2 | Fisher's | G-test | Trends test | ||
| SNP-based | – | 145 (323) | 133 (289) | 125 (297) | 133 (296) |
| 0.5 | 0 (0) | 0 (0) | 0 (0) | 0 (0) | |
| 0.8 | 0 (0) | 89 (272) | 0 (0) | 130 (303) | |
| 0.9 | 106 (270) | 151 (307) | 90 (261) | 154 (338) | |
| 0.95 | 184 (371) | 153 (334) | 162 (348) | 126 (300) | |
| e-h* | – | 238 (463) | 211 (454) | 223 (446) | 228 (504) |
| 0.5 | 20 (194) | 275 (574) | 15 (139) | 279 (641) | |
| 0.8 | 188 (616) | 284 (607) | 225 (644) | 413 (682) | |
| 0.9 | 293 (611) | 394 (662) | 322 (640) | 262 (595) | |
| 0.95 | 404 (734) | 401 (686) | 433 (696) | 30 (435) | |
| un-h† | – | 301 (646) | 292 (602) | 291 (616) | 239 (528) |
| 0.5 | 308 (768) | 381 (775) | 304 (748) | 254 (682) | |
| 0.8 | 249 (865) | 299 (772) | 287 (887) | 399 (788) | |
| 0.9 | 332 (815) | 509 (774) | 372 (808) | 164 (622) | |
| 0.95 | 506 (854) | 377 (755) | 575 (863) | 18 (440) | |
*Equal-haploblock.
†Unequal-haploblock.
DISCUSSION
In this paper, we presented a practical approach to the data solicitation problem. Our technique helps biomedical researchers choose the most useful datasets for scientific discovery using their own GWAS algorithms, without direct access to the content of the confidential dataset. It leverages a unique feature of the human genome, linkage equilibrium, to reduce the dimensions of the data. As a result, a much higher utility level than the straightforward SNP-based approach can be maintained, without undermining the differential-privacy protection of the data. Furthermore, we provide data users a utility estimate method so that they can compare the utilities of multiple pilot datasets under their own association test algorithms. Combining these two methods offers an effective way for data users to test their algorithms on the pilot data released by different human genomic projects without going through a complicated user agreement process to get all datasets. Based on our evaluation results, the user can solicit the useful datasets (eg, from different diseases, or from different cohorts of patients with the same disease, or even the genomic data on different loci) for different research purposes.
On the other hand, our attempt only sketches the surface of this privacy-preserving data selection problem. Even for GWAS, we only touched univariate associate tests in which SNPs are examined separately and therefore breaking SNP sequences into haploblocks does not impair their utility. When it comes to more sophisticated multivariate GWAS, the whole haploblocks need to be inspected and tested together. An example is the LASSO method that employs the pairwise correlation in the association test to increase its sensitivity.26 Although it is conceivable that the proposed techniques can be extended to this setting, more studies need to be performed to understand the effectiveness in utility estimation. Also, the results reported here are based on a relatively small locus involving 200 SNP sites. Association tests on this scale have been performed in practice as in validation studies of previously identified disease-susceptible SNPs,21,22 but in most cases of GWAS, researchers need to look at loci involving thousands (or even more) of SNP sites. In this case, even higher dimensions must be tackled to control the level of noise that has to be added to the pilot data, which will be studied in future research.
CONCLUSION
In summary, we designed a novel method to solve the contradiction between the large amount of available human genomic data with valuable and sensitive information and re-identification risk of participants, which gives data owners and researchers a secure and timely way to share human genomic data.
CONTRIBUTORS
XW, XJ, and HT conceived and designed the project. YZ developed the software. YZ, XW, XJ, LOM, and HT analyzed the data and wrote the paper.
FUNDING
This work is partially supported by NHGRI/NIH (grant no: 1R01HG007078-01), NLM (R00LM011392, R21LM012060), NSF (grant no: CNS-1408874), and iDASH (NIH grant U54HL108460).
COMPETING INTERESTS
None.
PROVENANCE AND PEER REVIEW
Not commissioned; externally peer reviewed.
SUPPLEMENTARY MATERIAL
Supplementary material is available online at http://jamia.oxfordjournals.org/.
REFERENCES
- 1.Hardy J, Singleton A. Genomewide association studies and human disease. N Engl J Med 2009;360:1759–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cooper RS, Kaufman JS, Ward R. Race and genomics. N Engl J Med 2003;348:1166–70. [DOI] [PubMed] [Google Scholar]
- 3.Paw B, Tieu P, Kaback M, et al. Frequency of three Hex A mutant alleles among Jewish and non-Jewish carriers identified in a Tay-Sachs screening program. Am J Hum Genet 1990;47:698. [PMC free article] [PubMed] [Google Scholar]
- 4.Tsui LC. Mutations and sequence variations detected in the cystic fibrosis transmembrane conductance regulator (CFTR) gene: a report from the Cystic Fibrosis Genetic Analysis Consortium. Hum Mutat 1992;1:197–203. [DOI] [PubMed] [Google Scholar]
- 5.Thein SL. Genetic insights into the clinical diversity of β thalassaemia. Br J Haematol 2004;124:264–74. [DOI] [PubMed] [Google Scholar]
- 6.Homer N, Szelinger S, Redman M, et al. Resolving individuals contributing trace amounts of DNA to highly complex mixtures using high-density SNP genotyping microarrays. PLoS Genet 2008;4:e1000167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sankararaman S, Obozinski G, Jordan MI, et al. Genomic privacy and limits of individual detection in a pool. Nat Genet 2009;41:965–7. [DOI] [PubMed] [Google Scholar]
- 8. Policy for Sharing of Data Obtained in NIH Supported or Conducted Genome-Wide Association Studies (GWAS). http://grants.nih.gov/grants/guide/notice-files/NOT-OD-07-088.html.
- 9.Wang R, Fuga Li Y, Wang XF, et al. Learning your identity and disease from research papers: information leaks in genome wide association study. Proceedings of the 16th ACM Conference on Computer and Communications Security 2009. ACM. [Google Scholar]
- 10.Bush WS, Moore JH. Genome-wide association studies. PLoS Comput Biol 2012;8:e1002822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Price AL, Zaitlen NA, Reich D, et al. New approaches to population stratification in genome-wide association studies. Nat Rev Genet 2010;11:459–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Irit D, Nissim K. Revealing information while preserving privacy. Proceedings of the Twenty-second ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems 2003. ACM. [Google Scholar]
- 13.Dwork C, McSherry F, Nissim K, et al. Calibrating noise to sensitivity in private data analysis. Theory of Cryptography Conference (TCC) Springer, 2006:265–84. [Google Scholar]
- 14. Privacy preserving GWAS data sharing. Data Mining Workshops (ICDMW), 2011 IEEE 11th International Conference on 2011. IEEE. [Google Scholar]
- 15.Craig DW, Goor RM, Wang Z, et al. Assessing and managing risk when sharing aggregate genetic variant data. Nat Rev Genet 2011;12:730–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kaye J, Heeney C, Hawkins N, et al. Data sharing in genomics—re-shaping scientific practice. Nat Rev Genet 2009;10:331–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang S, Sparks L, Xie H, et al. Subtyping obesity with microarrays: implications for the diagnosis and treatment of obesity. Int J Obes 2009;33:481–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dwork C. Differential privacy. In: Automata, languages and programming. Burkhard M, auf der Heide FM, eds Springer, 2006:1–12. [Google Scholar]
- 19.Gabriel SB, Schaffner SF, Nguyen H, et al. The structure of haplotype blocks in the human genome. Science 2002;296:2225–9. [DOI] [PubMed] [Google Scholar]
- 20.Zhang K, Qin ZS, Liu JS, et al. Haplotype block partitioning and tag SNP selection using genotype data and their applications to association studies. Genome Res 2004;14:908–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gupta V, Khadgawat R, Ng HKT, et al. A Validation Study of Type 2 Diabetes-related Variants of the TCF7L2, HHEX, KCNJ11, and ADIPOQ Genes in one Endogamous Ethnic Group of North India. Ann Hum Genet 2010;74:361–8. [DOI] [PubMed] [Google Scholar]
- 22.Barnett GC, Coles CE, Elliott RM, et al. Independent validation of genes and polymorphisms reported to be associated with radiation toxicity: a prospective analysis study. Lancet Oncol 2012;13:65–77. [DOI] [PubMed] [Google Scholar]
- 23.Burton PR, Clayton DG, Cardon LR, et al. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 2007;447:661–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shimizu C, Jain S, Davila S, et al. Transforming growth factor-β signaling pathway in patients with Kawasaki disease. Circulation 2011;4:16–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Burns JC, Glodé MP. Kawasaki syndrome. Lancet 2004;364:533–44. [DOI] [PubMed] [Google Scholar]
- 26.Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc B 1996;58:267–88. [Google Scholar]