EFFECT ON PERFUSION VALUES OF SAMPLING INTERVAL OF CT PERFUSION ACQUISITIONS IN NEUROENDOCRINE LIVER METASTASES AND NORMAL LIVER

Abstract

Objective

To assess the effects of sampling interval (SI) of CT perfusion acquisitions on CT perfusion values in normal liver and liver metastases from neuroendocrine tumors.

Methods

CT perfusion in 16 patients with neuroendocrine liver metastases were analyzed by distributed parameter modeling to yield tissue blood flow, blood volume, mean transit time, permeability, and hepatic arterial fraction, for tumor and normal liver. CT perfusion values for the reference sampling interval of 0.5s (SI_0.5) were compared with those of SI datasets of 1s, 2s, 3s and 4s, using mixed-effects model analyses.

Results

Increases in SI beyond 1s were associated with significant and increasing departures of CT perfusion parameters from reference values at SI_0.5 (p≤0.0009). CT perfusion values deviated from reference with increasing uncertainty with increasing SIs. Findings for normal liver were concordant.

Conclusion

Increasing SIs beyond 1s yield significantly different CT perfusion parameter values compared to reference values at SI_0.5.

INTRODUCTION

CT perfusion offers a non-invasive means of evaluating tissue perfusion (1). There is particular interest in oncologic imaging, where there is a need for treatment prognostication, prediction and monitoring. There is also interest in developing better understanding of the pathophysiological processes at play in tumor development and treatment (2–5).

A variety of perfusion parameters can be derived from CT perfusion depending on the particular physiological model that is used to describe the behavior of tissue perfusion. One physiological model that is utilized in a commercially available CT perfusion platform is based on the distributed parameter model and deconvolution analysis. A range of tissue perfusion parameters can be derived from the resulting time-attenuation (density) curves acquired from the tissue region(s) of interest ROI(s) and vascular input(s) (6). These CT perfusion parameters include blood flow (BF), blood volume (BV), mean transit time (MTT) and permeability-surface area product (PS), and in the case of liver perfusion, also hepatic arterial fraction (HAF) (7).

One potential limitation of CT perfusion is the radiation burden involved in the acquisition of the CT images for analysis. These CT images are acquired at relatively high temporal sampling frequencies, typically with a temporal sampling interval of 1 second or less, during intravenous (IV) administration of contrast medium. The overall radiation exposure could be reduced if the temporal sampling interval (SI) could be increased (i.e. sampling frequency reduced or “subsampled”). However, before incorporating such strategies into CT perfusion acquisition protocols, it is clearly necessary to gain an understanding of its impact, if any, on resultant perfusion parameter values.

There have only been a few studies which have investigated the effects of temporal sampling intervals on resulting CT perfusion values (8–17). These studies, which have been undertaken with a variety of different physiological and CT perfusion models, in the brain, lung and colorectal tumors, have come to varying conclusions. Some studies have suggested that increasing sampling intervals to 3s are satisfactory, while others have concluded that sampling intervals should not be reduced below 1s (9, 12, 16, 17).

To the best of our knowledge, there have been no studies which have investigated the effect of sampling intervals on CT perfusion parameter values in liver tumors and tissue, and in particular, one implementing the dual vascular (arterial and portal venous) inputs that are relevant to this particular organ (7). In oncology, the liver is frequently involved by primary and secondary tumors, and hence is an organ of interest in treatment evaluations.

The aim of this study was to evaluate the effects of increases in sampling interval of CT data acquisition on resultant CT perfusion parameter values, utilizing the distributed parameter model, in liver tumors and normal liver.

MATERIALS AND METHODS

Patients

This retrospective study was approved by our institutional review board (IRB), with waiver of informed consent and was HIPAA (Health Insurance Portability and Accountability Act) compliant. The patients for the current study were drawn from two earlier IRB approved prospective clinical trials. The two clinical trials were for patients with metastatic neuroendocrine tumors who were treated by bevacizumab (VEGF (vascular endothelial growth factor) inhibitor), everolimus (mTOR (mammalian target of rapamycin) inhibitor), or pazopanib (VEGFR inhibitor), between April 2007 and September 2009, and in which CT perfusion was undertaken before and after initiation of therapy. The trials allowed for prior antineoplastic, but not VEGF- or mTOR-inhibitor, therapies. Novartis and Genentech provided partial funding support for conduct of the study, and everolimus and bevacizumab, respectively. One of the authors (A.G.C.) is employed by General Electric; the other authors, however, have full control of inclusion of data and information submitted for publication.

The patients, inclusion and exclusion criteria, and liver target lesion selections in the current study were identical to our previous study (18). In brief, the patients had participated in two treatment protocols for patients with metastatic neuroendocrine tumors and had CT perfusion of a target lesion in the liver, which was clinically or radiologically considered malignant, based on biopsy of other lesions, widespread metastatic disease and/or increase in size of lesions (biopsy of the selected target lesions were considered excessively invasive). Other inclusion criteria included a) patient age older than 18 years, b) Eastern Cooperative Oncology Group (ECOG) performance status score of 0–2, c) serum creatinine concentration of less than 1.5 mg/dL, and absence of contraindications to CT, e.g., severe allergy to contrast medium and pregnancy. A single target lesion, required to be a well-demarcated, contrast-enhancing solid mass larger than 2.5 cm in longest diameter, had been identified on review of previous imaging studies in each patient by a radiologist (C.S.N. with more than 10 years’ experience in interpreting CT studies). In both clinical studies, CT perfusion had been undertaken before and after one and/or two cycles of therapy according to the specific trial.

CT Perfusion Scanning Technique

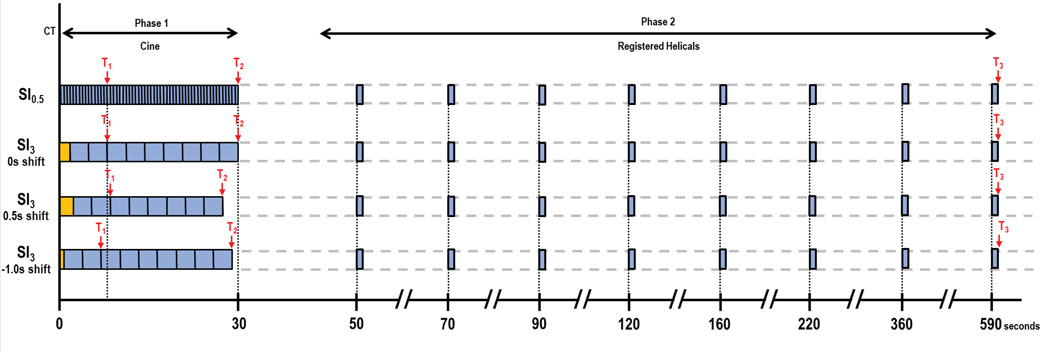
CT perfusion imaging was obtained with a 64-row multidetector CT scanner (VCT, GE Healthcare, Waukesha, WI). The CT perfusion scans were obtained in two phases: Phase 1, continuous (or “cine”) acquisition during a breath-hold, followed by Phase 2, consisting of eight intermittent short breath-hold helical scans, as described previously (18), and outlined in Figure 1. The CT perfusion scans were preceded by localization scans without contrast, to identify the CT coordinates of the target lesion, which consisted of a 20 cm z-axis inspiratory breath-hold helical scan as follows: tube voltage, 120 kV; tube current, 60 mA; slice thickness, 5 mm; slice interval, 5 mm; pitch factor, 0.984:1; speed 39.37; rotation speed, 0.8 second; field of view, 32–40 cm; and matrix, 512 × 512.

FIGURE 1.

Schematic of subsampling and shifting (not to scale)

Top row:	Reference dataset (SI0.5). 0.5s sampling interval in Phase 1, combined with 8 anatomically registered Phase 2 images. T1, pre-enhancement set-point; T2, Post-enhancement set-point; T3, last second phase set-point.
Second row:	Subsampled dataset, T1=t0. Orange block, baseline data-points added to ensure comparability of baseline values across all sampling intervals.
Third row:	Subsampled dataset. Sampling interval same as second row, but T1=shifted forward.
Bottom row:	Subsampled dataset. Sampling interval same as second row, but T1=shifted backward

After the localization image, Phase 1 (“cine”) scans were performed at the mid-point of the target lesion, with a 30-second inspiratory breath-hold and a 4 cm “slice” utilizing the cine mode (8i cine mode, comprising eight 0.5-cm contiguous slices) with the following settings: tube voltage, 120 kV; tube current, 90 mA; rotation speed, 1.0 seconds; field of view, 32–40 cm; matrix, 512 × 512. Data acquisition started 5 seconds after intravenous injection of 50 mL of a nonionic contrast agent (ioversol [Optiray], 320 mg of iodine/mL; Mallinckrodt, Inc., St. Louis, MO) using an automatic injector (MCT/MCT Plus; Medrad, Pittsburgh, PA) and an injection rate of 7 mL/second. This was followed by a normal saline flush with the same parameters. Images were reconstructed every half second and to a thickness of 0.5-cm.

Phase 2 (“delayed”) scans were eight intermittent short inspiratory breath-hold helical scans, each of 3.6s duration, with the following settings: tube voltage, 120 kV; tube current, 90 mA; slice thickness, 5 mm; slice interval, 5 mm; pitch factor, 0.984:1; speed 39.37; rotation speed, 0.8 second. The first Phase 2 helical scan commenced 20 seconds after the end of the Phase 1 acquisition; the subsequent seven helical scans were obtained at increasing intervals (at 70s, 90s, 120s, 160s, 220s, 360s and 590s after commencement of Phase 1, as shown in Figure 1). The images were reconstructed to 0.5cm thickness (as for the Phase 1 images). The estimated effective dose for this CT perfusion protocol was 28 mSv. When required for clinical purposes, the CT perfusion study was followed by routine staging CT scans of chest, abdomen, and/or pelvis, using further intravenous administration of 100 mL of contrast medium.

CT Perfusion analyses

The CT perfusion analyses and liver tumor and normal liver ROIs utilized in the current study were identical to those of our previous study (18). In brief, of the 90 patients enrolled in the two clinical trials above, 47 had CT perfusion studies of metastases in the liver which were reviewed visually by four observers independently to carefully identify those with negligible motion in their acquired Phase 1 CT images (E.F.A., D.H.H. (each with more than 15 years’ experience in CT perfusion), A.G.C. (with more than 10 years’ experience in image registration), and C.S.N.). The absence of motion in the Phase 1 data of the selected patients removed the need to anatomically register the Phase 1 images and thus provided Phase 1 images (for the total duration of Phase 1), which had not undergone any additional post-processing. This removed a potential confounding factor from the subsequent adjustments discussed below. 16 such patients were identified, which formed the cohort for our study.

Before the CT perfusion analyses were undertaken, the Phase 2 images of each patient dataset were anatomically registered with the Phase 1 images using a semi-automated rigid registration algorithm as previously described (19–21). This resulted in CT perfusion datasets consisting of fifty-nine 8-contiguous 0.5cm-slice cine images temporally sampled at 0.5s from the Phase 1 acquisition, together with eight anatomically matched 8-contiguous 0.5cm-slice images from the Phase 2 acquisition. These resultant images formed the reference dataset for our subsequent analyses.

Reference CT perfusion analysis

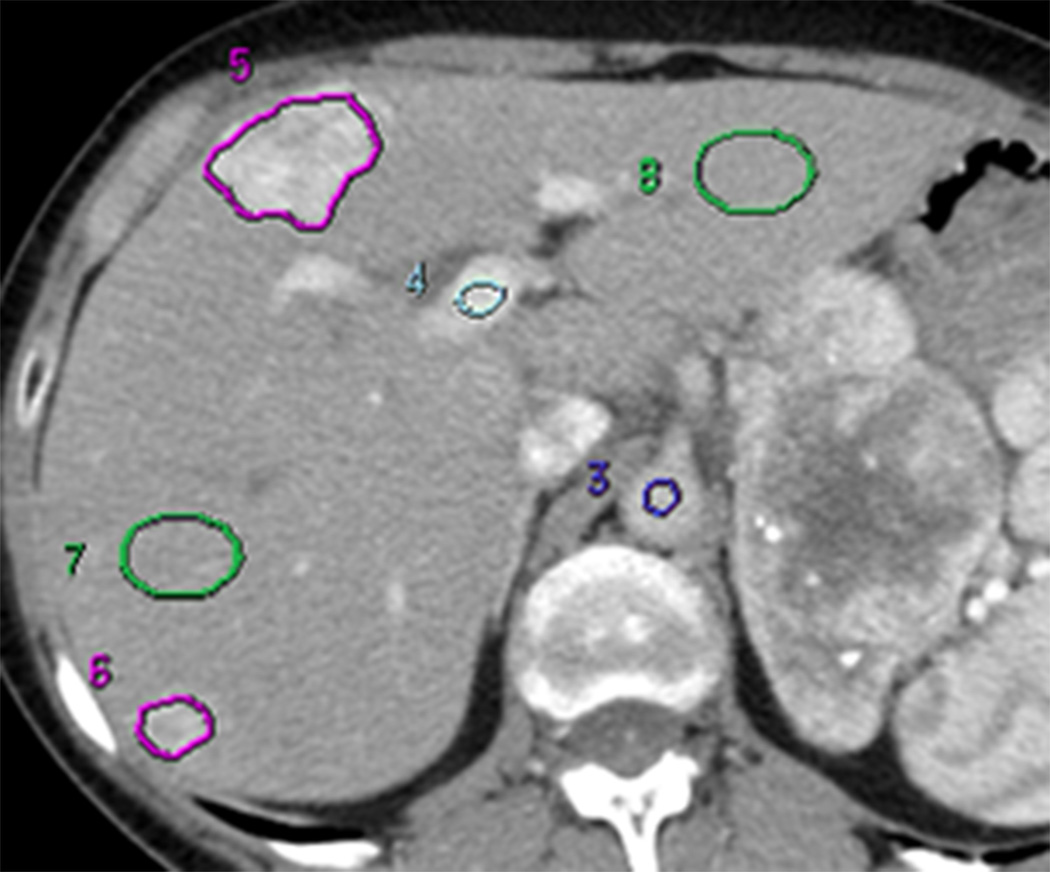
The above reference datasets, utilizing a temporal sampling interval of 0.5s, were analyzed using commercially available CT perfusion software on a workstation (CT Perfusion 4 version 4.3.1, Advantage Workstation 4.4; GE Healthcare, Waukesha, WI). The perfusion software utilizes the distributed parameter model. We utilized the Liver Protocol of the vendor software, which utilizes a dual vascular input algorithm. Regions of interest (ROI) were placed in the abdominal aorta and in the portal vein on the source images to provide these vascular inputs (C.S.N.) (Figure 2a). Three set-points were then determined: a pre-enhancement set-point (T₁=t₀), which corresponded to the time when the arterial signal first began to rise; a post-enhancement set-point (T₂), which corresponded with the final time point of the Phase 1 data acquisition; and the last second phase set-point (T₃), which corresponds to the final Phase 2 image (Figure 1, first row; Figure 2b). Perfusion parametric maps were generated of BF, BV, MTT, PS and HAF values.

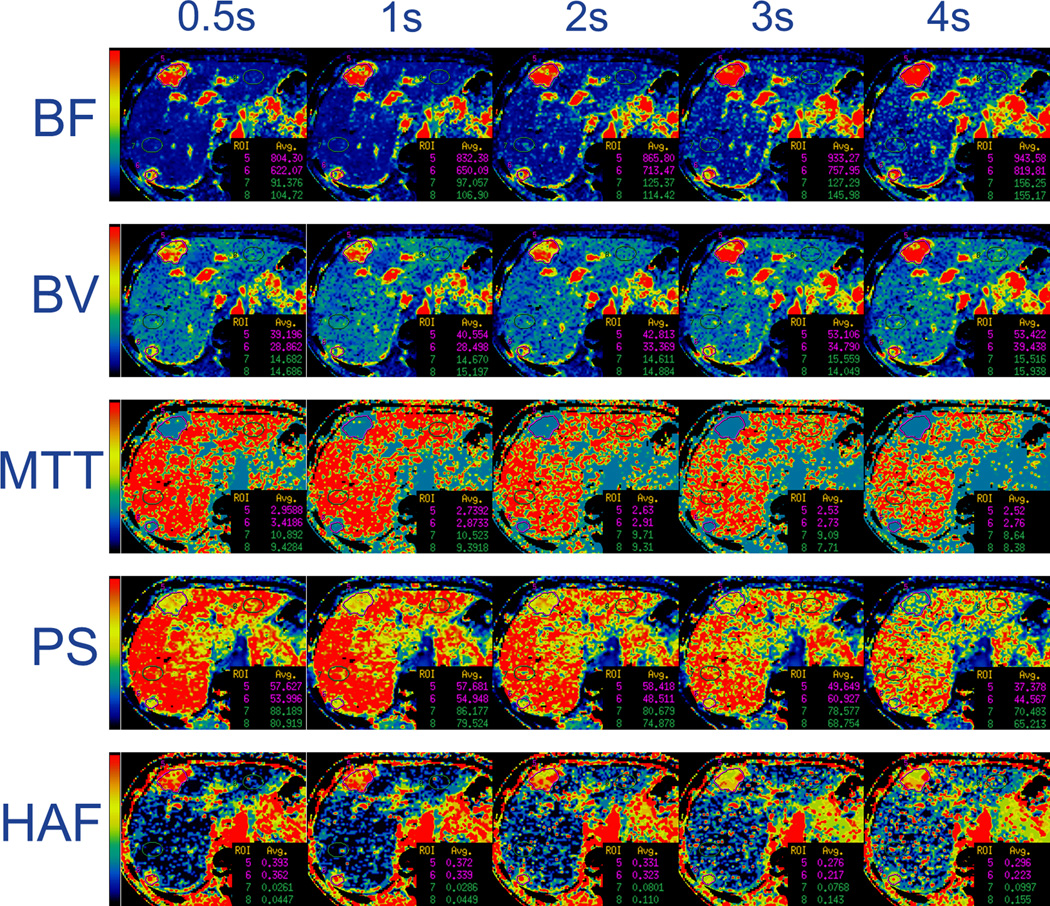
FIGURE 2. 61 year old woman with liver metastases from neuroendocrine tumor.

(a) Image from CT perfusion dataset

(b) Parametric maps for BF, BV, MTT, PS and HAF (by rows, respectively), with illustrative examples of reference (SI_0.5) and sampling intervals of 1s, 2s, 3s and 4s (left to right columns, respectively). Tumor and normal liver ROIs = purple and green outlines, respectively.

BF, in mL/min/100g; BV, in mL/100g; MTT, in seconds; PS, in mL/min/100g; HAF, ratio without units. The color scales are identical for each row of parametric maps. Note, for example in the first row, the increasing BFs of tumor and background normal liver with increasing sampling intervals

Liver tumor and normal liver ROIs

For each of the eight axial slice locations of each dataset, a liver lesion ROI was drawn freehand around the periphery of the target tumor, using an electronic cursor and mouse, with reference to the source cine CT images and perfusion maps, displaying the images at soft tissue windows (width = 350 HU, level = 40 HU) (E.F.A and D.H.H., in consensus). Large vessels and artifacts were avoided. Wherever possible, a second tumor ROI was delineated, provided it fulfilled the same criteria as the primary target lesion and was greater than 1.5 cm in diameter. There were a total of 25 tumor ROIs (all 16 patients had at least one tumor (the target identified at enrollment); and 9 had a second tumor).

Parallel analyses were undertaken for normal liver parenchyma on associated CT slices. Circular or oval ROIs were delineated in normal liver regions (“normality” was based on the absence of visible tumor); these ROIs were as large as possible and placed to avoid vessels and artifacts. We delineated two normal liver ROIs on each of the 8 slices where possible; if possible, separate ROIs were placed in the left and right lobes (C.S.N.). There were 30 separate normal liver tissue ROIs: 12 patients had one ROI each in the right and left lobes; 3 patients had two ROIs in the right lobe (which were averaged); and one patient did not have delineable normal tissue, resulting in 27 lobe-specific normal liver ROIs.

Average tumor BF, BV, MTT, PS and HAF values were obtained from the CT levels in which tumor and normal liver ROIs were drawn, and the mean values across all CT levels were computed. All ROIs were saved within the software to enable identical placement in all the subsequent analyses.

Temporal subsampling and CT perfusion analysis

The above reference datasets for each patient, which were based on a temporal sampling of 0.5 seconds from the Phase 1 component of the acquisition (SI_0.5), were re-analyzed with temporal sampling intervals of 1, 2, 3 and 4 seconds applied to the Phase 1 data. CT perfusion analyses were undertaken of the combined subsampled Phase 1 images and the reference Phase 2 images.

The 1s sampling interval (SI₁) dataset was achieved by selecting alternate images from the original SI_0.5 8-slice Phase 1 cine dataset, and loading these with the corresponding eight anatomically registered 8-slice Phase 2 images into the software. The 2s sampling interval (SI₂) dataset was achieved in a similar fashion by selecting every fourth image from the SI_0.5 Phase 1 data. The 3s sampling interval (SI₃) dataset was achieved by selecting every sixth image from the original SI_0.5 dataset, and similarly for the SI₄ dataset, every eighth image (Figure 1, second row).

It should be noted that the above subsampling manipulations were carried out only on the cine Phase 1 data, and not the eight delayed Phase 2 data; thus, final subsampled datasets consisted of subsampled Phase 1 data combined with unaltered (and anatomically registered) Phase 2 data.

Temporal shifting and CT perfusion analysis

The above analyses were initially undertaken with T₁ fixed at the time-point that had been determined for the reference dataset (T₁ is the time-point when the arterial concentration-time curve is noted to rise, T₁=t₀, abbreviated to T₁=0 in the following).

Subsequently, each subsampled data was analyzed following application of a “temporal shift”. The need to include temporal shifting in consideration of an analysis of subsampling is that there may be uncertainty as to the T₁ time-point of the more sparsely populated subsampled data; indeed, the “true” T₁=0 time-point in the reference 0.5s data may not have been actually acquired or represented in the subsampled data. In order to simulate the reality of such subsampled datasets, we applied both positive and negative temporal shifts relative to the subsampled T₁ time-point. Although in principle one could explore the full range of possible shifts for any subsampled data, we conservatively considered that although analysts may stray on the side of the upslope of the time attenuation curve of the aorta, in practice only small incursions in this direction are likely. Thus, for the SI₁ dataset, temporal shifts in T₁ relative to t₀ of −0.5s and +0.5s were investigated. This was achieved by analyzing the 1s sampling interval dataset a further two times in addition to the T₁=0 described above, each time using a different pre-enhancement set-point time (T₁), which was shifted from the original reference pre-enhancement set-point time at t₀ by −0.5s and +0.5s. For the SI₂ dataset, two further temporal shifts, of −1.0s and −1.5s, were imposed, which resulted in a total of 5 temporal shifts (−1.5s, −1.0s, −0.5s, 0s, +0.5s). For the SI₃ dataset, 7 temporal shifts were investigated (−2.5s, −2.0s, −1.5s, −1.0s, −0.5s, 0s, +0.5s); and for the SI₄ dataset, 9 temporal shifts were investigated (−3.5s, −3.0s, −2.5s, −2.0s, −1.5s, −1.0s, −0.5s, 0s, +0.5s) (Figure 1, third and bottom rows).

Subsampling/shifting inevitably affects the number of available data-points from the reference data prior to T₁, from which baseline vascular and tissue attenuation values for the algorithm are determined; and this is exacerbated by baseline data which may be intrinsically noisy. We therefore ensured that there were the same number of pre-T₁ data-points in the subsampled/shifted datasets as in the 0.5s reference; this was achieved for each patient by randomly choosing images from the acquired images prior to T₁ and inserting the necessary number of these images prior to T₁ to standardize the total number of baseline images for each patient’s subsampled/shifted datasets.

All the resultant subsampled/shifted datasets were analyzed in the CT perfusion software using the same arterial, portal venous and tissue ROIs as for the reference analyses. Mean BF, BV, MTT, PS and HAF values were obtained for each tissue ROI at each CT level (Figure 2b).

Statistical Analysis

Summary statistics for the CT perfusion parameters (BF, BV, MTT, PS and HAF) were obtained by subsampling intervals (1s, 2s, 3s, and 4s). All CT perfusion parameters were transformed to the logarithmic scale prior to analysis to adjust for skewness in the raw data. Statistical analysis was carried out using R 3.0.1 (R Foundation, Vienna, Austria).

Mixed-effects modeling was used to estimate deviations for each subsampling interval from reference for each CT perfusion parameter using software package “lme4”. Observations acquired under the full range of possible pre-enhancement shifts were included in the inference after preliminary analyses revealed that for some CT parameters (notably MTT and PS) the extent of variability associated with temporal shifting was nontrivial. Nested random intercepts were used to account for correlation induced by repeated sampling from multiple temporal shifts within each region and multiple regions within each patient, inducing compound symmetric covariance structure. Each of the 25 tumor and 27 normal regions contributed 3, 5, 7, and 9 deviations from reference at SIs 1s, 2s, 3s, and 4s, respectively, resulting in a minimum of 50 (in tumor at 1s) and up to 216 degrees of freedom (in normal at 4s).

For each CT perfusion parameter, the estimated differences and limits of the corresponding interval estimates (99% confidence intervals for mean) were back-transformed to the raw scale to obtain ratios for each of the 4 sampling intervals. P-values were derived from two-sided tests of the null hypothesis (mean ratio=1) using Wald chi-square. Outliers were evident for BV in normal liver (at 3s and 4s), suggesting deviation from normality. Thus, Wald tests were repeated using the robust estimation method (22). Implementation used software package “robustlmm”. Adjustment for multiple comparisons used Bonferroni’s correction, resulting in a significance threshold of p<0.0125. Piecewise polynomial interpolation was used to evaluate the effect of subsampling over the interval of 0.5s to 4s.

Relative variance contributions attributable to temporal shifting were estimated for each CT perfusion parameter using mixed-effects analysis of variance (ANOVA) with fixed effects to characterize the four subsampling intervals, heteroscedastic error variance by subsampling interval, and nested random effects with structure identical to that used in aforementioned mixed-model.

RESULTS

The study consisted of 16 patients and 25 metastatic lesions to the liver from neuroendocrine tumors. The median age of the patients was 57.5 years (range, 42.0 to 69.7 years), with 6 male (median, 54.1 years (range, 42.0 to 69.7 years)), and 10 female (median, 59.3 years (range, 43.6 to 66.3 years)). There were 25 separate tumor ROIs and 27 lobe-specific (right or left lobe) normal liver ROIs. The median longitudinal diameter of the tumors was 5.1 cm (range, 1.7 – 16.0 cm), and the median size of the tumor ROIs was 1525 mm² (range, 50 – 16000 mm²). The mean size of the normal liver ROIs was 460 mm² (range, 100 – 1300 mm²).

Effect of subsampling

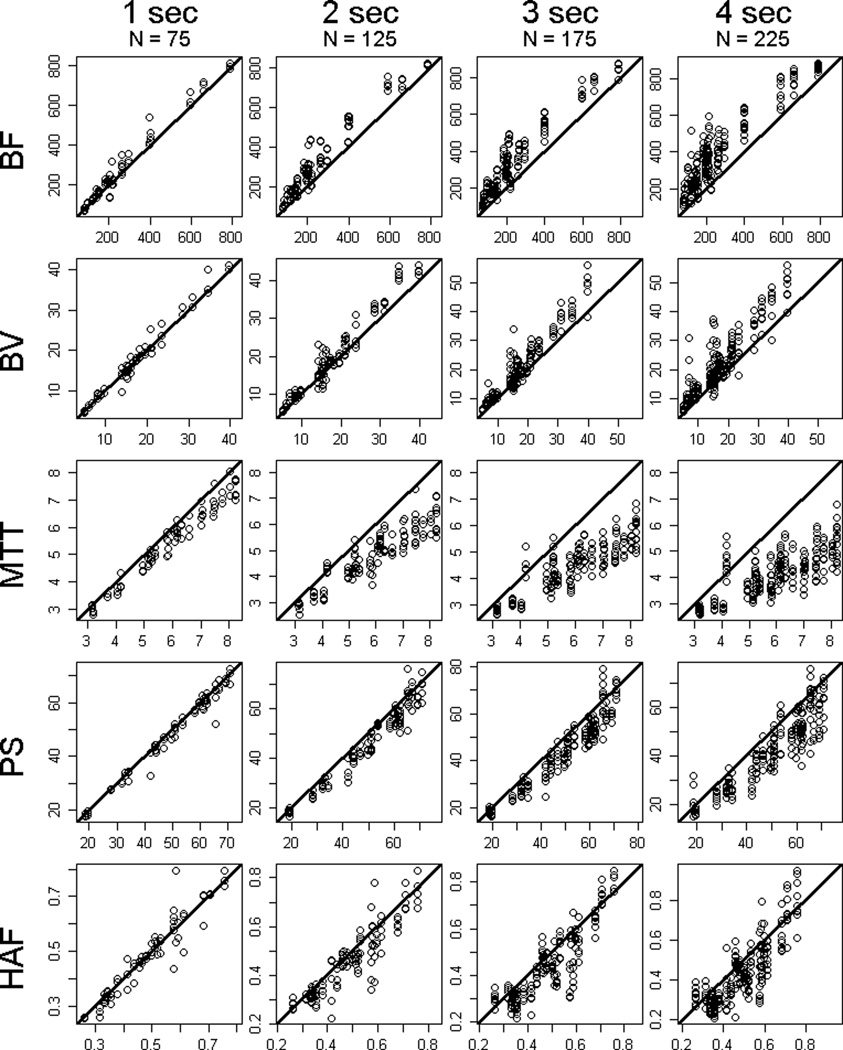
Summary statistics of the raw data by sampling interval, for tumor and normal liver, are presented in Table 1. Scatter-plots of the raw data by sampling intervals compared to reference, for tumor and normal liver, are presented in Figure 3 and 4, respectively.

TABLE 1.

Summary of raw data by CT perfusion parameter and sampling interval.BF, in mL/min/100g; BV, in mL/100g; MTT, in seconds; PS, in mL/min/100g; HAF, ratio without units.

		Tumor		Normal Liver
Parameter	Sampling Interval	Median	Inter-quartile range	Median	Inter-quartile range
BF	0.5s	200.7	139.5 – 263.8	134.1	88.4 – 182.9
	1s	216.5	145.4 – 314.9	140.0	91.0 – 190.9
	2s	268.8	180.1 – 391.6	166.0	114.7 – 236.5
	3s	296.3	206.1 – 437.4	194.4	132.2 – 270.7
	4s	339.7	234.9 – 465.2	222.0	151.7 – 297.0
BV	0.5s	15.5	9.7 – 20.8	14.9	11.8 – 18.7
	1s	15.9	9.5 – 20.6	15.0	11.5 – 17.8
	2s	17.6	10.7 – 22.8	15.8	12.1 – 18.7
	3s	17.7	11.9 – 25.1	16.2	12.1 – 20.0
	4s	19.4	13.8 – 26.9	17.0	12.2 – 21.1
MTT	0.5s	6.08	5.13 – 7.04	9.05	7.73 – 9.49
	1s	5.62	4.63 – 6.51	8.61	7.48 – 9.22
	2s	4.95	4.13 – 5.61	7.41	6.60 – 8.11
	3s	4.60	3.88 – 5.13	6.76	5.83 – 7.36
	4s	4.19	3.50 – 4.71	6.14	5.39 – 6.83
PS	0.5s	51.0	42.0 – 62.0	79.4	69.6 – 87.2
	1s	50.9	37.7 – 60.6	76.8	68.7 – 85.4
	2s	48.5	33.1 – 58.4	70.2	63.3 – 79.8
	3s	47.0	32.7 – 55.3	66.5	57.7 – 74.3
	4s	42.4	31.1 – 52.5	62.7	54.5 – 70.2
HAF	0.5s	0.48	0.36 – 0.58	0.16	0.07 – 0.29
	1s	0.48	0.35 – 0.58	0.18	0.08 – 0.31
	2s	0.46	0.33 – 0.53	0.19	0.11 – 0.31
	3s	0.42	0.32 – 0.54	0.21	0.13 – 0.32
	4s	0.40	0.31 – 0.51	0.24	0.16 – 0.33

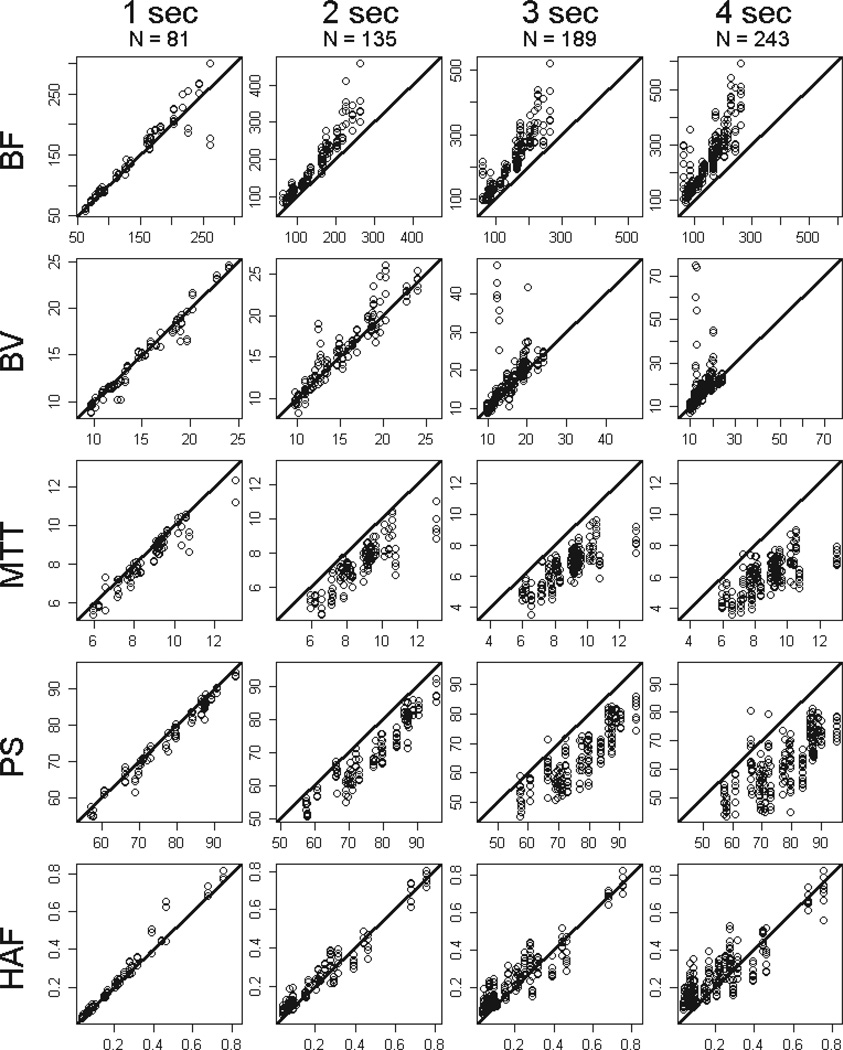
FIGURE 3.

Raw data plots for tumor BF, BV, MTT, PS and HAF (by rows, respectively), by sampling intervals of 1s, 2s, 3s and 4s (left to right columns, respectively). N reflects the number of subsampled differences observed among the 25 tumor regions acquired under the various temporal shifts. y-axis = subsampled parameter value, x-axis = reference parameter value. Solid line = slope of unity.

BF, in mL/min/100g; BV, in mL/100g; MTT, in seconds; PS, in mL/min/100g; HAF, ratio without units.

FIGURE 4.

Raw data plots for normal liver BF, BV, MTT, PS and HAF (by rows, respectively), by sampling intervals of 1s, 2s, 3s and 4s (left to right columns, respectively). N reflects the number of subsampled differences observed among the 27 regions in normal liver acquired under the various temporal shifts.

y-axis = subsampled parameter value, x-axis = reference parameter value. Solid line = slope of unity. BF, in mL/min/100g; BV, in mL/100g; MTT, in seconds; PS, in mL/min/100g; HAF, ratio without units.

The quantitative effects of sampling interval on CT perfusion values compared to reference, for tumor and normal liver, are presented in Table 2 and in Figure 5. The first row of Table 2 indicates, for example, that subsampling at 1s resulted in tumor BF significantly higher than reference, with a mean ratio of 1.06, i.e. higher or over-estimated by 6% (p=0.0009). The data for tumor indicate that subsampling resulted in significantly different CT perfusion values compared to reference values for essentially all our sampling intervals of 1s through 4s, and for essentially all CT perfusion parameters (p≤0.0009); the only exceptions were for BV and HAF at 1s.

TABLE 2.

Summary of ratios of CT perfusion parameters (subsampled/reference) estimated using mixed-effects modeling. Interval and point estimates for the mean ratios (subsampled/reference) are provided for each CT perfusion parameter, in tumor and normal liver. A ratio >1 indicates subsampled results were larger than reference. Boldface values represent statistically significant differences after adjusting for multiple comparisons using Bonferroni’s correction.

		Tumor			Normal Liver
Parameter	Sampling Interval	Mean Ratio	99% Confidence Interval	P-value	Mean Ratio	99% Confidence Interval	P-value
BF	1s	1.06	1.02 – 1.12	0.0009	1.03	0.99 – 1.07	0.10
	2s	1.31	1.22 – 1.40	<0.0001	1.28	1.22 – 1.34	<0.0001
	3s	1.47	1.32 – 1.64	<0.0001	1.46	1.35 – 1.58	<0.0001
	4s	1.63	1.44 – 1.84	<0.0001	1.64	1.47 – 1.82	<0.0001
BV	1s	0.99	0.96 – 1.03	0.71	0.98	0.96 – 1.01	0.10 [0.19*]
	2s	1.10	1.06 – 1.15	<0.0001	1.03	0.99 – 1.07	0.05 [0.13*]
	3s	1.20	1.13 – 1.27	<0.0001	1.09	0.97 – 1.21	0.06 [0.10*]
	4s	1.29	1.18 – 1.41	<0.0001	1.13	0.98 – 1.29	0.03 [0.05*]
MTT	1s	0.93	0.91 – 0.94	<0.0001	0.96	0.94 – 0.98	<0.0001
	2s	0.82	0.78 – 0.87	<0.0001	0.83	0.80 – 0.87	<0.0001
	3s	0.77	0.71 – 0.83	<0.0001	0.76	0.72 – 0.80	<0.0001
	4s	0.71	0.65 – 0.78	<0.0001	0.70	0.65 – 0.75	<0.0001
PS	1s	0.97	0.95 – 0.99	0.0002	0.98	0.97 – 0.99	0.0002
	2s	0.94	0.91 – 0.96	<0.0001	0.91	0.89 – 0.93	<0.0001
	3s	0.90	0.87 – 0.94	<0.0001	0.85	0.82 – 0.88	<0.0001
	4s	0.86	0.82 – 0.91	<0.0001	0.80	0.76 – 0.84	<0.0001
HAF	1s	0.99	0.96 – 1.02	0.52	1.09	1.04 – 1.13	<0.0001
	2s	0.93	0.89 – 0.97	<0.0001	1.23	1.05 – 1.43	0.0012
	3s	0.89	0.82 – 0.96	0.0003	1.34	1.05 – 1.72	0.0028
	4s	0.87	0.80 – 0.94	<0.0001	1.49	1.10 – 2.03	0.0011

^*p-values resulting from robust estimation (as described in Statistical analysis).

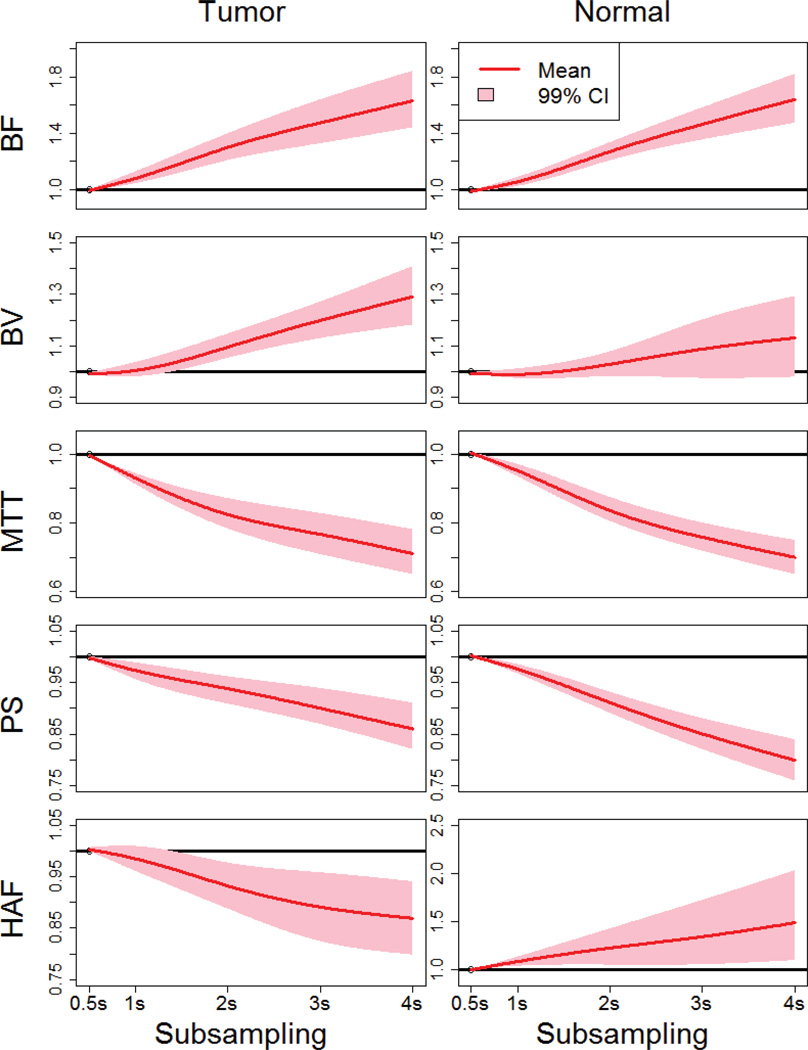
FIGURE 5.

Estimated ratios for subsampled/reference values for the CT perfusion parameters, for tumor and normal liver.

The estimated means and 99% confidence intervals (CI) are provided as functions of subsampling. y-axes = ratios of subsampled values to values at SI_0.5

Note: pink regions that do not encompass the horizontal black line of unity are significantly different.

BF values for tumor were over-estimated increasingly compared to reference by 6%, 31%, 47% and 63%, with increasing sampling intervals from 1s, 2s, 3s and 4s, respectively (p≤0.0009). BV values were also over-estimated, by 10%, 20% and 29%, with increasing sampling intervals from 2s, 3s and 4s, respectively (p<0.0001). In comparison, MTT and PS values were under-estimated increasingly compared to reference by 7%, 18%, 23% and 29% (p<0.0001), and 3%, 6%, 10% and 14% (p≤0.0002), with increasing sampling intervals from 1s, 2s, 3s and 4s, respectively. HAF values were under-estimated, by 7%, 11%, and 13%, with increasing sampling intervals from 2s, 3s and 4s, respectively (p≤0.0003). The widths of the confidence intervals for these parameter values increased with increasing sampling intervals, reflecting increasing uncertainty in the estimations of the parameter values.

The results for normal liver showed similar trends as for tumor, except that significant differences were not detected with BV. Also, HAFs were over-estimated with subsampling for normal liver, as compared to under-estimated for tumor; nevertheless, as for other parameters, the trend of increasing departures from reference with increasing sampling intervals were still evident (Table 2, Figure 5).

Relative contributions of shifting and sampling intervals

Variation due to temporal shifting was smaller than variation attributable to subsampling interval, but varied in magnitude by CT parameter. In tumor, temporal shifting accounted for 18% of the total variance of MTT and 6–11% of total variance for BF, BV, PS, and HAF. Similarly, in normal liver, 6–12% of the total variance was attributable to temporal shifting.

DISCUSSION

Our results demonstrate that subsampling, or increases in sampling interval, greater than 1s yield CT perfusion parameter values that deviate significantly from reference values acquired with 0.5s sampling. And furthermore, departures from reference values increased with increasing sampling intervals. For example, BF values for tumor were over-estimated increasingly from 6% to 63%, and PS values were under-estimated increasingly from 3% to 14%, with increases in sampling intervals from 1s to 4s, respectively. At 4s sampling intervals, BV was over-estimated by 29%, and HAF and MTT under-estimated by 13% and 29%, respectively. The overall results for tumor and normal liver parenchyma were similar, suggesting that the findings are robust.

There have been relatively few previous studies that have investigated the effects of subsampling using the distributed parameter physiological model and these have come to differing views. In a study of patients with cerebrovascular disease, one study suggested that subsampling resulted in significant differences for BF, BV and MTT, and recommended that sampling intervals should not depart from their reference of 0.5s (9). In comparison, two studies of tumors in abdomino-pelvic locations, have suggested that 2s sampling intervals might be satisfactory. One study with colorectal tumors reported no significant trends in BV and PS with subsampling up to 4s, but found significant over-estimation of BF and under-estimation of MTT at 3s; notably, these conclusions were in relation to a reference of 1s (10). Interestingly, the other similar study of body tumors, investigating rectal and retroperitoneal tumors, reported that BF values were under-estimated, and MTT values were over-estimated with subsampling (14), which is at some variance from the current study and that of Goh et al. (10). Two recent studies of patients with lung tumors have also come to opposing views (15, 16).

Comparison with the above studies is extremely difficult, not just because of differences in organ system/tissue, acquisition techniques, and CT perfusion software versions, but importantly, in their methods of statistical analyses. For example, t-tests, Wilcoxon and analysis of variance were used in three of the studies (9, 10, 14, 15), all of which fail to account for repeated measures and thus to properly differentiate between sources of variability attributable to the effect of subsampling and heterogeneity between patients. Another study based their conclusions on an assessment of Pearson’s correlation coefficients (14), which simply tests the proximity of data to a straight line, with no consideration of the slope of that line or of potential correlations of measurements from the same patient. Other studies using physiological models other than the distributed parameter model have also reached differing conclusions regarding subsampling (8, 11–13, 17, 23).

The current and a previous study (16) have incorporated consideration of shifts in T₁ in their evaluations of subsampling, unlike other studies which have limited their analyses to a fixed T₁=0. This is an important consideration since an actual acquisition employing subsampling may not include or capture the T₁=0 time-point in its dataset. Our variance component analysis showed that shifting contributed up to 18% of the total variation. Thus, neglecting shifting will likely under-estimate the impact of subsampling on CT perfusion values. Shifting in T₁ alone inevitably affects MTT, since the vascular input “start” times are necessarily displaced. Reductions in sampling interval, in addition to shifts in T₁, affect the profile of the vascular input curves, typically reducing the peak heights and areas under the curve; these apparent reductions in vascular input functions probably contribute to the apparent over-estimations in tissue BF and BV with subsampling.

In this work on liver tissues, it has been possible to derive HAF since our CT perfusion analysis included incorporation of the dual vascular input which more correctly represents the perfusion of hepatic tissues than single (arterial) supply, as utilized in some other liver-related CT perfusion studies (24). Estimates of HAF for normal liver were approximately 20%, which is as expected; for tumor they were substantially higher (approximately 50%), as might be expected for a highly vascular tumor, such as carcinoid. BF, BV, MTT and PS showed similar trends with subsampling for tumor and normal liver; in contrast, HAF showed differing trends when comparing tumor and normal liver, which may be a reflection of the complex interaction of arterial and portal flow with subsampling.

Our acquisition protocol extended over 590 seconds, which we have previously shown allows for reliable estimations of CT perfusion values (18). The current analysis suggests that subsampling has more profound effects on some parameters than others: for example, BF values departed from reference by 6%, 31%, 47% and 63% with increasing sampling intervals from 1s to 4s, respectively; while departures in PS values were smaller at 3%, 6%, 10% and 14%, respectively. This might be expected from a modeling perspective, since PS relies more heavily on the more delayed parts of the data acquisition (Phase 2), which in our analysis was not altered. In contrast, BF is heavily influenced by the initial portions of the data acquisition, which was inevitably much more affected by our systematic adjustments with sampling intervals and shifting within Phase 1 of our dataset. Of note, our observed effects of subsampling, which were found to be significant for essentially all CT perfusion parameters, were the result of sampling manipulations only within the first 30 seconds of acquired data.

Subsampling offers the possibility of reducing radiation exposure. For example, with the protocol employed, subsampling at 1s, 2s, 3s, or 4s would reduce radiation exposures by approximately 30%, 44%, 49% and 52%, respectively. It also gives the opportunity for more extended tissue coverage by allowing the incorporation of CT table z-axis “shuttling” or “toggling” into CT perfusion acquisitions. Our finding that subsampling significantly affects CT perfusion parameter values suggests that some calibration for such studies will be required. It will also be recognized that subsampling introduced more non-systematic variation into the estimation of CT perfusion parameter values, and that uncertainty increased with increasing sampling intervals; this increases variability and reduces scan-rescan reproducibility, which in turn impacts on the powering of clinical trials.

We recognize and acknowledge several limitations in our study. We had a relatively small number of patients; however, it should be noted that correct modelling of the effects of subsampling utilized information acquired from all 25 tumor and 27 normal liver regions and up to 9 temporal shifts, which contributed up to 216 degrees of freedom for the chi-squared tests. Our study was limited only to liver tissue and one specific tumor type. It did, however, incorporate dual vascular inputs, and our results for normal liver parenchyma paralleled our findings for tumor, suggesting that the findings are robust. Our cohort of 16 CT perfusion studies was not restricted to simply pre- or post-treatment evaluations, which could be considered a limitation; however, a heterogenous treatment population could be considered advantageous, since the object of this study was essentially a technical evaluation, in which therapeutic interventions would not be anticipated to be relevant. We recognize that what we have considered “normal liver parenchyma” may not have been entirely normal, since our patients had an underlying malignancy, evidence of at least macroscopic focal liver disease and possible prior exposure to systemic therapies. Further exploration with other tumors and tissues need to be considered. Comparisons across other CT perfusion platforms and implementing different physiological modeling were beyond the scope of this work and would require further investigation.

Our analysis was inevitably constrained by our specific CT perfusion acquisition protocol, which did not contain fully and highly sampled temporal data throughout the acquisition. Such an ideal dataset would have required excessive and unacceptably high radiation burdens to acquire.

In conclusion, our study of subsampling in the context of the distributed parameter model suggests that sampling intervals beyond 1s result in significant differences in CT perfusion parameter values in liver tissues when compared to 0.5s reference. Although subsampling is an attractive proposition, resultant CT perfusion values are more variable and can be significantly different from reference values by up to 63% or more. Its implementation may be partially mitigated if correlation tables could be developed and were available.