Regression to the Mean and Changes in Risk Behavior following Study Enrollment in a Cohort of US Women at Risk for HIV

Abstract

Purpose

Reductions in risk behaviors are common following enrollment in HIV prevention studies. We develop methods to quantify the proportion of change in risk behaviors that can be attributed to regression to the mean versus study participation and other factors.

Methods

A novel model that incorporates both regression to the mean and study participation effects is developed for binary measures. The model is used to estimate the proportion of change in the prevalence of “unprotected sex in the past 6 months” that can be attributed to study participation versus regression to the mean in a longitudinal cohort of women at risk for HIV infection who were recruited from ten US communities with high rates of HIV and poverty. HIV risk behaviors were evaluated using audio computer-assisted self-interviews at baseline and every 6 months for up to 12 months.

Results

The prevalence of “unprotected sex in the past 6 months” declined from 96% at baseline to 77% at 12 months. However, this change could be almost completely explained by regression to the mean.

Conclusions

Analyses that examine changes over time in cohorts selected for high or low risk behaviors should account for regression to the mean effects.

Introduction

In HIV and STI prevention trials reported risk behaviors are often observed to decline over the course of the study, even in the control group^1,2. Such declines may be attributed to a number of factors, including counseling messages and services provided by the study, a general increase in feelings of self-worth due to study participation, healthy survivor effects, aging of the participants, and/or the Hawthorne effect³. However, an important alternative explanation that should be considered, and can be quantified, is the phenomenon of regression to the mean⁴.

Regression to the mean (RTM) is a statistical phenomenon that occurs when study participants are selected for extreme values of characteristics or behaviors that vary over time. RTM predicts that subsequent measures of those characteristics or behaviors will, on average, be closer to the underlying population mean than the original values. For example, if subjects are selected such that 100% of participants have a particular behavior at enrollment, then (assuming the behavior varies over time) RTM predicts that the prevalence of that behavior will decline as the study progresses, even in the absence of any intervention. However, it is not clear how much of a decline might be expected due to RTM, and how rapidly the decline might occur.

RTM has been studied extensively, usually in the context of continuous measures (e.g. blood pressure⁵, heights of fathers and sons⁶, and medical costs⁷) or count data (sex acts, sex partners⁸). However, little has been written about RTM in the context of binary measures (e.g. unprotected sex in the past 6 months) even though such measures are common in epidemiologic and behavioral studies. In this manuscript we develop methods for estimating the expected change in the prevalence of a selected binary behavior due to RTM. We apply these methods to data from the HIV Prevention Trials Network Women's HIV SeroIncidence Study HPTN 064⁹ to quantify the amount of change in a key risk behavior – unprotected sex in the past 6 months – that is associated with study participation versus RTM.

Methods

Study Design

HPTN 064 was a multi-site, longitudinal cohort study designed to estimate HIV incidence among women at elevated risk for HIV infection. Details regarding the study design have been previously described⁹. In brief, eligible women were enrolled between May 2009 and July 2010 from 10 urban and periurban communities in six geographic areas of the US (Atlanta, GA; Baltimore, MD; New York City, NY; Newark, NJ; Raleigh-Durham, NC; Washington, DC) using venue-based recruitment. Specifically, women were recruited during randomly selected venue-time intervals within each community. Women entering the venue during the recruitment interval were sequentially or systematically (e.g. every 4^th woman) approached for screening. Women who met inclusion criteria (see below) and agreed to enroll were followed at 6 month intervals for either 6 or 12 months, depending on date of enrollment. All participants completed HIV rapid testing and audio computer-assisted self-interviews (ACASI) at baseline and each follow-up visit. The ACASI included questions regarding sexual behavior as well as socioeconomic factors, food insecurity, mental health, history of sexually transmitted infections (STIs), domestic violence, health perceptions, substance use, and social support.

Inclusion Criteria and Definitions

Eligible individuals were 18 to 44 years of age, self-identified as a woman (inclusive of transgender women) and reported, during a face-to-face screening interview, at least one episode of unprotected vaginal and/or anal sex with a man in the 6 months before enrollment (based on the screening question “When did you last have unprotected sex with a man?”, where sex was defined as vaginal or anal sex). Two additional inclusion criteria were that individuals:

1. Reported one or more of the following in the past 6 months, except for incarceration which could have occurred within the past 5 years: a) illicit injection and/or non-injection drug use (e.g. heroin, cocaine, crack cocaine, methamphetamine, and/or use of prescription drugs apart from those prescribed by a licensed provider), b) alcohol dependence (defined as CAGE Score ≥2)¹⁰, c) binge drinking, defined as consuming ≥4 drinks at one time, d) incarceration (jail and/or prison ≥24 hours), e) self-reported history of sexually transmitted infections (STIs): gonorrhea, chlamydia, or syphilis, f) exchange of sex for commodities (e.g., drugs, money, shelter), g) a male sexual partner with reported history of any of the following: injection or non-injection drug use, STIs, HIV diagnosis, history of binge drinking (consuming ≥5 drinks at one time), alcohol dependence, (CAGE Score ≥2), or incarceration (jail and/or prison ≥24 hours within past 5 years).

2. Reside in census tracts (except Bronx and Harlem where zip codes were used) that ranked in the top 30^th percentile of HIV prevalence and where >25% of inhabitants lived below the US federal poverty threshold, as defined by the 2008 United States Census Bureau^11,12.

Exclusion criteria included self-reported history of a previous positive HIV test, current HIV prevention trial enrollment, current/past participation in an HIV vaccine trial, or anticipated absence for >2 consecutive months during the follow-up period.

Outcomes

The outcome of this analysis is unprotected vaginal or anal sex with any of the three most recent male partners during the past 6 months. This measure is based on the woman's ACASI report of her behavior with each of her three most recent partners and was consistently collected at baseline and each follow-up visit. Responses to the question “About how many times did you and this partner have vaginal (anal) sex without using a condom in the last 6 months?” for up to three partners were combined to create a measure that was coded as 1 if the woman reported unprotected sex with any partner, 0 if she reported no partners or only protected sex with all partners, and missing if she did not complete the follow-up visit or (rarely) if she indicated sex with partners but did not indicate whether a condom was used.

Due to the inclusion criteria, we expected that all enrolled women would respond “yes” to the unprotected sex questions on the ACASI at baseline. However, as noted above, a woman was eligible for participation if she indicated during screening that she had had unprotected sex with any man during the past 6 months, whereas the ACASI asked about the three most recent partners only. Thus, there are occasional discrepancies between the screening responses and the baseline ACASI responses. We detail these inconsistencies in the Results section.

Statistical Methods

Women who screened for the HPTN 064 study and met all the study eligibility criteria, except they may not have had unprotected sex in the past 6 months, will be referred to as the “unselected” population. We have data on the unprotected sex outcome at the screening and/or baseline visit on all participants in the unselected population (subject to the discrepancies mentioned above, screening and baseline results are equivalent for enrolled women). We have data at 6 and 12 months (depending on retention) only on participants who met all eligibility criteria, including the unprotected sex criterion, and enrolled. This subset of participants represents the “selected” population.

Define X_i =1 if a participant reports unprotected sex (with a man, in the past 6 months) at visit i (i = 0, 1, 2 corresponding to the baseline, 6 month and 12 month visits, respectively) and 0 otherwise. The following logistic regression model is used to capture the association between repeated measurements of X over time and the possibility that participation in a research study may affect X,

$$\text{logit}\left(Pr\left({\mathrm{X}}_{\mathrm{i}}=1\right)\right)={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1{\mathrm{X}}_{\mathrm{i}-1}+{\mathrm{\alpha }}_2{\mathrm{E}}_{\mathrm{i}}$$ (1)

where E_i is 1 if the participant was participating in the study during the preceding 6 months (the period during which X_i was measured), and 0 otherwise. In the present analysis, E_i is 0 only at the baseline visit (i = 0). Standard maximum likelihood methods are used for parameter estimation for model (1) (see appendix).

In model (1), the log odds ratio of unprotected sex at the current visit increases by α₁ if the participant reported unprotected sex at the previous visit, compared to if she did not report unprotected sex at the previous visit. α₁ plays a role similar to correlation in studies of continuous measures. Small values of α₁ (near 0) lead to rapid regression to the mean (typically characterized by a steep decline in behavior from enrollment to the first followup visit); large values imply that complete regression will take longer. Based on model (1) we may derive the probability of unprotected sex in the unselected population, which we denote as P_all (see appendix for derivation). In the absence of an intervention or study effect, P_all represents the prevalence that the selected population will regress towards following enrollment. For example, denote the baseline prevalence in the selected population by P_selected (e.g. if the behavior is required for eligibility then P_selected = 1). We expect to observe a change in prevalence from Pselected to P_all over time simply due to RTM.

The parameter α₂ in model (1) quantifies the effect of study participation on the prevalence of the behavior. If α₂ = 0, then there is no study effect while negative/positive values of α₂ imply that the prevalence of the behavior will decline/increase, beyond that predicted by regression to the mean, following study participation. The (long-term) on-study prevalence of the behavior may also be derived from model (1) and is denoted by P_onstudy (see appendix for derivation).

The difference between P_all and P_onstudy quantifies the “study effect” and the ratio

$$\frac{{\mathrm{P}}_{\text{all}}-{\mathrm{P}}_{\text{onstudy}}}{{\mathrm{P}}_{\text{selected}}-{\mathrm{P}}_{\text{onstudy}}}$$ (2)

quantifies the proportion of the observed change in behavior from baseline that is associated with study participation. Negative values of (2) imply that the change in prevalence of the behavior over the course of the study is less than would be expected due to RTM. For instance, if we have selected for a high risk behavior, then a negative value for (2) implies that the prevalence of the behavior has not declined over the course of the study as much as predicted by RTM; effectively, the study is associated with an increase in the prevalence of the behavior.

Estimation in model (1) depends critically on having complete information on the prevalence of the behavior, X, in the unselected population. In the HPTN 064 study, this information was collected during screening for the key selection variable “unprotected sex with a male in the past 6 months” but was not available for other behaviors or characteristics (e.g. substance use, food insecurity, foregone medical care) that may be of interest.

Results

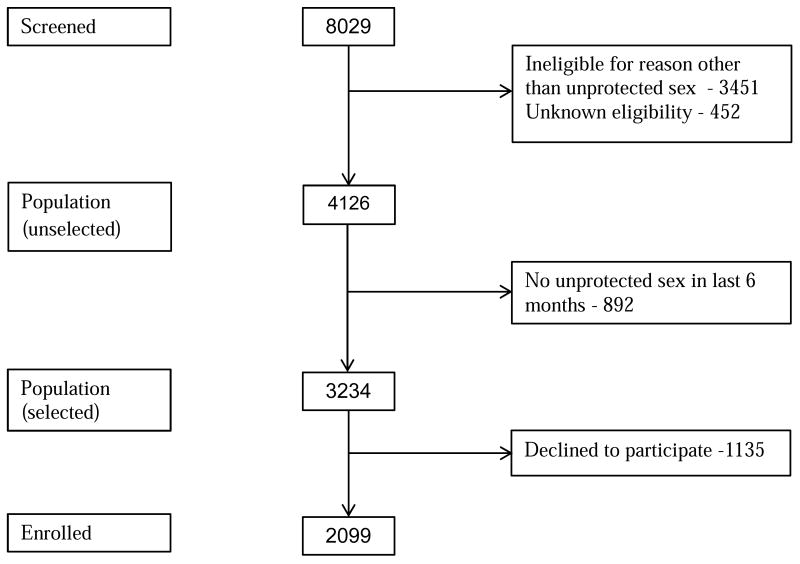
A total of 8029 women were screened for HPTN 064 (figure 1). Of those, 4126 women satisfied all eligibility criteria, aside from the requirement of unprotected sex in the last 6 months. Thus, these 4126 women represent (a sample from) the unselected population. At screening, a total of 3234 of these women (78.4%) reported unprotected sex with a male during the past 6 months (screened “positive”) and 2099 of these (64.9%) chose to participate in HPTN 064. Details on followup and retention are provided elsewhere^9,13.

Figure 1. Study Flow Chart: Screening and Eligibility.

Table 1 shows the proportion of women reporting unprotected sex (with at least one of the three most recent partners) at each visit. Note that 91 of 2099 enrolled women (4.3%) indicated on the baseline ACASI that they had not had unprotected sex (with any of the last three male partners) in the past 6 months. To make the data on unenrolled women comparable to the data on the enrolled women, we assume that 4.3% (49) of the 1135 eligible, screen positive women who chose not to enroll would also have responded “no” to the ACASI questions about unprotected sex, and we adjust the number of unenrolled women reporting unprotected sex from 1135 to 1086 (no information is available regarding what proportion of the 892 eligible women who reported no unprotected sex with a male during the past 6 months at screening might have answered “yes” to the unprotected sex questions if asked via ACASI, so these women are treated as if they would have responded “no” to the ACASI at baseline). After this adjustment, we estimate that 75% of women (3094/4126) in the unselected population would have responded “yes” at screening to the ACASI questions about any unprotected sex in the past 6 months with the last three partners.

Table 1.

Data from the HPTN 064 study for the measure “Any vaginal/anal sex with a male partner without condom in last 6 months” among individuals otherwise eligible for enrollment. 1 indicates unprotected sex; 0 indicates no unprotected sex; a period (.) indicates missing.

	Screening	ACASI
		Baseline	6 months	12 months	N	Nadj 1
	Not enrolled (2027)
	0	.	.	.	892	941
	1	.	.	.	1135	1086
	Enrolled (2099)
	1	0	.	.	5
	1	0	0	.	7
	1	0	1	.	12
	1	0	0	0	25
	1	0	1	0	9
	1	0	0	1	12
	1	0	1	1	20
	1	0	.	0	0
	1	0	.	1	1
	1	1	.	.	114
	1	1	0	.	72
	1	1	1	.	3672
	1	1	0	0	120
	1	1	1	0	190
	1	1	0	1	98
	1	1	1	1	10133
	1	1	.	0	6
	1	1	.	1	28
Observed proportions	.78 .751	.96	.83	.77

¹Rate of unprotected sex in the past 6 months (UPS) at screening are adjusted to be comparable to the ACASI measure of UPS collected during the study (see text for a description of the difference in the two measures). Among the 2099 women who enrolled in the study, 91 (4.3%) women reported UPS at screening but stated they had had no UPS on the ACASI. Among women who did not enroll in the study, we assume that, similar to enrolled women, 49 (4.3%) of the 1135 unenrolled women who responded “yes” to the screening question would have responded “no” on the ACASI question. Thus, the adjusted proportion of UPS at screening is (2099 - 91 + 1135 - 49)/4126.

²Includes 1 women whose ACASI responses was missing at baseline

³Includes 2 woman whose ACASI response were missing at baseline

The prevalence of unprotected sex in the past 6 months is observed to decline from 0.96 at baseline to 0.77 at 12 months (table 1). The adjusted data from table 1 was used to estimate the parameters of model (1). We estimate that the long-term on-study prevalence of unprotected sex is 0.74 (95% CI: 0.71 – 0.77) (table 2). Of this decline in unprotected sex during the study (from 0.96 to 0.74), only 4.4% (95% CI: -10%, 17%) cannot be explained by RTM and may be associated with study participation (see text following equation (2) for interpretation of a negative percentage). If no adjustments are made to the screening results (i.e. using N instead of N^adj from table 1), then 10% of the decline in unprotected sex during the study may be associated with study participation.

Table 2.

Estimated model parameters and derived probabilities/proportions for the outcome, unprotected sex with a male in the past 6 months. Percent change due to study participation is computed from equation (2) in the manuscript.

		Estimate (95% confidence interval)
Parameter estimates	α0	-0.186 (-0.34,-0.11)
	α1	1.91 (1.68,2.03)
	α2	-0.036 (-0.14,0.019)
Observed prevalence at baseline		0.96 (0.95, 0.97)
Estimated pre-study probability1		0.75 (0.74,0.76)
Estimated on-study probability2		0.74 (0.71,0.77)
% of change from baseline due to study		4.4% (-10%, 17%)

¹estimated as $\frac{e^{{\alpha }_0}(1+e^{{\alpha }_0+{\alpha }_1})}{1+2e^{{\alpha }_0}+e^{2{\alpha }_0+{\alpha }_1}}$ (see appendix)

²estimated as $\frac{e^{{\alpha }_0+{\alpha }_2}(1+e^{{\alpha }_0+{\alpha }_1+{\alpha }_2})}{1+2e^{{\alpha }_0+{\alpha }_2}+e^{2{\alpha }_0+{\alpha }_1+2{\alpha }_2}}$ (see appendix)

Discussion

When individuals are selected for high or low values of a time-varying quantity (e.g. presence of a risk behavior or biologic marker) and then measured again on that quantity, regression to the mean is inevitable. This phenomenon has been demonstrated in a wide variety of settings including education (e.g.. test scores¹⁴), medicine (e.g. treatment for hypertension⁵) and sports (e.g., the “sophomore slump”¹⁵), among others. Although less often discussed in the context of binary outcomes, the same principle applies – if a sample of individuals is selected to have a high or low prevalence of a time-varying behavior then, over time, the prevalence of that behavior will regress towards the prevalence in the unselected population.

In this manuscript we develop a model for RTM for binary measures that allows simultaneous estimation of the regression effect and study effect in the context of a prospective cohort selected for certain high risk behaviors. Applying these methods to HPTN 064, we found that most of the observed change over the course of the study in unprotected sex in the last 6 months could be explained by RTM. Three key assumptions must be considered in interpreting this result. First, in HPTN 064 only a subset of the eligible women (65%) enrolled in the cohort. We assume that the women who enrolled in the study are representative of all the women who were eligible. Second, among women who enrolled, we assume there is no differential dropout with respect to the behavior of interest. Since retention in HPTN 064 was high (≥ 93%⁹) there is little potential for bias due to loss to followup (although the fact that, by design, only 77% of women were enrolled for 12 months of followup decreases our sample size and increases the uncertainty of our estimates). Third, unlike the multivariate normal distribution for continuous data, there is no unique model for multivariate binary data. Thus, other models for the joint distribution of the X_i (eq. 1) could be proposed and these could lead to different estimates of the RTM effect. However, in one other model that we explored (a beta-binomial model), the results were qualitatively similar to those presented here (data not shown).

Importantly, estimation of the regression effect requires information on the prevalence of the behavior of interest in the unselected population. Obtaining these data could increase study costs (although it would be acceptable to collect data on a random subset of the unselected population). For this reason these data may not be systematically collected and, in any event, are typically not included in published data. Thus, it is difficult to quantitatively assess the RTM effect in other published studies that report declines in high risk behaviors during study participation. However, it is interesting to note that in the HVTN 906 study¹, a study with similar design and unprotected sex eligibility requirements as HPTN 064, the prevalence of unprotected vaginal sex in the past 6 months declined from 99.6% at enrollment to 76.1% at 18 months, a result remarkably similar to that seen here. It is reasonable to hypothesize that a substantial portion of this decline may be due to RTM.

Model (1) assumes a constant study effect (quantified by α₂) over the course of followup. Given the relatively brief followup in HPTN 064, a more complex model is not possible for these data. However, with a longer followup, model (1) could be extended to allow for a time-varying or transient study effect. Such an approach could be used to model e.g. a rapid initial decline in a high risk behavior followed by a partial return to a level representing the long term prevalence (strong initial study effect waning over time). Such a pattern was observed by Bartholow et al.¹⁶

In this manuscript, we have focused on change in the prevalence of a behavior that has been directly selected for based on study eligibility criteria. However, RTM may also explain changes in behaviors that are not subject to direct selection if those behaviors are highly correlated with the measures that form the eligibility criteria. For example, the behavior “condom use at last sex” is expected to be strongly (inversely) correlated with the selection variable “unprotected sex in the last 6 months”. Thus, direct selection on the latter measure may result in indirect selection on the former. As a consequence, we expect “condom use at last sex” to exhibit some RTM effect over the course of the study. If screening data on the prevalence of such indirectly selected measures are available, then the methods outlined above may be used to estimate the RTM effect. In the absence of such screening data (as is the case for “condom use at last sex” in HPTN 064) it may be possible to estimate the RTM effect in an indirectly selected measure based on the strength of its association with the directly selected measure(s). For example, a sensitivity analysis presented in Hodder et al.⁹ suggested that 30 – 60% of the observed increase in “condom use at last sex” could be attributed to RTM (stated differently, 40 – 70% associated with study participation). Development of methods to more precisely quantify this indirect selection effect is an area for future research.

The idea that participation in a research study can result in beneficial behavioral changes in high risk individuals, above and beyond any intervention provided, is pervasive. The analyses presented here do not totally discount this possibility, but they do show that the benefits of study participation may be substantially less than a naïve analysis that ignores RTM would suggest. To fully understand the relative contribution of study participation versus RTM among individuals selected for study participation on the basis of high risk behaviors, it is important to measure the prevalence of the behaviors of interest in the unselected population and to account for regression effects. Declines in high risk behaviors beyond those predicted by RTM may be attributable to study participation or other factors.

Abbreviations

ACASI

Audio computer-assisted self-interview

HIV

Human Immunodeficiency virus

HPTN

HIV Prevention Trials Network

RTM

Regression to the mean

STI

Sexually transmitted infections

US

United States

Appendix

In HPTN 064 women were evaluated at baseline, 6 and 12 months (i = 0, 1, 2, respectively). Let X_i = value of the variable or behavior of interest at visit i, i = 0,1,2. We assume that values of X₀ are available for all women - for women who are not eligible by the unprotected sex criterion, or do not enroll, this information comes from the response to the screening questionnaire. The typical enrolled participant has values X₀, X₁, X₂. We write the joint distribution as

$$\mathrm{P}\left({\mathrm{X}}_0,{\mathrm{X}}_1,{\mathrm{X}}_2\right)=\mathrm{P}({\mathrm{X}}_2|{\mathrm{X}}_1)\mathrm{P}({\mathrm{X}}_1|{\mathrm{X}}_0)\mathrm{P}({\mathrm{X}}_0)$$ (A1)

and assume the following model

$$\text{logit}(Pr({\mathrm{X}}_{\mathrm{i}}|{\mathrm{X}}_{\mathrm{i}-1}))={\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1{\mathrm{X}}_{\mathrm{i}-1}+{\mathrm{\alpha }}_2{\mathrm{E}}_{\mathrm{i}}$$

where E_i is 1 if the woman was participating in the study during the 6 months preceding visit i, and 0 otherwise. If X₁ or X₂ is missing, then the joint distribution for that participant is obtained by summing (A1) over the missing value.

Assuming that the underlying prevalence of the behavior in the unselected population is in steady state, we can show that

$$\mathrm{P}\left({\mathrm{X}}_0=1\right)={\mathrm{P}}_{\text{all}}=\frac{e^{{\alpha }_0}\left(1+e^{{\alpha }_0+{\alpha }_1}\right)}{1+2e^{{\alpha }_0}+e^{2{\alpha }_0+{\alpha }_1}}.$$

Proof: Note that P(X₀ = 1) = E(X₀). Assuming that the behavior is in steady state in the unselected population, E(X₀) = E(X_-i) = p. Then

$$\begin{array}{ccc}E(X_0)& =& E(E(X_0|X_{-1}))\\ p& =& \frac{\left(1-p\right)e^{{\alpha }_0}}{1+e^{{\alpha }_0}}+\frac{p{e}^{{\alpha }_0+{\alpha }_1}}{1+e^{q_0+{\alpha }_1}}\\ p& =& \frac{e^{{\alpha }_0}(1+e^{{\alpha }_0+{\alpha }_1})}{1+2e^{{\alpha }_0}+e^{2{\alpha }_0+{\alpha }_1}}\end{array}$$

In practice, the fitted values of the α will be such that P_all is simply equal to the prevalence of the behavior in the unselected population.

More importantly, the predicted long-term, steady state prevalence in the unselected population after exposure to the study is

$${\mathrm{P}}_{\text{onstudy}}=\frac{{\mathrm{e}}^{{\mathrm{\alpha }}_0+{\mathrm{\alpha }}_2}(1+{\mathrm{e}}^{{\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1+{\mathrm{\alpha }}_2})}{1+2{\mathrm{e}}^{{\mathrm{\alpha }}_0+{\mathrm{\alpha }}_2}+{\mathrm{e}}^{2{\mathrm{\alpha }}_0+{\mathrm{\alpha }}_1+2{\mathrm{\alpha }}_2}}$$

Proof: Assuming that the behavior is in steady state after exposure to the study, E(X_i) = E(Xi_-1) = p. Then

$$\begin{array}{ccc}E(X_0)& =& E(E(X_i|X_{i-1}))\\ p& =& \frac{(1-p)e^{{\alpha }_0+{\alpha }_2}}{1+e^{{\alpha }_0+{\alpha }_2}}+\frac{p{e}^{{\alpha }_0+{\alpha }_1+{\alpha }_2}}{1+e^{q_0+{\alpha }_1+{\alpha }_2}}\\ p& =& \frac{e^{{\alpha }_0+{\alpha }_2}(1+e^{{\alpha }_0+{\alpha }_1+{\alpha }_2})}{1+2e^{{\alpha }_0+{\alpha }_2}+e^{2{\alpha }_0+{\alpha }_1+2{\alpha }_2}}\end{array}$$

The difference between P_onstudy and P_all represents the study effect.

Let

• p₀ = Pr(X₀ = 1)

• p_i(r)=Pr(X_i= 1|X_i-1 = r)

• nx₀(x) = Count of number of observations at time 0 with X₀=x among all individuals

• nx_i(x | r) = Count of number of observations at time i with X_i=x and X_i-1=r, i = 1,2

We use maximum likelihood to estimate α₀, α₁ and α₂. The log-likelihood is

$$\ell =\mathrm{n}{\mathrm{x}}_0(1)log({\mathrm{p}}_0)+\mathrm{n}{\mathrm{x}}_0(0)log(1-{\mathrm{p}}_0)+{\sum }_{i=1}^2{\sum }_{r=0}^1\mathrm{n}{\mathrm{x}}_{\mathrm{i}}(1|\mathrm{r})log({\mathrm{p}}_{\mathrm{i}}(\mathrm{r}))+\mathrm{n}{\mathrm{x}}_{\mathrm{i}}(0|\mathrm{r})log(1-{\mathrm{p}}_{\mathrm{i}}(r))$$

and standard methods may be used to obtain parameter estimates and standard errors. The delta method may be used to compute standard errors for derived quantities such as P_all and P_onstudy.