Abstract
The effectiveness of vaccinating males against the human papillomavirus (HPV) remains a controversial subject. Many existing studies conclude that increasing female coverage is more effective than diverting resources into male vaccination. Recently, several empirical studies on HPV immunization have been published, providing evidence of the fact that marginal vaccination costs increase with coverage. In this study, we use a stochastic agent-based modeling framework to revisit the male vaccination debate in light of these new findings. Within this framework, we assess the impact of coverage-dependent marginal costs of vaccine distribution on optimal immunization strategies against HPV. Focusing on the two scenarios of ongoing and new vaccination programs, we analyze different resource allocation policies and their effects on overall disease burden. Our results suggest that if the costs associated with vaccinating males are relatively close to those associated with vaccinating females, then coverage-dependent, increasing marginal costs may favor vaccination strategies that entail immunization of both genders. In particular, this study emphasizes the necessity for further empirical research on the nature of coverage-dependent vaccination costs.
1 Introduction
The sexually transmitted human papillomavirus (HPV) is a significant global public health burden. Almost all cervical cancers, up to 90% of anal cancers, and up to 60% of oropharyngeal cancers are caused by HPV [1]. In the USA alone, the incidence of new HPV-related cancer cases in 2009 exceeded 35,000, with more than a third of cases occurring in the male population [2]. Although screening has led to a significant decrease in cervical cancer incidence and mortality in developed countries, there has been an increase in other HPV-related cancers for which population screening is not currently performed [3, 4]. The introduction of effective prophylactic vaccines against HPV-16 and HPV-18, the two types responsible for 70% of cervical cancers, as well as most anal and oropharyngeal HPV-related cancers, provides an additional strategy for preventing morbidity and mortality. Although both commercially available HPV vaccines were originally approved for use in girls and women only, the quadrivalent vaccine (Gardasil © Merck, Inc., Whitehall Station, NJ) was approved by the US Food and Drug Administration in 2009 for use in boys and men. Despite vaccination of boys being recommended by the Centers for Disease Control and Prevention [5], vaccine coverage in adolescent males remains low in the United States, where it is currently around 13.9% [6].
Whether allocating further resources to increase low coverage in adolescent males is more effective than vaccinating females alone remains controversial. Existing studies vary in their conclusions, with most finding that targeting females alone is most cost effective: see Elbasha and Dasbach [7] (see also [8]), Taira et al. [9], Kim et al. [10, 11], Brisson et al. [12], Bogaards et al. [13], Chesson et al. [14], and [15] for a review. A common assumption in all of these studies is that the vaccination costs consist of direct costs (i.e., vaccine price) only. However, several recent publications indicate that an increase in coverage might be subject to additional marginal costs of vaccine distribution. In fact, the number of preadolescent and early adolescent girls in the USA who have completed the full vaccine series appears to have plateaued around 37% [6], which is a much lower coverage level than was assumed by previous analyses (e.g., 75% in [11]). In addition, the willingness of parents to have their preadolescents vaccinated may be decreasing, with 44% of US parents opposing vaccination [16]. Together, these findings suggest that a further increase in female coverage will require costly education and outreach programs to reach the unvaccinated population, resulting in increasing marginal costs in addition to direct vaccine costs. The necessity to study the potential impact of these additional costs on optimal resource allocation has been emphasized previously [7, 13], but to our knowledge the issue has not yet been addressed explicitly.
In this study, we develop an agent-based modeling framework to assess the impact of coverage-dependent marginal vaccination costs on optimal resource allocation policies for vaccination against HPV. We do so by considering two different scenarios. First, we assess globally optimal resource allocation in the case of new vaccine programs. In this scenario, which is particularly relevant to countries without an HPV vaccination program, we seek to identify allocation policies that yield a maximum decrease in disease burden. In the second scenario, we optimize the distribution of resources in the case where a positive fraction of the population is already vaccinated.
2 Model Description and Validation
Various groups have developed mathematical models to optimize vaccination strategies against HPV [7–15]. Among these models, there are stochastic agent-based models (e.g., [12]), deterministic compartment models (e.g., [13]), and hybrid models (e.g., [11]). Over the past years, it has been emphasized that the heterogeneity of sexual networks plays an important role in disease transmission (see [17] for a detailed discussion). In particular, time-ordering [18, 19], assortativity [20], and concurrency [21] of relationships in sexual networks are now recognized as important mechanisms affecting the spread of sexually transmitted infections. Acknowledging the importance of these mechanisms, we develop a stochastic agent-based model (ABM), in which stochastic infection dynamics of SIR/S-type take place on a dynamic random graph model of sexual network evolution. In addition, we develop a compartment model (CM) that provides an analytically tractable simplification of the ABM and yields qualitatively similar results despite its simplicity.
2.1 Model Development
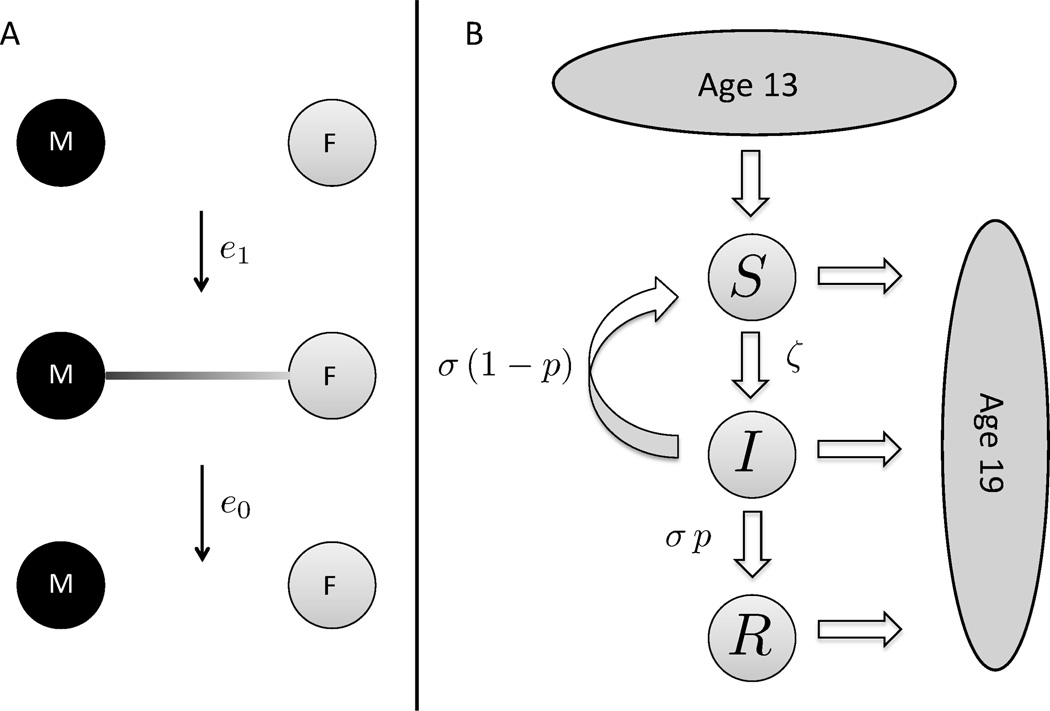
We consider a cohort of sexually active adolescents, containing N females and N males. Individuals enter the cohort at age 14 and leave when they turn 19 years old. Depending on the magnitude of N, the model can describe, for example, the network of students in a single high school, or the entire adolescent population in a given town or geographic region. For simplicity, we consider only heterosexual relationships; the role of bi- and homosexual relationships is addressed in Section 4. As illustrated in Figure 1A, each of the N2 possible male-female pairs (edges) in the cohort initiates a relationship at rate e1 and can engage in sexual activity until dissolution of the relationship, which occurs at rate e0. The rates e1 and e0 vary by edge, enforcing assortative mixing according to age and sexual activity level. Regarding the latter, we follow [22] and categorize individuals into four groups, L0, …,L3, ranging from low (L0) to high (L3) sexual activity. In keeping with studies of teenage sexual networks, we allow for concurrency, i.e. individuals are permitted to have more than one relationship simultaneously [23–25].
Figure 1. Stochastic model dynamics.
(A) The N male (black) and N female (grey) nodes initiate and dissolve relationships at rates e1 and e0, respectively. The edge rates depend on the age and sexual activity levels of the associated individuals. (B) The disease dynamics on the random graph are of SIR/S-type with immigration and death. Susceptible individuals (Sm/f) enter the network at age 14, with a probability υm/f of being vaccinated (Rm/f). Disease transmission takes place between infected (Im/f) and susceptible nodes, and the infection rate ζm/f of a given node depends on the current number of infected partners. Infected individuals clear the virus at rate σ. Upon clearing the virus, individuals enter the compartments of recovered nodes (Rm/f) with probability pm/f or re-enter the compartments of susceptible nodes (Sm/f) with probability 1 − pm/f. Individuals age deterministically and leave the system upon turning 19 years old, so that the total number of individuals in the system is conserved.
We model the dynamics of genital infections with HPV-16 and HPV-18 only. In fact, HPV-16/18 are the main oncogenic strains and account for roughly 70% of HPV-associated cancers [1]. Moreover, they are the only oncogenic strains covered by vaccines currently available to the public. There is currently no compelling evidence for either synergy or competition between vaccine types and non-vaccine types [26, 27]. Consequently, we assume that transmission, acquisition and clearance of HPV-16/18 are independent of co-infection with other strains. As illustrated in Figure 1B, susceptible individuals can become infected when engaging in sexual activity with infected individuals. We denote the per-relationship transmission rate from infected females (males) to susceptible males (females) by βfm (βmf). The total numbers of susceptible and infected females are denoted by Sf and If, respectively, with analogous notation for males. Most HPV infections are transient [28], and we assume that infected individuals clear the virus at rates σf and σm, respectively. The number of recovered females (males) is denoted by Rf (Rm). Since we are interested in different vaccination strategies, we introduce υf (υm), the fraction of vaccinated females (males). For the purpose of this study, we only consider completed vaccinations (3 doses), and we assume a vaccine efficacy of 100%. A detailed description of the ABM is found in Appendix A.
2.2 Large Population Limit
In addition to the ABM, we introduce a deterministic CM. Due to its simplicity, the CM is analytically tractable, and enables more systematic analyses such as the roadmap to herd immunity in Section 3.4. To derive the CM, we neglect network heterogeneity and assortativity in the ABM approach and pass to the large population limit (N → ∞). The resulting deterministic transmission model is described by the following set of ordinary differential equations (see Appendix B for details):
| (1) |
where the equations for the female variables are analogous, with the subscripts interchanged. The notation is the same as for the ABM, expect that βfm and βmf are now effective transmission rates, corresponding to the per-relationship transmission rates from the ABM model multiplied by a scaling factor related to effective network connectivity. Note that we have normalized the variables by the total population size, so they represent relative fractions rather than absolute numbers. A brief discussion of basic properties of system (1) and its basic reproductive number ℛ* is found in Appendix B.1.
2.3 Model Parametrization
The parametrization of the network part of the ABM was partially based on estimates provided in the work of Van de Velde and colleagues [22]. To enable a direct parameter comparison between our and Van de Velde’s model, we had to rescale our edge formation rate e1 by a dimensionless scaling factor ℰ. In a first step, we parametrized the network part of the ABM. To account for parameter uncertainty (i.e. large prior ranges) we applied a dynamic re-sampling scheme for most network parameters (see Appendix A.3 for details). More precisely, during simulations we re-sampled these parameters uniformly across their prior ranges every Δt = 0.025 years (≈ 10 days). The scaling factor ℰ on the other hand was inferred by fitting the degree distribution of the simulated sexual network to the degree distribution of a high school sexual network described in [23], see Appendix A.4 for details. Once the network part of the model was parameterized, we used longitudinal data on prevalence of HPV-16/18 in adolescents [29] together with vaccine uptake data [30] to infer the viral transmission and clearance rates. We tested 1000 prior sets for the disease parameters, from which only 26 sets satisfied our criteria of a good fit. We call these the Posterior Sets, and all ABM results throughout this study are presented in terms of these Posterior Sets, which are listed in Table 8. A detailed description of the ABM parametrization is found in Appendices A.2–A.5, and a summary of the ABM parameters and their prior ranges is given in Table 1.
Table 8. Posterior Set.
The 26 posterior parameter sets retained after calibration of the model to prevalence data, see text for details. Units for rates: per year.
| Set # | βfm | βmf | σ |
|---|---|---|---|
| 1 | 42.8 | 145.8 | 0.63 |
| 2 | 42.8 | 166.4 | 0.63 |
| 3 | 42.8 | 187.0 | 0.63 |
| 4 | 63.4 | 187.0 | 0.77 |
| 5 | 84.0 | 63.4 | 0.63 |
| 6 | 84.0 | 125.2 | 0.77 |
| 7 | 84.0 | 145.8 | 0.77 |
| 8 | 84.0 | 166.4 | 0.77 |
| 9 | 84.0 | 187.0 | 0.77 |
| 10 | 104.6 | 63.4 | 0.63 |
| 11 | 104.6 | 104.6 | 0.77 |
| 12 | 104.6 | 125.2 | 0.77 |
| 13 | 104.6 | 145.8 | 0.77 |
| 14 | 125.2 | 63.4 | 0.63 |
| 15 | 125.2 | 104.6 | 0.77 |
| 16 | 125.2 | 125.2 | 0.77 |
| 17 | 145.8 | 104.6 | 0.77 |
| 18 | 145.8 | 125.2 | 0.77 |
| 19 | 145.8 | 187.0 | 0.91 |
| 20 | 166.4 | 84.0 | 0.77 |
| 21 | 166.4 | 104.6 | 0.77 |
| 22 | 166.4 | 187.0 | 0.91 |
| 23 | 187.0 | 84.0 | 0.77 |
| 24 | 187.0 | 104.6 | 0.77 |
| 25 | 187.0 | 166.4 | 0.91 |
| 26 | 187.0 | 187.0 | 0.91 |
Table 1. Model parameters: summary.
Prior ranges are for dynamically sampled and inferred parameters only; Group 1: fixed parameters, Group 2: dynamically re-sampled parameters, Group 3: parameters sampled for each individual separately. Units for rates: per year.
| Parameter | Name | Prior range | Value | Group | Type | Refs. |
|---|---|---|---|---|---|---|
| Λ(a, a′) | age mixing matrix | – | Table 2 | 1 | fixed | [44] |
| ε | e1 scaling | – | 1.5 | 1 | inferred | [23] |
| θ(g, a, l) | initiation rate | Table 3 | – | 2 | sampled | [22] |
| σ̂(a, l) | dissolution rate | Table 4 | – | 2 | sampled | [22] |
| κ | assortative degree | [65, 140] | – | 2 | sampled | [22] |
| ρ(l) | activity level fractions | Table 5 | – | 3 | sampled | [22] |
| βmf | m-f transmission | [1.6, 187] | Posterior Set | 1 | inferred | [46–48] |
| βfm | f-m transmission | [1.6, 187] | Posterior Set | 1 | inferred | [46–48] |
| σ | clearance rate | [0.63, 1.88] | Posterior Set | 1 | inferred | [49, 50] |
| pm | prob. of immunity | [0,1, 0.85] | – | 3 | sampled | [22] |
| pf | prob. of immunity | [0.2, 0.9] | – | 3 | sampled | [22] |
To parametrize the CM, we used the 26 Posterior Sets from the ABM, and rescaled the viral transmission rates by a network connectivity parameter to account for the differences in network structure between the ABM and the CM. For each Posterior Set, the connectivity parameter was estimated separately by fitting the CM-derived prevalence levels to the empirical data as described above for the ABM. CM results throughout this study are presented in terms of the 26 Posterior Sets (including the network connectivity parameter). Details on the CM parametrization are found in Appendix B.2.
2.4 The Costs and Benefits of Vaccination
Conclusions drawn from mathematical vaccination models naturally depend on the underlying choices of cost and benefit measures. Several authors have called for a more detailed analysis of the relationship between these measures and optimal vaccination strategies against HPV [7, 13]. Here, we follow their call and assess how coverage-dependent costs impact optimal vaccination strategies. Since the nature of these cost functions is largely unknown, we work with a general class of functions, subject to a few natural assumptions. More precisely, we assume that the cost of vaccinating a proportion υm of males and υf of females is a a non-negative function C(υm, υf) satisfying the following two conditions:
C(υm, υf) > 0 for all υm + υf > 0,
.
Condition (1) says that it always costs something to vaccinate an individual, while (2) accounts for a minimal per-person cost, cm/f > 0, of administering the vaccine. Importantly, these conditions do not specify the local curvature of the cost function, allowing for different scenarios. For example, one would expect to spend less money to raise coverage from 10% to 11% than to raise it from 40% to 41%, since a certain proportion of the population may be difficult to vaccinate [16]. However, the corresponding increasing marginal costs may not apply at all coverage levels. In fact, economies of scale and network externalities could play a role at higher coverage levels, leading to locally concave cost functions [31]. Examples of cost-function level curves in a fixed-resource setting where C(υm, υf) = K for some K > 0, are found in Figure 2a.
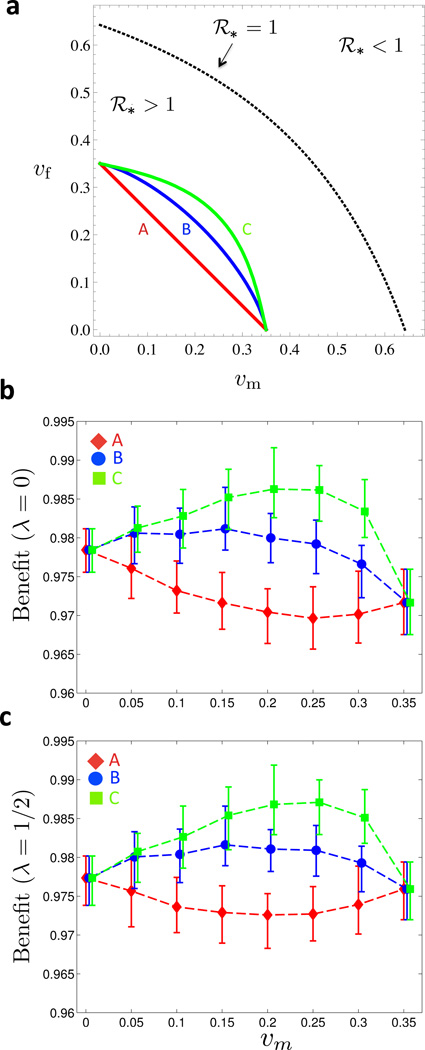
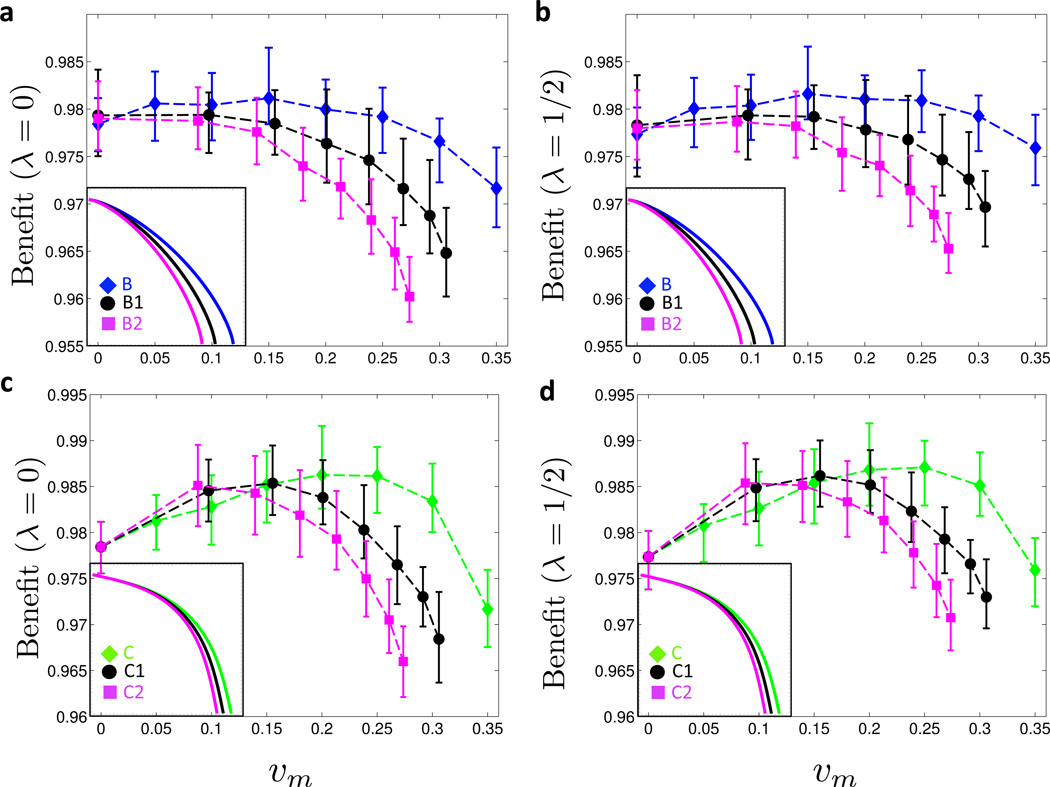
Figure 2. Benefit under symmetric cost curves.
(a) The three curves A, B and C are fixed-cost curves with differing levels of convexity (for the corresponding ratios of marginal administration to marginal fixed costs, see Figure 8): linear curve with no marginal costs associated with vaccine administration (A), mildly convex curve with high marginal costs of vaccine administration (B), and more convex curve with low marginal costs of vaccine administration (C). Maximal single-sex coverage is 35% for all three curves. In the region below the dotted line there is an endemic equilibrium (ℛ* > 1). Vaccination coverage on and above the dotted line confers herd immunity (ℛ* ≤ 1). (b) Moving along the level-sets of the cost functions A, B and C in (a), the vaccination benefit Bλ(υm, υf) is shown as a function of υm for λ = 0. (c) Same as (b) but with λ = 1/2. In (a) and (b), 25 simulations for each of the 26 Posterior Sets were run for 30 years. Prevalence levels were time-averaged between 15 and 30 years for each run, and the time averages were in turn averaged over the 25 realizations per Posterior Set. For each value of υm, the mean, minimum and maximum Benefits across the Posterior Set are represented by the symbol and the error bars, respectively. (Online version in color.)
To quantify the Benefits of vaccination, we introduce the benefit function Bλ(υm, υf),
| (2) |
where is the burden of infection, defined as
| (3) |
The latter is a weighted sum of the fraction of infected males and the fraction of infected females, and λ determines the sex-specific burden of infection. It ranges from λ = 0 (focus on female infections only) to λ = 1 (focus on male infections only). In fact, the potential costs associated with a male infection are different from the costs associated with a female infection: the probability to develop an HPV-associated disease is both sex- and site-specific. Considering that in the US and Europe roughly one in three HPV-related cancers affect men [2, 32], it seems reasonable to assume that λ ∈ (0, 1/2). Since the true value of λ is difficult to ascertain, we present the model results below for both the lower (λ = 0) and upper (λ = 1/2) bounds of this interval. As explained in Appendix C, we estimate the true value of λ to be of the order of λ ≈ 7 · 10−3, and model results obtained for this value are virtually identical to the lower bound λ = 0.
Finally, it is important to emphasize that a complete cost-effectiveness analysis is not feasible within our framework as such an analysis would require extending the cohort to all ages, and introducing additional models for cancer progression. Nevertheless, sufficient prevalence levels in adolescent populations are critical for the survival of HPV in the entire population. In this sense, the upper bound λ = 1/2, for which measures the cohort prevalence of infection, provides valuable information in itself.
3 Results
A key public health challenge with respect to HPV vaccination is the optimal allocation of available resources among the population. Since both males and females can develop symptomatic diseases that require medical intervention (e.g. genital warts and various cancer types), both sexes benefit from immunization. However, the optimal distribution of vaccines among males and females is difficult to establish. The most challenging part is the parametrization of the coverage-dependent costs of vaccination. To our knowledge there is currently no empirical data on these costs in the specific case of HPV. Despite several authors asking for more detailed analyses regarding the impact of marginal costs [7, 13], to our knowledge, no previous study has addressed this issue. The goal of our analysis is to assess their potential impact on optimal vaccine distribution in different scenarios: (i) in countries with no HPV vaccine programs in place, the central issue is how to allocate resources to set up the most efficient new vaccine program; (ii) in countries with ongoing vaccine programs, the main issue is how to invest newly allocated resources such that herd immunity-conferring coverage levels are approached most efficiently. In Section 3.1 we address scenario (i) under the assumption of symmetric cost curves and homogeneous vaccine uptake. Next, we study the impact of asymmetric cost curves in Section 3.2, and assortative vaccine uptake in Section 3.3. Finally, scenario (ii) is addressed in Section 3.4.
3.1 Global Analysis: When a Mixed Protocol is Optimal
In this section, we characterize the globally optimal resource distribution among both sexes. Thereby, the aim is to determine the optimal strategy along fixed cost curves, C(υm, υf) = K, where K > 0 is the amount of allocated resources. This scenario is particularly relevant for low-resource countries with a current lack of HPV vaccine programs.
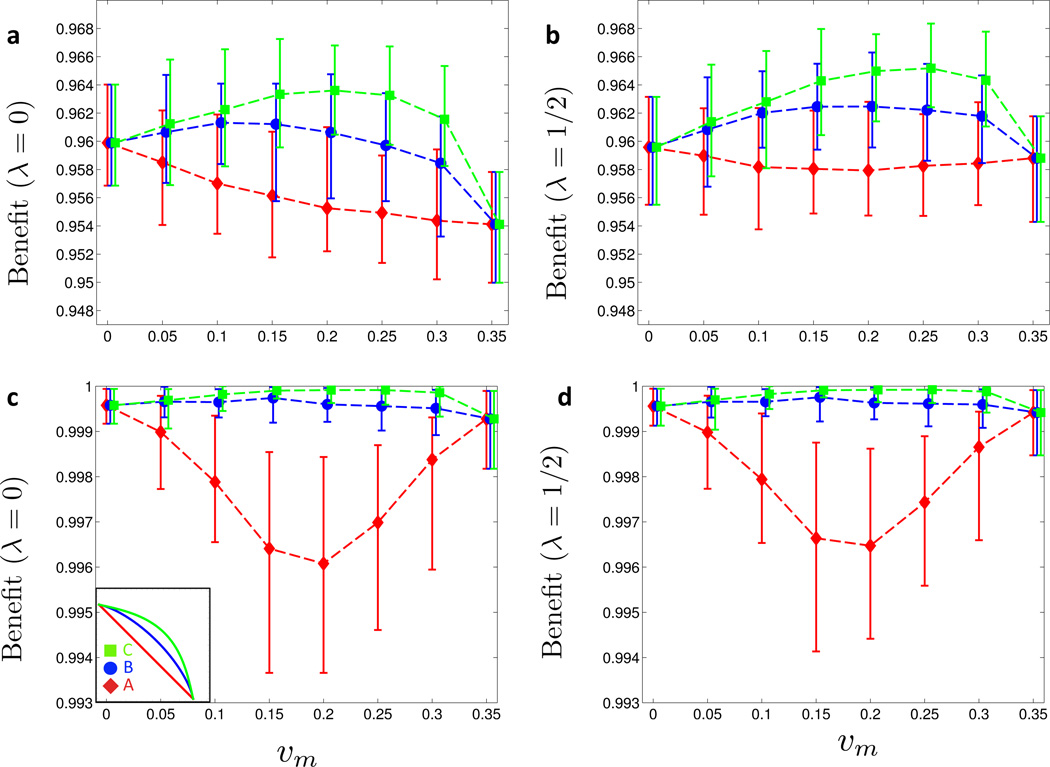
Based on ABM simulations, we determine the vaccine benefit along three symmetric cost function level sets, see curves A, B, and C in Figure 2a, and present the results for λ = 0 in Figure 2b, and for λ = 1/2 in Figure 2c. We point out two interesting observations. First, incorporating coverage-dependent marginal costs drastically changes the shape of the benefit curve. For the linear cost curve A, the optimal strategy entails female-only vaccination (υm = 0), and the benefit decreases as resources are shifted towards males (υm > 0). In contrast, for increasing convexity in the cost curve (curves B and C), the benefit increases as υm becomes positive. In particular, the maximum benefit is achieved for a mixed vaccination strategy where both genders are vaccinated, and the height of the peak correlates with the convexity of the cost curve. Second, the impact of coverage-dependent costs is, qualitatively speaking, independent of the λ value: the optimal strategy is mixed, whether we focus on female prevalence (λ = 0) or population prevalence (λ = 1/2). The only qualitative difference between the two cases is found at the end points (υm = 0 and υm = 0.35) of the benefit curve: while female-only vaccination is more beneficial in the case λ = 0, the two pure strategies perform almost identically in the case λ = 1=2.
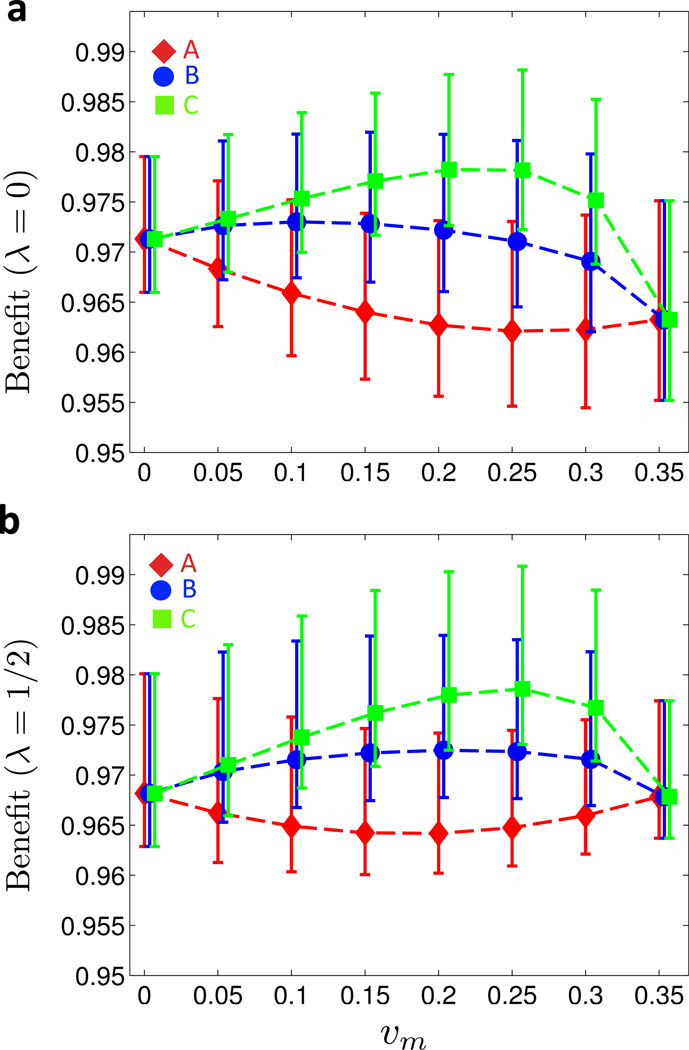
To ascertain whether the above observations were due to particular features of assortativity and heterogeneity in the ABM, we repeated the analysis using the homogeneously mixing CM from Section 2.2. Interestingly, as shown in Figure 3, the benefit curves are qualitatively very similar, underscoring the robustness of the above observations with respect to coverage-dependent marginal costs.
Figure 3. Compartment model: benefit under symmetric cost curves.
(a) Moving along the cost curves A, B and C in Figure 2a, the vaccination benefit Bλ(υm, υf) is shown as a function of υm for λ = 0. (b) Same as (a) but with λ = 1/2. In (a) and (b), the CM steady states for the 26 Posterior Sets were computed. For each value of υm, the mean, minimum and maximum Benefits across the Posterior Set are represented by the symbol and the error bars, respectively. (Online version in color.)
Finally, we considered potential limitations due to our assumption of a closed sexual network of 14–18 year old adolescents. In fact, there is data suggesting that up 35–40% of females in this age group have sexual relationships with males who are at least 3 years older [39], raising questions about our choice of network closure. To assess the potential impact of such relationships on our results, we repeated the simulations from Figure 2 in the presence of additional relationships between females in the network and older males outside the network. In these simulations, external males were assigned a probability of being infected with HPV-16/18, and they could transfer the disease to their female partners inside the network, see Appendix E for details. The simulation results (Figure 9) show that adding external males causes changes in the overall prevalence levels. Since 20–29 years old males have higher prevalence levels of HPV-16/18 than younger males inside the network, see Appendix E for estimates, the external relationships increase the disease burden among females considerably. This is reflected by the fact that the average benefit for λ = 0 (female-only benefit), Figures 9a) and c), is smaller than for λ = 1/2 (population benefit), Figures 9b and d), respectively. However, despite the impact on female prevalence, a comparison between Figure 9 and Figure 2 (no external relationships) shows that adding external relationships does not change the qualitative nature of the benefit curves. Most importantly, mixed vaccination strategies remain optimal for the nonlinear cost curves B and C.
Figure 9. Impact of external relationships.
The simulation of Figure 2 is repeated for a scenario with both network internal and external relationships. In (a) and (b), the prevalence of HPV-16/18 among external males was set to pext = 0.12 · υm, and in (c) and (d) it was set to 0.5 · pext.
3.2 Impact of Asymmetric Cost Curves
The analysis in Section 3.1 was based on the gender symmetric cost curves in Figure 2a. In other words, we assumed identical marginal costs of vaccination for males and females. Despite proved efficacy against infection with HPV-16/18 and the development of lesions in males [33,34], vaccine uptake in male adolescents (13.9%) is considerably lower than in female adolescents (37%) [6]. One possible reason for the differential uptake may be a general lack of awareness and knowledge about the role of HPV in cancers other than cervical cancer [35]. Together, the preference to vaccinate females over males [36], and the low vaccine uptake in male adolescents, suggest that the marginal costs associated with male vaccination may be higher than the marginal costs associated with female vaccination. To assess the potential impact of this gender specific asymmetry on the optimal allocation of resources, we repeated the analysis from Section 3.1 with asymmetric cost curves.
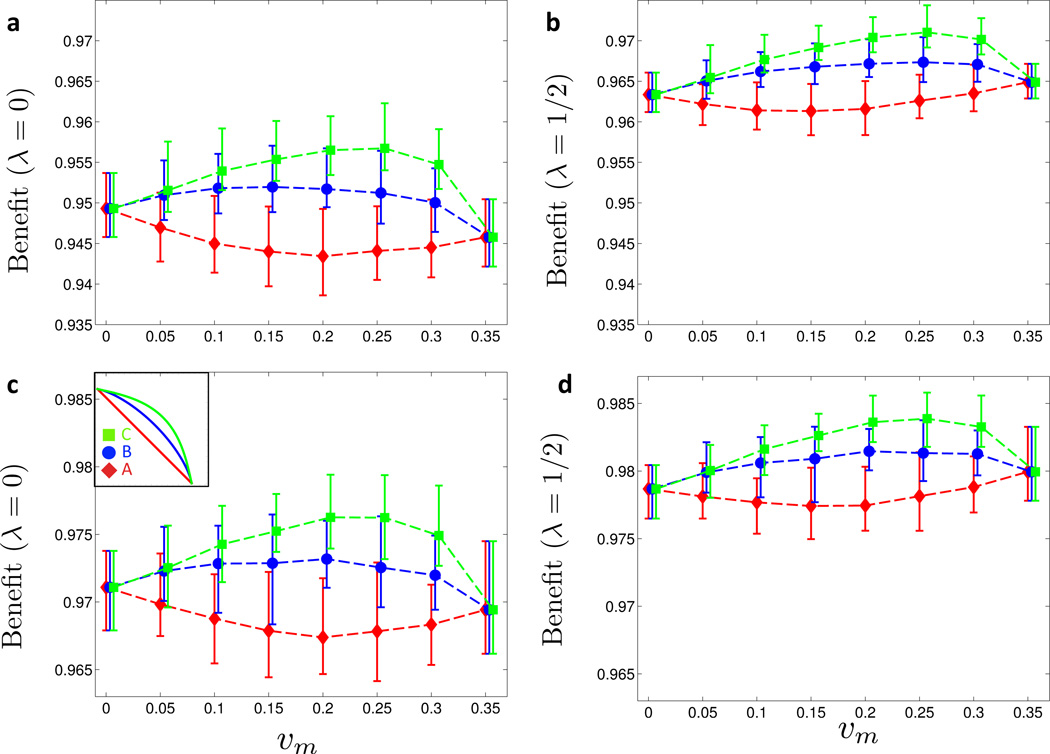
First, starting from the mildly convex (but symmetric) cost curve B (see Figure 2a), we added a 25% and 50% increase in male over female marginal costs, leading to the asymmetric cost curves B1 and B2, respectively, see inset of Figure 4a. As illustrated in Figures 4a for λ = 0 and Figure 4b for λ = 1/2, the asymmetry in the cost curves counterbalances the effect of the increasing marginal costs: in comparison to the symmetric B curve, the global maximum of the benefit function is shifted toward υm = 0 for curves B1 and B2.
Figure 4. Benefit under asymmetric cost curves.
(a) and (b) Cost curve B from Figure 2a is rendered asymmetric (curves B1 and B2 in insets). Moving along these asymmetric cost curves, the benefit Bλ(υm, υf) is shown for λ = 0 in (a) and for λ = 1/2 in (b). (c) and (d) Cost curve C from Figure 2a is rendered asymmetric (curves C1 and C2 in insets). Moving along these asymmetric cost curves, the benefit Bλ (υm, υf) is shown for λ = 0 in (c) and for λ = 1/2 in (d). For details on averaging and meaning of symbols and error bars, see Figure 2. (Online version in color.)
As shown in Figures 4c and 4d, the impact of cost asymmetry on the benefit is smaller when starting from the more convex cost curve C from Figure 2a. Here, increasing the marginal costs for male vaccination by 25% (C1) and 50% (C2), respectively, still shifts the maximum benefit toward υm = 0, but the optimal strategy clearly remains of mixed type, consisting of positive male and female coverages.
3.3 Impact of Assortativity in Vaccine Uptake
In the US, the recommended age of HPV vaccination in preteens is 11–12 years [30]. Since this is generally before onset of sexual activity, future sexual activity levels are not known at the time of vaccination. For this reason, most modeling studies assume uniform distribution of the vaccine across the population. However, many socioeconomic and sociodemographic factors that are associated with sexual behavior are also associated with vaccine uptake, and hence it is likely that vaccine uptake is associated with future sexual activity levels; see [20] and references therein for a detailed discussion of this issue. In this section, we address how differential vaccine uptake across sexual activity levels may affect the role of increasing marginal costs on resource allocation. For this purpose we repeat the analysis from Section 3.1, and analyze two different scenarios of uptake, where vaccine uptake levels are either negatively or positively correlated with sexual activity.
To study the case of a negative correlation of vaccine uptake with sexual activity, allocated vaccines are distributed across the population such that an individual in the lowest activity level (L0) is twice as likely to receive a given vaccine than an individual in the lower intermediate level (L1), 4 times as likely than an individual in the upper intermediate level (L2), and 8 times as likely than an individual in the highest activity level (L3). For each allocated vaccine we then draw an individual at random with the above relative weights, and either set the individuals’ status to vaccinated, or repeat the draw in case the individual had already received a vaccine. This process is iterated until all allocated vaccines are distributed. As shown in Figure 5a for λ = 0 and Figure 5b for λ = 1/2, the benefit curves for this distribution scheme are qualitatively similar to the ones obtained under a uniform distribution of vaccines, see Figures 2b and 2c for comparison. However, the average benefit is about two percentage points lower when vaccine uptake correlates with lower sexual activity (Figure 5a–b). This highlights the dominant role of high activity individuals in the spread of HPV.
Figure 5. Assortative vaccine uptake (symmetric cost curves).
The symmetric cost curve analysis of Figure 2 is repeated with different types of assortative vaccine uptake. (a) and (c) Vaccine uptake correlates negatively with sexual activity level: at the beginning of the year, vaccines are distributed among the sexual activity levels as follows: L0 (low activity) with probability 1/2, L1 and L2 with probabilities 1/3 and 1/6, respectively, and L3 (high activity) with probability 0. The benefit Bλ (υm, υf) along the three symmetric cost curves A, B and C (see inset in (c)) is computed for λ = 0 (a) and λ = 1/2 (b). (c) and (d) Vaccine uptake correlates positively with sexual activity level: at the beginning of the year, vaccines are distributed among the sexual activity levels as follows: L3 (high activity) with probability 1/2, L2 and L1 with probabilities 1/3 and 1/6, respectively, and L0 (low activity) with probability 0. The benefit Bλ (υm, υf) along the three symmetric cost curves A, B and C (see inset in (c)) is computed for λ = 0 (c) and λ = 1/2 (d). (Online version in color.)
Regarding the case of a positive correlation between sexual activity and vaccine uptake, the vaccines are distributed the other way around: an individual in the highest activity level (L3) is twice as likely to receive a vaccine than an individual in the upper intermediate activity level (L2), 4 times as likely than an individual in the lower intermediate level (L1), and 8 times as likely than an individual in the lowest activity level (L0). As seen in Figure 5c for λ = 0 and Figure 5d for λ = 1/2, this vaccine distribution scenario considerably changes the benefit curves in comparison to the case of uniform distribution across the population, see Figures 2b (λ = 0) and 2c (λ = 1/2), respectively. For the linear cost curve A, the benefit of vaccination remains highest for single-sex vaccination strategies (υm = 0 and υm = 0.35), but for the convex cost curves B and C, the benefit becomes nearly constant and is close to 1, which means that the disease burden has nearly vanished.
3.4 Local Analysis: Roadmap to Herd Immunity
In the previous three sections, we focused on the scenario of new vaccination policies: assuming an initial coverage level of zero (υm = υf = 0), we determined how to best distribute budgeted resources such that the overall disease burden was minimized. In the current section, we focus on an alternative scenario with initial nonzero coverage levels, (υm, υf) ≠ (0, 0), and we are interested in how to distribute newly allocated resources. In other words, given the current coverage, we seek to determine whether the next dollar should be invested in male or female vaccination to decrease the disease-related burden. This question, raised previously by Elbasha and colleagues [7], is complicated by the fact that marginal costs and Benefits, and hence the optimal strategy, depend on the current coverage levels.
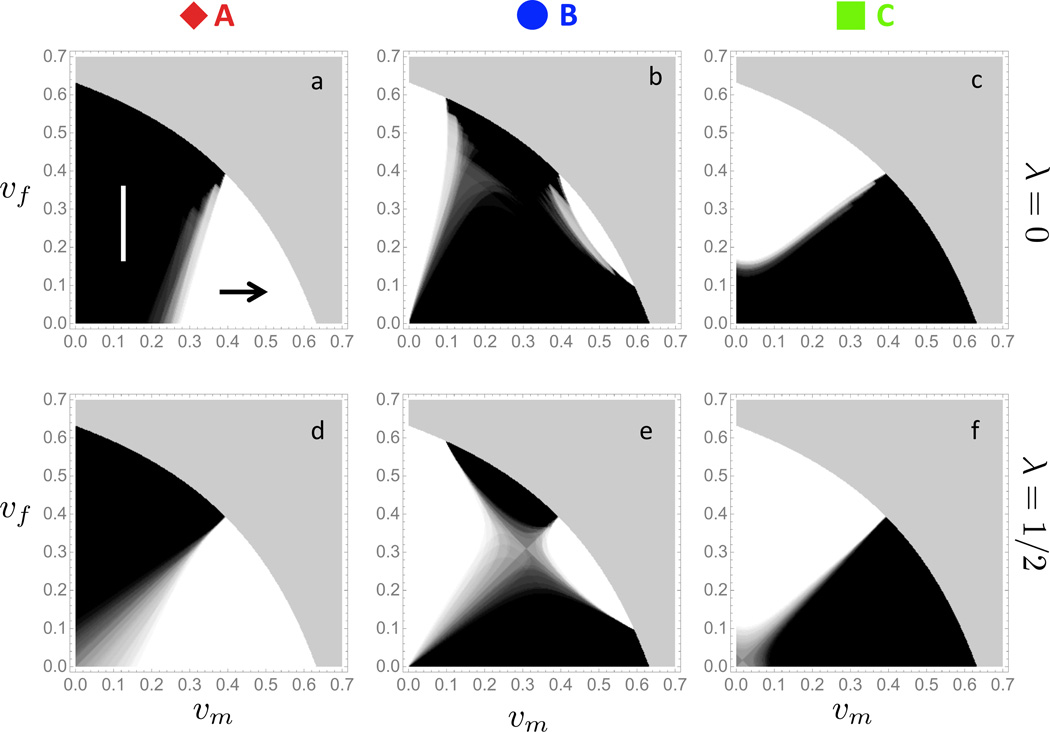
We present the results of our analysis in the form of a “roadmap to herd immunity” as shown in Figure 6. More precisely, for each level of coverage corresponding to a point in the (υm, υf)-plane, we calculate the locally optimal strategy as follows. First, we compute the marginal benefit to marginal cost ratio of vaccinating males, , and the corresponding quantity for females, . If rm > rf at the given coverage level, then it is marginally more effective to allocate new resources towards the vaccination of males. Conversely, if rm < rf at the current coverage level, then vaccinating more females is marginally more effective. To quantify the uncertainty introduced by the 26 different parameter combinations in the Posterior Set, we proceeded as follows. For each coverage level (υm, υf), we only retained the parameter sets that were endemic (ℛ* > 1), and eliminated all others. Next, we determined the optimal strategy for the endemic parameter combinations, added their individual “votes” and normalized so that the uncertainty is visually represented in color between black (spend new resources on females) and white (spend new resources on males). As illustrated in Figure 6, the magnitude of λ (rows) and the convexity of the cost-curve (columns) have a significant impact on the locally optimal strategy.
Figure 6. Roadmap to herd immunity.
The optimal allocation of new resources is analyzed as a function of current coverage levels υm and υf across the 26 Posterior Sets. Plain black regions (↑) indicate zones of current coverage levels in which allocating additional resources towards females is most effective for all Posterior Sets; plain white regions (→) indicate zones in which allocating resources towards males is most effective for all Posterior Sets; regions where the 26 Posterior Sets exhibit disagreement with respect to optimal allocation, the color interpolates between black (increase in female coverage is optimal) and white (increase in male coverage is optimal) according to the respective number of votes for either strategy; the grey zone in the upper right corner of each panel corresponds to herd immunity conferring coverage levels (ℛ* < 1). The following combinations of cost curves (see Figure 2a for reference) and λ values are examined: (a) cost curve A and λ = 0, (c) cost curve B and λ = 0, (c) cost curve C and λ = 0, (d) cost curve A and λ = 1/2, (e) cost curve B and λ = 1/2, (f) cost curve C and λ = 1/2. (Online version in color.)
4 Discussion
In most countries with HPV vaccine programs, male vaccine coverage is low in comparison with female coverage. Whether allocation of resources to increase male vaccination is more effective than continuing to vaccinate females alone remains a subject of debate among experts. Several groups have addressed this issue using mathematical modeling [7–15], but there is currently no consensus on an optimal vaccination strategy. However, recent empirical findings may shed new light onto the ongoing debate about optimal resource allocation. In fact, the coverage level of HPV vaccination among US females has stagnated over the past three years, and there is increasing opposition among parents towards getting their daughters vaccinated [16, 37]. These circumstances are likely to result in significant coverage-dependent marginal costs of vaccine administration, because a further increase in coverage will require costly education and outreach programs to reach the unvaccinated population. In light of these findings, we developed an agent-based model of adolescent sexual networks to examine the impact of coverage-dependent marginal costs on optimal vaccination strategies against HPV. Our model framework accounts for several aspects of real-world sexual networks, such as time-ordered and concurrent relationships, as well as assortativity by age and sexual activity levels. 26 Posterior Sets (Table 8) for the main disease parameters (gender specific transmission rates and clearance rates) were inferred by fitting the model to US prevalence data before and after introduction of the vaccine, and we accounted for all Posterior Sets when presenting the simulation results. Focusing on the two scenarios of pre-existing and new vaccination programs, our results suggest that if the costs associated with vaccinating males are close to those associated with vaccinating females, then coverage-dependent, increasing marginal costs favor vaccination strategies that entail immunization of both genders. The potential impact of increasing marginal administration costs has been previously noted [7, 13], but not formally modeled. To our knowledge, this is the first study to explicitly address the issue of coverage-dependent marginal costs in the context of HPV vaccination.
4.1 Global Analysis
First, we considered the problem of optimal allocation of fixed resources in Section 3.1, assuming gender symmetric cost curves and uniform vaccine distribution. Specifically, we asked when the optimal allocation of resources would involve “mixed” strategies, that is vaccinating positive fractions of both males and females. We found that the nature of the coverage-dependent marginal costs plays a significant role in determining the optimal allocation of resources. While the optimal strategy entails female-only vaccination for linear cost curves (curve A), an increase in convexity in the cost curves (curves B and C) means a shift of the optimal strategy towards equal distribution of resources among males and females, see Figure 2.
Next, we relaxed the assumption of gender symmetry in the cost curves in Section 3.2. Acknowledging that the marginal administration costs may – e.g. due to a general lack of awareness of the role of HPV in diseases other than cervical cancer – be higher for males than females, we assessed optimal resource allocation for asymmetric cost curves. We found the implications of asymmetry to depend on the convexity of the cost curves, see Figure 4. In the case of mildly convex cost curves (curve B), increasing the degree of asymmetry (curves B1 and B2) pushes the optimal strategy from “mixed” back to “female-only” vaccination. In the case of a more convex cost curve (curve C), the optimal strategy remains “mixed”, even when the male marginal costs are 25–50% higher than the female marginal costs (curves C1 and C2).
To conclude the discussion of global resource allocation, we assessed how a possible association between sexual activity and vaccine uptake would impact the optimal strategy in Section 3.3. Here, we found that a negative correlation between sexual activity and vaccine uptake has very little impact on the optimal strategy, see Figures 5a and 5b. This is due to the fact that a large fraction of individuals belongs to the the lower sexual activity groups L0 and L1, and hence uniform uptake across the population is virtually identical to negatively correlated uptake across the activity levels. In contrast, if vaccine uptake is positively correlated with sexual activity, see Figures 5c and 5d, then the overall vaccine benefit increases independently of the cost curve, and increasing convexity (curves B and C) results in disease eradication across all combinations of male and female vaccine coverage.
4.2 Local Analysis
Next, we assessed optimal allocation of new resources in the case of countries with a pre-existing vaccine program, such as the USA. From the results presented in Figure 6, it is clear that the optimal allocation depends critically on the value of the sex-specific disease burden λ and the nature of the marginal cost curves, and that any future recommendation will require an empirical assessment of these curves. In particular, considering the current coverage in the USA (υm = 13.9%; υf = 37%), the optimal strategy changes from “spend new resources on females” in the case of a linear cost curve (curve A) to “spend new resources on males” in the case of convex cost curves (curves B and C).
Our results have implications beyond the USA. First, countries that have not fully implemented an HPV vaccination program should carefully consider the costs and Benefits of both-sex vs girls-only vaccination. In fact, our results suggest that the highest benefit from a vaccine program may be achieved with a both-sex strategy, provided that the there are considerable coverge-dependent marginal costs, and provided that these costs are comparable in magnitude between males and females. Second, a nine-valent vaccine is currently in development, with the potential to prevent up to 90% of cervical cancers [38]. Particularly in settings where organized screening is not currently available, the degree of reduction through vaccination could be comparable, or perhaps even better, than screening. Policy makers with limited resources might be faced with the choice of introducing a screening program or a vaccination program, in which case both-sex vaccination may play an important role.
4.3 Limitations
When interpreting the above results, it is important to be aware of the various limitations that come with the chosen modeling approach.
In a trade-off between realism and model simplicity, we restricted our modeling approach to a closed sexual network of 14–18 years old adolescents, representative of the setting of e.g. a high school or a small town. This choice reduces the model complexity and the number of parameters considerably, but it comes with the limitation that relationships outside the network cannot be accounted for explicitly. Since up to 35–40% of females aged 15–19 have sexual relationships with males who are 3 or more years older [39], we performed additional simulations to assess the sensitivity of our results to the presence of relationships between females in the network with older males outside the network, see Appendix E. Since 20–29 years old males have higher prevalence levels of HPV-16/18 than younger males inside the network, the external relationships lead to an overall increase in disease burden inside the network. However, we found that adding external relationships did not change the qualitative nature of the benefit curves: mixed vaccination strategies remained optimal for sufficiently nonlinear cost curves.
Our choice of four different sexual activity levels (L0–L4), together with the parametrization of the corresponding partnership initiation and dissolution rates, is likely to have a significant impact on the network topology and the spread of the virus across the cohort. The average activity distribution of 25% (fraction of individuals in activity level L0), 53% (L1), 20% (L2), and 2% (L3), puts a rather large weight on the lower end of the sexual activity spectrum (L0 and L1). Even though the prior ranges used for the sexual activity levels are based on epidemiological data, see Appendix A.3 for details, it is important to emphasize that different activity weights (e.g. more individuals in the higher activity levels) could yield quantitative changes in our results. This limitation is particularly relevant for the vaccine assortativity analysis of Section 3.3, which depends strongly on the activity distribution.
Another important determinant of the network connectivity is the degree of concurrency. To calibrate our sexual network model, we used the degree distribution of a real-life high school network as reported by Bearman et al. [23]. Even though Bearman and colleagues performed, to our knowledge, the most comprehensive study of an adolescent sexual network to date, their study has several limitations, which in turn may have influenced the results presented in the current study. More precisely, the students in the Bearman network may not have been representative of students from similar schools [23], and the number of reported relationships was truncated, which may have introduced considerable bias in the inferred degree distribution [40].
In our model, sexual mixing is explicitly assortative by gender, age and sexual activity level. However, there are a number of additional factors such as socioeconomic status and race/ethnicity that have been shown to determine sexual mixing patterns [41]. Since these attributes are not accounted for the in the current model, we cannot comment on their potential impact on the predicted Benefits under increased male vaccination.
Since we focused on prevalence of genital HPV-16/18 infections in the population of 14–18 years old adolescents, our framework is not amenable to a complete cost-effectiveness analysis. Costs incurred by infections with low-risk HPV types causing genital warts, as well as oral and anal HPV infections would also need to be included. Additionally, the incidence of most HPV-related cancers is much smaller in individuals aged 14–18 years than in subpopulations of older individuals, and an age-structured modeling approach would be required to assess the costs due to HPV-related cancers. Nevertheless, sufficient prevalence levels in adolescent populations are critical for the survival of HPV in the entire population, and incidence levels peak – particularly in females – at a young age [42, 43]. Therefore, reduction of the virus among adolescents is the crucial first step towards herd immunity.
Finally, our models only describe heterosexual relationships, and it is a priori not clear how the inclusion of bi- and homosexual individuals would affect our conclusions. Importantly, sexual orientation is usually not defined by the age of vaccine administration, which makes it impossible to target groups by sexual orientation. This issue will be addressed in future work.
In summary, our analysis shows that coverage-dependent marginal costs may, depending on their true magnitude, play a critical role in optimizing the distribution of resources among female and male vaccination programs, both in the USA and elsewhere. In light of our findings, the conclusions of previous cost-benefit analyses of male vaccination that employed linear cost curves may need to be re-evaluated carefully. Most importantly, since there is currently a lack of empirical data on the marginal administration costs of HPV vaccination, more research is needed to quantify the true cost curves and make specific policy recommendations.
Highlights.
Evidence suggests that marginal HPV vaccination costs may increase with uptake
We assess the impact of increasing marginal costs on optimal resource allocation
We find that increasing marginal costs may favor both-sex HPV vaccination
More empirical research on cost curves is needed for policy recommendations
Acknowledgments
The authors are grateful to Rick Durrett and Cathrine Hoyo for stimulating discussions. MDR is thankful to Xiaoyu Jiang for fruitful conversations.
Appendix
A Agent-based model
A.1 Model structure and dynamics
Network structure
The model consists of a closed cohort of sexually active adolescents, containing N females and N males. Individuals enter the cohort at age 14 and leave when they turn 19 years old. Aging of the population is modeled deterministically, and an equal number of individuals are in each age group. The 2N individuals (graph nodes) can engage in sexual relationships (graph edges), break up existing relationships, and transmit HPV-16/18 along active network edges. Each node in the network has three characteristics: gender g ∈ {m, f}, age a ∈ {1, 2, …, 5} (where a = 1 stands for age group 14, etc.) and sexual activity level l ∈ {0, 1, 2, 3} (where l = 0 corresponds to the lowest activity level L0, etc.).
Network dynamics
Similarly to previous studies [20, 22], we adopt a female-centric perspective to define the network dynamics. Each female initiates new relationships at rate e1(a, l), depending on both her age (a) and activity level (l). Once a female node decides to initiate an edge, a male node is chosen according to the assortative mixing matrix M(a, l, a′, l′), whose elements describe the probability that a female of type (a,l) chooses a male of type (a’,l’). We allow for concurrent relationships, but enforce a penalty for increasing per-node concurrency as follows: if a female node chooses a male node (according to the mixing matrix M), the node is accepted with probability (#f + 1)−1(#m + 1)−1, where #f and #m are the number of already active relationships of the female and male node, respectively. Like this, the acceptance probability is 1 for two single nodes, and decreases with an increasing number of already existing relationships. If a relationship is rejected, we repeat the process and pick a new male in agreement with the assortativity matrix M, until a partner is accepted. One key advantage of this simple rejection rule is its independence from additional parameters. Furthermore, without this rule, we were unable to fit the cumulative degree distribution of a real-life sexual network, see Appendix A.4. Finally, edges are dissolved by the female node at rate e0(a, l).
Disease dynamics
Each node is either susceptible (S), infected (I) or recovered (R). Incoming nodes are either susceptible or vaccinated, in which case they fall into the category of recovered nodes (assuming a 100% vaccine efficacy throughout the study). Transmission of the virus can take place along active edges between infected and susceptible nodes. The transmission rates are gender specific: βmf between infected male and susceptible female, and βfm between infected female and susceptible male. Infected individuals clear the virus at rates σf, σm. Upon clearing the virus, previously infected nodes either develops immunity with probability pf, pm and becomes recovered, or go back to the pool of susceptible nodes otherwise.
A.2 Simulations
The model was simulated for N = 1500 in discrete time, with a time stepping interval of Δt = 0.025 years (≈ 10 days). All simulations were performed with the software MATLAB (© 1984–2014, The Mathworks, Inc). At each time step, the network parameters were re-sampled (see below for details), and we proceeded in 5 steps.
Edge dissolution: each female engaged in at least one relationship dissolves one of her relationships with probability Δt e0(a, l).
Edge formation: each female activates an edge with probability Δt e1(a, l), and chooses a male partner according to the mixing matrix M and the rejection rule for concurrent relationships (see above).
Recovery of infected nodes: each infected individual clears its infection with probability Δt σf or Δt σm, and either becomes recovered (probability pf or pm) or susceptible otherwise.
Disease transmission: along active edges between susceptible and infected individuals the virus is transmitted with probability Δt βmf if the male is infected, and with probability Δt βfm if the female is infected.
Once a year, the individuals in age group a = 5 leave the cohort, and the remaining age groups move up to the next age level. The now empty age group a = 1 is filled with the incoming group of susceptible and recovered (if vaccinated) individuals.
A.3 Network parametrization
To parametrize the network dynamics, we relied in part on prior estimates from the work of Van de Velde et al. [22]. Since their network model is slightly different to ours (they do not allow for concurrent relationships), we made the following adjustments.
-
In [22], only single women can initiate a relationship. Therefore, our edge formation rate e1(a, l) is related to [22]’s female relationship initiation rate θ(f, a, l) according to
where Ntotal(f, a, l) and Nsingle(f, a, l) are the total number of females and the number of single females in compartment (a, l) at stationarity, respectively. Noticing that in [22] the expected number of singles in compartment (a, l) is
where σ̂(a, l) is [22]’s edge dissolution rate (we denote their σ by σ̂ to avoid confusion with our clearance rate σ), we find that
where(4) Because our model does, in contrast to Van de Velde’s model, allow for concurrency, and because (4) is only an approximation, we introduced an ad hoc scaling factor ℰ and replaced (4) by
Importantly, ℰ is the only free parameter in the network dynamics, see below for details on the inference of ℰ.(5) Our relationship dissolution rate e0(a, l) corresponds directly to [22]’s dissolution rate σ̂(a, l).
- To characterize the mixing matrix M, we defined
where Λ(a, a′) is the age mixing matrix between females of age a and males of age a′, and Γ(l, l′|a′) is the activity level mixing matrix between females of activity l and males of activity l′, conditioned on having chosen the age group a′ for the potential male partner. To parametrize the age mixing matrix Λ(a, a′), we used empirical data on age assortativity in sexual relationships from [44]. Since our model cohort is closed, we discarded relationships that are connected to the outside of the 14–18 year bracket, and renormalized the in-cohort mixing probabilities reported in Table 2 of [44].
- For the sexual activity mixing matrix Γ(l, l′|a′) we followed the rationale in [22]. After correction of their expression for Γ (see [45] for details), we obtained
where N(m, a′, l′) is the number of males in group (a′, l′), θ(m, a′, l′) is the partnership formation rate of males in group (a′, l′), and W(l, l′) is the preference matrix, defined in terms of the assortative degree parameter κ as(6)
Table 2. Age mixing matrix Λ(a, a′).
Each entry specifies the probability of a female in age group a to choose a male partner in age group a′. Values derived from Table 2 in [44] after excluding partnerships outside the model age range of 14–18 years.
| a\a’ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0.277 | 0.198 | 0.197 | 0.197 | 0.131 |
| 2 | 0 | 0.318 | 0.228 | 0.227 | 0.227 |
| 3 | 0 | 0 | 0.54 | 0.23 | 0.23 |
| 4 | 0 | 0 | 0 | 0.705 | 0.295 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Regarding the numerical parameter values (see Table 1 for an overview), we performed a dynamic re-sampling scheme for most network parameters to account for parameter uncertainty. We classified the networks parameters into the following groups:
Group 1. The age mixing matrix Λ(a, a′) and the scaling factor ℰ were kept constant throughout all simulations. Λ(a, a′) is given in Table 2 and ℰ was obtained by inference, see Table 1.
- Group 2. The parameters θ(g, a, l), σ̂(a, l) and κ, which together specify the edge rates e0 and e1 as well as the activity matrix Γ(l, l′|a′), were re-sampled dynamically after each time step, using prior ranges obtained from the literature, see Tables 3 and 4 for the ranges of θ and σ̂, respectively, and Table 1 for the prior range of κ. For σ and κ, we sampled from uniform distributions between the lower and upper bounds of the reported prior ranges. The sampling for θ was more involved. In fact, since sexual activity generally increases between ages 14 and 18, we assumed θ(g, a, l) to be a linearly increasing function of age. More precisely, for each update we drew two random numbers r1 and r2 uniformly on [0,1] and [r1, 1], respectively, and then determined θ(g, a, l) in terms of the lower θL(g, a, l) and upper bounds θU(g, l) of the prior range as follows:
Group 3. The distribution of incoming individuals across the sexual activity levels was done probabilistically, and the respective fractions in each level, ρ(l), were drawn uniformly from their prior range (see Table 5) and then normalized to sum to unity. The prior ranges in Table 5 were derived in the Supporting Information of [22] based on data from the Canadian PISCES study [51]. In short, the four groups L0–L3 correspond to 0–2, 2–10, 11–39 and 40+ lifetime sex partners, and normal and abnormal Pap cohorts in the PISCES study were used to derive upper and lower bounds for the fraction of females in the respective activity groups. The male prior ranges for the different activity levels coincide with the female prior ranges, but males have higher partnership initiation rates than females in the same activity group, see Table 3.
Table 3. Relationship initiation rates θ(g, a, l): prior ranges.
Lower θL and upper θU bounds of prior ranges for θ(f, a, l) and θ(m, a, l) as reported in [22]. Units for rates: per year.
| θL(f, l) | θU(f, l) | θL(m, l) | θU(m, l) | |
|---|---|---|---|---|
| l=0 | 0.44 | 1.05 | 0.53 | 1.73 |
| l=1 | 0.74 | 1.78 | 0.9 | 2.94 |
| l=2 | 2.04 | 4.31 | 2.47 | 7.12 |
| l=3 | 4.29 | 8.74 | 5.21 | 14.41 |
Table 4. Relationship dissolution rates σ(f, a, l): prior ranges.
Lower σL and upper σU bounds of prior ranges for σ(f, a, l) as reported in [22]. Units for rates: per year.
| σ̂L(f, l) | σ̂U(f, l) | |
|---|---|---|
| l=0 | 0.1 | 0.74 |
| l=1 | 0.12 | 0.88 |
| l=2 | 0.14 | 1.04 |
| l=3 | 0.32 | 2.4 |
Table 5. Fraction of individuals in different sexual activity groups: prior ranges.
Lower ρL and upper ρU bounds of prior ranges for the estimated fraction of individuals in each sexual activity group as reported in [22].
| ρL(l) | ρU(l) | |
|---|---|---|
| l=0 | 0.16 | 0.36 |
| l=1 | 0.41 | 0.67 |
| l=2 | 0.14 | 0.27 |
| l=3 | 0.01 | 0.02 |
A.4 Network calibration
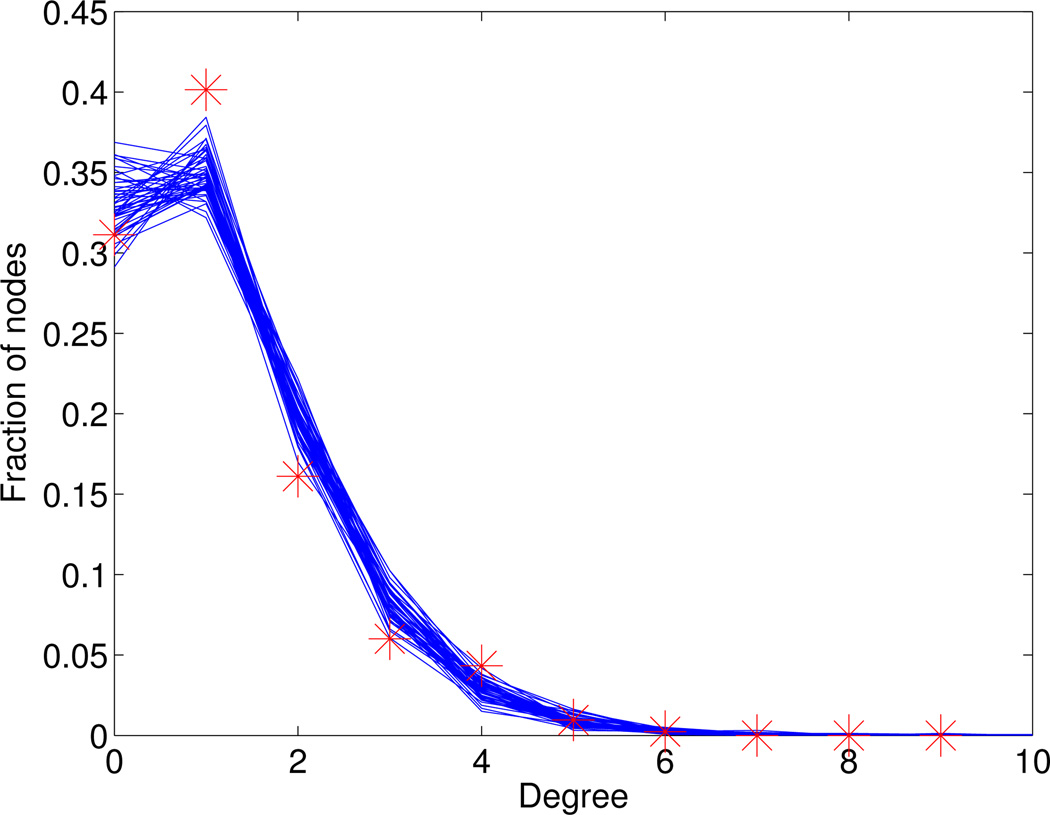
The only free parameter in the above network model is the scaling factor ℰ appearing in the definition of e1 in (5). To estimate the value of ℰ, we used the cumulative graph of a real-life high school sexual network [23]. From Figure 2 in [23], we extracted the degree distribution of the cumulative graph over 18 months, see Table 6. Running our network model to steady-state and then computing the cumulative graph over an 18 months period, we compared the obtained degree distribution to the real-life distribution from [23], and estimated ℰ = 1.5, using a least square-fit starting from a prior range ℰ ∈ [1,2]. The optimal fit is shown in Figure 7.
Table 6. Empirical degree distribution of adolescent sexual network.
From Figure 2 in [23] we determined the degree distribution (total population) of the cumulative sexual network graph over a period of 18 months in Jefferson high school.
| Degree | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7+ |
|---|---|---|---|---|---|---|---|---|
| Fraction | 0.3113 | 0.4014 | 0.1611 | 0.0601 | 0.0433 | 0.0096 | 0.0024 | 0 |
Figure 7. Degree distribution of sexual network.
For ℰ = 1.5, the network is first run until stationarity, and then the degree distribution of the cumulative network graph over 18 months (50 simulations, solid lines) is compared to the empirical degree distribution (star) as reported in [23].
A.5 Disease dynamics parametrization
The disease-related parameters are the transmission rates βmf and βfm, the clearance rates σm/f and the probabilities pm/fof developing immunity agai of developing immunity against re-infection with HPV-16/18 after clearing the virus. Following the group definitions introduced for the network parameters in Section A.3, the probabilities pm/f were placed into Group 3 (updated for each incoming cohort), and were assumed to be person-specific, that is they were sampled uniformly at random from the ranges in Table 1 for each incoming individual. The remaining disease parameters βmf, βfm and σm/f were used to fit the model-derived prevalence levels to empirically measured prevalence data of infections with HPV-16/18 among adolescents. Based on evidence about gender-specific differences in transmission rates [46, 47], we introduced two independent rates βfm and βmf. Regarding the virus clearance, data suggests similar rates for males and females [49, 50], and hence we used a single rate σ = σm = σf. Of note, gender-related differences in the immune response are captured in the probabilities pm/f.
Data about the vaccine impact on prevalence levels is still scarce, and, to our knowledge, good estimates are only available for females, see [29]. The prevalence levels reported in [29] together with the corresponding vaccine uptake levels from the CDC [37] are summarized in Table 7. Even though [29] only reports on female prevalence levels, we are not aware of any evidence that there is a significant difference between pre-vaccine male and female prevalence levels, see also [52]. In particular, using the same calibration intervals for males and females is compatible with the very broad pre-vaccine estimates of 1.3–72.9% (males) and 14%–90% (females) in [53]. To infer posterior values for the transmission and clearance rates, we sampled 1000 parameter triples (βfm, βmf, σ) uniformly across prior ranges (see Table 1), ran 50 realizations of the process for each parameter triple over 30 years, time-averaged each realization between years 15 and 30, and finally averaged the 50 time-averages to obtain a representative prevalence level for each parameter triple. We only retained parameter sets that met the following criteria of a good fit. 1) Both male (Im/N) and female (If /N) pre-vaccine prevalence levels (year 2006) were within the 95% confidence interval reported in [29]. 2) Post-vaccine female prevalence levels (year 2010) were within the 95% confidence interval reported in [29]. According to this procedure, we retained a Posterior Set of 26 parameters triples (βfm, βmf, σ) among the 1000 tested sets, see Table 8.
Table 7. Prevalence intervals for model calibration.
All values in %. For female prevalence of HPV-16/18 before (2006) and after (2010) introduction of the vaccine we used 95% confidence intervals from [29]. In absence of reliable pre-vaccine prevalence estimates for males, we followed [52, 53] and used the same confidence intervals as for females. Vaccine uptake levels (υm, υf) as reported by the CDC [37].
| Year | If/N | υf | Im/N | υm |
|---|---|---|---|---|
| 2006 | [5.8, 8.7] | 0 | [5.8, 8.7] | 0 |
| 2010 | [2.5, 5] | 32 | - | 0 |
B Deterministic compartment model
B.1 Model description
To derive the deterministic CM, we neglect the heterogeneous network structure, i.e. we consider the continuous-time jump Markov process (Sm, Sf, Im, If,Rm,Rf)t on the complete bipartite graph. The transition rates for the male population then given by
| (7) |
The rates for the female population can easily be obtained by interchanging the m and f indices in (7). Next, we pass to the large population limit to average out the stochastic fluctuations in the system. To this end, it is convenient to introduce the sub-population fractions for all state variables as , where X ∈ {Im, If, Sm, Sf, Rm,Rf}. Using standard results from the theory of Markov processes, see e.g. [54], the large population limit (N → ∞) yields the following system of mean field equations for the male population fractions,
| (8) |
The mean field equations for the female population are obtained similarly by simply interchanging the indices m and f. Rescaling time as t = γ−1t̃ results in the following set of dimensionless parameters: β̃mf = βmf/γ, β̃fm = βfm/γ, σ̃m = σm/γ, σ̃f = σf/γ, and γ̃ = 1. Introducing the rescaled time in (8) and omitting tildes, we obtain
| (9) |
Naturally, we only study solutions of (9) such that (Sm, Sf, Im, If,Rm,Rf) ∈ [0,1]6 as well as
It is important to emphasize that the mean field equations (9) are not merely the large population limit of the full stochastic ABM introduced above. Indeed, we first discarded the network heterogeneity before taking the limit N → ∞. Nevertheless, we expect the original ABM to exhibit similar qualitative features as the jump-process (7) and the compartment model (9). This resemblance is illustrated by direct comparison of the qualitative features displayed in Figures 2 and 3.
The long-term dynamical behavior of the system (1) has been well-characterized. For certain parameter regimes, there is a disease-free equilibrium with (Im, If) = (0, 0), and it is stable if and only if the basic reproduction number ℛ* for the CM satisfies ℛ* ≤ 1. In the current context, ℛ* is defined as the expected number of same-sex secondary infections of an infected individual. In fact, the potentially asymmetric transmission βfm and βmf require that this number be defined atypically, and we define it as the expected number of secondary infections in the same sex, when a single infected individual is introduced to a susceptible population. The reason for this modified definition is so that ℛ* > 1 is the condition for the existence of an endemic, and the sex of the initially infected individual does not matter. It is possible for the expected number of males infected by a single initially infected female to be less than 1, and still have an endemic state (ℛ* > 0) in our model. In the case where our model is symmetric (parameters for males and females are identical), our definition of ℛ* is the square of the traditional reproduction number ℛ0. According to the above definition,
| (10) |
If ℛ* ≤ 1, then the disease-free equilibrium is globally asymptotically stable [55], a situation known as herd immunity. On the other hand, if ℛ* > 1, then the disease-free equilibrium is unstable, and there is exactly one endemic equilibrium point, given by (recall that all rates were rescaled by γ)
| (11) |
where β̅ = βmfβfm, s̄ ≡ (1+σf)(1+σm). Furthermore, if ℛ* > 1, then this endemic equilibrium is globally asymptotically stable, which means that the endemic equilibrium exists and is globally asymptotically stable if and only if ℛ* > 1 [55].
B.2 Model parametrization
The CM dynamics are characterized by 4 parameters only: 1/γ, which is the average time spent in the cohort, the gender-specific transmission rates βmf and βfm, as well as the clearance rate σ. While 1/γ is fixed to 5 years for our purposes, we used the 26 Posterior Sets from the ABM for the remaining parameters. In addition, the two transmission rates βfm and βmf were rescaled by a network connectivity parameter δ to account for the fact that the network structures in the ABM and the CM are inherently different. In other words, we replaced βmf and βfm by δβmf and δβfm, respectively. To obtain the best estimate of δ we proceeded analogously to the fitting procedure for the transmission and clearance rates in Section A.5: for each of the 26 Posterior Sets we estimated δ by fitting the model-derived pre- and post-vaccine prevalence levels to the empirical data in Table 7.
C Estimation of λ
By definition, λ is the average cost of a male genital infection relative to the cost of a female genital infection. To determine the average cost of an infection, we have to compute the probability that an infected individual will eventually develop precancer or cancer, and assess the costs incurred by the different types of HPV-associated diseases. More precisely, the average costs C̄f and C̄m for females and males are given by
| (12) |
where pf,i and pm,i are the gender-specific probabilities of progression from infection to disease of type i, cf,i is the gender-specific cost associated with diagnosis of disease type i, and Nf and Nm are the total numbers of diseases associated to infection with HPV-16/18. Once C̄m and C̄f have been estimated, the relative cost of male infections is given by
| (13) |
It remains to estimate the parameters in (12).
Diseases to be included for females are cervical intraepithelial neoplasia (CIN) 1, CIN 2, CIN 3, cervical cancer, vaginal cancer and vulvar cancer (Nf = 6). For males, we include penile cancer only (Nm = 1). Since we do not model anal or oral HPV infections or infections with low-risk types, we exclude anal and oropharyngeal cancers as well as genital warts for the estimate of λ.
To estimate the probability of progression, we first determine the fraction of cases associated with HPV for each cancer type. Then we calculate the risk of progression by combining the lifetime risk of HPV infection with the overall population incidence levels of the different cancers. For details see Table 9 and caption. Of note, CIN 1, 2 and 3, and cervical cancer are sequential disease stages, and we assume here that incident cases in either stage had gone unnoticed through the previous stages.
To estimate the disease-related costs, we use again the data from [14], see Table 10 below.
Table 9. Risk of progression.
The following estimates are used to calculate the above probabilities. 1) Fractions of cancers associated with HPV infection as reported in [2]: 100% for cervical cancer, and 40% each for vulvar, vaginal and penile cancers. 2) Lifetime incidence risk of the different cancers from Table 2 in Chesson et al. [14]. 3) An estimated 79% lifetime risk of HPV infection according to the study by Syrianen et al. [56].
| CIN 1 | CIN 2 | CIN 3 | Cervix | Vulva | Vagina | Penis | |
|---|---|---|---|---|---|---|---|
| pf | 5.8 · 10−3 | 3.6 · 10−3 | 1.5 · 10−3 | 1.6 · 10−4 | 2.4 · 10−5 | 7.6 · 10−6 | - |
| pm | - | - | - | - | - | - | 1.4 · 10−5 |
Table 10. Estimated costs per cancer case.
| CIN 1 | CIN 2 | CIN 3 | Cervix | Vulva | Vagina | Penis | |
|---|---|---|---|---|---|---|---|
| Cost | 1,959 | 3,642 | 4,135 | 33,894 | 35,693 | 19,697 | 18,528 |
Using the tabulated values (Tables 9 and 10) and equations (12) and (13), we find estimates of C̄m = 0.26, C̄f = 37.16 and estimated value of
Finally, we emphasize that our analysis does not include potential costs incurred by oral and anal HPV infections as well as infections with low-risk strains of HPV. Since this would require considering oral-anogenital HPV transmissions as well as explicit modeling of low-risk vaccine strains (HPV-6/11), our current framework is not suitable for a complete analysis.
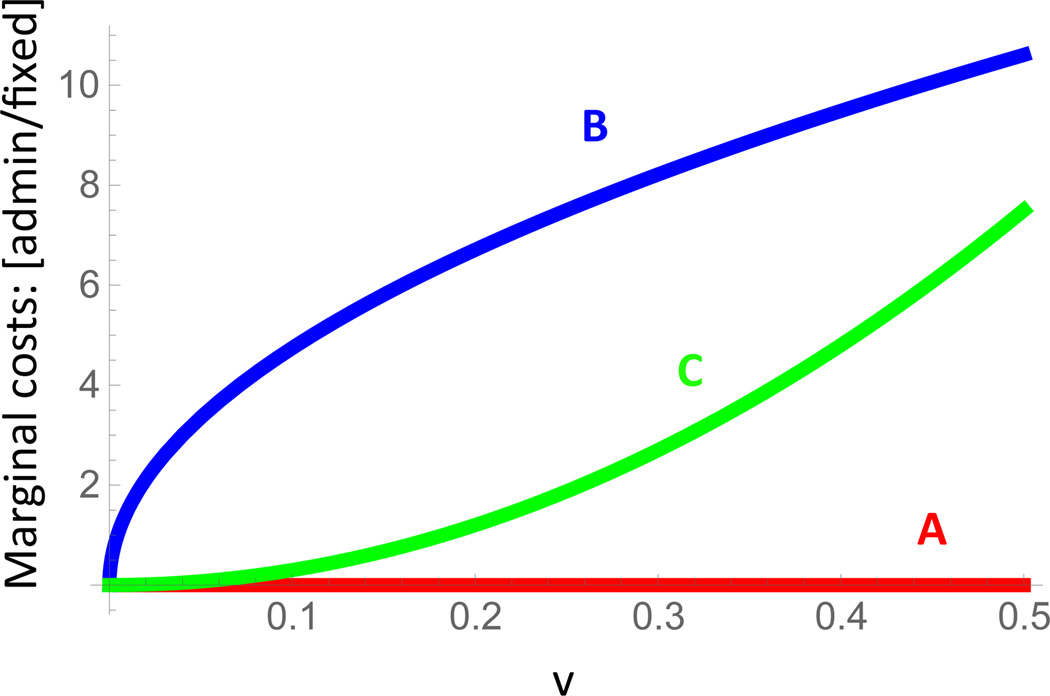
D Marginal costs: administration vs fixed
To provide a better understanding of the different cost function level sets in Figure 2a, the ratio of marginal costs of vaccine administration to marginal fixed costs (vaccine price) is shown for curves A, B, and C in Figure 8.
Figure 8. Ratio of marginal administration to marginal fixed costs.
For the cost function level sets in Figure 2a, the ratio of marginal costs of vaccine administration to marginal fixed costs (vaccine price) is shown for increasing single sex coverage v. For curve A there are no marginal administration costs, and the mildly convex cost curve has steeper marginal administration costs (relative to marginal fixed costs) than the more convex curve C.
E The role of external relationships
The model developed in this manuscript consists of a closed dynamic network of 14–18 years old adolescents. In particular, it does not account for potential relationships with older sex partners outside the network. Since an estimated 37% of adolescent females have relationships with males who are 3 or more years older [39], we assess here the impact of external relationships on the model results. To this end, and according to the above estimate, we introduce an internal partnership initiation rate , where e1(a, l) is the partnership initiation rate used in all other simulations, and an external partnership initiation rate . The network internal dynamics remain unchanged except for the replacement of e1 by , whereas the external relationships are modeled as follows:
Each female who is currently not in an external relationship initiates a relationship with a male aged 20–29 years at rate .
The external male entering the sexual relationship with the internal female is assumed to be infected with HPV-16/18 with probability pext.
The relationship with the external edge is dissolved at the usual rate e0(a, l). During an ongoing relationship with an infected external male, a susceptible internal female can get infected according to the male-to-female transmission rate βmf.
The only additional parameter in these dynamics is pext, the likelihood of an external male being infected with HPV-16/18. To assess the most extreme scenario – corresponding to a maximal injection of virus from outside the network – we assumed that the prevalence of HPV-16/18 in external males corresponds to the peak-prevalence in absence of any vaccine, only reduced by the male vaccine uptake υm. In particular, we ignored further reductions due to herd immunity effects because these can only be estimated by explicitly extending the model to account for older individuals. Due to a lack of data, the peak prevalence of HPV-16/18 among men aged 20–29 years needed to be estimated indirectly. Thereby, we assumed that the ratio of peak HPV-16/18 prevalence between males and females before the introduction of the vaccine is equal to the ratio of peak incidence of genital warts between males and females. The estimated pre-vaccine peak prevalence of HPV-16/18 in females aged 20–29 years was estimated at 15% [29]. Next, based on Figure 2 in Patel et al. [57], we estimated the ratio of male to female peak incidence rates of genital warts to be approximately 0.79. Combining these estimates, we found an estimated peak prevalence of HPV-16/18 in males aged 20–29 years of 12%, and the respective estimate for the HPV-16/18 prevalence of external males in our simulations is pext = 0.12 · υm. The corresponding simulation results for the most extreme scenario (pext) as well as an intermediate scenario (0.5·pext) are shown in Figure 9. As expected, the relationships of internal females with external males (whose HPV-16/18 prevalence is higher than the one of internal males) leads to an overall decrease of the vaccine benefit, see Figure 2 for comparison. For both values of HPV prevalence among external males, the female-only benefit (λ = 0) is roughly one percentage-point lower than the population benefit (λ = 1/2), compare Figures 9a) and c) with b) and d), respectively. This is due to the fact that accounting for relationships with external males increases primarily the prevalence of HPV among internal females, but not males. Finally, and most importantly, we remark that the qualitative observation from Figure 2 remains unaltered when accounting for relationships with older males: the vaccine benefit is highest for mixed vaccination regimes for the convex cost curves B and C.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest
MDR, KM, DPH and DJS have no conflicts of interest. ERM has received research funding from Merck, Inc., manufacturer of Gardasil, in the past, and currently serves as a consultant to Merck on issues regarding HPV vaccination. He is currently receiving research support from GSK, Inc., manufacturer of Cervarix, through a contract with Duke University, to evaluate the reproductive outcomes and associated costs resulting from HPV-related cervical neoplasia. Neither Merck or GSK have been involved in any way with the research described in this paper, and the results have not been presented or shared with employees or external consultants of either company.
References
- 1.Crow JM. HPV: The global burden. Nature. 2012;488(7413):S2–S3. doi: 10.1038/488S2a. [DOI] [PubMed] [Google Scholar]
- 2.Jemal A, Simard EP, Dorell C, Noone AM, Markowitz LE, et al. Annual report to the Nation on the Status of cancer, 1975–2009, Featuring the Burden and trends in Human Papillomavirus (HPV)–Associated cancers and HPV Vaccination coverage levels. J Natl Cancer Inst. 2013;105(3):175–201. doi: 10.1093/jnci/djs491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Simard EP, Ward EM, Siegel R, Jemal A. Cancers with increasing incidence trends in the United States: 1999 through 2008. CA - Cancer J Clin. 2012;62(2):118–128. doi: 10.3322/caac.20141. [DOI] [PubMed] [Google Scholar]
- 4.Shiels MS, Pfeiffer RM, Chaturvedi AK, Kreimer AR, Engels EA. Impact of the HIV epidemic on the incidence rates of anal cancer in the United States. J Natl Cancer I. 2012;104(20):1591–1598. doi: 10.1093/jnci/djs371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.for Disease Control C, Prevention. HPV Vaccine is Recommended for Boys; 2014. [accessed August-2014]; [Online]. http://www.cdc.gov/features/hpvvaccineboys/.
- 6.Stokley S, Jeyarajah J, Yankey D, Cano M, Gee J, Roark J, et al. Human Papillomavirus Vaccination Coverage Among Adolescents, 2007–2013, and Postlicensure Vaccine Safety Monitoring, 2006–2014, United States. MMWR Morbidity and mortality weekly report. 2014;63(29):620–624. [PMC free article] [PubMed] [Google Scholar]
- 7.Elbasha EH, Dasbach EJ. Impact of vaccinating boys and men against HPV in the United States. Vaccine. 2010;28(42):6858–6867. doi: 10.1016/j.vaccine.2010.08.030. [DOI] [PubMed] [Google Scholar]
- 8.Elbasha EH, Dasbach EJ, Insinga RP. Model for assessing human papillomavirus vaccination strategies. Emerg Infect Dis. 2007;13(1):28. doi: 10.3201/eid1301.060438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Taira AV, Neukermans CP, Sanders GD. Evaluating human papillomavirus vaccination programs. Emerg Infect Dis. 2004;10(11):1915. doi: 10.3201/eid1011.040222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kim J, Andres-Beck B, Goldie S. The value of including boys in an HPV vaccination programme: a cost-effectiveness analysis in a low-resource setting. Brit J Canc. 2007;97(9):1322. doi: 10.1038/sj.bjc.6604023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kim JJ, Goldie SJ. Cost effectiveness analysis of including boys in a human papillomavirus vaccination programme in the United States. Brit Med J. 2009;339 doi: 10.1136/bmj.b3884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brisson M, van de Velde N, Franco EL, Drolet M, Boily MC. Incremental impact of adding boys to current human papillomavirus vaccination programs: role of herd immunity. J Infect Dis. 2011;204(3):372–376. doi: 10.1093/infdis/jir285. [DOI] [PubMed] [Google Scholar]
- 13.Bogaards JA, Kretzschmar M, Xiridou M, Meijer CJ, Berkhof J, Wallinga J. Sex-specific immunization for sexually transmitted infections such as human papillomavirus: insights from mathematical models. PLoS medicine. 2011;8(12):e1001147. doi: 10.1371/journal.pmed.1001147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chesson HW, Ekwueme DU, Saraiya M, Dunne EF, Markowitz LE. The cost-effectiveness of male HPV vaccination in the United States. Vaccine. 2011;29(46):8443–8450. doi: 10.1016/j.vaccine.2011.07.096. [DOI] [PubMed] [Google Scholar]
- 15.Seto K, Marra F, Raymakers A, Marra CA. The Cost Effectiveness of Human Papillomavirus Vaccines. Drugs. 2012;72(5):715–743. doi: 10.2165/11599470-000000000-00000. [DOI] [PubMed] [Google Scholar]
- 16.Darden PM, Thompson DM, Roberts JR, Hale JJ, Pope C, Naifeh M, et al. Reasons for not vaccinating adolescents: National Immunization Survey of Teens, 2008–2010. Pediatrics. 2013;131(4):645–651. doi: 10.1542/peds.2012-2384. [DOI] [PubMed] [Google Scholar]
- 17.Durrett R. Some features of the spread of epidemics and information on a random graph. P Natl Acad Sci USA. 2010;107(10):4491–4498. doi: 10.1073/pnas.0914402107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moody J. The importance of relationship timing for diffusion. Soc Forces. 2002;81(1):25–56. [Google Scholar]
- 19.Carvalho AM, Goncalves S. Epidemics Scenarios in the Romantic Network. PloS One. 2012;7(11):e49009. doi: 10.1371/journal.pone.0049009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Malagón T, Joumier V, Boily MC, Van de Velde N, Drolet M, Brisson M. The impact of differential uptake of HPV vaccine by sexual risks on health inequalities: A model-based analysis. Vaccine. 2013;31(13):1740–1747. doi: 10.1016/j.vaccine.2013.01.026. [DOI] [PubMed] [Google Scholar]
- 21.Goodreau SM. A decade of modelling research yields considerable evidence for the importance of concurrency: a response to Sawers and Stillwaggon. Journal of the International AIDS Society. 2011;14(1):12. doi: 10.1186/1758-2652-14-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Van de Velde N, Brisson M, Boily MC. Understanding differences in predictions of HPV vaccine effectiveness: A comparative model-based analysis. Vaccine. 2010;28(33):5473–5484. doi: 10.1016/j.vaccine.2010.05.056. [DOI] [PubMed] [Google Scholar]
- 23.Bearman PS, Moody J, Stovel K. Chains of Affection: The Structure of Adolescent Romantic and Sexual Networks1. American Journal of Sociology. 2004;110(1):44–91. [Google Scholar]
- 24.Doherty IA, Minnis A, Auerswald CL, Adimora AA, Padian NS. Concurrent partnerships among adolescents in a Latino community: the Mission District of San Francisco, California. Sex Transm Dis. 2007;34(7):437–443. doi: 10.1097/01.olq.0000251198.31056.7d. [DOI] [PubMed] [Google Scholar]
- 25.Rosenberg MD, Gurvey JE, Adler N, Dunlop MB, Ellen JM. Concurrent sex partners and risk for sexually transmitted diseases among adolescents. Sex Transm Dis. 1999;26(4):208–212. doi: 10.1097/00007435-199904000-00004. [DOI] [PubMed] [Google Scholar]
- 26.Chaturvedi AK, Katki HA, Hildesheim A, Rodríguez AC, Quint W, Schiffman M, et al. Human papillomavirus infection with multiple types: pattern of coinfection and risk of cervical disease. J Infect Dis. 2011;203(7):910–920. doi: 10.1093/infdis/jiq139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Goldman B, Rebolj M, Rygaard C, Preisler S, Ejegod DM, Lynge E, et al. Patterns of cervical coinfection with multiple human papilloma virus types in a screening population in Denmark. Vaccine. 2013 doi: 10.1016/j.vaccine.2012.12.084. [DOI] [PubMed] [Google Scholar]
- 28.Evander M, Edlund K, Gustafsson Å, Jonsson M, Karlsson R, Rylander E, et al. Human papillomavirus infection is transient in young women: a population based cohort study. J Infect Dis. 1995;171(4):1026–1030. doi: 10.1093/infdis/171.4.1026. [DOI] [PubMed] [Google Scholar]
- 29.Markowitz LE, Hariri S, Lin C, Dunne EF, Steinau M, McQuillan G, et al. Reduction in Human Papillomavirus (HPV) Prevalence Among Young Women Following HPV Vaccine Introduction in the United States, National Health and Nutrition Examination Surveys, 2003–2010. J Infect Dis. 2013 doi: 10.1093/infdis/jit192. [DOI] [PubMed] [Google Scholar]
- 30.for Disease Control C, Prevention. HPV Vaccination for Preteens and Teens; 2014. [accessed July-2014]; [Online]. http://www.cdc.gov/vaccines/who/teens/vaccines/hpv.html.
- 31.Bishai D, McQuestion M, Chaudhry R, Wigton A. The costs of scaling up vaccination in the worlds poorest countries. Health Affairs. 2006;25(2):348–356. doi: 10.1377/hlthaff.25.2.348. [DOI] [PubMed] [Google Scholar]
- 32.Stanley M. Perspective: Vaccinate boys too. Nature. 2012;488(7413):S10–S10. doi: 10.1038/488S10a. [DOI] [PubMed] [Google Scholar]
- 33.Giuliano AR, Palefsky JM, Goldstone S, Moreira ED, Jr, Penny ME, Aranda C, et al. Efficacy of quadrivalent HPV vaccine against HPV infection and disease in males. New England Journal of Medicine. 2011;364(5):401–411. doi: 10.1056/NEJMoa0909537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Palefsky JM, Giuliano AR, Goldstone S, Moreira ED, Jr, Aranda C, Jessen H, et al. HPV vaccine against anal HPV infection and anal intraepithelial neoplasia. New England Journal of Medicine. 2011;365(17):1576–1585. doi: 10.1056/NEJMoa1010971. [DOI] [PubMed] [Google Scholar]
- 35.Blödt S, Holmberg C, Müller-Nordhorn J, Rieckmann N. Human Papillomavirus awareness, knowledge and vaccine acceptance: A survey among 18–25 year old male and female vocational school students in Berlin, Germany. The European Journal of Public Health. 2011:ckr188. doi: 10.1093/eurpub/ckr188. [DOI] [PubMed] [Google Scholar]
- 36.Liddon N, Hood J, Wynn BA, Markowitz LE. Acceptability of human papillomavirus vaccine for males: a review of the literature. Journal of Adolescent Health. 2010;46(2):113–123. doi: 10.1016/j.jadohealth.2009.11.199. [DOI] [PubMed] [Google Scholar]
- 37.Human Papillomavirus Vaccination Coverage Among Adolescents, 20072013, and Postlicensure Vaccine Safety Monitoring, 20062014 United States. Centers for disease control and prevention: Morbidity and Mortality Weekly Report. 2014;63(29):620–624. [PMC free article] [PubMed] [Google Scholar]
- 38.Serrano B, Alemany L, Tous S, Bruni L, Clifford GM, Weiss T, et al. Potential impact of a nine-valent vaccine in human papillomavirus related cervical disease. Infect Agent Cancer. 2012;7(1):38. doi: 10.1186/1750-9378-7-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Darroch JE, Landry DJ, Oslak S. Age differences between sexual partners in the United States. Family planning perspectives. 1999:160–167. [PubMed] [Google Scholar]
- 40.Boily MC, Brisson M, Drolet M, Malagon T. Response. J Nat Cancer Inst. 2013;105(10):750–751. doi: 10.1093/jnci/djt084. [DOI] [PubMed] [Google Scholar]
- 41.Santelli JS, Lowry R, Brener ND, Robin L. The association of sexual behaviors with socioeconomic status, family structure, and race/ethnicity among US adolescents. American Journal of Public Health. 2000;90(10):1582. doi: 10.2105/ajph.90.10.1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Winer RL, Lee SK, Hughes JP, Adam DE, Kiviat NB, Koutsky LA. Genital human papillomavirus infection: incidence and risk factors in a cohort of female university students. American journal of epidemiology. 2003;157(3):218–226. doi: 10.1093/aje/kwf180. [DOI] [PubMed] [Google Scholar]
- 43.Partridge JM, Hughes JP, Feng Q, Winer RL, Weaver BA, Xi LF, et al. Genital human papillomavirus infection in men: incidence and risk factors in a cohort of university students. Journal of Infectious Diseases. 2007;196(8):1128–1136. doi: 10.1086/521192. [DOI] [PubMed] [Google Scholar]
- 44.Kaestle CE, Morisky DE, Wiley DJ. Sexual intercourse and the age difference between adolescent females and their romantic partners. Perspectives on Sexual and Reproductive Health. 2002:304–309. [PubMed] [Google Scholar]
- 45.Walker R, Nickson C, Lew JB, Smith M, Canfell K. A revision of sexual mixing matrices in models of sexually transmitted infection. Statistics in medicine. 2012;31(27):3419–3432. doi: 10.1002/sim.5545. [DOI] [PubMed] [Google Scholar]
- 46.Hernandez BY, Wilkens LR, Zhu X, Thompson P, McDuffie K, Shvetsov YB, et al. Transmission of human papillomavirus in heterosexual couples. Emerg Infect Dis. 2008;14(6):888. doi: 10.3201/eid1406.070616.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Widdice L, Ma Y, Jonte J, Farhat S, Breland D, Shiboski S, et al. Concordance and Transmission of Human Papillomavirus Within Heterosexual Couples Observed Over Short Intervals. J Infect Dis. 2013;207(8):1286–1294. doi: 10.1093/infdis/jit018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Burchell AN, Coutlée F, Tellier PP, Hanley J, Franco EL. Genital transmission of human papillomavirus in recently formed heterosexual couples. J Infect Dis. 2011;204(11):1723–1729. doi: 10.1093/infdis/jir644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Giuliano AR, Lee JH, Fulp W, Villa LL, Lazcano E, Papenfuss MR, et al. Incidence and clearance of genital human papillomavirus infection in men (HIM): a cohort study. The Lancet. 2011;377(9769):932–940. doi: 10.1016/S0140-6736(10)62342-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Moscicki AB, Ellenberg JH, Farhat S, Xu J. Persistence of human papillomavirus infection in HIV-infected and-uninfected adolescent girls: risk factors and differences, by phylogenetic type. J Infect Dis. 2004;190(1):37–45. doi: 10.1086/421467. [DOI] [PubMed] [Google Scholar]
- 51.Drolet M, Brisson M, Maunsell E, Franco EL, Coutlée F, Ferenczy A, et al. The psychosocial impact of an abnormal cervical smear result. Psycho-Oncology. 2012;21(10):1071–1081. doi: 10.1002/pon.2003. [DOI] [PubMed] [Google Scholar]
- 52.Satterwhite CL, Torrone E, Meites E, Dunne EF, Mahajan R, Ocfemia MCB, et al. Sexually transmitted infections among US women and men: prevalence and incidence estimates, 2008. Sexually transmitted diseases. 2013;40(3):187–193. doi: 10.1097/OLQ.0b013e318286bb53. [DOI] [PubMed] [Google Scholar]
- 53.Dunne EF, Nielson CM, Stone KM, Markowitz LE, Giuliano AR. Prevalence of HPV infection among men: a systematic review of the literature. Journal of Infectious Diseases. 2006;194(8):1044–1057. doi: 10.1086/507432. [DOI] [PubMed] [Google Scholar]
- 54.Kurtz TG. Solutions of ordinary differential equations as limits of pure jump Markov processes. J Appl Probab. 1970;7(1):49–58. [Google Scholar]
- 55.Elbasha EH. Global stability of equilibria in a two-sex HPV vaccination model. Bull Math Biol. 2008;70(3):894–909. doi: 10.1007/s11538-007-9283-0. [DOI] [PubMed] [Google Scholar]
- 56.Syrjanen K, Hakama M, Saarikoski S, Väyrynen M, Yliskoski M, Duba Prevalence, incidence, and estimated life-time risk of cervical human papillomavirus infections in a nonselected Finnish female population. J Sex Transm Dis. 1990;17(1):15–19. [PubMed] [Google Scholar]
- 57.Patel H, Wagner M, Singhal P, Kothari S. Systematic review of the incidence and prevalence of genital warts. BMC Infect Dis. 2013;13(1):39. doi: 10.1186/1471-2334-13-39. [DOI] [PMC free article] [PubMed] [Google Scholar]