Atlas-based head modeling and spatial normalization for high-density diffuse optical tomography: In vivo validation against fMRI

Abstract

Diffuse optical imaging (DOI) is increasingly becoming a valuable neuroimaging tool when fMRI is precluded. Recent developments in high-density diffuse optical tomography (HD-DOT) overcome previous limitations of sparse DOI systems, providing improved image quality and brain specificity. These improvements in instrumentation prompt the need for advancements in both i) realistic forward light modeling for accurate HD-DOT image reconstruction, and ii) spatial normalization for voxel-wise comparisons across subjects. Individualized forward light models derived from subject-specific anatomical images provide the optimal inverse solutions, but such modeling may not be feasible in all situations. In the absence of subject-specific anatomical images, atlas-based head models registered to the subject’s head using cranial fiducials provide an alternative solution. In addition, a standard atlas is attractive because it defines a common coordinate space in which to compare results across subjects. The question therefore arises as to whether atlas-based forward light modeling ensures adequate HD-DOT image quality at the individual and group level. Herein, we demonstrate the feasibility of using atlas-based forward light modeling and spatial normalization methods. Both techniques are validated using subject-matched HD-DOT and fMRI data sets for visual evoked responses measured in five healthy adult subjects. HD-DOT reconstructions obtained with the registered atlas anatomy (i.e. atlas DOT) had an average localization error of 2.7 mm relative to reconstructions obtained with the subject-specific anatomical images (i.e. subject-MRI DOT), and 6.6 mm relative to fMRI data. At the group level, the localization error of atlas DOT reconstruction was 4.2 mm relative to subject-MRI DOT reconstruction, and 6.1 mm relative to fMRI. These results show that atlas-based image reconstruction provides a viable approach to individual head modeling for HD-DOT when anatomical imaging is not available.

1. Introduction

Functional magnetic resonance imaging (fMRI) techniques have played an important role in advancing neuroscience research, both basic and translational (Bullmore, 2012; Fox and Greicius, 2010; Matthews et al., 2006; Raichle, 2009). However, fMRI is impractical or impossible in many situations, e.g., when experimental interventions are incompatible with a high magnetic field or in clinical evaluation of critically ill patients. High-density diffuse optical tomography (HD-DOT) provides an alternative to fMRI for measuring blood oxygen level dependent (BOLD) signals in the brain (Bluestone et al., 2001; Boas et al., 2004; Joseph et al., 2006; Zeff et al., 2007). By using overlapping measurements and a forward model that describes the light propagation in the underlying tissue, HD-DOT generates three-dimensional images of differential changes in the concentration of oxygenated and deoxygenated hemoglobin. Compared to previous versions of diffuse optical imaging systems, HD-DOT provides significant improvements in brain specificity (Gregg et al., 2010; Saager et al., 2011) and spatial resolution (Boas et al., 2004; Habermehl et al., 2012; Koch et al., 2010; White and Culver, 2010; Zeff et al., 2007). These advances in instrumentation motivate the development and use of realistic head models for accurate DOT reconstruction and spatial normalization methods for voxel-wise comparisons across subjects. When HD-DOT is combined with anatomically accurate head models derived from individual structural images, usually MRI or CT, the technique can provide lateral resolution at the gyral-level and localization errors on the order of ~5 mm (Eggebrecht et al., 2012). However, subject-specific structural imaging may be impractical in certain situations, e.g., bedside monitoring of critically ill patients who cannot be transported to an MRI scanner. An alternative strategy, compatible with portability, is to build realistic head models from standard atlases that are registered to the subject’s head surface (anatomy) using cranial fiducials. Standard atlases are attractive because they also provide a common coordinate system for statistical comparisons across subjects. In this paper, we use a standard MRI-based atlas in order to evaluate: i) image quality of atlas-based head models for HD-DOT reconstruction and ii) spatial normalization for the creation of atlas HD-DOT group maps. To our knowledge, this is the first study to systematically evaluate these aspects of HD-DOT with voxel-wise comparisons against fMRI, currently the gold standard in non-invasive functional neuroimaging.

Multiple strategies have been used for building models of the human head for DOT reconstruction. An early simple approach used layered hemispherical models, in which each layer has homogeneous optical properties associated with a particular tissue type, e.g., skull, scalp, and brain (Zeff, 2007, White 2009). Concentric shell models are attractively simple but inaccurate (Dehaes et al., 2011; Heiskala et al., 2009). An alternative strategy is to use a population-based anatomical model, as frequently used in EEG inverse source reconstruction (Baillet et al., 2011; Litvak et al., 2011; Tadel et al., 2011). While some studies have previously compared subject-MRI DOT to atlas DOT reconstructions, in both adult (Cooper et al., 2012; Custo et al., 2010) and neonates (Gibson et al., 2003; Heiskala et al., 2009), these analyses have been restricted to numerical simulations or low spatial resolution data sets and did not provide comparisons to subject-matched fMRI.

In this study, we used high quality visually evoked responses of healthy adult volunteers. Due to its highly detailed spatial functional organization, the visual cortex has traditionally served as a benchmark for validating neuroimaging systems such as PET (Fox et al., 1987) and fMRI (Engel et al., 1994). For the generic head template, we chose the ICBM152 atlas (Fonov et al., 2012; Mazziotta et al., 2001) because it exhibits a high contrast-to-noise ratio and well-preserved fine structural detail without being subject to the idiosyncrasies of a single head anatomy. To compute the mapping from the atlas to the subject-specific coordinate system, we used a set of cranial fiducials based on the extended 10/20 international system (Chatrian et al., 1988). While previous work has used fiducial-based affine transformations to register atlas anatomy to subject-specific anatomy (Fuchs et al., 2002; Singh et al., 2005; Tsuzuki et al., 2007), here we used a non-linear registration based on B-spline transformations (Lee et al., 1997) that provides a superior fitting in areas that exhibit high curvature such as the occipital region.

DOT reconstructions obtained with the registered atlas anatomy (i.e. atlas DOT) were compared to reconstructions obtained with the subject-specific anatomical images (i.e. subject-MRI DOT) and to subject-matched BOLD fMRI data at the single subject level. Additionally, group level comparisons were performed in atlas space. All comparisons were evaluated in terms of localization error and three-dimensional overlaps. Overall the atlas DOT reconstructions showed a good agreement with results obtained with both subject-MRI DOT reconstructions and fMRI data, thereby providing support for the use of atlas HD-DOT as surrogate for fMRI when anatomical imaging is not available.

2. Methods

The different processing steps involved in the atlas head modeling and spatial normalization methods are outlined in Figure 1.

Figure 1.

Flowchart of atlas-based head modeling in subject space and spatial normalization in atlas space. DOT_subject-MRI denotes subject-MRI DOT reconstruction; DOT_atlas denotes atlas DOT reconstruction. Solid boxes denote measurements/data: MRI (cyan); DOT (orange); cranial fiducials (green). Open boxes denote processing steps: head modeling (magenta); DOT reconstruction (orange); fMRI preprocessing (cyan); spatial normalization and grouping (red); voxel-wise comparisons (green). See text for further details.

2.1 Subjects and protocol

Five healthy adult participants (aged 21–30 years) were recruited for this study. The research was approved by the Human Research Protection Office at Washington University School of Medicine, and informed consent was obtained from each participant before scanning. The visual stimuli consisted of angularly sweeping reversing checkerboard wedges (10 Hz reversal) rotating around a white cross located at the center of the screen on a 50% background. The grid rotated 10 times at 10°/sec to complete a sweep of the entire visual field every 36 seconds. Gray screens were also presented for 30 seconds before and after the complete sweep sequence (Engel et al., 1994; Warnking et al., 2002).

2.2 High-density DOT system and acquisition

Subjects were seated in an adjustable chair in a low ambient light room facing a 19-inch LCD screen at a viewing distance of 90 cm. All measurements were performed with a continuous wave high-density DOT imaging system (Zeff et al., 2007). The instrument consists of 24 source positions and 28 detector positions interleaved in a high-density array. Each source position has LEDs emitting at two near-infrared wavelengths (750 and 850 nm). Optical fibers are coupled to a flexible plastic cap that is attached to the head by means of Velcro straps. Source-detector (SD) pair measurements at multiple distances (namely, first- through fourth-nearest neighbors at 13, 30, 39 and 47 mm, respectively) were sampled simultaneously at a frame rate of 10 Hz. A set of fiducial points were also measured during the HD-DOT scan in order to determine the location of the optode array relative to the head. Specifically, fiducial points were measured on the subject’s head surface (including nasion, inion, and pre-auricular points) as well as the outer four corners of the optode array using an RF pen based 3D digitizer (FastTrack, Polhemus, USA).

2.3 fMRI acquisition

All MRI scans were collected on a Siemens Trio (Erlagen, Germany) 3T scanner. Anatomical T1-weighted (T1) MPRAGE (echo time (TE) = 3.13 ms, repetition time (TR) = 2400 ms, flip angle = 8°, 1 × 1 × 1 mm isotropic voxels) and T2-weighted (T2) scans (TE = 84 ms, flip angle = 120°, 1 × 1 × 4 mm voxels) were taken at each session. Functional images were collected using a series of asymmetric gradient spin-echo echo-planar (EPI) sequences (each brain volume had a TE = 27 ms, TR = 2000 ms, flip angle = 90°, 4 × 4 × 4 mm voxels) to measure the blood-oxygenation-level-dependent (BOLD) contrast. In keeping with standard methods for performing BOLD analysis, we transformed the BOLD data to a standard 3 mm isotropic voxelated space.

2.4 Head modeling in subject space

We used the non-linear ICBM152 atlas from the Montreal Neurological Institute (Fonov et al., 2012; Mazziotta et al., 2001) for the generic head model. This atlas was generated from 152 MRI volume images from a normative young population (aged 18.5–43.5 years), which were non-linearly co-registered and averaged in Talairach space. Average T1 and T2 volumes consist of 1mm isotropic voxels (Fig. 2a). In comparison to other standard MRI-based templates, the non-linear ICBM152 exhibits high spatial resolution and an increased contrast-to-noise ratio throughout the head.

Figure 2.

Atlas-based head modeling in subject space. (a) T1 and T2 volumes of the ICBM152 non-linear atlas were used to segment the atlas into five tissue types: scalp (red), skull (light blue), CSF (cyan), gray matter (orange) and white matter (yellow). (b) An atlas finite element model (FEM) was created based on the segmentation. (c) A set of external fiducials based on the extended 10/20 international standard was measured on both the atlas FEM (blue) and the subject FEM (red). (d) The atlas mesh (blue) was linearly registered to the subject’s head (red) using an affine transformation computed from the cranial fiducials. (e) A non-linear registration based on a B-spline transformation was applied to the affine-transformed atlas mesh in order to improve the local fitting. Note the significant improvement in the spatial correspondence provided by the non-linear registration. (f) The optical grid was placed on the warped atlas FEM to compute the forward light model.

In order to create an atlas head model, we first segmented the atlas into five tissue types: scalp, skull, CSF, gray matter (GM) and white matter (WM). Brain tissue segmentation was based on tissue masks included in the atlas database, while extra-cerebral tissue (i.e., skull and scalp) was obtained using standard image processing techniques such as thresholding and morphological operations (Fig. 2a). To generate a finite element model (FEM), a tetrahedral head mesh was computed from the segmented atlas using Mimics 3D modeling software (Materialize, Belgium). The number of nodes and elements was in the range of 5×10⁵ and 4×10⁶, respectively, with a maximum inter-node distance of 5 mm on the mesh surface and 3 mm within the mesh volume (Fig. 2b). Following the same procedure, a subject FEM was created based on the subject-specific anatomical images (Fig. 2c).

A set of cranial fiducials (see Supplementary Figure 1) based on the extended 10/20 international system was measured on both the atlas FEM and subject FEM (Fig. 2b–c) following the procedure described in (Jurcak et al., 2007). The registration of the atlas FEM to the subject’s anatomy was accomplished in two steps. First, a linear registration was performed by an affine transformation computed from the cranial fiducials (Fig. 2d). Then, a non-linear registration based on a B-spline transformation (Lee et al., 1997) was applied to the affined-transformed atlas FEM in order to improve the local fitting (Fig. 2e).

The optical imaging array of sources and detectors was mapped onto the warped atlas FEM by using the previously defined affine transformation from atlas to subject and a subsequent spring-relaxation energy-minimization algorithm (Joseph et al., 2006). Tissue-specific optical properties (absorption coefficient, μ_a, and scattering coefficient, μ_s) were assigned to each node based on the atlas segmentation (see Supplementary Table 1). Using the warped atlas FEM and the optodes positions, a sensitivity matrix was computed using NIRFAST, a software package for modeling light transport in tissue based on the diffusion approximation to the radiative transport equation (Dehghani et al., 2003). The sensitivity matrix converts the SD pair measurements into a three-dimensional reconstruction of absorption changes within the head model.

2.5 DOT data analysis and reconstruction

Raw detector light levels were decoded to source-detector pair (SD-pair) data, V_i(t), and converted to time-series log-ratio data, y_i(t) = − log(V_i(t))/〈V〉. The data was then high-pass filtered (0.02 Hz cutoff) to remove long term drifts. In order to minimize systemic and superficial signal contamination, we regressed out an average of the first nearest-neighbor measurements from all of the individual measurements (Gregg et al., 2010; Saager et al., 2011; Zeff et al., 2007), and a subsequent low-pass filter (0.5 Hz cutoff) removed any residual pulse signal. Measurements that exhibited high temporal variance (>7.5%) were considered corrupted by motion artifacts and removed from further analysis. Across all sessions and subjects, this procedure kept the following percentages of nearest neighbor (nn) measurements: 100% of 1st nn, 95% of 2nd nn, 65% of 3rd nn, and 19% of 4th nn. Thus reconstruction was mostly based on 1st and 2nd nearest neighbor measurements with some additional information from 3rd and 4th nearest neighbor measurements. Sensitivity matrices were inverted following procedures described previously (Dehghani et al., 2009), where the Tikhonov regularization constant was λ = 0.01 and the spatially variant regularization parameter was β = 0.01. Time-series log-ratio data for each SD-pair measurement was converted into time-series 3D images of absorption changes for both 750 nm and 850 nm. To do this, we multiplied the log-ratio data by the inverted sensitivity matrix pertaining to a given subject’s light model. Concentration changes of oxyhemoglobin (ΔHbO₂), deoxyhemoglobin (ΔHbR) and total hemoglobin (ΔHbT) were obtained from absorption changes using spectral decomposition and the extinction coefficients of HbO₂ and HbR at the two wavelengths (Wray et al., 1988). All DOT volumes were defined in a 2 mm isotropic voxelated space, and temporally downsampled to 1 Hz.

2.6 fMRI data analysis

Preprocessing of MRI data was performed according to the methods described in (Shulman et al., 2010). Briefly, whole-brain normalization and data realignment were applied to correct for signal intensity changes across scans and head movement within and across scans, respectively. Each fMRI volume was aligned to its associated T1 volume using a 9-parameter affine transformation (no shearing), which in turn, was mapped to a representative brain target defined in Talairach space. After these preprocessing steps, fMRI data of each subject was resampled to a 2 mm isotropic voxelated space for the purpose of comparison with DOT data. In order to measure percentage changes of the BOLD signal, we divided out the average intensity value for each voxel from the fMRI data. Additionally, the fMRI data was spatially smoothed to match the point spread function of HD-DOT (13 mm) and temporally interpolated to 1 Hz to match HD-DOT data rates.

2.7 Group maps in atlas space

Two operations, namely, spatial normalization and statistical grouping, were involved in the computation of group maps for subject-MRI DOT reconstructions, atlas DOT reconstructions, and BOLD fMRI data. For the spatial normalization, we applied affine transformations from subject to atlas space to each individual volume using the inverse of the affine transformation derived in section 2.4. After co-registering each volume in atlas space, we concatenated the normalized volumes for all subjects and computed the signal-to-noise ratio of the hemodynamic response at each voxel. The signal-to-noise ratio, or voxel-wise t-value, was defined as the mean of the baseline-to-activation amplitude divided by its standard deviation across blocks and subjects, i.e.

$${\mathrm{t}}_{\text{voxel}}=\frac{\text{mean}(\text{activation}-\text{baseline})}{\sqrt{var(\text{activation}-\text{baseline})}}\sqrt{{\mathrm{N}}_{\text{blocks}}-1}.$$

Each activation is defined by the timing of when the checkerboard wedge is presented at the center of each visual quadrant (e.g. upper right quadrant = 45°). For each stimulus block (36 seconds), activation refers to the amplitude of the signal during a 5 seconds window centered on the timing of the defined visual presentation angle. Baseline refers to the amplitude of the signal during a 5 seconds window centered at 18 seconds after the activation window (e.g. out of phase). The variable N_blocks refers to the total number of stimulus blocks for all runs and subjects.

2.8 Quantitative image metrics of atlas performance

All comparisons were restricted to the field of view (FOV) of the HD-DOT system, as defined by the sensitivity matrix obtained for each subject. For comparisons between group maps, a FOV mask was defined as the intersection of the individual FOVs across subjects defined in atlas space. To evaluate the performance of the atlas-based DOT reconstructions, we divided the FOV into four visual quadrants and computed the center of mass of the activation at the center of each quadrant. To quantify the spatial error, we considered the following metrics:

1. Localization error: calculated as the Euclidean distance between the center of mass of two activations.

2. Dice coefficient: calculated as the ratio of the overlapping voxels between two activations to the total number of activated voxels. This value should be equal to 1 if there is a complete overlap between both activations, and zero if there is no overlap.

3. Overlap Percentage: calculated as the fraction of one activation that is correspondent in space with the other activation.

2.9 Data Visualization

Cortical surface representations based on the atlas and each subject’s T1 volumes were generated to facilitate three-dimensional visualization of the functional data. The surfaces were created using FreeSurfer (Dale et al., 1999; Fischl et al., 2001), while the surface mapping was performed using Caret (Van Essen et al., 2001).

3. Results

Individual comparisons in subject space

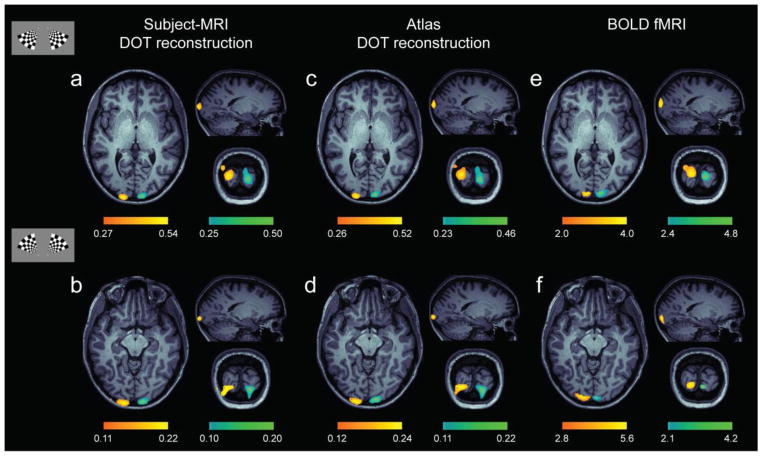
As a result of the detailed anatomical head modeling and the dense spatial sampling, well localized cortical activation maps were obtained for individual subjects using either subject-MRI DOT or atlas DOT reconstructions (Figure 3a–d). The similarity of the results indicates that the registration between atlas and subject-specific anatomy is suitable for generating individualized functional maps. In addition, there is a good spatial agreement between the atlas DOT responses and the measured BOLD fMRI activations at the single subject level (Figure 3c–f). All single-subject activation maps, either for DOT or fMRI data, were computed from block averaged responses from a set of eight repetitions. To aid visualization, all activations, corresponding to changes in oxyhemoglobin in the case of the HD-DOT maps, were thresholded at 50% of the peak response and overlaid onto the corresponding subject’s T1-weighted intensity map. Similar functional maps were obtained for deoxyhemoglobin and total hemoglobin for both subject-MRI DOT and atlas DOT reconstructions defined in subject space (Supplementary Figure 2).

Figure 3.

Functional responses to stimuli located in four visual quadrants (example shown in inset) for a single subject. Activation maps are based on subject-MRI DOT reconstructions (a–b), atlas DOT reconstructions (c–d), and BOLD fMRI (e–f) responses matched for Subject 1. All activations were thresholded at 50% of the peak response and overlaid on axial, sagittal and coronal slices of the subject’s T1-weighted intensity map. HD-DOT activations correspond to ΔHbO₂ concentration (μM). BOLD fMRI activations correspond to percentage changes (%) of the BOLD signal.

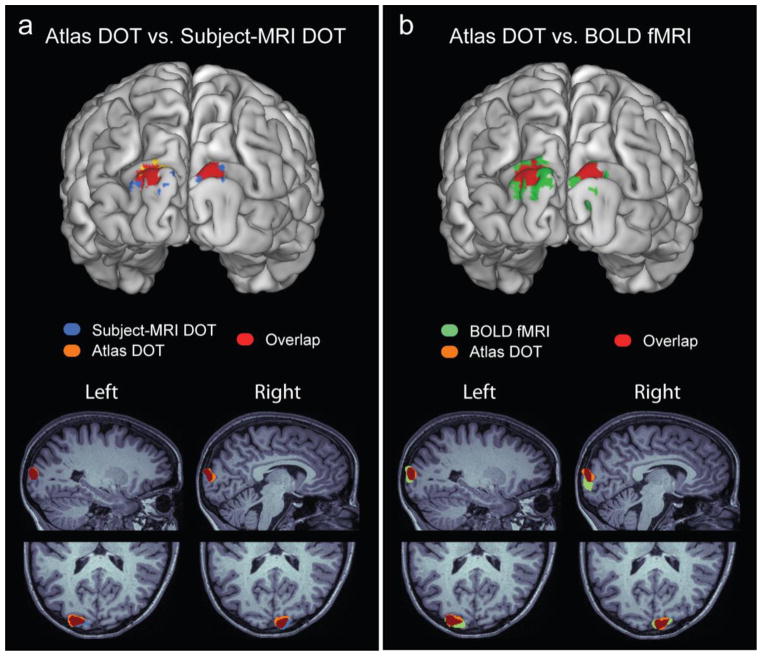
To facilitate spatial comparisons between the different modalities, we projected the volumetric activations and their spatial overlap onto subject-specific cortical surfaces generated with Freesurfer. Cortical responses obtained with atlas and subject-MRI head modeling exhibit significant spatial overlap within single subjects (Figure 4a), which is consistent with the results shown in the volumetric slices (Figure 3a–d). Similarly, atlas DOT and BOLD responses show comparable spatial extents (Figure 4b). While the DOT activations lie on the same gyri as the BOLD activations, the DOT activations are, relative to BOLD, weighted towards the surface (Fig. 4b). This is particularly evident in the cortical responses mapped onto the ventral region of the visual cortex, located deeper into the head where HD-DOT has lower sensitivity (Zhan et al., 2012).

Figure 4.

Spatial overlaps of cortical responses to lower visual stimuli measured on a single subject (Subject 3). (a) Subject-MRI DOT activations and atlas DOT activations exhibit a significant spatial overlap. (b) Atlas DOT activations and BOLD fMRI activations also show comparable spatial extents. All activations (thresholded at 50% of the peak value) were projected on the subject-specific pial cortical surface (top row), and overlaid on sagittal and axial slices of the associated T1 volume (bottom row).

To quantify the performance of the atlas head modeling in subject space, we computed multiple image metrics relative to subject-MRI DOT reconstructions and BOLD fMRI responses. Comparisons to subject-MRI DOT produced an average localization error of (2.7 ± 1.1) mm for all subjects and contrasts. Similarly, the average dice coefficient is (0.66 ± 0.04), while the average overlap percentage is (77 ± 3)%. We then repeated the error computation relative to the BOLD fMRI responses. In this case, the average localization error is (6.6 ± 1.4) mm, while the average dice coefficient and overlap percentage are (0.33 ± 0.09) and (47 ± 10)%, respectively. It is worthwhile to mention that the discrepancy between overlap percentage and dice coefficient is likely due to differences in the size of the focal activations measured with DOT and fMRI. While both metrics are sensitive to the relative locations of the activations, dice coefficient is also sensitive to their relative sizes. This means that if a smaller activation is completely contained within a larger one, the dice coefficient will be a small value. All image metrics relative to subject-MRI DOT and BOLD fMRI responses for each subject and hemodynamic contrast are summarized in Tables 1 and 2, respectively.

Table 1.

Quantitative error metrics for subject-MRI DOT versus atlas DOT reconstructions for all five subjects and contrasts computed in subject space.

Subject	Localization error (mm)			Dice coefficient			Spatial overlap (%)
	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT
1	2.6	3.2	2.7	0.64	0.62	0.63	69	70	69
2	1.4	1.5	1.6	0.76	0.77	0.74	83	82	84
3	2.4	2.5	2.3	0.66	0.66	0.67	72	71	72
4	4.8	4.4	3.5	0.54	0.56	0.62	76	82	76
5	3.1	1.6	2.9	0.71	0.71	0.68	83	87	77
Mean +/− S.D.	2.9 +/− 1.2	2.6 +/− 1.2	2.6 +/− 0.7	0.66+/− 0.08	0.66+/− 0.08	0.67+/− 0.05	77 +/− 6	78 +/− 8	76 +/− 6

Table 2.

Quantitative error metrics for atlas DOT reconstructions versus BOLD fMRI for all five subjects and contrasts computed in subject space.

Subject	Localization error (mm)			Dice coefficient			Spatial overlap (%)
	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT
1	6.7	6.9	6.6	0.25	0.23	0.25	33	31	32
2	6.8	6.9	6.7	0.29	0.29	0.29	40	41	39
3	3.4	3.6	3.2	0.51	0.51	0.5	84	82	83
4	10.3	10.5	6.2	0.31	0.29	0.37	34	33	53
5	6.6	7.9	6.6	0.32	0.28	0.32	39	36	39
Mean +/− S.D.	6.8 +/− 2.4	7.2 +/− 2.5	5.9 +/− 1.5	0.34 +/− 0.10	0.32 +/− 0.11	0.35 +/− 0.10	46 +/− 21	45 +/− 21	49 +/− 20

Group comparisons in atlas space

In order to spatially normalize the different data sets (atlas DOT, subject-MRI DOT and fMRI) for group comparisons, we registered each individual volume to atlas space using an affine transformation and performed statistical grouping (Figure 5). All t-maps were thresholded at 50% of the peak t-value and overlaid onto the atlas T1-weighted intensity map. In order to visualize the extent of the group responses along the cortical ribbon, we also projected the functional volumes on a pial cortical surface derived from the atlas T1 generated with Freesurfer. Qualitatively, all t-maps show strong focal activations for both dorsal and ventral responses, indicating that there is a good spatial alignment among the individual functional responses mapped in atlas space.

Figure 5.

Group t-maps in atlas space. Voxel-wise t-values were computed across all five subjects for subject-MRI DOT reconstructions (a–b), atlas DOT reconstructions (c–d), and BOLD fMRI responses (e–f). All t-maps (thresholded at 50% of the peak t-value) were overlaid on axial, sagittal and coronal slices of the atlas T1-weigthed intensity map and projected on the atlas pial cortical surface. HD-DOT t-maps are based on ΔHbO₂.

Comparisons between group t-maps obtained with subject-MRI DOT and atlas DOT reconstructions show a remarkable spatial correspondence (Figure 5a–d), which is more clearly demonstrated by the spatial overlaps projected on the atlas cortical surface (Figure 6a). This result is also confirmed by the quantitative image metrics computed for all three contrasts (Table 3). Specifically, the average localization error computed across all visual quadrants and contrast is 4.2 mm, while the average dice coefficient and overlap percentage are 0.51 and 63%, respectively.

Figure 6.

Spatial overlaps of group t-maps defined in atlas space. (a) Subject-MRI DOT and atlas DOT group maps exhibit a remarkable spatial overlap. (b) Atlas DOT and BOLD fMRI group maps also show comparable spatial extents. All maps were thresholded at 50% of the peak response and projected on the atlas-based pial cortical surface using Caret. (c) Scatter plots of the t-values obtained for subject-MRI DOT and atlas DOT group maps though the entire field of view. (d) Scatter plots obtained for atlas DOT and BOLD fMRI group maps. Note that all t-values are normalized to the maximum of each corresponding map.

Table 3.

Quantitative error metrics obtained for all group t-maps and contrasts computed in atlas space.

	Localization error (mm)			Dice coefficient			Spatial overlap (%)
	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT	ΔHbO2	ΔHbR	ΔHbT
DOTsubject vs. DOTatlas	4.6	4.1	4.0	0.57	0.44	0.53	68	56	65
DOTatlas vs. fMRI	5.5	6.0	6.9	0.46	0.48	0.47	65	64	63

Comparisons between group t-maps obtained with atlas DOT and BOLD fMRI also show good spatial agreement (Figure 5c–f), particularly in the dorsal region of the occipital cortex, as evidenced by the spatial overlaps depicted in Figure 6b. In order to quantify the spatial mismatch between both maps, we recomputed the image metrics for all contrasts across the four visual quadrants (Table 3). In this case, the average localization error is 6.1 mm, while the average dice coefficient and overlap percentage are 0.47 and 64%, respectively.

Taking advantage of the spatial co-registration between the different group maps, we also compared the time courses within a region of interest of 9 × 9 × 9 mm of the visual cortex. Figure 7 shows the temporal responses averaged across subjects corresponding to subject-MRI DOT (blue), atlas DOT (orange) and BOLD fMRI (green) functional maps. Note that the temporal correlation among the different modalities is remarkably high within the region of interest and consistent across different stimulus blocks.

Figure 7.

Average time series across all subjects obtained from a region of interest of the group maps corresponding to subject-MRI DOT activations (blue), atlas DOT activations (orange) and BOLD fMRI activations (green). HD-DOT temporal responses correspond to ΔHbO₂ concentration.

4. Discussion

Atlas-based head modeling in subject space

The improved image quality of HD-DOT (Joseph et al., 2006; Koch et al., 2010; Zeff et al., 2007) motivates the use of higher fidelity head models. In a previous work (Eggebrecht et al., 2012), we implemented subject-specific head modeling and demonstrated that the average localization error between subject-MRI DOT and BOLD fMRI is (4.4 ± 1.1) mm. In this paper, we proposed a general pipeline for building atlas-based head models that provide accurate DOT reconstructions without requiring subject-specific anatomical images. Our in vivo results show that atlas DOT activations are quantitatively comparable to subject-MRI DOT and fMRI activations. In particular, the average localization error relative to fMRI is ~6 mm, which is within the average gyral width, and smaller than the typical point spread function of the DOT imaging system (~13 mm).

Previous work has evaluated the accuracy of atlas-guided DOT reconstructions using numerical simulations (Cooper et al., 2012) and in vivo data (Custo et al., 2010; Habermehl et al., 2012). However, two of these studies (Cooper et al., 2012; Custo et al., 2010) used sparse imaging arrays with lower lateral resolution that introduce considerable localization errors (~18 mm relative to subject-MRI DOT reconstructions, see (Cooper et al., 2012)). Relatively good agreement was found between HD-DOT and fMRI for lateral displacements using a homogeneous head model for somatosensory mapping (Habermehl et al., 2012); however this study did not compare subject-MRI DOT versus atlas DOT reconstructions.

A realistic generic head model can integrate the detailed internal structure provided by an anatomical atlas and the subject’s external head shape accomplished by means of a warping procedure. In principal, the anatomical atlas would provide high definition structural images of a representative population. However, the linear averaging often involved in the atlas construction reduces the anatomical resolution and undermines tissue segmentation procedures. Consequently, single subject atlases such as the standard Colin27 (Holmes et al., 1998) have been considered (Cooper et al., 2012; Custo et al., 2010; Habermehl et al., 2012) since they provide higher image quality that facilitate the segmentation process. But as single subject templates, they do not capture anatomical variability and so are prone to introduce errors in the reconstruction due to structural differences between atlas and subject anatomies. Hence, in this study, we used the ICBM152 head template because it exhibits high spatial resolution and contrast without being subject to the idiosyncrasies of a single head anatomy.

The warping procedure that co-registers the atlas to the subject-specific anatomy should account for overall differences in head size and orientation as well as local differences between the atlas and each individual anatomy. In this work, we used a non-linear registration that provides improved fitting in regions that exhibit high curvature such as the occipital region (Fig. 2e). Our results show strong spatial agreement between the functional responses obtained with both subject-MRI DOT and atlas DOT reconstructions (Fig. 3a–d and Fig. 4a), with an average localization error smaller than 3 mm and an average overlap of 77% across all subjects. These results are in agreement with the simulations performed by Heiskala et al. (Heiskala et al., 2009), where they evaluated the performance of an infant atlas using a high-density grid and elastic deformations to register the individual volumes to a single subject atlas.

The DOT maps can be evaluated in greater detail against the gold standard of fMRI. Hence, to further validate the technique, we acquired subject-matched BOLD fMRI data during a non-concurrent scanning session. Our results demonstrate that the localization and spatial extent of the atlas DOT responses are qualitatively similar to the activations measured with BOLD fMRI (Fig. 3c–f and Fig. 4b). Moreover, as we mentioned above, quantitative comparisons reveal that the average localization error (6.6 mm) lies within the average gyral width.

Group maps in atlas space

Aligning functional maps across multiple subjects is a crucial step that precedes the statistical analysis of group data. The use of spatial transformations to project single subject data into a common atlas space, such as the Talairach space, has greatly aided PET (Fox et al., 1985; Seitz et al., 1990) and fMRI studies (Evans et al., 1992; Evans et al., 1991). Though not current practice, spatial normalization is also possible with optical data. While the most common approach has been to average optical data in measurement space, Amyot et al. (Amyot et al., 2012) considered spatial co-registration of optical images using affine transformations based on landmark points measured with a tracker device. While their method produced a localization error of 13 mm relative to fMRI, comparisons of our results to this study are limited by differences in study design, as they did not evaluate localization errors relative to subject-matched fMRI data but rather used results reported in the fMRI literature. More importantly, the individual maps used in the group analysis were limited to topographic reconstructions of sparse data sets.

Herein, we evaluated spatial normalization of three-dimensional subject-specific DOT volumes to a common atlas space following the approaches common in fMRI and PET. We mapped each individual volume to atlas space using affine transformations and created group maps for subject-MRI DOT, atlas DOT and BOLD fMRI data. Group maps, obtained from the statistical combination of normalized volumes, are expected to exhibit an increased signal-to-noise ratio relative to individual maps. On the other hand, anatomic variability between subjects can affect the ability to extract well localized activations from group maps. This discrepancy could be potentially amplified in the case of DOT reconstructions where spatial localization strongly depends on the accuracy of the anatomical head model. However, our results show well localized activations in group maps obtained with both subject-MRI DOT and atlas DOT data (Fig. 5a–d), illustrating the validity of using spatial normalization techniques for HD-DOT data sets. Moreover, qualitative comparisons to fMRI maps show good spatial agreement with atlas DOT group maps (Fig. 5c–f), which demonstrate that the proposed atlas-based head models provide enough accuracy to generate DOT group maps with good spatial localization. The localization error relative to fMRI is ~6 mm, which is in the range of the typical intersubject variability for group averaged fMRI in the visual cortex (~7 mm, see (Belliveau et al., 1991; Kang et al., 2003)). These comparisons can also be performed in the temporal domain, where we demonstrate a significant temporal correlation between HD-DOT and BOLD fMRI signals (Fig. 7).

Finally, the average errors relative to subject-MRI DOT and BOLD fMRI obtained in atlas space are within the same range of the average errors obtained in subject space. This result suggests that spatial normalization and statistical grouping techniques can be potentially extended to HD-DOT maps without strongly affecting the reliability of functional localization in HD-DOT group maps.

Further considerations

There exists a wide variety of statistical techniques for grouping fMRI data in the context of functional neuroimaging (Beckmann et al., 2003; Hagler et al., 2006). However, the general assumptions of standard fMRI analyses will need to be evaluated specifically within the context of HD-DOT due to differences in the modalities (e.g. the depth sensitivity of HD-DOT is more variable than fMRI). An interesting work in this direction is the simulation study by Abdelnour et al. (Abdelnour and Huppert, 2011) where they explored whether a random effects-model can improve group-level analysis compared to individual subject level image reconstructions followed by averaging of topographic maps. Although this topic exceeds the scope of the current paper, future developments of statistical parametric mapping techniques specifically tailored for DOT applications will bring more insight into group comparisons of HD-DOT functional maps. In particular, for the studies of higher order brain functions, such as language and attention, which require fast stimuli presentations and generally have lower signal-to-noise ratios than primary sensory functions, the event related SPM methods will be highly valuable.

An effective brain monitoring tool should provide an extended coverage, beyond the occipital cortex, over other relevant cortical areas such as the motor, temporal and frontal cortices. Additionally, when applying HD-DOT to clinically interesting populations, extensions might be required. For instance, for premature infants, domain-specific atlases such as neonatal brain templates might be useful (Fonov et al., 2012; Kuklisova-Murgasova et al., 2011). While the current analysis is restricted to the visual cortex of adult subjects, this paper provides a general pipeline for building atlas-based head models for HD-DOT applications that can be extended to a wide variety of populations and brain regions.

Accurately determining the transformation from the atlas to the subject coordinate space, to provide the atlas-based head models fitted to the individual anatomy is an important consideration for clinical application. Fiducial-based methods are likely to be the most common approach for a clinical setting. In the current study, we used an idealized data set of fiducials measured directly on the subject FEM (Fig 2c), in order to establish the fundamental performance of the atlas head modeling. It will be important to verify that experimental fiducial measurements obtained with a 3D digitizer do not introduce significant errors in the co-registration. A recent work by Shamir et al. (Shamir et al., 2009) estimates that the fiducial localization error is within a range of 0.5–2 mm, depending on the anatomical landmark. This suggests that the current results will translate to experimental fiducial measurements without a significant loss in image quality.

In conclusion, our in vivo evaluations demonstrate that the proposed atlas-based head models provide good spatial localization (~6 mm) across subjects with a broad variety of head shapes and sizes. Voxel-wise comparisons relative to fMRI responses reveal that the average localization error lies within the average gyral width. The validity of using spatial normalization techniques for HD-DOT data is supported by HD-DOT group maps that show good spatial agreement with fMRI group maps. These results strongly support the potential for atlas-based HD-DOT to serve as a surrogate of fMRI in clinical scenarios. These promising results motivate future validation studies that involve other brain regions and populations as well as methodological advances in other areas of HD-DOT technology.

Abbreviations

HD-DOT

high-density diffuse optical tomography

DOI

diffuse optical imaging

HbO₂

oxyhemoglobin

HbR

deoxyhemoglobin

HbT

total hemoglobin

FOV

field of view