Skip to main content
NCBI home page
Heredity logoLink to Heredity
. 2015 Jan 14;114(6):552–563. doi: 10.1038/hdy.2014.123

Joint-multiple family linkage analysis predicts within-family variation better than single-family analysis of the maize nested association mapping population

F Ogut 1, Y Bian 1, P J Bradbury 2, J B Holland 1,3,*
PMCID: PMC4434247  PMID: 25585918

Abstract

Quantitative trait locus (QTL) mapping has been used to dissect the genetic architecture of complex traits and predict phenotypes for marker-assisted selection. Many QTL mapping studies in plants have been limited to one biparental family population. Joint analysis of multiple biparental families offers an alternative approach to QTL mapping with a wider scope of inference. Joint-multiple population analysis should have higher power to detect QTL shared among multiple families, but may have lower power to detect rare QTL. We compared prediction ability of single-family and joint-family QTL analysis methods with fivefold cross-validation for 6 diverse traits using the maize nested association mapping population, which comprises 25 biparental recombinant inbred families. Joint-family QTL analysis had higher mean prediction abilities than single-family QTL analysis for all traits at most significance thresholds, and was always better at more stringent significance thresholds. Most robust QTL (detected in >50% of data samples) were restricted to one family and were often not detected at high frequency by joint-family analysis, implying substantial genetic heterogeneity among families for complex traits in maize. The superior predictive ability of joint-family QTL models despite important genetic differences among families suggests that joint-family models capture sufficient smaller effect QTL that are shared across families to compensate for missing some rare large-effect QTL.

Introduction

Quantitative trait locus (QTL) mapping has been exploited to dissect the genetic architecture of a trait and predict phenotypes for marker-assisted selection. Most QTL mapping studies in plants have been based on biparental populations; comparisons of QTL detected in mapping populations often reveal distinct sets of QTL (Blanc et al., 2006; Holland, 2007; Sneller et al., 2009). Joint analysis of multiple families permits evaluation of more QTL across different genetic backgrounds compared with single-family analysis (Sneller et al., 2009); the probability that a QTL will be polymorphic in at least one population is higher across multiple families derived from diverse parents (Blanc et al., 2006). Joint analysis of multiple related populations can integrate genetic heterogeneity into QTL models, simultaneously estimate the effects of more than two alleles per locus and incorporate the effects of different linkage phases and intensities of linkage disequilibrium in subpopulations (Rebaï and Goffinet, 2000; Blanc et al., 2006; Verhoeven et al., 2006; Holland, 2007; Yu et al., 2008; Sneller et al., 2009). Joint-family analysis has the potential for greater power of QTL detection, more accurate estimation of QTL effects, better resolution of QTL positions and more direct insight about the distribution of functional allelic variation across multiple families compared with single-family QTL analysis (Rebaï and Goffinet, 2000; Verhoeven et al., 2006; Blanc et al., 2006; Yu et al., 2008; Buckler et al., 2009; Coles et al., 2010; Steinhoff et al., 2011; Würschum, 2012).

The choice of QTL model for analysing multiple families jointly depends on assumptions about the consistency of QTL effects across families (Blanc et al., 2006; Würschum et al., 2012). A related issue is the relative power of joint-family and single-family analysis for detecting rare QTL (those QTL segregating in only one or a small proportion of families). Single-family analysis has higher power than joint-family analysis to detect a rare QTL with large effect (Li et al., 2011). Thus, joint-family analysis trades off some power to detect rare QTL for improved capacity to identify and estimate the effects of QTL shared across families. Therefore, it is of interest to empirically evaluate the accuracy of joint- and single-family methods across a range of distinct traits to determine if this tradeoff is worthwhile.

The goal of this study is to compare the characterisation of trait genetic architecture by joint-multiple family QTL mapping versus single-family QTL analysis in terms of their accuracy of QTL identification and effect estimation. We used data from the maize nested association mapping (NAM) population, which comprises 25 biparental mapping families all sharing a common reference parent. In this design, a rare QTL is one that segregates in only one or a few families, whereas a common QTL segregates in many families because most founders carry a functionally distinct allele than the reference parent at the QTL. We re-analysed data from six quantitative traits, representing distinct aspects of growth and development of maize plants using an updated dense consensus linkage map. Because these are real data, we do not know the true positions or effects of QTL underlying trait variation. Therefore, we compared the predictive value of QTL models based on the two different mapping methods using cross-validation. Although genotype value prediction is not the primary objective of either method, the relative accuracy of their estimates of QTL effects can be compared on the basis of their predictive ability in independent test data sets using cross-validation. We also tested the effect of marker density on the prediction ability of single-family analysis and evaluated the consistency of QTL detection among individual families and between single- and joint-family QTL analysis methods.

Materials and methods

Data

The development of the maize NAM population was described in detail by Buckler et al. (2009) and McMullen et al. (2009). Briefly, the maize NAM population consists of about ~5000 recombinant inbred lines (RILs) derived from crosses between the reference parent inbred line B73 and 25 diverse inbred lines. For this study, 4421 RILs were used, representing biparental cross family sizes from 121 to 191 RILs (Supplementary Table S1) remaining after removing lines with >8% heterozygosity or resulting from pollen contamination, or with lower quality genotyping-by-sequencing marker data. For this study, we selected six diverse traits: cob length (Brown et al., 2011), tassel length (Brown et al., 2011), leaf length (Tian et al., 2011), southern leaf blight (Kump et al., 2011), days to anthesis (Buckler et al., 2009) and seed oil content (Cook et al., 2012). Detailed information about field experimental designs, trait measurements and analysis of phenotype data can be found in the studies by Kump et al. (2011), Cook et al. (2012) and Hung et al. (2012). Traits were measured in three to eight environments (Supplementary Table S2). Predicted mean values of each RIL across environments for each trait were used as phenotype values for QTL mapping in this study (Supplementary File S1).

We used a consensus genetic linkage map derived from all 25 NAM families for linkage analysis. A genotyping-by-sequencing protocol (Elshire et al., 2011; Glaubitz et al., 2014) was used to score single-nucleotide polymorphisms (SNPs) on 4892 available NAM RILs. Marker values were imputed at 0.2-cM intervals. Sequence coverage for genotyping-by-sequencing was low (~0.5 × ), resulting in >50% missing data at many sites and detection of only a single allele at about 80% of heterozygous sites. Therefore, imputation was required to recover missing data and correctly call heterozygous sites. We used the Full-Sib Family Haplotype Imputation method described in Swarts et al. (2014). Briefly, each observed SNP call was numerically recoded as 0 (homozygous for B73 allele), 1 (heterozygous) or 2 (homozygous for non-B73 parent). Then the Viterbi algorithm (Rabiner, 1989) was applied to the resulting sequence to identify probable heterozygous loci and genotype calling errors. Sites were then chosen at 0.2-cM intervals and missing values for each site imputed as 2* (probability allele came from the non-B73 parent) based on the nearest non-missing flanking markers. Where both flanking marker alleles came from the same parent, the imputed value was either 0 or 2. Where the alleles at different flanking markers came from different parents, the imputed value was intermediate and based on the relative distance from the two markers. The resulting data set represents markers phased and imputed to represent identity-by-descent states at each position relative to each individual family, and thus we do not have any missing marker data in the imputed data set even if the parents were not polymorphic at some markers. We used the dense 0.2-cM resolution linkage map (with 7386 markers) for single-family analysis (Supplementary Files S2 and S3). We also used a subset of 1478 markers equally spaced 1 cM apart for single-family analysis and joint-linkage analysis (Supplementary Files S4 and S5).

Data analysis

Each trait was analysed separately. For both single-family and joint-family analyses, QTL were detected with step-wise regression using Proc GLMSelect in SAS version 9.3 (SAS Institute, 2011). In single-family analysis, each of the 25 biparental families was analysed independently using the model y=μ+Xβ+ɛ, where y is the n × 1 vector of RIL phenotype values, μ is the intercept, X is the n × m matrix consisting of m vectors of expected numbers of non-B73 alleles for each RIL at each of the m SNP markers, β is the m × 1 vector of QTL allele effects to be estimated and ɛ is the n × 1 vector of random residuals. Step-wise regression was used to select the subset of SNP markers significantly associated with the phenotypes (QTL), and QTL allele effects were estimated simultaneously from the final model step.

The model for joint-family analysis was y=μ+τα+Xβ+ɛ, where y is the n × 1 vector of trait values, μ is the intercept, τ is the n × 25 incidence matrix for family mean effects, α is the vector of 25 family effects, X is the n × 25m incidence matrix for marker-population combinations, β is the vector of 25m × 1 marker effects, m is the number of markers, n is the number of observations (RILs) and ɛ is the n × 1 vector of random residuals. The critical differences between single-family and joint-family models are the inclusion of family main effects and the nesting of SNP effects within families in the joint-family analysis. SNP effects were nested in families to reflect the potential for unique QTL allele effects within each family.

For single-family analysis, each of the four significance thresholds (P=0.0001, 0.001, 0.01 and 0.05) were used for markers to enter or exit the model at each step, whereas three significance thresholds (P=0.0001, 0.001 and 0.01) were used for joint-family analysis. The original NAM QTL studies sometimes included the intermated B73 × Mo17 (IBM) family (Lee et al., 2002), resulting in 26 biparental families, however, we excluded the IBM family from this study and used only the 25 NAM families per se. An exception to this was that two NAM families (derived from crosses with the sweet corn inbreds IL14H and P39) were not included in the analysis of seed oil content due to their extreme kernel phenotypes (Cook et al., 2012).

Cross-validation

Before conducting cross-validation, a baseline analysis for each trait was performed by first conducting step-wise regression on the full data set to estimate the proportion of phenotypic variation associated with QTL models. Next, the predictive ability of single-family and joint-family methods based on step-wise regression model was evaluated via fivefold cross-validation. Cross-validation sampling was stratified by biparental family, so that in each cross-validation fold, ~80% of the RILs within each family were selected for inclusion in the training data set, with the remaining 20% allocated to the validation data set. Each of the five cross-validation folds was disjoint, such that each line was included in exactly four training sets and one validation set. For a given training data set, QTL models were selected for each family separately via step-wise regression for single-family analysis, whereas for joint-family methods a single-QTL model was selected for the entire training data set. For each training data set, QTL model selection was conducted using each significance threshold for each method. Thus, for each training data set, we created 100 single-family QTL models (25 families × 4 thresholds) and 3 joint-family QTL models (1 for each of the 3 thresholds). We recorded the proportion of variation explained by the QTL model within each training data set (R2-value). Prediction abilities for each model created for a given training data set were evaluated by predicting the phenotype of each of the 20% of RILs in the validation data set using estimated QTL effects and SNP genotypes at QTL included in the model. Observed phenotypes for those lines were regressed on the QTL model-based prediction values, and the prediction ability (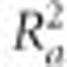Inline graphic value) was recorded for each cross-validation (Supplementary Files S6 and S7). To enable direct comparison of prediction abilities from single-family and joint-family analyses, we evaluated prediction ability within each family separately using both single-family and joint-family QTL prediction models.

The entire process of cross-validation, including sampling, QTL model selection and evaluation of prediction ability was replicated 50 times for single-family analysis and 10 times for joint-family analysis. The mean prediction ability for each combination of trait, QTL modelling procedure and significance threshold was evaluated as the mean coefficient of determination (Ra2) from regression of predicted RIL values on observed RIL values within each single-family validation data set. Since each replication of the process involved five folds of training and validation data sets, we performed a total of 50 replicates × 5 folds per replicate × (25 families × 5 traits+23 families × 1 trait (oil content)) × 4 significance thresholds=148 000 single-family analyses and a total of 10 replicates × 5 folds per replicate × 6 traits × 3 significance thresholds=900 joint-family analyses.

Detection and removal of collinear markers

Due to high correlation among nearby markers in the dense linkage maps used here, automated model selection can select groups of markers with high collinearity. Therefore, we conducted an additional analysis to automate detection of collinear marker sets selected by step-wise regression, delete nearly redundant collinear markers and refit reduced models. Markers were detected as involved in a collinearity if they had inflated s.e. (greater than the mean of the distribution of s.e.) and were within 5 cM of another marker in the selected model (Supplementary Figure S1). The mean of the s.e. of the QTL effects in the selected model was calculated for each combination of analysis method, trait, significance threshold, replicate and fold. After detection of collinear marker groups, only the marker entering the model first among that group was retained in the final reduced model. Within-family prediction abilities were re-calculated for the reduced models.

Repeatability of QTL from single-family and joint-family methods

To evaluate the concordance between QTL selected with high frequency in single-family and joint-family analyses, we first computed the resample model inclusion probabilities (RMIP) for each marker within each combination of trait, marker and analysis method at a single common significance threshold (α=0.01; Supplementary Figure S2). RMIP measures the proportion of training data set samples in which a particular SNP was selected in the final regression model. RMIPs of each SNP across 250 replicate-folds for each family using the single-family QTL analysis method or across 50 replicate-folds for the joint-family method were computed for each trait. The results for each trait were then summarised as the sum of RMIP values for all markers within 10-cM windows within each chromosome. Genomic windows with RMIP sum values ⩾0.1 or RMIP sum values ⩾0.5 were declared as well-supported QTL intervals at two different levels of significance. We then computed the total number of well-supported QTL intervals across all single-family analyses, and compared their overlap with well-supported QTL intervals from joint-family analysis for the same trait and RMIP sum threshold level.

The concordance between single-family and joint-family methods for QTL detection for each trait was also assessed by computing the correlation coefficient of RMIP values from single-family and joint-family QTL analyses methods at each SNP without imposing any RMIP threshold. In addition, we estimated correlations between methods on the basis of RMIP sum values for 10-cM bins. The comparisons between RMIP values of single- and joint-family analyses at a common test-wise P-value threshold have different overall type I error rates, since each marker was tested 25 times across the single-family analyses. Therefore, we also performed comparisons of RMIP values for joint-family analysis conducted with P=0.01 threshold and single-family analysis conducted with P=0.0001, since it was the threshold evaluated closest to the Bonferroni-corrected P-value of 0.01/25.

The correspondence between similarity of a family's single-family model to the joint-family model and the within-family prediction ability was measured by estimating the correlation between the pairwise RMIP correlation at α=0.0001 across 10-cM bins and the within-family validation Ra2 for single- or joint-family models. We estimated the correlation between this similarity measure and the predictive ability within each family from the two QTL modelling procedures.

Results

Effect of number of markers on the prediction ability (Ra2)

Previous NAM joint-family QTL analyses relied on a linkage map based on 1106 SNP markers with some gaps of up to 15 cM (McMullen et al., 2009). A denser linkage map based on genotypes obtained from genotyping-by-sequencing (Elshire et al., 2011) of the NAM RILs with SNPs located every 0.2 cM (7386 SNPs total) was recently created. Computational memory limitations prevented our use of this dense map for most of the joint-family linkage analyses, so we conducted most analyses for this study using a map with one marker every 1 cM selected from the denser map. To determine if QTL prediction ability was limited by use of the 1-cM resolution map versus the 0.2-cM resolution map, we compared single-family analysis using the two maps with fivefold cross-validation. There was no significant difference in mean prediction abilities for single-family analysis between 1-cM and 0.2-cM resolution maps (Supplementary Figure S3). Predictive ability of single-family analysis was optimal at the marker selection threshold of P=0.01 for both map densities (Supplementary Figure S3). Since prediction ability decreased at P=0.05 threshold for single-family analysis, we did not consider this threshold in further analyses.

To check the effect of the higher density linkage map on joint-linkage analysis, we also conducted one fivefold cross-validation analysis of joint-linkage mapping of CL with the 0.2 cM resolution map. Predictive ability of the joint-family model was the same as with the 1 cM map for P=0.0001 and 0.001 thresholds (r2=0.22 in all cases), but was worse for the denser map at P=0.01 (r2=0.16 compared with r2=0.19 for the 1 cM map). Therefore, resolution of the 1-cM linkage map did not limit predictive ability of joint-linkage analysis.

Prediction abilities (Ra2) of joint-family and single-family QTL analysis methods

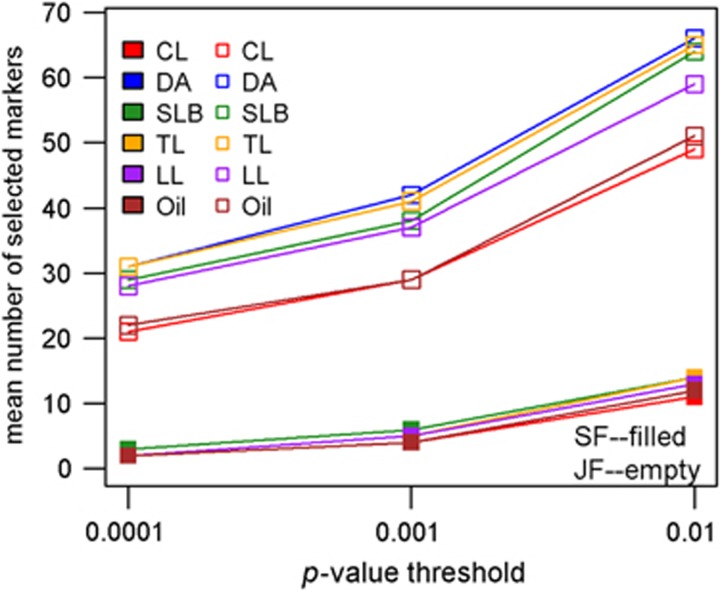
The number of QTL selected in final models varied among traits and increased with higher P-value thresholds (Figure 1). For all traits and significance thresholds, joint-family prediction models had more QTL than single-family prediction models (Figure 1). Furthermore, since each QTL fit in the joint-analysis model involved estimating 25 allele effect estimates (or 23 allele effects for oil), the total number of parameters estimated in joint-family models was always much greater than for any one single-family model.

Figure 1.

Figure 1

Open in a new tab

Mean number of markers selected in the prediction models obtained from single-family and joint-family QTL analyses methods for all traits and three significance levels.

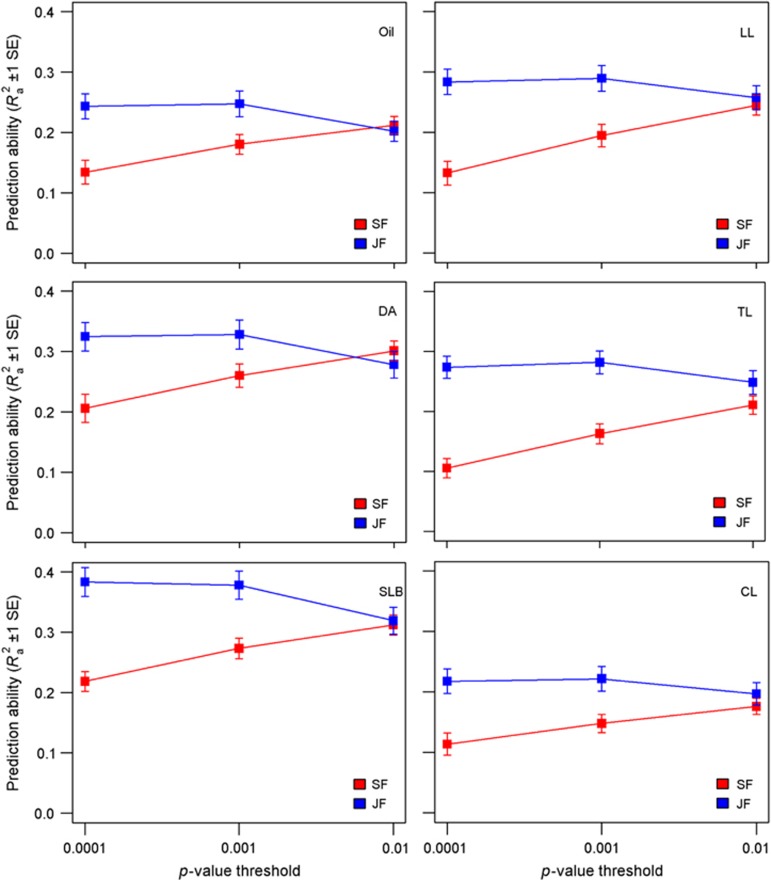
The mean prediction abilities within families were estimated from single-family and joint-family methods by cross-validation for all traits and for three significance levels (P=0.0001, 0.001 and 0.01) using the 1-cM resolution map (Figure 2). In most cases, joint-family analysis had higher mean prediction abilities than single-family QTL analysis. The joint-family method had the highest mean prediction abilities at α=0.0001, ranging from 0.22±0.02 for CL to 0.38±0.02 for SLB. As the stringency of the significance level decreased to α=0.01, however, the mean prediction ability of the joint-family method decreased slightly. In contrast, the response of single-family prediction ability to relaxing the QTL significance threshold was the reverse, reaching its optimum at α=0.01. Even at the α=0.01 threshold, however, joint-family QTL analysis provided similar or slightly better mean prediction abilities than single-family analysis for all traits (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Mean prediction abilities (Ra2±1 s.e.) within families for joint-family (JF) and single-family (SF) QTL analyses for each of the six traits and three P-value thresholds for inclusion of markers in step-wise regression models.

Differences in prediction abilities between joint-family and single-family QTL analyses methods varied among families (Supplementary Figures S4 and S5). Even at P-value thresholds where joint-family analysis was substantially better on average than single-family analysis, it was sometimes observed that single-family analysis was better for one or a few families (Supplementary Figures S4 and S5). Prediction abilities from joint-family analysis were higher than from single-family analysis for nearly all families and traits at α=0.0001, but were better in only about half of the families at α=0.01 for some traits (Supplementary Figure S4).

Within- and across-family mean prediction abilities (Ra2) from joint-family method

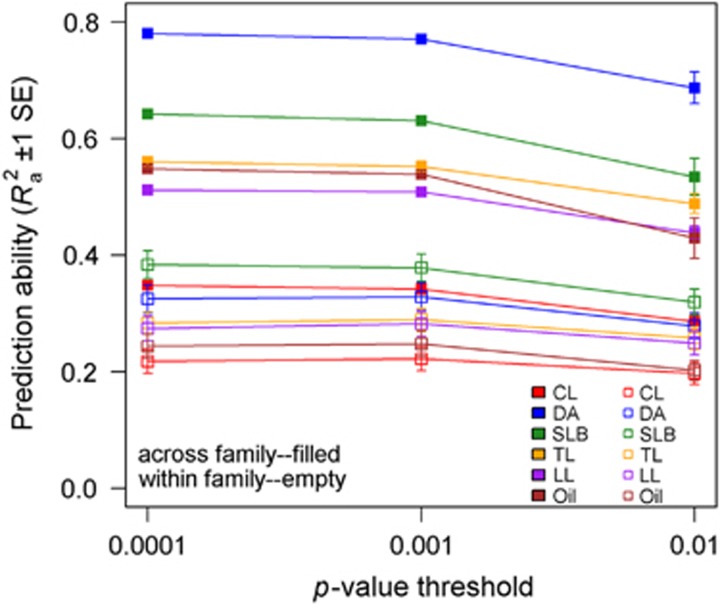
Joint-family analysis permits the prediction of RIL values for multiple families from a common model; we compared mean prediction abilities within and across families for six traits at three significance levels (P=0.0001, 0.001 and 0.01). The mean prediction abilities within and across families were highest when α=0.0001 and decreased as α increased (Figure 3). Prediction ability computed across families was always higher (in some cases twice as high) than within families (Figure 3; Supplementary Table S4).

Figure 3.

Figure 3

Open in a new tab

Within-and across-family mean prediction abilities (Ra2±1 s.e.) for six traits and three P-value thresholds for inclusion of markers in joint-family regression models.

Variance (R2) explained by single-family and joint-family methods

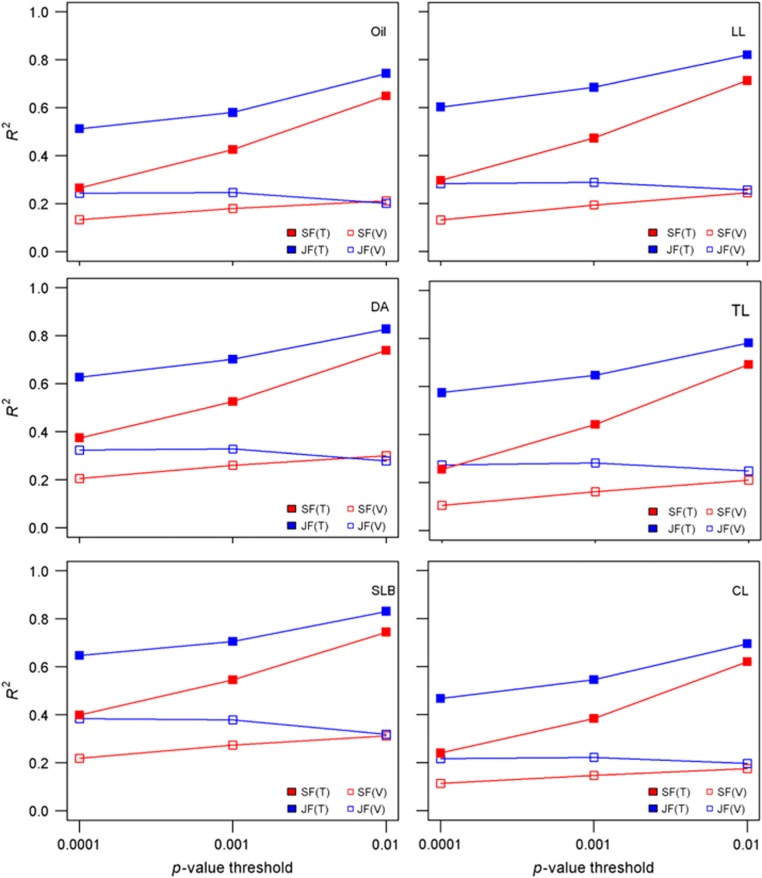
The optimism (Bleeker et al., 2003) of within-family predictive ability in the training data sets was substantial, as shown by the discrepancy between mean within-family R2 in the training sets compared with the prediction ability (Ra2) measured in validation data sets for both single-family and joint-family methods and for every combination of trait and significance thresholds (Figure 4). The difference between variation associated with models in training and validation data sets increased for both single- and joint-family methods as QTL significance thresholds were relaxed. For example, the difference between mean R2 values in training and validation data sets for oil content increased from 14% (single-family method) or 27% (joint-family method) at α=0.0001 to 43% (single family) or 54% (joint family) at α=0.01 (Figure 4).

Figure 4.

Figure 4

Open in a new tab

Within-family mean R2 from training data and Ra2 from validation sets obtained from joint-family (JF) and single-family (SF) QTL analyses for each of six traits and three P-value thresholds for inclusion of markers in models. SF(T) is the mean model R2 for single-family analysis in training data sets, SF(V) is the mean Ra2 for single-family analysis in validation sets, JF(T) is the mean model R2 for joint-family analysis in training data sets and JF(V) is the mean Ra2 for joint-family analysis in validation sets.

Detection and deletion of collinear markers

Prediction abilities of single-family and joint-family QTL analyses slightly increased after detection and deletion of collinear markers from the QTL models for all traits, with the greatest improvement occurring for the least stringent P-value thresholds (Supplementary Table S3). Joint-family QTL analysis still provided higher within-family prediction abilities than single-family QTL analysis across traits after removal of collinear markers (Supplementary Table S3).

Repeatability of QTL within and across families

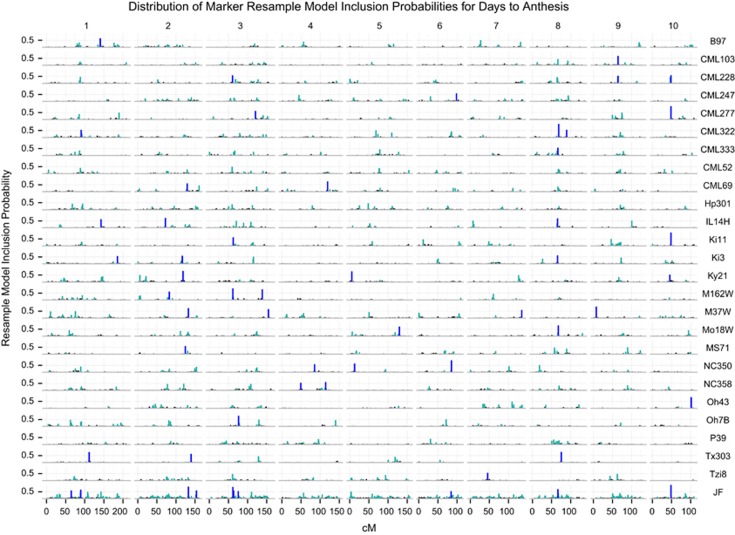
To test if consistency of detection of a QTL across families is related to the probability of the QTL being selected in the joint-family model, we compared the positions of QTL selected within each single-family analysis to QTL positions selected by joint-family analysis. For each SNP, we computed the proportion of analyses in which the SNP was selected for inclusion in a final QTL model (RMIP; results for days to anthesis are presented in Figure 5, results for other traits are presented in Supplementary Figure S6). To simplify comparisons and account for the fact that different but tightly linked SNPs can be selected to represent a common QTL in different data samples, we also made comparisons on the basis of 10-cM linkage map bins by summing RMIP values across all markers within each bin.

Figure 5.

Figure 5

Open in a new tab

The concordance between markers selected in multiple regression models by single-family and joint-family (JF) methods for days to anthesis. The resample model inclusion probabilities (RMIP) from repeated data samples at α=0.01are shown for each marker on each of the 10 chromosomes of maize (one marker per cM) for each single-family (indicated by the non-B73 founder) or by joint-family (JF) analysis. Markers with RMIP<0.1 are in black, markers selected with RMIP between 0.1 and 0.5 are in turquoise and markers selected with RMIP⩾0.5 are in dark blue.

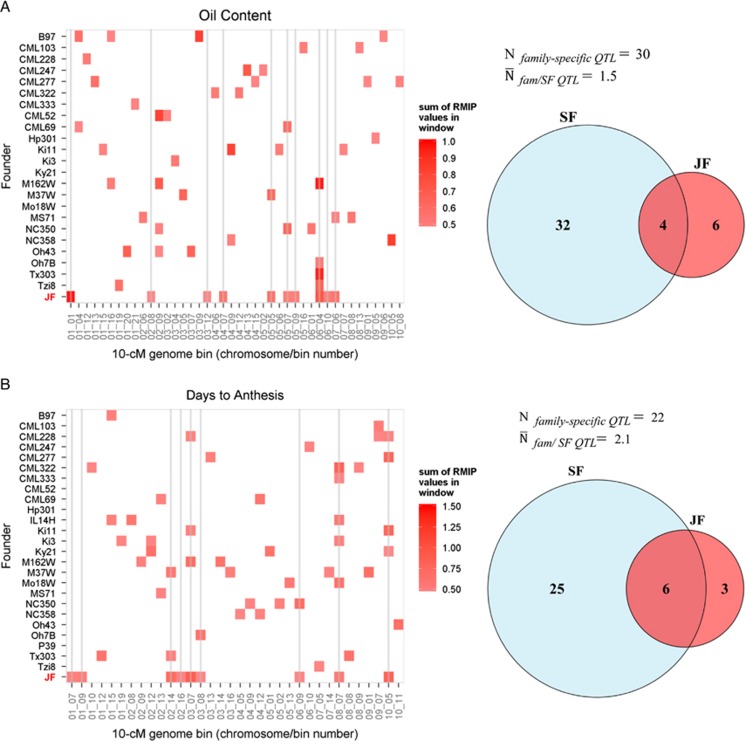
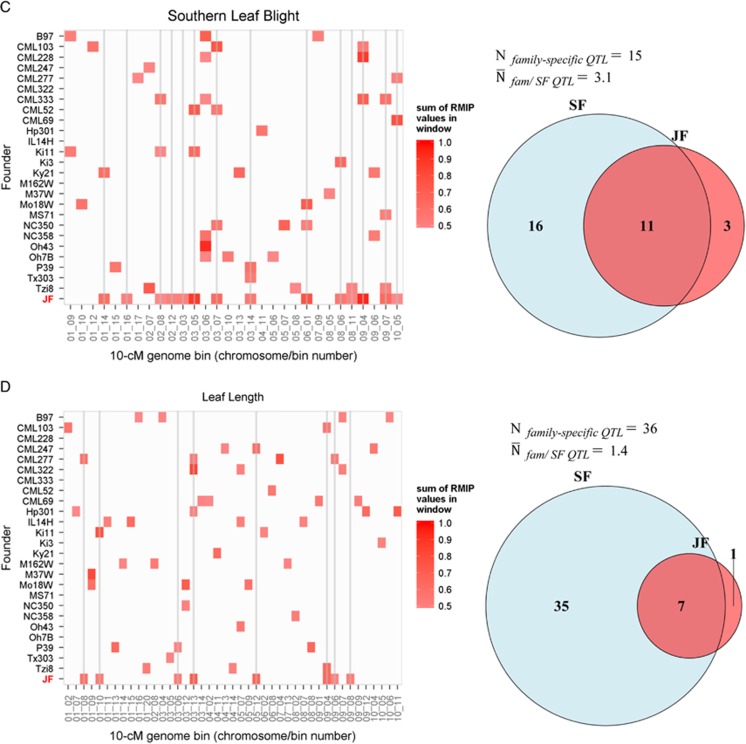
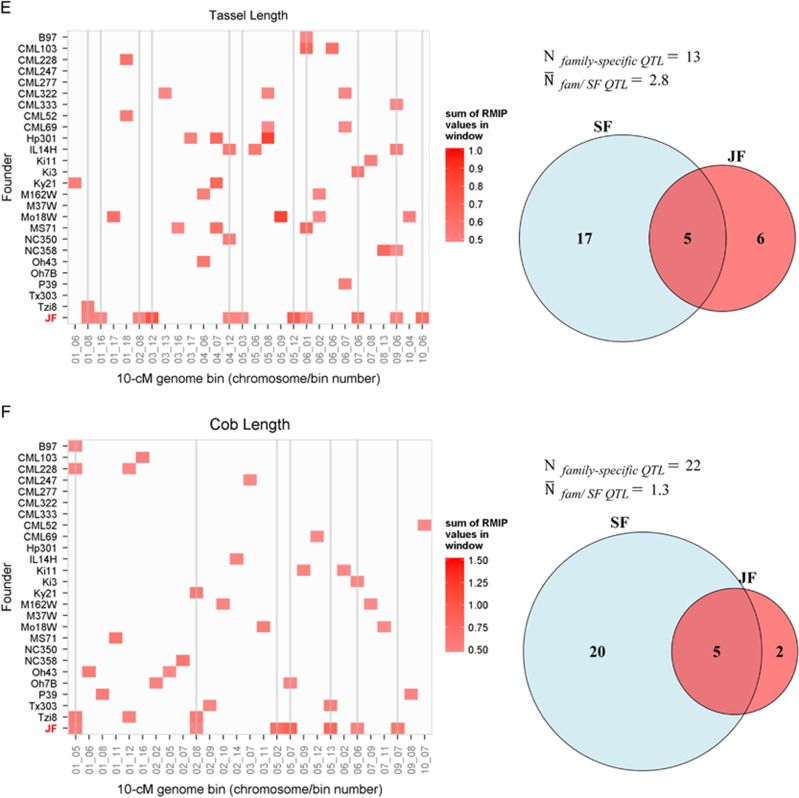
To focus on the most robust QTL detected with each method and to facilitate visual display of genomic bin RMIP values across families and methods, we compared 10-cM genome windows with sum RMIP values of at least 50% at a common P-value threshold of α=0.01. The number of robust QTL intervals (sum RMIP values at least 50%) detected in at least one family with single-family analysis ranged from 22 (TL) to 42 (LL) (Table 1; Figure 6). Most robust QTL identified by single-family analysis were detected in only one family (Figures 5 and 6). The number of these family-specific QTL intervals ranged from 13 (TL) to 36 (LL) across families, and the mean number of families in which a QTL interval was detected using single-family analysis ranged from 1.3 (CL) to 3.1 (SLB) (Figure 6). More QTL were shared among families for DA, SLB and TL than other traits. The joint-family method detected from 7 (CL) to 14 (SLB) robust QTL (Table 1). The concordance of robust QTL selected between single-family and joint-family methods was generally limited, but highly variable among traits (Figure 6). For example, 25 robust QTL were detected in at least 1 family for CL using single-family analysis, 3 of which were detected in >1 family (Figure 6). Of the seven robust CL QTL detected with joint linkage, five overlapped with robust single-family QTL (Table 1; Figure 6). In contrast, 36 robust single-family QTL were identified for oil, but only 4 of these overlapped with the 10 robust joint-family QTL (Table 1; Figure 6).

Table 1. The concordance between robust QTL detected by SF and JF methods calculated as the sum of RMIP from repeated data samples across all markers within each 10-cM genome window and trait.

Trait Sum RMIP⩾0.1
 Sum RMIP⩾0.5
  SF only QTL JF only QTL QTL detected with both methods SF only QTL JF only QTL QTL detected with both methods
CL 55 2 77 20 2 5
DA 48 1 96 25 3 6
SLB 45 4 89 16 3 11
LL 52 1 88 35 1 7
TL 49 3 85 17 6 5
Oil 46 2 82 32 6 4
Similar global type I error rates (JF α=0.01, SF α=0.0001)
 CL 11 41 38 5 3 4
 DA 15 53 44 9 2 7
 SLB 8 41 52 6 5 9
 LL 20 38 51 13 2 6
 TL 8 41 47 8 10 1
 Oil 8 43 41 8 8 2
Open in a new tab

Abbreviations: JF, joint family; QTL, quantitative trait locus; RMIP, resample model inclusion probabilities; SF, single family.

Comparisons are made between models selected with equal test-wise type I error rates (α=0.01) or with similar global type I error rates based on a Bonferroni correction for multiple testing across single families (α=0.01 for JF; α=0.0001~0.01/25 for SF). Two sum RMIP value thresholds were compared with declare robust QTL: windows with minimum sum RMIP of 0.1 or 0.5. SF only QTL: the number of robust QTL intervals detected in at least one family only with the single-family method. JF only QTL: the number of robust QTL intervals detected only with the joint-family method.

Figure 6.

Figure 6

Figure 6

Figure 6

Open in a new tab

The concordance between robust QTL detected by single-family (SF) and joint-family (JF) methods at the resolution of 10-cM windows for each trait. Resample model inclusion probabilities (RMIP) from repeated data samples at α=0.01were summed for all markers within a window. Only robust genome bins with sum RMIP values of at least 0.5 are displayed in colour. Vertical lines intersect robust QTL windows detected by JF to help compare JF with SF results. Venn diagrams for each trait indicate the total number of robust QTL windows detected with either or both SF or JF analyses. The number of robust QTL detected in only one family by SF analysis (Nfamily-specific QTL) and the mean number of families in which each of these robust QTL were detected by single-family analysis (Inline graphic) are also displayed for each trait. A, oil content; B, days to anthesis; C, southern leaf blight; D, leaf length; E, tassel length; F, cob length.

Comparison of robust QTL detected by single- and joint-family methods relied on imposing an arbitrary threshold to define a ‘robust' QTL. Visual inspection of histograms of the number of models in which each QTL was included (Figure 5 and Supplementary Figure S6) suggests that many of the most robust QTL (RMIP⩾50%) were rare, being detected in few families. By relaxing the threshold of QTL declaration to a 10-cM window with minimum sum RMIP of 10%, we observed better concordance between single-family and joint-family QTL compared with the 0.5 RMIP threshold (Table 1).

To make comparisons between the sets of markers included in different analyses without imposing any RMIP threshold, we also estimated the correlation coefficients of RMIP values for each marker individually and for each sum RMIP values in 10-cM bins between single- and joint-family methods at α=0.01 (Table 2). The concordances between RMIP values of individual markers in single-family and joint-family methods were moderate and ranged from 0.45 to 0.53 across traits (Table 2). At the resolution of 10-cM bins, consistencies between single-family and joint-family methods were higher, ranging from 0.64 to 0.77 (Table 2).

Table 2. Pearson correlation coefficients (r) of RMIP values between single-family and joint-family QTL analyses applied to random 80% data subsamples of the full data set.

Correlation (r) between RMIP values from single-family versus joint-family analysis
Trait RMIP per marker Sum RMIP per 10-cM bin
Equal test-wise type I error rates (JF α=0.01, SF α=0.01)
 CL 0.49 0.77
 DA 0.50 0.72
 SLB 0.51 0.67
 LL 0.45 0.64
 TL 0.48 0.74
 Oil 0.53 0.67
Similar global type I error rates (JF α=0.01, SF α=0.0001)
 CL 0.38 0.62
 DA 0.43 0.61
 SLB 0.42 0.51
 LL 0.29 0.47
 TL 0.21 0.50
 Oil 0.42 0.51
Open in a new tab

Abbreviations: JF, joint family; QTL, quantitative trait locus; RMIP, resample model inclusion probabilities; SF, single family; SNP, single-nucleotide polymorphism.

Comparisons are made between models selected with equal test-wise type I error rates (α=0.01) or with similar global type I error rates based on a Bonferroni correction for multiple testing across single families (α=0.01 for JF; α=0.0001~0.01/25 for SF). RMIPs were calculated for each SNP separately and also as sums over markers within 10-cM genome bins.

RMIP comparisons between single- and joint-family models at a common P-value threshold are confounded with a higher global type I error rate for single-family models, since each marker is tested 25 times independently among the single-family models. Therefore, we also made the comparisons of QTL model RMIP profile similarity between joint-family models with markers selected at P=0.01 and single-family models with markers selected at P=0.0001, similar to the Bonferroni-corrected type I error rate of P=0.01/25. This adjustment reduced the correlation between single- and joint-family RMIP values (Table 2) because it resulted in a much higher proportion of QTL positions unique to the joint-family analysis, although it reduced the proportion of QTL unique to single-family analyses (Table 1).

Germplasm grouping of the families had little discernible relationship to within-family prediction ability, with the exception of flowering time (DA) and disease resistance (SLB), for which the tropical-derived families tended to have higher prediction ability (Supplementary Figure S5).

Discussion

Previous empirical QTL mapping studies have demonstrated that joint-family mapping methods are generally better than single-family mapping in terms of the number of QTL detected, the likelihood statistics for QTL, the precision of QTL position estimates and the proportion of variation accounted for by the QTL (Blanc et al., 2006; Coles et al., 2010; Steinhoff et al., 2011). However, since the true QTL positions and effects are unknown in empirical studies, these studies could not independently validate the superiority of joint-family analyses. Simulation studies (for example, the study by Li et al. (2011)) permit comparison of models for their accuracy to detect true QTL positions and effects, but they are also limited by the difficulty in modelling ‘true' genetic architectures that reflect reality (Myles et al., 2009; Wimmer et al., 2013). Cross-validation approaches using empirical data offer an alternative approach that can also be useful to compare models based on their ability to predict genotypic values of individuals or lines that were not included in the selection and estimation of QTL parameter estimates (Utz et al., 2000; Schön et al., 2004).

Previous reports of trait variation accounted for by joint-family linkage models in the maize NAM population (Buckler et al., 2009; Kump et al., 2011; Tian et al., 2011; Hung, Shannon, et al., 2012) were ‘optimistic' (Bleeker et al., 2003), being biased upward by estimating the variation accounted by the model with the same data used to estimate the QTL model parameters (Figure 4; Schön et al., 2004). In addition, since NAM comprises 25 distinct biparental families, the joint-linkage models account for among-family differences with a population main effect, which alone often accounts for a substantial portion of the observed variation (Supplementary Table S4; Figure 3). The cross-validation ability of genotype predictions across families is highly influenced by the population main effect estimates, which alone have prediction abilities of 21–69% across families (Supplementary Table S4).

Single-family and joint-family analyses had distinct optimum thresholds for selecting markers in prediction models. Prediction ability of single-family models improved with less stringent thresholds and were optimal at P=0.01, but then declined when the threshold was relaxed further to P=0.05 (Figure 2; Supplementary Figure S3), whereas joint-family models were optimal at P=0.0001 (Figure 2). The higher stringency threshold optimum for joint-family analysis compared with single-family analysis is congruent with a simulation of QTL-based selection (Blanc et al., 2008). The drop-off of predictive ability in single-family analysis between P=0.01 and 0.05 thresholds contrasts with results of previous simulations of QTL-based selection (Hospital et al., 1997; Bernardo and Charcosset, 2006), however. In those previous studies, the optimal thresholds for single-family QTL-based prediction were often much higher, for example, P=0.40 (Bernardo and Charcosset, 2006). One likely cause of the higher optimal thresholds for inclusion of markers in the prediction model observed in this study was the higher marker density. For example, Hospital et al. (1997), Bernardo and Charcosset (2006) and Blanc et al. (2008) simulated marker densities from one marker per 5–50 cM, compared with one marker per cM in this study. With more markers available for selection, the possibility of highly collinear markers being selected in the prediction models is greater. Results from our collinearity reduction procedure indicate that collinearity was not a major problem at stringent P-value thresholds, but clearly caused overfitting of models at the most relaxed threshold (Supplementary Table S3).

The highly parameterized nature of joint-linkage models also rendered them susceptible to overfitting, even though the combined data set was much larger than typical biparental QTL studies. The number of parameters estimated in joint-linkage models was sometimes very large, with many QTL detected and 25 allele effects estimated per QTL. For example, the mean number of markers fit in joint-family models at the P=0.01 threshold was >60 for some traits (Figure 1), resulting in 60 × 25=1500 allele effect parameter estimates. For this reason, the higher stringency in the range of thresholds tested improved the predictive ability of the joint-linkage models. Further increases in the QTL detection stringency would be counterproductive, however, as joint-linkage models seem to gain predictive power over single-family models by including larger numbers of QTL.

Diverse models have been used to relate marker variation to trait variation in multiple family mapping studies. Würschum (2012) reviewed these models and noted a primary distinction between models that estimate the marker allele effect across families based on identity by state (association analysis models), and those that estimate a marker allele effect based on identity-by-descent (linkage analysis models). In this study, we tested only linkage analysis models, but linkage and association analyses are complementary and can be combined in the analysis of the maize NAM population (Kump et al., 2011; Tian et al., 2011).

Among identity-by-descent linkage analysis models, there is another major division between models that assume consistent effects of IBD QTL alleles across families (‘connected models') and those that allow IBD QTL allele effects to vary across families (‘disconnected models' Rebaï and Goffinet, 2000; Blanc et al., 2006). The optimal IBD linkage model for multiple family analysis appears to vary among studies and traits; disconnected models are superior when QTL allele effects vary considerably across families, possibly due to epistatic interactions with the family genetic background (Blanc et al., 2006; Coles et al., 2010; Steinhoff et al., 2011, 2012). The precise form of connected or disconnected models used for linkage analysis depends on the mating design used to construct inter-related mapping families, and previous multiple family mapping studies have investigated a wide range of mating schemes (Wu and Jannink, 2004; Blanc et al., 2006; Verhoeven et al., 2006; Coles et al., 2010; Steinhoff et al., 2011). The maize NAM population is a reference mating design (in which all biparental families have a common parent), which represents one extreme of multiple family designs. In the reference design, there is no distinction between connected and disconnected models because although the reference allele can be modelled as consistent (‘connected') across families, the effect of the other founder allele in each family is unique and cannot be tested for variation across families. The reference design offers an important practical benefit of improving the adaptation of diverse mapping families, permitting the value of QTL alleles from unadapted germplasm sources to be compared in reasonably adapted genetic backgrounds. The reference design also enables efficient sampling of allelic diversity for a fixed number of populations (equal to the allelic sampling of the single round robin design and better than diallels), but may have reduced power of detecting connected QTL allele effects compared with other designs. The results of this study suggest that joint-family analysis of the maize NAM design may be underpowered to detect strong but rare QTL; compensating for this is its ability to detect more commonly segregating but smaller effect QTL. Further, these results indicate value in conducting and comparing both single- and joint-family analyses of maize NAM to identify both common and rare QTL. The most commonly segregating robust QTL we observed across all traits were detected in four to six individual families (Figure 6). An oil content QTL on chromosome 6 was detected in >50% of training sets for four single families and for joint analysis (Figure 5 and Supplementary Figure S6); we believe this QTL represents the large effect of the DGAT gene (Cook et al., 2012). Two flowering time (DA) QTL with RMIP>50% were detected in four families and in joint analysis (Figures 5 and 6). The chromosome 8 QTL represents a region that contains the known flowering time loci Vgt1 and Zcn8 (Salvi et al., 2007; Buckler et al., 2009; Hung, Shannon, et al., 2012) and the chromosome 10 QTL represents the effect of the major photoperiod gene ZmCCT (Hung, Shannon, et al., 2012; Yang et al., 2013). The robust chromosome 3 SLB QTL in the genome bin between 40 and 50 cM was detected in six individual families but not in joint-linkage analysis (Figure 5 and Supplementary Figure S6). However, robust QTL were detected in each adjacent 10-cM window in two to three families and in joint-linkage analysis. Initial mapping studies of this region detected a single QTL, but higher resolution analysis using the intermated B73 × Mo17 population identified two distinct QTL in that family that were apparently fused into a single-QTL signal within smaller, lower resolution RIL families (Balint-Kurti et al., 2007). It seems likely that the QTL detected in the 40–50-cM window in many families is in fact an intermediate position that absorbs most of the effects of two or more linked QTL, and that the joint-family analysis was able to separate these effects due to its larger population size and sampling of more recombinations in this region (Li et al., 2011).

The existence of many rare QTL in the diverse founders sampled for NAM should minimise the effectiveness of joint-linkage analysis in this population compared with other possible mating designs that would provide higher replication of rare founder QTL. The joint-linkage model would fit 25 allele effects, only 1 of which should be significant to capture the effect of a single-rare QTL. Thus, it would seem difficult for the joint-family analysis to capture a large number of rare QTL effects in a single model; in this situation single-family analysis should be better able to capture rare allele effects and provide better prediction ability. Nevertheless, we observed that even in this non-optimal situation, joint-family analysis almost always outperformed single-family analysis in terms of prediction ability at a common threshold (Figure 2). This apparent contradiction could occur because of the allelic effect series at QTL observed in joint-linkage results. The allelic series implies that a locus tends to either have no significant effect across all families (no QTL) or has effects in multiple families, even if the effects are distinct. Joint-family analysis will have an advantage in cases where QTL positions are shared across families by increasing the power to include the QTL positions in the prediction model. The consistency of QTL positions across families can be inferred from the high overall correlations between sum RMIP values of genome windows (Table 2) despite the limited congruence of robust QTL effects (Figure 6).

Single-family analysis used in combination with joint-family analysis may help identify rare QTL that may be of biological interest and targets for follow-up genetic analyses. The two analysis approaches should be considered complementary. As an example, M37W carries its most robust QTL for days to anthesis at 5 cM on chromosome 9 (RMIP=0.80), but this position is selected in <4% of models for other single families or for joint linkage (Figure 5). Thus, joint linkage has low power, but analysis of the B73 × M37W family alone has high power to detect this rare QTL. In contrast a QTL was detected at 60 cM on chromosome 9 at RMIP>0.10 in six single-family models, but joint-family analysis detected this QTL in 38% of models, more than in any single family (Figure 5), demonstrating the power of joint linkage to detect shared QTL with higher power than single-family analysis. An alternative strategy would be to implement a more parsimonious joint-linkage analysis that selects only specific QTL alleles (and constrains unselected allele effects to zero) rather than fitting effects of all alleles at every QTL in the model. Such an approach might capture the complementary strengths of single- and joint-family analyses in a single model. Further research will be required to develop this method and compare it to the joint-linkage model used in this study. Finally, model averaging procedures could be used to combine results from single- and joint-family QTL analysis for genotype prediction, but as interest turns towards prediction and away from understanding the underlying genetics of trait variation genomic selection procedures would be the appropriate baseline comparison (Guo et al., 2012; Wimmer et al., 2013). Indeed, Lehermeier et al. (2014) demonstrated that joint analysis of related families with genomic prediction models can improve predictions over family-specific genomic prediction models.

Data Archiving

Raw phenotype data were reported in Hung et al. (2012) and are available at http://panzea.org/db/gateway?file_id=Hung_etal_2012_Heredity_data. Phenotype mean values and linkage map information and scores are available at http://www.panzea.org/db/gateway?file_id=Ogut_etal_2014_Heredity_supplement.

Acknowledgments

Research supported by US Department of Agriculture, Agricultural Research Service and the National Science Foundation grants IOS-1238014 and IOS-0820619.

The authors declare no conflict of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Information
Click here for additional data file. (1.7MB, doc)

References

  1. Balint-Kurti PJ, Zwonitzer JC, Wisser RJ, Carson ML, Oropeza-Rosas MA, Holland JB, et al. Precise mapping of quantitative trait loci for resistance to southern leaf blight, caused by Cochliobolus heterostrophus race O, and flowering time using advanced intercross maize lines. Genetics. 2007;176:645–657. doi: 10.1534/genetics.106.067892. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bernardo R, Charcosset A. Usefulness of gene information in marker-assisted recurrent selection: a simulation appraisal. Crop Sci. 2006;46:614–621. [Google Scholar]
  3. Blanc G, Charcosset A, Mangin B, Gallais A, Moreau L. Connected populations for detecting quantitative trait loci and testing for epistasis: an application in maize. Theor Appl Genet. 2006;113:206–224. doi: 10.1007/s00122-006-0287-1. [DOI] [PubMed] [Google Scholar]
  4. Blanc G, Charcosset A, Veyrieras J-B, Gallais A, Moreau L. Marker-assisted selection efficiency in multiple connected populations: a simulation study based on the results of a QTL detection experiment in maize. Euphytica. 2008;161:71–84. [Google Scholar]
  5. Bleeker SE, Moll HA, Steyerberg EW, Donders ART, Derksen-Lubsen G, Grobbee DE, et al. External validation is necessary in prediction research. J Clin Epidemiol. 2003;56:826–832. doi: 10.1016/s0895-4356(03)00207-5. [DOI] [PubMed] [Google Scholar]
  6. Brown PJ, Upadyayula N, Mahone GS, Tian F, Bradbury PJ, Myles S, et al. Distinct genetic architectures for male and female inflorescence traits of maize. PLoS Genet. 2011;7:1–14. doi: 10.1371/journal.pgen.1002383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Buckler ES, Holland JB, Bradbury PJ, Acharya CB, Brown PJ, Browne C, et al. The genetic architecture of maize. Science. 2009;325:714–718. doi: 10.1126/science.1174276. [DOI] [PubMed] [Google Scholar]
  8. Coles ND, McMullen MD, Balint-Kurti PJ, Pratt RC, Holland JB. Genetic control of photoperiod sensitivity in maize revealed by joint multiple population analysis. Genetics. 2010;184:799–812. doi: 10.1534/genetics.109.110304. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cook JP, McMullen MD, Holland JB, Tian F, Bradbury P, Ross-Ibarra J, et al. Genetic architecture of maize kernel composition in the nested association mapping and inbred association panels. Plant Physiol. 2012;158:824–834. doi: 10.1104/pp.111.185033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Elshire RJ, Glaubitz JC, Sun Q, Poland JA, Kawamoto K, Buckler ES, et al. A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE. 2011;6:1–10. doi: 10.1371/journal.pone.0019379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Glaubitz JC, Casstevens TM, Lu F, Harriman J, Elshire RJ, Buckler ES. TASSEL-GBS : a high capacity genotyping by sequencing analysis pipeline. PLoS ONE. 2014;9:e90346. doi: 10.1371/journal.pone.0090346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Guo Z, Tucker DM, Lu J, Kishore V, Gay G. Evaluation of genome-wide selection efficiency in maize nested association mapping populations. Theor Appl Genet. 2012;124:261–275. doi: 10.1007/s00122-011-1702-9. [DOI] [PubMed] [Google Scholar]
  13. Holland JB. Genetic architecture of complex traits in plants. Curr Opin Plant Biol. 2007;10:156–161. doi: 10.1016/j.pbi.2007.01.003. [DOI] [PubMed] [Google Scholar]
  14. Hospital F, Moreau L, Lacoudre F, Charcosset A, Gallais A. More on the efficiency of marker-assisted selection. Theor Appl Genet. 1997;95:1181–1189. [Google Scholar]
  15. Hung H-Y, Browne C, Guill K, Coles N, Eller M, Garcia A, et al. The relationship between parental genetic or phenotypic divergence and progeny variation in the maize nested association mapping population. Heredity. 2012;108:490–499. doi: 10.1038/hdy.2011.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hung H-Y, Shannon LM, Tian F, Bradbury PJ, Chen C, Flint-Garcia SA, et al. ZmCCT and the genetic basis of day-length adaptation underlying the postdomestication spread of maize. Proc Natl Acad Sci USA. 2012;109:E1913–E1921. doi: 10.1073/pnas.1203189109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kump KL, Bradbury PJ, Wisser RJ, Buckler ES, Belcher AR, Oropeza-Rosas MA, et al. Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat Genet. 2011;43:163–168. doi: 10.1038/ng.747. [DOI] [PubMed] [Google Scholar]
  18. Lee M, Sharopova N, Beavis WD, Grant D, Katt M, Blair D, et al. Expanding the genetic map of maize with the intermated B73 x Mo17 (IBM) population. Plant Mol Biol. 2002;48:453–461. doi: 10.1023/a:1014893521186. [DOI] [PubMed] [Google Scholar]
  19. Lehermeier C, Kramer N, Bauer E, Bauland C, Camisan C, Campo L, et al. Usefulness of multiparental populations of maize (Zea mays L.) for genome-based prediction. Genetics. 2014;198:3–16. doi: 10.1534/genetics.114.161943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Li H, Bradbury P, Ersoz E, Buckler ES, Wang J. Joint QTL linkage mapping for multiple-cross mating design sharing one common parent. PLoS ONE. 2011;6:e17573. doi: 10.1371/journal.pone.0017573. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. McMullen MD, Kresovich S, Villeda HS, Bradbury P, Li H, Sun Q, et al. Genetic properties of the maize nested association mapping population. Science. 2009;325:737–740. doi: 10.1126/science.1174320. [DOI] [PubMed] [Google Scholar]
  22. Myles S, Peiffer J, Brown PJ, Ersoz ES, Zhang Z, Costich DE, et al. Association mapping: critical considerations shift from genotyping to experimental design. Plant Cell. 2009;21:2194–2202. doi: 10.1105/tpc.109.068437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proc IEEE. 1989;77:257–286. [Google Scholar]
  24. Rebaï A, Goffinet B. More about quantitative trait locus mapping with diallel designs. Genet Res. 2000;75:243–247. doi: 10.1017/s0016672399004358. [DOI] [PubMed] [Google Scholar]
  25. Salvi S, Sponza G, Morgante M, Tomes D, Niu X, Fengler KA, et al. Conserved noncoding genomic sequences associated with a flowering-time quantitative trait locus in maize. Proc Natl Acad Sci USA. 2007;104:11376–11381. doi: 10.1073/pnas.0704145104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. SAS Institute 2011. SAS/STAT 9.3 User's Guide. SAS Instutue Inc: Cary, NC, USA.
  27. Schön CC, Utz HF, Groh S, Truberg B, Openshaw S, Melchinger AE. Quantitative trait locus mapping based on resampling in a vast maize testcross experiment and its relevance to quantitative genetics for complex traits. Genetics. 2004;167:485–498. doi: 10.1534/genetics.167.1.485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Sneller CH, Mather DE, Crepieux S. Analytical approaches and population types for finding and utilizing QTL in complex plant populations. Crop Sci. 2009;49:363–380. [Google Scholar]
  29. Steinhoff J, Liu W, Maurer HP, Würschum TC, Friedrich HL, Ranc N, et al. Multiple-line cross quantitative trait locus mapping in European elite maize. Crop Sci. 2011;51:2505–2516. [Google Scholar]
  30. Steinhoff J, Liu W, Reif JC, Della Porta G, Ranc N, Würschum T. Detection of QTL for flowering time in multiple families of elite maize. Theor Appl Genet. 2012;125:1539–1551. doi: 10.1007/s00122-012-1933-4. [DOI] [PubMed] [Google Scholar]
  31. Swarts K, Li H, Navarro JAR, An D, Romay MC, Hearne S, et al. Novel methods to optimize genotypic imputation for;ow-coverage, next-generation sequence data in crop plants. Plant Genome. 2014;7:1–12. [Google Scholar]
  32. Tian F, Bradbury PJ, Brown PJ, Hung H, Sun Q, Flint-Garcia S, et al. Genome-wide association study of leaf architecture in the maize nested association mapping population. Nat Genet. 2011;43:159–162. doi: 10.1038/ng.746. [DOI] [PubMed] [Google Scholar]
  33. Utz HF, Melchinger AE, Schön CC. Bias and sampling error of the estimated proportion of genotypic variance explained by quantitative trait loci determined from experimental data in maize using cross validation and validation with independent samples. Genetics. 2000;154:1839–1849. [PMC free article] [PubMed] [Google Scholar]
  34. Verhoeven KJF, Jannink J-L, McIntyre LM. Using mating designs to uncover QTL and the genetic architecture of complex traits. Heredity. 2006;96:139–149. doi: 10.1038/sj.hdy.6800763. [DOI] [PubMed] [Google Scholar]
  35. Wimmer V, Lehermeier C, Albrecht T, Auinger H-J, Wang Y, Schön C-C. Genome-wide prediction of traits with different genetic architecture through efficient variable selection. Genetics. 2013;195:573–587. doi: 10.1534/genetics.113.150078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Wu X-L, Jannink J-L. Optimal sampling of a population to determine QTL location, variance, and allelic number. Theor Appl Genet. 2004;108:1434–1442. doi: 10.1007/s00122-003-1569-5. [DOI] [PubMed] [Google Scholar]
  37. Würschum T. Mapping QTL for agronomic traits in breeding populations. Theor Appl Genet. 2012;125:201–210. doi: 10.1007/s00122-012-1887-6. [DOI] [PubMed] [Google Scholar]
  38. Würschum T, Liu W, Gowda M, Maurer HP, Fischer S, Schechert A, et al. Comparison of biometrical models for joint linkage association mapping. Heredity. 2012;108:332–340. doi: 10.1038/hdy.2011.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Yang Q, Li Z, Li W, Ku L, Wang C, Ye J, et al. A CACTA-like transposable element in ZmCCT attenuated photoperiod sensitivity and accelerated the postdomestication spread of maize. Proc Natl Acad Sci USA. 2013;110:16969–16974. doi: 10.1073/pnas.1310949110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Yu J, Holland JB, McMullen MD, Buckler ES. Genetic design and statistical power of nested association mapping in maize. Genetics. 2008;178:539–551. doi: 10.1534/genetics.107.074245. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
Click here for additional data file. (1.7MB, doc)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES