Significance
Functional connectivity MRI has revolutionized our understanding of brain architecture. Correlated changes in oxygen levels reveal networks of regions. These networks, each linked to particular functions, are conserved across individuals and species. Normal development, learning, and mental disorders are associated with subtle network changes, providing insight into how brains work. Remarkably, the basis of functional connectivity remains unknown. Although some studies have reported data consistent with an oscillatory process, the leading hypothesis involves emergent, arrhythmic dynamics of complex and distributed networks (the “criticality” hypothesis). By using a new electrode-based technique, we show that functional connectivity is not related to criticality, but instead to specific and potentially localizable oscillatory processes. This finding provides a tool to identify the mechanisms underlying functional connectivity.
Keywords: resting-state functional connectivity, band-limited, criticality, oxygen polarography, oscillation
Abstract
The mechanism underlying temporal correlations among blood oxygen level-dependent signals is unclear. We used oxygen polarography to better characterize oxygen fluctuations and their correlation and to gain insight into the driving mechanism. The power spectrum of local oxygen fluctuations is inversely proportional to frequency raised to a power (1/f) raised to the beta, with an additional positive band-limited component centered at 0.06 Hz. In contrast, the power of the correlated oxygen signal is band limited from ∼0.01 Hz to 0.4 Hz with a peak at 0.06 Hz. These results suggest that there is a band-limited mechanism (or mechanisms) driving interregional oxygen correlation that is distinct from the mechanism(s) driving local (1/f) oxygen fluctuations. Candidates for driving interregional oxygen correlation include rhythmic or pseudo-oscillatory mechanisms.
Resting-state functional connectivity MRI (rs-fcMRI) analyses provide insight into the functional architecture of the brain. The method is based on slow correlations (e.g., 0.01–0.1 Hz) in blood oxygen level-dependent (BOLD) signal across the brain. The pattern of these slow correlations has been used to trace out functional networks and to describe how these networks develop, change with experience, vary across individuals, and are disturbed in disease (1–8). Slow BOLD fluctuations and their correlations are thought to reflect neuronal processes, yet the underlying mechanisms remain unknown (9, 10). We used a high temporal resolution method, oxygen polarography, to characterize the dynamics of oxygen fluctuations and thereby gain insight into the underlying neuronal mechanisms.
Two types of dynamics commonly observed in the brain may be associated with two distinct types of underlying mechanisms or processes. Dynamics with narrow band-limited power may reflect the influence of specific pacemaker units. For instance, the occipital alpha rhythm, which dominates the EEG during relaxed wakefulness, may originate from an alpha pacemaker unit, which consists of a specialized subset of gap-junction–coupled thalamocortical neurons that exhibit intrinsic rhythmic bursting at alpha frequencies (11–13). Although much evidence supports this oscillatory model of resting-state activity (e.g., refs. 14 and 15), the dominant hypothesis in the field is that correlations arise from neural activity propagating within an anatomically constrained small world network (e.g., refs. 16 and 17). This model predicts scale-free dynamics, also known as 1/f dynamics (17, 18). With 1/f dynamics, event amplitude varies inversely with frequency, so that large events are rare whereas small events are common. More precisely, power may vary inversely with frequency raised by a (small) exponent: P ∝ 1/fβ, with typical exponents from 0 to 3 (19). The 1/f dynamics are a hallmark of a complex dynamic system operating at a critical point, at which the system is balanced between ordered and disordered phases (20–22), although 1/f dynamics may also arise in other noncritical systems (23). The fact that various neural signals, such as local field potentials, show 1/f characteristics has inspired models of the brain as operating at a critical point through a process of self-organization (17, 24–28).
Local BOLD fluctuations have a 1/f power spectrum (29–31). This has led to the suggestion that the slow correlations of resting-state connectivity may reflect a critical process (18, 19). This assumes that the dynamics of interregional oxygen correlation match the dynamics of local fluctuations. Indeed, three studies report that BOLD correlations vary inversely with frequency (1/f), much like local oxygen (32–34). However, Sasai et al. (35), Achard et al. (36), and Cordes et al. (37) report instead that oxygen correlation peaks around 0.04–0.06 Hz, with less correlation at lower frequencies—a band-limited pattern that is distinctly different from 1/f (38–40). Finally, other studies report that BOLD correlations reach a plateau at low frequencies, a result that is intermediate between 1/f and band-limited dynamics (41, 42).
We used oxygen polarography to directly measure the spectrum of interregional oxygen correlation. Polarography is an invasive alternative to BOLD fMRI that allows robust recording of local oxygen fluctuations with higher temporal resolution, higher frequency specificity, and broader frequency range than can be achieved with standard fMRI techniques. We measured oxygen fluctuations in the default network [bilateral posterior cingulate cortex (PCC) area 23] and the visual/attention network (bilateral V3) in the awake, resting macaque. Here, we report that correlations between homotopic regions are band limited rather than 1/f. Further, we show that the variance of local oxygen fluctuations can be separated into a 1/f component and a band-limited component. Only the band-limited component relates to long-range correlation. This suggests that there is a band-limited mechanism (or mechanisms) driving interregional oxygen correlation that is distinct from the mechanism(s) driving local (1/f) oxygen fluctuations. The fact that correlation is band limited is suggestive of a rhythmic or pseudo-oscillatory mechanism.
Results
Polarography Captures Long-Range Oxygen Correlation.
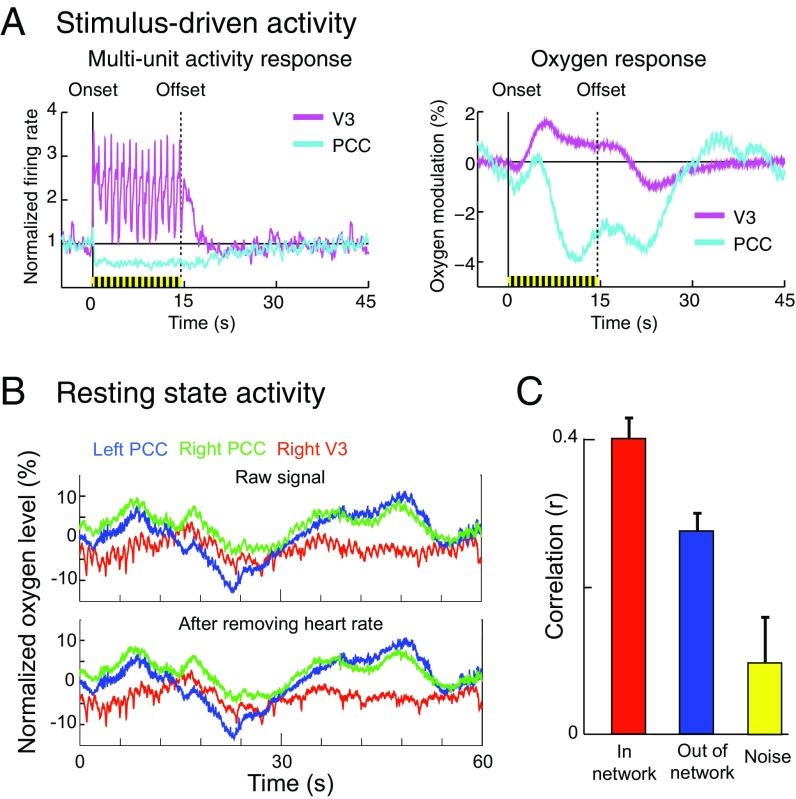
We recorded resting-state oxygen level simultaneously from four sites in two monkeys: two sites in the default mode network (left and right PCC) and two sites in the visual/attention network (left and right V3). To verify electrode placement, we first obtained visually evoked responses at each of these sites. As previously reported (43), both multiunit firing rate and oxygen level were elevated in V3, and both were suppressed in PCC (Fig. 1A). This confirms that our recording sites are located in two functionally distinct networks: V3 is part of the task-positive, visual/attention network, whereas PCC is part of the task-negative, default mode network.
Fig. 1.
(A) Visually driven activity in V3 and PCC. The visual stimulus is a 1-Hz flash for 15 s (yellow and black bar). A, Left shows firing rate normalized to the rate in the 5 s before stimulation and A, Right shows the oxygen modulation. In V3, both unit activity and oxygen level are activated during visual stimulation, and in PCC, both are suppressed. (B) Example data (normalized oxygen level) obtained from three electrodes in a minimally restrained animal at rest in complete darkness. B, Lower shows the same data after regressing out heart rate. (C) Within each network, oxygen signals (left vs. right V3, left vs. right PCC) are strongly correlated with one another (“In network,” r = 0.40 ± 0.03, n = 31 polarographic electrode pairs). Out-of-network signals (left V3 vs. left PCC, left V3 vs. right PCC, right V3 vs. right PCC, right V3 vs. left PCC) are also correlated, but less so (r = 0.28 ± 0.02, n = 62 electrode pairs). The correlation between noise signals, recorded from outside the brain, is 0.10 ± 0.06 (P = 0.13, n = 42). Both in-network and out-of-network correlations are significantly higher than noise correlation (both P < 0.005), and the difference between in-network correlation and out-of-network correlation is significant (P < 0.005).
After visual stimulation, we recorded 30–60 min of resting-state data, where monkeys were left alone and resting in the dark room. Similar to BOLD recorded with fMRI, oxygen level fluctuated slowly, over the course of tens of seconds or longer, changing by up to ∼10% of the baseline value (Fig. 1B, Upper) (44). Unlike BOLD, prominent pulsations (∼1% of the baseline value) occurred at just above 1 Hz. In separate experiments we recorded simultaneous electrocardiograms to show that these pulsations correspond to heart beats (Fig. S1). In conventional BOLD, these pulsations are aliased into lower frequencies due to the low sampling rate of fMRI. With our high temporal resolution, this does not occur. However, modulation of heart rate by respiration rate and other low-frequency factors will contaminate measures of interregional oxygen correlation regardless of sampling rate (45). To minimize this contamination, we analyzed correlations only after regressing out the heart rate signal (Fig. 1B, Lower). See SI Text for additional discussion regarding the comparison between oxygen polarography and BOLD fMRI.
To determine whether long-range correlations in oxygen can be seen using polarography, we first bandpass filtered the oxygen signals into the standard fcMRI frequency range (0.1–0.01 Hz). Fig. 1C shows that polarographic oxygen is correlated across long distances. Correlations are significantly larger within a network (in-network correlation, recorded from sites in opposite hemispheres) than correlations across networks (out-of network correlation) (P < 0.005). Both in-network and out-of-network correlations are greater than zero (rin = 0.40 ± 0.03, nin = 31, P < 0.0001; rout = 0.28 ± 0.02, nout = 62, P < 0.0001). The positive out-of-network correlation is surprising, because many fcMRI studies find that the visual/attention and default mode networks are anticorrelated with one another; that is, their out-of-network correlation is negative (44). Such anticorrelation may or may not be the result of preprocessing steps whose purpose is to remove common signals (46). In fact, it has been shown that the so-called “global signal” is in fact particularly prominent in regions including visual cortex and pericingulate regions (47). To test whether the positive out-of-network correlation that we observed was specific to the particular sites that we used, to their physical proximity, or to their lying within or close to the occipital lobe, we performed additional control experiments. We recorded from two additional pairs of visual/attention and default mode network sites: the intraparietal sulcus (IPS) and PCC and the anterior cingulate cortex (ACC) and V3 (Fig. S2). All out-of-network correlations were significantly positive, even for pairs at the most extreme distance (ACC vs. V3: rout = 0. 20 ± 0.03, P < 0.001). Distance may affect the strength of out-of-network correlation, although this analysis is confounded by network identity (Fig. S2). Hemispheric location (within vs. across hemispheres) did not affect out-of-network correlations (rout [within hemisphere] = 0.29 ± 0.05, rout [across hemisphere] = 0.26 ± 0.03, P = 0.4).
Out-of-network correlations could be driven by artifactual signals not related to oxygen level. The yellow bar in Fig. 1C and the yellow dot in Fig. S2 represent the correlation between noise signals recorded from soft tissue or fluid immediately adjacent to the brain. This correlation was very low (rnoise = 0.10 ± 0.06, nnoise = 42, P = 0.13), ruling out non-oxygen–related artifacts (e.g., correlated electrical circuit noise and movement artifacts) as sources for the high in- and out-of-network correlations. Taken together, our results demonstrate that oxygen polarography can capture long-range, network-dependent oxygen correlation and serve as an MR-independent measure of functional connectivity.
Oxygen Correlation Is Band Limited.
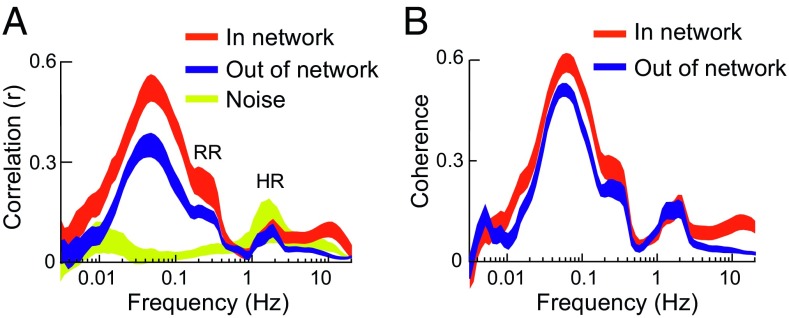
To gain insight into the mechanism(s) driving interregional oxygen correlation, we wished to evaluate the frequency structure of just that portion of the signals that is correlated between regions. Because we cannot precisely isolate the correlated signal, we instead estimated its frequency spectrum by computing correlation as a function of frequency. To accomplish this, we filtered the heart-rate–regressed oxygen signals into half-octave frequency bands from 0.003 Hz to 20 Hz and then computed correlation for each band. Fig. 2A shows that both in- and out-correlations are present only in a band-limited window between 0.01 Hz and 0.4 Hz, with a peak at 0.06 Hz, and not present below 0.01 Hz or between 0.4 Hz and 5 Hz. This frequency structure suggests that the correlated signal is not 1/f but band limited.
Fig. 2.
(A) Oxygen correlation as a function of frequency, mean ± 1 SEM. Both in- and out-of-network correlations are band limited from 0.01 Hz to 0.4 Hz. Peak correlation is at 0.06 Hz. Data recorded from outside the brain show no significant correlation at these frequencies. The peak just above 1 Hz and the shoulder just above 0.1 Hz reflect residual effects of heart rate (HR) and respiratory rate (RR), present after regression of HR (SI Text). (B) Coherence (baseline removed; Materials and Methods and Fig. S4) shows band-limited effects similar to those seen in correlation.
There are several additional features in the data, including a prominent peak at 1 Hz and a shoulder at 0.3 Hz. Both are significantly decreased after regressing out heart rate (Fig. S3). Respiration is known to modulate heart rate and BOLD signals, and the respiratory rate in monkeys is close to 0.3 Hz (48). Therefore, the features at 1 Hz and 0.3 Hz likely reflect residual effects of heart rate and respiration, respectively. A small peak at 10 Hz appears only for in-network correlations and may reflect a previously undescribed high-frequency, network-specific coupling. The yellow trace in Fig. 2A represents the correlation found in the soft tissue outside of the brain and demonstrates that the frequency dependence of correlation is a brain-specific finding and is not related to extraneous factors such as noise or filtering in our system.
Correlation captures the instantaneous temporal dependence between two signals. If there is a time lag between two otherwise similar signals, then correlation will underestimate that similarity. Consider two otherwise identical sine waves, one of which is shifted in time by one-quarter cycle. One signal perfectly predicts the other, and therefore there is 100% temporal dependence between the two. However, because of the phase shift, their correlation coefficient is zero. Coherence, unlike correlation, captures temporal dependence even in the face of phase shifts. Unlike correlation, the coherence between two sine waves of the same frequency is always 1, regardless of phase lead or lag. In general, shifting two signals in time will change their correlation but will have no effect on their coherence.
Fig. 2B shows that, like correlation, coherence is also band limited from 0.01 Hz to 0.4 Hz. Other related measures such as synchrony and wavelet amplitude correlation give similar results (Fig. S4). The pattern for in-network (PCC–PCC and V3–V3) recording sites was found in all animals tested, and a very similar pattern of band-limited correlation was also seen in all out-of-network pairs, including the out-of-network correlations between V3 and PCC, IPS and PCC, and V3 and ACC (Fig. S5). We conclude that interregional oxygen signals show band-limited temporal dependence, not 1/f.
Local Oxygen Has Both a 1/f Component and a Band-Limited Component.
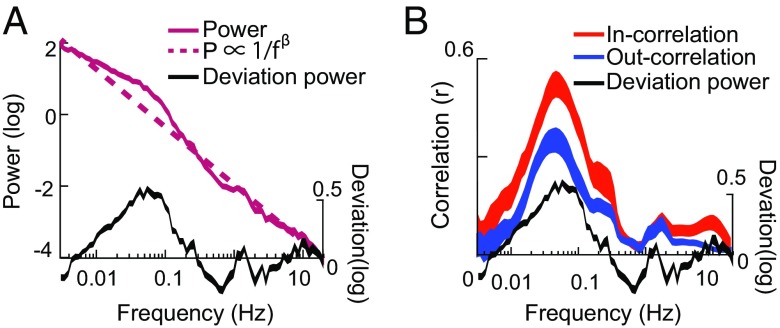
Previous MRI studies report that the local BOLD power spectrum is 1/f from 0.01 Hz to 0.23 Hz (29). Our polarography data extend this finding to a range of 0.003–20 Hz. When plotted on log–log axes, a 1/fβ relationship appears as a straight line with a slope of β. Fig. 3A reveals a P ∝ 1/fβ relationship with an exponent of 1.74. Together, Figs. 2 and 3A show that local power is predominantly 1/f whereas long-range correlation is band limited. This situation might arise in one of two ways. In one scenario, oxygen fluctuations are driven by at least two distinct mechanisms. One mechanism is entirely local and has 1/f characteristics; that is, it has high power at low frequencies and low power at high frequencies. The other mechanism independently drives fluctuations that are correlated across regions. This mechanism is band limited, with most of its power concentrated between 0.01 Hz and 0.4 Hz (Fig. 2).
Fig. 3.
(A) Power in the local oxygen signal as a function of frequency. A log-linear (1/f) model fit (dashed dark red line) accounts for most of the power in the raw oxygen (solid dark red line). Subtracting the log-linear fit from the observed power leaves a residual that we call the “deviation power” (black line). (B) The frequency profile of the local deviation power is similar to the frequency profile of long-range correlation, both within network (“In-correlation”) and across networks (“Out-correlation”).
In the second scenario, oxygen fluctuations are driven by sources that have a 1/f spectrum, and fluctuations that are coupled across regions are a band-limited component of this 1/f spectrum. (In neither scenario do we include known nonneural sources of oxygen fluctuations, e.g., heart rate, which is band limited at around 1 Hz.) The power (or equivalently, the variance) of two independent processes will add together. Therefore, we can distinguish between the two scenarios by asking whether the local power is best described as the sum of a 1/f component and a band-limited component (supporting the first scenario) or as purely 1/f (supporting the second scenario).
The data support the first scenario, that is, separate 1/f and band-limited sources. On closer examination, the local power spectrum deviates from a strict P ∝ 1/fβ fit, and the largest deviation occurs over the same range of frequencies at which long-range correlations appear (0.01–0.4 Hz). When this frequency range is excluded, the exponent of the best 1/f fit is 1.65. We call the difference between the 1/f fit (Fig. 3A, dashed dark red line) and the observed power (Fig. 3A, solid dark red line) the “deviation power” (Fig. 3A, black line). Fig. 3B shows that the deviation power has the same frequency profile as the interregional oxygen correlation. The match is similar for both in-network correlation (r = 0.89, P < 0.0001) and out-of-network correlation (r = 0.78, P < 0.0001), although it is stronger in network than out of network (P = 0.047). This relationship between the 1/f fit and the observed power is also significant if, instead of using the mean power averaged across all sessions, the relationship is computed session by session (r = 0.37 ± 0.04, n = 31, mean ± SEM, P < 0.05 for in network and r = 0.24 ± 0.04, n = 62, P < 0.05 for out of network). To summarize, local power deviates from a strict 1/f relationship, and this deviation matches the frequency profile of long-range oxygen correlation. Because the power from independent processes will add together, this pattern can be most parsimoniously explained by the idea that at least two independent mechanisms drive oxygen fluctuations. One mechanism is 1/f and local, and the second is band limited and nonlocal. (We cannot rule out that the two mechanisms may be partially rather than fully independent.)
As a further test of the two-source model, we asked whether the deviation power cofluctuates with interregional oxygen correlation in time. Briefly, we used a sliding-window strategy (2-min wide, 10-s increments) to estimate the time courses of (i) the local deviation power and (ii) the interregional correlation strength. The time courses were estimated over a half-octave band centered at 0.06 Hz. We chose this frequency band because this is where we measure the highest deviation power and the strongest interregional correlation. We then calculated the correlation coefficient between the time course of average deviation power from each pair of electrodes and the time course of the long-range correlation coefficient between those same two electrodes. The fluctuations of local deviation power are significantly correlated with the fluctuations in long-range correlation, both for in-network (r = 0.29 ± 0.05, P < 0.05) and out-of-network electrode pairs (r = 0.13 ± 0.04, P < 0.05). The relationship is significantly stronger in network compared with out of network (P = 0.03). These results confirm that local deviation power is significantly related to long-range correlation. The relationship exists for both in-network pairs and out-of network pairs, but is stronger for in-network pairs.
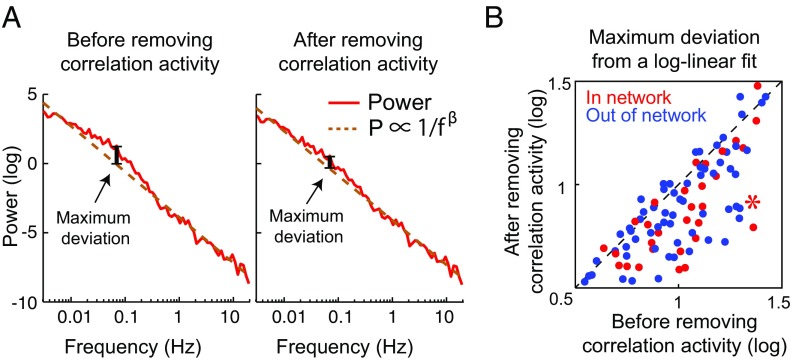
As a final test of the two-source model, we evaluated the impact of removing correlated power on the local power spectrum. If the two-source model is accurate, then removing the power associated with the long-range correlation (the correlated power) from the locally measured power should make the remaining power more consistent with the P ∝ 1/fβ spectrum (Fig. 4A). We estimated the correlated power based on a linear regression model (Materials and Methods). Removing the correlated power significantly improved the fit of the local oxygen signals to a 1/fβ model. For each individual session and recording site (n = 93), removing the correlated power either reduces the maximum deviation from a strict P ∝ 1/fβ spectrum or else leaves it essentially unchanged; that is, all of the data points fall close to or below the diagonal identity line (Fig. 4B). In no case did removal of the correlated power substantially increase the deviation from a 1/f fit; that is, no points are well above the identity line. In summary, our data support a two-source model in which oxygen fluctuations are driven by the sum of long-range band-limited sources and a local 1/f source. The removal of the correlated power from a single distal electrode does not produce a perfectly linear fit; that is, after removal a positive deviation often remains in the 0.01- to 0.4-Hz range (e.g., Fig. 4A, Right). This is consistent with a model in which there are independent band-limited contributions from multiple long-range networks, and our manipulation removes only one of those contributions.
Fig. 4.
Maximum deviation from a log-linear fit. (A) The oxygen power spectrum was expressed in log–log scale and then fitted by a linear function [log(Power) = −β × log(f) + k or P ∝ 1/fβ] before (A, Left) and after (A, Right) removing correlated activity. The maximum deviation was computed as the maximum difference between the observed power spectrum and the linear fit (vertical black lines). (B) Maximum deviation before and after removing correlated activity. Each individual data point corresponds to a single session’s recording from a single pair of in-network (red circles) or out-of-network oxygen signals (blue circles). The maximum deviation was reduced or largely unchanged as a result of removing the correlated portion of the signal. The asterisk corresponds to the data in A.
Differences in Frequency Content Across Networks.
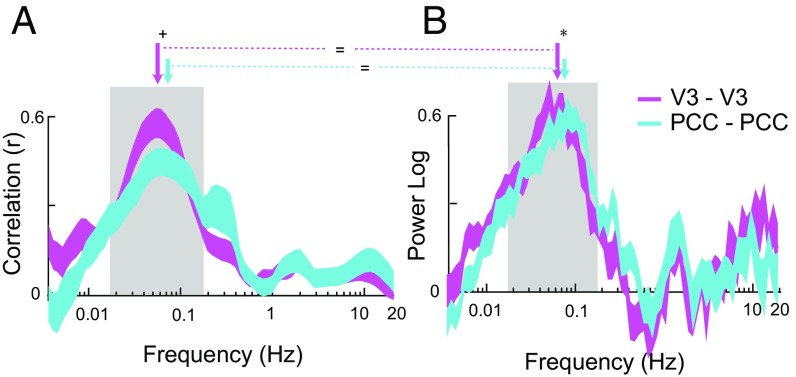
To investigate whether the frequency content of correlation is similar or different for different networks, we compared correlation and power deviation across frequencies in the visual/attention network (left V3 and right V3) and in the default mode network (left PCC and right PCC). Fig. 5 shows that the frequency profiles of the visual/attention and default networks are broadly similar, whether assessed by oxygen correlation (Fig. 5A) or by power deviation (Fig. 5B). Both networks are band limited from 0.01 Hz to 0.4 Hz.
Fig. 5.
(A) The frequency profiles of oxygen correlations from the visual/attention and default networks are nearly identical. The default network has a trend toward a higher peak correlation frequency than the visual attention network (V3) (0.072 ± 0.009 Hz vs. 0.056 ± 0.004 Hz, respectively; P = 0.09 for the difference). (B) The deviation power profiles from the two networks are also similar, although the small difference in the peaks of the deviation power is significant (0.076 ± 0.005 Hz vs. 0.054 ± 0.004 Hz, respectively; P < 0.05 for the difference). The peak frequencies revealed by correlation analysis (A) vs. deviation power (B) are not significantly different from one another for either network (P > 0.5 for each).
To compare band-limited correlations in the two networks more closely, we compared the frequencies at which the peak effect (correlation or deviation power) occurs, computed electrode pair by electrode pair. There is no significant difference in the values obtained using one or the other method (Pvisual/attention = 0.7, Pdefault = 0.6). The peak correlation frequencies (Fig. 5A, arrows) show a trend toward being higher in the default network than in the visual/attention network (0.072 ± 0.009 Hz vs. 0.056 ± 0.004 Hz, respectively; P = 0.09). This difference is significant for the peak deviation power (Fig. 5B, 0.054 ± 0.004 Hz vs. 0.076 ± 0.005 Hz, P < 0.05). In sum, correlation within the two networks occurs at a similar range of frequencies (0.01–0.4 Hz), but the peak effect is 0.02 Hz higher in the default network compared with the visual/attention network. Finally, the fact that the same peak frequencies are seen within each network when using either long-range correlation or local deviation power further supports the two-source model.
Eyes Open vs. Eyes Closed.
Both local fluctuations and long-range correlations were stronger when the eyes were closed compared with open. Effects were similar across areas and networks, with greater effects in network compared with out of network (SI Text). The published data from human fMRI are inconsistent on this point (Table S1). See SI Text for discussion.
Discussion
Interregional correlation of fluctuations in BOLD signals has been used to reveal the functional architecture of large-scale brain networks. To gain insight into the origin of BOLD correlation, we used a high temporal-resolution measurement, oxygen polarography, to further probe oxygen fluctuations and their correlation. We simultaneously recorded oxygen from two sites in the default mode network (bilateral posterior cingulate) and from two sites in the visual/attention network (bilateral V3) in each of two resting macaques across multiple experimental sessions.
We found that long-range oxygen correlation occurs only in a restricted-frequency window of 0.01–0.4 Hz (Fig. 2; see SI Text for discussion regarding the upper bound). In contrast, the variance or power of local oxygen levels is inversely proportional to frequency (1/f, or more completely, P ∝1/fβ with β = 1.7) across the full range of tested frequencies (0.003–20 Hz) (Fig. 3A). This indicates that the (band-limited) process or processes driving interregional correlation are distinct from the (1/f) process(es) driving local oxygen fluctuations. On closer inspection, the power spectrum of local oxygen fluctuations deviates slightly from a strict 1/fβ fit. The profile of this deviation closely matches the frequency profile of the long-range oxygen correlation (Fig. 3B). This is exactly what would be predicted if the band-limited mechanism or mechanisms driving interregional oxygen correlation are independent of the mechanism(s) driving the local 1/fβ fluctuations. Finally, the fact that correlation is band limited suggests that long-range oxygen correlations are driven by a rhythmic or pseudo-oscillatory mechanism. The fact that the peak frequency is higher in one network than in the other (Fig. 5) is consistent with two separate driving mechanisms, but could also arise from a single mechanism with slightly different effects on the two networks (41).
Oxygen Polarography Captures Interregional Oxygen Correlation.
fcMRI has established that blood oxygen levels in widely separated brain areas fluctuate in synchrony. This finding was established by sampling volumes 2–3 mm on a side at 1- to 3-s intervals. We modified an existing technique, oxygen polarography, to examine long-range oxygen correlations. Oxygen polarography has been used to study the vascular control of oxygen levels in the brain and more recently to examine the relationship between local oxygen levels and neuronal activity (43, 49–52). Fluctuations in local oxygen level were an incidental finding in many early polarography studies, but they were believed to be driven by local autoregulation (e.g., refs. 53 and 54). Burgess et al. have observed slow fluctuations (∼0.1 Hz) that are correlated between left and right medial geniculate in rats (55). However, the importance of interregional oxygen correlation did not become apparent until fcMRI revealed that long-range BOLD correlations can be used to delineate functionally relevant brain networks (44, 56).
Polarographic oxygen signals can be recorded using modified glass pipettes (Clarke electrodes), platinum, or carbon paste electrodes (49–52). Electrode tip sizes can range from microns to millimeters. We recorded simultaneously from multiple areas, using independently controlled platinum microelectrodes with ∼30-μm exposed tips. Our design was optimized for robustness (required for use in an awake behaving animal), high spatial specificity, and high temporal resolution. In our design, oxygen levels are recorded from a sphere of brain parenchyma 30–100 μm in diameter (vol = 0.00001–0.0005 mm3). We temporally filtered the analog oxygen signal at 20 Hz before digitizing at 1,000 Hz.
Remarkably, the signals obtained through fMRI and polarography are largely similar, despite differences in sampled volume and temporal resolution and despite the fact that polarography samples tissue oxygen rather than blood oxygen. The amplitude and time course of stimulus-evoked responses in both task-positive and task-negative areas are similar for the two techniques (43), as is the finding of interregional correlations (Fig. 1). In our data, exactly as in fcMRI before global signal regression (see below), most correlations are positive. Scholvinck et al. (57) have found electrophysiological evidence for widely shared neural activity at rest in nonhuman primates, which could correspond to the positive correlation that we see in the polarographic oxygen signals between PCC and V3.
A direct comparison between the functional connectivity revealed by polarography and fcMRI is complicated by differences in preprocessing. Before computing correlations in fcMRI data, a mean signal (the global signal) is computed and then regressed out of each voxel’s data. Some portion of the global signal is clearly artifactual, including variance due to head movements, respiration, and aliasing from heart rate. Some variance is of neural origin. The neurally derived portion of the global signal could reflect a specific global neural signal, as shown in Scholvinck et al. (57), or merely an average of neural activity throughout the brain (46). Global signal regression (GSR) will distort correlation by imposing a substantial negative bias, because the sum of the correlations across all of the contributing signals must necessarily be less than or equal to zero as a result of GSR (Fig. S6; see ref. 46 for proof). In addition, GSR might fundamentally alter the correlation pattern by biasing correlations differently in different regions, depending on the true underlying correlation structure (58). Nevertheless, GSR remains in wide use for fcMRI data, and this is fully justified by the fact that GSR is effective in removing artifactual variance in fcMRI data and greatly improves the delineation of networks within the brain (59).
Although GSR is appropriate for fcMRI preprocessing, it would be inappropriate to apply GSR to our polarographic data. Artifactual sources are greatly attenuated in polarographic data compared with MRI data. Sampling rates are higher so aliasing of heart and respiration rate is not an issue; heart and respiration rate effects can be resolved and removed from the data. In addition, we did not observe shared signals in our control recordings from nonneural tissue (Fig. 1B). This result argues that our system is not susceptible to correlations resulting from nonneural sources, including motion artifacts, which are the major artifactual source in fcMRI data. Thus, applying GSR to polarography data will not yield empirical benefits in artifact removal as in fcMRI. If we were to nonetheless blindly apply GSR in the current study, then the sum of all of our correlations would necessarily be negative. This would occur whether or not a shared signal is actually present; it is a mathematical consequence of the operation and independent of the physiology. With thousands of signals, as in typical fMRI analyses, the sum of the correlations after regression approaches zero; with fewer signals the sum is progressively more negative (Fig. S6). Thus, with our current state of knowledge, applying GSR to our data is inappropriate for both theoretical and practical reasons. We cannot rule out the possibility that our results may be affected by the inclusion of a globally shared neural signal that is removed from the fMRI data by GSR. However, our most important finding—that interregional correlation is band limited—still applies, because the difference between in-network and out-of-network correlation is itself strongly band limited (Fig. 2A).
Interregional Oxygen Correlation Is Independent of Local Fluctuations and Is Band Limited.
The temporal and spatial features of interregional oxygen correlation can provide clues to the origin of the correlation. Local BOLD fluctuations have 1/f power spectra (Fig. 3A) (29–31). From this it has been suggested that neural activity corresponding to interregional BOLD correlation may also have a 1/f power spectrum (19). Furthermore, the topology of connectivity, as assessed by correlations, itself shows a 1/f character. Only a few voxels are strongly correlated with many other voxels outside of their own network (“hub nodes”), whereas many voxels show a few internetwork correlations (60, 61). Such 1/f features are a signature of a system operating around criticality, a state where the system balances between ordered and disordered phases and has a maximum number of metastable states (62). Taken together, these findings have inspired a heuristic model in which interregional oxygen correlation results from self-organized criticality (24–28).
A key assumption of the heuristic model is that the spectrum of interregional correlation is 1/f. Although some studies have obtained results consistent with a 1/f pattern, other studies report opposite results. Salvador et al. (33) separate BOLD into three frequency bands (0–0.08 Hz, 0.08–0.17 Hz, and 0.17–0.25 Hz) and show that correlation is strongest at the lowest-frequency band, consistent with a 1/f spectrum. Ciuciu et al. (32) also argue that BOLD coherence is 1/ f. In contrast, Wu et al. (41) show that correlation first increases as frequency decreases and then plateaus at 0.04–0.06 Hz. Achard et al. (36) show that wavelet correlation, which is similar to coherence, peaks around 0.03–0.06 Hz and drops at lower frequencies. Sasai et al. (35) measure mean-squared coherence and find that the prefrontal and occipital regions show high coherence only in a narrow frequency range (0.04–0.1 Hz). Network structure is most clear for fMRI at 0.02–0.06 Hz (33, 36, 37). Additional indirect support of band-limited behavior can be seen in studies of quasi-periodic patterns in the BOLD signal, which have a center frequency of around 0.05 Hz (63–66). Other indirect support can be found in the fact that gamma-band power, a putative neural correlate of BOLD (but see ref. 43), is coherent within the default mode network only over a narrow frequency range (31). Still other studies find mixed results regarding the frequency content of BOLD correlation (37, 42). Thus, some results have been consistent with a 1/f pattern and others have been consistent with a band-limited pattern.
Two main issues may explain the lack of agreement across studies. To distinguish band-limited from 1/f effects, a wide range of frequencies is helpful. Many studies of correlation acquire only 5–10 min of data, which limits their range at the low-frequency end. Range is limited at the high end by sampling rate. A typical 5-min fMRI dataset provides a theoretical frequency range of 1.3 decades (0.17–0.0033 Hz) and a usable range of less than 1 decade. (The usable range is reduced at the high end because the Nyquist limit cannot be reached under real-world conditions and is reduced at the low end because at least three or four cycles are required for a reproducible estimate.) Second, most measures of coherence (but not mean-squared coherence, used by ref. 35) are compromised by a mathematical artifact that produces an apparent 1/f effect (Fig. S7). This bias is surprisingly strong, yet few studies remove or otherwise compensate for it (32, 35). In addition, Zhang et al. (40) show that artifacts, such as head motion and systemic physiological fluctuations in pulsation, can mask the frequency structure of the “true” correlation. To address these issues, we use oxygen polarography, which is less susceptible to artifactual correlations (Figs. 1B and 2A), and collect polarographic data for 40 min, providing at least four cycles of data over four frequency decades (0.0017–20 Hz), and correct our analysis of coherence for the artifactual 1/f contamination.
We show that interregional oxygen correlation is band limited from 0.01 Hz to 0.4 Hz with a peak at 0.06 Hz, not 1/f (Fig. 2). In addition, we show that the power spectrum of oxygen fluctuations measured at each electrode can be explained as the sum of a 1/f process plus a band-limited process (Fig. 3A). Both the frequency profile and the temporal fluctuations of the deviation power match those of the interregional correlation (Fig. 3B). This relationship exists for both in-network pairs and out-of-network pairs, but is stronger for in-network pairs. Our results indicate that the signal underlying interregional correlation has a band-limited spectrum that is distinct from the 1/f pattern of local oxygen fluctuations. The fact that the relationship is stronger for in-network pairs supports that the deviation power reflects both network-specific and network-nonspecific correlations (such as the global signal shown in ref. 57). In-network pairs capture both network-specific and network-nonspecific correlations, whereas out-of-network pairs capture only network-nonspecific correlation, and thus in-network pairs show a stronger relationship between their correlation and their local deviation power.
Our results do not address whether criticality exists in the brain. They do, however, strongly suggest that interregional correlation is neither a result nor a reflection of criticality. More generally, our results challenge the view that functional connectivity arises from neural activity propagating within an anatomically constrained network (e.g., refs. 16 and 17). This would predict that correlation has a flat spectrum (Fig. S8). Instead, we show that oxygen correlation is band limited. The band-limited aspect of interregional correlation is highly suggestive of rhythmic or pseudo-oscillatory mechanisms, perhaps reflecting resonant mechanisms or circuits (15, 67–69).
Interregional correlations could be driven by oscillatory modules, perhaps in subcortical nuclei, which consist of small sets of cells and generate band-limited patterns of firing that are then transmitted to widespread cortical and subcortical regions. Indeed, simple oscillator-based models of functional connectivity exist (e.g., ref. 70). However, these models focus on oscillators with fast dynamics, on the order of tens to hundreds of milliseconds. Our results point to oscillators with dynamics several orders of magnitude slower.
An alternative possibility is that band-limited correlation that we measure using polarography is unrelated to the functional connectivity measured using BOLD and instead reflects local vasomotion or Mayer waves, both of which are low-frequency (∼0.1 Hz) oscillations in cerebral hemodynamics. For several reasons, we do not believe this is the case. First, we see greater correlation within known cortical networks than across networks. Local vasomotion is a spontaneous oscillation of local blood vessel tone and is unlikely to drive long-range correlations (53, 71) (but see ref. 63). Mayer waves are produced by oscillations of arterial pressure and can drive long-range correlations, but these correlations would not reflect functional network structure (72). Second, our control recordings from soft tissue should be as susceptible to local vasomotion and Mayer waves as signals recorded from the brain (73). However, our control recordings do not show band-limited correlation. Third, local vasomotion sporadically occurs in a range of pathological conditions or subjects under anesthesia but appears to be rare in healthy awake subjects; its occurrence may reflect a form of hemodynamic dysregulation (71). In contrast, fcMRI is a consistent phenomenon, seen in essentially all subjects. We have found band-limited oxygen correlations in all four awake, resting monkeys that we tested (Fig. S5). The odds of all four animals showing the same rare vascular behavior are quite low. Fourth, the characteristic frequency of local vasomotion and Mayer waves is 0.1 Hz, which is almost an octave above the center frequency that we observe. Fifth, local vasomotion and Mayer waves are sinusoidal, with a large amount of power in a very narrow frequency range (53, 71, 72). The signals we have recorded are not sinusoidal but aperiodic (Fig. 1A). In sum, although we cannot rule out that local vasomotion or Mayer waves contribute to oxygen correlation, these facts all suggest that the band-limited correlation that we observe reflects the same phenomenon that is revealed by resting-state fcMRI in humans and is of neural origin.
Materials and Methods
Animals, Behavior, and Stimulus.
Two macaques served as subjects in this study. Animals were cared for and handled in accordance with the Guide for the Care and Use of Laboratory Animals, and all procedures were approved by the Washington University Animal Studies Committee (74). During recording, macaques were fully hydrated and sat with heads fixed in a dark room. Behavior was unconstrained, and the animals had no expectation of a task or reward. Animals naturally relaxed in the setup. The velocity of spontaneous eye movements typically slowed and the eyelids often partially or fully closed (64% and 17% of the time, respectively, for the two monkeys). Results discussed below are similar for the two monkeys, and thus the data are combined. Data from two additional macaques were collected for results reported in the SI Text.
Recording.
Electrodes were targeted to V3 and PCC, using anatomical MRI images and physiology (43). Briefly, each animal’s brain was accessed via bilateral 15-mm (internal diameter) chronic custom recording chambers. T1 weighted MRI images (magnetization prepared rapid acquisition gradient echo imaging 0.5-mm isotropic voxels) were obtained using a custom phantom in the chamber that provides visualization of the chamber and allows for the virtual projection of a chamber-based coordinate system down into the brain. In one monkey, two small manganese injections were placed to confirm alignment. Before data collection, boundaries for PCC and V3 recording regions were defined on the MRI image. The positions of PCC and V3 were further validated based on their respective oxygen and electrophysiological responses to visual stimulation, which were recorded immediately before the resting-state data (43).
To record oxygen signals, we used specialized platinum microelectrodes [FHC inventory no. UE(LS3)] as a cathode. An Ag/AgCl reference electrode (Grass Technologies) was placed on the back of the head at a location with minimal underlying musculature and no response to body or limb movements. The skin was lightly abraded to minimize sweat and movement potentials, and a layer of Ten20 EEG paste was applied. The platinum cathode was polarized at −0.8 V relative to the reference electrode (Unisense PA2000). The current required to maintain the polarization is proportional to oxygen level. This signal was filtered at 20 Hz and sampled and stored at 1 kHz, using the Plexon MAP system.
We recorded oxygen signals simultaneously from left and right PCC and left and right V3. Twenty datasets (10 from each monkey) with an average length of 40 min were recorded.
Analysis.
All analyses were performed with custom software written in Matlab (MathWorks). Oxygen polarographic signals, like BOLD signals, reflect relative rather than absolute oxygen levels. Therefore, the polarographic signals, like BOLD data, were expressed as percentage of deviation from the mean signal level.
Heart-rate removal.
We identified individual heart rate pulsations, using a recursive template-matching approach. We started with a 1-s Gaussian-derived generic heartbeat template. We identified putative beat times as the moments at which the template had greatest linear correlation with the data, using a sliding-window approach (1-s window with increment of 1 ms). We used these times to generate a beat-triggered average of the oxygen signal. We then replaced the heartbeat template with this beat-triggered average and repeated the analysis. Four iterations were performed to refine our estimates of the beat template and the beat times. The estimated heartbeat effect was then regressed out of the oxygen signals, taking into account instantaneous heart rate, using the method of Fekete et al. (75).
Bandpass filtering.
Bandpass filtering was accomplished by first high-pass filtering and then low-pass filtering. Chebyshev-type II filters were designed with a defined passband and stopband. The transition band of each filter was one octave wide, and the stopband was set to −80 dB. For the correlation in Fig. 1B, the −3-dB points for the low- and high-pass filters were set to 0.01 Hz and 0.1 Hz, respectively. For correlation in Fig. 2A, oxygen signals were filtered into individual frequency bands, using filters with half-octave passbands.
Correlation and coherence.
Correlation was calculated as Pearson’s r. To calculate coherence, we decomposed each oxygen signal into a time-frequency representation. We extracted the instantaneous amplitude A(t, f) and analytical phase ψ(t, f) as a function of time and frequency by applying the Hilbert transform to each half-octave band. To confirm that our results were not influenced by the specific filters used or by the use of the Hilbert transform, we repeated the decomposition and subsequent analyses, using a continuous wavelet transform with a complex Morlet wavelet (43). These two approaches generated nearly identical results.
Coherence at the frequency (f) is defined as
where is the expectation or mean value across time (t). Coherence measures the degree of consistency of the phase difference Φx,y(t, f) = ψx(t, f) − ψy(t, f) across time. It ranges over the interval 0–1. The more consistent the phase difference is across time, the higher the coherence value. All statistics on correlation and coherence were done after applying Fisher’s Z transform (76).
Estimations of instantaneous phase at neighboring time points by a Hilbert or wavelet transform are based on a finite interval. This results in the phase of neighboring time points being nearly identical, because they are estimated based on overlapping data. Even phase estimates of time points that are more widely separated will show some level of artifactual consistency. This artifactual consistency in phase within individual signals produces artifactual consistency in the phase differences across signals. This in turn leads to artifactual nonzero values for coherence even for completely independent signals. Fig. S7 shows the bias between two 8-min independent synthetic signal streams. The bias approaches 1 for a single cycle of data. This reflects the fact that, with a single cycle of data, phase can hardly vary as a function of time, and therefore the phase difference between two independent streams remains nearly constant for the entire cycle, and coherence thus approaches 1. As the number of data cycles in each stream increases, the bias decreases, but even with 1,000 cycles of data (corresponding to a frequency of just over 1 Hz for an 8-min data stream) the bias is still significantly greater than zero. The result is that, for most data lengths, there will be a substantial bias toward a 1/f characteristic.
To estimate and remove the bias, we constructed two independent synthetic signals, each with the same duration and power spectrum as the recorded oxygen signals. We then calculated their coherence. This process was repeated 100 times and the resultant values were averaged to compute the mean expected bias. For the analysis illustrated in Fig. 2B, the mean expected bias was subtracted out so that a value of zero corresponds to the consistency of phase differences that would be obtained by chance were the null hypothesis true (no coherence).
Power spectrum and deviation power.
The power spectrum was obtained using the multitaper technique (77, 78), which efficiently improves spectral estimates by using multiple Slepian tapers. When power and frequency are expressed in log units, the 1/f power spectrum is captured by a linear function,
where f is frequency, β is the power exponent, and k is the offset. The deviation power (Fig. 3) was calculated as the difference between the actual power and the power predicted by a linear fit.
Removal of correlated power.
We wished to estimate power in a signal after removing the power that is associated with a correlated signal. Consider two signals, expressed as vectors and , whose correlation coefficient is . Both and can be written as the sum of a shared component plus a unique component,
| [1] |
| [2] |
where , , and are unit-length vectors corresponding respectively to the shared component, the unique component in , and the unique component in . and , and , and and are all orthogonal to each other. and are the relative weights of the shared component () in and , respectively. If the fraction of the total signal that is shared is similar in and , then , and based on [1] and [2] the shared power and the unique power are expressed as
| [3] |
| [4] |
The correlation between and is by definition
| [5] |
We can substitute the values from Eqs. 1 and 2 into Eq. 5. Because , , and are all orthogonal to each other, most of the terms in the dot product go to zero, leaving
| [6] |
Therefore, from Eqs. 3, 4, and 6,
Thus, the unique power in a signal that is left over after removing the power that is associated with a correlated signal is simply, for each frequency band, 1 minus the Pearson correlation coefficient, multiplied by the total power.
Supplementary Material
Acknowledgments
We thank Drs. Ralf Wessel and ShiNung Ching for helpful discussions on data analysis. We thank Dr. Olaf Sporns for providing the source code of the model described in ref. 17. This research was supported by National Institutes of Health Grants R21 MH093858 and R01 MH102471.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1419837112/-/DCSupplemental.
References
- 1.Buckner RL, Krienen FM, Yeo BT. Opportunities and limitations of intrinsic functional connectivity MRI. Nat Neurosci. 2013;16(7):832–837. doi: 10.1038/nn.3423. [DOI] [PubMed] [Google Scholar]
- 2.Power JD, Fair DA, Schlaggar BL, Petersen SE. The development of human functional brain networks. Neuron. 2010;67(5):735–748. doi: 10.1016/j.neuron.2010.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Harmelech T, Preminger S, Wertman E, Malach R. The day-after effect: Long term, Hebbian-like restructuring of resting-state fMRI patterns induced by a single epoch of cortical activation. J Neurosci. 2013;33(22):9488–9497. doi: 10.1523/JNEUROSCI.5911-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Qin S, et al. Hippocampal-neocortical functional reorganization underlies children’s cognitive development. Nat Neurosci. 2014;17(9):1263–1269. doi: 10.1038/nn.3788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kerestes R, Davey CG, Stephanou K, Whittle S, Harrison BJ. Functional brain imaging studies of youth depression: A systematic review. NeuroImage Clin. 2014;4:209–231. doi: 10.1016/j.nicl.2013.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Menon V. Developmental pathways to functional brain networks: Emerging principles. Trends Cogn Sci. 2013;17(12):627–640. doi: 10.1016/j.tics.2013.09.015. [DOI] [PubMed] [Google Scholar]
- 7.Meijer FJ, Goraj B. Brain MRI in Parkinson’s disease. Front Biosci. 2014;6:360–369. doi: 10.2741/E711. [DOI] [PubMed] [Google Scholar]
- 8.Dennis EL, Thompson PM. Typical and atypical brain development: A review of neuroimaging studies. Dialogues Clin Neurosci. 2013;15(3):359–384. doi: 10.31887/DCNS.2013.15.3/edennis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nir Y, et al. Interhemispheric correlations of slow spontaneous neuronal fluctuations revealed in human sensory cortex. Nat Neurosci. 2008;11(9):1100–1108. doi: 10.1038/nn.2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He BJ, Snyder AZ, Zempel JM, Smyth MD, Raichle ME. Electrophysiological correlates of the brain’s intrinsic large-scale functional architecture. Proc Natl Acad Sci USA. 2008;105(41):16039–16044. doi: 10.1073/pnas.0807010105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hughes SW, et al. Synchronized oscillations at alpha and theta frequencies in the lateral geniculate nucleus. Neuron. 2004;42(2):253–268. doi: 10.1016/s0896-6273(04)00191-6. [DOI] [PubMed] [Google Scholar]
- 12.Hughes SW, Crunelli V. Thalamic mechanisms of EEG alpha rhythms and their pathological implications. Neuroscientist. 2005;11(4):357–372. doi: 10.1177/1073858405277450. [DOI] [PubMed] [Google Scholar]
- 13.Lorincz ML, Crunelli V, Hughes SW. Cellular dynamics of cholinergically induced alpha (8-13 Hz) rhythms in sensory thalamic nuclei in vitro. J Neurosci. 2008;28(3):660–671. doi: 10.1523/JNEUROSCI.4468-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cabral J, et al. Exploring mechanisms of spontaneous functional connectivity in MEG: How delayed network interactions lead to structured amplitude envelopes of band-pass filtered oscillations. Neuroimage. 2014;90:423–435. doi: 10.1016/j.neuroimage.2013.11.047. [DOI] [PubMed] [Google Scholar]
- 15.Cabral J, Kringelbach ML, Deco G. Exploring the network dynamics underlying brain activity during rest. Prog Neurobiol. 2014;114:102–131. doi: 10.1016/j.pneurobio.2013.12.005. [DOI] [PubMed] [Google Scholar]
- 16.Deco G, et al. Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. J Neurosci. 2013;33(27):11239–11252. doi: 10.1523/JNEUROSCI.1091-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci USA. 2007;104(24):10240–10245. doi: 10.1073/pnas.0701519104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.He BJ, Zempel JM, Snyder AZ, Raichle ME. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010;66(3):353–369. doi: 10.1016/j.neuron.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.He BJ. Scale-free brain activity: Past, present, and future. Trends Cogn Sci. 2014;18(9):480–487. doi: 10.1016/j.tics.2014.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bak P. How Nature Works. Oxford Univ Press; Oxford: 1997. [Google Scholar]
- 21.Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett. 1987;59(4):381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- 22.Jensen HJ. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge Univ Press; Cambridge, UK: 1998. [Google Scholar]
- 23.Mitzenmacher M. A brief history of generative models for power law and lognormal distributions. Internet Math. 2004;1(2):226–251. [Google Scholar]
- 24.Levina A, Herrmann JM, Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat Phys. 2007;3(12):857–860. [Google Scholar]
- 25.Millman D, Mihalas S, Kirkwood A, Niebur E. Self-organized criticality occurs in non-conservative neuronal networks during Up states. Nat Phys. 2010;6(10):801–805. doi: 10.1038/nphys1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Rubinov M, Sporns O, Thivierge J-P, Breakspear M. Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput Biol. 2011;7(6):e1002038. doi: 10.1371/journal.pcbi.1002038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Poil S-S, Hardstone R, Mansvelder HD, Linkenkaer-Hansen K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J Neurosci. 2012;32(29):9817–9823. doi: 10.1523/JNEUROSCI.5990-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Linkenkaer-Hansen K. Self-Organized Criticality and Stochastic Resonance in the Human Brain. Helsinki University of Technology; Espoo, Finland: 2002. [Google Scholar]
- 29.He BJ. Scale-free properties of the functional magnetic resonance imaging signal during rest and task. J Neurosci. 2011;31(39):13786–13795. doi: 10.1523/JNEUROSCI.2111-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bullmore E, et al. Colored noise and computational inference in neurophysiological (fMRI) time series analysis: Resampling methods in time and wavelet domains. Hum Brain Mapp. 2001;12(2):61–78. doi: 10.1002/1097-0193(200102)12:2<61::AID-HBM1004>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ko AL, Darvas F, Poliakov A, Ojemann J, Sorensen LB. Quasi-periodic fluctuations in default mode network electrophysiology. J Neurosci. 2011;31(32):11728–11732. doi: 10.1523/JNEUROSCI.5730-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ciuciu P, Abry P, He BJ. Interplay between functional connectivity and scale-free dynamics in intrinsic fMRI networks. Neuroimage. 2014;95:248–263. doi: 10.1016/j.neuroimage.2014.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Salvador R, et al. A simple view of the brain through a frequency-specific functional connectivity measure. Neuroimage. 2008;39(1):279–289. doi: 10.1016/j.neuroimage.2007.08.018. [DOI] [PubMed] [Google Scholar]
- 34.Salvador R, Suckling J, Schwarzbauer C, Bullmore E. Undirected graphs of frequency-dependent functional connectivity in whole brain networks. Philos Trans R Soc Lond B Biol Sci. 2005;360(1457):937–946. doi: 10.1098/rstb.2005.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sasai S, Homae F, Watanabe H, Taga G. Frequency-specific functional connectivity in the brain during resting state revealed by NIRS. Neuroimage. 2011;56(1):252–257. doi: 10.1016/j.neuroimage.2010.12.075. [DOI] [PubMed] [Google Scholar]
- 36.Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J Neurosci. 2006;26(1):63–72. doi: 10.1523/JNEUROSCI.3874-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cordes D, et al. Mapping functionally related regions of brain with functional connectivity MR imaging. Am J Neuroradiol. 2000;21(9):1636–1644. [PMC free article] [PubMed] [Google Scholar]
- 38.Kiviniemi V, Kantola JH, Jauhiainen J, Hyvärinen A, Tervonen O. Independent component analysis of nondeterministic fMRI signal sources. Neuroimage. 2003;19(2 Pt 1):253–260. doi: 10.1016/s1053-8119(03)00097-1. [DOI] [PubMed] [Google Scholar]
- 39.Niazy RK, Xie J, Miller K, Beckmann CF, Smith SM. Spectral characteristics of resting state networks. Prog Brain Res. 2011;193:259–276. doi: 10.1016/B978-0-444-53839-0.00017-X. [DOI] [PubMed] [Google Scholar]
- 40.Zhang YJ, et al. Determination of dominant frequency of resting-state brain interaction within one functional system. PLoS ONE. 2012;7(12):e51584. doi: 10.1371/journal.pone.0051584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wu CW, et al. Frequency specificity of functional connectivity in brain networks. Neuroimage. 2008;42(3):1047–1055. doi: 10.1016/j.neuroimage.2008.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cordes D, et al. Frequencies contributing to functional connectivity in the cerebral cortex in “resting-state” data. Am J Neuroradiol. 2001;22(7):1326–1333. [PMC free article] [PubMed] [Google Scholar]
- 43.Bentley WJ, Li JM, Snyder AZ, Raichle ME, Snyder LH. Oxygen level and LFP in task positive and task negative areas: Bridging BOLD fMRI and electrophysiology. Cereb Cortex. 2014 doi: 10.1093/cercor/bhu260. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fox MD, et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci USA. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Birn RM. The role of physiological noise in resting-state functional connectivity. Neuroimage. 2012;62(2):864–870. doi: 10.1016/j.neuroimage.2012.01.016. [DOI] [PubMed] [Google Scholar]
- 46.Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: Are anti-correlated networks introduced? Neuroimage. 2009;44(3):893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fox MD, Zhang D, Snyder AZ, Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101(6):3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Teichert T, Grinband J, Hirsch J, Ferrera VP. Effects of heartbeat and respiration on macaque fMRI: Implications for functional connectivity. Neuropsychologia. 2010;48(7):1886–1894. doi: 10.1016/j.neuropsychologia.2009.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Thompson JK, Peterson MR, Freeman RD. Single-neuron activity and tissue oxygenation in the cerebral cortex. Science. 2003;299(5609):1070–1072. doi: 10.1126/science.1079220. [DOI] [PubMed] [Google Scholar]
- 50.Masamoto K, Vazquez A, Wang P, Kim SG. Trial-by-trial relationship between neural activity, oxygen consumption, and blood flow responses. Neuroimage. 2008;40(2):442–450. doi: 10.1016/j.neuroimage.2007.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mathiesen C, et al. Activity-dependent increases in local oxygen consumption correlate with postsynaptic currents in the mouse cerebellum in vivo. J Neurosci. 2011;31(50):18327–18337. doi: 10.1523/JNEUROSCI.4526-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lowry JP, et al. Real-time electrochemical monitoring of brain tissue oxygen: A surrogate for functional magnetic resonance imaging in rodents. Neuroimage. 2010;52(2):549–555. doi: 10.1016/j.neuroimage.2010.04.187. [DOI] [PubMed] [Google Scholar]
- 53.Cooper R, Crow HJ, Walter WG, Winter AL. Regional control of cerebral vascular reactivity and oxygen supply in man. Brain Res. 1966;3(2):174–191. doi: 10.1016/0006-8993(66)90075-8. [DOI] [PubMed] [Google Scholar]
- 54.Clark LC, Jr, Misrahy G, Fox RP. Chronically implanted polarographic electrodes. J Appl Physiol. 1958;13(1):85–91. doi: 10.1152/jappl.1958.13.1.85. [DOI] [PubMed] [Google Scholar]
- 55.Burgess D. Correlation between oxygen cycles in contralateral regions of the brain. Stroke. 1973;4(3):374. (abstr) [Google Scholar]
- 56.Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- 57.Schölvinck ML, Maier A, Ye FQ, Duyn JH, Leopold DA. Neural basis of global resting-state fMRI activity. Proc Natl Acad Sci USA. 2010;107(22):10238–10243. doi: 10.1073/pnas.0913110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Saad ZS, et al. Trouble at rest: How correlation patterns and group differences become distorted after global signal regression. Brain Connect. 2012;2(1):25–32. doi: 10.1089/brain.2012.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Power JD, et al. Methods to detect, characterize, and remove motion artifact in resting state fMRI. Neuroimage. 2014;84:320–341. doi: 10.1016/j.neuroimage.2013.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.van den Heuvel MP, Stam CJ, Boersma M, Hulshoff Pol HE. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage. 2008;43(3):528–539. doi: 10.1016/j.neuroimage.2008.08.010. [DOI] [PubMed] [Google Scholar]
- 61.Bassett DS, Bullmore E. Small-world brain networks. Neuroscientist. 2006;12(6):512–523. doi: 10.1177/1073858406293182. [DOI] [PubMed] [Google Scholar]
- 62.Beggs JM, Timme N. Being critical of criticality in the brain. Front Physiol. 2012;3:163. doi: 10.3389/fphys.2012.00163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Majeed W, Magnuson M, Keilholz SD. Spatiotemporal dynamics of low frequency fluctuations in BOLD fMRI of the rat. J Magn Reson Imaging. 2009;30(2):384–393. doi: 10.1002/jmri.21848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Thompson GJ, Pan WJ, Magnuson ME, Jaeger D, Keilholz SD. Quasi-periodic patterns (QPP): Large-scale dynamics in resting state fMRI that correlate with local infraslow electrical activity. Neuroimage. 2014;84:1018–1031. doi: 10.1016/j.neuroimage.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Thompson GJ, et al. Neural correlates of time-varying functional connectivity in the rat. Neuroimage. 2013;83:826–836. doi: 10.1016/j.neuroimage.2013.07.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Majeed W, et al. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. Neuroimage. 2011;54(2):1140–1150. doi: 10.1016/j.neuroimage.2010.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Buzsáki G, Logothetis N, Singer W. Scaling brain size, keeping timing: Evolutionary preservation of brain rhythms. Neuron. 2013;80(3):751–764. doi: 10.1016/j.neuron.2013.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jensen O, Bonnefond M, VanRullen R. An oscillatory mechanism for prioritizing salient unattended stimuli. Trends Cogn Sci. 2012;16(4):200–206. doi: 10.1016/j.tics.2012.03.002. [DOI] [PubMed] [Google Scholar]
- 69.Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32(1):9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Cabral J, Hugues E, Sporns O, Deco G. Role of local network oscillations in resting-state functional connectivity. Neuroimage. 2011;57(1):130–139. doi: 10.1016/j.neuroimage.2011.04.010. [DOI] [PubMed] [Google Scholar]
- 71.Rayshubskiy A, et al. Direct, intraoperative observation of ∼0.1 Hz hemodynamic oscillations in awake human cortex: Implications for fMRI. Neuroimage. 2014;87:323–331. doi: 10.1016/j.neuroimage.2013.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Julien C. The enigma of Mayer waves: Facts and models. Cardiovasc Res. 2006;70(1):12–21. doi: 10.1016/j.cardiores.2005.11.008. [DOI] [PubMed] [Google Scholar]
- 73.Nikulin VV, et al. Monochromatic ultra-slow (∼0.1 Hz) oscillations in the human electroencephalogram and their relation to hemodynamics. Neuroimage. 2014;97:71–80. doi: 10.1016/j.neuroimage.2014.04.008. [DOI] [PubMed] [Google Scholar]
- 74. Committee on Care and Use of Laboratory Animals (1996) Guide for the Care and Use of Laboratory Animals (Natl Inst Health, Bethesda), DHHS Publ No (NIH) 85-23.
- 75.Fekete T, Rubin D, Carlson JM, Mujica-Parodi LR. The NIRS Analysis Package: Noise reduction and statistical inference. PLoS ONE. 2011;6(9):e24322. doi: 10.1371/journal.pone.0024322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Rosenberg JR, Amjad AM, Breeze P, Brillinger DR, Halliday DM. The Fourier approach to the identification of functional coupling between neuronal spike trains. Prog Biophys Mol Biol. 1989;53(1):1–31. doi: 10.1016/0079-6107(89)90004-7. [DOI] [PubMed] [Google Scholar]
- 77.Thomson DJ. Spectrum estimation and harmonic analysis. Proc IEEE. 1982;70(9):1055–1096. [Google Scholar]
- 78.Percival DB. Spectral Analysis for Physical Applications. Cambridge Univ Press; Cambridge, UK: 1993. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.