Topology, structures, and energy landscapes of human chromosomes

Significance

Various cell types emerge from their nearly identical genetic content for a multicellular organism, in part, via the regulation of the function of the genome—the DNA molecules inside the cell. Similar to the way catalytic activity is lost when proteins denature, the function of the genome is tightly coupled to its 3D organization. A theoretical framework for picturing the structure and dynamics of the genome will therefore greatly advance our understanding of cell biology. We present an energy landscape model of the chromosome that reproduces a diverse set of experimental measurements. The model enables quantitative predictions of chromosome structure and topology and provides mechanistic insight into the role of 3D genome organization in gene regulation and cell differentiation.

Abstract

Chromosome conformation capture experiments provide a rich set of data concerning the spatial organization of the genome. We use these data along with a maximum entropy approach to derive a least-biased effective energy landscape for the chromosome. Simulations of the ensemble of chromosome conformations based on the resulting information theoretic landscape not only accurately reproduce experimental contact probabilities, but also provide a picture of chromosome dynamics and topology. The topology of the simulated chromosomes is probed by computing the distribution of their knot invariants. The simulated chromosome structures are largely free of knots. Topologically associating domains are shown to be crucial for establishing these knotless structures. The simulated chromosome conformations exhibit a tendency to form fibril-like structures like those observed via light microscopy. The topologically associating domains of the interphase chromosome exhibit multistability with varying liquid crystalline ordering that may allow discrete unfolding events and the landscape is locally funneled toward “ideal” chromosome structures that represent hierarchical fibrils of fibrils.

The genome’s 3D organization is thought to play a crucial role in many biological processes, including gene regulation, DNA replication, and cell differentiation (1). A theoretical framework for picturing the structure and dynamics of chromosomes thus promises significantly to advance our understanding of cell biology. It is a challenge to develop from first principles an energy landscape theory for chromosomes analogous to that for proteins, which has proved rather successful in providing quantitative insights into protein folding thermodynamics, kinetics, and evolution as well as providing protein structure prediction schemes (2–4). The difficulty arises from several factors, the first being the complexity of the team of molecular players that contribute to chromosome organization. Although one chromosome is made of a single DNA molecule, an array of different proteins is involved in its 3D organization (5); of these only a few have been fully characterized. Even at the shortest length scales, the double-stranded DNA is wrapped by core histone proteins into nucleosomes, which can go on to form higher-order structures such as the proposed 30-nm fibers upon stabilization by histone proteins H1 (6). Long-range contacts between genomic loci can also form in the presence of CCCTC-binding factor (CTCF) (7). The second difficulty is that the chromosome is large in molecular terms. It is so large, in fact, that its dynamics can be so slow that the chromosome may be a far from equilibrium structure, unlike most folded proteins (8, 9). To complicate matters further, chromosome organization has been reported to be variable and to depend both on cell type and phase in the cell cycle (10, 11). There are apparently thus many global attractors on any realistic chromosome landscape. An energy landscape theory built at atomistic resolution using physicochemical interactions of known components for chromosome organization seems thus currently out of reach. Here we explore a way to skirt some of the difficulties by using a maximum entropy approach to derive an effective equivalent equilibrium energy landscape for chromosomes by using physical contact frequencies measured in chromosome conformation capture experiments.

Results

Maximum Entropy Inferred Chromosome Models.

Hi-C experiments provide a good measure of the frequency of spatial contacts between genomic loci (12, 13). These data have been incorporated into computer simulations to build structural models in a variety of ways. Many approaches start by mapping the contact frequencies onto preferred spatial distances between the corresponding genomic loci. The resulting distances can be directly used to construct a potential much like the associative memory models of protein folding (14). They can also be used as constraints to derive a unique chromosome structure using algorithms resembling NMR protein structure determination (15, 16). Because the experimental contact frequencies are ensemble averages from a population of cells that potentially vary in chromosome conformation (17–20), the explicit form of this mapping to specific spatial distances is not known and may not be unique. In this study, we propose a method that confronts the issue of the averaging involved and directly reproduces the observed contact frequencies using an ensemble of chromosome conformations.

We use the maximum entropy principle to derive what might be considered a minimally biased information theoretic energy landscape. Using an approximate statistical mechanical treatment of the ensemble and computer simulations, we develop an efficient iterative algorithm to find an ensemble of chromosome conformations consistent with a pseudo-Boltzmann distribution for an effective energy landscape that reproduces the experimentally measured pairwise contact frequencies (see SI Text, Inverse Statistical Mechanics and the Maximum Entropy Ensemble). We emphasize that the inferred energy landscape must be regarded as at best an effective one. It is an effective landscape because not only are the crucial protein partners left out, but also the model employs a very coarse-grained description of the chromosome itself, being only at the resolution of 40,000 bp. At the same time, the validity of the pseudo-Boltzmann distribution can be questioned because doubtless there are nonequilibrium effects that allow the structures found in the cell nucleus to be formed under kinetic, not thermodynamic, control. Nevertheless, as shown by Wang and Wolynes (21, 22), effective equilibrium landscapes can provide accurate descriptions of even highly nonequilibrium systems in favorable (but not universal) circumstances. The tabula rasa starting point for our modeling describes the chromosome as a generic homopolymer, a chain of beads on a string that is confined in a spherical wall mimicking the effect of the nuclear envelope to yield a volume fraction of 0.1 (9). Owing to the excluded volume, one might expect strong topological constraints due to the possible knotting of such a confined chain. However, in vivo the cell nucleus typically contains a large quantity of topoisomerases that might relieve such constraints (23). Therefore, to mimic the effect of topoisomerases that can enable chain crossing, a soft-core repulsive potential is applied between pairs of beads rather than a strong hardcore excluded volume (10). A detailed mathematical definition of the model is provided in SI Text, Simulation Details of Chromosome Models. We denote the potential energy function for this homopolymeric backbone model as $U\left(r\right)$. To fit the experimental data, we also need to encode a geometrical signal for contact formation. A rigorous description of this encoding would involve a quantitative understanding of the physical chemistry of the cross-linking reactions as well as the readout processes. For simplicity, thus, we assume the measured contact probability between genomic loci is a scalar function of the pairwise distance $r$ between those loci, $f\left(r\right)$, where $f$ is roughly a square-well function. A biased energy landscape that can fit the observations that would be consistent with the maximum entropy principle can thus be written as a sum of the tabula rasa homopolymer energy and a pair interaction term with coefficients to be determined: $U_{ME}\left(r\right)=U\left(r\right)+{\displaystyle {\sum }_i{\alpha }_i{f}_i\left(r_{ab}\right)}$ (24–26), where the index i loops over the pairs of contacts and $a,b$ indicate the two genomic loci involved in forming the $i$-th contact pair. The coefficients ${\alpha }_i$ are Lagrangian multipliers that may be determined using an iterative optimization procedure to ensure that contact frequencies predicted from the simulation ultimately match the experimental measurements, that is, $\langle f_i\left(r_{ab}\right)\rangle =f_{i,\exp }$, where the bracket $\langle \mathrm{\cdot }\rangle$ indicates the ensemble average. As a proof of principle, in Fig. S1 we show that the iterative inverse statistical mechanics algorithm we have developed indeed is able accurately to reproduce the structure of a small protein [with root-mean-squared displacement (RMSD) <2Å] from pair contact information alone. At the same time such an information theoretic energy landscape provides a picture of the free energy landscape near the basin of minima. This encourages us to apply the approach to finding effective landscapes for the human chromosome 12 in both embryonic stem and mature fibroblast cells starting from the contact maps measured by Ren and coworkers (27).

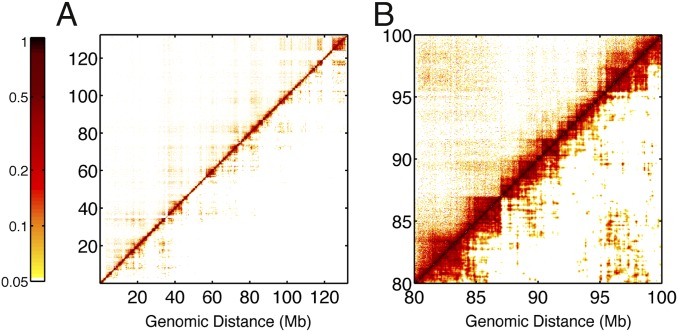
Fig. 1 A and B compare the experimental mature cell chromosome contact maps (upper triangles) with the simulated ones obtained via the iterative algorithm (lower triangles). The corresponding plots for the stem cell chromosome are shown in Fig. S2. Fig. 1B is the zoomed-in version of Fig. 1A showing only the genomic region 80–100 Mb, as an illustration of the finer structure. For both cell types, the derived landscapes accurately reproduce the contact map. This is quite remarkable given that the two cell types exhibit strikingly different contact maps, with the mature cell chromosome forming stronger and denser long-range contacts. Results for the human chromosome 11 obtained in the same way also agree well with experiment and are shown in Fig. S2.

Fig. 1.

Comparison between contact probabilities obtained from experiments and simulations. (A) Contact probability maps for the mature cell chromosome as determined in Hi-C experiments by Ren and coworkers (27) (upper triangles) and as sampled in simulations based on the information theoretic energy landscape (lower triangles). (B) Zoomed-in version of A in the genomic region 80–100 Mb.

Often, rather than examining the whole contact matrix, only the contact probability as a function of genomic distance between loci has been used to compare theories and models with measured data. In Fig. S2C, log-log plots of this quantity for the experimentally determined contact probability versus genomic distance are shown for the stem cell (light blue) and the mature cell (light red) chromosome. The corresponding lines from the landscape simulations are drawn in darker colors. Two dashed black lines with critical exponents of −1.0 and −1.5 are drawn as guides for the eye. These two exponent values have previously been predicted by two different homopolymer pictures of the chromosome and have been used to test these pictures. The exponent −1.5 corresponds to a fully equilibrated globule whereas the exponent −1.0 is predicted for a homopolymeric fractal globule, whose conformations are kinetically limited owing to the rapid nonequilibrium collapse of an originally unknotted chain (28). The present simulation models that assume a kind of effective equilibrium but with heterogeneous interactions closely reproduce the experiments across the entire range over 100 Mb for all cases.

Structural Characterization of Human Chromosomes.

Examining the ensemble of chromosome conformations obtained with the optimized information theoretic energy landscape that reproduces the Hi-C contact map suggests some deeper ways of characterizing the ensemble. In particular, one can use many body correlation functions and statistical landscape characterization through inherent structure analysis to find the themes of local organization. To that end, we first determine the mean squared fluctuation of the distances between loci separated at various genomic distances. This quantity characterizing a polymeric trajectory would grow linearly for an ideal random coil. In contrast, as shown in Fig. S3A, consistent with the 3D FISH experiments (29), the mean squared displacements plateau at long genomic separations for both the stem cell (blue) and the mature cell (red) chromosome. Quantitative comparison with the experiment also allows the estimation of an effective persistence length scale of 150 nm per 40,000 bp (see Fig. S4A and SI Text, Physical Units of Chromosome Models). We note this length scale would be consistent with forming a 30-nm fiber at a nucleosome line density of 1.3, a density that lies in the range of experimental observations (30). A comparison of the probability distributions for the radius of gyration of the entire chain is shown in Fig. S3B. The stem cell chromosome has a size similar to that for an uncollapsed homopolymeric backbone model of the measured persistence length, but the mature cell chromosome adopts smaller and more collapsed conformations. The increase in compactness from the stem cell to the mature cell chromosome is consistent with the chromatin condensation and gene silencing that are observed experimentally during cell differentiation (31).

To characterize the heterogeneity of the sampled chromosome structures, we perform quality threshold clustering using the RMSD of atom-pair distances as a metric over the ensemble of simulated conformations. For neither of the cell types is there a dominant cluster that would signal a well-defined unique chromosome structure. Instead, each ensemble exhibits several different clusters of structures of the chromosome that have rather comparable statistical weights. The central structures from the top two clusters are shown in Fig. 2 for the stem cell (SC1 and SC2) and the mature cell (MC1 and MC2) chromosome. Representative structures for other clusters are shown in the Fig. S3. For comparison, an example configuration of the reference homopolymeric backbone model is also shown in Fig. S3C. Both the stem cell chromosome and the backbone-only model adopt overall spherical structures, which arise from the confinement wall that is included to mimic the nuclear envelope. Consistent with its smaller radius of gyration, the mature cell chromosome seems more collapsed. Despite the structural heterogeneity of the simulated ensembles, the chromosome conformations for both cell types can be readily distinguished from those of the starting homopolymeric backbone model because they appear segregated by sequence. For example, one sees that the red colors at the 5′ end cluster together, as also do the yellow colors in the other end of the chromosome. However, the red colors are spread all over the place for the homogeneous backbone model. These still frames from the simulation already indicate there is a difference in the topology of chromosomes from the homogeneous backbone model, a point that will be made clearer in the following section.

Fig. 2.

Structural characterization of the chromosome ensembles. Central structures of the top two most populous clusters for the stem cell (SC1 and SC2) and the mature cell (MC1 and MC2) chromosome.

Light microscopy and in situ hybridization experiments show that chromosomes occupy mutually exclusive domains that form territories inside the nucleus (32). The underlying mechanism for this segregation is not yet known. Our optimized chromosome models also support such territory formation (see SI Text, Chromosome Territories). As shown in Fig. S2K, for the optimized landscapes, both in the stem and mature cell models, the chromosomes 11 and 12 do indeed segregate and restrict their motions to more limited regions.

Topological Landscape for Human Chromosomes.

Characterizing the topology of human chromosomes has been of great interest. The issue of chain knotting is clearly biologically relevant, as witnessed by the fact that topoisomerases have evolved in even the simplest cellular organisms (33). Entanglements in complex knotted conformations would pose potential kinetic barriers for DNA replication and transcription in the absence of such topoisomerases. Thus, it has been argued that the chromosome should be unknotted (8). The so-called fractal globule model suggests the reason for a lack of knots is a kinetic effect coming from rapid collapse. If topoisomerases are sufficiently active, however, the chain could topologically equilibrate, so the reason for unknottedness (if indeed that is the case) would have to be sought elsewhere. The Hi-C experiments are indeed consistent with the predictions for the fractal globule model in many aspects. For example, the power-law scaling of contact probability as a function of genomic distance for human chromosomes does show a slope of approximately −1, which is consistent with the prediction from the fractal globule model (12). Nevertheless, as pointed out by many authors, the slope for the power-law scaling does vary dramatically among different cell types (34) (see also Fig. S2C). In addition, other models can also give rise to a slope of −1 (35, 36). What topologies are found for the optimized chromosome landscapes inferred using statistical mechanical information theory?

We characterize the topological state of an individual chromosome configuration by using the minimal length/diameter ratio as an easily computable topological invariant (see SI Text, Knots and the Topological Characterization of Chromosomal Configurations). Fig. 3A presents the probability distributions of this knot invariant for the stem cell (blue) and the mature cell (red) chromosome conformational ensembles. As a comparison, the probability distribution for the input homogeneous backbone model is also shown in yellow. The homopolymeric backbone model is highly knotted, as expected from entropic considerations for such long, locally flexible chains (37). In contrast to the homogeneous backbone model, however, both the stem cell and the mature cell chromosome ensembles have topological distributions peaked near the trivial and the simple trefoil knot. The mature cell chromosome does exhibit conformations composed by compounding a few simple knots. As discussed in SI Text, these knots are tight, being formed from two locally intertwined loop configurations. These knots can be effectively eliminated via a simple coarse-graining procedure (dotted line). We find that the key to unknotting lies precisely in the formation of topologically associating domains (see SI Text, Topologically Associating Domains in Chromosome), which locally rigidify the chain. Forming these domains effectively renormalizes the persistence length of the chromosome. Because these domains are approximately 1 Mb in size, an entire chromosome of 0.1 billion bp can be pictured as being a coarse-grained polymer that has only around 100 beads. Computer simulations show that more than 100 beads are needed to sample with high likelihood even a single knot (38). For a polymer of such a small equivalent size, therefore, heavy knotting is not expected to occur. To support this argument, we examined another energy landscape for the chromosome using a model that only includes the local topologically associating domain (TAD) signals from the mature cell chromosome by excluding the more genomically distant interactions in determining the energy function. The corresponding knot invariant distribution shown in Fig. S5I indicates that this model also adopts knotless conformations. Of course, because the derived energy landscape is only an effective information theoretic construct, it is still possible that nonequilibrium effects are the actual source of the effective short range in sequence interactions that prevent knotting. Rapid kinetic collapse constraints may well be the origin of forming the topologically associating domains, but certainly one must entertain other possibilities involving specific protein actors.

Fig. 3.

Topological characterization of the chromosome ensembles. (A) The probability distributions of the minimal length/diameter ratio that is a topological invariant. These are shown for the mature cell (MC, red), the stem cell (SC, blue) chromosome, and for the tabula rasa backbone model (BB, yellow). The probability distribution of the mature cell chromosome computed using coarse-grained representations is shown as a green dotted line. Example polymer configurations with minimal length/diameter ratio for the trivial knot, the trefoil knot, and a complex knot are also shown, and arrows indicate their corresponding values of the topological invariant. (B) Relaxation of the mature cell (red) and the stem cell (blue) chromosome topology measured with the average knot invariant as a function of time when topoisomerases are sufficiently active. (Inset) The corresponding plot without the presence of topoisomerase. The shaded regions represent the SDs.

Not only is the structural distribution of chromosome conformations interesting, but so also is the dynamics of chromosome reorganization (39). It has been argued that owing to the exceedingly long timescale of topological relaxation, the interphase chromosome may never equilibrate and thus closely resembles in topology the metaphase chromosome that transforms to this state (9). These kinetic arguments, however, have been based on homopolymeric models for the chromosome. Here we examine the kinetics of chromosome unknotting using both the optimized energy landscape having the small excluded volume force mimicking the presence of strong topoisomerase activity and a model with larger excluded volume forces that would not allow knots to unravel, as would happen without sufficient topoisomerases.

Starting from equilibrium configurations of the homogeneous backbone model with complex knots, we turn on the optimized contact potentials at time 0. Fig. 3B presents the relaxation of the average minimal length knot invariant for the stem cell (blue) and for the mature cell chromosome (red). The simulations shown in the main figure have the smaller excluded volume forces that mimic the presence of topoisomerase, through a soft-core potential that allows chain crossing. Results for the model with a full excluded volume effect modeling what happens when there is insufficient topoisomerase are plotted in the inset. With sufficient topoisomerase, equilibrium knotless conformations are reached within the simulation time equivalent to 3 h in the laboratory, much less than the cell cycle of human cells. However, when topoisomerase is absent, the inferred relaxation timescale vastly exceeds the cell life cycle. For the stem cell chromosome, the knotted conformations are significantly relaxed after about 300 h on the laboratory timescale, whereas for the mature cell chromosome the relaxation is too slow to be observed on our simulation timescale. Apparently, the higher density of the more collapsed chromosome conformations of the mature cell causes jamming that substantially increases the timescale.

In Search of an Ideal Chromosome Structure.

As shown in Fig. 2 and in Fig. S3, instead of one single structure, an ensemble of chromosome conformations is needed to reproduce the contact map. How tight is the structural ensemble? We quantify the similarities among the sampled chromosome structures on various length scales. We know that even for a protein in the denatured thermodynamic state, local secondary and even tertiary structures resembling the final folded structure persist (40, 41). Likewise, the chromosome conformation ensemble inferred from Hi-C experiments may well share local structural motifs characterizing a more energetically important and organized chromosome structure. Many experiments indeed already report finding chromosome motifs (42). One way to look for these motifs is to study chromosome conformations at a low information theoretic temperature. As for protein folding, although the unfolded ensemble is favored by entropy and thus dominates at high information theoretic temperature, a tighter ensemble reflecting a nearly unique most probable folded structure could emerge below a folding temperature.

To investigate chromosome structures at low effective temperatures, we performed simulated annealing runs in which the equivalent temperature T is linearly decreased from 2 to 0.2 over 18 million steps. The temperature $T=1.0$ corresponds with the physical ensemble as sampled in the interphase state. To characterize the relation of these energy minima or “inherent structures” to the ensemble (43), we use a collective variable $Q$, a measure of the fraction of common contacts formed, to quantify the similarity between quenched inherent structures (the mathematical definition of $Q$ is provided in SI Text). When a single structure dominates as in protein folding, $Q$ to the unique native structure can serve as an excellent reaction coordinate for conformational changes, as it does for describing protein folding where the energy landscape is known to be funneled. $Q$ ranges from 0 to 1 with higher values corresponding to higher structural similarity. Fig. S6A shows the ensemble average $\langle Q\rangle$ over all of the pairs of structures for the stem cell (blue) and the mature cell (red) ensembles obtained at various temperatures. For neither of the cell types does the chromosome relax toward a unique structure. The “uniqueness” of the folded structure for a protein is usually visually apparent when the average $\langle Q\rangle$ exceeds 0.5. When the $\langle Q\rangle$ at different length scales is determined, as shown in Fig. S6B for the mature cell chromosome, it becomes clear that the wide breadth of distribution of structures mainly manifests itself at large length scales. In contrast, the chromosomes do exhibit high structural similarity in their inherent structure ensembles when one probes at short genomic regions of approximately 1 Mb in size, the length scale on which the formation of topologically associating domains has been observed.

The relatively low $\langle Q\rangle$ at large length scales suggests the presence of glassy behavior that is typical of random heteropolymers where the interactions fluctuate strongly as a function of sequence. To study the role of the heterogeneity of the interactions between genomic loci, we examined a smoothed average contact potential that varies only as a function of genomic distance $V\left(i-j\right)$, but otherwise is homogeneous (see SI Text, The Ideal Homogeneous Chromosome). Fig. S6C shows this sequence averaged ideal homogeneous potential $V\left(i-j\right)$ of the contact energies for both the stem cell (blue) and the mature cell (red) chromosome. Consistent with its more compact structure, the mature cell chromosome has a larger contact energy at long genomic distances. Nevertheless, the contact potentials for both cell types exhibit large fluctuations, which lead to the observed heterogeneity and to the small $\langle Q\rangle$ in the average even for the quenched structural ensemble containing the local energy minima, which are individually the most probable structures. Owing to possible experimental noise in the contact map that may arise from intrinsic low resolution and the mixture of cell cycles, however, the significance of the observed heterogeneity in the contact potential is presently difficult to evaluate and may well be overestimated.

To simplify our understanding of the origins of chromosome structural themes, it is therefore interesting to examine the conformational ensemble that would be predicted for the homogenized polymer model having only the averaged contact potential $V(i-j)$ acting uniformly throughout the sequence. When quenched using the same simulation protocol as was used for the heterogeneous model, this idealized chromosome model exhibits quite clearly some extremely long-range correlated fibril-like structural features (see Fig. 4C for an example conformation). To quantitatively characterize the fibril structure, we calculate the correlation of a unit vector between beads separated by 4 in sequence. The strong oscillatory behavior of the correlation function, shown as the yellow line in Fig. 4A, is a quantitative measure of the presence of fibril structures. Fourier transforming this correlation function, as shown in Fig. 4B, further reveals that there are actually two layers of fibrils in the ideal chromosome. The first layer has a periodicity of ∼0.25 Mb, and the second layer has a periodicity corresponding to around 5 Mb. The two layers of fibrils can also be seen from the density map shown in Fig. S6D, with the genomic and spatial distances forming the two axes, respectively. Fig. 4C further shows that the 0.25-Mb peak corresponds to a 300-nm fibril and the 5-Mb peak corresponds to a 600-nm fibril superstructure. We note that the hierarchical layers of fibril structures are reminiscent of the liquid crystal-like conformations that have been observed for dinoflagellate chromosomes (44) and are consistent with the hierarchical metaphase chromosome model supported by light microscopy experiments (42).

Fig. 4.

Chromosome structures at low information theoretic temperature. (A and B) The orientational order parameter along the genome (A) and its Fourier transform (B) for the mature cell chromosome at temperature $T=1.0$ (red) corresponding to the experimental data and at the lower information theoretic temperature $T=0.2$ (blue) as well as for the ideal homogenized chromosome model (IC). (C and D) Example conformations of the ideal (C) and the mature cell (D) chromosome at $T=0.2$.

As shown by the correlation functions and their power spectra in Fig. 4 A, B, and D, signatures of fibril structure also actually appear in the optimized interphase chromosome having heterogeneous interactions (red lines), although they are much weaker. The fibril structures are more evident at the low information theoretic temperature $T=0.2\hspace{0.17em}$ as shown as blue lines, although the heterogeneity by itself leads to broadening of the peak around 0.25 Mb. For human interphase chromosomes, signals of local fibril-like structures have indeed been picked up in light microscopy experiments and these have led to specific suggestions of a hierarchical fiber of fibers model for chromosomes (42). The scattering intensity profile computed from the present landscape shown in Fig. S6E indicates that these fibril features would be hard to detect in small-angle X-ray scattering experiments of the type whose results have been used to argue against such models (45).

Folding Free-Energy Profiles of Topologically Associating Domains.

It has been suggested that the topologically associating domains, within which long-range contacts between DNA sequences are formed, provide structural units that could be a dynamical basis for coordinating gene regulation (46). For example, folding of topologically associating domains can bring enhancers and promoters that are separated by large genomic distances close to each other. Such a correlation between structure and function argues for the importance of specific interactions in guiding the 3D organization of topologically associating domains, and thus justifies the use of landscape theory to study chromosome folding. The present model, in addition to allowing an examination of global chromosome dynamics, allows us to explore the energy landscape of individual domains and their coupling to neighboring ones while still remaining agnostic regarding detailed biochemical and biophysical mechanisms that actually give rise to the effective landscape.

We first search for generic structural features of the set of topologically associating domains identified in the mature cell chromosome 12. To measure the structure similarity within each of these collapsed globules, we again determine the pairwise $Q$ in the ensemble of each defined topologically associating domain at $T=1.0$. As shown in Fig. S6G, most of the topologically associating domains have an average $\langle Q\rangle$ around 0.5. These high $\langle Q\rangle$ values indicate that topologically associating domains exhibit strong structural regularity, which is consistent with the orientational ordering characterized in Fig. 4. The liquid crystal-like orientational ordering shown in Fig. 4 would indeed even be predicted for collapsed globules of locally ordered chain with excluded volume, just as it is for proteins (47).

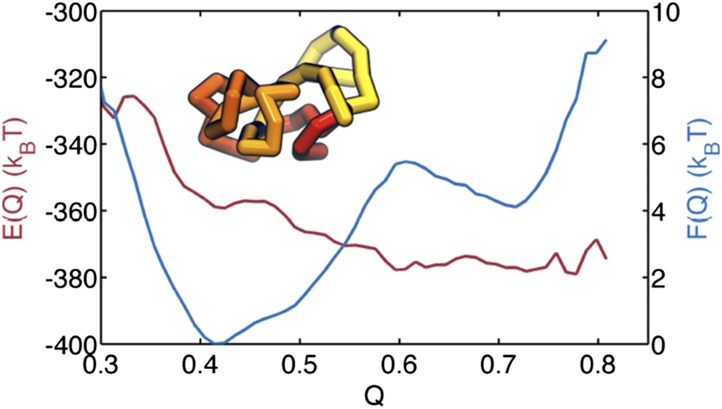
Landscapes can be found for all of the local domains and various behaviors are found as described in SI Text. To highlight what can be learned, we discuss the analysis of the thermodynamics of one particular topologically associating domain between genomic region 40.76–42.6 Mb, as highlighted with a star in Fig. S6G. Similar analyses for other regions are provided in the Figs. S7 and S8. Here we study the free-energy profile over the reaction coordinate $Q$ relative to a reference structure shown in Fig. 5, Inset. The free energy $F\left(Q\right)$, which is shown in Fig. 5 in blue, exhibits two basins around $Q=0.4$ and $Q=0.8$ respectively. The average energy $E\left(Q\right)$, however, decreases to a minimum at the rather high value of $Q=0.8$. The double-well feature of the free-energy profile indicates a possible cooperative transition between the two ensembles of conformations and supports the idea that topologically associating domains may undergo two state transitions as in recent models of stochastic gene regulation (48–50). We also can investigate the coupled landscapes for neighboring topologically associating domains. As seen in Fig. S9, there are some pairs showing significant cooperative coupling.

Fig. 5.

Landscape characterizations for a topologically associating domain between genomic region 40.76–42.6 Mb. Average energy $E$ (red) and free energy $F$ (blue) at $T=1.0$ as a function of $Q$. (Inset) The reference structure used for the calculation of $Q$.

Discussion

As witnessed by the blossoming of the protein-folding field, energy landscape theory provides powerful statistical mechanical tools for the quantitative study of heteropolymers. For a complex macromolecule such as the chromosome, an effective energy landscape inferred using an information theoretic approach provides an interesting alternative to landscapes derived directly from physicochemical interactions of its constituents given by first principles. The power of the inferred energy landscape has been partially revealed by the prediction of an “ideal chromosome” model that nicely bridges the seemingly disordered interphase chromosome that provides the input data here with the more condensed metaphase chromosome structure suggested by microscopy leading to a proposed hierarchical model (42). With the coming availability of contact probability maps for metaphase chromosomes (10), it will be of great interest quantitatively to investigate the phase diagram of chromosome structures at different stages of the cell cycle and further to evaluate the significance of the suggested ideal chromosome model as a starting point for dynamical analysis. Equally interesting will be the study of the structure–dynamics–function relationships that are crucial to understanding protein biology, but now in the much more complex context of gene regulation, and seek possible structural imprints of epigenetic memory in chromosome conformation (11).