Significance
Assortative mating, the tendency of men and women who marry to have similar social characteristics, is a commonly observed phenomenon in human societies. This study shows that assortative mating could result from structural causes independent of human agents’ preference, because unmarried persons who newly enter marriage are systematically different from those who married earlier. Thus, assortative mating could result from selection, not by rational choice, but by the dynamics of social structures.
Keywords: assortative mating, structural effect, Gale–Shapley model, encounter mating model, composition heterogeneity
Abstract
Assortative mating—marriage of a man and a woman with similar social characteristics—is a commonly observed phenomenon. In the existing literature in both sociology and economics, this phenomenon has mainly been attributed to individuals’ conscious preferences for assortative mating. In this paper, we show that patterns of assortative mating may arise from another structural source even if individuals do not have assortative preferences or possess complementary attributes: dynamic processes of marriages in a closed system. For a given cohort of youth in a finite population, as the percentage of married persons increases, unmarried persons who newly enter marriage are systematically different from those who married earlier, giving rise to the phenomenon of assortative mating. We use microsimulation methods to illustrate this dynamic process, using first the conventional deterministic Gale–Shapley model, then a probabilistic Gale–Shapley model, and then two versions of the encounter mating model.
We take assortative mating to mean the tendency of men and women who marry to have similar social characteristics (i.e., homogamy), although, broadly speaking, assortative mating may refer to any nonrandom mixing of spousal characteristics. Assortative mating is a commonly observed phenomenon in human societies (1–10). In the existing literature in both sociology and economics, this phenomenon has mainly been attributed to individuals’ conscious preferences for homogamy. On the one hand, sociologists have argued that people with similar attributes are likely to have similar values, interests, tastes, economic resources, and lifestyles, and individuals often value these similarities when selecting marriage partners. On the other hand, economists have explained assortative mating by stressing complementarities of marriage partners’ attributes. For example, Becker (11) showed that, under a market equilibrium, marriage partners are likely to be associated in traits that are complementary in producing household goods. In other words, people with similar attributes tend to enter marriage as long as these attributes reinforce each other in improving family welfare.
Sociologists have long been aware that assortative mating, as in friendship formation, may also result from structural forces that sort individuals into separate social contexts by similarity in attributes (2, 4, 12–17). In a modern society, it is safe to assume that experiences and social activities leading to marriage, such as dating, require that a man and a woman get to know each other and interact. This is true even when dating takes place in cyberspace. Social structure may induce or constrain assortative mating because it defines the social spaces in which such interactions take place. In the sociology literature, social structure is said to define the exposure to mating opportunities (i.e., potential persons with whom to interact). When persons with different attributes are segregated into different social contexts, assortative mating ensues even when they do not prefer to marry persons with similar attributes, because they do not have a chance to meet, or are not exposed to, persons with dissimilar attributes.
In this paper, we show that patterns of assortative mating may arise from another structural source even if individuals do not have assortative preferences or possess complementary attributes: dynamic processes of marriages in a closed population. For a given cohort of youth in a finite population, as the percentage of married persons increases, unmarried persons who newly enter marriage are systematically different from those who married earlier, giving rise to the phenomenon of assortative mating. To put it in the causal framework of recent literature, a dynamic process could lead to changes in the population composition of the untreated pool (i.e., the pool of unmarried individuals) when treatment propensity (i.e., the propensity of getting married) is systematically associated with treatment effects (i.e., the utilities of the couple getting married) (18). We use microsimulation methods to illustrate this dynamic process, using first the conventional deterministic Gale–Shapley model, then a probabilistic model, and then two versions of the encounter mating model.
Assumptions and Models
We start with a hypothetical finite population with a sex ratio of one, including N males and N females. We assume that all marriages are heterosexual. To preserve parsimony and for convenience, we assume that individuals consider a unidimensional attribute of potential marriage partners: mate desirability. To demonstrate the influence of changing population structure alone in generating assortative mating, we assume that preference for mate desirability is invariant across all members of the opposite sex. Let and represent mate desirability, respectively, for males and females. In this hypothetical setup, a person’s desirability as a marriage partner, or , affects the utility from marrying him/her independently. That is, the contribution of the desirability of a potential partner to the overall utility for the decision maker does not depend on the attributes of the decision maker. This is what we mean by “no assortativeness” in individuals’ preference. Below, we discuss three models with which to characterize the dynamic process of marriage formation. In all three models, we treat monogamous marriage as an absorbing state and do not allow polygamy, divorce, or remarriage.
The Gale–Shapley Model.
The Gale–Shapley model was originally introduced to solve the problem of stable matching (19). It proposes an iterative algorithm that consists of a number of rounds. In the first round, each male proposes to his preferred female. Each female who receives more than one proposal rejects all but her preferred choice among those who have proposed to her. In the original algorithm proposed by Gale and Shapley (19), she “does not accept him yet, but keeps him on a string to allow for the possibility that someone better may come along later.” In other words, they are provisionally engaged but not necessarily going to marry. Here, the Gale–Shapley algorithm requires that the males but not the females have full information about their potential partners. We slightly modify the process to assume that both sexes have full information about all potential partners. Thus, if the female’s preferred suitor happens to be her preferred choice among all available males, they instantly get married and exit the marriageable pool. In this modification, both sexes, instead of only the males, act with full information at each round; thus, we expedite the matching process without altering the final results. In each subsequent round, all unengaged males, that is, those who failed to be matched during the last round, propose to their next choices. As in the first round, each female receiving proposals rejects all but her preferred suitor among those unmarried. If he is also her preferred choice among all available males, they get married and exit the marriageable pool; otherwise, they return to the marriageable pool. This process continues until everyone is married. It can be proved that as long as each person has a fixed preference ranking of potential spouses, this algorithm is guaranteed to produce complete and stable matching. That is, everyone is married (assuming equal numbers of males and females), and there are no two people of opposite sexes who are not married to one another but would both prefer marrying each other to remaining with their current spouses.
A crucial assumption that enables the Gale–Shapley algorithm to produce stable marriages is that each person has a fixed preference ranking of potential spouses. The preference ranking, in turn, can be derived from a utility model. Here, we assume that all individuals of one sex assign utility to each potential mate of the opposite sex based on the person’s desirability. Incorporating our assumption of universal preference, we can write the ith male’s utility for marrying the jth female as a univariate function of :
| [1a] |
where denotes the jth female’s attribute. Similarly, gives the jth female’s utility from marrying the ith male:
| [1b] |
where denotes the ith male’s attribute. Here, linear function is used without loss of generality; the functional form that links utility with mate desirability will not affect our major findings.
Combined with the above specification for utility, the Gale–Shapley algorithm also predicts assortative marriages. In fact, as long as and are truly continuous, that is, there are no ties in and , marriage partners will be matched to each other exactly according to their relative ranks within their respective sexes. To see this, consider the sequential process. At the beginning, all males prefer the most desirable female, and all females prefer the most desirable male, resulting in a match between the top-ranked male and the top-ranked female. Because marriage is an event leading to an absorbing state, a matched pair is immediately removed from the marriageable pool. Thus, in the second round, marriage occurs between the second-ranked male and the second-ranked female. Consequently, in the rth round of marriage, male of rank r according to is matched to female of rank r according to . This process is replicated until everyone in the population is married. Because this model does not involve any randomness in utility based on mate desirability, we call this model the deterministic Gale–Shapley model (i.e., model 1).
The Probabilistic Gale–Shapley Model.
In our second model, we modify the conventional Gale–Shapley model by adding a noise component to the male’s and female’s utility from marriage (Eq. 1). Thus, we rewrite the ith male’s utility from marrying the jth female at time t as
| [2a] |
and the jth female’s utility from marrying the ith male at time t as
| [2b] |
It is evident that Eqs. 2a and 2b are of the same form as the random utility model widely used for studying discrete choice in econometrics (20). Following convention for the discrete-choice model, we assume that and are independent and identically distributed as a type I extreme value distribution.
For reasons to be given later, the choice set at time t consists of all unmarried individuals of the opposite sex and the option of remaining single. For males, we denote the state of being single by . For females, we denote the state of being single by . For the state of being single, we normalize the systematic part of the utility function of Eq. 2 at zero, yielding
| [2c] |
| [2d] |
With the utility model thus modified by the time-varying noise component, we again apply the same Gale–Shapley matching algorithm as was discussed earlier. In each round, each male makes a marriage proposal to his most preferred female or prefers to remain single, and the female will accept the proposal if and only if this male is her most desired male and she considers marriage to him preferable to being single. That is, a marriage occurs if the preferences between a male and a female are reciprocal. However, owing to the noise component, there is no guarantee that exactly one pair will be matched in each round. Because this model adds randomness to the first model, we call it the probabilistic Gale–Shapley model (also called model 2).
The Encounter Mating Model.
The Gale–Shapley model, in either its original form or our modified form, assumes that some or all individuals have full information about the attributes of all potential marriage partners in the entire population. Such an assumption is hardly true in reality, because marriage possibility is conditional on exposure to and encounter of potential partners. As an alternative to the two Gale–Shapley algorithm-based models, we learn from models in biological science (21) and propose the third model: the encounter mating model (also called model 3A).
The encounter mating model also breaks the matching process into consecutive rounds, with each round comprising two steps. In the first step, a randomly selected pair of male and female encounter one another. In the second step, male evaluates the desirability of female , and female simultaneously evaluates the desirability of male . A marriage occurs only when both potential partners are satisfied with each other, akin to Logan’s two-sided logit model (22, 23). To implement this idea, we keep the same utility model as in the probabilistic Gale–Shapley model (i.e., Eq. 2). One important difference between the encounter mating model and the probabilistic Gale–Shapley model, however, pertains to the size of choice set in each round. Whereas individuals compare all available marriage partners and the state of being single in the probabilistic Gale–Shapley model, they are faced with a binary choice in the encounter mating model: marry or not marry. As before, to model this binary choice, we normalize the systematic part of the utility function for being single to zero (Eqs. 2c and 2d). As a result, the probability that the ith male is willing to marry the jth female given their encounter can be expressed simply as a binary logit model (24):
| [3a] |
Similarly, gives the probability that the jth female is willing to marry the ith male given their encounter:
| [3b] |
Obviously, the intercept terms , affect the marriage probability in Eq. 3. In other words, they represent the utility gain from getting married relative to staying single that is unaffected by the potential partner’s attributes. The higher the intercept terms , , the higher utility of getting married relative to staying single, respectively, for men and women.
By construction the two potential partners’ decisions are assumed to be independent, and the joint probability that the ith male and the jth female marry given their encounter should be the product of and :
| [4] |
For our simulation exercise to be shown later in the paper, we further characterize the dynamic features of this model with two conditions. First, an encounter between a male and a female is assumed to be random and sequential. That is, a random pair of potential mates encounter first and then decide whether to marry before the next random encounter occurs. Second, as before, marriage is considered an absorbing state, and thus we do not allow polygamy, divorce, or remarriage. In our implementation, a marriage removes the two marrying partners from the marriageable pool for subsequent rounds. If an encountered couple do not marry, however, they return to the unmarried pool. We then start over to let another pair encounter and simulate their marital decision. We iterate this process until all people in the hypothetical population are married.
Waiting Cost.
In extending the deterministic Gale–Shapley model to the probabilistic Gale–Shapley model and the encounter mating model, we aimed to add more realism. However, the two extensions still fall short of realism because they ignore the cost of waiting. If waiting is costless, the rational behavior under the encounter mating model would be to reject until a highly desirable (i.e., optimal or nearly optimal) match shows up. This is impossible in reality, of course, because it might take unrealistically too many iterations for such a match to occur. In actual marriage markets, young persons wishing to get married have limited time in which to consider a limited number of potential marriage partners in a very large population. Given the time constraint, waiting is costly, because each unsuccessful encounter shortens the remaining time and probably the quality of the marriageable pool. As we will illustrate later, another reason why waiting is costly is that our model predicts that the general quality of available mates declines with time. This is particularly true if one objective of marriage is childbearing, because fertile years are limited, especially for women.
Hence, it is essential to a realistic model of marriage that individuals incur a cost for waiting to marry, comparable to our earlier modification that they do not have full information about all potential marriage partners. Thus, to our baseline encounter mating model we now propose an a priori time-increasing cost of being single ( for every unmarried individual. Because we wish to keep time scale-free, we parameterize the cost ( as an increasing function of the proportion of individuals of a given sex who have married. In a closed system, is determined by the number of persons who have exited the state of being single by time t, denoted as In other words, individuals become increasingly impatient as they observe an increasing number of peers getting married in the population. However, we assume that individuals do not have more information about the remaining population beyond . In reality, the cost of waiting may not be equal between men and women owing to sex differences in the age pattern of fecundity. Thus, the specification for could be sex-specific. However, for simplicity, simulation in this paper assumes the same parameterization for men and women. More specifically, we parameterize this cost of being single as
where takes a positive value. This amounts to a decrease in the systematic part of utility of being single with time:
| [5a] |
| [5b] |
For the encounter mating model, the incorporation of the cost factor amounts to increasing the intercept terms , in the utility models (Eq. 2) so as to increase the overall probability of realization in the binary logit models (Eq. 3). Therefore, the binary logit models of Eqs. 3a and 3b translate into
| [6a] |
| [6b] |
This model explicitly compares the utility of marrying a potential partner to the utility of being single, which declines with time. Henceforth, we call this model the extended encounter mating model (also called model 3B).
Microlevel Simulation
We demonstrate the dynamic process of assortative mating using microlevel simulation (or an agent-based model). In our simulation, a hypothetical population is composed of 5,000 males and 5,000 females (i.e., n = 5,000). Individual characteristics, and , are assumed to follow standard normal distributions. We set and . We simulate the dynamic matching process according to the deterministic Gale–Shapley model, the probabilistic Gale–Shapley model, and the encounter mating model, as described in the previous section. For each of these models, we track the attributes of married couples at each time point and present them in two time series, one for each sex. Time points at which no successful marriage occurs are removed, because they provide no information to our study.
Before we discuss the results, we define several quantities of interest. The first quantity is the correlation ( between the husband’s and wife’s attributes, and , across all of the matched pairs. The correlation is a simple, crude measure of assortative mating. The second quantity is the running correlation between and within an interval of 100 pairs matched adjacently in time, that is,
The third quantity is the cumulative correlation between and for the matched pairs up to , that is,
Obviously, , the cumulative correlation up to the last marriage, is the same as the correlation for the overall population. The fourth quantity is the cumulative correlation ( between and that is encountered up to . Because it takes a very large number of encounters for a match to occur, for computational easiness we randomly select one of the encountered pairs for inclusion in the calculation of this quantity between two consecutive matches ( and ), that is,
The fifth quantity is the running averages ( and of the attributes of the newly married and , within an interval of 100 pairs matched adjacently in time, that is,
The sixth quantity is the average time to marriage for a certain group, measured as the average number of rounds before one gets married.
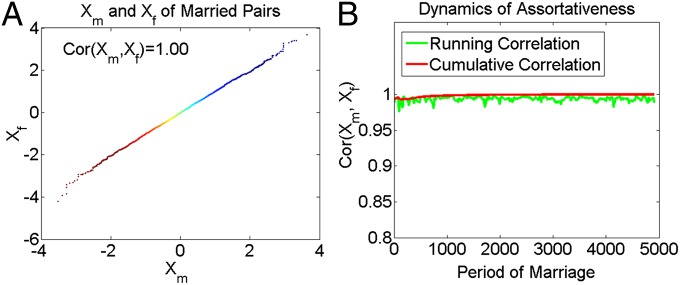
In Fig. 1, we present the assortative mating results produced by the deterministic Gale–Shapley model (model 1). Fig. 1A is a scatterplot of and , showing that males and females in marriages are perfectly matched by their respective ranks on and . The correlation between and is 1.00. The colors of the dots represent time of marriage, with bluer points corresponding to earlier marriages and redder points corresponding to later marriages. The results clearly reveal that individuals with higher and scores are married earlier, and those with lower scores are married later. Fig. 1B is the running correlation and cumulative correlation by period of marriage. It suggests that the running correlation between the male’s and female’s attribute remains high and fairly stable, even when we examine it in small time windows.
Fig. 1.
(A and B) Assortative mating in the deterministic Gale–Shapley model. In A, gradations of color are used to represent marriages formed in different time periods. Specifically, bluer points correspond to earlier marriages, and redder points correspond to later marriages.
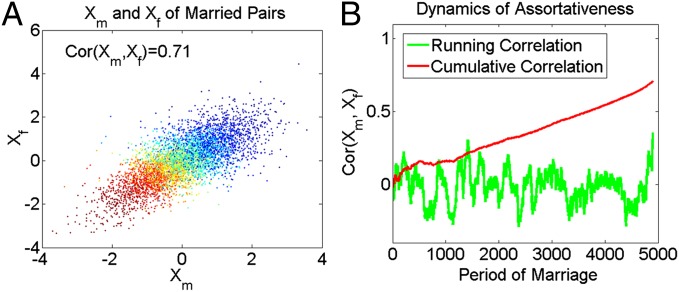
In Fig. 2, we present analogously the assortative mating resulting from the probabilistic Gale–Shapley model (model 2). Fig. 2A is a scatterplot of and . The overall correlation between and is 0.71, indicating a high assortativeness in marriage. Again, the colors of the dots show that individuals with higher and scores are married earlier, and those with lower scores are married later. Fig. 2B suggests that the addition of a probabilistic component in model 2 shrinks the running correlation between the male’s and female’s attribute to almost zero when we examine assortativeness in small time intervals. The cumulative correlation, however, increases as more pairs are accumulated over time. This pattern suggests that assortativeness of attributes between husbands and wives mainly results from time selectivity of persons entering marriage (with persons of higher attributes entering marriage earlier), but it disappears if we control for waiting time to marriage.
Fig. 2.
(A and B) Assortative mating in the probabilistic Gale–Shapley model. In A, gradations of color are used to represent marriages formed in different time periods. Specifically, bluer points correspond to earlier marriages, and redder points correspond to later marriages.
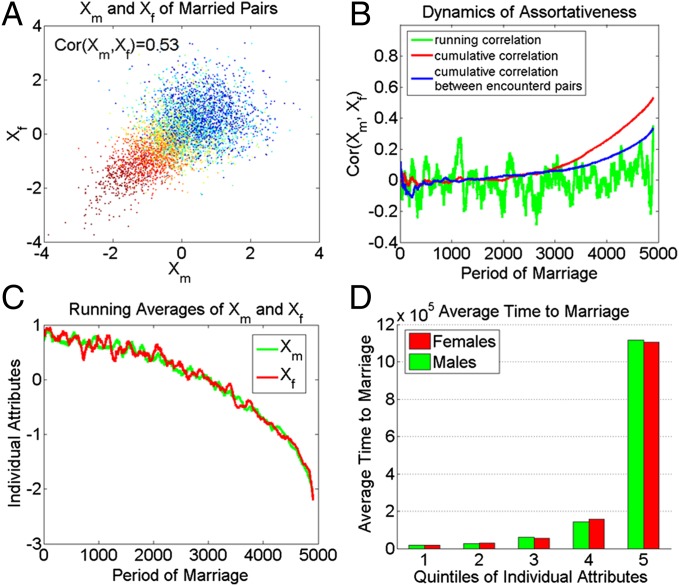
As we stated earlier, we consider the encounter mating model a more realistic model for marriage. We present simulation results for this model, in both the baseline version (model 3A) and the extended version with waiting cost (model 3B). We display the results from the baseline encounter mating model (model 3A) in Fig. 3 in four panels. Fig. 3 A and B show the overall correlation at 0.53, indicating a much smaller, but more plausible, degree of assortativeness than in the previous two models based on the Gale–Shapley algorithm. In Fig. 3B, the cumulative correlation among the matched pairs increases gradually as more individuals are married (red line). A large part of this increase is driven by an increase in homogeneity in the unmarried pool, which is reflected in the increasing assortativeness in and among the encountered pairs (blue line). Qualitatively speaking, the results are similar to those from model 2, in that the running correlation stays close to zero (except for the end), but the cumulative correlation rises with time, particularly at the end. Fig. 3C shows the running average of male’s and female’s attributes by time of marriage. It reveals steady declines in the scores of the attributes for husbands and wives over time. Fig. 3D shows the average time to marriage by quintiles of individual attributes. Consistent with our proposition of a sequential selection of available population, individuals ranked in lower quintiles on attributes are married much later than those ranked in higher quintiles.
Fig. 3.
(A–D) Assortative mating in the encounter mating model. In A, gradations of color are used to represent marriages formed in different time periods. Specifically, bluer points correspond to earlier marriages, and redder points correspond to later marriages.
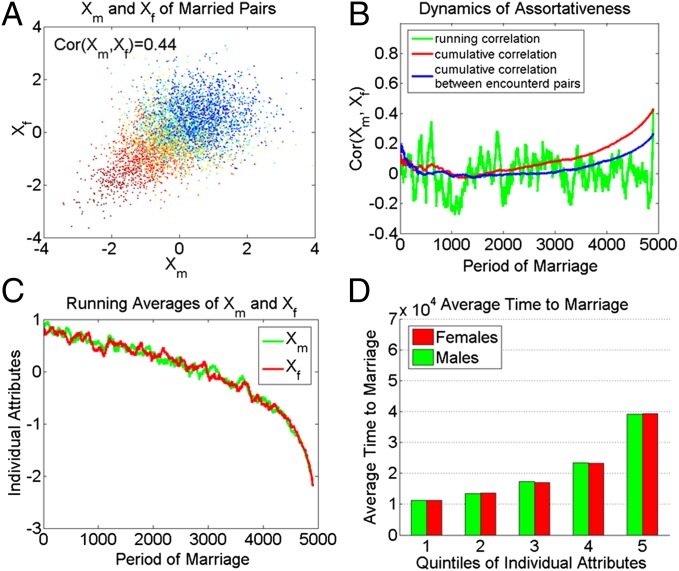
Fig. 4 shows the results from the extended encounter mating model (model 3B). The pattern is qualitatively similar to that of the simpler encounter mating model, model 3A. However, a notable finding is that the inclusion of an increasing cost of being single with time further dilutes assortativeness, leading to an overall correlation of 0.44. The reason is that a rising waiting cost causes the entry into marriage to be less selective in spouses’ attribute attractiveness, which in turn reduces assortativeness owing to compositional changes. For the same reason, shown in Fig. 4D, differences in average marriage time across the five quintiles are less pronounced in the extended encounter mating model than in the baseline encounter mating model.
Fig. 4.
(A–D) Assortative mating in the encounter mating model with increasing cost of being single. In A, gradations of color are used to represent marriages formed in different time periods. Specifically, bluer points correspond to earlier marriages, and redder points correspond to later marriages.
Our results are not sensitive to the choice of our measure using the correlation coefficient. In the sociological literature on assortative mating, frequency tables cross-classifying categorical attributes of husbands and wives are typically analyzed with log-linear models. Table S1 displays four such cumulative frequency tables with and discretized into quintiles at four times: 25, 50, 75, and 100% of the population having been married under the encounter mating model with waiting cost. In Table S2, we present key results of a log-linear analysis of the tables, which are consistent with findings revealed in Fig. 4.
Conclusion
In this paper, we show that patterns of assortative mating may arise from a structural source even if individuals do not have assortative preferences or possess complementary attributes: dynamic changes of those waiting for marriage in a closed system. For a given cohort of youth in a finite population, as the percentage of the married increases, unmarried persons who newly enter marriage are systematically different from those who married earlier, giving rise to the phenomenon of assortative mating. We have used microsimulation methods to illustrate this dynamic process, using first the conventional deterministic Gale–Shapley model, then a probabilistic Gale–Shapley model, and then two more realistic versions of the encounter mating model.
Our consideration of more realistic model specifications, such as the addition of a probabilistic element to the conventional Gale–Shapley model, the adoption of the encounter mating model due to the lack of full information, and the addition of the time-increasing waiting cost, all lead to a lessening of assortativeness between husband and wife. In our final model, the extended encounter mating model with waiting cost, the overall correlation in attributes between husband and wife is only 0.44, far below the perfect correlation in the case of the conventional deterministic Gale–Shapley model.
Supplementary Material
Acknowledgments
We thank Robert Mare and Christine Schwartz for their comments on an earlier version of the paper. This work was supported by National Institutes of Health Grant R01-HD-074603.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1504811112/-/DCSupplemental.
References
- 1.Kalmijn M. Shifting boundaries: Trends in religious and educational homogamy. Am Sociol Rev. 1991;56(6):786–800. [Google Scholar]
- 2.Mare RD. Five decades of educational assortative mating. Am Sociol Rev. 1991;56(1):15–32. [Google Scholar]
- 3.Qian Z. Breaking the racial barriers: Variations in interracial marriage between 1980 and 1990. Demography. 1997;34(2):263–276. [PubMed] [Google Scholar]
- 4.Kalmijn M. Intermarriage and homogamy: Causes, patterns, trends. Annu Rev Sociol. 1998;24(24):395–421. doi: 10.1146/annurev.soc.24.1.395. [DOI] [PubMed] [Google Scholar]
- 5.Smits J, Ultee W, Lammers J. Educational homogamy in 65 countries: An explanation of differences in openness using country-level explanatory variables. Am Sociol Rev. 1998;63(2):264–285. [Google Scholar]
- 6.Raymo JM, Xie Y. Temporal and regional variation in the strength of educational homogamy. Am Sociol Rev. 2000;65(5):773–781. [Google Scholar]
- 7.Schwartz CR, Mare RD. Trends in educational assortative marriage from 1940 to 2003. Demography. 2005;42(4):621–646. doi: 10.1353/dem.2005.0036. [DOI] [PubMed] [Google Scholar]
- 8.Qian Z, Lichter DT. Social boundaries and marital assimilation: Interpreting trends in racial and ethnic intermarriage. Am Sociol Rev. 2007;72(1):68–94. [Google Scholar]
- 9.Schwartz CR. Earnings inequality and the changing association between spouses’ earnings. AJS. 2010;115(5):1524–1557. doi: 10.1086/651373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Torche F. Educational assortative mating and economic inequality: A comparative analysis of three Latin American countries. Demography. 2010;47(2):481–502. doi: 10.1353/dem.0.0109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Becker GS. A theory of marriage: Part I. J Polit Econ. 1973;81(4):813–846. [Google Scholar]
- 12.Blau PM, Schwartz JE. Crosscutting Social Circles: Testing a Macrostructural Theory of Intergroup Relations. Academic; New York: 1984. [Google Scholar]
- 13.Lichter DT, LeClere FB, McLaughlin DK. Local marriage markets and the marital behavior of black and white women. Am J Sociol. 1991;96(4):843–867. [Google Scholar]
- 14.Lichter DT, McLaughlin DK, Kephart G, Landry DJ. Race and the retreat from marriage: A shortage of marriageable men? Am Sociol Rev. 1992;57(6):781–799. [Google Scholar]
- 15.Lichter DT, Anderson R, Hayward M. Marriage markets and marital choice. J Farm. 1995;16(4):412–431. [Google Scholar]
- 16.McPherson JM, Smith-Lovin L, Cook JM. Birds of a feather: Homophily in social networks. Annu Rev Sociol. 2001;27:415–444. [Google Scholar]
- 17.Zeng Z, Xie Y. A preference-opportunity-choice framework with applications to intergroup friendship. AJS. 2008;114(3):615–648. doi: 10.1086/592863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xie Y. Population heterogeneity and causal inference. Proc Natl Acad Sci USA. 2013;110(16):6262–6268. doi: 10.1073/pnas.1303102110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gale D, Shapley LS. College admissions and the stability of marriage. Am Math Mon. 1962;69(1):9–14. [Google Scholar]
- 20.McFadden D. In: Frontiers in Econometrics. Zarembka P, editor. Academic; New York: 1974. pp. 105–142. [Google Scholar]
- 21.Gimelfarb A. Processes of pair formation leading to assortative mating in biological populations: Encounter-mating model. Am Nat. 1988;131(6):865–884. doi: 10.1016/0040-5809(88)90032-9. [DOI] [PubMed] [Google Scholar]
- 22.Logan JA. Opportunity and choice in socially structured labor markets. Am J Sociol. 1996;102(1):114–160. [Google Scholar]
- 23.Logan JA, Hoff PD, Newton MA. Two-sided estimation of mate preferences for similarities in age, education, and religion. J Am Stat Assoc. 2008;103(482):559–569. [Google Scholar]
- 24.Powers DA, Xie Y. Statistical Methods for Categorical Data Analysis. 2nd Ed Emerald; Bingley, UK: 2008. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.