Significance
Societies around the world make massive investments in ecosystem restoration projects to mitigate habitat loss, conserve biodiversity, and boost ecosystem services. We use a return-on-investment framework to assess the value of coordinating restoration efforts in space and time to maximize ecological connectivity between the Laurentian Great Lakes and their tributaries, which are fragmented by hundreds of thousands of dams and road crossings. We show that coordinating restoration efforts across the entire region is nine times more cost-effective than local-scale planning. Similarly, a single lump sum investment is up to 10 times more cost-effective than a series of annual allocations. These dramatic economic and ecological efficiencies provide ample incentive for coordinating conservation efforts across broad spatial and temporal scales.
Keywords: freshwater, conservation, connectivity, prioritization
Abstract
In many large ecosystems, conservation projects are selected by a diverse set of actors operating independently at spatial scales ranging from local to international. Although small-scale decision making can leverage local expert knowledge, it also may be an inefficient means of achieving large-scale objectives if piecemeal efforts are poorly coordinated. Here, we assess the value of coordinating efforts in both space and time to maximize the restoration of aquatic ecosystem connectivity. Habitat fragmentation is a leading driver of declining biodiversity and ecosystem services in rivers worldwide, and we simultaneously evaluate optimal barrier removal strategies for 661 tributary rivers of the Laurentian Great Lakes, which are fragmented by at least 6,692 dams and 232,068 road crossings. We find that coordinating barrier removals across the entire basin is nine times more efficient at reconnecting fish to headwater breeding grounds than optimizing independently for each watershed. Similarly, a one-time pulse of restoration investment is up to 10 times more efficient than annual allocations totaling the same amount. Despite widespread emphasis on dams as key barriers in river networks, improving road culvert passability is also essential for efficiently restoring connectivity to the Great Lakes. Our results highlight the dramatic economic and ecological advantages of coordinating efforts in both space and time during restoration of large ecosystems.
Habitat loss and fragmentation are leading drivers of declining biodiversity and ecosystem services worldwide (1–3). Landscape corridors and dam removals are popular and effective strategies for mitigating fragmentation (4, 5). To implement these projects efficiently, societies around the world are developing regional and even continental-scale plans for restoring ecosystem connectivity (6). These plans set ecosystem-level conservation objectives and identify priority regions for investment, but individual project selection (e.g., a specific dam removal or habitat corridor) is generally dictated by opportunism and politics. When poorly coordinated, these piecemeal mitigation efforts may be an inefficient means of achieving ecosystem-level objectives. Transboundary coordination is known to increase the cost-effectiveness of nature reserve networks (7–9), but the benefits of coordination are likely to be even greater for connectivity efforts in rivers because the dendritic nature of drainage basins makes them highly susceptible to fragmentation (10–12). Migratory fishes, which support major fisheries and ecosystem processes, are particularly vulnerable to life cycle disruption by the millions of dams and road crossings that fragment the world’s rivers (13, 14).
Here, we investigate the value of coordinating restoration efforts in space and time to maximize ecological connectivity between the Laurentian Great Lakes and their tributaries. The Great Lakes Basin (GLB) contains 21% of the world’s surface freshwater and is home to more than 33.5 million people (15). High societal dependence on lake-derived ecosystem services includes US$7 billion annually in economic activity related to recreational fishing (16). Historically, breeding migrations of dozens of native fish species formed an important ecological link between the Great Lakes and their tributaries (17). Today, hundreds of thousands of dams and road culverts partially or fully block historical fish migration routes (18). There is growing investment in removing or modifying these structures, but project selection has been largely opportunistic and driven by local priorities.
Barrier removal projects to restore tributary connectivity are selected and funded by a diverse set of actors operating independently at different spatial scales across the GLB. Most road crossings are managed by counties or states, whereas impacts of dams are addressed at the watershed, state, federal, or even international level. Funding to restore connectivity is often disbursed as small, one-time investments, but large pulses of public investment are occasionally available, as within the $1.2 billion Great Lakes Restoration Initiative (19). Although connectivity restoration efforts have been piecemeal, the GLB has a long history of collaborative management of shared resources, including binational treaties regarding fisheries, invasive species, and water quality (20). The success of these initiatives demonstrates that large-scale coordination is feasible and that large pulses of spending can be arranged when justified.
We used a return-on-investment framework to analyze potential efficiency gains from coordinating barrier removals at a range of spatial scales (county, tributary, state, lake, nation, or GLB-wide) and temporal scales (a single “pulse” of investment vs. the same amount allocated as a series of 2, 5, or 10 “trickle” investments). Return-on-investment approaches are known to outperform alternative strategies such as purely minimizing cost, and maximizing benefit irrespective of cost (21). Our mathematical optimization model identifies the portfolio of barrier removal projects that provides the greatest increase in total tributary channel length (hereafter “habitat”) accessible to migratory fishes for a given budget. Channel length serves as a surrogate for gains in spawning habitat across the entire fish community and is widely used in restoration planning in lieu of high-resolution spawning habitat maps for individual species.
We applied this model to a comprehensive barrier inventory for the GLB, encompassing 6,692 dams and 232,068 road crossings georeferenced within the 661 largest tributary watersheds (18). For each of these structures, we estimated the direct economic cost of restoring full passability (removal of dams or retrofitting road culverts) and the net upstream habitat that would become available, and we used estimates of the current passability of each culvert (22). Barrier passability is defined as the proportion of fish able to pass through or over a barrier to migrate upstream. Because dozens of partially passable structures often separate headwater spawning grounds from the Great Lakes, we calculated the net probability that a migratory fish could reach the area upstream of a particular barrier as the product of that barrier’s passability and the passability of all downstream barriers (hereafter, the “cumulative passability” of a barrier). Similarly, the net benefit of any barrier removal includes not only full access to the unobstructed area immediately upstream but also partial access to areas above successive upstream barriers until cumulative passability declines to zero.
Results and Discussion
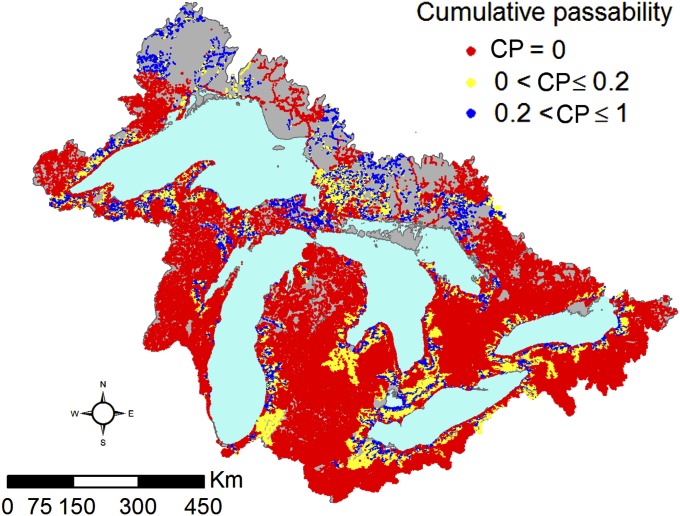
Across the basin, we find that the cumulative passability of dams and road crossings is remarkably low: less than 14% of tributary channel length is fully accessible to migratory fishes (Fig. 1). Cumulative passability is typically much lower than the passability of individual road crossings, highlighting the need for a riverscape perspective in restoration planning.
Fig. 1.
Cumulative passability (CP) of 6,692 dams and 232,068 road crossings in the GLB. Nearly 87% of the total river channel length is at least partially inaccessible to adfluvial fishes (CP < 1), including 64% that is entirely inaccessible (CP = 0). Gray background represents areas without barriers or lacking barrier data.
Our optimization model shows that barrier removals can efficiently restore access to tributary habitat, but only when prioritized strategically. When investments were optimized for the entire basin—the most cost-efficient spatial scale of decision making—the amount of habitat accessible to migratory fishes could be doubled for $70 million (Fig. 2A) by restoring fish passage at 299 dams and 180 road crossings at an average individual cost of $200,000 and $57,000, respectively. Both dam and road- crossing projects are critical components of efficient strategies, with road crossings becoming increasingly important at higher levels of investment (Fig. 2B). Failure to consider both classes of barriers leads to striking inefficiencies: optimizing removal of only dams created access to 24% less habitat than addressing both dams and road crossings jointly across the GLB, whereas prioritizing road crossings alone was 88% less efficient (SI Methods).
Fig. 2.
(A) Return-on-investment curves for six spatial scales of coordination. (B) Number of dams, road crossings, and total projects in the whole-basin solution portfolios. (C) Increase in habitat that could be achieved with an investment of $50 million or $100 million at six spatial scales of coordination. (D) Budget required to achieve a 50% or 100% increase in habitat at each spatial scale.
Considering the spatial scale of project selection, the cost efficiency of barrier removal was relatively unaffected by optimizing at the national or lake scales rather than the entire GLB, but declined dramatically when investments were optimized separately for each state, county, or tributary (Fig. 2A). For an investment of $100 million, for example, a portfolio of projects optimized for the entire GLB would provide a 119% increase in habitat (Fig. 2C). Dividing the same $100 million among tributaries would provide only a 14% increase in habitat even when optimized within each watershed. Correspondingly, to double the accessible tributary length, $70 million is needed if coordinated across the GLB or divided among the five lakes, but $690 million would be required if barrier removals were optimized for each tributary individually (Fig. 2D). In these analyses, funding to each spatial unit was proportional to the number of barriers it contained. Results were similar for alternative distribution rules (SI Methods).
The allocation of restoration funding through time also proved critical; a one-time pulse of investment is much more efficient than providing the same amount in an annual trickle when funds are divided among small spatial units (Fig. 3A). However, when site selection was optimized for the GLB or states, there was little difference among the return-on-investment curves for a pulse vs. a trickle of investment. For $100 million delivered as a pulse to counties, accessible habitat could be increased by 52%, whereas the same amount provided as a series of annual investments over a decade would return only a 5% increase (Fig. 3B). To obtain a 100% increase in habitat, $350 million would be required for the county-pulse model, whereas $950 million would be required for the county-trickle model (Fig. 3C).
Fig. 3.
(A) Return-on-investment curves for all combinations of three spatial and four temporal scales of coordination. Temporal coordination scenarios represent the entire budget allocated as a single pulse of investment (labeled 1 × 100%) vs. the same total amount allocated as a series of 2, 5, or 10 trickle investments, during which 50%, 20%, or 10% of the total budget is disbursed per funding cycle (labeled 2 × 50%, 5 × 20%, and 10 × 10%, respectively). Note that temporal curves overlap at GLB and State spatial scales. (B) Increase in habitat that could be achieved with an investment of $50 million or $100 million for six space by time allocation scenarios. (C) Budget required to achieve a 50% or 100% increase in habitat for six space by time allocation scenarios.
Differences in cost efficiency across spatial and temporal scales of allocation are driven by two factors. First, when the total budget is divided among spatial units (e.g., counties), some funding is inevitably directed toward areas that lack high-return projects. Thus, a purely local-scale model of planning, in which each spatial unit receives an equitable share of funding, can inadvertently force funds to be spent on inefficient projects. Similar trade-offs between equity and conservation outcomes exist for marine protected areas (23). Second, when the budget is finely divided in space and time, only a subset of possible projects are affordable, which sharply constrains aggregate efficiency. For example, a total budget of $300 million allocated under the county-scale, annual trickle model yields an average of just $123,000 per year per county, making 79% of dams (Fig. 4A) and 23% of road crossings unaffordable regardless of potential habitat gains (Fig. 4B).
Fig. 4.
Costs of barrier removal relative to funding levels under various spatial and temporal allocation scenarios. (A) For dam removal, the frequency histogram of project costs is compared with per-county budgets under four scenarios: $100 million total budget allocated among counties as a series of 10 annual investments (a 10 × 10% trickle approach), $300 million trickle, $100 million allocated as a single pulse, and $300 million pulse. Vertical line position on the horizontal axis marks the funding available to each county under each of the four scenarios. (B) For road crossings, retrofitting costs are compared with the same four budget scenarios.
Our analyses offer two key lessons that elucidate how regional coordination and collaboration can boost the efficiency of large-scale restoration efforts. First, we find that large-scale, transboundary coordination can be dramatically more efficient than even optimized local-scale planning. Interestingly, several intermediate spatial scales of coordination (nations and lakes) were nearly as efficient as whole-basin coordination. In the GLB, a variety of conservation and management issues are coordinated at the federal, state, and lake levels (20). Such intermediate-sized planning units may be a useful compromise that offers most of the economic efficiency of large-scale planning while facilitating consideration of local and regional management goals and logistical constraints (24). Our findings differ from those pertaining to the design of nature reserve networks, where international coordination has been shown to be two to three times more cost-effective than national-level coordination (7–9). This difference likely arises from the nature of the targets; reserve networks designed to maximize coverage of a list of species inevitably become more efficient when biodiversity targets can be met jointly across geopolitical units. In contrast, the target in our analyses is simply gains in access to upstream habitat, regardless of which unit they occur in or what species benefits. Presumably, the efficiency of meeting connectivity targets for multiple species would be lower at the lake and nation scales than for the entire GLB if species distributions were taken into account.
The second lesson is illustrated by the extreme inefficiency of local-scale planning when combined with annual trickle budgets. This inefficiency arises when annual budgets are not large enough to remove key dams that are both expensive and occur low in a tributary, thereby forcing expenditure on low-cost, low-reward projects. Where planning at a local scale is essential (e.g., within a high-priority watershed), some of this inefficiency could be mitigated by a one-time strategic pulse of investment sufficient to complete an expensive project. Subsequent trickle investments could then boost overall returns through relatively inexpensive road-crossing upgrades. Policy makers should, therefore, ensure that allocation levels are sufficient to afford certain expensive high-priority projects within their jurisdiction and that funding is allocated toward projects that specifically leverage other completed or planned barrier removals.
The GLB has a long tradition of binational management of shared resources, suggesting that transaction costs associated with coordination (7) would be modest and that large-scale coordination is feasible. Existing binational treaties (e.g., the Great Lakes Water Quality Agreement), institutions (e.g., the Great Lakes Fishery Commission), and interagency agreements [e.g., the Joint Strategic Plan for Management of Great Lakes Fisheries (20)] are important precedents for basin-wide coordination to address key conservation issues. Indeed, formal and informal frameworks for coordinating investments in connectivity across the GLB are beginning to emerge. Given the growing focus on barrier removals by a large number of local, state, federal, and nongovernmental organization actors, our findings underscore the benefits of a collaborative framework for prioritizing investments in connectivity across the GLB.
Although our analyses focused on coordination for ecological objectives only, the political realities of infrastructure maintenance may also create opportunities for cost-efficient conservation investments. All infrastructure has a finite life span, and proper maintenance is costly in aggregate. Future investments in maintenance or replacement of dams and road crossings will come from many sources with various objectives, but ecological outcomes will generally be secondary to public use and safety issues. Thus, a promising conservation strategy is to leverage ongoing infrastructure maintenance activities by supporting low-cost, high-return add-ons to infrastructure projects that are already underway for other reasons (18, 25). In addition, using ecological restoration value as a tie-breaker in selection of infrastructure projects might enhance connectivity at no cost whatsoever.
We stress that large-scale coordination does not necessitate purely top-down, centralized planning. Self-organized or facilitated cooperation among local actors can represent a form of large-scale planning, but one that leverages the local resources and expertise that can be crucial for on-the-ground restoration success. In the GLB, numerous locally driven initiatives play essential roles in conservation efforts (24). Large-scale prioritization could complement local efforts by establishing overarching conservation targets and ensuring that individual projects align in ways that reconnect isolated habitats and populations (24, 26, 27). Moreover, we recognize that local-scale decision making is often rooted in unpredictable reductions in the economic or sociopolitical costs of a particular project. Such opportunities can be entirely worthwhile even if they were not prioritized when using standardized cost data.
Our model does not account for tributary habitat conditions, the spatial distribution of beneficiary species, or the likelihood of species invasions, all of which mediate the ecological benefits of barrier removals (28, 29). Unfortunately, these important management considerations have not been systematically mapped across the entire GLB, so they cannot be incorporated into current optimization models. However, previous work elsewhere suggests that, in some cases, project selection is less sensitive to the distribution of beneficiary species than to spatial variation in project costs (30). We also recognize that the decision to remove a specific barrier often involves multiple stakeholders with differing social and economic values and perspectives (31). Although socioeconomic factors often have enormous importance in individual project selection (32), this perspective is difficult to quantify systematically across the entire GLB for purposes of conservation planning. Nevertheless, our general findings on the relative efficiency of large-scale planning are likely to be robust to further consideration of the ecological costs and benefits of particular barrier removals due to statistical averaging of these costs and benefits over the enormous number of barriers in our analysis. Thus, it is unlikely that refining our estimates of removal costs, habitat gains, or other factors would alleviate the disparities in relative cost efficiency between large- and small-scale project selection, or pulsed and trickled funding patterns.
Given that most of the world’s large freshwater and terrestrial ecosystems are heavily fragmented (13, 33), our finding that spatial and temporal coordination is critical for maximizing returns on societal investments in restoring connectivity is relevant in many conservation contexts. Moreover, the same concepts and mathematical tools could be applied proactively to minimize the impacts of new roads and dams (34–36). This is a critical conservation problem given estimates that the global road network will increase 60% in length between 2010 and 2050 (36). Similarly, our approach could be adapted to identify cases where it would be beneficial to retain existing barriers or construct new barriers to inhibit the spread of invasive species and pathogens (37). In the GLB, for example, more than 60 barriers have been constructed or modified to control the spread of invasive sea lampreys (38). Optimization models can also be expanded to account for risk of infrastructure failure or habitat loss under climate change (39). In each of these contexts, our results on restoring aquatic connectivity, and previous work on transboundary coordination in nature reserve networks (7–9), illustrate the benefits of coordinating investments in both space and time. These dramatic economic and ecological efficiencies provide ample incentive for coordinating restoration efforts across broad spatial and temporal scales.
Methods
Optimization Model.
We developed a mathematical optimization model that, for a given budget, identifies the portfolio of barrier removal projects that provides the greatest net increase in accessibility-weighted tributary habitat available to migratory fishes. Barrier passability is defined conceptually as the proportion of fish able to pass through or over a barrier while migrating upstream (11). We define the cumulative passability of a barrier as the product of that barrier’s passability and the passability of all downstream barriers. Cumulative passability thus represents the probability that a fish can migrate between the Great Lakes and the tributary channel immediately upstream of a barrier. This is equivalent to the definition of “accessibility” in ref. 11. In calculating cumulative passability, we treat successive passage events as independent, which is typical in fish passage prioritization analyses (12). It is not our intent to address performance differences among individual fish based on swimming ability. For the strongest individuals, our passability ratings would be underestimates, or if fatigue leads to diminishing swimming ability with each barrier passed, then our cumulative passability ratings would be overestimates.
Our model extends that of ref. 11 to account for differences in barrier passability ratings and upstream habitat length for multiple species. Specifically, we consider a set of fish guilds, where a guild represents a group of species exhibiting similar swimming abilities and thus having similar likelihood of being capable of passing a particular barrier.
In this study, we only consider projects that restore full passability to a barrier location. We also assume that each barrier has only a single proximate downstream barrier. Our formulation thus omits braided channels, deltas, and artificial connections via drainage channels. This modest simplification is essential for model tractability and captures the large majority of tributary network patterns in our study area.
Given the following decision variables:
our mathematical formulation of the fish passage barrier removal problem is as follows:
| [1] |
s.t.
| [2] |
| [3] |
| [4] |
Here, G is the set of all fish guilds, indexed by g; J is the set of all natural and artificial barriers, indexed by j; JArt is the subset of artificial barriers; Dj is the set of all barriers downstream from and including j; R is the set of planning regions, indexed by r; hj,g is the net amount of habitat for guild g between barrier j and its immediate upstream barriers or the range limit for guild g, in stream kilometers; is the initial passability for guild g at barrier j; pjg is the increase in passability for guild g given mitigation of barrier j; cj is the cost of mitigating barrier j, in US dollars; br is the available budget for region r, in US dollars; and is the cumulative passability (i.e., accessibility) of barrier j for guild g.
The objective function [1] maximizes total accessibility-weighted habitat upstream of each barrier over all barriers and guilds . We weighted all guilds equally for the analyses in this paper. Eqs. 2 give the cumulative passability of barrier for guild . The passability for guild at any intervening barrier in set is simply equal to the initial passability for guild plus the potential increase in passability for guild given mitigation of barrier . Multiplying the passability of all barriers in yields the cumulative passability of barrier for guild . Inequalities [3] specify that the sum of the project costs within a given planning region cannot exceed the available budget br allocated to that region. We modeled budget allocations br as proportional to the number of barriers in a region (results in Figs. 2–4) or proportional to human population (results in SI Methods). Leftover funds were not carried over to other planning regions or time periods. Last, constraints [4] specify that all barrier mitigation decision variables must be binary.
Note that the above model is nonlinear. An exact linear formulation of the problem was devised by introducing a series of probability chains (40) to evaluate cumulative passability terms [2]. A probability chain is a newly proposed technique from the operations research field for linearizing certain classes of high-order polynomial terms such as [2]. See SI Methods for linearization methods and an example return-on-investment analysis using a small fish passage barrier network.
Data and Submodels.
Here, we describe data and submodels for the calculation of project costs, passability, and upstream habitat for each of the 238,760 potential barriers in our analysis. For these calculations, we derived geomorphic and road network covariates from widely available spatial datasets using ArcGIS 10.2 (41). We obtained road surface type (paved or gravel/dirt) and road class (interstate highway, regional highway, or local road), where available, from the US Census Bureau’s TIGER roads layer (42) and Land Information Ontario’s Ontario Road Network (43). We estimated road width by assuming that interstate highways are six lanes wide, regional highways are four lanes wide, and local roads are two lanes wide, and that these three road classes have widths of 25.6 m (84 ft), 18.3 m (60 ft), and 11 m (36 ft), respectively. The stream polylines are a merged dataset derived from the US Geological Survey’s National Hydrography Dataset (44) and the Canadian National Hydro Network (45). To ensure all stream network polylines were strictly dendritic, we manually removed braided and artificial channels and then used the Check Network Topology tool in FLOWS, version 9.3 (46), using ArcGIS 10.2. We calculated upstream drainage area at each barrier using a 30 × 30-m digital elevation model (47).
Our database of 238,760 structures is a subset of the 276,027 dams and road crossings reported in ref. 18. Our dataset is smaller because we omit barriers on very small drainages that drain directly to the Great Lakes. These smallest drainages were omitted because most barrier removal projects focus on larger tributaries that host spawning migrations of a wider range of species. Although the source barrier dataset is the most comprehensive available for the GLB, it also omits natural barriers (e.g., waterfalls) and dams and road crossings that have not been mapped in federal or state databases. These additional barriers may reduce realized habitat gains relative to those reported here. These data gaps are likely to be systematic, however, such that our core findings on the relative efficiencies of planning at different spatial and temporal scales still hold.
Project Cost.
For each of the 238,760 structures in our analysis, we used data on completed project costs (for dams) or estimates of material, labor, and personnel costs (for road crossings) to predict the cost of restoring full passability at a structure. Specifically, we model the cost of removing a dam or the cost of replacing a road-crossing structure with a “fish-friendly” culvert or bridge.
To estimate dam removal costs, we used data from 108 completed dam removal projects in the GLB compiled by American Rivers, a nonprofit organization. Completed projects spanned the period 1965–2013, with 95 of 108 dam removals completed after 1990. To represent historical project costs in 2012 US dollars, we used the Consumer Price Index, an index of inflation published by the US Bureau of Labor Statistics (48). After converting historical project costs to 2012 US dollars, we created a statistical model to predict the cost of removing a dam based on characteristics of that dam. Because our aim was to apply this model to the majority of the 6,692 dams in our dataset, we used as model covariates only those that were widely available for the majority of the dams in the GLB. Dam height was the most consistently available attribute, available for ∼75% of dams in our database. Although dam age, purpose and ownership are often important determinants of removal cost, this information is available for only a small subset of the dams in the GLB. Furthermore, we focused solely on infrastructure costs; we did not consider costs associated with removing or mitigating contaminated impounded sediments (4, 29), or the ecological and economic costs of suppressing species invasions into the newly accessible habitat. Accounting for these additional costs could potentially alter the balance of road crossings and dams in optimal project portfolios.
To predict dam removal costs using dam height, we fit a simple linear regression model (R2 = 0.30) to relate dam removal costs, in 2012 US dollars, to the log10 of dam height, in meters:
We then used this equation to predict dam removal costs for each of the 4,897 dams in our dataset with recorded field-measured height data. For the 1,795 dams for which we had no height information, we assumed that the median dam removal cost (US$173,032.50) was applicable in lieu of height data. To test whether this assumption affected our results, we compared the value of the objective function calculated using the median dam removal cost to the values of the objective when replacing these cost estimates with one of eight different values in the range $113,000 (representative of a dam 2.13 m tall) to $261,000 (representative of a dam 5.22 m tall). The differences in objective function values were less than 1% in all cases, except for the first scenario (setting the removal cost of these 1,795 dams to $113,000), which was 1.3% different from the results in Fig. 2.
Dams for which we had no height data are very unlikely to be large dams with a removal cost greater than $261,000. Our database includes height data for all GLB dams within the US National Inventory of Dams, which is stated to include all dams that are equal to or greater than 6 ft (1.83 m) in height and 50 acre-feet (61.7 ML) in storage, as well as all dams that are equal to or greater than 25 ft (7.62 m) in height and exceed 15 acre-feet (18.5 ML) in storage.
For each of the 232,068 road crossings in our analysis, we used data on material and personnel costs to estimate the total cost of replacing the road-crossing structure with a fish-friendly culvert or bridge. The main drivers of project costs are stream width, road width, road fill depth, and road surface. Details are presented in SI Methods.
Upstream Habitat.
For each of the 238,760 structures in our analysis, we estimated the amount of habitat upstream of that structure by measuring the net tributary length (hjg in the model) between each structure and its nearest set of upstream structures. For this calculation, we used RivEX (49) and ArcGIS 10.2 (41) to sum the distance of all upstream polylines up to the closest set of upstream structures or the river source.
We chose to use tributary length as a measure of habitat because it is a simple metric that integrates restoration benefit across the community of native beneficiary species, whose preferred habitat is patchy and spatially variable across the GLB. Analyses aimed at generating restoration plans for particular species or groups of species are possible using our model by replacing tributary length with more specific estimates of the amount and quality of each habitat type. In each case, the set of priority barriers identified will depend on the set of species chosen and the weightings assigned to those species.
Structure Passability.
We assumed that all dams in our analysis had zero passability and that removing a dam would restore full passability. Although a small subset of dams may in reality be partially passable to certain fishes (due to low height or having a fish passage structure), passability data for dams are not consistently available across the GLB. Fish passage structures are absent from most dams in the GLB, and even where present, salmonid-inspired passage structures may not work well for the weak leapers that dominate the native migratory fish assemblage (50).
For road crossings, we assumed that all intersections with streams of Strahler order >4 were likely to be bridges (22) and therefore fully passable to migratory fishes (∼7.4% of the road crossings in our analysis). For structures over streams with a Strahler order ≤4, we used structure-specific passability estimates from ref. 22. In brief, field-surveyed data from 2,235 culverts across nine watersheds in the GLB were used to create a statistical model linking culvert passability to geographic information system (GIS)-derived landscape geomorphic covariates. In this model, the passability of a culvert is the product of two independent dimensions, culvert outlet drop and culvert outlet water velocity, each of which is estimated independently using a boosted regression tree model. The predictive power of these models as measured by the area under the receiver operating characteristic curve ranged from 0.64 to 0.69, suggesting reasonable ability to predict passability of road crossings from GIS-derived landscape covariates.
Supplementary Material
Acknowledgments
We thank S. Januchowski-Hartley for developing initial barrier maps and passability estimates, and S. Carpenter, M. Guyette, M. Herbert, M. Khoury, and B. Lalasz for helpful comments on the project. Funding was provided by the Upper Midwest and Great Lakes Landscape Conservation Cooperative, The Nature Conservancy’s Great Lakes Project, the University of Wisconsin, the David and Lucille Packard Foundation, the University of Michigan Water Center, and the US Fish and Wildlife Service. The findings and conclusions of this article are those of the authors and do not necessarily represent the view of the US Fish and Wildlife Service.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1423812112/-/DCSupplemental.
References
- 1.Sala OE, et al. Global biodiversity scenarios for the year 2100. Science. 2000;287(5459):1770–1774. doi: 10.1126/science.287.5459.1770. [DOI] [PubMed] [Google Scholar]
- 2.Tilman D, et al. Forecasting agriculturally driven global environmental change. Science. 2001;292(5515):281–284. doi: 10.1126/science.1057544. [DOI] [PubMed] [Google Scholar]
- 3.Fahrig L. Effects of habitat fragmentation on biodiversity. Annu Rev Ecol Syst. 2004;34(1):487–515. [Google Scholar]
- 4.Bednarek AT. Undamming rivers: A review of the ecological impacts of dam removal. Environ Manage. 2001;27(6):803–814. doi: 10.1007/s002670010189. [DOI] [PubMed] [Google Scholar]
- 5.Damschen EI, Haddad NM, Orrock JL, Tewksbury JJ, Levey DJ. Corridors increase plant species richness at large scales. Science. 2006;313(5791):1284–1286. doi: 10.1126/science.1130098. [DOI] [PubMed] [Google Scholar]
- 6.Beier P, Spencer W, Baldwin RF, McRae BH. Toward best practices for developing regional connectivity maps. Conserv Biol. 2011;25(5):879–892. doi: 10.1111/j.1523-1739.2011.01716.x. [DOI] [PubMed] [Google Scholar]
- 7.Kark S, Levin N, Grantham HS, Possingham HP. Between-country collaboration and consideration of costs increase conservation planning efficiency in the Mediterranean Basin. Proc Natl Acad Sci USA. 2009;106(36):15368–15373. doi: 10.1073/pnas.0901001106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mazor T, Possingham HP, Kark S. Collaboration among countries in marine conservation can achieve substantial efficiencies. Divers Distrib. 2013;19(11):1380–1393. [Google Scholar]
- 9.Moilanen A, et al. Edge artefacts and lost performance in national versus continental conservation areas. Divers Distrib. 2013;19(2):171–183. [Google Scholar]
- 10.Hermoso V, Linke S, Prenda J, Possingham HP. Addressing longitudinal connectivity in the systematic conservation planning of fresh waters. Freshw Biol. 2011;56(1):57–70. [Google Scholar]
- 11.O’Hanley JR, Tomberlin D. Optimizing the removal of small fish passage barriers. Environ Model Assess. 2005;10(2):85–98. [Google Scholar]
- 12.Kemp PS, O’Hanley JR. Procedures for evaluating and prioritising the removal of fish passage barriers: A synthesis. Fish Manag Ecol. 2010;17(4):297–322. [Google Scholar]
- 13.Nilsson C, Reidy CA, Dynesius M, Revenga C. Fragmentation and flow regulation of the world’s large river systems. Science. 2005;308(5720):405–408. doi: 10.1126/science.1107887. [DOI] [PubMed] [Google Scholar]
- 14.McIntyre PB, et al. In: Conservation of Freshwater Fishes. Closs GP, Krkosek M, Olden JD, editors. Cambridge Univ Press; Cambridge, UK: [Google Scholar]
- 15.Austin J, Dezenski E, Affolter-Caine B. The Vital Connection: Reclaiming the Great Lakes Economic Leadership in the Bi-National US-Canadian Region. The Brookings Institution; Washington, DC: 2008. [Google Scholar]
- 16. Southwick Associates (2008) Sportfishing in America: An Economic Engine and Conservation Powerhouse (American Sportfishing Association, Alexandria, VA)
- 17.Bogue MB. Fishing the Great Lakes: An Environmental History, 1783–1933. Univ of Wisconsin Press; Madison, WI: 2000. [Google Scholar]
- 18.Januchowski-Hartley SR, et al. Restoring aquatic ecosystem connectivity requires expanding inventories of both dams and road crossings. Front Ecol Environ. 2013;11(4):211–217. [Google Scholar]
- 19.Great Lakes Restoration Initiative 2010 Great Lakes Restoration Initiative Action Plan, FY2010–FY2014. Available at glri.us/pdfs/glri_actionplan.pdf. Accessed April 13, 2015.
- 20.Dochada MR. In: Great Lakes Fisheries Policy and Management. Taylor WW, Ferreri CP, editors. Michigan State Univ Press; East Lansing, MI: 1999. [Google Scholar]
- 21.Murdoch W, Ranganathan J, Polasky S, Regetz J. Using return on investment to maximize conservation effectiveness in Argentine grasslands. Proc Natl Acad Sci USA. 2010;107(49):20855–20862. doi: 10.1073/pnas.1011851107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Januchowski-Hartley SR, Diebel M, Doran PJ, McIntyre PB. Predicting road culvert passability for migratory fishes. Divers Distrib. 2014;20(12):1414–1424. [Google Scholar]
- 23.Halpern BS, et al. Achieving the triple bottom line in the face of inherent trade-offs among social equity, economic return, and conservation. Proc Natl Acad Sci USA. 2013;110(15):6229–6234. doi: 10.1073/pnas.1217689110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pearsall DR, et al. “Make no little plans”: Developing biodiversity conservation strategies for the Great Lakes. Environ Pract. 2013;15(04):462–480. [Google Scholar]
- 25.Doyle MW, Havlick DG. Infrastructure and the environment. Annu Rev Environ Resour. 2009;34:349–373. [Google Scholar]
- 26.Berkes F. Rethinking community-based conservation. Conserv Biol. 2004;18(3):621–630. [Google Scholar]
- 27.Zbicz DC. Imposing transboundary conservation: Cooperation between internationally adjoining protected areas. J Sustain For. 2003;17(1-2):21–37. [Google Scholar]
- 28.McLaughlin RL, et al. Unintended consequences and trade-offs of fish passage. Fish Fish. 2012;14(4):580–604. [Google Scholar]
- 29.Stanley EH, Doyle MW. Trading off: The ecological effects of dam removal. Front Ecol Environ. 2003;1(1):15–22. [Google Scholar]
- 30.Bode M, et al. Cost-effective global conservation spending is robust to taxonomic group. Proc Natl Acad Sci USA. 2008;105(17):6498–6501. doi: 10.1073/pnas.0710705105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Johnson SE, Graber BE. Enlisting the social sciences in decisions about dam removal. Bioscience. 2002;52(8):731–738. [Google Scholar]
- 32.Hoenke KM, Kumar M, Batt L. A GIS based approach for prioritizing dams for potential removal. Ecol Eng. 2014;64:27–36. [Google Scholar]
- 33.Saunders DA, Hobbs RJ, Margules CR. Biological consequences of ecosystem fragmentation: A review. Conserv Biol. 1991;5(1):18–32. [Google Scholar]
- 34.Ziv G, Baran E, Nam S, Rodríguez-Iturbe I, Levin SA. Trading-off fish biodiversity, food security, and hydropower in the Mekong River Basin. Proc Natl Acad Sci USA. 2012;109(15):5609–5614. doi: 10.1073/pnas.1201423109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Laurance WF, Balmford A. Land use: A global map for road building. Nature. 2013;495(7441):308–309. doi: 10.1038/495308a. [DOI] [PubMed] [Google Scholar]
- 36.Laurance WF, et al. A global strategy for road building. Nature. 2014;513(7517):229–232. doi: 10.1038/nature13717. [DOI] [PubMed] [Google Scholar]
- 37.Rahel FJ. Intentional fragmentation as a management strategy in aquatic systems. Bioscience. 2013;63(5):362–372. [Google Scholar]
- 38.Lavis DS, Hallet A, Koon EM, McAuley TC. History of and advances in barriers as an alternative method to suppress sea lampreys in the Great Lakes. J Great Lakes Res. 2003;29(1):362–372. [Google Scholar]
- 39.Ando AW, Mallory ML. Optimal portfolio design to reduce climate-related conservation uncertainty in the Prairie Pothole Region. Proc Natl Acad Sci USA. 2012;109(17):6484–6489. doi: 10.1073/pnas.1114653109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.O’Hanley JR, Scaparra MP, Garcia S. Probability chains: A general linearization technique for modeling reliability in facility location and related problems. Eur J Oper Res. 2013;230(1):63–75. [Google Scholar]
- 41.ESRI . ArcGIS Desktop: Release 10.2. Environmental Systems Research Institute; Redlands, CA: 2013. [Google Scholar]
- 42.US Census Bureau 2010 TIGER/Line Shapefiles. Available at www.census.gov/geo/maps-data/data/tiger.html. Accesssed April 13, 2015.
- 43.Land Information Ontario 2010 Ontario Road Network Shapefiles. Available at www.ontario.ca/environment-and-energy/land-information-ontario. Accessed April 13, 2015.
- 44.US Geological Survey 2009 National Hydrography Dataset. Available at nhd.usgs.gov/. Accessed April 13, 2015.
- 45.Natural Resources Canada 2007 National Hydrography Network. Available at www.geobase.ca. Accessed April 13, 2015.
- 46.Theobald D, et al. Functional Linkage of Waterbasins and Streams (FLoWS) v1 User’s Guide: ArcGIS Tools to Analyze Freshwater Ecosystems. Natural Resource Ecology Laboratory, Colorado State University; Fort Collins, CO: 2006. [Google Scholar]
- 47.US Geological Survey 2012 Shuttle Radar Topography Mission Finished Grade Product. Available at https://lta.cr.usgs.gov/SRTM. Accessed April 13, 2015.
- 48.US Bureau of Labor Statistics 2013 Consumer Price Index. Available at www.bls.gov/cpi/. Accessed April 13, 2015.
- 49.Hornby D. 2008 RivEX. Available at www.rivex.co.uk/. Accessed April 13, 2015.
- 50.Stuart IG, Mallen-Cooper M. An assessment of the effectiveness of a vertical-slot fishway for non-salmonid fish at a tidal barrier on a large tropical/subtropical river. Reg Rivers Res Manage. 1999;15(6):575–590. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.