Strain and the optoelectronic properties of nonplanar phosphorene monolayers

Significance

Phosphorene is a new 2D atomic material, and we document a drastic reduction of its electronic gap when under a conical shape. Furthermore, geometry determines the properties of 2D materials, and we introduce discrete differential geometry to study them. This geometry arises from particle/atomic positions; it is not based on a parametric continuum, and it applies across broad disciplinary lines.

Abstract

Lattice kirigami, ultralight metamaterials, polydisperse aggregates, ceramic nanolattices, and 2D atomic materials share an inherent structural discreteness, and their material properties evolve with their shape. To exemplify the intimate relation among material properties and the local geometry, we explore the properties of phosphorene––a new 2D atomic material––in a conical structure, and document a decrease of the semiconducting gap that is directly linked to its nonplanar shape. This geometrical effect occurs regardless of phosphorene allotrope considered, and it provides a unique optical vehicle to single out local structural defects on this 2D material. We also classify other 2D atomic materials in terms of their crystalline unit cells, and propose means to obtain the local geometry directly from their diverse 2D structures while bypassing common descriptions of shape that are based from a parametric continuum.

Two-dimensional materials (1–20) are discrete surfaces that are embedded on a 3D space. Graphene (1, 2) develops an effective Dirac-like dispersion on the sublattice degree of freedom and other 2D atomic materials exhibit remarkable plasmonic, polariton, and spin behaviors too (18–20).

The properties of 2D materials are influenced by their local geometry (12–17, 21–29), making a discussion of the shape of 2D lattices a timely and fundamental endeavor (24, 30–32). A dedicated discussion of the shape of 2D materials is given here within the context of nets. Nets are discrete surfaces made from vertices and edges, with vertices given by particle/atomic positions (31–34). The discrete geometry that originates from these material nets is richer than its smooth counterpart because the net preserves the structural information of the 2D lattice completely, yielding exact descriptions of shape that remain accurate as the lattice is subject to arbitrarily large structural deformations (15, 16), as the particle/atomic lattice becomes the net itself.

A discrete geometry helps address how strain influences chemistry (35), how energy landscapes (36–38) correlate to nonplanar shapes, and it provides the basis for a lattice gauge theory for effective Dirac fermions on deformed graphene (39, 40). In continuing with this program, the optical and electronic properties of phosphorene cones will be linked to their geometry in the present work. At variance with 2D crystalline soft materials that acquire topological defects while conforming to nonplanar shapes (12–15), the materials considered here have strong chemical bonds that inhibit plastic deformations for strain larger than 10% (41).

The study is structured as follows: We build conical structures of black and blue phosphorene, determine their local shape, and link this shape to the magnitude of their semiconducting gap. It is clear that a discrete geometry applies for arbitrary 2D materials.

Results and Discussion

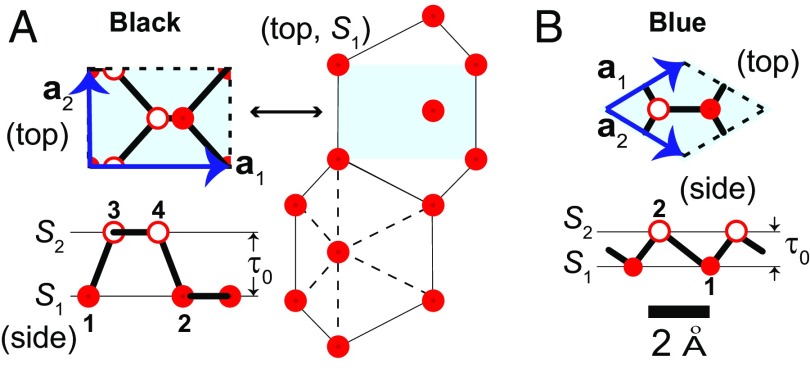
Phosphorene (8, 9) has many allotropes that are either semiconducting or metallic depending on their 2D atomistic structure (42–44). The most studied phase, black phosphorene (Fig. 1A), has a semiconducting gap that is tunable with the number of layers, and by in-plane strain (26, 27, 45, 46). Theoretical studies of defects on planar phosphorene indicate that dislocation lines do not induce localized electronic states (47), and algorithms to tile arbitrary planar 2D phosphorene patterns have been proposed as well (44). Unit cells of planar monolayers of black and blue phosphorene are displayed in Fig. 1.

Fig. 1.

Unit cells for (A) black and (B) blue phosphorene monolayers that are formed by two sublayers ($S_1$ and $S_2$) separated by a distance ${\tau }_0$. Sublayers in black phosphorene are irregular––distances among nearest atoms belonging to the same sublayer are not identical––as emphasized by the dashed lines joining atoms belonging to sublayer $S_1$ on the rightmost structure in A.

Four invariants from the metric (g) and curvature (k) tensors determine the local geometry of a 2D manifold (24, 30):

$$\text{Tr}\left(g\right),\text{Det}\left(g\right),\hspace{0.5em}H\equiv \text{Tr}\left(k\right)/2\text{Tr}\left(g\right),\hspace{0.5em}K\equiv \text{Det}\left(k\right)/2\text{Det}\left(g\right),$$ [1]

where Tr (Det) stands for trace (determinant), H is the mean curvature, and K is the Gaussian curvature.

An infinite crystal can be built from these unit cells, and the geometry of such ideal planar structure can be described by $\text{Tr}\left(g\right)=1$, $\text{Det}\left(g\right)=1$ (i.e., no strain), $H=0$, and $K=0$ (i.e., no curvature) at both sublayers $S_1$ and $S_2$. In addition, their thickness τ is equal to ${\tau }_0$ before a structural distortion sets in: These five numbers quantify the local reference, flat geometry. [In principle, Tr(g) and Det(g) will be functions of the lattice constant, but here they are normalized with respect to their values in the reference crystalline structures seen in Fig. 1, to enable direct comparisons of the metric among black and blue phosphorene monolayers. ${\tau }_0=2.27$ (1.26) Å for black (blue) phosphorene in these planar reference structures.]

Now, structural defects can induce nonzero curvature and strain (35), and may also be the culprits for the chemical degradation of layered phosphorene. To study the consequences of shape on the optical and electronic properties of phosphorene monolayers, we create finite-size conical black and blue phosphorene monolayers, characterize the atomistic geometry, and investigate the influence of shape on their semiconducting gap. [We have proposed that hexagonal boron nitride could slow the degradation process while allowing for a local characterization of phosphorene allotropes (48), and a study of chemical reactivity of nonplanar phosphorene will be presented elsewhere.]

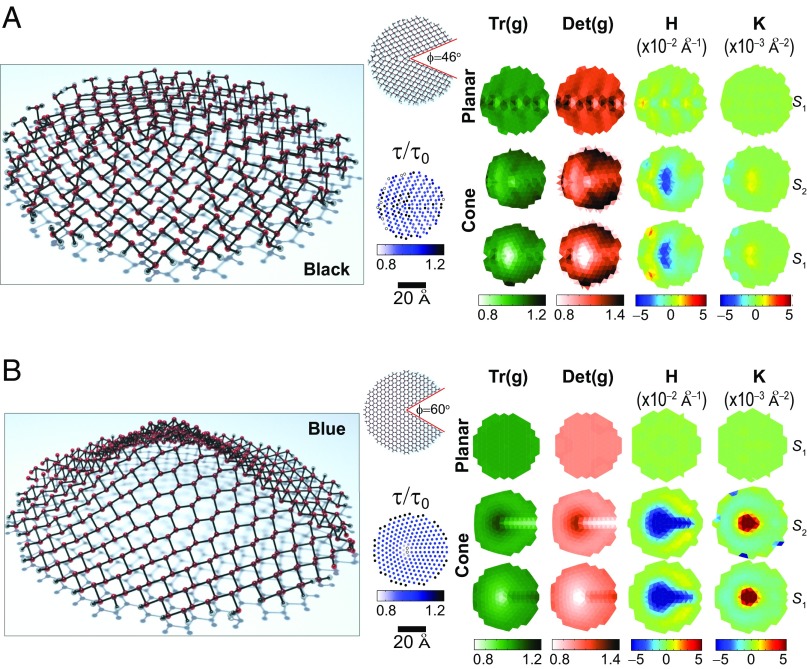
Phosphorene cones are built from finite disk-like planar structures that have hydrogen-passivated edges (Fig. 2). The black phosphorene cone seen in Fig. 2A is created as follows: We remove an angular segment—that subtends a $\varphi =46°$ angle—from a planar structure that has a dislocation line (47). The two “ridges” that are highlighted by the red segments on the planar structure in Fig. 2A are joined afterward to create a disclination line. Atoms are placed in positions dictated by an initial (analytical) conical structure, and there is a full structural optimization via molecular dynamics at the ab initio level to relieve structural forces throughout (Methods).

Fig. 2.

(A) Black and (B) blue phosphorene cones are built by removing the angular segments in white from the planar structures (as illustrated at the upper-right corner of the conical structures), joining the cut structures along the red (disclination) lines, and a subsequent structural optimization. The discrete local geometry of these conical structures at sublayers $S_1$ and $S_2$ is given by four local invariants [$\text{Tr}\left(g\right)$, $\text{Det}\left(g\right)$, H, and K] that are obtained at each atomic position. These invariants are contrasted with the geometry of planar structures [$\text{Tr}\left(g\right)=1$, $\text{Det}\left(g\right)=1$, $H=0$, and $K=0$] that is depicted at the uppermost row for sublayer $S_1$. The change in relative height $\tau /{\tau }_0$ is shown at each atomic position as well. Features such as (i) strain induced by the dislocation line in planar black phosphorene, (ii) a sensible compressive strain near the apex, (iii) curvature lacking a radial symmetry, and (iv) the lack of significant changes in τ on conical black phosphorene, are clearly seen. The disclination line on the blue phosphorene cone is reflected on the metric invariants and on H: This disclination has a semicylindrical shape, which yields an overall radially symmetric Gaussian curvature K. In addition, a decrease of τ, and an in-plane compression (elongation) at sublayer $S_1$ ($S_2$) near the apex can also be seen on the blue phosphorene cone.

Blue phosphorene has a (buckled) honeycomb structure reminiscent of graphene, so the conical structure seen to the left of Fig. 2B was generated by removing an angular segment subtending a $\varphi =60°$ angle on planar blue phosphorene, and following prescriptions similar to those used in creating the black phosphorene cone afterward.

The subplots displayed to the right in Fig. 2 A and B show the local discrete geometry at individual atoms (Eq. 1; see details in Methods). For each allotrope, the data are arranged into three rows that indicate the geometry of the planar structure at sublayer $S_1$, and the local geometry of the cones at sublayers $S_1$ and $S_2$. An additional plot shows the value of $\tau /{\tau }_0$ that tells us of local vertical compression.

There is strain induced by the dislocation line on the planar black phosphorene structure, as indicated by the color variation on the $\text{Tr}\left(g\right)$ and $\text{Det}\left(g\right)$ plots, which implies having atoms at closer/longer distances than in the reference structure, Fig. 1. A slight curvature on the black phosphorene planar structure, induced by the dislocation line, is also visible in the H plot in Fig. 2A. The planar blue phosphorene sample does not have any dislocation line, and for that reason the metric shows zero strain [$\text{Tr}\left(g\right)=1$ and $\text{Det}\left(g\right)=1$] and zero curvature ($H=0$ and $K=0$) on that reference structure (Fig. 2B).

The black phosphorene conical structure seen in Fig. 2A has the following features: A compression near its apex, as displayed by the white color on the metric invariants; this compression is not radial-symmetric. An asymmetric elongation is visible toward the edges. In addition, there is a radially asymmetric nonzero curvature; the observed asymmetry reflects the presence of the dislocation/disclination axis, which provides the structure with an enhanced structural rigidity. This rigidity is confirmed by the ratio $\tau /{\tau }_0$ close to unity, which indicates almost no vertical compression–elongation of this conical structure (Fig. 2A).

The blue phosphorene cone has a more apparent radial symmetry, except for the disclination line that is created by the conical structure, as reflected on the metric invariants and on H. There is compression (elongation) at the apex, and elongation (compression) along the disclination line in sublayer $S_1$ ($S_2$). The disclination line has a semicylindrical shape and hence a zero radius of curvature along the disclination line, resulting in a zero Gaussian curvature along such line; the Gaussian curvature looks radially symmetric overall.

Fig. 2 indicates that the blue phosphorene cone acquires the largest curvatures of these two cones. This is so because the angular segment removed from the planar blue phosphorene sample has a comparatively larger value of ϕ. One notes the rather smooth curvature at the apex on the blue phosphorene conical structure after the structural optimization.

The change of τ with respect to ${\tau }_0$ is created by an out-of-plane strain or by shear. The blue phosphorene cone shows out-of-plane compression near the apex. The distance among planes in black phosphorene is closer to its value in an ideal planar structure throughout, showing scatter around the dislocation line.

The main point from Fig. 2 is the strain induced by curvature. The strain pattern observed in that figure is far more complex than those reported before for planar phosphorene (26, 27, 45, 46), and the discrete geometry captures the strain pattern with the precision given by actual atomic positions. We will describe the tools that lead to this geometry based from atoms later on (Methods), but we describe the effect of shape on the material properties of these cones first.

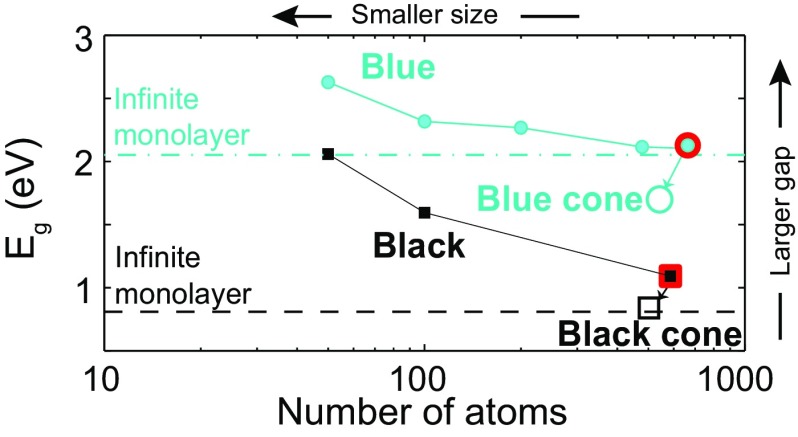
Black and blue phosphorene monolayers are both semiconducting 2D materials with a direct bandgap, and we investigate how this semiconducting gap evolves with their shape. The semiconducting gap $E_g=$ is equal to 1.1 (2.2) eV for the finite-size planar black (blue) phosphorene monolayers on display in Fig. 2, before the removal of the angular segments. These electronic gaps are highlighted at the rightmost end of Fig. 3. All gaps were computed after a structural optimization, to avoid unbalanced forces on these samples that would bias their magnitude (Methods).

Fig. 3.

The semiconducting gap of planar black and blue phosphorene monolayer disks increases as the number of atoms decreases. Even though the number of atoms must be reduced to create a conical shape from a planar structure, the gap decreases on conical structures with such decrease of the number of atoms, as indicated by open ticks and the tilted arrows: This reduction of the gap on a conical structure thus has a purely geometrical origin. (Dash and dash-dot lines indicate these gaps when the number of atoms is infinite.)

We determine size effects on the semiconducting gap on planar structures first: The magnitude of the gap $E_g$ increases as the number of atoms decreases on strain-free disk-like planar structures, as seen in Fig. 3. For an infinite number of atoms––i.e., for a fully periodic planar 2D crystal––the gap converges to the values indicated by the dash and dash-dot lines on Fig. 3, namely, 0.8 eV and 2.0 eV for black and blue phosphorene, respectively. These magnitudes were obtained from standard density-functional theory (8, 42). Although we acknowledge that other methods describe the dielectric properties more accurately on smaller samples (27), our focus is on the trend the gap follows, and given that the trend is geometrical in nature, it will stand correct despite the particular method used in computing the semiconducting gap.

The conical structures have fewer atoms than their parent planar structures once the angular segments seen in Fig. 2 A and B are removed. We learned in the previous paragraph that the electronic gap increases as the number of atoms is decreased on planar structures. Following that argument, one may expect the semiconducting gap for the conical structures to be larger than the one observed on their parent planar structures.

However, instead of increasing with the removal of atoms, the gap decreases dramatically on the conical structures, going down to 0.84 (1.70) eV for the black (blue) phosphorene cone, as indicated by the open red symbols, and the tilted arrows in Fig. 3: Shape influences phosphorene’s material properties. A practical consequence of this result is that optical probes could provide a measure of the local shape of phosphorene. The relation between the semiconducting gap and a nonplanar shape has been observed in transition metal dichalcogenide monolayers recently (25), and we establish here that structural defects on semiconducting 2D materials create a similar effect. Let us next address the reason for such reduction of the semiconducting gap.

The semiconducting gap is a global material property. On finite samples it is possible to project the electronic density onto individual atoms to learn about the spatial localization of the electronic states below and above the Fermi level, whose energy difference is equal to the electronic gap. Those states are known as the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), and they were spin-degenerate in all of the samples we studied. Additionally, the nth electronic orbital below (above) the HOMO (LUMO) is labeled HOMO$-n$ (LUMO$+n$).

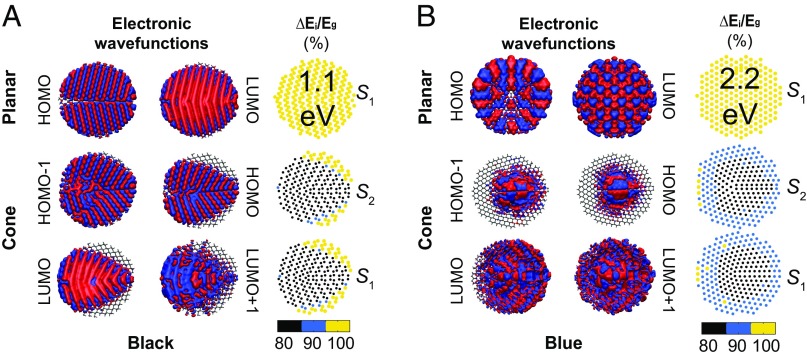
The HOMO and LUMO states cover the entire planar black and blue phosphorene structures (Fig. 4) and are thus delocalized. On the other hand, the conical samples have orbitals below and above the Fermi energy that display a certain amount of localization.

Fig. 4.

A remarkable reduction of the semiconducting gap occurs due to the strain induced by the conical shape, and regardless of phosphorene allotrope. The local distribution of $\mathrm{\Delta }{E}_i$ correlates with the extent of the electronic wavefunctions shown below and above the Fermi level for (A) black and (B) blue phosphorene.

Such effect is most visible for the HOMO and HOMO$-1$ states for the blue phosphorene cone in Fig. 4B. Thus, unlike a dislocation line (47) the pentagon defect that is responsible for the curvature of the blue conical structure is localizing the HOMO state within an $\sim 10$ Å radius. Given that the pentagon defect originates curvature itself, we conclude that curvature leads to a reduction of the electronic gap on this system.

Given the localization observed on some of these orbitals, we can further ask: At a given atomic position, what is the first orbital with a nonzero density at such location below and above the Fermi energy? This question can be rephrased in terms of the difference in energy among the first orbitals below and above the Fermi level that have a nonzero probability density at a given atomic location: In the third column in Fig. 4 A and B we display such energy difference $\mathrm{\Delta }{E}_i$ at every phosphorus atom i. There exists a clear correlation among $\mathrm{\Delta }{E}_i$ and the localization pattern of the orbitals below and above the Fermi energy, as should be the case. The reduction on the semiconducting gap on the cones is emphasized by normalizing $\mathrm{\Delta }{E}_i$ in terms of $E_g$, which yields a 20% reduction of the semiconducting gap for both allotropes: a nonplanar geometry that is created by structural defects on any phosphorene allotrope will lead to a sizable reduction of the semiconducting gap.

To end this work, we must state that the discrete geometry used to tell the shape of the phosphorene conical structures applies to other 2D atomic materials with varied unit cells, some of which are listed here: (i) Regular honeycomb lattices [graphene (2, 39, 40, 49) and hexagonal boron nitride (4)]. (ii) Low-buckled honeycomb hexagonal lattices [silicene and germanene (5); we established that freestanding stanene (50) is not the structural ground state]. (iii) “High-buckled” hexagonal close-packed bilayers of bismuth (51), tin, and lead (52). (iv) Thin trigonal–prismatic transition-metal dichalcogenides (53, 54). (v) Materials with buckled square unit cells––quad-graphs (31)––such as AlP (7).

Structures (i)–(iv) are equilateral triangular lattices with a basis, for which individual planes represent regular equilateral triangular nets; and structure (v) realizes a regular quad-graph.

Low-buckled structures (silicene, germanene, blue phosphorus), hexagonal close-packed bilayers (bismuth, tin, and lead), and black phosphorus have two parallel sublayers, S₁ and S₂. Transition-metal dichalcogenides and AlP have three parallel sublayers S₁–S₃. The discrete geometry clearly stands for other 2D materials that do not form strong directional bonds (12, 14) as well.

Concluding Remarks

Shape is a fundamental handle to tune the properties of 2D materials, and the discrete geometry provides the most accurate description of 2D material nets. This geometry was showcased on nonplanar phosphorene allotropes for which the electronic gap decreases by 20% with respect to its value on planar structures. The discrete geometry can thus be used to correlate large structural deformations to intended functionalities on 2D materials with arbitrary shapes.

Methods

Creation of Conical Structures.

Consider structures having atomic positions at planar disks; these positions can be parameterized by $r_i$, ${\theta }_i$, and $z_i=\left\{0,{\tau }_0\right\}$. Calling ϕ the angular segments being removed from these planar structures, the range of the angular variable ${\theta }_i$ is $[\mathrm{0,2}\pi -\varphi ]$, and the conical structures are initially built by the following transformation: $r_i^{\prime }=r_i\sqrt{1-\left({\varphi }^2/4{\pi }^2\right)}$, ${\theta }_i^{\prime }=\left(2\pi /\left(2\pi -\varphi \right)\right){\theta }_i$, and $z_i^{\prime }=z_i-r_i\left(\varphi /2\pi \right)$. These conical structures containing about 500 atoms undergo a structural optimization via ab initio (Car–Parinello) molecular dynamics (55) with the SIESTA code (56, 57), until forces are smaller than 0.04 eV/Å.

Calculation of the Electronic Gap of Phosphorene Samples.

We obtain $\mathrm{\Delta }{E}_i$ as follows: Let $E_F$ be the charge neutrality level or Fermi energy, and ${\rho }_i\left(E\right)$ the density of electronic states projected onto atom i. We call $E_i^A$ ($E_i^B$) the first energy level observed on ${\rho }_i\left(E\right)$ lying above (below) $E_F$ at atom i, and report $\mathrm{\Delta }{E}_i/E_g\equiv \left(E_i^A-E_i^B\right)/E_g$ in Fig. 4. We note that all structures we worked with had a final net zero spin polarization on spin-polarized calculations.

A Discrete Geometry Based on Triangulations at Atomic Positions.

There is an extrinsic and continuum (Euclidean) geometry in which material objects exist. These material objects are made out of atoms that take specific locations to generate their own intrinsic shape.

The intrinsic shape of 2D atomic materials can be idealized as a continuum: The basic assumption of continuum mechanics is that a continuum shape is justified at length scales l much larger than interatomic distances that are characterized by a lattice parameter $a_0$ ($l\gg a_0$). The common understanding of shape arises from within this continuum perspective that is based on the differential geometry of 2D manifolds. This continuum approximation is valid down to interatomic scales ($l\le a_0$) for slowly varying deformations, but not when curvature concentrates at atomic-scale bonds or pleats, such as in the examples provided in refs. 11 and 14. And so, whereas these sharp structures may be disregarded or approximated within the context of a continuum surface, we hold the opinion that an intrinsic geometry that is exact at the atomic scale must form part of the theoretical toolset to deal with 2D materials. The discrete geometry to be described in the next paragraphs bypasses descriptions of shape that are based on an effective continuum, and it brings an understanding of the shape of material nets at a fundamental level.

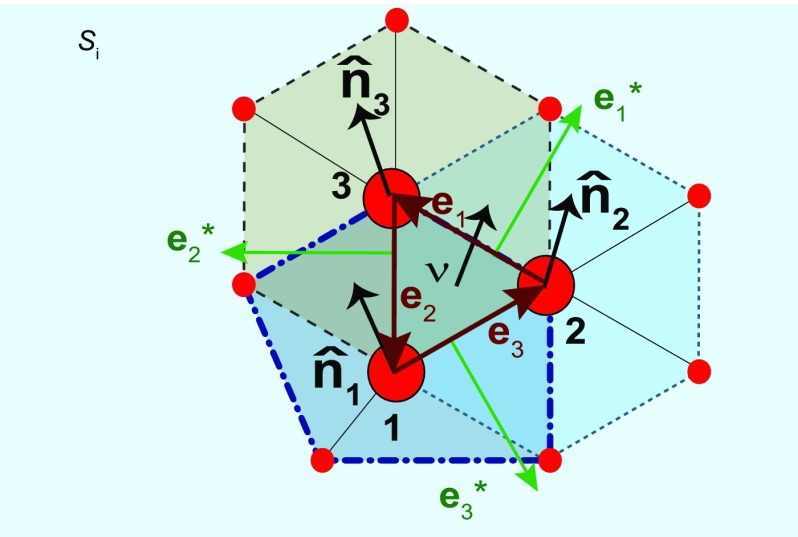
Consider three directed edges ${\mathbf{e}}_1$, ${\mathbf{e}}_2$, and ${\mathbf{e}}_3$, such that ${\mathbf{e}}_1+{\mathbf{e}}_2+{\mathbf{e}}_3=\mathbf{0}$, and define $Q_l^I\equiv {\mathbf{e}}_l\cdot {\mathbf{e}}_l$ ($l=\mathrm{1,2,3}$), representing the square of the smallest finite distance among atoms on the 2D lattice. This is the discrete analog of the infinitesimal length element $d{s}^2$ (Fig. 5).

Fig. 5.

Discrete tensors based on triangulations are expressed in terms of averaged normals ${\widehat{\mathbf{n}}}_j$, edges ${\mathbf{e}}_j$, the normal of the triangle $\mathit{\nu }$, and dual edges ${\mathbf{e}}_j^{*}\equiv {\mathbf{e}}_j\times \mathit{\nu }$ ($j=\mathrm{1,2,3}$). These tensors can be used in quad-nets, irregular lattices, and structures containing defects as highlighted by the pentagon surrounding atom 1.

Now consider the change in orientation among normals ${\widehat{\mathbf{n}}}_j$ and ${\widehat{\mathbf{n}}}_k$, and project such variation onto their common edge ${\mathbf{e}}_l$: This is, define $Q_l^{II}\equiv \left({\widehat{\mathbf{n}}}_k-{\widehat{\mathbf{n}}}_j\right)\cdot {\mathbf{e}}_l$ (see Fig. 5; $j,k,l$ are permutations of integers 1, 2, and 3). The reader may recall that the curvature tensor is defined as $\widehat{n}\cdot \left(\partial g_{\alpha }/\partial {\xi }_{\beta }\right)$, but the discrete tensor carries a constant edge, and it rests on changes of the local normals instead. In the previous equation, ${\widehat{\mathbf{n}}}_l$ is the average over individual normals at triangulated area elements within the polygon surrounding atom l and highlighted by dashed lines. The dual edge is defined by ${\mathbf{e}}_l^{*}\equiv {\mathbf{e}}_l\times \mathit{\nu }$, with $\mathit{\nu }$ the normal to the triangle formed by atoms 1, 2, and 3 and $A_T$ is the triangle area ($-{\mathbf{e}}_2\times {\mathbf{e}}_1=2A_T\mathit{\nu }$).

This way, the discrete metric tensor takes the following form on the basis given by dual edges*:

$$g=-\frac{1}{8A_0^2}{\displaystyle \sum _{\left(j,k,l\right)}\left(Q_j^I-Q_k^I-Q_l^I\right){\mathbf{e}}_j^{*}\otimes {\mathbf{e}}_j^{*}},$$ [2]

with $A_0$ the area of the triangulated area element at the reference (nondeformed and defect-free) plane.

The discrete curvature tensor has an identical structure:

$$k=-\frac{1}{8A_T^2}{\displaystyle \sum _{\left(j,k,l\right)}\left(Q_j^{II}-Q_k^{II}-Q_l^{II}\right){\mathbf{e}}_j^{*}\otimes {\mathbf{e}}_j^{*}}.$$ [3]

The parentheses $\left(j,k,l\right)$ indicate a sum of three terms, as follows: ($j=1$, $k=2$, $l=3$), (2, 3, 1), and (3, 1, 2). Eqs. 2 and 3 become 3$\times$ 3 matrices with explicit values for $Q_l^I$, $Q_l^{II}$, and ${\mathbf{e}}_j^{*}$ from atomic positions (Fig. 5). For instance, the discrete curvature tensor has eigenvalues {0, $k_1$, $k_2$} at each triangulated area element, yielding $H=\left(k_1+k_2\right)/2$ and $K=k_1{k}_2$. The geometrical invariants reported at point $\mathbf{j}$ are averages over their values at individual triangles sharing this vertex.

Topological defects (exemplified by a pentagon seen by a dot-dash line in Fig. 5) break translation symmetry, making it impossible to recover a crystalline structure by means of elastic deformations. However, Eqs. 2 and 3 provide a geometry along topological defects seamlessly still, as seen in the geometry provided in Fig. 2.

The computation of the distribution of the thickness τ in both conical structures was performed by finding for each atom in the lower sublayer $S_1$ the three nearest neighbors on the upper sublayer $S_2$. The distance between the centroid of these three atoms and the atom in question at the $S_1$ sublayer amounts to the thickness τ of the structure at that specific atom.