Interactions of the KWK₆ cationic peptide with short nucleic acid oligomers: demonstration of large Coulombic end effects on binding at 0.1–0.2 M salt

Abstract

We quantify Coulombic end effects (CEE) on oligocation–nucleic acid interactions at salt concentrations ([salt]) in the physiological range. Binding constants (K_obs; per site, at zero binding density) for the +8-charged C-amidated oligopeptide KWK₆ and short single-stranded DNA oligonucleotides [, where 6 ≤ |Z_D| ≤ 22 is the number of DNA phosphates] were determined as a function of [salt] by fluorescence quenching. For the different DNA oligomers, K_obs values are similar at high [salt], but diverge as [salt] decreases because −S_aK_obs ≡ −∂ln K_obs/∂ln a_± increases strongly with |Z_D|. For binding of KWK₆ near 0.1 M salt, −S_aK_obs is 5.5 ± 0.2 for dT(pdT)₂₂, 4.0 ± 0.2 for dT(pdT)₁₀ and 2.9 ± 0.2 for dT(pdT)₆, as compared with 6.5 ± 0.3 for poly(dT). Similarly, at 0.1 M salt, K_obs per site for poly(dT) exceeds K_obs for dT(pdT)₂₂ by 7-fold, for dT(pdT)₁₀ by 50-fold and for dT(pdT)₆ by 700-fold. We interpret the reductions in K_obs and |S_aK_obs| with decreasing |Z_D| as a significant CEE that causes binding to the terminal regions of a nucleic acid to be weaker and less salt dependent than interior binding. We analyze long oligonucleotide-KWK₆ binding data in terms of a trapezoidal model for the local (axial) salt cation concentration on single-stranded DNA to estimate the size of the CEE to be at least seven phosphates on each end at 0.1 M salt.

INTRODUCTION

Oligonucleotides are regularly used as models for polymeric nucleic acids in a wide range of applications, including NMR and crystallographic structural studies, spectroscopic investigations of physical properties, and in the thermodynamic characterization of processes, such as conformational changes and binding interactions. To relate studies of oligonucleotides to those of polymeric nucleic acids, it is necessary to understand how oligomers differ from polymeric nucleic acids. A major source of such differences is the increased contribution of end effects to the behavior of oligonucleotides versus polynucleotides. Two examples are fraying of helices at their ends and end binding modes of ligands to DNA. Another effect, termed the ‘Coulombic end effect’ (CEE), is important for charge–charge interactions with other species, including proteins, DNA-binding drugs, cationic peptides and salt ions. CEEs are particularly important determinants for the relative stabilities of hairpin and dimer duplex forms of a self-complementary (palindromic) DNA or RNA sequence (1,2).

Many in vivo and in vitro processes involve oligocationic ligands and/or oligomeric nucleic acids. Are the effects of salt concentration on the thermodynamics of these processes different for oligomeric and polymeric nucleic acids at physiological salt concentration? Most physiological functions of RNA and DNA directly involve binding or folding and are therefore very sensitive to [salt]. Short (oligomeric) RNA structures and their conformational transitions play important roles in RNA function in vivo. CEEs should be significant in all processes involving small RNAs, including binding of oligomeric RNA strands to polymeric or oligomeric nucleic acids in the mechanism of gene regulation, silencing and ribozyme catalysis (3). Recently discovered small (22 nt) interfering RNAs (siRNAs) bind to the complementary portion of their target mRNA and tag it for degradation (4). CEEs are predicted to be more important for many polymeric RNA conformations than for DNA because RNA is folded in short secondary and tertiary structures of higher charge density and radius, e.g. tRNA. Short hairpins in such structures are often protein binding sites (5–7). Anomalously, small [salt] dependences of the binding constant have been reported for the binding of proteins to ends of short telomeric DNA (8) and in the binding of cationic (+6) neomycin and other amino glycosides to a short 27 nt RNA hairpin containing the conserved A site in the 16S RNA of the 30S ribosome subunit (9).

Three experimental approaches, and corresponding nonlinear Poisson-Boltzmann (NLPB) and Monte Carlo (MC) calculations, have been used to characterize CEEs. ²³Na-NMR on a 20 bp oligonucleotide duplex showed a much smaller relaxation enhancement than for 160 bp double-stranded DNA (dsDNA), consistent with a smaller average local Na⁺ concentration at the surface of the 20-mer than for 160 bp DNA, as predicted by NLPB analysis for a cylindrical model of the DNA (10). Effects of oligonucleotide length (number of phosphate charges) on the [salt] dependence of the melting temperature T_m of helical nucleic acids have been characterized [(2) and references therein], as have the effect of the length of both an oligocation ligand and the nucleic acid lattice on the [salt] dependence of the binding constant K_obs [(11–23) and references therein].

Non-specific binding to polymeric DNA or RNA of a series of oligocationic peptides (13–18), polyamines (19) and cobalt hexammine (20), spanning the range of ligand charge 2 ≤ |Z_L| ≤ 10, have been investigated extensively. In general, binding is largely Coulombic. At high [salt] (∼0.5 M) where binding of these cationic ligands is weak, K_obs is small (typically of order unity) and insensitive to oligocation charge (|Z_L|). At lower [salt], K_obs exhibits a very strong power dependence on [salt] with an exponent (SK_obs ≡ ∂lnK_obs/∂ln[salt] or S_aK_obs ≡ ∂lnK_obs/∂lna_±) proportional to the oligocation valence [SK_obs ≈ −0.9Z_L for binding to polymeric ds nucleic acids and SK_obs ≈ −0.7Z_L for binding to polymeric single-stranded (ss) nucleic acids]. Thus, as [salt] increases, K_obs decreases strongly, approaching unity when extrapolated to 1 M salt. Record et al. [(21); see (12) for a review] used an approximate analytic polyelectrolyte theory to analyze SK_obs of these experiments and to conclude that salt ion release is the driving force for binding as [salt] is reduced. In this analysis, the authors proposed that ion release from the short oligocation L^Z+ contributed much less to SK_obs than that from polyanionic DNA as a result of a CEE for L^Z+. Only recently this proposal has been tested.

Zhang et al. (22) compared binding of an oligocation (KWK₆) to a polymeric and oligomeric dT nucleic acids. At 0.1 M salt, binding of the octacationic oligopeptide to a site on polymeric dT was between one and two orders of magnitude stronger than to a site on dT(pdT)₁₀, whereas |S_aK_obs| was between 50 and 100% larger for poly(dT) than for dT(pdT)₁₀. Conversely, K_obs for KWK₆ binding to the oligomer versus to the polymer were similar at high salt (>0.4 M Na⁺). Analysis of these results led Zhang et al. (22) to propose that ∼75% of S_aK_obs for KWK₆ binding to poly(dT) comes from ion release from the DNA polyelectrolyte, and the remaining 25% from ion release from KWK₆ at 0.1 M salt. Later work (23) demonstrated that affinities and the magnitudes of [salt] dependences of L⁸⁺ binding to DNA oligomers (with 15, 39 and 69 charges) decreased monotonically as the DNA charge (and length) decreased.

Despite the extant experimental evidence for the significance of CEEs, their importance at experimental salt conditions is not widely recognized and is still debated, as evidenced by the presence of opposing views in Chapters 8 and 11 of a current treatise on nucleic acids (24). This controversy has been summarized recently (2). NLPB calculations and analysis of experimental data for conformational transitions of hairpin (one-strand) and two-stranded DNA oligomers at 0.01–1 M 1:1 salt show that CEEs are an important determinant of the ln[salt] derivative (ST_m) of the transition temperature T_m in this [salt] range, and that the CEE explains the different dependences of ST_m on DNA helix length (|Z_D|) for hairpin and two-stranded oligomeric DNA helices (2).

The work presented here quantifies the binding thermodynamics of KWK₆ (L⁸⁺) with a series of short dT-oligomers (6 ≤ |Z_D| ≤ 22) to characterize the transition from polyelectrolyte to oligoelectrolyte behavior. We observe that the per site binding constant K_obs and its salt activity (a_±) derivative, S_aK_obs, decrease strongly with decreasing number of phosphates per oligonucleotide for lengths |Z_D| ≤ 22. The monotonic dependence of S_aK_obs on the number of DNA residues (charges) in oligocation binding processes provides a direct experimental approach to quantify the CEE and demonstrate its importance for ligand–nucleic acid interactions. We develop a qualitative model to describe the salt dependence of oligolysine–DNA association on the basis of predicted trapezoidal (parabolic) axial profile of ion accumulation around the DNA lattice for long (short) oligonucleotides. Analysis of previously published ‘long’ oligomer binding data in terms of this model indicates that the CEE spans at least 7 nt at each end of a ssDNA at 0.1 M [salt]. In a forthcoming paper, we present a unified analysis of experimental data of the current paper and previous results (22,23) that provides a parametric predictive functional form of the dependence of S_aK_obs on DNA charge |Z_D|, and quantitatively relate the |Z_D|-dependence of S_aK_obs to the reduced salt cation accumulation characteristic of the CEE.

MATERIALS AND METHODS

Buffers and reagents

All reagents used were reagent grade, purchased from Sigma Chemical Company (St Louis, MO), Fisher Scientific (Pittsburgh, PA) or Aldrich Chemical Company, Inc. (Milwaukee, WI). All solutions were prepared with 18 MΩ cm⁻¹ deionized water. All DNA and peptide solutions used in the titrations described below contained 0.2 mM Na₂EDTA, 5 mM sodium cacodylate, pH 6.0 and enough sodium acetate (‘NaOAc’) to bring the total salt concentration to the indicated salt concentration.

Peptide

KWK₆-NH₂, (K, l-lysine; W, l-tryptophan), was synthesized using a Perceptive Biosystems Pioneer Peptide Synthesizer with standard Fmoc (fluorenyl-9-methoxycarbonyl) pentafluorophenyl chemistry, purified via high-performance liquid chromatography (HPLC) (see Supplemental Material), and characterized using matrix-assisted laser desorption ionization mass spectroscopy (Biochemistry Instrumentation Facility, Madison, WI). Stock peptide concentrations were determined spectrophotometrically from the tryptophan absorbance at 280 nm in 6 M guanidinium chloride using ɛ₂₈₀ = 5690 M⁻¹ cm⁻¹ (25). The extinction coefficients of the KWK₆ dissolved in the buffer described above were then experimentally measured to calculate the inner-filter corrections for the fluorescence titrations (, ). The resulting oligopeptide inner-filter correction is small relative to the corresponding correction due to the DNA concentration (see below).

Single-stranded oligo(dT) DNA

The oligonucleotides dT(pdT)₆, dT(pdT)₁₁, dT(pdT)₁₄ and dT(pdT)₂₂ were synthesized using an Applied Biosystems 391 PCR-mate automated synthesizer with phosphoramidite chemistry and then purified to >98% homogeneity by using polyacrylamide gel electrophoresis as described elsewhere (26,27). Stock solutions of these oligonucleotides were prepared by dialysis, first against a solution of 10 mM disodium phosphate, pH 6.0, 2 mM Na₂EDTA and 100 mM sodium chloride; followed by three sequential dialyses against 0.5 mM NaOAc at 4°C [SpectraPor dialysis tubing, 1000 MWCO for the dT(pdT)₂₂ and dT(pdT)₁₄ oligomers, and 100 MWCO for the dT(pdT)₁₁ and dT(pdT)₆ oligomers]. The DNA nucleotide concentration was determined from the 260 nm absorbance with a Beckman DU-600 spectrophotometer using an extinction coefficient of ɛ₂₈₀ = 8100 M⁻¹ (nucleotide) cm⁻¹ (28) with a multiplicative conversion factor |Z_D|/(|Z_D|−1) to convert into phosphate concentration, where |Z_D| is the number of phosphates in the oligomer. Extinction coefficients of each DNA were measured for use with the inner-filter corrections [, , at 0.075 M NaOAc, at 0.105 M NaOAc, at 0.035 M NaOAc and at 0.015 M NaOAc; in all cases]. At high DNA concentrations, the inner-filter correction can be as large as 20%.

Fluorescence titrations

Oligopeptide binding to oligo(dT) DNA was monitored by tryptophan fluorescence quenching with an SLM-Amino 8000C spectrofluorometer (Spectronic Instruments, Rochester, NY). The excitation wavelength was 296 nm with a bandpass of 4 nm, and the emission wavelength was 350 nm with a bandpass of 4 nm. These wavelengths were chosen to minimize the inner-filter corrections and DNA absorbance (29). Solutions of the oligopeptides (0.5–5.1 μM) and DNA (1–4 mM DNAP) used in the fluorescence titrations were prepared from freezer stocks and diluted to obtain identical buffer and salt concentrations (pH 6 in 5 mM sodium cacodylate, 0.2 mM Na₂ EDTA and enough NaOAc to bring the total Na⁺ concentration to 0.1 M Na⁺ [dT(pdT)₂₂, dT(pdT)₁₄, dT(pdT)₁₁], 0.075 M Na⁺ [dT(pdT)₁₁], 0.035 M Na⁺ [dT(pdT)₆] or 0.015 M Na⁺ [dT(pdT)₆].

Use of fluorescence spectroscopy in the determination of binding parameters

The extent of tryptophan fluorescence quenching is defined as

where F_obs is the observed fluorescence intensity and F₀ is the initial fluorescence intensity of the free ligand (i.e. oligopeptide). All fluorescence intensities were corrected for background fluorescence, dilution, inner-filter contributions and photobleaching effects as described above and elsewhere (22,29).

‘Reverse titrations’, where the peptide is titrated with DNA, were executed at fixed excess salt concentration to generate binding isotherms. Titrations were typically performed in duplicate or triplicate at 25°C over a range of oligopeptide concentrations (12–17 reverse titrations for each DNA length). At the conclusion of almost all reverse titrations, a ‘saltback titration’ was performed in which the equilibrated KWK₆–DNA solutions were titrated with a high salt solution (1.00 M NaOAc, 5 mM sodium cacodylate, pH 6, 0.2 mM Na₂EDTA; see Buffers and reagents). The increase in fluorescence (and therefore the decrease in the quenching, Q_obs) was monitored as the salt concentration of the solution increased. After all corrections were applied (i.e. background fluorescence, dilution, inner-filter, photobleaching of KWK₆ and photobleaching of the rhodamine reference), >97% of the original fluorescence signal of the free oligopeptide was recovered, indicative of complete reversibility of oligopeptide-DNA complex formation.

Analysis of the oligopeptide–DNA binding isotherms

Determination of equilibrium binding constants from fluorescence quenching

Ligand binding densities (ν) and the concentration of unbound oligopeptide ([P_F]) were calculated using ligand binding density function (‘LBDF’) analysis (29), a model-independent method to show that fluorescence quenching, Q_obs (Equation 1), is proportional to the concentration of bound peptide, [P_B], and thus proportional to binding density (ν = [P_B]/[D_T]; see Supplemental Material). [P_T] and [D_T] are the total molar concentrations of KWK₆ and of DNA phosphate, and Q_max, the maximum quenching, is attained when all peptide is bound (i.e. when [P_B]/[P_T] = 1). To calculate the average binding constant, K_obs, of KWK₆ with individual sites on dT(pdT)₂₂, dT(pdT)₃₉ and dT(pdT)₆₉, the dependence of ν on [P_F] was analyzed using a finite lattice model (23,30). This model incorporates anti-cooperativity for large ligand (overlap) effects but neglects CEEs and assumes that all potential binding sites have the same binding constant K_obs:

where

and

In Equations 2–4, Ω_j is the number of arrangements of j ligands (with net charge, |Z_L|) on a DNA lattice with |Z_D| phosphates, to a maximum of J_max ligands bound. Binding modes in which a peptide extends beyond the end of the DNA lattice are disallowed. The partition function Σ is the sum over all states of binding (30). The Epstein model assumes that there are ||Z_D| − |Z_L|| + 1 potential binding sites with no overhanging ligands and assumes that K_obs is the same for all sites, regardless of site position or the presence of other bound ligands. Because this isotherm neglects differences in binding affinity caused by CEEs near the ends of the lattice, the zero binding density value of K_obs is interpreted as an average over all possible sites (see Discussion).

Titration data for the oligomers from dT(pdT)₆ to dT(pdT)₁₅ were fit to a 1:1 binding model (Equation 5) [mathematically equivalent to the Epstein finite lattice binding model (Equation 2)]:

The (‖Z_D| − |Z_L‖ + 1) term accounts for the statistical degeneracy (number of ways) of binding the shorter oligomer to the longer one, assuming as above that all sites have the same K_obs, and that no binding occurs with overhanging ends.

The nonlinear least squares program NONLIN (31) was used to fit Equations 2 and 5 to the fluorescence quenching data obtained from reverse titrations via the LBDF proportionalities (see Supplemental Material). K_obs was fit with Q_max fixed to the LBDF value (Table 1) and also with Q_max floated (Table SII).

Table 1. Fitted values of the binding constants K_obs, salt derivatives (SK_obs and S_aK_obs), and 1 M intercepts (K₀) for the binding of KWK₆ to dT-mers using LBDF values of Q_max.

dT-mer	|ZD|	Qmax (%)	log10 Kobs ([Na+] = 0.105 M)	–SKobsa	log10 K0a (1 M Na+)	–SaKobsa	log10 K0a (a± = 1 M)
poly(dT)	169b	90 ± 2c	6.45 ± .33d	6.36 ± .21ce	0.27 ± .15ce	6.54 ± .28ce	−0.70 ± .22ce
dT (pdT)69	69f	93 ± 2c	6.23 ± .16	5.83 ± .11	0.43 ± .12	6.14 ± .14	−0.50 ± .12
dT (pdT)39	39f	94 ± 2	5.98 ± .10	5.63 ± .10	0.50 ± .07	5.93 ± .12	−0.40 ± .10
dT (pdT)22	22	95 ± 1	5.60 ± .04	5.26 ± .22	0.48 ± .17	5.54 ± .16	−0.39 ± .14
dT (pdT)15	15f	93 ± 2	5.33 ± .07	4.77 ± .27	0.60 ± .23	5.05 ± .22	−0.19 ± .30
dT (pdT)14	14	92 ± 1	5.24 ± .05	4.80 ±.33	0.47 ± .28	5.08 ± .38	−0.32 ± .37
dT (pdT)11	11	86 ± 1	4.91 ± .03	4.20 ± .31	0.74 ± .26	4.47 ± .36	0.03 ± .35
dT (pdT)10	10b	90 ± 2	4.72 ± .04	3.75 ± .12	0.95+0.05−0.10	3.96 ± .15	0.34 ± .14
dT (pdT)6	6	76 ± 1g	3.59 ± .29d	2.64 ± .20h	1.01 ± .21	2.85 ± .23	0.53 ± .23

Errors are reported with 95% confidence intervals unless otherwise noted (see Materials and Methods for details of Q_max and log K_obs error determination). Fits to the reverse titration isotherms are shown in Figure 1 and to the salt dependence are in Figure 2A and B.

^aS_aK_obs, SK_obs and logK₀ were determined within 0.083 M ≤ a_± ≤ 0.19 M (0.105–0.25 M [Na⁺]) using the LBDF determined Q_max, unless otherwise indicated.

^bSaltback data (15) reanalyzed within the range considered here.

^cValues determined at 0.196 M Na⁺ because binding is too tight at 0.106 M Na⁺ for accurate estimation.

^dLinearly extrapolated to 0.105 M [Na⁺] using Equation 6.

^eS_aK_obs, SK_obs and logK₀ were determined within 0.15 M ≤ a_± ≤ 0.19 M (0.195–0.25 M [Na⁺]).

^fSaltback data (16) reanalyzed within the range considered here.

^gQ_max value for dT (pdT)₆ at 0.035 M Na⁺. dT (pdT)₆ at 0.015 M Na⁺ has .

^hTwo point determination of S_aK_obs and logK₀. logK_obs = 4.82 ± 0.04 at 0.035 M Na⁺ and logK_obs = 5.79 ± 0.06 at 0.015 M Na⁺. The reported error in logK_obs was calculated via propagation of the logK_obs error at these two salt concentrations.

Error determination in analysis

For each DNA oligomer, reverse titrations spanning the range of oligopeptide concentrations 0.5–5.1 μM were performed in replicate, as described above. All fitted parameters are reported with 95% confidence intervals unless otherwise indicated. One such exception is in the log K_obs values determined directly from reverse titrations. Because of the high number of experimental points involved (typically 60 points or more), fitted errors in log K_obs were usually well below 0.5%. To get a better estimation of error in log K_obs, fits of the reverse titration data were performed constraining Q_max at its upper bound value and its lower bound value. The error in log K_obs was then estimated by using the widest possible error range (i.e. using the lower bound logK_obs found at the upper Q_max fit and the upper bound logK_obs value resulting from the lower bound Q_max fit). Even using this extreme definition of error in logK_obs (reported in Tables 1 and SII), errors in log K_obs are in the order of 1%.

We conclude that 95% confidence interval as reported in Tables 1 and SII provide a realistic statement of the uncertainty in SK_obs ≡ ∂ln K_obs/∂ln[salt] and S_aK_obs ≡ ∂ln K_obs/∂lna_±. When it was necessary to interpolate or extrapolate values of logK_obs using Equation 6, error in S_aK_obs (SK_obs) and in logK₀ was propagated to estimate the error in logK_obs.

Analysis of the salt dependence of log K_obs or ΔG_obs^o

Over the range of salt concentration examined, the dependence of K_obs on salt (mean ionic) activity for each oligonucleotide was well described as a power law dependence with a [salt]-independent exponent. The K_obs (Equations 2 and 5) necessary to exhibit the observed ν (via Q_obs and Equations S1–S3) at the known peptide and DNA concentrations present in the solution was calculated at each point of the saltback titration. The exponent S_aK_obs and the extrapolated (a_± = 1 M) reference binding constant K₀ were then determined from the [salt] dependence of K_obs (12,21),

The results from the NONLIN least-squares fitting analysis are reported for both fitted values of Q_max (Table SII) and from LBDF analysis (Table 1). The S_aK_obs data reported here are the linear least squares fits using 95% confidence intervals (see above) of the logK_obs versus log a_± for data within the salt range of 0.1–0.25 M unless specified otherwise.

The oligopeptide tryptophan fluorescence was independent of [NaOAc] >0.07 M, but decreases monotonically by 20% in the range 0.006–0.07 M NaOAc in the absence of DNA (data not shown). As a result, saltback titrations for dT(pdT)₆ are difficult to interpret unambiguously. Therefore, S_aK_obs and logK₀ were estimated from Equation 6 using two well-determined values of K_obs (from data of 12 reverse titrations) at 0.015 and 0.035 M [Na⁺]. K_obs at 0.105 M Na⁺ for dT(pdT)₆ was then obtained from Equation 6 assuming S_aK_obs to be independent of salt concentration in this range.

RESULTS

Reverse and saltback titrations to quantify KWK_6^–oligo(dT) binding: behavior of Q_obs and Q_max

Tryptophan fluorescence quenching was monitored during reverse titrations and saltback titrations (see Materials and Methods) to determine the thermodynamics of binding of the octacationic oligopeptide ligand KWK₆ to ssDNA with |Z_D| equal to 6,11,14 and 22. Ligand binding density functional analysis (‘LBDF’) (29) demonstrates that the corrected fluorescence quenching, Q_obs, of KWK₆ in the presence of the oligonucleotides studied here is proportional to the ratio of bound ligand to total ligand ([P_B]/[P_T]) (see Supplemental Material Figure S1). This model-independent result, analogous to that obtained previously for poly(dT) (17,22) allows the calculation of ligand binding density directly from the fluorescence quenching data. For dT(pdT)₂₂ and dT(pdT)₁₄ at 0.105 M Na⁺, dT(pdT)₁₁ at 0.105 M and 0.075 M Na⁺ and dT(pdT)₆ at 0.015 and 0.035 M Na⁺, values of Q_max determined from extrapolation to the condition where all the peptide is bound ([P_B]/[P_T] = 1) (Table 1) were the same within error as values of Q_max (Table SII in Supplemental Data) found by nonlinear least-squares fitting of reverse titration data to the Epstein or 1:1 binding models as appropriate (cf. Figure 1 and Materials and Methods). As part of this work, previously published data (22,23) for poly(dT), dT(pdT)₆₉, dT(pdT)₃₉, dT(pdT)₁₅ and dT(pdT)₁₀ were reanalyzed. The differences between fitted versus LBDF determinations of Q_max were within 1 SD for all cases except dT(pdT)₁₅ at 0.106 M Na⁺.

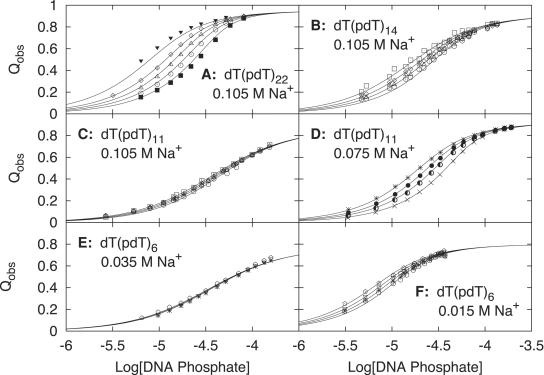
Figure 1.

Reverse titrations. Reverse titration binding isotherms obtained at constant ligand concentration by monitoring fluorescence quenching as a function of increasing DNA concentration at pH 6.0 and 25°C. The solid line curves are the theoretical fits to the Epstein model for the specified ligand concentrations using a site size n = 8 and the K_obs and LBDF Q_max values denoted in Table 1. (A) KWK₆ binding to dT(pdT)₂₂ at 0.105 M Na⁺ and initial peptide concentrations of 0.49 μM (black inverted triangles), 1.03 μM (open diamonds), 1.48 μM (open triangles), 2.06 μM (open circles) and 2.94 μM (black squares). (B) KWK₆ binding to dT(pdT)₁₄ at 0.105 M Na⁺ and initial peptide concentrations of 0.59 μM (open squares), 1.03 μM (open diamonds), 1.48 μM (open triangles) and 2.06 μM (open circles). (C) KWK₆ binding to dT(pdT)₁₁ at 0.105 M Na⁺ and initial peptide concentrations of 0.59 μM (open squares), 1.03 μM (open diamonds), 1.48 μM (open triangles) and 2.06 μM (open circles). (D) KWK₆ binding to dT(pdT)₁₁ at 0.075 M Na⁺ and initial peptide concentrations of 1.73 μM (asterisks), 2.54 μM (black circles), 3.40 μM (half moons) and 5.08 μM (crosses). (E) KWK₆ binding to dT(pdT)₆ at 0.035 M Na⁺ and initial peptide concentrations of 0.97 μM (open pentagons), 1.29 μM (open inverted triangles) and 1.62 μM (asterisks). (F) KWK₆ binding to dT(pdT)₆ at 0.015 M Na⁺ and initial peptide concentrations of 0.98 μM (open pentagons), 1.30 μM (open inverted triangles), 1.60 μM (asterisks) and 1.94 μM (open circles).

Q_max for KWK₆-oligo(dT) complexes may depend on DNA length for the shorter lengths studied here. Considering only values of Q_max determined at 0.105 M Na⁺, the quenching upon binding of KWK₆ to dT(pdT)₁₁ and dT(pdT)₁₀ (86 ± 1 and 90 ± 2%, respectively) are smaller than the average Q_max value (93.5 ± 1.3%) observed at higher |Z_D| (Figure S2). Values of Q_max for binding of KWK₆ to dT(pdT)₆ at 0.015 and 0.035 M NaOAc (80 and 76%, respectively) are smaller than observed for longer dT-oligomers, but a significant [salt] dependence of peptide fluorescence and Q_max below 0.1 M salt contributes to this effect.

Reverse titrations of KWK₆ with DNA at constant [salt]

Figure 1 shows reverse titration binding isotherms for KWK₆ binding to dT(pdT)_|ZD| (where |Z_D| = 22, 14, 11 and 6) at the indicated salt concentrations. Q_obs, directly proportional to the percentage of bound peptide (Equation S1), increases as the total DNA phosphate concentration increases. Eventually, at high [DNA], the fluorescence quenching reaches a plateau, indicating saturation of the peptide. At higher initial peptide concentration, the titration curves as detected by fluorescence quenching shift to higher DNA concentration and sharpen (Figure 1). Complexes with weaker binding affinity (e.g. dT(pdT)₁₁–KWK₆ versus dT(pdT)₂₂–KWK₆, both at 0.105 M Na⁺) require higher [DNA] to achieve saturation at a given KWK₆ concentration. As the binding affinity decreases, isotherms differing in initial oligopeptide concentration coalesce (compare Figure 1A versus C): as K_obs decreases, the number of complexes becomes less sensitive to the concentration of DNA present because binding is weaker.

The curves represent global nonlinear fits (Table 1) to the non-cooperative Epstein binding model (Equation 2) for dT(pdT)₂₂ or to the mathematically equivalent 1:1 binding model (Equation 5) for the shorter oligomers. LBDF Q_max values (Table 1) were used to calculate the average binding density (Equations 2, 5 and S2) in these determinations. In all cases, especially for the shorter oligos (|Z_D| ≤22), global fits using the Epstein isotherm and the 1:1 binding model describe the reverse titration data extremely well. Values of the per site binding constant K_obs at zero binding density obtained from this fits are an average for all |Z_D|−7 sites on the DNA oligomer. As |Z_D| increases, the per site K_obs at fixed [salt] increases dramatically (Table 1). K_obs at 0.105 M NaOAc is 5-fold larger for KWK₆ binding to |Z_D| = 22 than to |Z_D| = 11 and 20-fold larger for binding to |Z_D| = 11 relative to the extrapolated value of K_obs of |Z_D| = 6 at this salt concentration. This decrease in K_obs with decreasing |Z_D| indicates a strong CEE in L⁸⁺ binding at 0.1 M salt (see Discussion).

[Salt] dependence of KWK₆–DNA binding

The complexes formed in each reverse titration shown in Figure 1 were titrated with buffered 1 M NaOAc (see Materials and methods and Supplementary Material). Complexes dissociated with increasing [salt] as indicated by a monotonic decrease in the fluorescence quenching. At sufficiently high [salt], Q_obs is reduced to <2% for all oligo(dT) lengths studied, indicating that complex formation is fully reversible and that binding is highly [salt] dependent, consistent with previous observations (17,22,23,29).

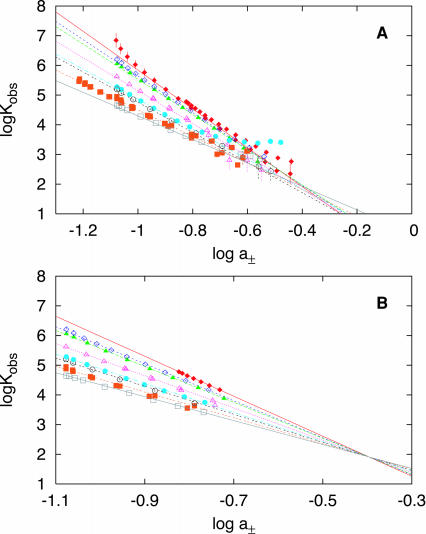
K_obs is determined from Q_obs as a function of [salt] via the Epstein finite lattice isotherm or the 1:1 binding model and LBDF-derived binding densities (Figures 1 and S3). Figures 2 and S4 show the variation of logK_obs with salt activity and [salt]. Values of |S_aK_obs|, evaluated over a specified [salt] range (Table 1), decrease from the polymer limit as DNA length decreases. In Figure 3, as |Z_D| decreases, |S_aK_obs| (plotted as a fraction of the experimental value of |S_aK_obs| for polymeric dT) exhibits a hyperbolic dependence on |Z_D|. For large |Z_D| (|Z_D| ≥ 39), |S_aK_obs| decreases gradually with decreasing |Z_D|: we refer to such oligomers as long (see Discussion). The decrease becomes much more pronounced for the shorter DNA lengths studied here (|Z_D| ≤ 22): we refer to such oligomers as short (see Discussion). These same data, when plotted versus reciprocal number of DNA charges, is approximately linear over the full range studied, and extrapolation to infinite DNA length (|Z_D|→∞) provides an independent determination of the S_aK_obs for poly(dT) (−6.4 ± 0.1) (cf. Figure 3, inset).

Figure 2.

S_aK_obs analysis. Log-log plot of K_obs versus mean ionic activity (a_±) of NaOAc for KWK₆ binding to poly(dT) (red diamonds), dT(pdT)₆₉ (open purple diamonds), dT(pdT)₃₉ (green triangles), dT(pdT)₂₂ (open pink triangles), dT(pdT)₁₅ (light blue circles), dT(pdT)₁₄ (open black circles), dT(pdT)₁₁ (orange squares) and dT(pdT)₁₀ (open gray squares). The lines in (A) represent the least squares linear fits of all data between 0.1 and 0.25 M NaOAc using the parameters summarized in Table 1. The solid and dashed lines in (B) represent the global fits of the indicated data to Equation 6, constrained to intersect at a single extrapolated value (see Table SIII in the Supplementary Material).

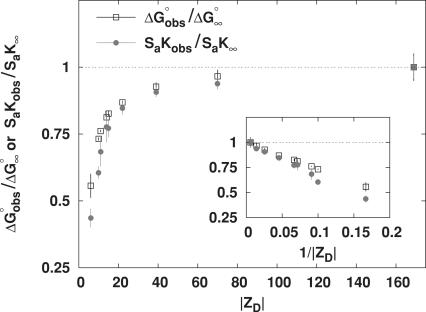
Figure 3.

Dependence of 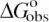(0.1 M Na⁺) and S_aK_obs on number of DNA charges |Z_D|. Values of 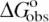at 0.1 M Na⁺ (open squares) and S_aK_obs (circles), normalized by the corresponding quantities for binding of KWK₆ to poly(dT), are plotted against the number of DNA charges |Z_D|. Reanalysis of data published previously (22,23) and current work are detailed in Table 1. S_aK_obs was determined as the slope of Equation 6 fit in the loga_± range of −1.1 to −0.72 (∼0.1–0.25 M [Na⁺]; cf. Figure 2B). All 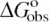values were determined from reverse titrations with the exception of dT(pdT)₆, for which 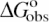was obtained by linear extrapolation of the logK_obs vesus loga_± to 0.105 M Na⁺ (Equation 6). The inset plots the same data versus 1/|Z_D|.

For each dT(pdT)_|ZD| oligomer, |S_aK_obs| decreases with increasing [salt] above ∼0.3 M Na⁺. At higher [salt], values of K_obs for the binding of KWK₆ to DNA oligomers with different |Z_D| appear to converge into a common curve (independent of Z_D). Nevertheless, the data are well fit in the range of 0.1–0.25 M salt by a constant S_aK_obs, and thus values for S_aK_obs and the extrapolated logK_obs at a_± = 1 M (logK₀) were determined using linear least squares analysis. Figure 2A suggests that the linear extrapolation of the low [salt] range logK_obs versus log[salt] data to higher [Na⁺] may intersect at a common point within the uncertainty of the fit. If the data are globally constrained to have a common intersection point (Figure 2B), the resulting S_aK_obs values (Table SIII) are within error of those analogously determined from fitting individual KWK₆-oligomers (Table 1). Allowing for the possibility of two intersection points, e.g. one for longer length DNA [poly(dT)–dT(pdT)₃₉] and another for shorter lengths [dT(pdT)₂₂–dT(pdT)₁₀], does not significantly improve the fit. The intersection on Figure 2B occurs at a_± = 0.40 ± 0.04 M Na⁺ ([Na⁺] = 0.53 M) with a logK_obs of 1.91 ± 0.20. This point represents an extrapolated reference state describing the DNA-length independent contribution to the binding of KWK₆ to a ssdT-oligomer. Interestingly, the analogous fitting of logK_obs versus log[Na⁺] (Figure S4) results in the same reference point (logK_ref = 1.89 ± 0.20, [Na⁺]_ref = 0.55 ± 0.07 M), although analysis on the mean activity scale exhibits a better statistical fit on the basis of the variance. Studies of binding of a series of oligocationic ligands (13,17) to polymeric nucleic acids also yield a common intersection point between 0.5 and 1 M salt.

Values of S_aK_obs for poly(dT), dT(pdT)₆₉, dT(pdT)₃₉, dT(pdT)₁₅ and dT(pdT)₁₀ reported in Table 1 differ in some cases from values published previously (22,23) because a smaller salt range was considered (0.1–0.25 versus 0.1–0.3 M Na⁺) for consistency with other oligo(dT) lengths investigated in this study.

Dependence of ΔG_obs^o on |Z_D|

Values of at 0.105 M Na⁺ and 25°C, either determined directly by reverse titration (Figure 1) or via Equation 6 using S_aK_obs and log K₀, were normalized by the corresponding value for poly(dT) and plotted as a function of DNA charge in Figure 3. The general features in the plot of versus |Z_D| at 0.105 M Na⁺ are similar to those seen for S_aK_obs/S_aK_∞ versus increases strongly with increasing |Z_D| when |Z_D| ≤ 15, but is only weakly dependent on DNA length for oligonucleotide lengths |Z_D| ≥ 39 phosphates. As |Z_D| increases above |Z_D| = 22, (expressed per site on the DNA lattice) gradually approaches for poly(dT). Above |Z_D| = 39, both (0.1 M) and S_aK_obs are within uncertainty of the values for poly(dT). Deviations of from the poly(dT) limit are approximately linear in 1/|Z_D|, as are deviations of S_aK_obs from the poly(dT) limit (Figure 3, inset).

The range of |Z_D| where is strongly dependent on |Z_D| is the same as that where S_aK_obs is strongly dependent on |Z_D|. Thus, short oligomers defined above in terms of strong effect of length (|Z_D|) on K_obs exhibit strong effect of length on the salt dependence S_aK_obs as well. In Discussion, we relate this behavior to the presence (for long oligomers) or absence (for short oligomers) of a polyion-like interior region in the surface axial counterion distribution.

DISCUSSION

The Coulombic end effect

The Coulombic interactions of nucleic acids with salt ions in solution create strong radial gradients of ion density, accumulating salt cations and excluding salt anions in the vicinity of the nucleic acid. The binding of an oligocationic ligand changes these gradients and gives rise to the remarkably large dependence of the equilibrium constant on [salt]. Binding constants of oligiocationic ligands to polymeric nucleic acids exhibit power dependences on [salt] (cf. Equation 6) with exponents SK_obs, which are proportional to the ligand charge (11,12). For example, the K_obs for binding L⁸⁺ to polymeric ss- or ds-DNA is predicted to change by 5–7 orders of magnitude for each decade change in [salt]. A general, model-independent thermodynamic analysis (12,32) connects the [salt] derivative SK_obs of a charged biopolymer process to the change in salt ion preferential interaction coefficients

where ΔΓ is the change in preferential interaction coefficients describing interactions of salt ions with product and with reactants, and Δ|Z| = |Z_LD| − |Z_D| − |Z_L|, where Z_LD, Z_D, and Z_L are charges of ligand-DNA complex (LD), DNA (D) and ligand (L), respectively (12,32). The difference ΔΓ describes the redistribution of the salt ions caused by the local neutralization of peptide and DNA charges upon complexation. This redistribution is the molecular origin of the salt ion release upon binding (12,33).

The Coulombic interactions of salt ions and ligands with phosphates in the terminal regions of a nucleic acid are very different than those involving interior phosphates of a long nucleic acid (1,2,12,22,23,33–35). Binding of a cationic ligand to the terminal regions is predicted (33) and deduced from experiment [Figure 3 and (22,23)] to be less [salt] dependent and weaker at low [salt] than interior binding. We call these differences CEEs. The CEE should be especially important when comparing effects of [salt] on processes involving short nucleic acid oligomers (lacking a polyelectrolyte-like interior region, as discussed below) with those of the corresponding polyion. CEEs cause the strong dependencies on DNA chain length (|Z_D|) of SK_obs for oligocation binding reported here [see also (22,23)]. Computational (both GCMC and NLPB) analyses (22,23,33) show that the strong reduction in S_aK_obs with decreasing |Z_D| for short oligos is a consequence of the CEE, arising from the reduced cation accumulation at the ends of all nucleic acids, and in the interior of sufficiently short nucleic acids.

CEE: axial dependence of surface concentrations of salt cations, anions; consequences for average K_obs, SK_obs

Monte Carlo simulations (33,36) and NLPB calculations [(2,35) and Figure S6] which model DNA as a primitive cylinder show that the salt cation concentration in the vicinity of the DNA surface is very high and uniform in the interior, but falls off strongly in the terminal regions of sufficiently long oligomers, resulting in a ‘trapezoidal’ axial profile of the local salt cation concentration. For these long oligomers, as |Z_D| increases, the length of the interior region increases, but the lengths of the terminal regions remain the same. The number of DNA phosphates charges (N_e) in each terminal region of a long oligomer does not change as |Z_D| increases. Short oligomers (e.g., less than 20 phosphates for ssDNA at 0.1 M salt [see Figure S6 and (36)] exhibit a ‘parabolic’ axial cation concentration distribution where the surface cation concentration in the interior region of DNA is predicted to increase with increasing number of phosphates (charges). Above ∼20 phosphates, a polyion-like interior is predicted.

In complexation, the salt ion concentration gradients in the vicinity of the DNA and the peptide are reduced, corresponding to a net salt ion release that drives complexation as the bulk salt concentration is reduced (33). If the DNA is long enough to have polyion-like interior region of sufficient length to bind the ligand, binding to those interior sites will exhibit the same K_obs and SK_obs as binding to the interior of a polyanionic DNA. The N_e terminal sites at each end of this long DNA include one or more phosphates in the terminal region of ion accumulation. As a consequence, binding to such sites exhibits less than the polyion level of ion release, and therefore is characterized by a weaker K_obs and a smaller contribution to SK_obs. The closer the terminal site is to the DNA terminus, the weaker the binding. |Z_L| + 2N_e (two full terminal regions of N_e phosphates each, and an interior of |Z_L| phosphates) is the minimal DNA chain length necessary to have at least one site that binds a Z_L-charged ligand with polyion values of K_obs and SK_obs. DNA oligomers with less than |Z_L| + 2N_e charges lack any such interior polyion-like site, and thus complexation at all sites is characterized by smaller K_obs and |SK_obs|. Because most of the binding of ligands to long oligos is to the polyion-like sites in the interior (and not to the weaker sites in the terminal regions), DNA oligomers with |Z_D| > |Z_L| + 2N_e exhibit only gradual reductions in overall (average) K_obs and |SK_obs|as |Z_D| decreases. Oligomers shorter than |Z_L| + 2N_e show strong reductions in K_obs and |SK_obs| with decreasing |Z_D| because in this length range binding to interior sites is weaker and releases fewer salt ions. For our experiments, the transformation from a strong to a weak dependence of K_obs and S_aK_obs on |Z_D| (Figure 3) occurs between dT(pdT)₃₉ and dT(pdT)₂₂; i.e. 22 < |Z_L| + 2N_e < 39 (for both logK_obs and SK_obs), suggesting that N_e is in the range of 7–15 since |Z_L| = 8 for KWK₆. The analysis in the following section tests this picture.

Implications for axial dependence of L^Z+ binding constant K_i and for length (|Z_D|) dependence of average K_obs, SK_obs at zero binding density

The trapezoidal model for the binding of L^Z+ to a long oligonucleotide (|Z_D| ≥ 39) partitions binding into two regimes: one consisting of the interior sites (those exhibiting polyelectrolyte binding affinity and forming the plateau region of the trapezoid), and the other made up of the two terminal regions of N_e binding sites each, where binding affinity decreases with increasing proximity to the termini of the DNA. If a DNA oligomer is long enough (|Z_D| ≥ |Z_L| + 2N_e), the interior sites demonstrate polymeric binding behavior, K_∞,

where PD_∞ is a complex of the peptide P at an interior DNA site and [D] and [P_F] are concentrations of free DNA and KWK₆ molecules. The trapezoidal model holds that all interior sites (as compared to the terminal sites described below) are identical and thus bind peptides with the same affinity, K_∞.

Binding of a peptide to a DNA near a terminus forms a complex PD_i, where i = 1 for a complex in which the peptide binds at the terminus of the nucleic acid, i = 2 for a complex starting at the second site from the end, and so on. In the low-binding density limit, the binding constant K_i for forming PD_i is

where K_i is always less than K_∞ for all sites i ≤ N_e away from a DNA terminus.

The zero binding density binding constants, K_obs, obtained from Epstein or 1:1 isotherms, are extrapolated values representing per site averages over all these potential oligocation binding sites. Neglecting binding modes where the peptide overhangs the nucleic acid, there are |Z_D| − |Z_L| + 1 = |Z_D| − 7 sites for KWK₆ (Z_L = 8) on the dT-oligomers with |Z_D| ≥ 8 phosphates. In the low-binding density (no multiple binding) limit, the relationship between K_obs and K_i is obtained from the McGhee-von Hippel definition of K_obs (37):

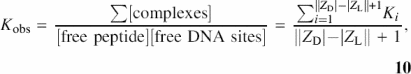
where the concentration of free lattice sites is (|Z_D| − |Z_L| + 1)[D] because there are (|Z_D| − |Z_L| + 1) sites on each DNA strand. The total concentration of complexes is a sum of all complexes, . Therefore, for long oligomers, K_obs is the weighted average of the polymeric interior sites and the terminal sites:

For oligomeric DNA strands long enough to exhibit an interior region with polymeric (polyelectrolyte) properties, ΣK_i is expected to be independent of |Z_D|. ΣK_i represents the sum of the binding constants for all binding sites in a single terminal region. Since the ΣK_i contribution to K_obs does not change for long oligomers, the long oligomer data can be easily analyzed as presented in the next section. However, such simplification is not possible for short oligomers because ΣK_i depends not only on the binding site i, but also on the DNA oligomer length |Z_D|. In a forthcoming paper, we develop a quantitative treatment that predicts K_i for both long and short DNA lengths. In the current analysis, we restrict consideration to long oligos only.

Behavior of K_obs, S_aK_obs as functions of |Z_D|, [salt]

In the binding of the KWK₆ octacation (L⁸⁺) to a dT oligoanion with |Z_D| negative charges, both the per site K_obs and |S_aK_obs| decrease strongly with decreasing |Z_D|, especially below |Z_D| = 39. Reduction of |Z_D| from 39 to 10 charges causes a 50% reduction in |S_aK_obs|. The behavior of logK_obs at 0.1 M salt mirrors that of S_aK_obs as seen in Figure 3 because the linearly extrapolated logK₀ intercepts are close to zero (Table 1). The small extrapolated K_obs seen at high salt concentrations is typical of non-specific interactions of oligocations (polyamines, oligolysines, etc.) with nucleic acid polyanions and indicates that salt ion release, quantified by S_aK_obs, represents the dominant driving force for complexation at low to moderate salt concentrations (11,12,14–17,21–23). Since K_obs is approximately independent of |Z_D| at high [salt], the variation in K_obs with |Z_D| at any lower [salt] is primarily a result of the variation of S_aK_obs with |Z_D|. Therefore, if we understand why S_aK_obs depends on DNA length, we can also understand the variation in K_obs.

If we assume that K_∞ = K_obs for |Z_D| = 169, Equation 11 predicts that the average number of sites at one end of a 39mer (|Z_D| = 39) is N_e = (7 ± 3) + ΣK_i/K_∞ at 0.2 M Na⁺ or N_e = (11 ± 4) + ΣK_i/K_∞ at 0.1 M Na⁺. Since ΣK_i/K_∞ must be a positive number, N_e must exceed 7 phosphates (∼25 Å) at 0.1 M salt.

At intermediate lengths (|Z_D| ≈ |Z_L| + 2N_e), binding of the oligocation to a significant portion of the DNA sites is predicted to be weaker than polymeric binding. Therefore, as the total number of sites decreases, the contribution of end sites increasingly dominates the average per site K_obs, as seen in Figure 3 and reported in Table 1. Even if the ΣK_i/K_∞ term is neglected at 0.2 M Na⁺, the first oligonucleotide long enough to have a single polymeric site is |Z_D| = (|Z_L| + 2N_e) ≈ 22 ± 6 for KWK₆ binding to ssDNA. Given these results, dT(pdT)₂₂ (|Z_D| = 22) is near the threshold of exhibiting polymeric binding. This is consistent with the results shown in Figure 3, where dT(pdT)₂₂ is at the transition between long and short oligomer binding behavior. Conversely, if there were no CEEs under these conditions, the ΣK_i/K_∞ term would equal N_e because there would be N_e polymeric sites for N_e phosphates. In this case, K_obs = K_∞ regardless of DNA length, in contrast to what is seen in Figure 3.

The number of end phosphates in the above analysis is greater than that estimated previously (23) because of the use of a trapezoidal (multistate) model instead of a two-state model for binding sites. The two-state model effectively divides each terminal region into half, treating the outward half as a uniform end region and inward half as part of the polymeric interior. As such, N_E is expected to be about half of the total number of end sites predicted by the trapezoidal model. Furthermore, once oligos are in the parabolic regime, as DNA charge decreases, the amount of salt cation accumulation within the oligo interior decreases, and thus the binding affinity decreases. As a result, the binding of a KWK₆ to dT(pdT)₁₀ will be weaker than a KWK₆ binding inside the terminal region of a long oligomer. Our previous phenomenological analysis (23) underestimated the ion release associated with end binding by assuming that it is represented by the S_aK_obs of KWK₆-dT(pdT)₁₀, therefore underestimating N_E as well, and is superseded by the current analysis.

Asymmetric contributions of L⁸⁺ and poly(dT) to S_aK_obs of binding at 0.1 M salt

The data of Table 1 allow us to refine our previous estimate (22) of the contribution of ion release from L⁸⁺ and from poly(dT) to S_aK_obs. Although binding of L⁸⁺ to dT(pdT)₈ was not investigated, the S_aK_obs for binding L⁸⁺ to dT(pdT)₈ should be well approximated by the average values of S_aK_obs for binding L⁸⁺ to dT(pdT)₆ and dT(pdT)₁₀: S_aK_obs = −3.4 ± 0.3. Ion release from the oligopeptide and the oligonucleotide should contribute approximately equally to this S_aK_obs; this contribution (−1.7) should be the same for L⁸⁺ binding to all larger dT-oligomers. Hence, for binding L⁸⁺ to poly(dT) where S_aK_obs = −6.5 ± 0.3 at 0.1 M salt, ion release from L⁸⁺ contributes ∼25% and ion release from poly(dT) contributes ∼75% of S_aK_obs. This asymmetry is a consequence of the CEE; L⁸⁺ is a short oligoelectrolyte and poly(dT) is a polyelectrolyte. CEEs are very important for L⁸⁺ but not for poly(dT) in this binding interaction.

Consequences of the CEE for multiple binding

Multiple-ligand binding events are important in the analysis of non-specific binding. In the data presented here, dT(pdT)₂₂ and longer lengths are in the multiple binding regime. Models frequently used for analyzing experimental titration data assume a uniform binding constant along DNA [e.g. the Epstein (30) and McGhee–von Hippel (37) models] and introduce cooperative or non-cooperative corrections for multiple binding via the cooperativity factor (37). This approach fits the data well, but does not address the important question of how much the binding differs between the center and the end of an oligomer. The binding affinity presumably depends not only on its position on the DNA but also on the number and positions of other bound ligands.

Binding of the first KWK₆ to a sufficiently short ssDNA (15–39 phosphates) is expected to reduce the effective K_obs for subsequent binding by requiring one or both ligands to bind at sites away from higher affinity interior sites and/or by reducing the overall amount of ion release for the next ligand. For example, binding of KWK₆ to the center site of a 39mer DNA strand should be as strong as binding to a site on poly(dT). In the 1:1 central complex on the 39mer, two 16mer regions remain on either side, which are too short to exhibit a trapezoidal ion distribution. Therefore, any second binding event must be weaker per site than the first. This is consistent with GCMC calculations (33), which predicted that ligand binding (modeled as the neutralization of |Z_L| charges in the center of a B-DNA strand) resulted in net reduction of the local counterion concentrations on either side of the site of complexation. Analysis of dT(pdT)₃₉ data allowing for varying microscopic binding constants is not straightforward as a result of the combinatorics of multiple binding modes; however, KWK₆-dT(pdT)₂₂ binding does not suffer this complication.

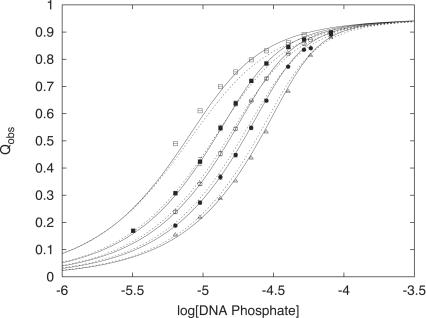
If we allow there to be two different average binding constants (K_obs,1 and K_obs,2) in the analysis of the dT(pdT)₂₂ reverse titration data (Figure 4), the binding density is defined as

Figure 4.

Comparison of fitting models for KWK₆ binding to dT(pdT) ₂₂ at 0.105 M Na⁺ with Z_L = 8, |Z_D| = 22, and Q_max = 0.95. Symbols are as defined in Figure 1. The dashed line represents the global fit to the Epstein model (Equation 2) with logK_obs = 5.605 ± 0.01. The solid line is the improved global fit to an Epstein model where two ligands can bind (Equation 12) with different affinities K_obs,1 and K_obs,2: logK_obs,1 = 5.734 ± 0.01 and logK_obs,2 = 5.434 ± 0.02. The F_χ-value (38), which tests the statistical significance of an increase in the number of fitting parameters, confirms that the use of two different binding constants describes KWK₆-dT(dT)₂₂ binding better (at a 95% confidence level) than the Epstein model with only one binding constant.

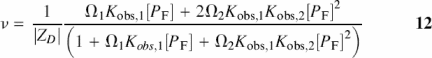
where Ω_j is as defined in Equation 4, the resulting fit is significantly better than that of the Epstein model where only one global K_obs is used. An F_χ-test (38) indicates that the improved quality of fit cannot be simply explained by the increase in the number of fitting parameters. At 0.1 M salt, K_obs,2 is a factor of two smaller than K_obs,1, and the two binding constants bracket the Epstein model K_obs (cf. Figure 4). The weaker K_obs,2 suggests that the first ligand binding event adversely affects the binding of a second KWK₆ oligopeptide. The significant difference between Epstein K_obs and K_obs,1 suggests that application of Epstein model to treat L^Z+-DNA binding may introduce error in K_obs and for more accurate treatments of experimental data one needs a binding isotherm that accounts for CEEs.

CONCLUSIONS

The current study uses a cationic oligopeptide (L⁸⁺) as a probe for the thermodynamics of CEEs on oligocation–nucleic acid interactions for a series of relatively short oligonucleotides. The CEE causes |SK_obs| and K_obs of L⁸⁺ binding at moderate to low salt concentration (≤0.3 M) to decrease strongly for short oligonucleotides (|Z_D| ≤ 22) relative to that seen for polymeric DNA. We propose a trapezoidal (for long oligomers) or a parabolic (for short oligos) axial counterion concentration model incorporating the CEE, and that oligolysine–DNA interactions are driven predominantly by salt ion release upon complex formation. Experimental data are qualitatively consistent with this model of ion accumulation along an oligomer. In particular, both logK_obs at fixed salt concentration and |S_aK_obs| increase strongly with increasing |Z_D| for DNA oligomers with no more than |Z_L| + 2N_e phosphates, where N_e is estimated to be ≥11 ± 4 phosphates at 0.1 M and ≥7 ± 3 phosphates at 0.2 M salt. When |Z_D| ≥ |Z_L| + 2N_e, the interior sites of the nucleic acid exhibit polymeric levels of ion accumulation, and binding becomes increasingly less sensitive to |Z_D|. Similarly, when multiple ligands (L⁸⁺) bind to an intermediate-length DNA lattice at low to moderate salt concentrations, a CEE introduced by the first binding event weakens the affinity of the second binding event, consistent with a decrease in the extent of ion accumulation around the DNA complex with the first ligand. Quantitative analysis of short oligomer data and a more precise determination of N_e will be presented in a subsequent paper.

We demonstrate that binding depends strongly on the nucleic acid charge for short sequences and that the behavior of these systems is markedly different from that involving long polynucleotides. As a consequence, binding studies with highly charged ligands that use short nucleic acid oligomers as models of interior regions of polymeric RNA or DNA may exhibit quite different SK_obs and therefore different K_obs at low to moderate [salt]. Binding to ends of polyanionic or oligoanionic RNA or DNA will also exhibit different SK_obs (and K_obs at low [salt]) from interior binding. Characterization of CEEs in oligocation binding provides the information needed to compare end and interior binding.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.