A Multi-scale Approach to Designing Therapeutics for Tuberculosis

Abstract

Approximately one third of the world’s population is infected with Mycobacterium tuberculosis. Limited information about how the immune system fights M. tuberculosis and what constitutes protection from the bacteria impact our ability to develop effective therapies for tuberculosis. We present an in vivo systems biology approach that integrates data from multiple model systems and over multiple length and time scales into a comprehensive multi-scale and multi-compartment view of the in vivo immune response to M. tuberculosis. We describe computational models that can be used to study (a) immunomodulation with the cytokines tumor necrosis factor and interleukin 10, (b) oral and inhaled antibiotics, and (c) the effect of vaccination.

Introduction

Tuberculosis (TB), a deadly infectious disease caused by the bacterium Mycobacterium tuberculosis, results in 1–2 million deaths per year worldwide. In 2013, an estimated 9 million new cases were diagnosed[1]. Control of the TB epidemic is limited by a complex and prolonged antibiotic regimen, development of antibiotic resistance, the lack of an effective vaccine and, more generally, by our incomplete understanding of the host-pathogen dynamics that underlie the disease, its progression, and treatment[2, 3]. Many of the challenges to the development of therapies for TB are captured by the following broad and as-yet-unanswered questions:

(1) What is the immune response to M. tuberculosis infection, and why does it often fail to eliminate the infection?

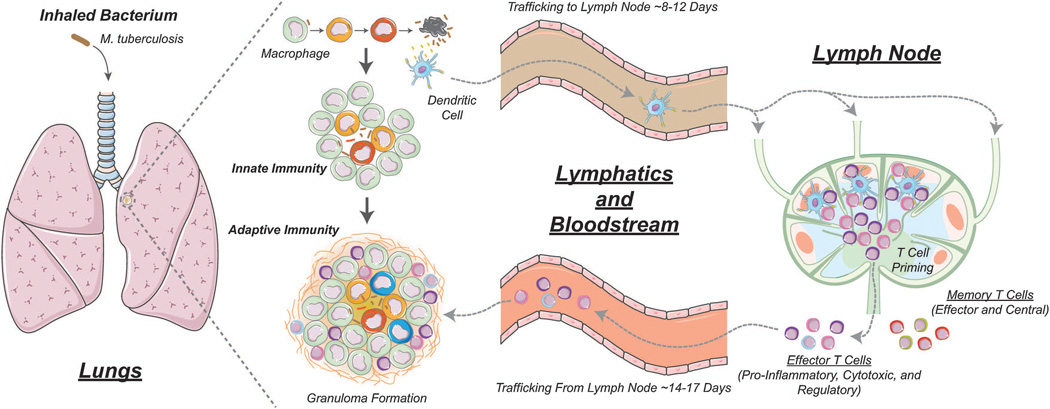
Figure 1 shows key aspects of the immune response to M. tuberculosis. M. tuberculosis is a respiratory pathogen that primarily causes infection in the lungs in adult humans and is transmitted via aerosolized droplets of bacteria from an infectious individual. Upon inhalation, bacteria reach the pulmonary alveoli and are phagocytosed by macrophages that line the alveolar space. Although some bacteria may be destroyed by macrophages through antimicrobial mechanisms, M. tuberculosis has evolved ways to evade protective host immune mechanisms (e.g. by preventing phagosome fusion with the lysosome), and as a consequence is able to multiply within macrophages[4, 5]. Dendritic cells (DCs), another phagocytic cell type, also internalize M. tuberculosis. DCs migrate through lymphatics to lung-draining lymph nodes (LNs) to prime an adaptive immune response. About 2–4 weeks after the initial infection, effector T cells, attracted by chemokines and pro-inflammatory cytokines from the lung site of infection, migrate back to lungs via the blood to mount an M. tuberculosis-specific immune response. The net result of these events is the formation of granulomas, roughly spherical collections of immune and lung cells, bacteria and infected cells.

Figure 1.

Overview of the immune response to M. tuberculosis infection. M. tuberculosis replicates within macrophages. Some bacteria are killed via non-pathogen specific processes (innate immunity). Dendritic cells present antigen to naïve T cells in the lymph node, generating effector T cells (CD4+ and CD8+) that travel back to the site of infection to kill bacteria (adaptive immune response). Granulomas form in lungs as a result of these events. In non-human primates, granulomas range in size from ~1–6 mm in diameter (median value 2 mm)[10, 12]. Multiple granulomas are present in a single host and likely each one is seeded by a single bacterium[10, 132]. Memory T cells (CD4+ and CD8+) are also generated by processes in the lymph node.

In TB, the battle between host and microbe plays out at the level of the granuloma. A classic caseous granuloma consists of a central necrotic area surrounded by layers of macrophages and then a smaller cuff of lymphocytes[4, 6]. The lymphocytic cuff primarily contains both CD4+ and CD8+ T cells, but other cell types, including B cells, neutrophils, DCs and fibroblasts are also observed[7, 8]. There are also many molecular mediators of granuloma dynamics, including cytokines interferon-γ (IFN-γ), tumor necrosis factor-α (TNF), and interleukin-10 (IL-10) and chemokines CXCL9/10/11, CCL2 and CCL5. Some, like IFN-γ, have been shown to be necessary to M. tuberculosis infection control, while others remain controversial. None have been shown to be sufficient for infection control. A central feature of almost all granulomas is a caseous necrotic center (dead immune cells and lung tissue), often trapping large numbers of bacteria that are unable to grow due to hypoxic conditions.

The role of a granuloma from a host-centric point of view is to contain infection, destroy bacilli, and limit pathology. From the bacterial point of view, however, the granuloma may serve as a niche for survival. If all granulomas present are capable of inhibiting or killing most mycobacteria present, humans develop a clinically latent infection. However, if a granuloma does not control bacterial growth, infection progresses, granulomas enlarge, and bacteria seed new granulomas; this results in progressive pathology and disease, i.e. active TB[5, 9–13]. Mechanisms that lead to an inability of the immune response to completely eliminate the pathogen are unknown but appear to be both host- and bacteria- related, making it difficult to identify those that would be suitable to manipulate for therapeutic purposes. Further, the immune response is necessarily limited; an overly-enthusiastic immune response, while possibly eliminating the bacteria, can do considerable damage to host lungs[11, 12, 14–16]. Perhaps latent disease is simply a compromise that, for the most part, works. However, a third of the world’s population is thought to have latent TB, providing a huge reservoir of contagion (contributing to the pool of active disease through reactivation); treating latent TB will be essential to the ultimate eradication of a disease that claims millions of lives each year[1].

(2) Why do some individuals develop latent disease while others develop active disease?

Humans and non-human primates infected with M. tuberculosis have multiple granulomas, from a few to ~25 granulomas[10, 12, 17]. The manifestation of the disease in an individual depends on how well the collection of granulomas can control infection. Following an initial infection with M. tuberculosis, ~10% of humans develop primary (active) TB, ~90% develop latent infection, and a few individuals likely clear the disease. Reactivation TB refers to the situation in which an individual with latent TB later develops active disease either due to reactivation of existing infection or a reinfection event[18]; there is a 10% per lifetime risk that can be greatly increased with immune-compromising events. It may be that some individuals with latent TB will never, or only rarely, develop reactivation TB, while for others the risk is much greater, i.e. there may be a spectrum of latency[19]. The factors that control these different outcomes are not well-understood. We do know that interfering with the immune system, either pharmacologically by delivering anti-TNF therapies (used in the treatment of some autoimmune diseases) or pathologically in the case of HIV-1 co-infection, both increase the risk of reactivation[5, 20–24].

(3) Why is a long time course of antibiotics needed, and why do antibiotics often fail?

Standard therapy for active TB includes an initial combination of 3–4 first-line oral antibiotics for two months followed by another 4–7 months of 2 oral antibiotics[25]. Long treatment periods appear to be required because of the presence of phenotypically drug-tolerant ‘persister’ bacteria, slow bacterial growth rates and high bacterial loads[26–29]. Known obstacles to treatment success (including patient non-compliance, drug toxicity, relapse, and drug resistance) are thought to be, at least in part, a result of the unusually long treatment regimens[1, 2, 30, 31]. The complex nature of the site of infection, namely granulomas, presumably further complicates treatment, as the dense and heterogeneous tissue itself may present an obstacle for antibiotics to reach the site of infection. Worldwide, TB has an 86% treatment success rate in new cases, leaving more than 1 million new patients without cure in 2013[1]. Thus there is a great need for both shorter treatment regimens and new antibiotics[32–34].

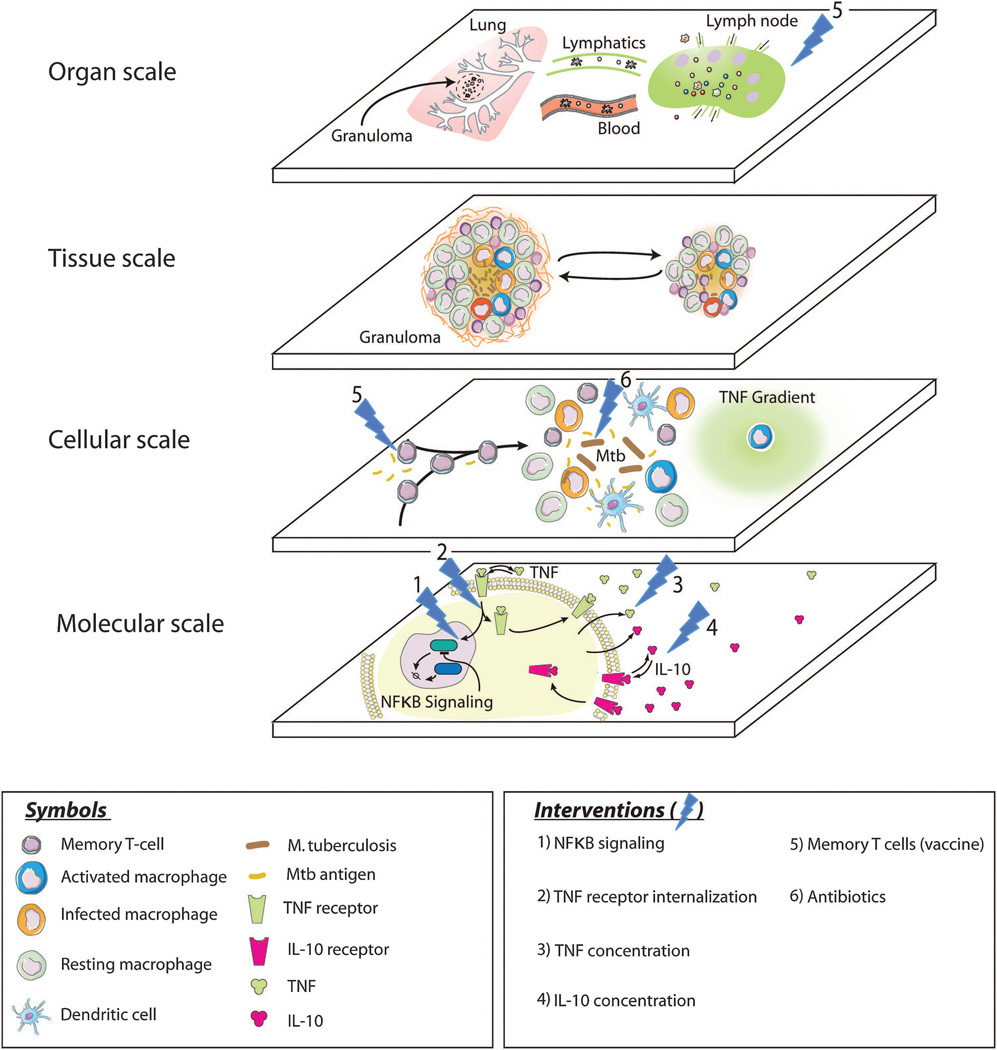
Underlying these three questions is a common theme: we currently have only limited insight into how the immune system fights M. tuberculosis and what constitutes protection from the bacteria. As a result, it is difficult to know how best to develop treatments and to approach vaccine development for TB. There are many reasons why these questions have been and remain difficult to address. Two reasons are particularly relevant for the discussion in this issue on in vivo systems biology. First, it should be clear from the above that, at a minimum, the lungs, draining LNs, blood, and lymphatic system participate in the host-pathogen dynamics that describe M. tuberculosis infection and its treatment (Figure 1), so it is difficult to study the disease “in a dish”. Most experimental studies focus on a single biological (length and/or time) scale of interest, e.g. examination of immune cells in the blood or a particular signaling pathway. Figure 2 highlights the different spatiotemporal scales at which host-pathogen dynamics operate. The smallest spatial scale shown, the molecular scale, also represents the fastest time scale. Receptor/ligand binding and trafficking as well as signal transduction pathways are included at this scale. Examples of assays that generate data for this scale include flow cytometry for receptor expression and fluorescently tagged reporters for gene expression[35–38]. The actions of individual cells, e.g. apoptosis, movement or secretion, are tracked at the cellular scale. Experiments such as microfluidic chemotaxis assays, TUNEL staining, and ELISA assays measuring cytokine production generate data for this scale[39–42]. The major event occurring at the tissue scale in TB is the formation of granulomas; necrosis and fibrosis are also tissue-level outcomes in TB. Experiments at this scale examine gross-pathology, histology, bacterial loads, cellular distribution and fibrosis[7, 12, 17, 43]. These tissue-scale events evolve over periods of weeks to years in humans. The largest spatial scale shown here is the organ scale. Here cells can traffic between the site of infection through blood to draining LNs and back again as well as to other body sites. Thus to understand the complex in vivo immune response to M. tuberculosis, it will be important to integrate information from experiments performed at multiple scales and on multiple physiological compartments (lung, blood, lymphatics, LNs).

Figure 2.

Multi-scale and multi-compartment view of host-pathogen dynamics during M. tuberculosis infection. Six potential interventions are also shown.

Second, the “design space” of both potential experiments and potential therapies is enormous. For example, the identities, dosing schedules, and concentrations of multiple antibiotics, cytokines and/or other immunomodulators can be varied across a wide range[44]. Animal models have been used for nearly 100 years in the study of TB and have provided much useful data. However, the animal models that are easiest to work with may not fully capture human disease. Mice are most commonly used because of the availability of reagents, genetically modified animals, and ease of use. But there is no true latent infection in mice; they become chronically and progressively infected, and eventually succumb to the disease. In addition, mouse granulomas are substantially different from human granulomas in terms of structure and organization[5, 6]. Other small organisms, e.g. guinea pigs, rabbits and zebrafish, have their own advantages and disadvantages[6, 45–47]. Recently, non-human primates, in particular Cynomolgus macaques, have emerged as the animal model most similar to humans in terms of spectrum of disease outcomes and pathology[6, 12]. The cost, technical, and ethical issues of working with macaques means that the number of animals studied, i.e. the fraction of design space that can be explored, is necessarily small. It is even more difficult and expensive to evaluate new therapies or vaccines in human clinical trials. Thus there is a crucial need for an approach that can efficiently narrow the design space of potential experiments and be used to identify, test, and optimize new therapies for TB.

We are convinced that a systems biology approach that integrates data from multiple model systems and over multiple length and time scales into a comprehensive multi-scale and multi-compartment view of the in vivo immune response to M. tuberculosis is necessary. This approach will allow us to identify and understand the mechanisms underlying host-pathogen dynamics and to improve on and identify new therapies. Here we discuss our computational models of M. tuberculosis infection, focusing on the multi-scale and multi-compartment influences that lead to granuloma formation and influence granuloma function – the ability to contain infection, and in the presence of minimal tissue damage and inflammation. We believe computational models provide valuable tools (among others) to aid in addressing the questions introduced above.

Methods

Computational model of granuloma formation and function

As explained above and in Figure 2, the “readout” of the lower and higher scale events – signaling pathways, cellular actions, and cellular input from LNs – are granulomas (occurring at the tissue scale) that may contain infection and may be accompanied by significant tissue damage and inflammation. Thus we have developed computational models of granuloma formation and function that are formulated such that information can be continually exchanged across scales and in both (higher/lower scales) directions[14, 20, 48–53].

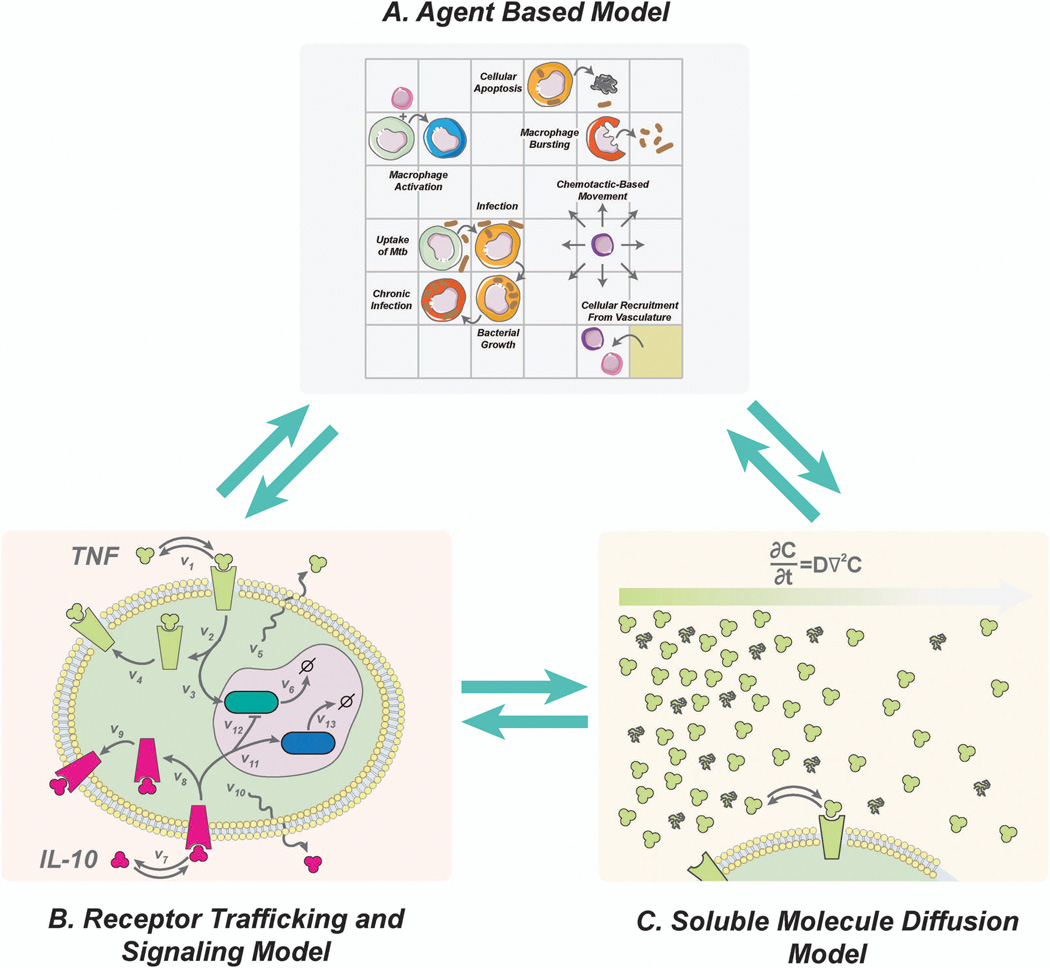
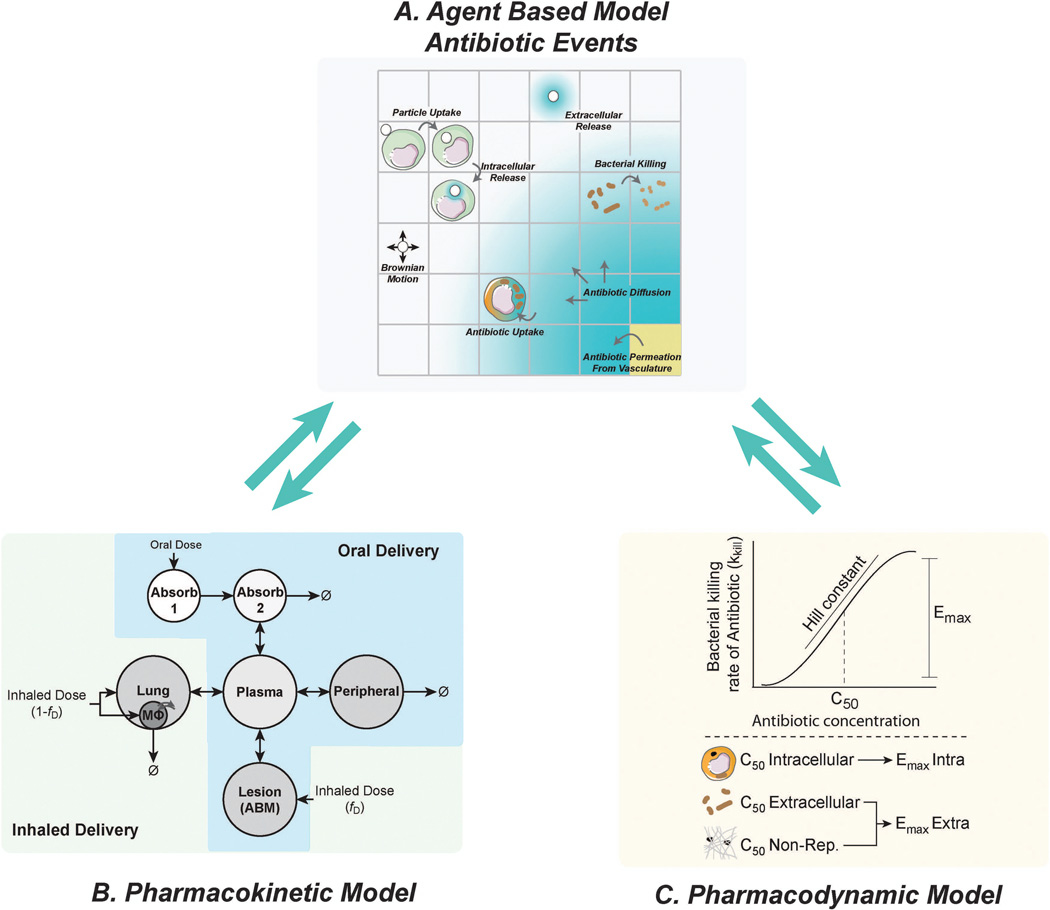
As shown in Figure 3, there are three central elements of our approach for following granuloma formation and function[54]. First, we use an agent-based model (ABM) to describe cellular behavior, including recruitment to the lung, changes of state (activation, infection, etc.), and movement (Figure 3A). Cells (agents) included are macrophages and T cells which can have multiple states (e.g. infected, activated, etc.). Bacteria are not represented as agents but rather as continuous functions in the extra- or intra-cellular environment. We track three different bacterial populations in our model: intracellular replicating, extracellular replicating and extracellular non-replicating bacteria. The simulation environment is two-dimensional and represents a 4–16 mm² cross-section of lung tissue. Probabilistic interactions between immune cells and with bacterial populations are described by a well-defined set of rules between immune cells and M. tuberculosis in the lung. Each simulation follows events over several hundred days, building over time to track thousands of individual cells (agents).

Figure 3.

Three elements of our computational approach to granuloma formation and function. (A) An agent-based model describes cellular actions. (B) Receptor binding, trafficking and signaling models are described with ODEs. (C) Molecular diffusion is described by partial differential equations. These model elements are linked, allowing information to be continually exchanged across scales.

Second, we capture receptor/ligand binding and trafficking and intracellular signaling events with ordinary differential equations (ODEs) that are solved within each agent (Figure 3B)[14, 48, 49, 52, 54]. For instance, the model can capture receptor-ligand binding and trafficking of cytokines, such as tumor necrosis factor-α (TNF) or interleukin-10 (IL-10), using ODEs[14]. The detail required in the model at this scale is determined by the questions being asked. For example, a detailed description of cytokines is necessary when trying to understand how cytokine availability and signaling contribute to infection control. If focus shifts to elucidating the dynamics of antibiotic treatment in granulomas, a detailed description of cytokines may not be necessary. Thus we use an approach we term tunable resolution, formulating fine-grained (detailed) and coarse-grained (less detailed) descriptions of the biological events occurring and toggling between these levels of resolution as needed.[55, 56] Third, we describe the diffusion of particular chemokines, cytokines, and other soluble ligands (e.g. anti-TNF antibodies, antibiotics) by solving the relevant partial differential equations (Figure 3C). Equations and parameters for these portions of the model are based on extensive biological data.

The three model elements are linked, allowing information to be continually exchanged across scales (Figure 3)[54]. Thus, our overall computational model of M. tuberculosis infection and granuloma formation is hybrid (formed from different mathematical formalisms). It is also multi-scale, incorporating molecular and cellular events explicitly with tissue-scale behavior (granuloma formation) as an emergent feature of the model (Figure 4). Among other tools, we use uncertainty and sensitivity analyses techniques to understand the relative importance of particular processes to granuloma formation and function[57].

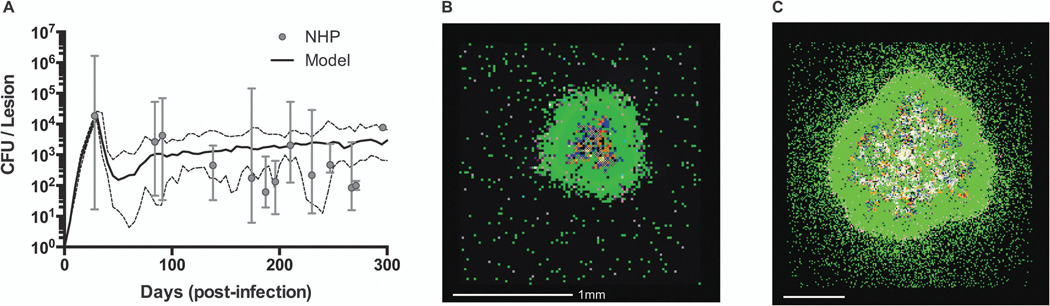
Figure 4.

Granuloma model calibration and snapshots. (A) Comparison of CFU/lesion data from non-human primates (NHP) with computational model predictions (median – solid black line, min/max – dashed black lines). Model detail and parameters are given in [52]. NHP data from 32 animals collected between 28 and 296 days post-infection has been previously published in[10, 17]. (B) Sample simulation snapshot shows a granuloma that is containing infection at 200 days post-infection. (C) Sample simulation snapshot with different parameter values than in (B) shows a granuloma that fails to contain infection. Snapshot legend colors: resting macrophages (green), infected macrophages (orange), chronically infected macrophage (red), activated macrophage (dark blue), pro-inflammatory T cell (pink), cytotoxic T cell (purple), regulatory T cell (aqua), extracellular bacteria (brown), and caseation (cross-hatch).

Although not discussed in detail here, our granuloma models have been developed, calibrated, and validated using extensive data from animal models, especially non-human primates (NHPs). Granuloma formation and function is quantified in the model by a variety of measurements capturing host immunity (e.g. macrophage and T cell numbers, states, locations and death), inflammation (e.g. cytokine levels, macrophage activation), granuloma metrics (e.g. granuloma size, caseation) and bacterial growth (e.g. total bacterial load, size and location of bacterial subpopulations). Figure 4A shows an example of model calibration to the number of bacteria (CFU, or colony-forming-units) per granuloma in non-human primates[10, 17, 52]. Figures 4B and 4C show snapshots from two simulations using different but physiologically realistic parameter values. We can predict features that map to a wide spectrum of those observed in primates, including granulomas that are able to contain bacteria (Figure 4B), granulomas that show bacterial overgrowth and dissemination (Figure 4C), and granulomas that clear bacteria completely, sometimes with extensive inflammation (not shown).

Immunomodulation simulations

The computational model for immunomodulation simulations was built in [14, 52] and modified here to allow for TNF and IL-10 depletion at various times during the course of infection. All model parameters can be found in[14, 52]. Additional parameters used here include the timing of IL-10 depletion (days 0, 25, 50, 75, and 100 post-infection) and the production rates of TNF and IL-10 (0.5–3.0 #/cell-s for TNF and 0.1–1.0 #/cell-s for IL-10).

Oral Antibiotic simulations

We use our computational model of the granuloma formation and function as described in [52] together with the ODEs describing the delivery of antibiotics to the granuloma from the bloodstream as in [58]. The antibiotic model is implemented on a larger simulation grid to accommodate more physiological granuloma sizes and vascular densities[58]. Equations and all parameter values can be found in [58]. Briefly, plasma pharmacokinetic (PK) parameters – absorption rate constant, intercompartmental clearance rate constant, plasma volume of distribution, peripheral volume of distribution and plasma clearance rate constant were calibrated to [59] guided by values in [60–62]. Granuloma PK parameters – extracellular degradation rate constant, cellular metabolism rate constant, effective diffusivity, cellular accumulation ratio, vascular permeability and permeability coefficient were calibrated to [60] guided by values in [63–68]. PD parameters – C₅₀ for intracellular M. tuberculosis (C_50,BI), extracellular replicating M. tuberculosis (C_50,BE), and extracellular non-replicating M. tuberculosis (C_50,BN); Hill constant for intracellular M. tuberculosis (H_BI), extracellular replicating M. tuberculosis (H_BE), and extracellular non-replicating M. tuberculosis (H_BN), maximum intracellular activity (E_max,BI) and maximum extracellular activity (E_max,BE) were calibrated to [17, 69–72]. Treatment is simulated by adding antibiotic doses to the first transit compartment in the plasma PK model and allowing the calibrated model to predict antibiotic concentrations and activity in in silico granulomas. Antimicrobial action is incorporated into the model by subtracting the local antibiotic killing rate (determined by the Hill curve) from the growth rate of the corresponding bacterial subpopulation (intracellular, extracellular replicating and extracellular non-replicating). Granuloma scale treatment outcomes in the model are quantified by CFU per granuloma (if not sterilized), time to sterilization (if sterilized) and percentage of granulomas sterilized (in a repository of granulomas).

Inhaled antibiotic simulations

We extend the computational model describing oral antibiotics to the granuloma as described above and in [58] to include inhaled dosing and antibiotic release of RIF and INH from a generalized carrier system. Carriers are modeled as distinct agents and behaviors include movement, macrophage phagocytosis of carriers, dispersal from macrophages, and extra- and intracellular degradation. Release of antibiotics from carriers occurs in both the intra- and extracellular environment and is described by diffusion of antibiotics through a spherical carrier and degradation of the carrier system. All model parameter can be found in [73]. Additional parameters used herein include changes to intracellular replicating, extracellular replicating, and extracellular non-replication C₅₀ values (20% to 180% of original values in [58]).

Vaccine simulations

We previously developed a two compartment computational model that links granuloma formation and LN dynamics [74]. Here we add an additional blood compartment to capture the recirculation of various T lymphocytes, using blood parameters from [75] and calibrated to NHP blood data. Here we set initial conditions such that the system starts with varying amounts of central and effector memory, helper (CD4+) and cytotoxic (CD8+) T cells. This is to mimic the scenario where vaccine has been administrated and immune memory has been established.

Simulation environment

The simulation environment consists of multi-threaded portable C++ code (~ 30,000 lines of code, with various options and analysis tools) currently targeted at Linux, Mac OS/X and Windows. We use the Boost library for general C++ functionality, openGL and ffmpeg libraries for graphics and video, Qt application framework for GUI, threading and open GL support, and the SDL application framework for use with openGL. We use Latin Hypercube Sampling (LHS), a stratified sampling without replacement technique [57], to efficiently explore parameter space to determine reasonable initial guesses of parameter values and for performing sensitivity analyses. We use uncertainty and sensitivity analyses to determine how parameter uncertainty affects model output(s), via a generalized correlation coefficient, the partial rank correlation coefficient (PRCC)[57]. Results are used to identify critical processes and mechanisms affecting treatment outcomes, to suggest strategies for model reduction [55] and to generate new hypotheses. Simulations, particularly the thousands of simulations required for uncertainty and sensitivity analyses, are computationally intensive [54] as each individual run can take several hours to days.

Results

Our computational models of granuloma formation and function can be used to probe therapeutic interventions that improve the ability of a granuloma to contain, or even eliminate, bacteria while minimizing tissue damage and inflammation. Several potential interventions with actions at different scales are shown in Figure 2 (interventions 1–6) and are discussed below. In each case, interventions at one location, or in one type of molecule or cell, impact events at other length and time scales, and we are especially interested in their effect on our main “readout”, granuloma formation and function. Below we describe four examples to highlight ways in which our approach can help the discovery of therapeutic interventions for M. tuberculosis infection. They are organized according to their scale to emphasize that there are multiple levels that should be considered when designing interventions opening up new avenues for exploration.

1. Immunomodulation focused on IL-10 and TNF

Data from human, animal, and mathematical models have demonstrated that pro-inflammatory cytokines, such as TNF, are essential to an efficient antimicrobial response against M. tuberculosis infection[22, 76, 77]. However, many anti-inflammatory cytokines are also present in granulomas[4, 5]. In particular, the regulatory cytokine IL-10 is of interest since it functions to inhibit cytokine and chemokine production (specifically TNF)[78–81]. It has recently been proposed that a balance of pro- and anti-inflammatory mediators (such as TNF and IL-10) in granulomas is an essential component of an efficient antimicrobial response with limited host-induced tissue damage[5, 82, 83]. Understanding how cytokines contribute to infection control at a single granuloma level has been difficult due to the myriad of cellular sources, differences among animal models, and limitations of detection methods for these mediators. From a therapeutic standpoint, we simply do not know whether manipulation of pro- and anti-inflammatory cytokines in granulomas would be useful in affecting infection outcomes.

In order to explore the therapeutic value of modulating cytokine levels, i.e. immunomodulation, we developed a version of our multi-scale computational model that incorporates IL-10 and TNF cytokine dynamics across multiple temporal and spatial scales (Figure 3)[14, 48, 52]. This model describes cytokine secretion, diffusion, degradation, and receptor-ligand binding and trafficking. We link these mechanisms across scales by allowing dynamics within each scale to influence behavior at other scales. For example, TNF binding and subsequent internalization affect TNF concentrations in the granuloma environment, affecting cellular apoptosis/necrosis. This systems biology-based approach allows us to explore the effect of immunomodulation strategies at the individual granuloma scale by performing virtual IL-10 knockouts, temporal IL-10 knockouts, and perturbing the balance of TNF and IL-10 levels in granulomas.

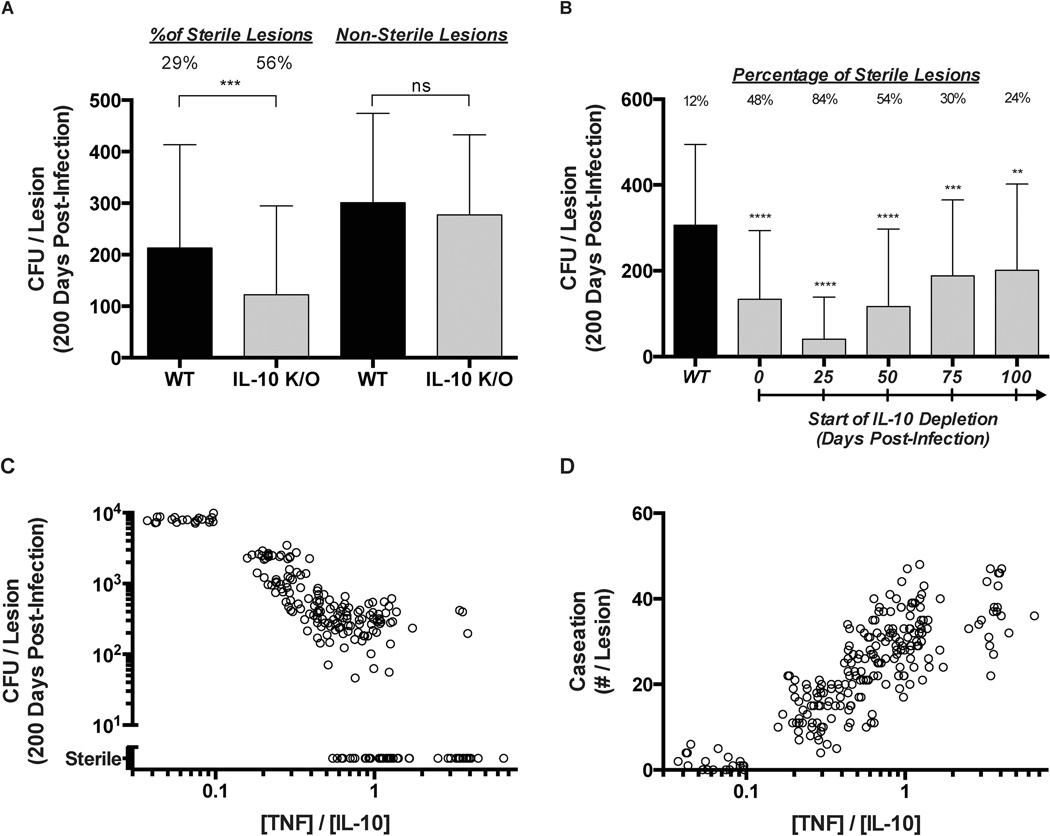
We first performed a virtual IL-10 deletion (referred to as IL-10 K/O) at the initialization of infection by setting IL-10 synthesis rates for all cells (agents) to zero (Figure 2, intervention 4). We observed a significant change (~2-fold increase) in the number of granulomas that achieve sterility (granulomas that kill all bacteria within) in the IL-10 K/O simulations as compared to the wild-type (WT) simulations (Figure 5A). The mean bacterial load per granuloma at 200 days post-infection is reduced ~1.75-fold in IL-10 KO simulations. However, when sterile granulomas are removed from the analysis of mean bacterial loads per granuloma, there is no significant difference between IL-10 KO simulations and WT simulations (Figure 5A). Thus, the model predicts that reduced bacterial loads in IL-10 KO simulations are due solely to the increased number of granulomas that are successfully able to sterilize bacteria. This suggests that IL-10 is a key regulator of granuloma sterility and that IL-10-focused treatment strategies might be able to improve infection outcome.

Figure 5.

Simulated immunomodulation of IL-10 and TNF in granulomas. (A) Left side: Mean CFU per lesion for WT and IL-10 deletion (IL-10 K/O) lesions at 200 days post-infection. Percent of lesions becoming sterile by 200 days is indicated. Right side: Mean CFU per lesion for WT and IL-10 deletion (IL-10 K/O) lesions that were non-sterile at 200 days post-infection. Error bars indicate SD. (B) CFU for WT and IL-10 deletions starting at day 25, 50, 75, or 100 days post-infection. Percent of lesions becoming sterile by 200 days is indicated. Error bars indicate SD. (C) CFU per lesion and (D) Number of caseated compartments per lesion for granulomas with differing ratios of mean TNF to IL-10 concentrations. The ratio of TNF to IL-10 was modulated by increasing/decreasing rates of TNF and/or IL-10 production from all cell types. Individual circles represent individual lesions.

In order to better understand whether IL-10 could be an effective therapeutic strategy, we performed virtual IL-10 deletions at days 25, 50, 75, and 100 post-infection. We observed an initial increase in the number of sterile granulomas depending on when IL-10 was removed from the system (Figure 5B), indicating that an increase in sterile granulomas due to deletion of IL-10 is a phenomenon that primarily occurs during the early immune response to M. tuberculosis. Unfortunately, the early increase in granuloma sterilization is coupled with increases in inflammation and tissue damage (not shown). Taken together, these predictions suggest that any therapeutic value of modulating IL-10 levels in granulomas may be present only at early times post-infection. However, because most patients typically present symptoms weeks to months after initially becoming infected with M. tuberculosis, this strategy is unlikely to be implemented in a clinical setting. It does, however, point to the importance of unbridling the immune response early in TB, which might be accomplished via a vaccine.

Similarly, modulating levels of TNF in granulomas could prove useful as a therapeutic strategy. In work with earlier generation granuloma models, we showed that altering TNF levels, TNF receptor internalization capabilities, or rates in the TNF-induced NFκB signaling pathway could alter granuloma outcomes, e.g. containment vs. dissemination of bacteria (Figure 2 – interventions 1–3)[20, 21, 48, 49]. Next, we modulated cellular production rates of both IL-10 and TNF within our granuloma simulations, thus changing the balance of TNF and IL-10 during infection [14, 52]. When the ratio of TNF to IL-10 in a granuloma is less than ~0.1, anti-inflammatory mechanisms dominate the immune response. We observe elevated bacterial loads (Figure 5C) with no granulomas achieving sterilization of bacteria. At the same time, however, the presence of caseation at the granuloma’s center, a measure of tissue damage, was reduced nearly 10-fold (Figure 5D). Conversely, when the ratio of TNF to IL-10 is greater than ~1.0, the immune response to M. tuberculosis infection is dominated by the pro-inflammatory response. In this case, significantly more granulomas are able to successfully sterilize (Figure 5C), but increased antimicrobial activity comes at the cost of increased tissue damage (Figure 5D). If the ratio of TNF to IL-10 is between these two extremes a trade-off exists between granuloma sterilization and tissue damage[14]. Thus controlling the balance of TNF and IL-10 in a granuloma, using exogenous antibodies or cytokines, could be an effective therapeutic strategy to shift granuloma outcomes from bacterial containment to sterilization. However, modulation of TNF and IL-10 must be done in a precise and perhaps a time-limited way to limit excessive inflammation and tissue damage. These results suggest that immunomodulation strategies focusing on balancing pro- and anti-inflammatory cytokines such as TNF and IL-10 could have significant therapeutic value, perhaps in combination with antibiotics.

2. Oral antibiotics

Our computational approach can also be used to examine the action of oral antibiotics during M. tuberculosis infection (Figure 2 – intervention 6). In particular, we wanted to understand the failure of current antibiotic treatments and to provide a tool for assessing how antibiotics or antibiotic dosing regimens might be altered to improve efficacy. To do this, we took a systems pharmacology approach, incorporating pharmacokinetic (PK) and pharmacodynamics (PD) elements into our computational models of granuloma formation and function (Figure 6)[58].

Figure 6.

Additions to the computational model of granuloma formation and function that allow for antibiotic dosing. (A) Granuloma PK of antibiotics described in the agent-based model include consideration of vascular permeability, diffusion and uptake by host cells. Inhaled antibiotics further include delivery particle deposition, movement and antibiotic release. (B) Host PK models describe movement of drug through the body and into the lung lesion (granuloma) using ODEs. The model for oral delivery (blue area) is expanded to allow inhaled delivery (blue + green areas). (C) PD are modeled independently of drug delivery method and are location- and bacterial subpopulation-specific. Killing rates are calculated using a Hill curve defined by the slope (Hill constant), maximum killing rate (E_max) and concentration where 50% activity is achieved (C₅₀). These parameters are specific for different bacterial subpopulations[58].

Current first-line antibiotics for TB are isoniazid (INH), rifampin (RIF), pyrazinamide (PZA) and ethambutol (EMB). Because INH and RIF are typically administered during the entire regimen and are arguably the most well-studied of the group[25], we focus on them here. We incorporated PK and PD models of orally-dosed INH and RIF into our computational model of granuloma formation[58]. PK are described by a classical two compartment (plasma and body) model with two absorption compartments (Figure 6B)[60, 84]. Antibiotic concentrations in the plasma compartment of the PK model are used to determine the movement of antibiotics into or out of the granuloma simulation grid (Figure 6A). Vascular permeation of antibiotics onto the ABM occurs at grid compartments designated as vascular sources (Figure 3A), and depends on antibiotic concentration gradients between blood and vascular source grid compartments. Antibiotics can diffuse and degrade on the simulation grid and enter host cells – which we refer to as granuloma PK. PD are modeled using a Hill curve [85] and antimicrobial action is determined for each grid compartment and host cell based on the local antibiotic concentrations (Figure 6C). PK and PD parameters were calibrated to experimental in vitro and in vivo data (rabbits and non-human primates) on INH and RIF[58].

Our systems pharmacology approach allows us to probe antibiotic treatment in the context of a granuloma in ways not previously possible, integrating antibiotic activities, immune response dynamics, and spatio-temporal aspects of an evolving granuloma. Furthermore, we can explore host variation in both immune responses and PK, to provide a view of the host factors that contribute to the heterogeneous nature of TB and treatment. The model allows for the following unique analyses: true side-by-side comparison of different treatment regimens and dose sizes in the same granulomas; prediction of time to sterilization; identification of early indicators of treatment outcome; identification of key host mechanisms and antibiotic attributes controlling treatment outcome (in terms of percentage of granulomas sterilized, time to sterilization and final bacterial load in non-sterilized granulomas). Therefore this adapted PK/PD granuloma model is an excellent tool for suggesting possible improvements or alterations to current antibiotic treatments, as well as exploring a large number of dosing regimens and antibiotic combinations to narrow the search space for animal studies and clinical trials.

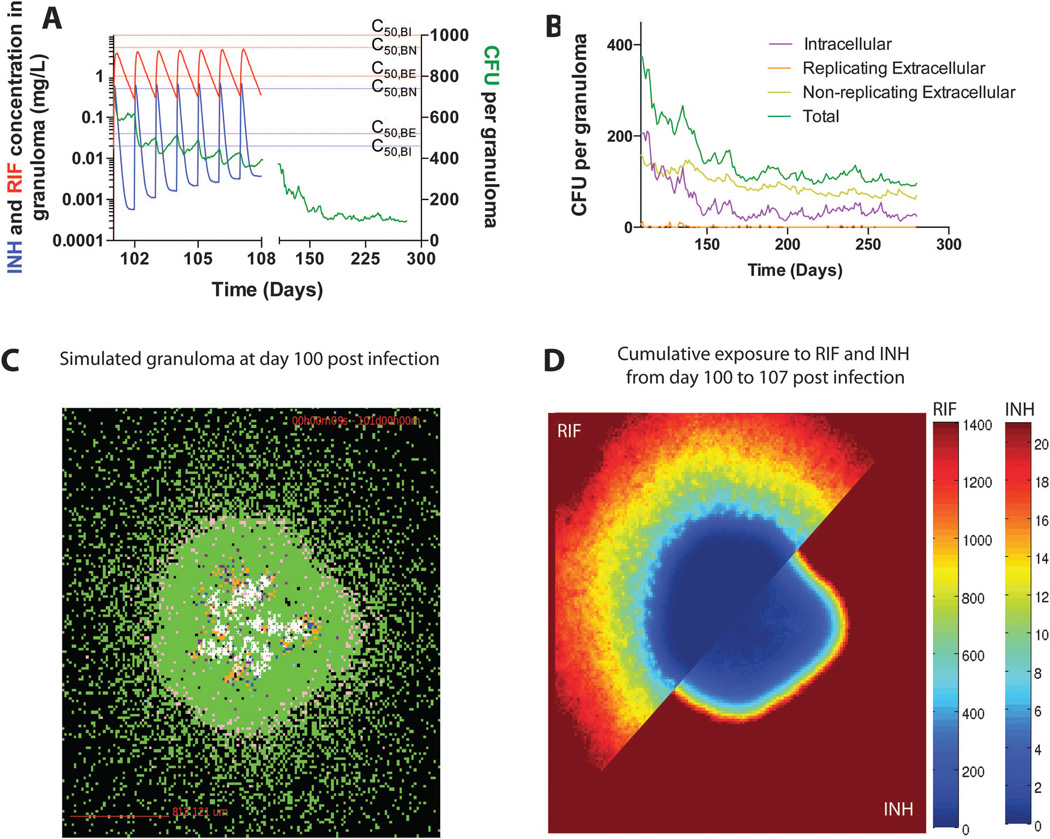
We illustrate model outcomes for a representative granuloma treated with daily oral dosing of both INH and RIF in Figure 7. We are able to evaluate granuloma PK, including average antibiotic concentrations for the granuloma as well as at specific locations in the granuloma. Average antibiotic concentrations remain below effective concentrations for the majority of dosing intervals inside granulomas (Figure 7A). Antibiotic concentration gradients form within granulomas, with lower concentrations, and therefore lower cumulative exposure, toward the center (Figure 7C and 7D). Simultaneous exposure to effective concentrations of both antibiotics inside the granuloma is infrequent. We note that monotherapy – exposure to effective concentrations of only a single antibiotic – can contribute to the development of or selection for drug resistant mutants[30, 86].

Figure 7.

Simulated antibiotic treatment of a representative granuloma. The granuloma is allowed to form for 100 days, after which treatment is initiated with daily doses of INH (15 mg/kg) and RIF (20 mg/kg) for an additional 180 days. These doses give plasma PK similar to that seen in humans[59]. (A) Average INH and RIF concentrations in the granuloma shown in panel C and the corresponding total bacterial load in the granuloma over time. C50 values (see Figure 6) for INH and RIF are indicated by dashed lines for each bacterial subpopulation (blue – INH; red – RIF). (B) Bacterial subpopulations in the granuloma over time during 180 days of treatment. (C) Snapshot of the granuloma on day 100, before treatment starts. (D) Cumulative exposure of the granuloma in panel C to RIF (top left) and INH (bottom right) over the first week of treatment, showing spatial distribution. Color bars are scaled between 0 and the EC80 (exposure where 80% of max efficiency is achieved) for each antibiotic.

Model results also provide insight into the spatial and temporal bacterial response to treatment. The bacterial populations of TB disease are heterogeneous and complex. We represent this heterogeneity by modeling three different bacterial subpopulations: intracellular replicating, extracellular replicating and extracellular non-replicating bacteria. These subpopulations have different susceptibilities to INH and RIF[70, 71] (reflected in differing C₅₀ (Figure 7A), Emax and Hill constant values), and we can track the response of each subpopulation to treatment in the representative granuloma (Figure 7B). Suboptimal antibiotic concentrations lead to bacterial growth between doses, likely a major factor contributing to the long treatment periods required for treating TB. As treatment progresses the intracellular and non-replicating extracellular bacterial subpopulations persist, while replicating extracellular populations are eliminated.

In addition to a daily dosing regimen, the Centers for Disease Control and Prevention (CDC) also approve alternative dosing regimens of two or three times weekly²⁵. Analysis of 500 simulated granulomas predicts that this intermittent dosing increases both the time to sterilization (clearance) and the percentages of granulomas not sterilized for INH and RIF treatment alone or in combination[58]. This is contradictory to findings obtained recently using a model based on non-specific antibiotic parameters for treatment of self-limiting infections[87]. However, treatment outcomes are clearly both antibiotic- and pathogen-specific. In our model, pre-treatment infection severity (including bacterial burden, host cell activation and host cell death) and antibiotic exposure are predictive of treatment outcome. Our results suggest that both host and bacterial attributes continue to play important roles during antibiotic treatment. Finally, we note that our results are based on individual granuloma simulations, although the expectation is that granulomas that fail to clear bacteria could lead to active TB.

3. Inhaled antibiotics

As described above, current oral antibiotic regimens of RIF and INH lead to poor antibiotic penetration into granulomas causing sub-optimal exposure. This necessitates lengthy treatment durations causing chronic toxicity and concerns with patient compliance[2, 34]. A proposed alternative strategy to oral delivery of antibiotics for TB is inhaled delivery. In this delivery mode, fabricated carriers loaded with antibiotics are dosed into the lungs via an aerosol delivery system[88, 89]. Delivery of antibiotics via an inhaled route may overcome many limitations of oral dosing for treatment of TB by providing direct dosing to the infection site, reduced systemic toxicity and clearance, and improved patient compliance with reduced dosing frequency[88–91]. To rationally design inhaled formulations of antibiotics for TB treatment, it is necessary to understand the contributions of PK, PD, and behavior of the carriers (e.g. drug release) at the site of infection. Measuring and understanding these dynamics in clinically relevant models (e.g. non-human primates) is difficult and costly. Thus, systems pharmacology approaches are needed to quickly assess the efficacy and dynamics of inhaled formulations for the treatment of TB.

We extend our existing computational model of granuloma function and antibiotic treatment discussed above to include inhaled dosing and antibiotic release from a generalized carrier system[73]. We modify the PK model to allow for dosing via both inhaled and oral routes by adding a non-infected lung compartment and an intracellular macrophage sub-compartment at pseudo-steady state (Figure 6B). Carriers are modeled as agents and behavior includes carrier movement, macrophage phagocytosis of carriers, dispersal from macrophages, and extra- and intracellular degradation (Figure 6A). In the non-infected lung and intracellular macrophage compartments, a homogenous representation of inhaled carriers is used. Release of antibiotics from carriers occurs in both the intra- and extracellular environment and is described by a diffusion-degradation equation with time varying boundary conditions[92–94]. We utilize the PD model constructed and calibrated in[58]. Using this model, we can begin to rationally design inhaled formulations of RIF and INH to be given at reduced dose frequencies (every two-weeks) with equivalent or better sterilizing capabilities as compared to conventional daily oral regimens. We can rapidly compare oral and inhaled doses, allowing us to assess whether existing antibiotics would be a promising candidates for inhaled formulations.

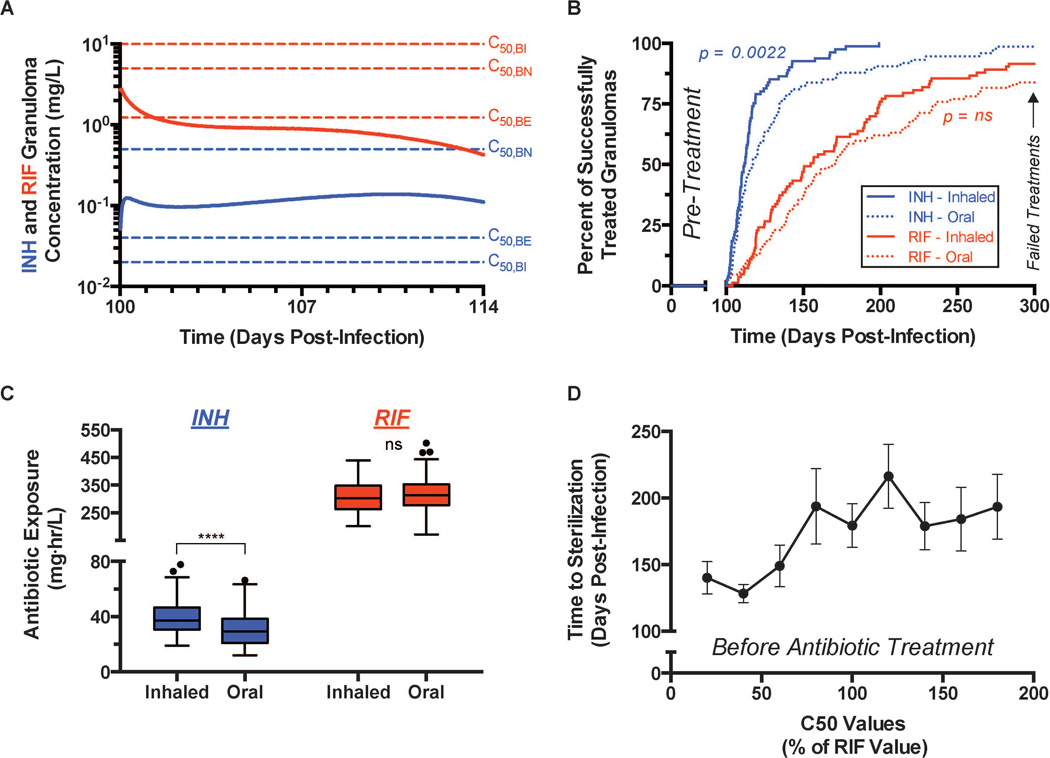
We illustrate model predictions showing behavior of an inhaled dose of either RIF or INH given once every two weeks in Figure 8. Based on model sensitivity analysis, we identified possible inhaled formulations of INH and RIF that lead to equivalent or reduced bacterial loads at 7 days post-treatment initiation compared to daily oral formulations. For an inhaled formulation the total two-week dose (inhaled – 1× dose; oral – 14× doses) of INH is 12-fold lower compared to the oral formulation, while the total two-week dose for an inhaled formulation of RIF is the same as in the oral formulation. The model predicts that antibiotic concentrations in granulomas remain more stable over an entire dosing window (2-weeks) with inhaled formulations (Figure 8A) than with daily oral doses (Figure 7A). In the case of INH, average granuloma concentrations are sustained above C₅₀ values for intra- and extracellular M. tuberculosis populations for the entire dosing window (Figure 8A). However, in the case of RIF, the inhaled formulation only eclipses the C₅₀ of extracellular M. tuberculosis immediately after dosing and never surpasses the C₅₀ for intracellular or non-replicating M. tuberculosis (Figure 8A). The average granuloma concentration of RIF slowly decreases, indicating that inhaled formulations cannot maintain effective concentrations of RIF over the two-week dosing window.

Figure 8.

Simulated antibiotic treatment of granulomas using inhaled formulations. Granulomas are allowed to form for 100 days, after which 200 days of treatment is simulated with inhaled formulations of INH and RIF dosed every two-weeks. (A) Mean INH (blue) and RIF (red) concentrations in the granuloma for the first 14-day dosing window. C50 values (see Figure 6) for INH and RIF are indicated by dashed lines for each bacterial subpopulation (blue – INH, red – RIF). (B) Percent of granulomas sterilized at indicated times after the initiation of treatment – INH (blue) and RIF (red). Inhaled formulations (solid lines) dosed every two-weeks are compared to daily oral dosing strategies (dashed lines). Granulomas still present at 300 days post-infection are considered failed treatments. (C) Mean INH (blue) and RIF (red) cumulative exposure in the granuloma for the first 14-day dosing window. Inhaled formulations dosed every two-weeks are compared to daily oral dosing strategies. (D) Mean time to granuloma sterilization when the C50 values (intracellular, extracellular, and non-replicating populations) of RIF are increased/decreased. RIF C50 values are given as a percentage of the original value. (A–C) * p ≤ 0.05, ** p ≤ 0.01, *** p ≤ 0.001, **** p ≤ 0.0001. INH – Inhaled (N = 81), Oral (N = 87). RIF – Inhaled (N = 83), Oral (N = 87).

We can also examine predicted treatment efficacy at the individual granuloma level for both drugs, comparing inhaled and oral formulations given once every two weeks and daily, respectively. There is no significant difference in successfully treated granulomas between the inhaled and oral formulations of RIF (Figure 8B). However, the inhaled formulation of INH sterilizes granulomas earlier than the oral formulation (Figure 8B). Treatment efficacy of inhaled formulations of RIF and INH, in comparison with their daily oral counterparts, is controlled by antibiotic concentrations mentioned above and the cumulative exposure in granulomas in a dosing window. A single inhaled dose of INH, given every two-weeks, leads to increased cumulative exposure in the granuloma compared to daily oral dosing (Figure 8C). A single inhaled dose of RIF, given every two-weeks, and daily oral dosing of RIF lead to similar cumulative exposure (Figure 8C).

An inhaled formulation of RIF may not be practical because effective concentrations of RIF cannot be maintained for an entire dosing window, there are early increases in peripheral toxicity (defined as cumulative exposure in the peripheral compartment), and the required two-week total dose would have to exceed ~90% w/w in a polymeric carrier formulation [73]. However, RIF is one of many rifamycin antibiotics with differing PD [95] and PK properties. To further illustrate the potential capabilities of our approach, we tested how PD properties of RIF and other rifamycin antibiotics could be altered to improve the feasibility of an inhaled formulation. For instance, if a RIF derivative could be synthesized with different C₅₀ characteristics would the efficacy of an inhaled formulation change? Using the same inhaled formulation of RIF as in Figure 8A–C, we varied the C₅₀ values for the three modeled bacterial populations. As C₅₀ values increase, the mean time to sterilize a granuloma remains constant or increases slightly (Figure 8D). When C₅₀ values are decreased by ~ 50%, the mean time to sterilization decreases dramatically from ~80–100 days of treatment to ~30–50 days of treatment (Figure 8D). Therefore, a RIF-derivative with different PD properties could make an inhaled formulation a practical possibility.

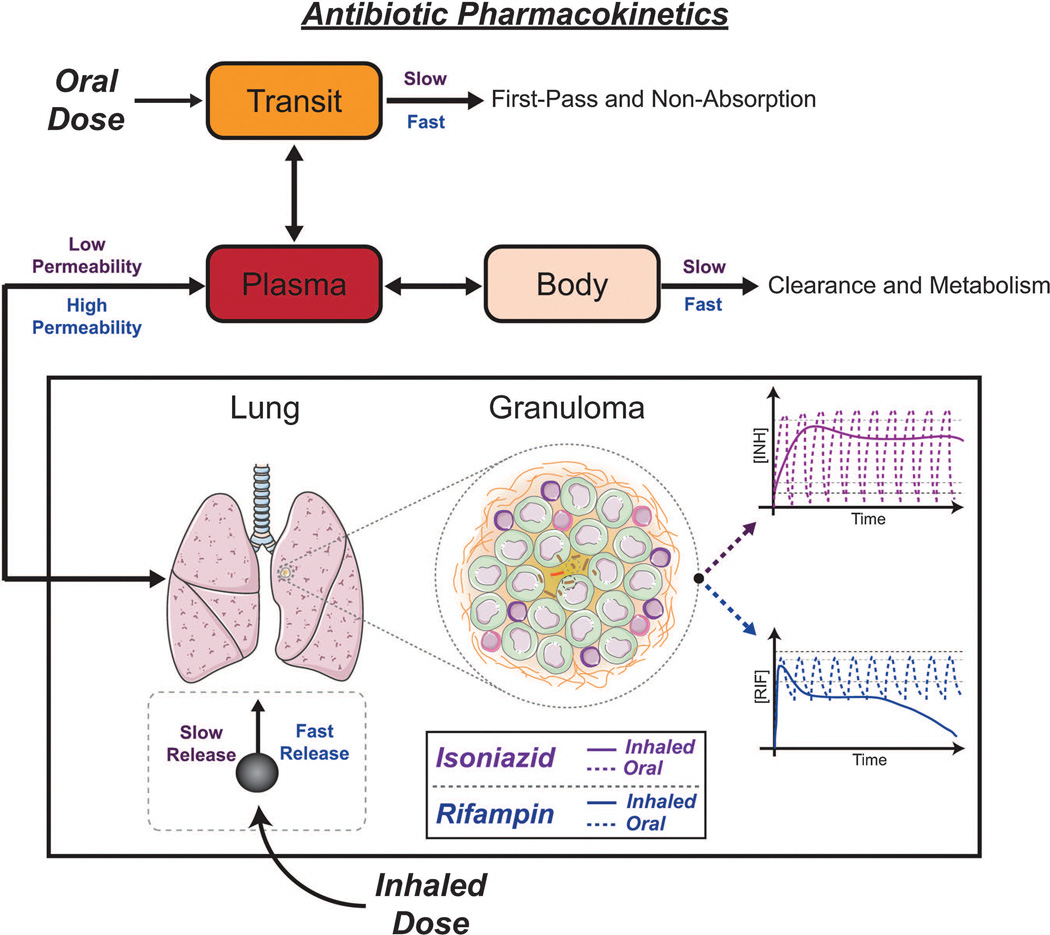
We summarize the findings from our computational models with regard to oral and inhaled delivery of the first-line antibiotics INH and RIF in Figure 9. When designing treatment regimens and delivery systems, it is important to consider all relevant dynamics. INH and RIF distribute differently within the host and are eliminated at different rates, leading to very different dynamics at the host level and the site of infection (granuloma). For inhaled antibiotic delivery, host-level PK together with the dynamics of the delivery system (slow or fast release from the carrier) lead to their different dynamics at the site of infection. These influences must be considered together with the granuloma dynamics in designing therapeutics.

Figure 9.

Antibiotic dynamics within granulomas are simultaneously influenced by host PK, granuloma PK, dosing regimens, and delivery route. Relative rates for INH and RIF are shown above (INH) or below (RIF) arrows. The transit compartment represents absorption in the gut and transit to systemic circulation. Oral and inhaled dosing regimens and inhaled carrier release kinetics need to be designed with host PK and granuloma PK in mind. For INH, slow distribution to other organs, slow clearance, and low permeability allow for slow inhaled carrier release kinetics (all relative to RIF). For RIF, rapid distribution to other organs, rapid clearance, and high permeability must be compensated for by fast inhaled carrier release kinetics.

4. Vaccines

The holy grail in TB therapy is the development of an effective vaccine (Figure 2 – intervention 6). When antigen is delivered to the body, antigen-presenting cells (APCs) (e.g. dendritic cells) present it in the context of MHC molecules to T cells circulating through LNs. T cells with specificity for that antigen/MHC complex bind, differentiate and proliferate to produce effector and memory T cells (Figure 1, right side). Central memory cells recirculate from blood to lymphoid organs, and can persist for years, awaiting activation by a second antigen challenge. Effector memory cells migrate to sites of infection. These cells have a shorter lifespan than central memory cells, but they can perform effector functions immediately after encountering a second antigen challenge. When vaccines are effective, these memory cells are able to protect an individual from disease.

To date there is still no efficacious vaccine against M. tuberculosis, although ~30 vaccines are in various stages of testing and clinical trials (www.aeras.org/annualreport)[96–100]. These trials are expensive, difficult, and time consuming to perform, and many result in a null outcome. Although many infants are vaccinated at birth with BCG (an attenuated M. bovis), this does not prevent infection or development of TB after childhood. Data suggest an effective vaccine must generate memory cells to multiple M. tuberculosis antigens that are expressed at multiple stages during infection[101]. However, there are currently no comprehensive approaches or tools that could significantly advance the development of vaccines. Perhaps not surprisingly, given the complexity of the host-pathogen dynamics, we do not yet understand what characteristics of an immune response correlate with protection against M. tuberculosis. Considering the high cost and time required to perform animal testing and human trials, computational models developed using a systems biology approach can be an important supplement for hypothesis generation to aid TB vaccine design, especially in the early stages.

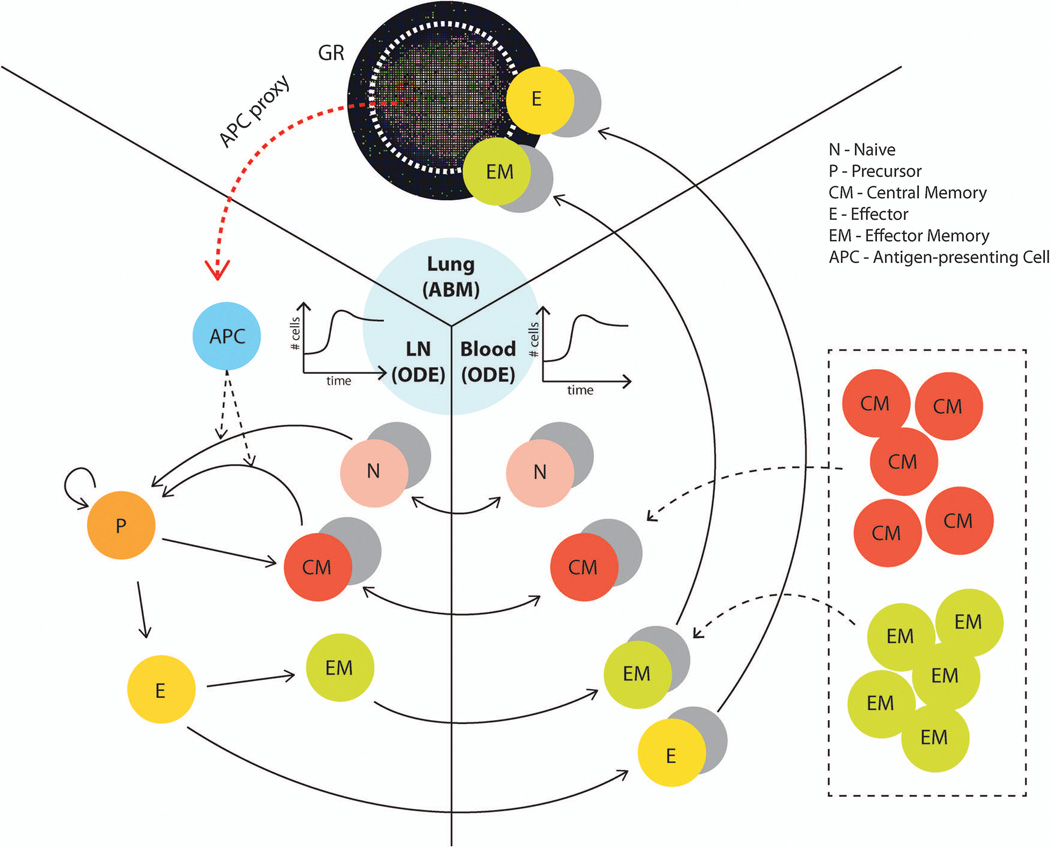
To study how memory cells generated from vaccination could influence the course of M. tuberculosis infection, we incorporated two additional physiological compartments – LNs and blood – into our computational model of the site of infection (lung granuloma). This 3-compartmental physiological model tracks relevant cells and molecules that participate in generation of adaptive immunity and ensuing responses during M. tuberculosis infection (Figure 10). Building on our previous work[74], we use an ODE model to capture the dynamics of cells within LNs, although we note that to address questions requiring an understanding of spatial dynamics within LNs we have also developed agent-based models[75, 102, 103]. ODEs describe the evolution of naïve, precursor, central memory, effector memory, and effector T cells for both CD4+ and CD8+ T cells. Naïve and central memory cells can be recruited to LNs and are primed or activated at a rate based on the number of antigen-bearing DCs in the LN[104]. Shown in Figure 1 is the lymphatic system, whereby DCs traffic from sites of infection (here, lung) to LNs. To simplify, we assume that antigen-bearing DCs are recruited into LNs at a rate proportional to the number of macrophages that interacted with M. tuberculosis at that time step. We refer to this as the “APC proxy” (Figure 10). After priming, T cells enter a precursor pool, where they begin to proliferate. Cells in this state are not allowed to exit the LN due to the early activation markers they express[105]. Precursor cells eventually differentiate into central or effector T cells, and a portion of the effector T cells become effector memory cells. We also model a blood compartment, allowing immune cells to traffic from the LN to the site of infection where they can participate in the immune response. Blood is a well-mixed compartment, and therefore we use ODEs to represent the dynamics. The lung, LN, and blood compartment models are linked via cell trafficking terms, and physiological scaling is used to correctly account for the appropriate volumes of the compartments.

Figure 10.

Three-compartment model framework for simulating the influence of memory cells (which can be generated by vaccines) on granuloma formation and function. The lung (site of infection) is represented with our agent-based model (GranSim) as described in previous sections, and two ODE models capture LN and blood dynamics. T cells that are tracked in LNs include: CD4+ and CD8+ T cells, and each of these can be further classified into: N (Naïve), CM (Central Memory), EM (Effector Memory), P(precursor cells), E (Effector). APCs such as DCs circulate from the lung to the LN to prime the adaptive immune response. The CM, EM, E and N classes can travel between LN and blood compartments as indicated by arrows. Only E and EM (total effector class) can travel to the infection site in the lung. Both M. tuberculosis-specific and non-specific T cells are accounted for in our model. For our in silico experiments, we changed the initial conditions of equations describing the number of different memory cells in the blood to represent the memory cells that we assume have been generated after vaccination (shown in box). The cell and bacterial time courses and granuloma spatial outcomes in the lung are tracked to assess the level of protection derived from the simulated vaccine.

An effective vaccine must trigger the immune response to generate a sufficient number of effector memory and central memory T cells that can act quickly in a recall response, preventing or controlling infection. Although the numbers required for successful protection are not known, our computational model can be used to generate predictions. Others have begun to explore this question as well, using mathematical modeling and bioinformatics approaches (www.epivax.com)[106]. For a simple illustration here, we assume that a vaccine will generate a particular level of M. tuberculosis-specific effector memory and central memory cells. These cells are assumed to be circulating post-vaccination in the blood compartment. A recall response (via introduction of M. tuberculosis, as in our earlier models) is then simulated to test whether infection with M. tuberculosis is cleared, controlled, or neither. In other words, simulations may suggest what levels of memory cells are required for vaccine efficacy.

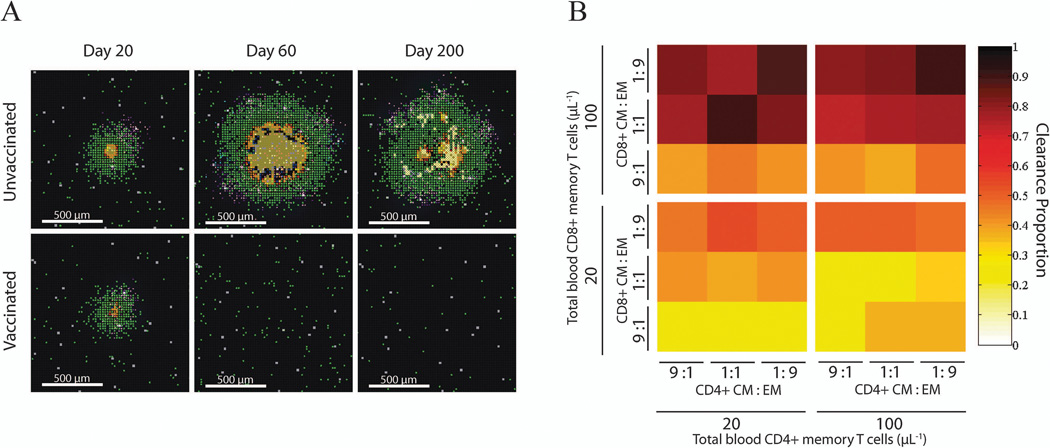
We can compare “unvaccinated” with “vaccinated” cases to learn more about the protection that memory cells can provide. For the unvaccinated case, infected macrophages, T cells and bacteria progress into a contained granuloma with a relatively stable structure over time (Figure 11A, upper row), as seen with our earlier models (e.g. Figure 4B). If there are a sufficient number of memory cells present as a result of vaccination prior to the infection, the granuloma may not form, or may resolve quickly after a short period of growth (Figure 11A, lower row). To test how levels of different types of memory cells affect protection, we varied the initial condition for the numbers of effector memory and central memory classes of both CD4+ and CD8+ T cells that are present in the blood compartment. We introduce M. tuberculosis infection into the lung during a scenario where the parameters are biased toward a host phenotype that can form a granuloma that can contain infection, and track how the presence of circulating memory cells affects granuloma outcomes. Each setup is replicated 50 times, and the probability that a granuloma clears its bacterial load is counted (Figure 11B). We see that increasing memory CD4+ T cells does not influence the outcome of a granuloma. However, the chance of sterilization (clearance) increases when more memory CD8+ T cells are present, especially when a high proportion of them are effector memory cells.

Figure 11.

Simulated effects of immune memory on granuloma outcomes. (A) Snapshots of granuloma progression over time with or without memory cells generated from vaccination. When no memory cells are present at the beginning (top row), the site with an initial infected macrophage develops into a granuloma and maintains the structure through the 200 days of simulation. With sufficient memory cells circulating (bottom row), a granuloma appears briefly but quickly resolves as the infection ends in bacterial clearance (sterilization). (B) Infection is simulated with different combinations of initial conditions for each type of memory cell (central, effector, CD4+ and CD8+ T cells). Four groups of simulations are run, each with a fixed low (20 µL⁻¹) or high (100 µL⁻¹) concentration for total CD4+ or CD8+ T memory cells. Within each group, the ratio of central memory (CM) to effector memory (EM) are set to 9:1, 1:1, or 1:9. Each scenario is simulated 50 times, and the outcomes of each granuloma are assessed. Shown in the color are the proportions of simulations that ended in a granuloma that cleared all bacteria. Clearance is defined as less than 500 macrophages and less than 10 replicating M. tuberculosis.

Even with this simple vaccine representation, we see that an appropriate vaccine for M. tuberculosis could greatly alter the outcome of infection. The goal now is to design a vaccine that generates the necessary levels and ratios of memory cells. In a recent study, using an agent-based LN model, we predicted that the relative abundance of different T cell subsets could be tuned by controlling the quantity and quality of APCs[75]. These computational studies, together with bioinformatics analyses, animal vaccine, and human trials, are necessary to both improve our understanding of what is needed to develop a successful vaccine for TB and to help narrow the design space of possibilities.

Discussion

Although TB has been around for thousands of years, much is still not understood about this complex infection. TB is a leading cause of death from infectious disease worldwide, second only to HIV-1/AIDS[1]. With a long and complicated antibiotic regimen required for TB treatment, there are a myriad of issues that can lead to treatment failure, including non-compliance, individual variations in antibiotic PK/PD, development of drug resistance, and differences among bacterial phenotypes. In recent years, several groups have taken a systems biology approach to identify critical metabolic and genetic regulatory pathways in the bacterium, with hopes of identifying new drug targets (e.g. [107–110] while others have focused on the alveolar macrophage host[111–113]. A Boolean network approach, while less mechanistic than our efforts here, has also identified critical roles for TNF and IL-10 [114]. These efforts have advanced our understanding of interactions and dynamics for both immune cells and pathogens. There is a rich literature of PK-PD computational models that include host immunity, antibiotic distribution into epithelial lung fluid or alveolar macrophages, for non-specific antibiotics as well as for INH and RIF [115–126]. None however examine the heterogeneous spatial distribution of antibiotics within granulomas, which we and others have shown to be critical to understanding and predicting antibiotic efficacy [58, 60, 127, 128].

Our approach here complements that work but focuses on the multi-scale and multi-organ influences that determine infection outcomes in vivo. The advantage of this approach is that it allows us to understand the impact of a molecular-scale perturbation (e.g. in a rate or molecular concentration) at a granuloma, a tissue-scale readout; similarly the impact of events in the lymph node (e.g. memory cell generation) at a granuloma can be examined. These insights can help us understand how to narrow the design space for therapeutics including vaccines. We can simultaneously incorporate systems pharmacology approaches to describe how well a particular drug will reach and influence the target (e.g. a signaling pathway in a macrophage).

An in vivo systems biology approach to TB has much to offer to hypothesis generation and therapeutic design. Computational models can integrate information from experimental work focused on molecular, cellular, and tissue scales. Iteration between experiments and modeling is essential to building reliable computational models and designing appropriate experiments. New biological findings can easily be added to the computational model. For example, we are now including additional cell populations (T cell subsets and neutrophils) that new data suggest are important to granuloma dynamics. In addition to the antibiotic studies described herein, other combinations of first-line and second-line antibiotics can be studied using our drug model platform to allow for rapid screening of a wide and unwieldy drug regimen space. We are also exploring immunomodulation in tandem with antibiotics [129–131]. Immunomodulation here refers to the addition/subtraction of cells and/or molecules (e.g. cytokines) to enhance the immune response. It stands to reason that boosting the immune system while reducing bacterial load could lead to more rapid control of infection. Several strategies have been tried in murine models (IFN-γ, GM-CSF, TNF, IL-12)[129, 130] and a few in humans (IL-2, GM-CSF, TNF, IFN-γ)[129, 131], but results are inconclusive. Again, the complexity of the immune response makes it difficult to identify which mechanisms are appropriate to modulate to increase control of infection while simultaneously minimizing tissue damage and extensive inflammation. Appropriate delivery to granulomas and proper timing, drug combinations and dosing are all likely to be key factors in successful therapy.

Although we have focused here on lung granulomas and the processes that affect them, more work is needed to understand how infection status correlates with the numbers and characteristics of granulomas that are observed in vivo; forthcoming NHP and human data will be useful for this. Finally, there is an urgent need to identify biomarkers of infection status and progression in TB. This is particularly true in developing countries where resources are limited and the need to parse whom to treat, and when, is urgent. We currently are exploring using machine learning as biomarker discovery tool for TB. In vivo systems biology can play a major role in these important aspects of TB intervention.

Tuberculosis causes 1–2 million deaths per year worldwide, and approximately one third of the world’s population is infected with M. tuberculosis. New therapeutic tools and approaches are desperately needed. We describe computational models of the immune response that integrate experimental data from multiple model systems and focus on the multi-scale and multi-compartment influences that determine infection outcomes in vivo. These models give insight into possible failure modes of current treatments and potential strategies involving, for example, immunomodulation with cytokines and inhaled antibiotics.