This work defines the biophysical mechanism of phosphoregulation of microtubule binding by the kinetochore NDC80 complex. Conformational plasticity of the disordered tail of its Hec1 subunit integrates outputs from multiple phosphorylations to serve as a rheostat, providing a new paradigm for accurate regulation of microtubule-binding affinity.
Abstract
Microtubule (MT) attachment to kinetochores is vitally important for cell division, but how these interactions are controlled by phosphorylation is not well known. We used quantitative approaches in vitro combined with molecular dynamics simulations to examine phosphoregulation of the NDC80 complex, a core kinetochore component. We show that the outputs from multiple phosphorylation events on the unstructured tail of its Hec1 subunit are additively integrated to elicit gradual tuning of NDC80-MT binding both in vitro and in silico. Conformational plasticity of the Hec1 tail enables it to serve as a phosphorylation-controlled rheostat, providing a new paradigm for regulating the affinity of MT binders. We also show that cooperativity of NDC80 interactions is weak and is unaffected by NDC80 phosphorylation. This in vitro finding strongly supports our model that independent molecular binding events to MTs by individual NDC80 complexes, rather than their structured oligomers, regulate the dynamics and stability of kinetochore-MT attachments in dividing cells.
INTRODUCTION
Dynamic interactions between microtubules (MTs) and kinetochores are vitally important for accurate cell division, but little is known about the biophysical basis for these attachments (reviewed in Joglekar et al., 2010; Grishchuk et al., 2012). Conceptually distinct models have been proposed to explain kinetochore-MT attachments, including structured protein oligomers (reviewed in Davis and Wordeman, 2007) and independent molecular binders (McIntosh et al., 2008; Civelekoglu-Scholey et al., 2013; Zaytsev et al., 2013, 2014; Keener and Shtylla et al., 2014). These different designs of the kinetochore-MT interface impose different thermodynamic and kinetic requirements on the MT-binding proteins that provide these molecular interactions, but discriminating between these models is difficult, because there is little quantitative information about the MT-binding properties of individual kinetochore proteins. This situation necessitates a thorough biophysical investigation of the molecular interactions between key kinetochore components and MTs. Because the stability of kinetochore MTs changes during mitosis, these studies should also examine the molecular mechanisms that provide accurate dynamic regulation of interactions between the MTs and kinetochore proteins.
The NDC80 complex is a major MT-binding component of the eukaryotic kinetochore, and it provides a direct link between kinetochores and MTs (Cheeseman et al., 2006; Tooley and Stukenberg, 2011; DeLuca and Musacchio, 2012). Each NDC80 complex is composed of two heterodimers: Spc24-Spc25 and Hec1-Nuf2 (Figure 1A). The dual calponin homology (CH) domain containing the Hec1-Nuf2 dimer directly binds MTs (Wei et al., 2007), and Hec1 also has an unstructured N-terminal 80–amino acid “tail” that is required for kinetochore-MT attachment in vivo (Guimaraes et al., 2008; Miller et al., 2008). This tail is an established target for phosphorylation during mitosis: from nine phosphorylation sites mapped in vitro, six sites have been confirmed to be phosphorylated in cells (DeLuca et al., 2006, 2011; Nousiainen et al., 2006; Ciferri et al., 2008; Malik et al., 2009; Santaguida and Musacchio, 2009). Early in mitosis, the Hec1 tail is heavily phosphorylated (DeLuca et al., 2011), and phosphorylation decreases down to zero to one phosphate in metaphase (Zaytsev et al., 2014). Previous work with purified NDC80 complexes in vitro demonstrates that the Hec1 tail can regulate NDC80-MT binding: multiple phosphorylations or introduction of phosphomimetic substitutions reduces the binding of NDC80 complexes for MTs, while a lack of phosphorylation promotes stronger binding (Cheeseman et al., 2006; Umbreit et al., 2012). Interestingly, in live cells, introducing different numbers of phosphomimetic mutations in the Hec1 tail results in a graded response of kinetochore affinity to MTs (Zaytsev et al., 2014). However, the effect of different numbers of phosphomimetic residues in the Hec1 tail on NDC80-MT binding in vitro has not been previously examined in a systematic and quantitative manner. In general, phosphorylations at multiple sites are known to elicit two types of response, leading to either a graded rheostat-like regulation or a switch-like regulation when the system responds abruptly to a critical number of phosphates (Serber and Ferrell, 2007; Salazar and Höfer, 2009). Whether Hec1 phosphorylation in vitro exhibits rheostasis or sets a threshold for NDC80-MT binding has not been determined.
FIGURE 1:
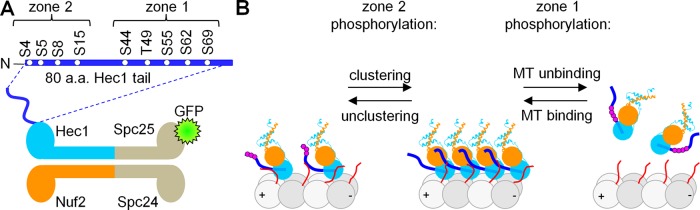
Hec1 tail phosphorylation and NDC80-MT interactions. (A) Schematic of the four-subunit NDC80 complex and the N-terminal tail of the Hec1 subunit. Residues phosphorylated by Aurora B kinase are indicated. (B) Simplified schematics of the zonal model of Hec1 tail phosphoregulation (based on Alushin et al., 2012). Different tubulins (α and β) are shown with different shades of gray, tubulin extensions are in red (shown only for two tubulin heterodimers). Plus (+) and minus (−) signs indicate MT polarity; other colors are as in A; phosphorylation events are depicted with purple circles.
Furthermore, different molecular mechanisms have been proposed to explain the phosphoregulation of the NDC80 complex and its implications for kinetochore-MT attachment in cells. In one model, phosphorylation of the Hec1 tail directly suppresses the binding of the NDC80 complex to the MT lattice (Guimaraes et al., 2008; Miller et al., 2008); this occurs at least in part via interactions between Hec1 and the C-terminal extensions of tubulin (Ciferri et al., 2008). Other studies suggest that phosphorylation of the Hec1 tail can regulate either NDC80-MT binding or NDC80-NDC80 oligomerization, depending on the location of this posttranslational modification (Alushin et al., 2010, 2012). Specifically, the latter model assigns different functional roles to different zones of the Hec1 tail (Figure 1B). Zone 2, made up of the amino acids 4–15, has been proposed to link the adjacent NDC80 complexes, promoting their clustering, and phosphorylations within this zone lead to molecular unclustering. Zone 1, which contains amino acids 44–69, which are proximal to the MT-binding CH domain of Hec1, has been proposed to bind directly to the MT lattice, so its phosphorylation specifically reduces NDC80-MT association (Alushin et al., 2012). To discriminate between these different molecular models, we carried out a systematic quantitative examination of the effects of targeted phosphomimetic substitutions on the binding and cooperativity of NDC80-MT interactions in vitro and in silico using molecular dynamics (MD) simulations.
RESULTS
The number of phosphomimetic substitutions, rather than their location within the Hec1 tail, dictates the characteristics of NDC80-MT interactions
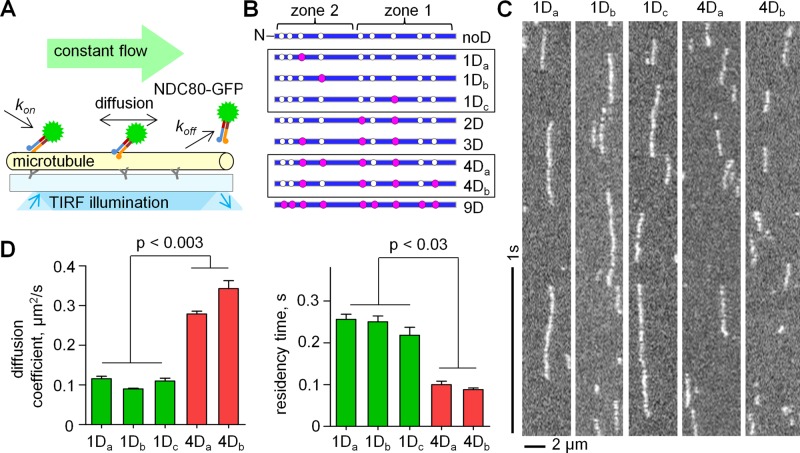
To establish how phosphorylation affects NDC80-MT interactions, we used single-molecule approaches in vitro, based on total internal reflection fluorescence (TIRF) microscopy (Figure 2A). “Bonsai” NDC80–green fluorescent protein (GFP) constructs with a shortened coiled-coil but normal MT-binding moieties were used with a different number of phosphomimetic substitutions in the tail of Hec1. The introduced aspartic acid residues (denoted with D) correspond to the in vitro–mapped Aurora B kinase target sites (Figures 1A and 2B). First, we probed the impact of the specific location of such substitutions on NDC80-MT interactions. Three mutants that differed only in the location of a single D residue and two mutants with randomly positioned 4D residues were constructed (Figure 2B, framed). Landings of these individual NDC80 complexes on the coverslip-attached MTs, their interaction with MTs, and their subsequent dissociation were recorded with high time resolution in BRB80 buffer, which is at near physiological ionic strength (Figure 2C and Supplemental Videos 1 and 2). Semiautomated analysis of the corresponding kymographs was done with custom-made programs (Supplemental Figure S1D) to plot the mean-squared displacement (MSD). While there were small differences in the diffusion coefficient (D) within each of these groups, diffusion of any 1D complex was statistically different from that of either of the two complexes with 4D substitutions (Figure 2D). Similar results were seen for residency time on the MT lattice. These data suggest that the number of mutations but not their position within the Hec1 tail plays a major role in driving the interactions between single NDC80 complexes and MTs.
FIGURE 2:
Single-molecule TIRF-microscopy characterization of NDC80 phosphomimetic mutants. (A) Schematic of the microscopy chamber with Taxol-stabilized MTs in vitro. NDC80 complexes with wild-type or phosphomimetic Hec1 proteins were flowed in continuously, and their binding and diffusion were recorded. (B) Hec1 tail constructs. Open circles are the known phosphorylation sites; purple circles are aspartic acid phosphomimetic substitutions. (C) Representative kymographs of 50 pM NDC80 complexes diffusing on MTs (5–10 ms exposure time). (D) Comparison of different proteins with 1D and 4D substitutions, see B. Bars are mean ± SEM for number of independent experiments (N = 2), in which n > 200 molecules were analyzed for each protein. Here and elsewhere, p value corresponds to Student's t test unless stated otherwise.
Increasing the number of phosphomimetic substitutions leads to a graded increase in NDC80 diffusion, concomitant with a decrease in the MT-binding residency time
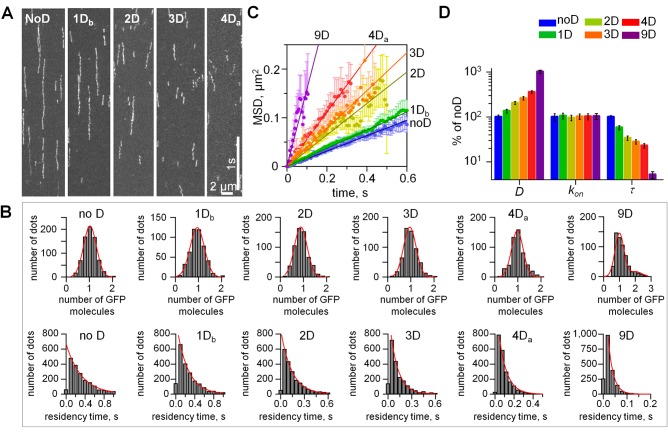
Next we carried out similar experiments using NDC80 complexes containing the wild-type Hec1 tail sequence and those with the number of D substitutions ranging from one to nine (Figure 3A). More than 95% of the recorded molecules were as bright as one GFP fluorophore, as expected in a single NDC80 complex (Figure 3B and Supplemental Figure S1). The diffusion coefficients for different complexes varied from 0.08 to 0.8 μm2/s (Figure 3C and Table 1), in a range similar to that of Saccharomyces cerevisiae NDC80 and Dam1 complexes (Gestaut et al., 2008; Grishchuk et al., 2008; Powers et al., 2009). Interestingly, with an increasing number of phosphomimetic substitutions, the diffusion coefficient increased exponentially (Figures 3D and Supplemental Figure S1E). The association (kon) and the dissociation (koff) rates were then determined. The kon for different phosphomimetic complexes were similar, indicating that mimicking phosphorylation did not significantly affect the rate of NDC80 complex binding to MTs (Figure 3D). The values of koff were used to calculate the residency time τ = 1/koff, over which the NDC80 complexes diffused on the MT lattice (Table 1). These data show that the MT binding of all complexes was transient, ranging from 20 to 420 ms depending on the number of phosphomimetic substitutions. The residency time decreased exponentially with the increasing number of phosphomimetic substitutions (Figure 3D and Supplemental Figure S1F), indicating that phosphorylation of the Hec1 tail can exert a broad-range tuning of the NDC80-MT binding.
FIGURE 3:
Quantitative TIRF analysis of single NDC80 molecules on MTs. (A) Representative kymographs of NDC80 phosphomimetic mutants on MTs. Exposure time: 10 ms. Soluble protein concentration was 50 pM for all proteins. (B) Top row, histograms of the integrated intensities for NDC80-GFP dots on the coverslip-attached MTs, >300 dots for each mutant. Background was subtracted, and data were normalized to the number of GFP molecules. For all proteins, >95% of dots had the intensity of a single GFP (95% confidence); therefore our data reported in Figures 2 and 3 correspond to single NDC80 complexes. Red lines are Gaussian fits. Bottom row, histograms of residency times for individual NDC80 complexes (at least 2000 dots for each protein). Dissociation rates (koff) for different NDC80 mutants were determined from the exponential fits. (C) MSD vs. time; for each mutant protein the tracks from at least 600 individual NDC80 complexes were averaged; data based on at least two independent experiments for each protein. Symbols are experimental data; lines are linear fits; error bars are SEM. (D) Single-molecule parameters for NDC80 phosphomimetic mutants plotted on a logarithmic scale. Values for noD protein were taken as 100% (Table 1). For 1D and 4D proteins average values are plotted. Bars are mean ± SEM for number of independent experiments (N ≥ 2), in which n > 600 molecules were analyzed for each protein.
TABLE 1:
Molecular parameters of NDC80-MT interactions measured in the single-molecule TIRF assay.
| Protein | NoD | 1D | 2D | 3D | 4D | 9D |
|---|---|---|---|---|---|---|
| Diffusion coefficient (D), μm2/s | 0.078 ± 0.006 (n = 719) | 0.106 ± 0.011 (N = 6, n = 2543) | 0.160 ± 0.003 (n = 712) | 0.204 ± 0.011 (n = 830) | 0.309 ± 0.033 (N = 4, n = 1381) | 0.793 ± 0.041 (n = 45) |
| Residency time (τ), ms | 417 ± 23 (n = 2682) | 240 ± 17 (n = 9202) | 143 ± 5 (n = 2779) | 117 ± 5 (n = 2652) | 94 ± 8 (n = 4869) | 22 ± 1 (n = 1877) |
| Association rate (kon)10−3, s−1nM−1 | 3.7 ± 0.5 (n = 2682) | 4.0 ± 0.3 (n = 1928) | 3.6 ± 0.3 (n = 2779) | 3.8 ± 0.3 (n = 2652) | 3.8 ± 0.4 (n = 2391) | 3.9 ± 0.4 (n = 1877) |
| Dissociation constant (KD), μM | 0.64 ± 0.09 | 1.01 ± 0.09 | 1.96 ± 0.09 | 2.24 ± 0.13 | 2.62 ± 0.31 | 12.00 ± 1.25 |
| Negative NDC80-MT binding energy (– ΔGoMT), kBT | 9.09 ± 0.06 | 8.75 ± 0.02 (N = 6) | 8.29 ± 0.04 | 8.01 ± 0.11 | 7.54 ± 0.03 (N = 4) | 6.45 ± 0.10 |
N, number of independent experiments; if not stated, N = 2; n, number of analyzed single molecules. Errors are SEM. Diffusion coefficient, residency time, and dissociation rate of 1D NDC80 are averages of data for S8D, S15D and S55D NDC80 proteins; data for 4D NDC80 are averages of S8,15,44,55D and S8,44,55,69D NDC80 proteins. Dissociation constant: KD = 1/(kon·τ). Negative NDC80-MT binding energy (−ΔGoMT) was calculated based on the diffusion coefficient; see Theoretical approaches to estimate MT-binding energy in Materials and Methods for details.
Increasing the number of phosphomimetic substitutions incrementally reduces the interaction energy between single NDC80 complexes and the MT lattice
The increase in both the diffusion coefficient and the dissociation rate in response to mimicking phosphorylation indicated a reduction in the energy of NDC80-MT interactions. To evaluate this change, we analyzed our single-molecule data with two theoretical approaches. First, we used an analytical model for the particle diffusing in a one-dimensional periodic potential field u(x) (Figure 4A; Festa and Galleani, 1978). This model explicitly links ΔGoMT, the energy for a particle's interaction with its binding site on the MT lattice, and the experimentally determined diffusion coefficient D:
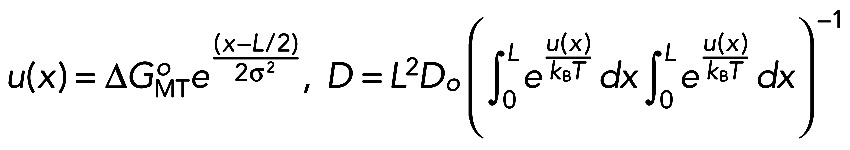 (1) (1)
|
FIGURE 4:
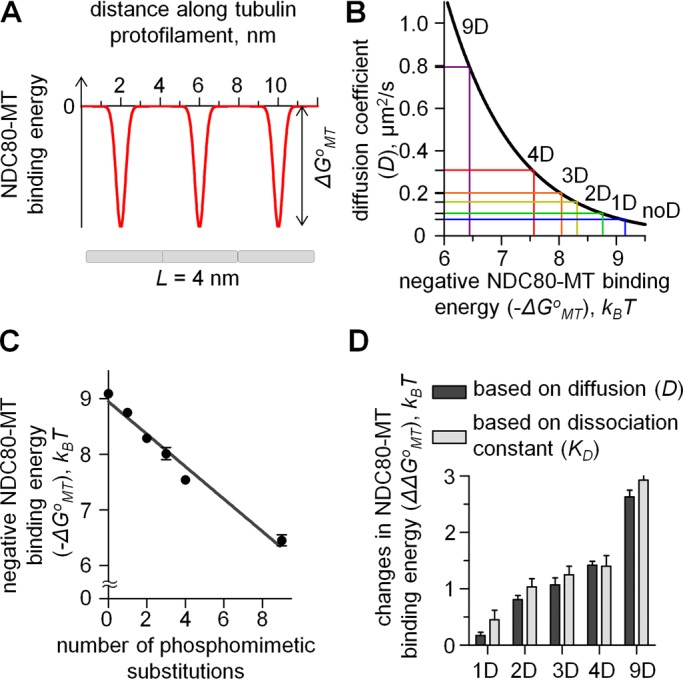
Quantitative TIRF analysis of single NDC80 molecules on MTs. (A) One-dimensional periodic energy landscape to model the site-specific interactions between a molecule and a linear array of subunits. Period is 4 nm, corresponding to the linear spacing of tubulin monomers in a tubulin protofilament. (B) Theoretical curve linking the diffusion coefficient and binding energy for a particle diffusing in a one-dimensional periodic potential was calculated as described in Materials and Methods. Horizontal lines show the measured diffusion coefficients for different NDC80 complexes in vitro. The 1D and 4D values correspond to the averaged diffusion coefficients for different 1D and 4D mutants, respectively. (C) NDC80-MT binding energy (ΔGoMT) estimated based on diffusion coefficient. Line is a linear fit. (D) Changes in NDC80-MT binding energy relative to noD NDC80 complex in response to phosphorylation were estimated based on diffusion coefficient and KD.
where ΔGoMT and σ are the depth and width of the potential well, respectively; Do is the diffusion coefficient in solution; x is the coordinate along a linear polymer with a potential period L; and kB is the Boltzmann constant. After specifying the model parameters relative to NDC80-MT interactions (as described in the Materials and Methods), we solved Eq. 1 numerically. With this approach, we estimate that the energy barrier for the diffusion of an unmodified NDC80 complex is 9.1 kBT (Figure 4B). This is a relatively strong binding, which is similar to the estimated MT interaction energy for Dam1 (Grishchuk et al., 2008) but smaller than that for diffusing Kip3 kinesin (Bormuth et al., 2009). The binding energy decreased linearly with increasing numbers of Ds, and for 9D NDC80, ΔGoMT was 6.5 kBT, a significantly smaller value than for noD NDC80 (Figure 4C).
In a second approach, we used the experimentally determined kon and τ to calculate the equilibrium dissociation constant KD = 1/(kon·τ). for various NDC80 complexes (Table 1). This ratio is linked to the NDC80-MT binding energy ΔGoMT via the following expression:
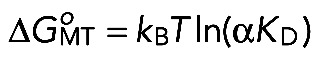 (2) (2)
|
where α is a coefficient that takes into account that NDC80 diffuses in an MT-bound state. This approach does not allow the calculation of ΔGoMT explicitly, because the value of α is unknown. However, Eq. 2 can be used to compare the binding energies of two molecular reactions with similar values of α:
 (3) (3)
|
where the superscript xD denotes a complex with x phosphomimetic substitutions. These two methods led to highly similar estimates of the change in NDC80-MT interaction energy in response to phosphorylation (Figure 4D). On average, each phosphomimetic residue results in the incremental decrease in NDC80-MT binding affinity by 0.30 ± 0.02 kBT (numbers are mean ± SEM here and below). Similar differences in binding energy per unit charge were observed previously for other systems (Okada and Hirokawa, 2000; Pufall et al., 2005; Lee et al., 2010).
NDC80-NDC80 interaction energy is weak relative to the energy of NDC80-MT binding
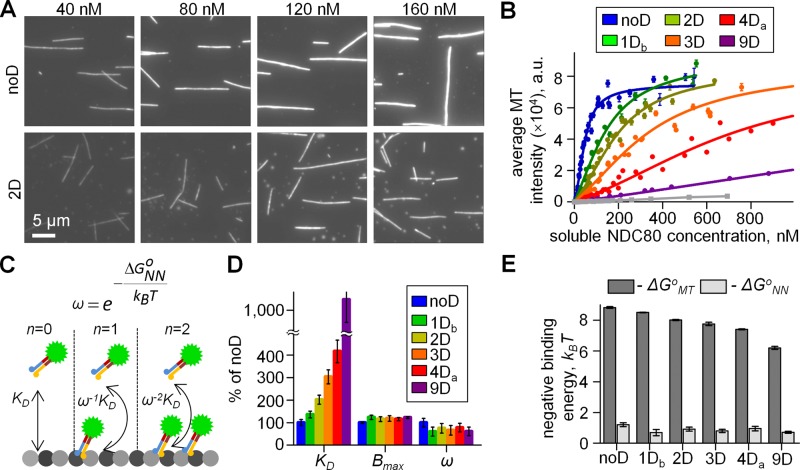
Previous biochemical studies of NDC80-MT interactions have suggested that NDC80 binding is cooperative (Cheeseman et al., 2006; Alushin et al., 2010; Umbreit et al., 2012), however, the estimates of this effect vary by orders of magnitude (Zaytsev et al., 2013). To quantify NDC80 cooperativity, we used the TIRF approach with MTs immobilized on the coverslip (Figure 1A). A wide range of soluble GFP-labeled NDC80 concentrations were introduced in a microscopy chamber with a constant flow to ensure that measurements were taken at a fixed level of soluble protein (Figures 2A and 5A; see Materials and Methods). We validated this approach by examining MT decoration density at <10 nM NDC80. At this low concentration, the MT intensity increased linearly with increasing NDC80 concentration, indicating that these changes were due to noncooperative, single-molecule interactions (Supplemental Figure S2). The slopes of these dependencies for different NDC80 phosphomimetic complexes were used to calculate ΔΔGoMT, producing highly similar estimates to the above two approaches (Supplemental Figure S2F) and thus demonstrating the accuracy of our MT-binding assay.
FIGURE 5:
Quantitative analysis of NDC80 phosphomimetic mutants using the TIRF-based MT-binding assay. (A) Representative images of the coverslip-attached MTs at indicated concentrations of NDC80 proteins. Each image is an average of 10 frames. (B) Quantification of data as in A. Solid lines are fitted with the model schematized in C. Number of independent experiments (N ≥ 3) for each protein. Gray line corresponds to Hec1Δ80, in which the entire Hec1 tail domain is deleted. (C) Molecular model of NDC80-MT and NDC80-NDC80 interactions: KD, dissociation constant; ω, cooperativity parameter; n, number of lateral contacts between MT-bound NDC80 complexes; ΔGoNN, interaction energy between adjacently bound NDC80 molecules on the MT lattice. (D) Molecular characteristics of the NDC80-MT interactions determined from data in B with the molecular model in C. Bmax (binding plateau), KD, and ω were used as fitting parameters to fit the experimental data. Values for noD protein were taken as 100% (Table 2). (E) NDC80-MT binding energy (ΔGoMT; same data as in Figure 4C) and the interaction energy between adjacently bound NDC80 molecules on the MT lattice (ΔGoNN). Kruskal-Wallis statistical test of ΔGoNN values results in p = 0.42, indicating absence of a trend.
At concentrations higher than 10 nM, all phosphomimetic complexes showed a slightly sigmoidal increase in their intensity of MT decoration (Figure 5B), indicating moderate cooperativity of NDC80-MT interactions. These binding curves were fitted with a molecular model based on McGhee and von Hippel (1974), which explicitly includes the intramolecular binding events (Figure 5C). Consistent with our estimates for ΔGoMT (Figure 4C), the parameter KD increased with the increasing number of D substitutions (Figure 5D). Moreover, the changes in ΔΔGoMT estimated from parameter KD were similar to the estimates obtained with the other three approaches (Supplemental Figure S2F). Interestingly, the binding plateau (parameter Bmax) was similar for all complexes tested, so mimicking phosphorylation did not affect the density of NDC80 complexes on the MT lattice at saturation (Table 2). Quantification of the intensity of a single GFP molecule under identical imaging conditions indicates that at saturation, different phosphomimetic complexes all bind at 1.9 ± 0.2 molecules per tubulin dimer, consistent with structural reports for nonmodified NDC80 (Wilson-Kubalek et al., 2008; Alushin et al., 2010). The value of the cooperativity parameter ω = 3.3 ± 0.4 for noD NDC80 was similar to that observed in MT-binding assays with unphosphorylated, full-length human NDC80 complexes (Umbreit et al., 2012). This value of ω corresponds to Hill's coefficient of 2.2 and indicates a relatively weak cooperativity, consistent with previous findings (Cheeseman et al., 2006; Ciferri et al., 2008; Umbreit et al., 2012). Using these values, we then estimated the energy of intramolecular NDC80-NDC80 interactions, ΔGoNN, as described in Zaytsev et al. (2013). The absolute value of ΔGoNN is <1.5 kBT for all phosphomimetic complexes, so the NDC80-NDC80 interactions are significantly weaker than the NDC80 complexes binding to MTs for all levels of NDC80 phosphorylation (Figure 5E).
TABLE 2:
Molecular parameters of NDC80-MT interactions measured in the TIRF MT-binding assay.
| Protein | NoD (N = 5) | 1Db (N = 3) | 2D (N = 5) | 3D (N = 3) | 4Da (N = 6) | 9D (N = 2) |
|---|---|---|---|---|---|---|
| Initial slopes, a.u./nM | 177 ± 16 | 133 ± 1 | 90 ± 3 | 59 ± 2 | 44 ± 3 | 18.6 ± 0.5 |
| Binding plateau (Bmax) × 104, a.u. | 7.6 ± 0.2 | 9.4 ± 0.7 | 8.8 ± 0.8 | 9.0 ± 0.9 | 8.7 ± 0.5 | 9.3 ± 0.2 |
| Cooperativity parameter (ω) | 3.33 ± 0.44 | 2.00 ± 0.40 | 2.50 ± 0.30 | 2.22 ± 0.24 | 2.60 ± 0.40 | 2.04 ± 0.13 |
| Dissociation constant (KD), μM | 0.53 ± 0.05 | 0.71 ± 0.04 | 1.06 ± 0.04 | 1.60 ± 0.07 | 1.92 ± 0.16 | 5.50 ± 0.11 |
| Negative NDC80-NDC80 binding energy (−ΔGoNN), kBT | 1.20 ± 0.13 | 0.69 ± 0.2 | 0.92 ± 0.13 | 0.80 ± 0.11 | 0.95 ± 0.15 | 0.71 ± 0.06 |
N, number of independent experiments. Errors are SEM. NDC80 mutants 1Db and 4Da correspond to S15D and S8,15,44,55D, respectively. Parameters Bmax, ω, and KD were obtained from the MT-binding assay; see Analyses of the in vitro data in Materials and Methods for details.
Cooperativity of NDC80-MT binding in vitro is not affected by Hec1 tail phosphorylation
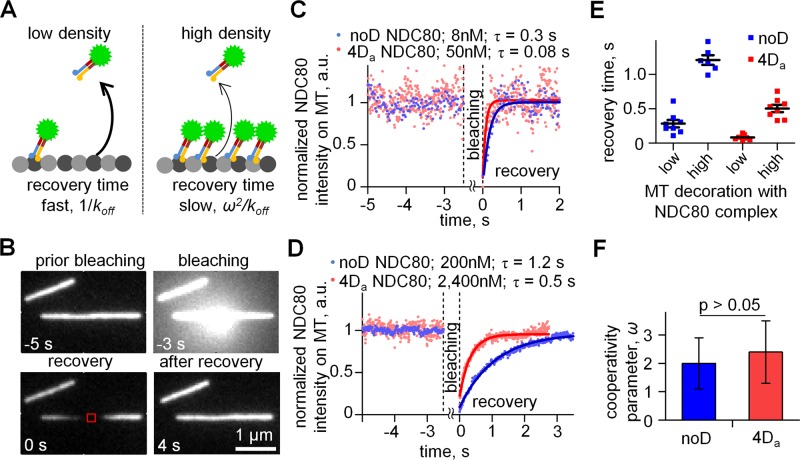
Published studies disagree on how phosphorylation affects cooperativity of NDC80-MT binding: while Alushin et al. (2012) concluded that cooperativity decreases for phosphorylated NDC80 complexes, this study did not report quantitative measures of cooperativity. On the other hand, the quantitative analyses of unmodified and 9D Hec1-containing NDC80 complexes suggested an increase in the cooperativity for phosphorylated NDC80 complexes (Umbreit et al., 2012); the experiments with these two complexes, however, were carried out under different experimental conditions. As reported in the preceding section, our quantitative TIRF-based assay for NDC80-MT binding showed that NDC80 cooperativity was not sensitive to the number of phosphomimetic substitutions (Table 2). To further test this conclusion, we developed a new experimental approach based on fluorescence recovery after photobleaching (FRAP). The rationale for this approach is that the recovery time for the intensity of NDC80-MT decoration after photobleaching should depend on the density of MT-bound NDC80 molecules (Figure 6A). Indeed, when the density of MT decoration is low, the recovery time corresponds to the lifetime of single-molecule binding (Bulinski et al., 2001), but the lifetime should increase at high MT decoration if the binding is cooperative. Therefore the ratio of the recovery times for two different degrees of MT decoration is an independent measure of binding cooperativity.
FIGURE 6:
FRAP-based analysis of NDC80-MT binding cooperativity. (A) Rationale for FRAP experiments. Higher density of NDC80 decoration increases the recovery time proportionally to ω2, so the recovery after photobleaching is expected to be slow (right panel) relative to the recovery at low NDC80 density (left panel). (B) Representative images of MTs decorated by GFP-labeled complexes of noD NDC80 (200 nM) during different experimental stages. MT was bleached for 3 s with a focused beam of a 488-nm laser (image at −3 s), and the intensity of the small MT segment (red square) was collected vs. time starting from 0 s, when the laser was turned off. (C and D) Representative intensity curves for low (C) and high (D) density of MT decoration. Lines are exponential fits. Different concentrations of soluble noD and 4Da proteins were used to reach the same degree of low and high MT decoration (Supplemental Figure S2H). (E) Recovery times for noD NDC80 and 4Da NDC80. Bars are means with SEM. (F) Mean ± SEM for cooperativity factor ω for noD NDC80 and 4Da NDC80 was determined as a square root of the ratio of the two recovery times in E.
We measured the recovery kinetics for two NDC80-GFP complexes (noD and 4Da) at two different MT decoration levels. The 4Da protein has 2 phosphomimetic substitutions in zone 2 of Hec1 tail, which has been suggested previously to inhibit cooperativity (Alushin et al., 2012). At a low level of MT decoration, both complexes recovered up to 95%, and the recovery times were very similar to the residency times of single molecules we have measured for these complexes (Figure 6, B and C, and Table 1). At a higher concentration of soluble protein and, hence, higher degree of MT decoration, both complexes showed relatively slow recovery, as expected (Figure 6, D and E). From the ratio of recovery times at high and low densities we determined that the cooperativity parameters for noD and 4Da NDC80 proteins were 2.0 ± 0.9 and 2.4 ± 1.1, respectively (Figure 6F). These values are not statistically different (p = 0.78, t test), and they are also consistent with the moderate cooperativity determined from the TIRF MT-binding assay (Table 2). Thus the FRAP-based method corroborates our above conclusion that phosphorylation of the Hec1 tail does not change appreciably the cooperativity of NDC80 binding.
MD simulations demonstrate significant conformational plasticity of the Hec1 tail, which binds the MT lattice via compact but random configurations
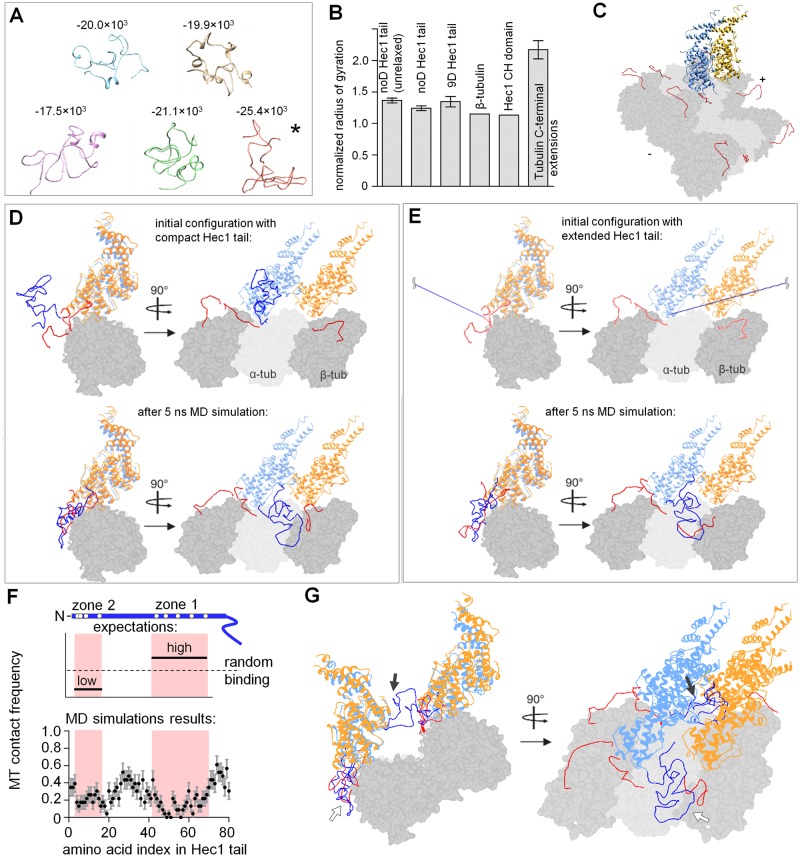
To gain mechanistic understanding of our in vitro results, we then used computational approaches. The average output of four different algorithms, which evaluate the propensity for intrinsic disorder based on the primary sequence, has confirmed that the Hec1 tail is likely to be structurally unstable (Supplemental Figure S3A; Ciferri et al., 2008; Guimaraes et al., 2008). Consistently, the ab initio predictions for the Hec1 tail, which we prepared with the Rosetta package (see Materials and Methods), were highly variable. Five structures with lower energy were selected and relaxed for 30 ns using MD simulations with AMBER99SB force field. Stability of one Hec1 tail configuration (Figure 7A, asterisk) was then followed for ∼1 μs, revealing that the Hec1 tail continuously evolves in solution (Supplemental Figure S3B). Interestingly, these unstable configurations were compact, with the normalized radius of gyration similar to those of β-tubulin and the Hec1 CH domain but smaller than that of the unstructured C-terminal extension of tubulin (Figure 7B). Thus utilizing the cartoon schematics of the Hec1 tail as an elongated linear extension of Hec1-Nuf2 heterodimer is likely to be inaccurate, and such simplifying cartoons should be treated with caution.
FIGURE 7:
MD simulations of the NDC80-MT binding interface. (A) Predictions for Hec1 tail (aa 1–80) conformations obtained using Rosetta with subsequent 30-ns optimization in GROMACS. Numbers show conformation energy in a.u., as obtained with GROMACS. Structure indicated with asterisk was used for MD simulations in a context of the NDC80-MT interface. (B) Normalized radius of gyration (Lobanov et al., 2008) was calculated for Hec1 tail structures after using ROSETTA only (“unrelaxed” tail structures); all other Hec1 structures were subsequently optimized in GROMACS. Analogous compactness analysis was done using available structures of β-tubulin, the Hec1 CH domain, and the tubulin C-terminal extensions, which are the least compact. For Hec1 tail and C-terminal extensions, bars are mean ± SEM; at least 5 different Hec1 tail conformations were averaged; for C-terminal extensions structures of 2 α-tubulin and 2 β-tubulin C-terminal extensions were averaged. (C) Snapshot of the MT surface patch used in MD simulations. Two adjacent NDC80 complexes with no Hec1 tails are shown in blue and yellow; tubulin C-terminal extensions are in red; plus (+) and minus (−) signs indicate MT polarity. (D) Representative structure of the MT-NDC80 interface obtained after 5-ns simulation in GROMACS. Two globular CH domains of the adjacent NDC80 complexes bound to the MT segment are shown in blue and yellow; tubulin monomers are in gray. The N-terminal tail of the left NDC80 complex (dark blue) was folded with Rosetta. Two adjacent tubulin protofilaments were present during the simulation but are not shown in this figure for clarity. (E) Views of the NDC80-MT patch as in D, but the initial configuration had a fully extended Hec1 tail. Another two example structures obtained after the MD simulations for this initial configuration are shown in Supplemental Figure S3D (Supplemental Video 3). (F) Residue-specific side-chain contact probability for the Hec1 tail with the MT after 5 ns of simulation. Top schematics show expectations for two different scenarios. In one, zone 1 becomes ordered at the MT-binding interface, leading to a “low” number of MT contacts relative to zone 2. Alternatively, MT binding may occur via random contacts. Bottom graph was calculated based on 23 simulations of the NDC80-MT interface starting from the unfolded tail. Pink highlights zones 1 and 2. (G) Representative example of the structure after 5 ns of the simulation when two pairs of the NDC80 complexes were positioned on neighboring protofilaments (Supplemental Video 4); white arrows, Hec1 tail that belongs to the front NDC80 complex; black arrows, Hec1 tail that belongs to the rear NDC80 complex positioned on the neighboring protofilament; total number of simulations: 5.
Next we analyzed Hec1 tail behavior in the context of a Hec1-Nuf2 heterodimer bound to the MT. A second heterodimer was positioned adjacently, using electron density maps generated in Alushin et al. (2010). Such composition allows examination of interactions between the Hec1 tail and the binding interface between two adjacent NDC80 dimers in the context of polymerized tubulins (Figure 7C). The tubulin C-terminal extensions, which are required for NDC80-MT interactions (Ciferri et al., 2008), were fused to α- and β-tubulins in the MT wall. These tubulin extensions and the compact Hec1 tail were then subjected to MD simulations, while the atomic positions of the globular protein domains remained fixed. The Hec1 tail quickly reoriented to form multiple contacts with the surface of the nearest tubulin dimer and one to two nearby tubulin C-terminal extensions (Figure 7D), and the system reached quasi steady state in ≤5 ns (Supplemental Figure S3C). Similar MT interactions were seen in additional 23 simulations, in which the tail was initially extended (Supplemental Video 3), so our results do not depend on initial tail configuration (Figure 7E).
Importantly, the exact final configurations of the MT-bound Hec1 tail were different, even when simulations started from an identical tail configuration (Figure 7E and Supplemental Figure S3D), suggesting that the tail did not become ordered upon binding to the MT. To test this conclusion, we examined whether zone 1 within the tail showed preferential binding to the MT, as expected based on the model in Alushin et al. (2012). This was done by calculating the frequency with which different Hec1 tail residues contacted the MT in different simulations. There was a considerable variability in which of the Hec1 residues contacted the MT (Figure 7F), suggesting that the Hec1 tail has no specific MT-binding conformation. Importantly, tail zones 1 and 2 had approximately equal probability to bind the MT (0.14 ± 0.08 and 0.20 ± 0.05, respectively; p = 0.6, t test). MT binding via the amino acids located in between these zones was slightly higher, but the differences with zones 1 and 2 were not significant (0.30 ± 0.11; p > 0.25). These results demonstrate that different areas of a randomly folded Hec1 tail can form a binding interface with the MT.
Hec1 tail exhibits weak interactions with adjacent Hec1-Nuf2 head domain in silico
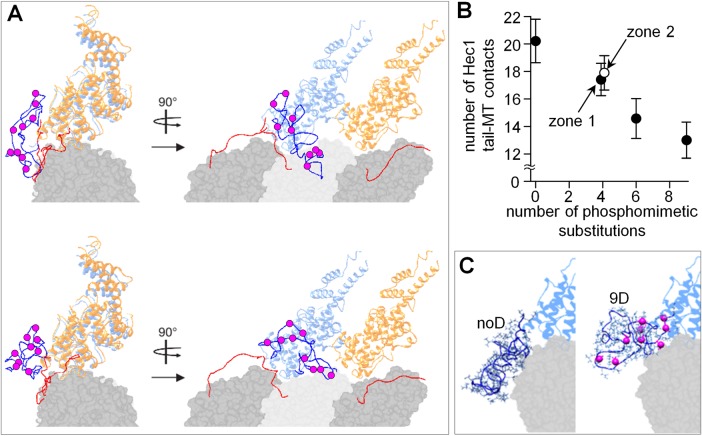
Interestingly, the tails in our simulations did not form extensive contacts with any of the two globular Hec1-Nuf2 domains or at their interface, even when the tail was initially extended such that it could potentially wrap around or lie in between the Hec1-Nuf2 heads during subsequent folding. To further examine the relative strength of molecular interactions between different tail zones and Hec1-Nuf2 heads, we sought a quantitative measure of these interactions based on the number of amino acid contacts. To test this approach, we first calculated the total number of amino acid contacts formed by one NDC80 complex (Hec1-Nuf2 head and its unmodified tail) with either the adjacent Hec1-Nuf2 head domain or the MT. The in silico “interactions” between one NDC80 complex and the MT were significantly stronger than the interaction of the NDC80 complex with the adjacent Hec1-Nuf2 head domain (Supplemental Figure S3E). This computational result is fully consistent with the relative strength of these binding interfaces in vitro (Figure 5E), validating this computational approach.
Next we determined the total number of amino acid contacts formed by the Hec1 tail with the adjacent Hec1-Nuf2 head: on average only 6.7 ± 4.7 contacts were found at this interface, while 20.2 ± 7.5 contacts were seen at the tail's interface with the MT. The relatively infrequent contacts between the Hec1 tail and the adjacent NDC80 complex indicate that the tail is unlikely to play a large role in promoting NDC80-NDC80 cooperativity. Interestingly, the Hec1 tail contacts with the adjacent Hec1-Nuf2 head were frequently via amino acids in zone 1, rather than zone 2 (average contact probability 0.18 ± 0.09 vs. 0.01 ± 0.02, p < 0.001, N = 23). This is opposite to the model in Alushin et al. (2012), which proposes that zone 2 becomes ordered at the interface with the adjacent Hec1-Nuf2 head.
Another significant difference between our MD simulations and the findings in Alushin et al. (2012) is that this structural study found an electron density (which authors attributed to zone 2 of the Hec1 tail) located at some distance from the MT surface and at the Nuf2 surface that is opposite to the junction between the Hec1 globular head and its tail (fig. 5 in Alushin et al., 2012). In contrast, in our MD simulations, the entire tail was located closely to the MT and it did not reach to the “back” surface of the adjacent Hec1-Nuf2 globule (Figure 7D). We hypothesize that this discrepancy might result from the different density of NDC80 complexes in these two studies: two adjacent subunits were examined in silico, while the electron density maps were generated by imaging MT surfaces fully saturated with NDC80 complexes. We mimicked such high surface density by positioning two pairs of NDC80 complexes on two neighboring protofilaments; two Hec1 tails were then simulated, one in the front row and one in the back (Figure 7G). Interestingly, the Hec1 tail that belonged to the NDC80 complex that had no neighbors on its N-terminal “front” side behaved as seen for the less-packed configuration, forming a compact globule near the MT surface “in front” of this subunit (Figure 7G, white arrows). However, the tail of the Hec1 subunit that was positioned in the back row did not bind to the MT surface due to steric hindrance by the NDC80 subunits located in front (Supplemental Video 4). This tail was seen in a compact configuration, but it reached to the Nuf2 subunit that belonged to the front row (Figure 7G, black arrows). Of note, this configuration is highly reminiscent of what was seen with electron microscopy reconstruction, suggesting that the density at the Nuf2 subunit, which was previously attributed to zone 2 of the tail of its binding Hec1 subunit, instead corresponds to the Hec1 tail that belongs to another heterodimer positioned on the neighboring protofilament. It remains to be seen whether such intramolecular contact between the Hec1 tail and the Nuf2 head has physiological significance, since it is revealed only when the NDC80 complexes are tightly packed on the MT wall.
Phosphorylation of the Hec1 tail leads to a graded tuning of its MT binding in silico
To analyze the phosphoregulation of the Hec1 tail-MT interactions in silico, we then modified the Hec1 tail sequence to insert D residues, analogous to our phosphomimetic proteins used in vitro. When all nine D residues were added, the tail compactness did not change considerably, and its compactness was similar to the unmodified tail (Figure 7B). Strikingly, the “phosphorylated” tail slightly “repelled” from the MT surface and the tubulin C-terminal extensions tended to avoid binding to it (Figure 8A and Supplemental Video 5). The average number of amino acid contacts between the tail and MT dropped from 20 to 13 (Figure 8B). The configuration of the 9D Hec1 tail was strikingly different from that seen for the unmodified tail (Figure 8C). Tail sequences with intermediate numbers of Ds showed a roughly linear dependency, in excellent agreement with our findings in vitro (Figure 4C). Moreover, the number of contacts formed with the MT by the 4D tail was highly similar when these modifications were in zone 1 versus zone 2 (Figure 8B), consistent with our experimental conclusion that the total number of substitutions but not their exact location determines the strength of the MT-Hec1 tail interaction.
FIGURE 8:
MD simulations of the Hec1 tail with phosphomimetic substitutions. (A) Two representative examples of the structures obtained after 5-ns MD simulation using the initially unfolded Hec1 tail with nine phosphomimetic substitutions (purple circles). (B) Average number of contacts (amino acids in the Hec1 tail) between the Hec1 tail and the MT. Simulations (N ≥ 16) were performed using Hec1 tails with the indicated number of phosphomimetic substitutions. Two different 4D complexes were analyzed with phosphomimetic mutations located in either zone 1 or zone 2; these symbols are slightly offset horizontally for clarity. (C) Representative conformations for noD NDC80 and 9D NDC80 Hec1 tails, viewed along the MT surface; the second NDC80 complex is not shown.
Finally, we examined the impact of tail phosphorylation on the cooperativity of NDC80-MT interactions by calculating the number of contacts formed by the modified Hec1 tails and the adjacent Hec1-Nuf2 domain. The in silico “interactions” between the phosphorylated NDC80 complex and the adjacent subunit were significantly weaker than between the NDC80 complex and the MT for the entire range of the number of D substitutions (Supplemental Figure S3E), analogous to our findings in vitro. Importantly, two tails with different 4D substitutions—in zone 1 (S49,55,62,69D) or 2 (S4,5,8,15D)—had a similarly low number of contacts with the neighboring NDC80 complex (Supplemental Figure S3F), indicating that location of phosphorylated residues has little impact on the strength of these interactions. Thus the results of the in vitro measurements for NDC80 phosphomutants are in quantitative agreement with the behavior of different Hec1 tails in silico.
DISCUSSION
NDC80 complexes function at the kinetochore as independent MT binders rather than within oligomeric clusters
The NDC80 complex is a core kinetochore MT-binding component, but how NDC80 molecules contribute to kinetochore-MT attachment is controversial. Structural work with purified NDC80 protein complexes has proposed that Hec1 tail phosphorylation affects oligomerization of NDC80 complexes, leading to their clustering or unclustering (Alushin et al., 2010, 2012). Phosphoregulation of NDC80 clustering is potentially important because it implies significant changes in the design of the kinetochore-MT interface during mitotic progression, which, depending on phosphorylation, could contain either independent NDC80 binders or oligomeric arrays. In contrast, our previous analysis of how Hec1 phosphorylation affects kinetochore affinity to MTs in live cells has led us to propose that NDC80 complexes function as independent molecular binders throughout mitosis (Zaytsev et al., 2014). These different views have prompted us to carry out a thorough investigation of the phosphoregulation of NDC80-MT binding in vitro.
With four different quantitative approaches, we demonstrate that the energy of MT binding for single NDC80 complexes changes incrementally with the number of phosphomimetic substitutions on the Hec1 tail (Figure 4D and Supplemental Figure S2F). We find, however, that NDC80 binding cooperativity is weak, and it is not affected by phosphorylation (Figure 5E). These in vitro results have been corroborated in a highly quantitative manner using MD simulations of NDC80-MT binding (Figures 8B and Supplemental Figure S3E). Together, these results provide important new insights about the molecular design of the kinetochore MT-binding interface composed of NDC80 molecules, since they permit estimation of the extent of NDC80 oligomerization at the kinetochore-MT binding interface. With the help of the residency time (τ) and cooperativity parameter (ω) reported in this study, we estimate computationally that ∼90% of NDC80 molecules could bind to kinetochore MTs at metaphase as monomers, 8% as dimers, and only 2% could potentially form larger clusters (Figure 9A; see Materials and Methods). Because only 12 NDC80 molecules are thought to be engaged in binding to one kinetochore MT, the chance of finding NDC80 oligomers with three subunits or larger at the kinetochore is negligible.
FIGURE 9:
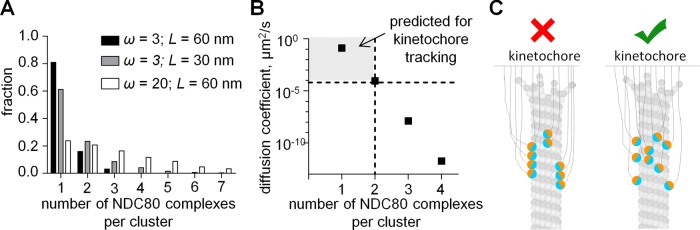
Structural arrangement of NDC80 molecules at the kinetochore. (A) Predicted size of the clusters of NDC80 molecules bound to the kinetochore-attached MT; ω, cooperativity factor; L, length of the MT segment available for NDC80 binding. (B) Predicted diffusion coefficient of 1D NDC80 clusters of different sizes. Clusters that diffuse slower than 6.4 × 10−5 μm2/s (below horizontal dashed line) cannot track a MT tip that disassembles faster than 1 μm/min, so the predicted maximal size for the tip-tracking 1D NDC80 complex is 2 subunits. (C) Models of the structural arrangement of the MT-bound NDC80 complexes at the kinetochore. NDC80 complexes have been suggested to form structured oligomers (left), but our data are more consistent with a model in which NDC80 complexes bind kinetochore MTs as monomers and, rarely, as dimers (right).
Our in vitro measurements reported here for NDC80 diffusion are also inconsistent with the presence of large oligomeric arrays of NDC80 at the ends of dynamic kinetochore MTs. Indeed, only monomers and dimers of NDC80 protein diffuse fast enough to be able to processively track the ends of kinetochore-attached MTs at 1 μm/min, the rate of chromosome motion (Figure 9B; Grishchuk et al., 2012). Larger NDC80 clusters are predicted to diffuse so slowly that they would not be able to follow the dynamic MT end, inhibiting kinetochore tracking. Thus the oligomeric arrays of NDC80 complexes are unlikely to be a functionally significant form of the kinetochore-MT molecular coupling mechanism. Our data are more consistent with the view that NDC80 complexes at the kinetochore interact with the MTs as individual molecular binders, which do not convert into oligomeric arrays in response to changes in Hec1 tail phosphorylation (Figure 9C). The results reported here provide important molecular evidence to support our model that the kinetochore MT-binding interface is composed of a molecular “lawn” of NDC80 complexes (Zaytsev et al., 2014).
Conformational plasticity of the Hec1 tail enables it to serve as a phosphorylation-controlled rheostat for tuning NDC80-MT binding
Structural study of NDC80-MT binding has previously led to the model in which two segments of the Hec1 tail become ordered upon binding to the MT: zone 2 at the interface with tubulin and zone 1 at the interface with a neighboring NDC80 head on the MT surface, forming interactions that can then be disrupted by phosphorylation (Alushin et al., 2012). However, our MD simulations of the Hec1 tail in the context of two adjacent MT-bound NDC80 complexes do not support this model and suggest that Hec1 tail configurations seen by electron microscopy may have resulted from molecular overcrowding. In silico, different amino acids in a randomly folded Hec1 tail that is not sterically restricted by the neighboring subunits form random interfaces with the MT and the adjacent NDC80 head. Zones 1 and 2 show no preferential affiliation with the MT, although there is a tendency of amino acids in zone 2 to contact the adjacent Hec1-Nuf2 head. Importantly, adding phosphomimetic substitutions does not change this general behavior, leading us to a new molecular model for the phosphoregulation of NDC80-MT interactions (Figure 10A).
FIGURE 10:
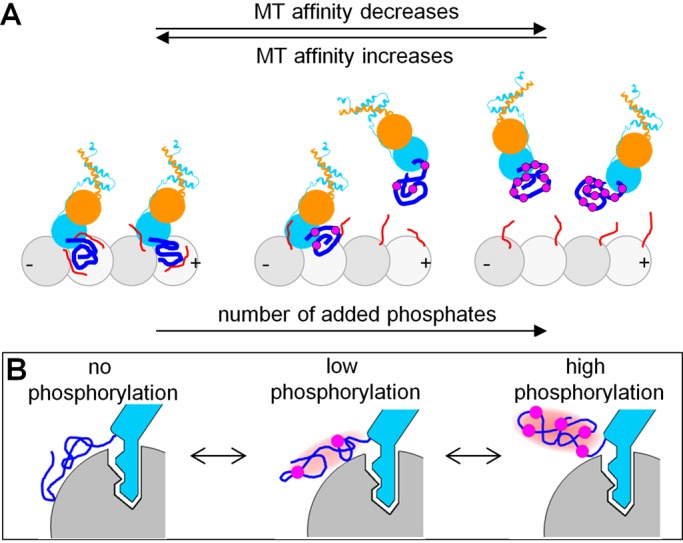
The Hec1 tail as a phosphorylation-controlled rheostat for tuning NDC80-MT binding. (A) Increasing numbers of Hec1 tail phosphorylations tune NDC80-MT affinity by reducing the energy of NDC80-MT binding, while NDC80 binding cooperativity is unchanged. Symbols are as in Figure 1B; note that the MT is rotated 180° relative to the schematic in Figure 1B. (B) Proposed dual mechanism to explain rheostasis of NDC80 (blue) binding to polymerized tubulin (gray). The site-specific lock-and-key binding by the globular head is assisted by the conformationally unstable protein extension, which additively integrates the output from multiple phosphorylation events (purple circles) regardless of their exact location.
The finding that the strength of NDC80-MT binding correlates with the number of phosphomimetic substitutions in the Hec1 tail, but not with their position, is striking. Insight into the underlying mechanism is provided by the MD simulations of the Hec1 tail in solution, which show that the Hec1 tail is conformationally unstable. Although the tail adopts a relatively compact structure, the exact positions of different amino acids within the soluble Hec1 tail are changing continuously. Importantly, such conformational plasticity dynamically randomizes the relative positions of phosphoresidues within the tail and ensures that, on average, each added phosphomimetic substitution reduces additively the number of contacts between the Hec1 tail and the MT (Figure 8B). Thus the dynamic plasticity of the Hec1 tail explains why the NDC80-MT binding affinity in vitro decreases linearly with the increasing number of phosphates and independently of their positions (Figure 4C).
Activity or binding of many intracellular proteins is regulated by single or multisite phosphorylation, which can switch protein interactions “on” or “off” (Salazar and Höfer, 2009). However, graded and dynamic adjustment of the binding affinity is problematic for proteins that interact strongly via a traditional lock-and-key mechanism, such as seen between the CH domain of Hec1 and its MT-binding site (>6 kBT). We propose that graded tuning of the MT binding in this case is realized with the help of an additional domain, which binds the MT less strongly but is amenable to adjustment by multisite phosphorylation, because such a domain can additively integrate the output from multiple phosphorylation events regardless of their specific locations (Figure 10B). The conformationally unstable Hec1 tail serves as a rheostat for tuning the binding in a 0–3 kBT range, or up to 30% of the total NDC80-MT binding affinity. This provides a molecular mechanism to explain how NDC80-MT binding elicits gradual and dynamic control of kinetochore-MT affinity during cell division (DeLuca et al., 2011; Zaytsev et al., 2014). Graded phosphoregulation has been proposed previously for the unstructured domains of the transcriptional activators Ets-1 (Pufall et al., 2005) and p53 (Lee et al., 2010) and the Kv2.1 potassium channel (Park et al., 2006), but NDC80 is the first MT-binding protein whose affinity is shown to be tuned in this manner. The dual mechanism of NDC80-MT interactions, which combines the strong and specific binding of the globular NDC80 “head” with the adjustable binding of an unstructured tail domain, provides a new paradigm for graded regulation of the binding affinity of MT-associated proteins.
MATERIALS AND METHODS
NDC80 “Bonsai” constructs and protein purification
Glutathione S-transferase (GST)-Bonsai-His6 was a generous gift from Andrea Musacchio, Max Planck Institute of Molecular Physiology, Dortmund, Germany (Ciferri et al., 2008). His6 was cloned onto the C-terminus of the Nuf2/Spc24 moiety using overlapping PCR. GFP (from pEGFP-N1 vector) was cloned onto the C-terminus of the Hec1/Spc25 moiety using modified SLIM, where a GFP PCR fragment containing sticky ends was obtained. This was then annealed with a GST-Bonsai PCR fragment containing complementary sticky ends (also obtained by site-directed, ligase-independent mutagenesis). NDC80 “Bonsai” constructs fused to GST were expressed in BL21-DE3 cells by induction with 0.4 mM isopropyl β-d-1-thiogalactopyranoside at 18°C for 16 h. Cells were harvested by centrifugation, and cell pellets were resuspended in lysis buffer (25 mM Tris, pH 7.6, 300 mM NaCl, 1 mM EDTA) supplemented with protease inhibitors and dithiothreitol (DTT; 1 mM final). All purifications were carried out at 4°C. Cell suspensions were subjected to sonication, and cell debris was pelleted by centrifugation at 40,000 rpm for 1 h. The supernatant was added to glutathione-agarose resin, and proteins were bound by gentle rotation for 1 h. Unbound protein was washed away, and bound protein was cleaved from GST and the glutathione resin by overnight incubation with Prescission Protease (GE Healthcare, Piscataway, NJ). Cleaved protein was then further purified by size-exclusion chromatography on a GE Superdex 200 HiLoad 16/60 column in lysis buffer supplemented with 5% glycerol and 1 mM DTT. Protein-containing fractions were pooled and concentrated, and glycerol was added to a final concentration of 20%. Small protein aliquots were stored at −80°C after snap-freezing in liquid nitrogen. Tubulin was purified from cow brains by thermal cycling (Hyman et al., 1991).
TIRF microscopy
All measurements were carried out at 32°C on a Nikon Eclipse-Ti microscope using a CFI APO 100× Nikon-TIRF NA 1.49 objective with an additional 1.5× magnification (pixel size: 90 nm) and the Perfect Focus system (Nikon, Melville, NY). A Coherent 488-nm diode laser was used as a light source with a Chroma (Bellows Falls, VT) C-TIRF Quad cube (final output: 10 mW). Data were acquired using Andor (Concord, MA) iXon3 camera in NIS-Elements software. Single-molecule measurements were carried out with the “Fast Kinetics” acquisition mode of the camera, equipped with OptoMask (CAIRN Research, Kent, UK) with camera settings: 10-MHz; 14-bit sensor readout mode; 999 EM gain; conversion gain: 5×; frame size: 220 × 120 pixels. In most single-molecule experiments, images were acquired continuously for 200 s at 100 frames/s (exposure time: 5 ms for 9D NDC80 phosphomutant and 10 ms for all other constructs). Coverslips (22 × 22 mm) were cleaned and silanized, as described in Volkov et al. (2014) and assembled in custom-made flow chambers (Volkov et al., 2014). Antitubulin antibodies (Serotec, Raleigh, NC) diluted 1:30 in BRB80 were flowed into the chamber and incubated for 10 min. After being washed with BRB80, 1% Pluronic F-127 (Sigma-Aldrich, St. Louis, MO) solution was added for 8 min; this was followed by another wash with BRB80 supplemented with 10 μM Taxol. Taxol-stabilized MTs were then flowed into the chamber and incubated for 15 min. NDC80 was diluted to the desired concentration in imaging buffer (K-Pipes 80 mM, pH 6.9, 4 mM Mg, 1 mM EGTA, 0.5 mg/ml casein, 4 mg/ml bovine serum albumin, 2 mM DTT, 0.1 mg/ml glucose oxidase, 68 μg/ml catalase, 20 mM glucose, 0.5% 2-mercaptoethanol, 10 μM Taxol) and then perfused continuously into the chamber at 15 μl/min during data acquisition to increase reproducibility of our experiments. For TIRF-based measurements of NDC80-MT binding affinity, NDC80 protein was dialyzed to exchange into BRB80 solution (pH 6.8), then ultracentrifuged in a Beckman Airfuge at 130,000 × g for 12 min; the supernatant was collected and kept on ice. The protein concentration of the resulting supernatant was measured with a Bio-Rad assay. Protein was diluted to specific concentrations in imaging buffer and flowed into the chamber for 4 min to achieve a steady state for NDC80-GFP decoration of MTs (Supplemental Figure S2A). Images of a field of decorated MTs were captured with the following camera settings: 1 MHz; 16-bit sensor readout mode; no EM gain; conversion gain: 5×; 256 × 256 pixels frame size. This procedure was repeated for 10–12 different fields to obtain images of at least 40 MTs for each protein concentration.
Analyses of the in vitro data
Illumination normalization procedure.
To account for unevenness of TIRF illumination, we normalized all fluorescence images before quantitative analysis as described in Volkov et al. (2014).
Photobleaching.
For measuring the photobleaching rate of GFP-labeled NDC80 complexes, protein was diluted with imaging buffer to 50 nM and incubated for 10 min in a chamber without MTs and without the blocking agent, Pluronic F127. Soluble protein was then washed out to exclude an exchange with the soluble protein pool during imaging. Time-lapse stacks were acquired with the same settings as used for acquiring the single-molecule data for NDC80-MT interactions. Average pixel intensity was plotted as a function of time and fitted exponentially. The measured GFP photobleaching time constant in our single-molecule assay was 1.9 ± 0.1 s.
Determining the molecular characteristics of single NDC80 complexes.
Positions of MTs (polymerized with nonfluorescent tubulin) on normalized images were determined with ImageJ (National Institutes of Health, Bethesda, MD) using average projections of image stacks in the GFP channel. Kymographs were built by drawing a line, 6 pixels in width, along the MT axis using MetaMorph 7.7 (Molecular Devices, Sunnyvale, CA). Different molecular characteristics were determined from the kymographs using custom programs developed using Mathematica 8.0 (Wolfram Research, Champaign, IL), as described below.
For determination of the diffusion coefficient D (μm2/s), the rectangular regions containing diffusion tracks were manually selected on the kymographs, such that each region contained the entire track of one complex while avoiding other complexes. The duration of each track was at least 10 frames or 100 ms. The position of the dot within this defined rectangular region for each time point was determined using a Gaussian fit. The position of the dot at the beginning of the track was set as 0, and the squared displacements for each time point were calculated. These displacements were averaged between >600 tracks to plot the MSD as a function of time (Figure 3C). The diffusion coefficient was determined as one-half the slope of this dependency.
For determination of the dissociation rate koff (s−1), all “landing” events on each kymograph were manually selected by clicking on the first and last points. Durations of these individual events were plotted as a histogram and fitted exponentially after excluding data in the first bin (50 ms; Figure 3B). The value of koff was obtained from the results of the fitting and corrected for photobleaching as described in Helenius et al. (2006).
Residency time τ (ms) for a given protein was calculated as 1/koff.
The association rate kon (s−1 nM−1) was determined as follows. First, the total number of binding events was obtained by integrating exponential fits (red exponential curves in Figure 3B) of the residency-time histograms. Second, the total observation time for these data was determined. Next the lengths of MTs used to obtain these data were summed to calculate total MT length. The association rate was calculated by dividing the total number of binding events by total observation time, total MT length, concentration of NDC80, and by 3250, the number of tubulin monomers in 1 μm of MT.
To measure the number of NDC80 complexes in the MT-associated NDC80-GFP dots, we first determined the fluorescence intensity of a single fluorophore by recording the time course of photobleaching for NDC80-GFP complexes nonspecifically attached to the coverslip surface (Volkov et al., 2014). Briefly, the changes in integrated intensity in a circle drawn around a fluorescent dot (diameter: 5 pixels) were then measured (Supplemental Figure S1A). These values for multiple dots were plotted as a histogram of integrated intensities and fitted with an equidistant Gaussian curve (Supplemental Figure S1B). The distance between Gaussian peaks corresponds to the intensity of a single GFP fluorophore under single-molecule imaging conditions. Determined value corresponds to (1.95 ± 0.03) × 104 a.u.
We then determined the intensities of MT-associated NDC80-GFP complexes using two different methods. In the first method, we manually determined integrated intensity of a circular area (diameter: 5 pixels) around each NDC80-GFP complex for the first frame when it appeared on an MT in our single-molecule experiments. Supplemental Figure S1C shows that > 95% of all MT-bound NDC80 complexes were in the form of monomers. To exclude the possibility of any bias introduced by manual analysis, we carried out an additional analysis. We developed a program using Mathematica software (Wolfram Research) to collect the maximum integrated intensity within a circular area (diameter: 5 pixels) for MT-bound complexes for all time frames of the imaging sequence (Figure 3B). Background intensities were obtained by applying the same algorithm as for the MT-associated NDC80 complexes but for MT-free areas, and the results were plotted on the same graph as the background. This approach determined the distribution of intensities of NDC80 complexes on the MT. The distance between two peaks is (1.87 ± 0.04) × 104 a.u., demonstrating that, in our single-molecule experiments, NDC80 complexes associate with MTs as monomers, consistent with the results of manual analysis.
Determining MT-binding affinity and cooperativity with the TIRF-based MT-binding assay.
Ten images for each field of the MTs decorated with NDC80-GFP complexes were averaged. MTs were selected using a rectangular 16-pixel-wide region (Supplemental Figure S2B). Using custom-written software in ImageJ, we plotted the peak intensities in this region along the MT length (Supplemental Figure S2C). The brightness of each MT was defined as the average level of the corresponding line scan. For each protein concentration, we analyzed at least 40 MTs. Fitting for data in Figure 5B was based on the model in McGhee and von Hippel (1974).
Calculating the density of NDC80 packing on the MT lattice at saturation.
The measured values of binding plateau Bmax in our TIRF-based MT-binding assay for all examined NDC80 proteins were similar: (8.4 ± 0.6) × 104 a.u. To calculate how this intensity value corresponds with the number of bound NDC80 molecules per tubulin dimer (N), we measured integrated intensity of a single NDC80-GFP molecule under same imaging conditions: 588 ± 21 a.u. (see Determining the molecular characteristics of single NDC80 complexes). From this integrated intensity and the width of the point-spread function for a single NDC80-GFP complex (3.4 pixels), we estimated the peak pixel value for a single NDC80-GFP molecule: 78 a.u. The Bmax intensity is then given by 78 a.u. × 3.4 pixels × 169 × N, where 169 is the number of tubulin dimers per pixel. Therefore, in our assays, the binding plateau Bmax at saturation was achieved with density N = 1.9 ± 0.2 molecules per tubulin dimer.
Analysis of NDC80 cooperativity using FRAP.
MT brightness was determined as mean intensity in the 5 × 5 pixel region centered on the image of a bleaching spot (red square in Figure 6B). Background signal was determined in the vicinity of the MT for each time, and these values were then subtracted from the MT brightness versus time curve. To determine whether diffusion of NDC80 complexes contribute to the observed recovery kinetics, we estimated the predicted recovery time τD, assuming that recovery takes places only due to diffusion (Sprague et al., 2004): τD = l2/D, where l is radius of focused beam (in our system l = 1.1 μm) and D is the NDC80 diffusion coefficient. For noD NDC80, we obtain τD = 13.8 s, much slower than the observed recovery time (0.29 ± 0.05 s), implying that diffusion contributes < 2% to recovery kinetics. A similar result was obtained for 4D NDC80 (τD = 3.2 s, and the observed recovery time is 0.084 ± 0.012 s). We conclude that the observed recovery kinetics reflect the continuous exchange of MT-bound NDC80 complexes with the soluble NDC80 pool.
Theoretical approaches to estimate MT-binding energy
Changes in the MT-binding energy for single NDC80 complexes were calculated using four independent approaches, which involved different experimental parameters. Values obtained from all four different approaches produced similar results.
Diffusion coefficient.
If a particle undergoes one-dimensional Brownian motion in a periodic potential field, its diffusion coefficient (D) can be calculated using an analytical model for the particle diffusing in a one-dimensional periodic potential field u(x), as in Festa and Galleani (1978) using Eq. 1. Our results show that, under saturating conditions, the NDC80 complex binds every tubulin monomer in the MT lattice (as described in Calculating the density of NDC80 packing on the MT lattice at saturation), so the period of the potential is equal to the tubulin monomer size (4 nm). Do for a protein with molecular weight 100 kDa in water is ∼30 μm2/s (Salmon et al., 1984). For typical protein–protein interactions, σ lies in the range 0.2–0.5 nm (Jiang et al., 2002); for our calculations, we used σ = 0.24 nm. Equation 1 was then solved for different phosphomimetic forms of NDC80 by using Mathematica software.
This model was also used to predict the diffusion coefficients for oligomeric clusters of multiple NDC80 molecules on the MT wall during metaphase (Figure 9B). Equation 1 was used with ΔG0MT for 1D NDC80 protein multiplied by the number of molecules in the cluster. Because 1D NDC80 can recapitulate normal kinetochore-MT attachments in metaphase cells, it was used for this estimate (Zaytsev et al., 2014).
Ratio of rates with which the protein associates (kon) and dissociates (koff) from the MT lattice.
During random Brownian motion in periodic potential, the probability of dissociating from the MT is proportional to Boltzmann's exponent:
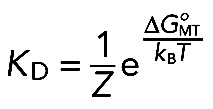 (4) (4)
|
where Z is a partition function (Landau and Lifshitz, 1969) and KD = koff/kon is the dissociation constant. This approach does not allow the calculation of ΔGoMT explicitly, because the value of Z is unknown. However, Eq. 4 can be used to compare the binding energies of two molecular reactions with similar Zs:
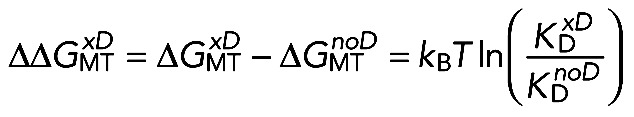 (5) (5)
|
where the superscript xD denotes a complex with x phosphomimetic substitutions. This approach led to the estimate of the change in NDC80-MT interaction energy in response to phosphorylation: 0.30 ± 0.02 kBT per phosphomimetic substitution.
Initial slopes of the intensity curves obtained with TIRF MT-binding assay.
For low-soluble protein concentrations (P), the intensity signal from bound NDC80 complexes (INDC80) can be estimated as a limit for binding equation in the following form using
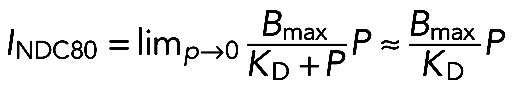 (6) (6)
|
Equation 6 shows that, at low P, the INDC80 is a linear function of P, and the slope for this dependency is a measure of 1/KD. The ratio of the dissociation constants for different mutants was estimated from Supplemental Figure S2E, and Eq. 6 was used to estimate ΔΔxDMT.
Dissociation constant.
This estimate was carried out using Eq. 5 but with KD values obtained from the TIRF MT-binding assay using the binding model (Figure 5B and Table 2).
MD simulations
Simulation parameters.
All simulations were performed on GPU NVidia Tesla C2075 with 1 fs step using the GROMACS 4.6.3 package and the AMBER99SB force field (Ponder and Case, 2003; Pronk et al., 2013). Generalized Born OBCII implicit solvent (Onufriev et al., 2004) and NVT-ensemble (constant temperature and volume) were used. Temperature was kept constant using a V-rescale thermostat (Bussi et al., 2007). Both electrostatic and Van der Waals interaction cutoffs were 10 Å.
Protein and MT structures.
PDB (Protein Data Base) structures were prepared using the Chimera 1.8 RC package (Pettersen et al., 2004) and the GROMACS pdb2gmx tool. Crystal structures of the Hec1 and Nuf2 CH domains of NDC80 complex (2VE7.pdb; Ciferri et al., 2008) were repaired by adding missing amino acid residues (from 203 to 210 in Hec1) and hydrogen atoms. The added peptide was subjected to “steepest decent” minimization (10,000 steps) and 30-ns relaxation, during which all other nonhydrogen atoms were fixed. The repaired structure was incorporated in 3IZ0.pdb (Alushin et al., 2010), which contains two adjacent NDC80 complexes bound to a tubulin dimer.
To obtain a short segment of the MT wall, we fitted the crystal structure of the tubulin dimer (1JFF.pdb; Löwe et al., 2001) into an MT electron density map (EMD5193; Sui and Downing, 2010) using three adjacent protofilaments, each containing three tubulin monomers (β-α-β tubulins). Tubulin C-terminal extensions were constructed with the Chimera Build Structure tool using the sequences for the α- and β-tubulin C-terminal extensions (UniProt Q2HJ86 aa 431–451 and UniProt Q6B856 aa 427–445, respectively) followed by 5-ns MD simulation in implicit solvent. The relaxed extensions were fused to tubulins in the MT wall segment using the Chimera tool Join Models tool.
The MT wall segment was then combined with NDC80 (modified 3IZ0.pdb) using the Chimera Match tool. The Hec1 tail (UniProt 014777 aa 1–80) was fused to the N-terminus of one of the MT-bound Hec1 proteins. In MD simulations, two initial Hec1 tail conformations were used. In one, the Hec1 tail was unfolded and fully extended. In the second set of simulations, the initial Hec1 tail configuration was obtained with the Rosetta 3.4 tool (Leaver-Fay et al., 2011) AbInitioRelax following a 30-ns simulation in implicit solvent.
For the simulations with high density of NDC80 complexes on the MT wall, two pairs of NDC80 complexes (modified 3IZ0.pdb) were placed on the neighboring MT protofilaments using the Chimera Match tool. Each pair of NDC80 complexes has one Hec1 tail fused to one of the Hec1 CH domains in the configuration obtained with the Rosetta 3.4 tool and relaxed as described above. All other simulation parameters were the same as above.
Other procedures and analyses.
The disorder probability of the first 250 amine acids of Hec1 were assessed with four online resources: DISOPRED2 (http://bioinf.cs.ucl.ac.uk/disopred; Ward et al., 2004); DISpro (http://scratch.proteomics.ics.uci.edu; Cheng et al., 2005); IUPred (http://iupred.enzim.hu/; Dosztányi et al., 2005); and OnD-CRF (http://babel.ucmp.umu.se/ond-crf/; Wang et al., 2009). For plotting root-mean-squared deviation (RMSD) as a function of time, RMSDs between all atom positions in the Hec1 tail for all time points separated by Δt were calculated. Values for the same Δt were averaged and plotted in Supplemental Figure S3B (black symbols). Total energy of the system plotted in Supplemental Figure S3C was calculated in GROMACS as a sum of the interaction energies between all pairs of atoms. To determine the number of contacts between the Hec1 tail and other polypeptides, we measured the distance between all atoms in these polypeptides. Two amino acids were considered in contact if at least two heavy atoms were at a distance shorter than the sum of their Van der Waals radii. To obtain the residue-specific contact probability between the Hec1 tail and the MT (surface of polymerized tubulins and their tails), we calculated the ratio Ni/Ntotal for each amino acid in the Hec1 tail, where Ni is the number of simulations at the end of which the amino acid number i in the Hec1 tail and MT were in contact, and Ntotal is the total number of the simulations.
Estimation of NDC80 oligomerization at the kinetochore
To estimate size of the NDC80 clusters on the surface of kinetochore-attached MTs, we used the model for stochastic protein binding from Zaytsev et al. (2013, see fig. 2B in this reference). This model allows us to link the residency time τ, cooperativity parameter ω, number of kinetochore-bound NDC80 molecules, and the number of their MT-binding sites with the size of the NDC80 clusters on the MT lattice. For this calculation, we used residency time τ = 0.24 s and cooperativity parameter ω = 3, the values we have measured for 1D NDC80 protein in vitro. We assumed that 12 NDC80 molecules could interact with the lattice of one kinetochore-attached MT (average of estimates from Johnson et al., 2010; Lawrimore et al., 2011; Aravamudhan et al., 2013). The number of NDC80 binding sites at the kinetochore-attached MT depends on the length L of the MT segment that the NDC80 molecules can reach from the kinetochore. The NDC80 molecules are positioned on average 60 nm from the MT plus end (Wan et al., 2009), similar to the length of an NDC80 molecule (Ciferri et al., 2005; Wei et al., 2005). Therefore, for our calculations, we assumed L = 30 or 60 nm. The number of NDC80 binding sites for these MT segments is 97 and 195, respectively. Using a twofold shorter MT wall segment or a much larger cooperativity parameter (ω = 20) increases the fraction of NDC80 dimers, but, together with monomers, they still represent the most frequent molecular forms, and the larger molecular clusters are found only rarely (<40%).
Supplementary Material
Acknowledgments
We thank F. I. Ataullakhanov for help with MD simulations and other insights and members of the DeLuca and Grishchuk labs, V. Barsegov, I. Cheeseman, and M. Lampson, for stimulating discussions. This work was supported in part by National Institutes of Health grants R01-GM098389 (to E.L.G.) and R01-GM088371 (to J.G.D.) and Russian Academy of Sciences Presidium grants for Mechanisms of the Molecular Systems Integration, Molecular and Cell Biology Programs and Russian Fund for Basic Research Grants 12-04-00111-a, 13-00-40188, 13-04-40188-H, and 13-04-40190-H to F. I. Ataullakhanov. E.L.G. is supported by a Research Scholar grant (RSG-14-018-01-CCG) from the American Cancer Society; J.G.D. is a Pew Scholar in the Biomedical Sciences.
Abbreviations used:
- CH
calponin homology
- DTT
dithiothreitol
- FRAP
fluorescence recovery after photobleaching
- GFP
green fluorescent protein
- GST
glutathione S-transferase
- MD
molecular dynamics
- MSD
mean-squared displacement
- MT
microtubule
- RMSD
root-mean-squared deviation
- TIRF
total internal reflection fluorescence.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E14-11-1539) on March 25, 2015.
REFERENCES
- Alushin GM, Musinipally V, Matson D, Tooley J, Stukenberg PT, Nogales E. Multimodal microtubule binding by the Ndc80 kinetochore complex. Nat Struct Mol Biol. 2012;19:1161–1167. doi: 10.1038/nsmb.2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alushin GM, Ramey VH, Pasqualato S, Ball DA, Grigorieff N, Musacchio A, Nogales E. The Ndc80 kinetochore complex forms oligomeric arrays along microtubules. Nature. 2010;467:805–810. doi: 10.1038/nature09423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aravamudhan P, Felzer-Kim I, Joglekar AP. The budding yeast point centromere associates with two Cse4 molecules during mitosis. Curr Biol. 2013;23:770–774. doi: 10.1016/j.cub.2013.03.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bormuth V, Varga V, Howard J, Schäffer E. Protein friction limits diffusive and directed movements of kinesin motors on microtubules. Science. 2009;325:870–873. doi: 10.1126/science.1174923. [DOI] [PubMed] [Google Scholar]
- Bulinski JC, Odde DJ, Howell BJ, Salmon TD, Waterman-Storer CM. Rapid dynamics of the microtubule binding of ensconsin in vivo. J Cell Sci. 2001;114:3885–3897. doi: 10.1242/jcs.114.21.3885. [DOI] [PubMed] [Google Scholar]
- Bussi G, Donadio D, Parrinello M. Canonical sampling through velocity rescaling. J Chem Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Cheeseman IM, Chappie JS, Wilson-Kubalek EM, Desai A. The conserved KMN network constitutes the core microtubule-binding site of the kinetochore. Cell. 2006;127:983–997. doi: 10.1016/j.cell.2006.09.039. [DOI] [PubMed] [Google Scholar]
- Cheng J, Randall AZ, Sweredoski MJ, Baldi P. SCRATCH: a protein structure and structural feature prediction server. Nucleic Acids Res. 2005;33:W72–W76. doi: 10.1093/nar/gki396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciferri C, De Luca J, Monzani S, Ferrari KJ, Ristic D, Wyman C, Stark H, Kilmartin J, Salmon ED, Musacchio A, et al. Architecture of the human ndc80-hec1 complex, a critical constituent of the outer kinetochore. J Biol Chem. 2005;280:29088–29095. doi: 10.1074/jbc.M504070200. [DOI] [PubMed] [Google Scholar]
- Ciferri C, Pasqualato S, Screpanti E, Varetti G, Santaguida S, Dos Reis G, Maiolica A, Polka J, De Luca JG, De Wulf P, et al. Implications for kinetochore-microtubule attachment from the structure of an engineered Ndc80 complex. Cell. 2008;133:427–439. doi: 10.1016/j.cell.2008.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Civelekoglu-Scholey G, He B, Shen M, Wan X, Roscioli E, Bowden B, Cimini D. Dynamic bonds and polar ejection force distribution explain kinetochore oscillations in PtK1 cells. J Cell Biol. 2013;201:577–593. doi: 10.1083/jcb.201301022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis TN, Wordeman L. Rings, bracelets, sleeves, and chevrons: new structures of kinetochore proteins. Trends Cell Biol. 2007;17:377–382. doi: 10.1016/j.tcb.2007.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLuca JG, Gall WE, Ciferri C, Cimini D, Musacchio A, Salmon ED. Kinetochore microtubule dynamics and attachment stability are regulated by Hec1. Cell. 2006;127:969–982. doi: 10.1016/j.cell.2006.09.047. [DOI] [PubMed] [Google Scholar]
- DeLuca KF, Lens SM, DeLuca JG. Temporal changes in Hec1 phosphorylation control kinetochore-microtubule attachment stability during mitosis. J Cell Sci. 2011;124:622–634. doi: 10.1242/jcs.072629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLuca JG, Musacchio A. Structural organization of the kinetochore-microtubule interface. Curr Opin Cell Biol. 2012;24:48–56. doi: 10.1016/j.ceb.2011.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosztányi Z, Csizmok V, Tompa P, Simon I. IUPred: Web server for the prediction of intrinsically unstructured regions of proteins based on estimated energy content. Bioinformatics. 2005;21:3433–3434. doi: 10.1093/bioinformatics/bti541. [DOI] [PubMed] [Google Scholar]
- Festa R, Galleani E. Diffusion coefficient for a Brownian particle in a periodic field of force. Physica A. 1978;90:229–244. [Google Scholar]
- Gestaut DR, Graczyk B, Cooper J, Widlund PO, Zelter A, Wordeman L, Asbury CL, Davis TN. Phosphoregulation and depolymerization-driven movement of the Dam1 complex do not require ring formation. Nat Cell Biol. 2008;10:407–414. doi: 10.1038/ncb1702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grishchuk EL, McIntosh JR, Molodtsov MI, Ataullakhanov FI. Force Generation by Dynamic Microtubule Polymers, Comprehensive Biophysics, vol. 4. Amsterdam: Elsevier; 2012. pp. 97–113. [Google Scholar]
- Grishchuk EL, Spiridonov IS, Volkov VA, Efremov A, Westermann S, Drubin D, Barnes G, Ataullakhanov FI, McIntosh JR. Different assemblies of the DAM1 complex follow shortening microtubules by distinct mechanisms. Proc Natl Acad Sci USA. 2008;105:6918–6923. doi: 10.1073/pnas.0801811105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guimaraes GJ, Dong Y, McEwen BF, Deluca JG. Kinetochore-microtubule attachment relies on the disordered N-terminal tail domain of Hec1. Curr Biol. 2008;18:1778–1784. doi: 10.1016/j.cub.2008.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helenius J, Brouhard G, Kalaidzidis Y, Diez S, Howard J. The depolymerizing kinesin MCAK uses lattice diffusion to rapidly target microtubule ends. Nature. 2006;441:115–119. doi: 10.1038/nature04736. [DOI] [PubMed] [Google Scholar]
- Hyman A, Drechsel D, Kellogg D, Salser S, Sawin K, Steffen P, Wordeman L, Mitchison T. Preparation of modified tubulins. Methods Enzymol. 1991;196:478–485. doi: 10.1016/0076-6879(91)96041-o. [DOI] [PubMed] [Google Scholar]
- Jiang L, Gao Y, Mao F, Liu Z, Lai L. Potential of mean force for protein-protein interaction studies. Proteins. 2002;46:190–196. doi: 10.1002/prot.10031. [DOI] [PubMed] [Google Scholar]
- Joglekar AP, Bloom KS, Salmon ED. Mechanisms of force generation by end-on kinetochore-microtubule attachments. Curr Opin Cell Biol. 2010;22:57–67. doi: 10.1016/j.ceb.2009.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston K, Joglekar A, Hori T, Suzuki A, Fukagawa T, Salmon ED. Vertebrate kinetochore protein architecture: protein copy number. J Cell Biol. 2010;189:937–943. doi: 10.1083/jcb.200912022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keener JP, Shtylla BA. Mathematical model of force generation by flexible kinetochore-microtubule attachments. Biophys J. 2014;106:998–1007. doi: 10.1016/j.bpj.2014.01.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau LD, Lifshitz EM. Statistical Physics, vol. 5. Oxford, UK: Pergamon; 1969. [Google Scholar]
- Lawrimore J, Bloom KS, Salmon ED. Point centromeres contain more than a single centromere-specific Cse4 (CENP-A) nucleosome. J Cell Biol. 2011;195:573–582. doi: 10.1083/jcb.201106036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leaver-Fay A, Tyka M, Lewis SM, Lange OF, Thompson J, Jacak R, Kaufman K, Renfrew PD, Smith CA, Sheffler W, et al. ROSETTA3: an object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011;487:545–574. doi: 10.1016/B978-0-12-381270-4.00019-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CW, Ferreon JC, Ferreon AC, Arai M, Wright PE. Graded enhancement of p53 binding to CREB-binding protein (CBP) by multisite phosphorylation. Proc Natl Acad Sci USA. 2010;107:19290–19295. doi: 10.1073/pnas.1013078107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lobanov MY, Bogatyreva NS, Galzitskaia OV. Radius of gyration is indicator of compactness of protein structure. Mol Biol. 2008;42:701–706. [PubMed] [Google Scholar]
- Löwe J, Li H, Downing KH, Nogales E. Refined structure of αβ-tubulin at 3.5 A resolution. J Mol Biol. 2001;313:1045–1057. doi: 10.1006/jmbi.2001.5077. [DOI] [PubMed] [Google Scholar]
- Malik R, Lenobel R, Santamaria A, Ries A, Nigg EA, Körner R. Quantitative analysis of the human spindle phosphoproteome at distinct mitotic stages. J Proteom Res. 2009;8:4553–4563. doi: 10.1021/pr9003773. [DOI] [PubMed] [Google Scholar]
- McGhee JD, von Hippel PH. Theoretical aspects of DNA-protein interactions: co-operative and non-co-operative binding of large ligands to a one-dimensional homogeneous lattice. J Mol Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- McIntosh JR, Grishchuk EL, Morphew MK, Efremov AK, Zhudenkov K, Volkov VA, Cheeseman IM, Desai A, Mastronarde DN, Ataullakhanov FI. Fibrils connect microtubule tips with kinetochores: a mechanism to couple tubulin dynamics to chromosome motion. Cell. 2008;135:322–333. doi: 10.1016/j.cell.2008.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller SA, Johnson ML, Stukenberg PT. Kinetochore attachments require an interaction between unstructured tails on microtubules and Ndc80(Hec1) Curr Biol. 2008;18:1785–1791. doi: 10.1016/j.cub.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nousiainen M, Silljé HH, Sauer G, Nigg EA, Körner R. Phosphoproteome analysis of the human mitotic spindle. Proc Natl Acad Sci USA. 2006;103:5391–5396. doi: 10.1073/pnas.0507066103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okada Y, Hirokawa N. Mechanism of the single-headed processivity: diffusional anchoring between the K-loop of kinesin and the C terminus of tubulin. Proc Natl Acad Sci USA. 2000;97:640–645. doi: 10.1073/pnas.97.2.640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Park KS, Mohapatra DP, Misonou H, Trimmer JS. Graded regulation of the Kv2.1 potassium channel by variable phosphorylation. Science. 2006;313:976–979. doi: 10.1126/science.1124254. [DOI] [PubMed] [Google Scholar]
- Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera—a visualization system for exploratory research and analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- Ponder JW, Case DA. Force fields for protein simulations. Adv Protein Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- Powers AF, Franck AD, Gestaut DR, Cooper J, Gracyzk B, Wei RR, Wordeman L, Davis TN, Asbury CL. The Ndc80 kinetochore complex forms load-bearing attachments to dynamic microtubule tips via biased diffusion. Cell. 2009;136:865–875. doi: 10.1016/j.cell.2008.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pronk S, Páll S, Schulz R, Larsson P, Bjelkmar P, Apostolov R, Shirts MR, Smith JC, Kasson PM, van der Spoel D, et al. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pufall MA, Lee GM, Nelson ML, Kang HS, Velyvis A, Kay LE, McIntosh LP, Graves BJ. Variable control of Ets-1 DNA binding by multiple phosphates in an unstructured region. Science. 2005;309:142–145. doi: 10.1126/science.1111915. [DOI] [PubMed] [Google Scholar]
- Salazar C, Höfer T. Multisite protein phosphorylation—from molecular mechanisms to kinetic models. FEBS J. 2009;276:3177–3198. doi: 10.1111/j.1742-4658.2009.07027.x. [DOI] [PubMed] [Google Scholar]
- Salmon ED, Saxton WM, Leslie RJ, Karow ML, McIntosh JR. Diffusion coefficient of fluorescein-labeled tubulin in the cytoplasm of embryonic cells of a sea urchin: video image analysis of fluorescence redistribution after photobleaching. J Cell Biol. 1984;99:2157–2164. doi: 10.1083/jcb.99.6.2157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santaguida S, Musacchio A. The life and miracles of kinetochores. EMBO J. 2009;28:2511–2531. doi: 10.1038/emboj.2009.173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serber Z, Ferrell JE., Jr Tuning bulk electrostatics to regulate protein function. Cell. 2007;128:441–444. doi: 10.1016/j.cell.2007.01.018. [DOI] [PubMed] [Google Scholar]
- Sprague BL, Pego RL, Stavreva DA, McNally JG. Analysis of binding reactions by fluorescence recovery after photobleaching. Biophys J. 2004;86:3473–3495. doi: 10.1529/biophysj.103.026765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui H, Downing KH. Structural basis of interprotofilament interaction and lateral deformation of microtubules. Structure. 2010;18:1022–1031. doi: 10.1016/j.str.2010.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tooley J, Stukenberg PT. The Ndc80 complex: integrating the kinetochore's many movements. Chromosome Res. 2011;19:377–391. doi: 10.1007/s10577-010-9180-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Umbreit NT, Gestaut DR, Tien JF, Vollmar BS, Gonen T, Asbury CL, Davis TN. The Ndc80 kinetochore complex directly modulates microtubule dynamics. Proc Natl Acad Sci USA. 2012;109:16113–16118. doi: 10.1073/pnas.1209615109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkov VA, Zaytsev AV, Grishchuk EL. Preparation of segmented microtubules to study motions driven by the disassembling microtubule ends. J Vis Exp. 2014;85 doi: 10.3791/51150. doi: 10.3791/51150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wan X, O'Quinn RP, Pierce HL, Joglekar AP, Gall WE, DeLuca JG, Carroll CW, Liu ST, Yen TJ, McEwen BF, et al. Protein architecture of the human kinetochore microtubule attachment site. Cell. 2009;137:672–684. doi: 10.1016/j.cell.2009.03.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Sauer UH. OnD-CRF: predicting order and disorder in proteins conditional random fields. Bioinformatics. 2009;24:1401–1402. doi: 10.1093/bioinformatics/btn132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward JJ, Sodhi JS, McGuffin LJ, Buxton BF, Jones DT. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J Mol Biol. 2004;337:635–645. doi: 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- Wei RR, Al-Bassam J, Harrison SC. The Ndc80/HEC1 complex is a contact point for kinetochore-microtubule attachment. Nat Struct Mol Biol. 2007;14:54–59. doi: 10.1038/nsmb1186. [DOI] [PubMed] [Google Scholar]
- Wei RR, Sorger PK, Harrison SC. Molecular organization of the Ndc80 complex, an essential kinetochore component. Proc Natl Acad Sci USA. 2005;102:5363–5367. doi: 10.1073/pnas.0501168102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson-Kubalek EM, Cheeseman IM, Yoshioka C, Desai A, Milligan RA. Orientation and structure of the Ndc80 complex on the microtubule lattice. J Cell Biol. 2008;182:1055–1061. doi: 10.1083/jcb.200804170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaytsev AV, Ataullakhanov FI, Grishchuk EL. Highly transient molecular interactions underlie the stability of kinetochore-microtubule attachment during cell division. Cell Mol Bioeng. 2013;6:393–405. doi: 10.1007/s12195-013-0309-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaytsev AV, Sundin LJ, DeLuca KF, Grishchuk EL, DeLuca JG. Accurate phosphoregulation of kinetochore-microtubule affinity requires unconstrained molecular interactions. J Cell Biol. 2014;206:45–59. doi: 10.1083/jcb.201312107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.