Ex-Vivo Lymphatic Perfusion System for Independently Controlling Pressure Gradient and Transmural Pressure in Isolated Vessels

Abstract

In addition to external forces, collecting lymphatic vessels intrinsically contract to transport lymph from the extremities to the venous circulation. As a result, the lymphatic endothelium is routinely exposed to a wide range of dynamic mechanical forces, primarily fluid shear stress and circumferential stress, which have both been shown to affect lymphatic pumping activity. Although various ex-vivo perfusion systems exist to study this innate pumping activity in response to mechanical stimuli, none are capable of independently controlling the two primary mechanical forces affecting lymphatic contractility: transaxial pressure gradient, ΔP, which governs fluid shear stress; and average transmural pressure, P_avg, which governs circumferential stress. Hence, the authors describe a novel ex-vivo lymphatic perfusion system (ELPS) capable of independently controlling these two outputs using a linear, explicit model predictive control (MPC) algorithm. The ELPS is capable of reproducing arbitrary waveforms within the frequency range observed in the lymphatics in vivo, including a time-varying ΔP with a constant P_avg, time-varying ΔP and P_avg, and a constant ΔP with a time-varying P_avg. In addition, due to its implementation of syringes to actuate the working fluid, a post-hoc method of estimating both the flow rate through the vessel and fluid wall shear stress over multiple, long (5 sec) time windows is also described.

1 Introduction

The lymphatic system is critical to some of the human body’s most basic functions, including maintaining tissue fluid balance, trafficking immune cells, and transporting lipid from the gut to the blood vasculature, among others [40]. Anatomically, lymphatic vessels begin in the interstitial tissue spaces, continuously merging downstream as branches into larger trunks termed the collecting lymphatics. These vessels consist of luminal lymphatic endothelial cells (LECs) surrounded by muscle cells that actively contract to propel fluid toward the venous circulation. This active pumping is crucial in lymphatic transport because interstitial fluid pressure alone is insufficient to move lymph against the adverse pressure gradient inherent to the system [2]. To aid in transferring this bulk of fluid, which recent estimates put at almost 8 liters per day for humans [25], the collecting lymphatics are separated into unit segments termed lymphangions [41, 29] by one-way valves. These anatomical structures are similar to those found in veins and help ensure unidirectional flow of lymph towards its exit at the left subclevian vein. However, unlike veins, these vessels can rapidly contract up to 75% of their diameter to rapidly eject fluid from one lymphangion to the next. It is noted that the endothelium in lymphangions, unlike that in the blood vasculature, is routinely exposed to oscillatory flow rates due to both the structure and pumping function of the collecting lymphatics [9].

The contraction dynamics of collecting lymphatic vessels (referred to as the intrinsic pump) are not predetermined and have been shown to be sensitive to changes in how they are mechanically loaded [27, 12, 7]. Since the formation of lymph can vary widely even during normal, physiologic circumstances [24], it seems reasonable to assume that lymphatics alter their behavior to optimize lymph transport due to their sensitivity to the local mechanical environment [12]. Many of these responses are, in part, endothelium mediated, and utilize similar mechanisms that have been known to regulate vasoactive responses in the blood vasculature [20, 3].

However, the magnitudes of the transmural pressure wall shear stress waveforms experienced by lymphatics are drastically different. Typical average values of these parameters are much lower than similarly sized microvessels [Table 1]. Additionally, wall shear stress values in lymphatics are not very well described by average values as the dynamic nature of the lymphatic pump continuously produces values that rang from −1 dynes/cm² during flow reversal before complete valve closure, to 10 dynes/cm² during the peak of systole [9]. Interestingly, these unique mechanical forces that lymphatics are exposed to have recently been implicated in guiding lymphatic development and differentiation [4, 39]. It is likely that lymphatics have specialized mechanotransduction pathways that regulate their response to this unique mechanical environment. Recently, vascular endothelial growth factor receptor-3, a growth factor receptor expressed differentially on LECs, was implicated in the lower shear stress sensitivity of lymphatics (Schwartz, M., Vascular Biology 2013, Oct 20–24, 2013, Hyannis, MA). The ability to expose isolated lymphatic vessels to these in vivo mechanical loading conditions will be crucial to further elucidating the molecular details involved in their mechanosensitvity.

Table 1.

Typical pressure and wall shear stress (WSS) values of the body’s microvessels [16, 26, 9].

Parameter	Arterioles	Venules	Capillaries	Collecting Lymphatics
Pressure (mmHg)	75–100	20–30	30–40	3–4
Average WSS (dynes/cm2)	50–60	10–30	20–50	< 1

One such example of this active behavioral modification may be found in the inhibition of lymphatic pumping amplitude, frequency, and tone in response to luminal fluid shear stress [12, 13]. Along with fluid shear stress, altering intraluminal (transmural) pressure in isolated lymphatic vessels has also been shown to result in differing contractile (pumping) responses [27, 16]. However, the magnitude of circumferential stress (or strain) imposed on a lymphatic vessel is not alone in affecting contraction: the rate of load applied to a vessel has also been shown to alter pump function [7]. Because these rate-sensitive changes proved to be different to that of the portal vein, it suggests that the lymphatics may have adapted to compensate for the rapidly varying changes in load that can occur in vivo. Moreover, the notion of a function-based pumping response is further supported by observations of lymphatic vessels exhibiting differential sensitivities to mechanical loading based on their anatomical location [13].

This clear relationship between lymphatic contractile function and mechanical loading is particularly interesting in the context of lymphatic pathologies that alter the mechanical environment surrounding the vessels. One such pathology is lymphedema, a disease characterized by gross swelling of the tissue estimated to affect over 130 million people worldwide [36, 37]. Clinically, lymphedema often manifests itself in the extremities, and there currently exists no effective cures or therapies for patients. Mechanically, lymphedema is likely to result in elevated transmural pressure in the affected area [15], and the accumulation of fibrotic tissue and adipocytes due to lymph stasis can drastically alter the mechanical environment surrounding the vessels [38]. However, although mechanics may play an integral role in lymphatic pathologies, it is crucial to first understand the role of mechanics during normal lymphatic function before we can unravel its implications in disease.

Unfortunately, current ex vivo experimental devices used in isolated lymphatic or blood vessel studies are inadequate to study the complex behavior of the intrinsic pump to dynamic mechanical loads. The most widely-used setup generally consists of two hydrostatic pressure columns separated by an isolated vessel [27, 23, 12, 32], which allows the experimenter to statically (or in a step-wise fashion) impose a pressure gradient and transmural pressure via the height of the columns. Others have developed more complex devices capable of imposing either a sinusoidal [30] or ramped intraluminal pressure [7] in isolated lymphatic vessels; however, none of these systems has the ability to dynamically adjust both the pressure gradient (which affects shear stress via flow rate) and average transmural pressure (which affects circumferential stress) simultaneously and arbitrarily. Likewise, investigators have constructed a wide array of ex vivo perfusion systems to impose varying flow rate and transmural pressure waveforms on isolated blood vessels [17, 5, 14, 1, 10, 33], but none can impose arbitrary pressure gradient and transmural pressure waveforms concurrently, independently, and automatically.

This shortcoming in capability may be attributed to the inherent complexity of multi-input, multi-output (MIMO) tracking control. Because these types of systems often have outputs with coupled dynamics, controlling these outputs to track independent dynamic signals is an extremely challenging task if using relatively simple feedback control schemes like on-off or PID control [14, 1]. Hence, more advanced controllers with predictive capabilities incorporating the system’s dynamics are necessary to advance the time-varying tracking capabilities of these perfusion systems. In this regard, significant strides have been made: El-Kurdi et al. reported the first system identification of an ex vivo vascular perfusion system to obtain a (MIMO) mathematical model that could be used for control [10]. However, to the authors’ knowledge no one has yet successfully included one of these models into a control scheme with MIMO tracking capabilities. This attribute of independent tracking could be especially significant in studying the lymphatics, where both intrinsic pumping and extrinsic factors (such as skeletal muscle contraction, respiration, and interstitial fluid formation) can result in widely-varying fluid loads even under normal, physiological conditions. Hence, the ability to impose arbitrary and dynamic waveforms for both transaxial pressure gradient and average transmural pressure within physiologically relevant ranges is necessary to properly study the contractile effects of lymphatic vessels subject to these assorted loads.

In order to study both the independent and coupled effects of these factors on lymphatic pump function in isolated vessels, the authors propose a novel ex vivo lymphatic perfusion system (ELPS) capable of controlling these two parameters within an excised rat lymphatic vessel [Fig. 1]. Specifically, this perfusion system is meant to independently control the two primary mechanical stimuli imposed on a lymphatic vessel: average transmural pressure, P_avg, which affects circumferential (hoop) stress; and transaxial pressure gradient, ΔP, which affects fluid shear stress via flow rate. The authors achieved this control capability using a linear, explicit model predictive control (MPC) scheme, which is implemented simply with an embedded microcontroller. Although the use of MPC is not new [35, 11, 28], it has never been implemented in a biomedical application such as this one. In short, a perfusion system with these control capabilities would be paramount in studying the physiological effects of biomechanical stimuli on lymphatic contractility and would allow single-factor studies to be performed that would be nearly impossible with in vivo models. The device and compensator designs for the proposed system are summarized henceforth.

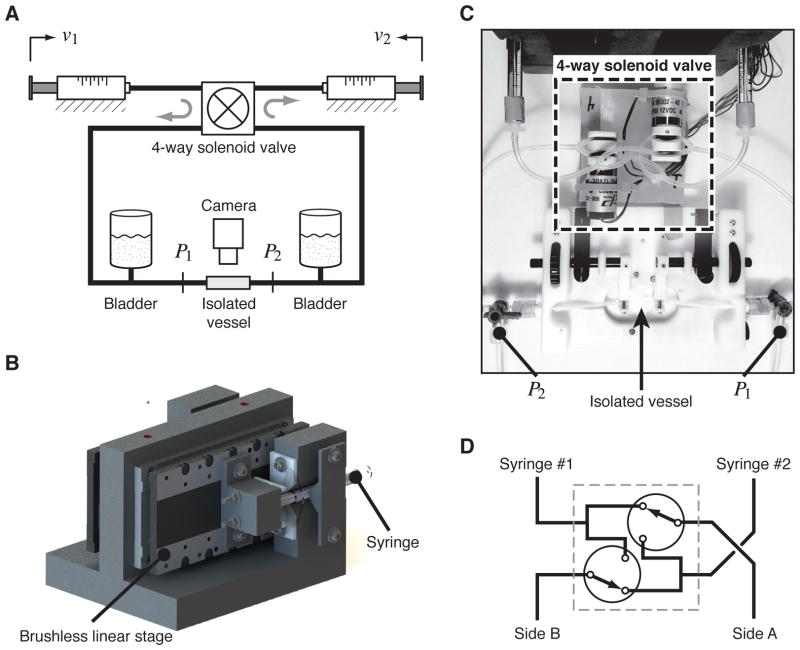
Figure 1.

Ex-vivo lymphatic perfusion system (ELPS). (a) Syringes are actuated by two linear stages to independently control both ΔP = P₁ − P₂ and P_avg = (P₁ + P₂)/2, during which a camera is recording the vessel’s contraction dynamics. (b) Custom-built mount for the brushless linear stages to actuate each syringe plunger. (c) Overhead photo showing a portion of the ELPS and highlighting the location of the four-way solenoid valve, location of measurements P₁ and P₂, and location of the isolated vessel. (d) High-level schematic of the 4-way solenoid valve, which is comprised of two 3/2 solenoid valves. In the setting shown, Syringe #1 is connected to Side A and Syringe #2 to Side B; when the valves are switched, Syringe #1 is connected to Side B and Syringe #2 to Side A.

2 Methodology

2.1 ELPS Design and Hardware

The primary control objective of the system is to track a pair of desired inputs, ΔP = P₁−P₂ and P_avg = (P₁ + P₂)/2, to be imposed on an isolated lymphatic vessel. In order to achieve this, the device [Fig. 1a] uses two independently-actuated glass syringes in a closed-loop configuration connected with two three-way pinch solenoid valves (Cole-Parmer, Vernon Hills, IL), connected in such a way to effectively form one four-way valve [Fig. 1c,d]. Thus, when one syringe has expelled a majority of its fluid, the four-way solenoid valve switches while the syringes begin to propagate in the opposite direction. In this way, the system can maintain the directionality of flow with respect to the vessel for an indefinite period of time [17]. The two glass syringes are independently actuated, which permits the precise generation of arbitrary pressure gradient and transmural pressure waveforms. Each syringe is 100 μL in volume (Hamilton Company USA, Reno, NV) and is actuated by a MX80L brushless linear stage (Parker Hannifin Corp., Rohnert Park, CA) through custom mounting hardware [Fig. 1b]. A ViX 250AH servo drive (Parker Hannifin Corp., Rohnert Park, CA) powers each linear stage, and each drive operates in velocity mode to internally control the velocity of the syringe plunger. A separate controller (compensator) provides a set of analog input voltages, u, to the servo drives, which resides in the range of ±10 V.

The system is connected by 1/16″ ID, 1/8″ OD Tygon^® tubing, with the exception of the small segments placed in the solenoid pinch valves that are made from silicone. In addition, two small fluid bladders are connected on each side of the fluid line in order to increase system compliance, helping mitigate high-frequency disturbances such as solenoid valve switching. The extraction and cannulation technique is similar to previous studies [13], where a ~1 cm thoracic duct segment (free of valves) is taken from a Sprague-Dawley rat and cannulated on two resistance-matched glass pipets (400–500 μm tip diameter). Both the system’s working fluid and the vessel bath are a physiological salt solution (PSS) (in mM: 145.0 NaCl, 4.7 KCl, 2.0 CaCl₂, 1.17 MgSO₄, 1.2 NaH₂ PO₄, 5.0 dextrose, 2.0 sodium pyruvate, 0.02 EDTA, and 3.0 MOPS). However, other types of media may be manually substituted after cannulation of the vessel: the authors have successfully disassembled the tubing and changed the working fluid to a calcium-free PSS post-experiment to observe the vessel’s tone-free diameter (data not shown).

Before operation of the ELPS, the vessel is warmed to 37°C for at least 20 min at P_avg ≈ 3 cmH₂O. After the vessel is equilibrated, a validation protocol is performed in order to ensure proper vessel functionality before experimentation. This protocol consists of 5 min of applied zero pressure gradient, followed by a steady pressure gradient (ΔP = 1 cmH₂O) that is also imposed for 5 min. Both of these conditions are imposed at an average transmural pressure, P_avg = 3 cmH₂O. In this way, inhibition of contraction frequency due to a steady imposed flow was confirmed, providing evidence of normal vessel functioning [12, 13]. Contraction frequency for both the no-flow and steady ΔP condition were compared for 5 thoracic ducts using a paired two-tailed t-test. Upon the start of each experiment, the diameter tracing is recorded in real-time via a custom LabView program using data from a bright-field camera capturing at 30 fps as in other studies [13]. Both diameter data and other sensor data are synchronized post-experiment using recorded timestamps.

The digital electronic hardware for the compensator consists of a Microchip 32-bit PIC32 microcontroller running at 80 MHz, providing adequate computational headroom for the control loop to run at 160 Hz. Specifically, the chipKIT Uno32 development board is used (Digilent, Pullman, WA), which is based on the Arduino Uno [6, 22]. The chipKIT Uno32 receives tracking commands serially at a baud rate of 921 kbps from a PC running a custom Python script, and it interfaces with the servo drives using a custom daughter board primarily consisting of two 32-bit LS7366R quadrature decoders for position measurement (LSI Computer Systems, Melville, NY) and a 16-bit, dual-channel AD5752 digital-to-analog converter (DAC) for the servo drive actuating signals (Analog Devices, Norwood, MA). In addition, the daughter board is connected to two 12-bit HSC 001PD digital pressure sensors for measuring both P₁ and P₂ (Honeywell, Golden Vally, MN). As with the Arduino, the software for this electronics platform uses high-level C++ functions to interface with basic hardware I/O, and in addition, the author has developed custom C++ drivers to easily interact with the components on the daughter board. Detailed schematics and source code are published on GitHub [21].

2.2 Control Scheme

The system may be described through the linear, discrete-time state-space equations,

$$\begin{array}{ll}\hfill {\mathbf{x}}_{k+1}& ={\mathbf{Gx}}_k+{\mathbf{Hu}}_k\\ \hfill {\mathbf{y}}_k& ={\left[\begin{array}{c}\mathrm{\Delta }P\\ P_{\text{avg}}\end{array}\right]}_k={\mathbf{Cx}}_k\end{array}$$ (1)

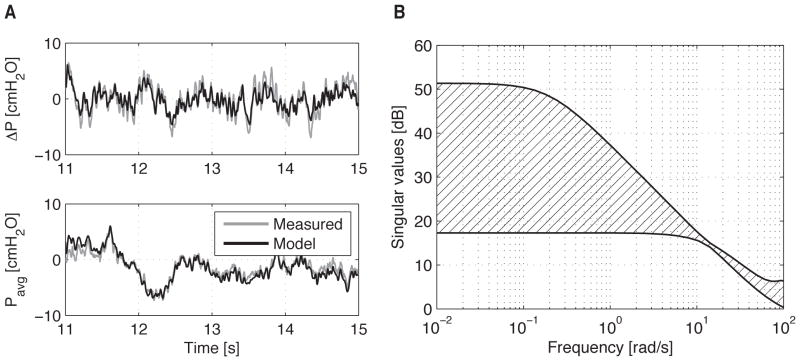
where x ∈ ℝ^n×1 is the state vector, G ∈ ℝ^n×n is the state matrix, and u ∈ ℝ^2×1 is the input vector (voltages to each servo drive). The output vector, y ∈ ℝ^2×1, represents the system output vector to be controlled, which is the transaxial pressure gradient, ΔP, and the average transmural pressure, P_avg. Due to the low pressures and pressure gradients this device produces, all nonlinear effects are ignored except for the saturation limit of the servo drives (±10 V). The matrices G, H, and C are all determined through standard linear identification techniques; specifically, the authors used MATLAB’s ssest() function, which initializes parameter estimates using a noniterative subspace technique before subsequently refining them using a prediction error minimization approach. It is noted that when using a black-box identification scheme such as this, the physical interpretation of the state variables, x, remains unknown since the state-space equations [Eq. (1)] have an infinite number of mathematical representations. In the case of this system, good agreement is achieved when n = 6 for a random binary input signal (±0.6 V) bandwidth-limited to 30 Hz and sampled at 300 Hz [Fig. 2a]. The singular value plot of the ELPS is shown in Fig. 2b. In short, this plot displays the minimum and maximum singular values of the ELPS, which form an outer region bounding the system’s frequency response (i.e. gain attenuation at each frequency).

Figure 2.

(a) ELPS validation data for the system identification using a rat thoracic duct. The input is a random binary signal (±0.6 V) with a frequency band of 0–30 Hz generated with MATLAB. (b) Singular value plot indicating the outer region bounding the frequency response of the ELPS.

The overall control objective of the system is to independently track the desired input wave-forms, y_d, (known a priori) as closely as possible while considering the input limitations of the actuators. Mathematically, we can describe this objective as minimizing a suitable quadratic cost function over some predictive time horizon, H_p:

$$J=\sum _{i=1}^{H_p}{\mathbf{e}}_{k+i}^{\top }{\mathbf{Q}}_i{\mathbf{e}}_{k+i}+{\mathbf{u}}_{k+i-1}^{\top }{\mathbf{R}}_i{\mathbf{u}}_{k+i-1}$$ (2)

where the tracking error vector, e, is the difference between the desired output vector, y_d, and the estimated output vector, ỹ; while the matrices Q_i and R_i are weighting matrices for both the tracking error and the input, respectively, at the i^th prediction step. These weighting matrices are chosen by the designer and, in a sense, effectively adjust the emphasis of the minimization between the tracking error (to enhance performance) and the velocity of the syringes (to increase stability). This particular control scheme is, in general, known as model predictive control (MPC), and has been used for decades in industrial settings where multi-input, multi-output (MIMO) systems are prevalent [35, 11, 28]. Defining the following vectors,

$${\mathbf{Y}}_d=\left[\begin{array}{c}{\mathbf{y}}_{d,k+1}\\ {\mathbf{y}}_{d,k+2}\\ ⋮\\ {\mathbf{y}}_{d,k+H_p}\end{array}\right],\stackrel{\sim }{\mathbf{Y}}=\left[\begin{array}{c}{\stackrel{\sim }{\mathbf{y}}}_{k+1}\\ {\stackrel{\sim }{\mathbf{y}}}_{k+2}\\ ⋮\\ {\stackrel{\sim }{\mathbf{y}}}_{k+H_p}\end{array}\right],\mathbf{U}=\left[\begin{array}{c}{\mathbf{u}}_k\\ {\mathbf{u}}_{k+1}\\ ⋮\\ {\mathbf{u}}_{k+H_p-1}\end{array}\right]$$ (3)

the cost function in Eq. (2) may be recast in matrix/vector form:

$$J={({\mathbf{Y}}_d-\stackrel{\sim }{\mathbf{Y}})}^{\top }\mathbf{Q}({\mathbf{Y}}_d-\stackrel{\sim }{\mathbf{Y}})+{\mathbf{U}}^{\top }\mathbf{RU}$$ (4)

where the weighting matrices Q = blkdiag (Q₁, Q₂,…, Q_Hp) and R = blkdiag (R₁, R₂,…, R_Hp).

Rewriting Eq. (4) in terms of the estimated state, ỹ = Cx̃, such that J = J(x̃, u), the stationarity condition, ∂J/∂U = 0^T, may then be used to solve for the optimal input vectors, U^*. Consequently, the control law governing these input vectors minimizes the quadratic cost function in Eq. (4). After a bit of algebra, this optimal control law may be written explicitly as

$$\begin{array}{l}{\mathbf{U}}^{\ast }={\left({\mathbf{K}}_{\mathit{CGH}}^{\top }{\mathbf{QK}}_{\mathit{CGH}}+\mathbf{R}\right)}^{-1}{\mathbf{K}}_{\mathit{CGH}}^{\top }\mathbf{Q}({\mathbf{Y}}_d-{\mathbf{K}}_{CG}{\stackrel{\sim }{\mathbf{x}}}_k)\\ \equiv \mathbf{K}({\mathbf{Y}}_d-{\mathbf{K}}_{CG}{\stackrel{\sim }{\mathbf{x}}}_k)\end{array}$$ (5)

where the gain matrices are defined as follows:

$${\mathbf{K}}_{CG}=\left[\begin{array}{c}\mathbf{CG}\\ {\mathbf{CG}}^2\\ ⋮\\ {\mathbf{CG}}^{H_p}\end{array}\right],{\mathbf{K}}_{\mathit{CGH}}=\left[\begin{array}{ccccc}\mathbf{CH}& \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{CGH}& \mathbf{CH}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ {\mathbf{CG}}^2\mathbf{H}& \mathbf{CGH}& \mathbf{CH}& \mathbf{0}& \mathbf{0}\\ ⋮& ⋮& ⋮& \ddots & \mathbf{0}\\ {\mathbf{CG}}^{H_p-1}\mathbf{H}& {\mathbf{CG}}^{H_P-2}\mathbf{H}& \cdots & \mathbf{CGH}& \mathbf{CH}\end{array}\right]$$ (6)

In addition, to obtain the input for just the current time, t_k, the control law in Eq. (5) may be written as

$${\mathbf{u}}_k^{\ast }={\mathbf{K}}_1({\mathbf{Y}}_d-{\mathbf{K}}_{CG}{\stackrel{\sim }{\mathbf{x}}}_k)$$ (7)

where K₁ represents the first two rows of K (since u ∈ ℝ^2×1). To obtain the estimated state, x̃_k, a standard Luenberger observer is employed,

$${\stackrel{\sim }{\mathbf{x}}}_{k+1}=\mathbf{G}{\stackrel{\sim }{\mathbf{x}}}_k+{\mathbf{Hu}}_k+\mathbf{L}({\mathbf{y}}_k-{\stackrel{\sim }{\mathbf{y}}}_k)$$ (8)

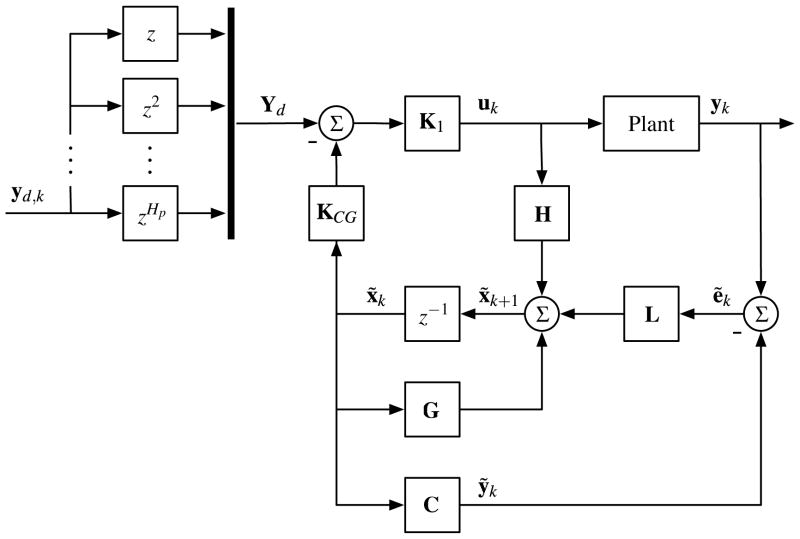
where L is a Kalman gain. Thus, this observer not only estimates the state, x̃, but it also acts to minimize measurement noise. In brief, the observer uses the system model to both predict the state vector at the next time step while also correcting for the error between the actual and predicted output at the current time step. All together, the control diagram is summarized in Fig. 3, and the MATLAB script used to generate the corresponding gain matrices in Eqs. (6)–(8) is also provided on the GitHub page listed in Section 2.1 [21].

Figure 3.

Explicit model predictive control (MPC) scheme with estimator used to compensate the plant, which consists of both the system in Fig. 1a and the servo drives.

2.3 Post-Experiment Shear Stress Estimation

Due to the utilization of precision syringes and position encoders in the ELPS (which have a 0.5 μm resolution), it is possible to estimate the average flow rate through the vessel over a certain window of time, Δt. Disregarding the transient dynamics by making this time window long (Δt = 5 sec used here; see Appendix A), the average volume of fluid displaced out of one syringe and into the other during this time window should accurately approximate the flow rate through the vessel imposed by the system,

$$\overline{Q}\approx A_c\frac{1}{2\mathrm{\Delta }t}{\left[\sum _k\mathrm{\Delta }{x}_{1,k}{\delta }_k-\sum _k\mathrm{\Delta }{x}_{2,k}{\delta }_k\right]}_{\mathrm{\Delta }t}$$ (9)

where A_c is the cross-sectional area of the syringe plunger, Δx_i,k = x_i,k−x_i,k−1 is the incremental position change (backwards difference) of the i^th syringe plunger at the k^th time sample, and

$${\delta }_k=\{\begin{array}{ll}\hfill 1,& \text{Solenoid}\text{OFF}\hfill \\ \hfill -1,& \text{Solenoid}\text{ON}\hfill \end{array}$$ (10)

Using this information, along with the mean diameter of the vessel, D̄, over the same time window, the authors calculate the estimated wall shear stress imposed on the vessel over time window Δt,

$${\overline{\tau }}_w=\frac{32\mu \overline{Q}}{\pi {\overline{D}}^3}$$ (11)

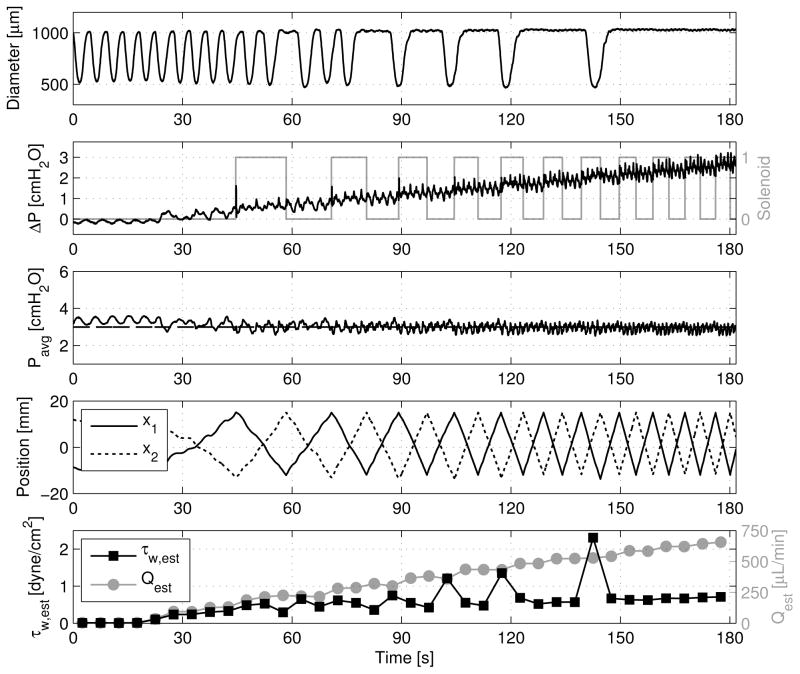
where μ is the dynamic viscosity of the fluid, taken to be that of water at 37°C. It is noted that this wall shear stress estimation assumes Poiseuille flow, which has been shown to be a sufficient constitutive relation for describing lymphatic fluid flow [8, 9, 34] due to the fact that both the Reynolds number and Womersley number are very low (calculated to be less than 20 and 0.8, respectively, in the current study’s experiments). Hence, one may calculate both Q̄ and τ̄_w every Δt units of time to study slowly changing phenomena during an experiment [Fig. 7].

Figure 7.

Example showing estimated shear stress, τ̄_w, calculated from estimated flow rate, Q̄, and mean diameter, D̄, over sequential time windows, Δt = 5 sec each, for a ramped ΔP. Transmural pressure remains constant at 3 cmH₂O, and the corresponding linear stage position, x₁ and x₂, are shown along with the solenoid state to help demonstrate the estimation procedure described in Section 2.3.

3 Results

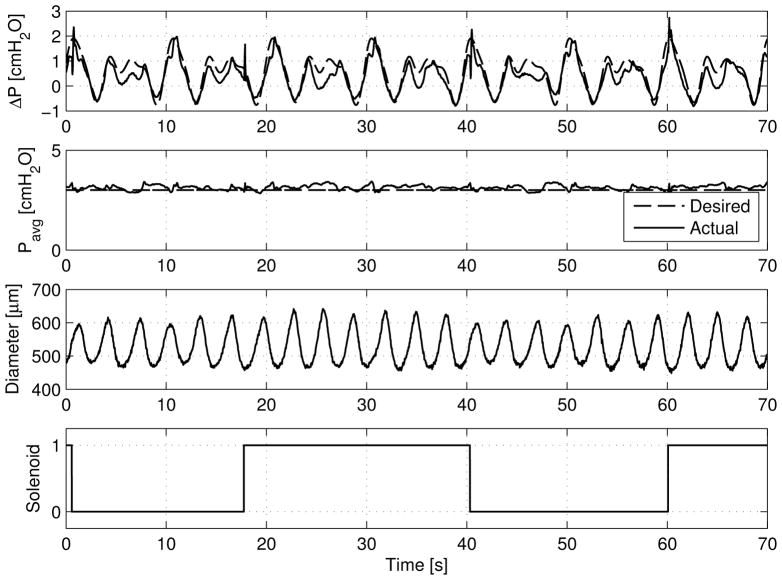
Figure 4 demonstrates this dynamic tracking performance of the ELPS. As shown, various waveform combinations are possible, including both a varying ΔP with a constant P_avg and a varying P_avg with a constant ΔP. Additionally, the ELPS can independently and concurrently track different time-varying ΔP and P_avg. In each of these cases, these pressure waveforms were applied on an actively pumping rat thoracic duct approximately 600 μm in diameter.

Figure 4.

Various arbitrary waveform combinations demonstrating ELPS tracking capabilities for both ΔP and P_avg. From left to right: time-varying ΔP with a constant P_avg, time-varying ΔP and P_avg, and a constant ΔP with a time-varying P_avg.

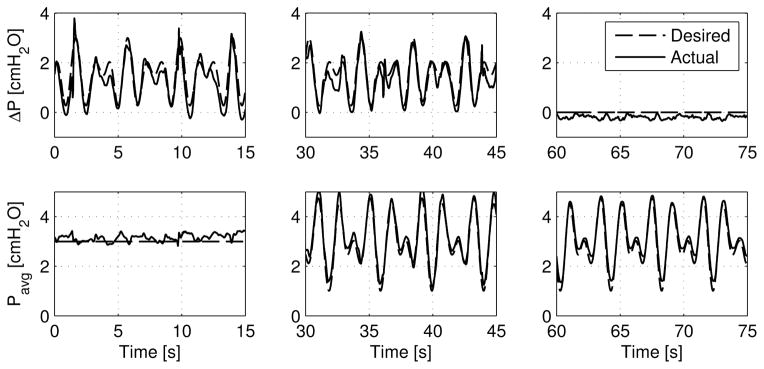
A more complete picture of the ELPS in operation may be seen in Fig. 5, where the ELPS simultaneously applied a constant P_avg (held at 3 cmH₂O) and an oscillatory ΔP based on a measured in vivo lymphatic waveform containing flow reversal. Specifically, the desired ΔP is a periodic function containing the first three harmonics of an oscillatory flow rate measured in the rat mesentery [19]. The corresponding diameter of the isolated rat thoracic duct is also shown along with the switching state of the solenoid valves, which is indicative of the volume of fluid being moved through the vessel. It is noted that the sharp spikes observed in the measured ΔP corresponds to these solenoid switching events, while the effect is less pronounced in the measured P_avg. Additionally, the authors have not observed any abnormal contractile responses of the vessel during solenoid valve switching during a validation protocol performed prior to experimentation [Fig. 6]. Because these switching events are brief (resulting ΔP modulations are typically < 0.25 sec) and have a relatively small magnitude, the authors believe they have negligible effect on normal lymphatic contractile function. To validate that the solenoid switching had no adverse effect on lymphatic pump function, the authors confirmed a significant reduction (p < 0.05) in contraction frequency upon the onset of a steady ΔP (1 cmH₂O) during the validation protocol in 5 separate vessels [Fig. 6b].

Figure 5.

Varying ΔP based on the first three harmonics of a measured in vivo waveform from a rat [19], while P_avg remains constant. The corresponding thoracic duct diameter and solenoid state are also shown.

Figure 6.

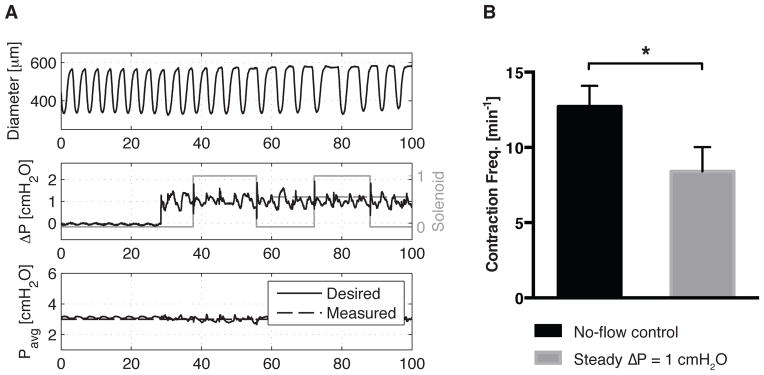
To validate proper vessel functionality before experimentation, a steady pressure gradient (ΔP = 1 cmH₂O) is imposed for 5 min after a no-flow condition (ΔP = 0), both at P_avg = 3 cmH₂O. (a) Despite switching events present after the onset of a steady ΔP, the resulting contraction profile does not display any apparent irregularities. (b) As expected from previous studies [12, 13], application of a steady ΔP results in a significant reduction in contraction frequency compared to a no-flow control (p < 0.05, n = 5). Error bars represent SEM.

However, although the number of solenoid switching events hints at the amount of fluid being transferred through the vessel, this information may be combined with position encoder measurements for the stages to estimate the flow rate over multiple, 5 second windows (detailed in Section 2.3). Thus, with the flow rate estimation and diameter information in hand, the imposed wall shear stress may be estimated as well. An example of this approximation may be seen in Fig. 7, where ΔP is ramped from 0 to 3 cmH₂O over 3 min while holding P_avg constant at 3 cmH₂O. For this experiment, the instantaneous Poiseuille flow assumption for calculating shear stress should hold as both the Reynolds number and Womersley number are always less than 20 and 0.8, respectively. As ΔP increases, the rate of solenoid switching also climbs, resulting in a rising Q̄. Nonetheless, as the flow rate increases, the thoracic duct’s contraction is inhibited, which leads to a higher mean diameter, D̄. The overall effect may be seen through τ̄_w—even as the flow rate continues to increase linearly, the estimated shear stress, τ̄_w, eventually levels off [Fig. 8]. In addition to observing dynamic trends, various functional metrics may also be calculated (as defined in many other lymphatic studies [12, 13, 9]) using the diameter data from the experiment. Table 2 shows several of these commonly used metrics for the diameter data in Fig. 7.

Figure 8.

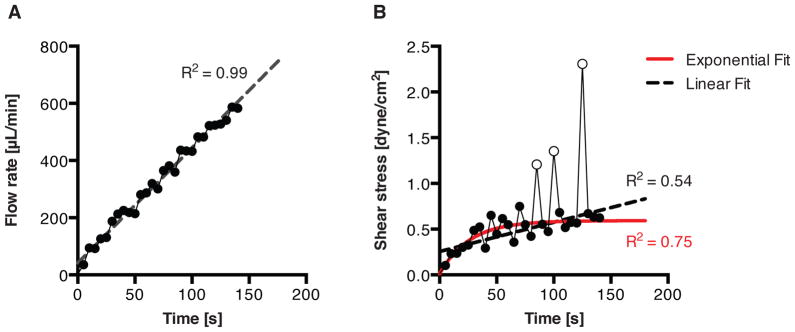
Estimated fits for the flow and shear stress profiles seen in Fig. 7. (a) The flow rate is confirmed to be linear, with R² = 0.99 for a linear fit. (b) However, the shear stress profile, which contains more point-to-point deviations due to the contractile activity of the vessel, is better fitted to an exponential function (R² = 0.75) than a linear function (R² = 0.54) since the shear stress begins to level off over time. To better visualize this trend, the three hollow points (corresponding to the last three contractions in Fig. 7 before complete flow inhibition) were excluded from both the linear and exponential fits.

Table 2.

Various metrics calculated from the diameter data in Fig. 7.

Metric	Value
Mean Diastolic Diameter [μm]	1019.5
Mean Systolic Diameter [μm]	502.0
Mean Contraction Frequency [min−1]	6.27
Fractional Pump Flow [min−1]	4.75
Mean RMS Velocity [μm/s]	147.1

4 Discussion

In order to impose arbitrary ΔP and P_avg waveforms on an isolated lymphatic vessel, the authors chose one of the simplest mechanical configurations: two opposing and independently-controlled pistons (syringes) located on each side of the vessel. In this way, the resulting system intrinsically has two dynamic modes—one which dictates ΔP when the syringes travel together, and one which dictates P_avg when the syringes operate in contrast. Additionally, the positive-displacement nature of the syringes, when coupled with the fast-moving MX80L brushless linear stages (which have a rate-limiting acceleration of 4 g’s), allows for quick alterations of both ΔP and P_avg. Careful thought was given to minimize the tubing length where possible in order to reduce the effects of fluid inertance; however, small fluid-air bladders composed of larger tubing where necessary to increase system compliance to a level where disturbances (such as solenoid switches) were also minimized. Thus, trade-offs had to be made in the system configuration between dynamic performance and robustness of operation: the effects of this trade-off may be seen in Fig. 2b, where significant gain attenuation begins to occur between 1 and 10 rad/s. To validate that P_avg by itself may be used to approximate the pressure distribution in the vessel during flow, the authors used Q̄ to calculate that less that 1% of the pressure-drop between P₁ and P₂ occurs within the vessel itself (assuming Poiseuille flow). This result is due to the fact that the length of the vessel is very small compared with the length of the cannula pipettes.

The authors have designed the system to operate within the range of known and anticipated in vivo loading conditions in healthy and diseased lymphatics. Thus, components were chosen (in particular, the syringe volume and the pressure transducers) that would provide the optimal operation within this range. The current limitation for the system in regards to the maximum pressure that can be generated so as to not exceed the capacity of the pressure transducers is 70 cmH₂O. The maximum flow rate that can be achieved is dictated by the speed of the brushless motors and the volume of syringe. For the 100 μL syringe used in these studies, this value is approximately 20 mL/min. It is possible that these two components could be replaced to allow for control across larger magnitudes or pressure and flow; however, future work would be necessary to optimize the control law for these new components.

System identification of the ELPS, as mentioned previously in Section 2.2, consisted merely of finding a suitable linear state-space model in the discrete-time domain. Although good agreement is seen between the model and the validation identification data [Fig. 2a], remaining discrepancies may be attributed to nonlinearities in the setup. Considering the relatively low pressures and flows imposed by the system, expansion of the tubing and air bladders is minimal and the Reynolds number is always small, suggesting mostly linear behavior for the system dynamics. However, static friction (stiction) inherent in the syringes and the electrodynamics of the linear motors themselves certainly contain nonlinearities. Indeed, the nonlinear cogging force present in the linear stages is most likely a major culprit considering this is a known limitation of direct-drive brushless motors [18].

It is important to note that the authors chose to use a lymphatic vessel segment free of valves during the ELPS identification in order to minimize system nonlinearities. Since the presence of one-way valves found in the collecting lymphatics could introduce significant nonlinearities in the system, the resulting model’s predictive nature would be greatly reduced. Likewise, as the presence of one-way valves would limit the application of fluid flow in a direction opposite to the valves, the authors deliberately chose to use valve-free vessel segments during experiments with the ELPS. In this way, the ELPS could impose transaxial pressure gradients (hence flow rates and corresponding wall shear stresses) of any directionality across the vessel’s endothelium. Of course, since the system model used is linear and based on a valve-free vessel segment, tracking control of the ELPS could cause unreliable operation when used with vessels with valves while imposing ΔP directionality in contrast to the valve direction. This aspect of the ELPS is certainly a limitation and would require further study to verify system compatibility with lymphatic vessels that contain valves.

Nevertheless, tracking control of the ELPS is quite advanced for ex vivo perfusion systems due to its ability to independently control both ΔP and P_avg—even though they may be time-varying. This capability is important: independent tracking control affords the ultimate flexibility to perform a wide range of experiments, including single-factor studies that aim to isolate specific mechanically-mediated mechanisms. For instance, the ability to single out shear-induced mechanisms is particularly interesting in light of the complex (and mostly oscillatory) flow rates experienced by the lymphatics in vivo [9, 19], where the ability to provide a dynamically-varying ΔP while holding P_avg constant would be necessary. Using an explicit MPC control law simplified for linear systems [Section 2.2], the compensator is able to utilize the predictive power of the identification model along with the feedback capabilities of the Kalman filter to generate plant inputs that minimize the desired performance objective (cost function). In other words, the MPC control law is designed in such a way to minimize both the multi-output tracking error and the multi-input voltage levels, which in turn increases both system performance and robustness. Although MPC and its application is not new, nobody has utilized such an advanced MIMO control scheme for an ex vivo perfusion system to track multiple signals.

However, despite its advanced nature, the way in which MPC was implemented in this case provides a very structured and simplified way of achieving the desired control performance for the system. Unlike many MPC algorithms that are nonlinear and require iterative solutions between time steps, the designer may employ an explicit linear control law [Eq. (7)] and state estimator [Eq. (8)] since the ELPS is described well through the linear state-space equations [Eq. (1), Fig. 2a]. Not only does this simplify hardware implementation, but it also allows for less-advanced electronics hardware to be used (such as the microcontroller platform used in this study). In order to adjust the controller performance, the designer merely needs to alter the weighting matrices, Q and R, based on desired emphasis between tracking performance and control robustness, and then recompute the gain matrix, K₁. This systematic approach to calculating the control gains is a major advantage compared to traditional controllers like PID, where finding the correct combination of gains to achieve comparable independent tracking performance would be extremely difficult (if not impossible) for MIMO systems.

Of course, the ELPS’s control system does have limitations. For instance, because the identification model and MPC control law are purely linear, the predictive capabilities of the system are restricted due to inherent nonlinear behavior. Thus, dynamic control performance could be improved by using a nonlinear MPC algorithm that takes various nonlinearities—such as the brushless linear stages’ cogging forces—into account. In addition, more advanced nonlinear control algorithms could also be used: sliding mode control, which is known for excellent disturbance rejection, could be a promising candidate to negate the disturbances caused by both the linear motors and solenoids. Nevertheless, despite these dynamic control limitations, the ELPS is certainly able to produce ΔP and P_avg waveforms within the frequency range of lymphatics, which has been shown to have primary components less than 1 Hz across both large and small animals [27, 16, 31, 9, 7, 19]. However, though the higher frequency components are small from a signal analysis standpoint, their relative biological or physiological importance remains unknown; thus, the system in its current form is limited in its ability to provide insight into the physiologic significance of these smaller, high-frequency components. Naturally, more straight-forward modifications to the ELPS, such as the addition of integral control, could also improve the tracking performance by eliminating steady-state error.

Another limitation of the ELPS is the inability to measure flow rate through the vessel in real time. Although recording this measurement at every sampling time would be desirable for estimating fluid shear stress, the flow rate through the vessel is very low (< 1 mL/min) and therefore difficult to measure with commercial flow sensors. Due to this limitation, the ELPS instead controls ΔP, which ultimately dictates the flow rate and is, therefore, commonly used in isolated lymphatic vessel studies [12, 13, 32]. Despite the inability to measure real-time flow rate, the authors have demonstrated a technique to estimate the applied flow rate through the vessel post hoc (and thus wall shear stress) over multiple, 5 second windows due to the positive-displacement nature of the syringes. Although this is certainly a limitation as real-time flow rate (and therefore peak shear stress) information would be essential to studying short-term shear stress dynamics, these estimated values do have the ability indicate trends over a longer time scale. For instance, as ΔP (and hence Q̄) is increased linearly to an abnormally high magnitude in Fig. 7, the consistent pumping of the vessel is actively reduced—eventually resulting in complete pumping inhibition (as expected). The estimated parameter, τ̄_w, demonstrates this phenomenon clearly: as vessel contraction is inhibited (thus increasing D̄), τ̄_w begins to curtail despite the linearly increasing Q̄ [Fig. 8]. This scenario could be representative of a normal physiological response of the collecting lymphatics to a large influx of lymph, where the lymphatic vessel would want to behave more as a conduit than a pump by reducing its overall resistance to the incoming fluid load.

In brief, the ELPS and its ability to independently control ΔP and P_avg waveforms make it unique among isolated lymphatic vessel systems and even state-of-the-art vascular ex vivo perfusion systems. As discussed, this capability is crucial for true single-factor studies that seek to isolate mechanically-mediated mechanisms specific to either fluid shear stress or circumferential stress. Furthermore, applying dynamic and differing ΔP and P_avg waveforms in concert could be helpful in teasing out potential interdependencies between mechanisms affected by these two significant mechanical forces. In all, the ELPS is a promising platform for studying the functional role of mechanics on isolated lymphatic vessels, allowing for new studies and potentially leading to significant discoveries relating to both physiologic and pathophysiologic cases of lymphatic fluid transport.

Nomenclature

A_c

cross-sectional area of syringe plunger

C

output matrix

D

diameter of vessel

e

output error vector

G

state matrix

H

input matrix

H_p

size of predictive time horizon

J

control objective/cost function

K

control gain matrix

L

Kalman gain matrix

n

size of state space

P_1,2

pressure on each end of cannula

P_avg

average transmural pressure

ΔP

transaxial pressure gradient

Q

estimated flow rate

Q

output error weighting matrix

R

input weighting matrix

Δt

time-averaging window

T_s

sampling time

u

input vector (voltages to servo drive)

U

vector of input vectors

v_avg

average velocity of both syringes

x

linear stage position

x

state vector

y

output vector

Y

vector of output vectors

z

Z-transform variable

δ

solenoid valve switching variable

μ

dynamic viscosity

τ_w

estimated wall shear stress

Subscripts and Superscripts

d

user-defined/desired quantity

*

optimal quantity

~

estimated via observer

–

mean over time window

Appendices

Appendix A: Time Window Length Calculation

In order to determine what constitutes a long Δt, we must first estimate the transient dynamics relating the instantaneous syringe velocity (averaged between the two syringes), v_avg, to the transaxial pressure gradient, ΔP. The instantaneous syringe velocity averaged between the two syringes is defined as follows:

$$v_{\text{avg}}(k)=\frac{\mathrm{\Delta }{x}_{1,k}{\delta }_k-\mathrm{\Delta }{x}_{2,k}{\delta }_k}{2T_s}$$ (A.1)

where T_s is the sampling time of the identification (see Section 2.3 for additional nomenclature). Thus, using the data from the identification experiment shown in Fig. 2, one may reconstruct another identification of a single-input, single-output (SISO) system with v_avg as the input and ΔP as the output. The validation data for this identification is shown in Fig. 9a (model order, n = 4, with good agreement), while the corresponding dynamic characteristics of this model is shown in Fig. 9b.

Figure 9.

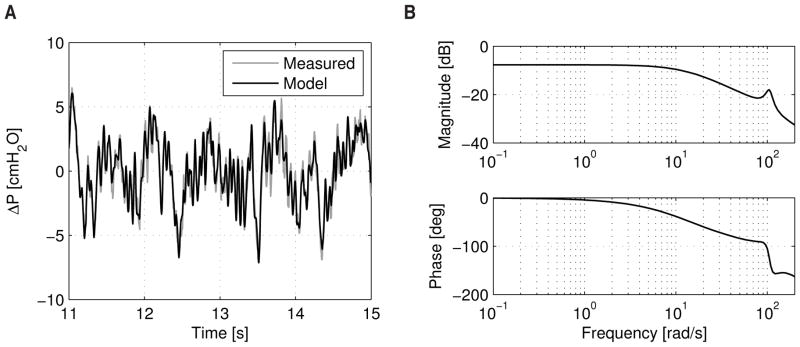
(a) Validation data (from the experiment in Fig. 2) for the SISO dynamic model of the ELPS with average instantaneous syringe velocity between the two syringes as the input and transaxial pressure gradient as the output. (b) Bode plot of this SISO model of the ELPS showing the frequency response.

Of course, this model does not take into account the dynamics between ΔP and the flow rate through the vessel, which certainly contain some fluid compliance and inertance. However, assuming these effects are on the same order of magnitude as between v_avg and ΔP (or smaller), a value of Δt much larger than these dynamics should suffice. To quantify the speed of these dynamics, the the 2% settling time, T_set, is found from simulating the model in Fig. 9 in response to a step input. For this model, T_set is approximately 0.3 sec; thus, to ensure Δt is long (> 10 T_set), the authors define:

$$\begin{array}{l}\mathrm{\Delta }t\gg T_{\text{set}}\\ =5sec\end{array}$$ (A.2)